Application of the Exp-Function and Generalized Kudryashov Methods for Obtaining New Exact Solutions of Certain Nonlinear Conformable Time Partial Integro-Differential Equations
Abstract
1. Introduction
2. Conformable Derivative and Its Properties
- (1)
- (2)
- for all
- (3)
- for all
- (4)
- (5)
- (6)
- If, in addition, f is differentiable, then .
3. Description of the Methods
3.1. Description of the Exp-Function Method
3.2. Description of the Generalized Kudryashov Method
4. Application of the Proposed Methods
4.1. Exact Solutions for the Conformable Time Second Integro-Differential KP Hierarchy Equation Using the Exp-Function Method
4.2. Exact Solutions for the (2 + 1)-Dimensional Conformable Time Partial Integro-Differential JM Evolution Equation Using the Generalized Kudryashov Method
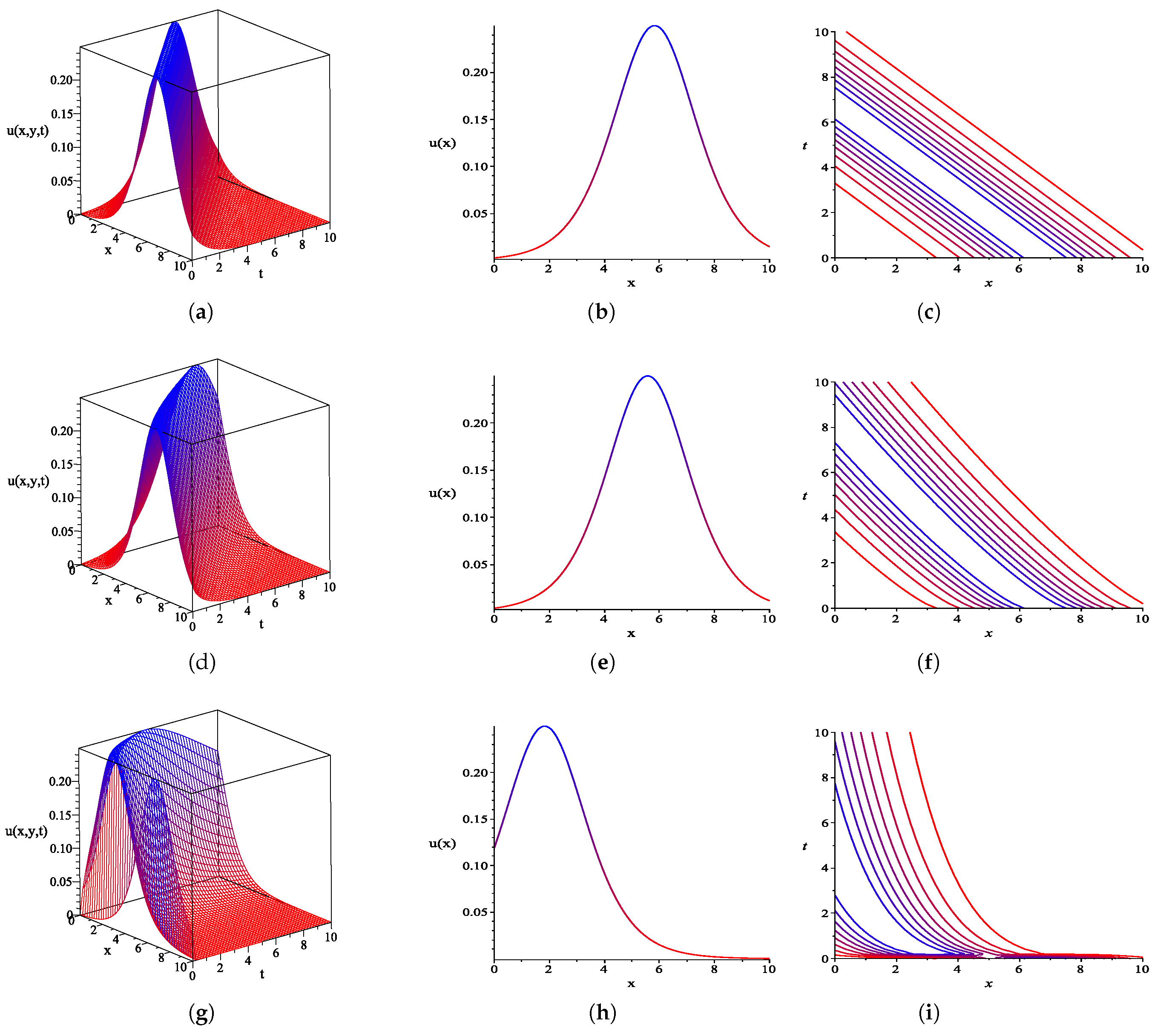
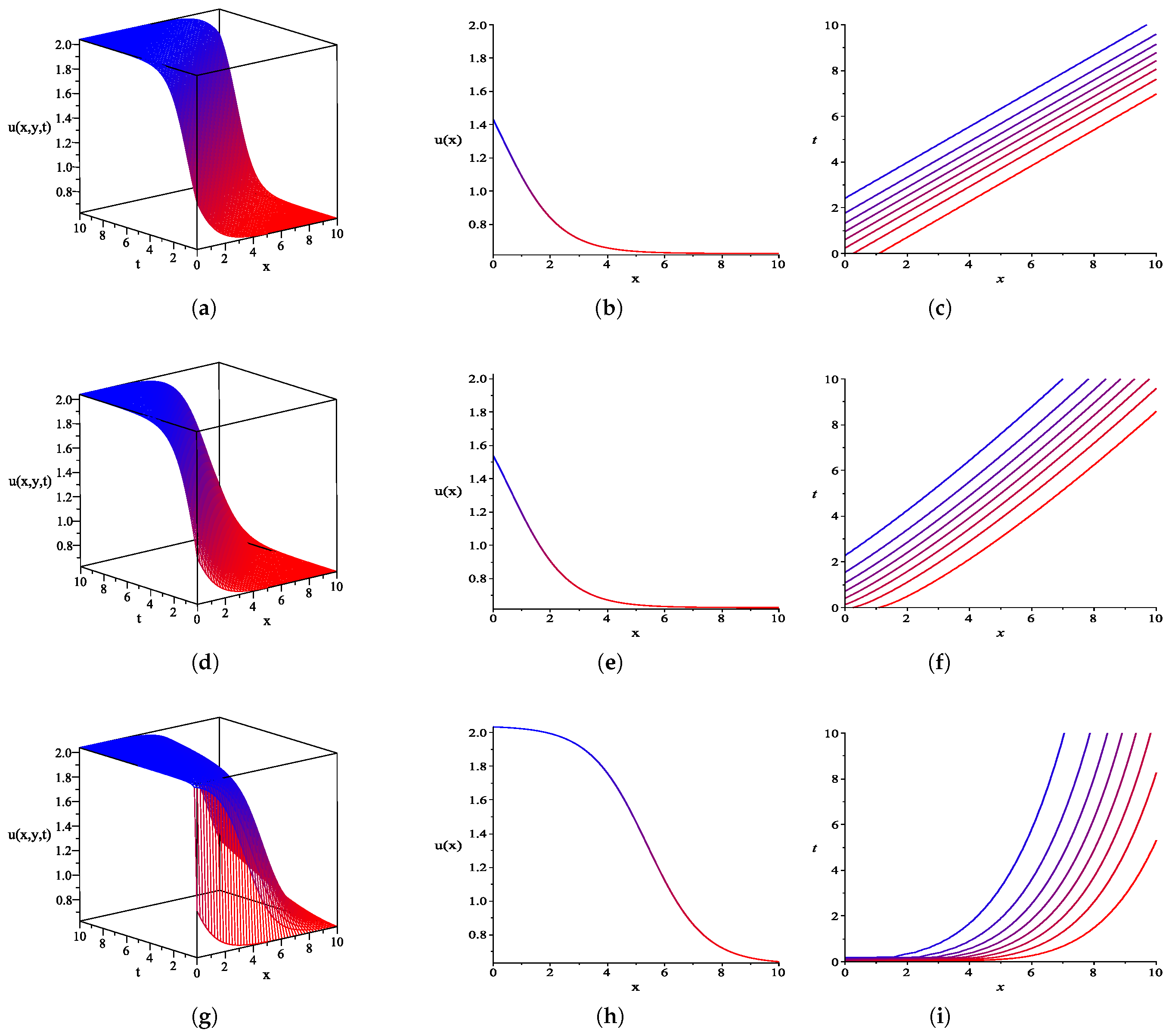
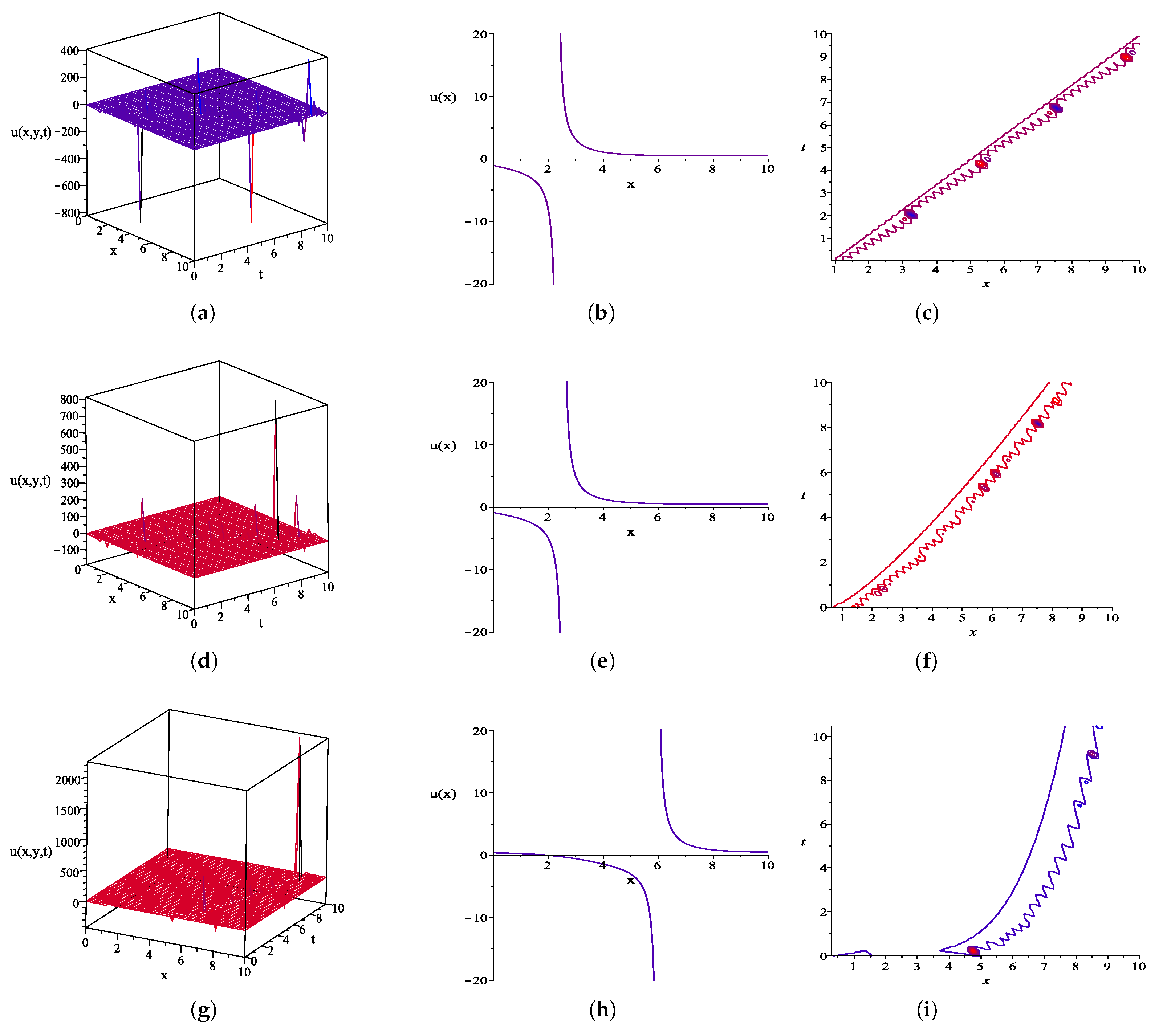
5. Some Graphical Representations
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ghafoor, A.; Firdous, S.; Zubair, T.; Iftikhar, A.; Zainab, S.; Mohyud-Din, S.T. (G′/G,1/G)-Expansion method for generalized ZK, Sharma-Tasso-Olver (STO) and modified ZK equations. Qscience Connect 2013, 2013, 24. [Google Scholar] [CrossRef]
- Aljahdaly, N.H. Some applications of the modified (G′/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Zheng, B.; Feng, Q. The Jacobi elliptic equation method for solving fractional partial differential equations. Abstr. Appl. Anal. 2014, 2014, 249071. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. Novel complex and hyperbolic forms to the strain wave equation in microstructured solids. Opt. Quantum Electron. 2018, 50, 14. [Google Scholar] [CrossRef]
- Eskitasçıoglu, E.; Aktas, M.B.; Baskonus, H.M. New complex and hyperbolic forms for Ablowitz-Kaup-Newell-Segur wave equation with fourth order. Appl. Math. Nonlinear Sci. 2019, 4, 105–112. [Google Scholar] [CrossRef]
- Seadawy, A.R. Three-dimensional nonlinear modified Zakharov-Kuznetsov equation of ion-acoustic waves in a magnetized plasma. Comput. Math. Appl. 2016, 71, 201–212. [Google Scholar] [CrossRef]
- Seadawy, A.R. Solitary wave solutions of two-dimensional nonlinear Kadomtsev-Petviashvili dynamic equation in dust-acoustic plasmas. Pramana 2017, 89, 49. [Google Scholar] [CrossRef]
- Shakeel, M.; Mohyud-Din, S.T.; Iqbal, M.A. Modified extended exp-function method for a system of nonlinear partial differential equations defined by seismic sea waves. Pramana 2018, 91, 1–8. [Google Scholar] [CrossRef]
- Yel, G.; Akturk, T. A new approach to (3 + 1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Appl. Math. Nonlinear Sci. 2020, 5, 309–316. [Google Scholar] [CrossRef]
- Ryabov, P.N.; Sinelshchikov, D.I.; Kochanov, M.B. Application of the Kudryashov method for finding exact solutions of the high order nonlinear evolution equations. Appl. Math. Comput. 2011, 218, 3965–3972. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Ryabov, P.N.; Fedyanin, T.E.; Kutukov, A.A. Evolution of pattern formation under ion bombardment of substrate. Phys. Lett. A 2013, 377, 753–759. [Google Scholar] [CrossRef]
- Sachs, E.; Strauss, A. Efficient solution of a partial integro-differential equation in finance. Appl. Numer. Math. 2008, 58, 1687–1703. [Google Scholar] [CrossRef]
- Singh, S.; Patel, V.K.; Singh, V.K. Convergence rate of collocation method based on wavelet for nonlinear weakly singular partial integro-differential equation arising from viscoelasticity. Numer. Methods Partial. Differ. Eqs. 2018, 34, 1781–1798. [Google Scholar] [CrossRef]
- Al-Khaled, K.; Darweesh, A.; Yousef, M.H. Convergence of numerical schemes for the solution of partial integro-differential equations used in heat transfer. J. Appl. Math. Comput. 2019, 61, 657–675. [Google Scholar] [CrossRef]
- Zadeh, K.S. An integro-partial differential equation for modeling biofluids flow in fractured biomaterials. J. Theor. Biol. 2011, 273, 72–79. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Xin, X. Explicit solutions, conservation laws of the extended (2 + 1)-dimensional Jaulent-Miodek equation. arXiv 2015, arXiv:1512.09196. [Google Scholar]
- Zheng, X.; Qiu, W.; Chen, H. Three semi-implicit compact finite difference schemes for the nonlinear partial integro-differential equation arising from viscoelasticity. Int. J. Model. Simul. 2020. [Google Scholar] [CrossRef]
- Kaewta, S.; Sirisubtawee, S.; Khansai, N. Explicit exact solutions of the (2 + 1)-dimensional integro-differential Jaulent-Miodek evolution equation using the reliable methods. Int. J. Math. Math. Sci. 2020, 2020, 2916395. [Google Scholar] [CrossRef]
- Yapman, Ö.; Amiraliyev, G.M.; Amirali, I. Convergence analysis of fitted numerical method for a singularly perturbed nonlinear Volterra integro-differential equation with delay. J. Comput. Appl. Math. 2019, 355, 301–309. [Google Scholar] [CrossRef]
- Hendi, F.; Al-Qarni, M. The variational Adomian decomposition method for solving nonlinear two-dimensional Volterra-Fredholm integro-differential equation. J. King Saud Univ. Sci. 2019, 31, 110–113. [Google Scholar] [CrossRef]
- Hasseine, A.; Attarakih, M.; Belarbi, R.; Bart, H.J. On the semi-analytical solution of integro-partial differential equations. Energy Procedia 2017, 139, 358–366. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Wang, Y. Topological soliton solutions for three shallow water waves models. Waves Random Complex Media 2018, 28, 508–515. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, X.Y. Soliton, breather, lump and their interaction solutions of the (2 + 1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation. Adv. Differ. Eqs. 2019, 2019, 332. [Google Scholar] [CrossRef]
- Seadawy, A.; Ali, A.; Aljahdaly, N. The nonlinear integro-differential Ito dynamical equation via three modified mathematical methods and its analytical solutions. Open Phys. 2020, 18, 24–32. [Google Scholar] [CrossRef]
- Bhrawy, A.; Alhuthali, M.S.; Abdelkawy, M. New solutions for (1 + 1)-dimensional and (2 + 1)-dimensional Ito equations. Math. Probl. Eng. 2012, 1–24. [Google Scholar] [CrossRef]
- Lin, L.; Zhu, S.; Xu, Y.; Shi, Y. Exact solutions of Gardner equations through tanh-coth method. Appl. Math. 2016, 7, 2374–2381. [Google Scholar] [CrossRef]
- Akbari, M.; Rasht, I. Application of Kudryashov method for the Ito equations. Appl. Math. 2017, 12, 136–142. [Google Scholar]
- Gepreel, K.A.; Nofal, T.A.; Alasmari, A.A. Exact solutions for nonlinear integro–partial differential equations using the generalized Kudryashov method. J. Egypt. Math. Soc. 2017, 25, 438–444. [Google Scholar] [CrossRef]
- Yin, Y.H.; Ma, W.X.; Liu, J.G.; Lü, X. Diversity of exact solutions to a (3 + 1)-dimensional nonlinear evolution equation and its reduction. Comput. Math. Appl. 2018, 76, 1275–1283. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.S.; Akbar, M.A.; Seadawy, A.R. New applications of the two variable (G′/G,1/G)-expansion method for closed form traveling wave solutions of integro-differential equations. J. Ocean Eng. Sci. 2019, 4, 132–143. [Google Scholar] [CrossRef]
- Alharbi, A.R.; Almatrafi, M.B. New exact and numerical solutions with their stability for Ito integro-differential equation via Riccati–Bernoulli sub-ODE method. J. Taibah Univ. Sci. 2020, 14, 1447–1456. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Yang, S.; Wang, L.; Zhang, S. Conformable derivative: Application to non-Darcian flow in low-permeability porous media. Appl. Math. Lett. 2018, 79, 105–110. [Google Scholar] [CrossRef]
- Anderson, D.R.; Camrud, E.; Ulness, D.J. On the nature of the conformable derivative and its applications to physics. arXiv 2018, arXiv:1810.02005. [Google Scholar]
- Anderson, D.R.; Ulness, D.J. Newly defined conformable derivatives. Adv. Dyn. Syst. Appl. 2015, 10, 109–137. [Google Scholar]
- Chung, W.S. Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 2015, 290, 150–158. [Google Scholar] [CrossRef]
- Lazo, M.J.; Torres, D.F. Variational calculus with conformable fractional derivatives. IEEE/CAA J. Autom. Sin. 2016, 4, 340–352. [Google Scholar] [CrossRef]
- Çenesiz, Y.; Baleanu, D.; Kurt, A.; Tasbozan, O. New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 2017, 27, 103–116. [Google Scholar] [CrossRef]
- Birgani, O.T.; Chandok, S.; Dedovic, N.; Radenovic, S. A note on some recent results of the conformable fractional derivative. Adv. Theory Nonlinear Anal. Appl. 2019, 3, 11–17. [Google Scholar]
- Gao, F.; Chi, C. Improvement on conformable fractional derivative and its applications in fractional differential equations. J. Funct. Spaces 2020, 2020. [Google Scholar] [CrossRef]
- Tasbozan, O.; Çenesiz, Y.; Kurt, A.; Baleanu, D. New analytical solutions for conformable fractional PDEs arising in mathematical physics by exp-function method. Open Phys. 2017, 15, 647–651. [Google Scholar] [CrossRef]
- Hosseini, K.; Manafian, J.; Samadani, F.; Foroutan, M.; Mirzazadeh, M.; Zhou, Q. Resonant optical solitons with perturbation terms and fractional temporal evolution using improved tan (ϕ (η)/2)-expansion method and exp function approach. Optik 2018, 158, 933–939. [Google Scholar] [CrossRef]
- Yaslan, H.Ç.; Girgin, A. Exp-function method for the conformable space-time fractional STO, ZKBBM and coupled Boussinesq equations. Arab. J. Basic Appl. Sci. 2019, 26, 163–170. [Google Scholar] [CrossRef]
- Ghany, H.A.; Hyder, A.A.; Zakarya, M. Exact solutions of stochastic fractional Korteweg de-Vries equation with conformable derivatives. Chin. Phys. B 2020, 29, 030203. [Google Scholar] [CrossRef]
- Biswas, A.; Sonmezoglu, A.; Ekici, M.; Mirzazadeh, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with fractional temporal evolution by generalized Kudryashov’s method. Optik 2018, 164, 303–310. [Google Scholar] [CrossRef]
- El-Ganaini, S.; Al-Amr, M.O. New abundant wave solutions of the conformable space-time fractional (4 + 1)-dimensional Fokas equation in water waves. Comput. Math. Appl. 2019, 78, 2094–2106. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Kadomtsev-Petviashvili hierarchy: N-soliton solutions and distinct dispersion relations. Appl. Math. Lett. 2016, 52, 74–79. [Google Scholar] [CrossRef]
- Gepreel, K.A. Exact solutions for nonlinear integral member of Kadomtsev-Petviashvili hierarchy differential equations using the modified (w/g)-expansion method. Comput. Math. Appl. 2016, 72, 2072–2083. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Liu, X.Q.; Wang, G.W. Symmetry reductions and exact solutions of the (2 + 1)-dimensional Jaulent-Miodek equation. Appl. Math. Comput. 2012, 219, 911–916. [Google Scholar] [CrossRef]
- Gu, Y.; Deng, B.; Lin, J. Exact traveling wave solutions to the (2 + 1)-dimensional Jaulent-Miodek equation. Adv. Math. Phys. 2018, 2018. [Google Scholar] [CrossRef]
- Ma, H.C.; Deng, A.P.; Yu, Y.D. Lie symmetry group of (2 + 1)-dimensional Jaulent-Miodek equation. Therm. Sci. 2014, 18, 1547–1552. [Google Scholar] [CrossRef]
- Matinfar, M.; Eslami, M.; Roshandel, S. The first integral method to study the (2 + 1)-dimensional Jaulent-Miodek equations. Pramana 2015, 85, 593–603. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. Some Applications of the (G′/G,1/G)-expansion method for finding exact traveling wave solutions of nonlinear fractional evolution equations. Symmetry 2019, 11, 952. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S.; Leekparn, T. Exact traveling wave solutions of the space-time fractional complex Ginzburg-Landau equation and the space-time fractional Phi-4 equation using reliable methods. Adv. Differ. Eqs. 2019, 2019, 219. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. New exact solutions of the conformable space-time Sharma-Tasso-Olver equation using two reliable methods. Symmetry 2020, 12, 644. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S. Soliton behaviours for the conformable space-time fractional complex Ginzburg-Landau equation in optical fibers. Symmetry 2020, 12, 219. [Google Scholar] [CrossRef]
- He, J.H.; Elagan, S.; Li, Z. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- Su, W.H.; Yang, X.J.; Jafari, H.; Baleanu, D. Fractional complex transform method for wave equations on Cantor sets within local fractional differential operator. Adv. Differ. Eqs. 2013, 2013, 97. [Google Scholar] [CrossRef]
- Güner, O.; Bekir, A.; Cevikel, A.C. A variety of exact solutions for the time fractional Cahn-Allen equation. Eur. Phys. J. Plus 2015, 130, 146. [Google Scholar] [CrossRef]
- Rahmatullah; Mohyud-Din, S.T.; Khan, U. Exact traveling wave solutions of fractional order Boussinesq-like equations by applying Exp-function method. Results Phys. 2018, 8, 114–120. [Google Scholar] [CrossRef]
- Guner, O.; Aksoy, E.; Bekir, A.; Cevikel, A.C. Different methods for (3 + 1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation. Comput. Math. Appl. 2016, 71, 1259–1269. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A. The Exp-function method for solving nonlinear space-time fractional differential equations in mathematical physics. J. Assoc. Arab. Univ. Basic Appl. Sci. 2017, 24, 277–282. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. Soliton solutions of some nonlinear evolution problems by GKM. Neural Comput. Appl. 2019, 31, 287–294. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaewta, S.; Sirisubtawee, S.; Sungnul, S. Application of the Exp-Function and Generalized Kudryashov Methods for Obtaining New Exact Solutions of Certain Nonlinear Conformable Time Partial Integro-Differential Equations. Computation 2021, 9, 52. https://doi.org/10.3390/computation9050052
Kaewta S, Sirisubtawee S, Sungnul S. Application of the Exp-Function and Generalized Kudryashov Methods for Obtaining New Exact Solutions of Certain Nonlinear Conformable Time Partial Integro-Differential Equations. Computation. 2021; 9(5):52. https://doi.org/10.3390/computation9050052
Chicago/Turabian StyleKaewta, Supaporn, Sekson Sirisubtawee, and Surattana Sungnul. 2021. "Application of the Exp-Function and Generalized Kudryashov Methods for Obtaining New Exact Solutions of Certain Nonlinear Conformable Time Partial Integro-Differential Equations" Computation 9, no. 5: 52. https://doi.org/10.3390/computation9050052
APA StyleKaewta, S., Sirisubtawee, S., & Sungnul, S. (2021). Application of the Exp-Function and Generalized Kudryashov Methods for Obtaining New Exact Solutions of Certain Nonlinear Conformable Time Partial Integro-Differential Equations. Computation, 9(5), 52. https://doi.org/10.3390/computation9050052







