Abstract
Thermal ablation is a minimally or noninvasive cancer therapy technique that involves fewer complications, shorter hospital stays, and fewer costs. In this paper, a thermal-ablation bioheat model for cancer treatment is numerically investigated, using a porous media-based model. The main objective is to evaluate the effects of a variable blood volume fraction in the tumoral tissue (i.e., the porosity), in order to develop a more realistic model. A modified local thermal nonequilibrium model (LTNE) is implemented including the water content vaporization in the two phases separately and introducing the variable porosity in the domain, described by a quadratic function changing from the core to the rim of the tumoral sphere. The equations are numerically solved employing the finite-element commercial code COMSOL Multiphysics. Results are compared with the results obtained employing two uniform porosity values (ε = 0.07 and ε = 0.23) in terms of coagulation zones at the end of the heating period, maximum temperatures reached in the domain, and temperature fields and they are presented for different blood vessels. The outcomes highlight how important is to predict coagulation zones achieved in thermal ablation accurately. In this way, indeed, incomplete ablation, tumor recurrence, or healthy tissue necrosis can be avoided, and medical protocols and devices can be improved.
1. Introduction
Thermal ablation is increasingly recognized as an important alternative in cancer treatments, for which the most common procedures applied are surgery, chemotherapy, and radiotherapy. Nevertheless, these common techniques pose critical issues such as they are too invasive for the human body, can reveal serious side effects, and are expensive in terms of financial costs for the national health service. Thermal ablation of tumors, instead, is a minimally invasive treatment option for cancer, which presents some advantages such as minor side effects, shorter hospital stays, and consequently lower costs [1,2,3]. It consists of focusing an energy source (commonly radiofrequency or microwave) in the target zone (the tumoral tissue) by means of a probe that causes the tissue destruction. Generally, the complete necrosis of tissue happens instantaneously at temperatures over about 60 °C, but lower temperatures with longer exposure times can be achieved [4]. The most common approach is a percutaneous treatment performed with the aid of imaging techniques. On the other hand, the main shortcoming of performing a thermal ablation is not achieving complete tissue ablation; therefore, the risk of a tumor recurrence is increased. In this context, in-depth knowledge of thermal therapy physics has a key role in modeling heat transfer in thermal therapies in order to develop increasingly accurate bioheat models for clinical applications [5], predicting the final necrotic tissue diameters and volumes. Over the years, various bioheat models have been proposed by the researchers, since 1948, when H. Pennes developed the first bioheat equation [6], which is still widely used for its simplicity but which reveals critical shortcomings due to the assumptions made, such as the perfusion rate is uniform in the tissue, the blood flow direction, and the artery–vein countercurrent arrangements are neglected, the arterial blood is considered at a constant temperature of about 37 °C, while the venous blood is in thermal equilibrium with tissue.
Thus, different models applied to thermal therapies have been developed trying to overcome these limitations, and they have been resumed in various review studies [7,8,9,10]. Furthermore, other thermodynamic approaches to cancer cell behaviors have been developed, such as the application of the constructal law [11,12]. According to a comparison made among the principal bioheat models [13], the most promising that combines good accuracy and acceptable complexity is the porous media-based [14] local thermal nonequilibrium model (LTNE), which was developed in 1997 by Xuan and Roetzel [15] and then modified during the years by different authors in order to take into consideration different vascular arrangements, tissue properties, and thermal treatments applications. Khaled and Vafai [16] discussed different diffusive applications and momentum transport by convection in porous media and concluded that the theory of porous media for heat transfer in biological tissues is the most appropriate since it contains fewer assumptions, compared to different bioheat models. Khanafer and Vafai [17] analyzed the development of the diffusion equation using local volume-averaging technique and the evaluation of the applications associated with the diffusion equation, such as works associated with magnetic resonance imaging and drug delivery. The aim was to develop new porous media-based models in biomedical applications. Nakyama and Kuwahara [18] developed a general set of bioheat transfer equations for blood flows and its surrounding biological tissue employing the volume averaging theory in the field of fluid-saturated porous media. They extended the two-energy equation model to a three-energy equation model in order to include the countercurrent heat transfer between closely spaced arteries and veins in the circulatory system and its effect on the peripheral heat transfer. Keangin and Rattanadecho [19,20] analyzed the heat transport on local thermal nonequilibrium in the porous liver and developed a two-layered porous model to study heat transfer and blood flow in an ex vivo liver tissue treated with microwave ablation. They compared two different antennas, (one slot vs. two slots), predicting numerically the temperature profiles, blood velocity, and coagulation zones, concluding that using a double slot antenna provides a wider region in porous liver than the single slot one. Dombrovsky et al. [21,22] developed a combined thermal model for transient temperature field during laser heating of embedded gold nanoparticles. They coupled a modified two-flux approximation model for the radiative heat transfer and a local thermal equilibrium equation for the temperature field. The authors concluded that the required uniform heating can be achieved even without gold nanoshells or other invasive procedures for some superficial tumors. Finally, Andreozzi et al. [23] developed a novel local thermal nonequilibrium model for biological tissue applied to multiple-antenna configurations for thermal ablation, using a porous media-based model modified in order to include water vaporization in tissue and blood separately based on their different water content.
According to the porous media theory, the biological medium can be divided into two different phases coexisting in the same domain, namely, the “tissue phase” and the “blood phase,” respectively. The first consists of cells and interstitial spaces among them, while the second one represents the blood vessels that infiltrate throughout the tissue. Moreover, the porosity is the blood volume fraction in the entire biological tissue domain, and it is a relevant parameter, especially when large vessels are considered.
In this work, in the following Material and Methods Section, a modified LTNE model is implemented in order to include the water content vaporization in the two phases separately and to introduce a variable porosity in the domain, described by a quadratic function based on the in vivo experimental measures made by Stewart et al. [24] in a rabbit liver tumor model. In the Results and Discussion Section, the results in terms of temperature fields and final coagulation diameters obtained are shown, comparing the variable-porosity model to the same model implemented employing uniform porosity values in the domain. The outcomes show very similar coagulation zones achieved for the two smallest blood vessels, whereas for the two largest vessels, the variable porosity model produces about the same results of using the smallest uniform porosity value, while the differences between the variable porosity model and the largest porosity yield bigger deviations as larger blood vessels are taken into account. The goal is to appreciate differences among the models, highlighting the key role of developing increasingly realistic bioheat models in thermal ablation of tumoral tissues in order to predict the coagulation zones achieved accurately.
2. Materials and Methods
The computational domain of tumoral tissue is represented by two concentric spheres displayed in Figure 1. The external sphere radius r1 = 3.10 cm defines the tissue boundary, while the inner sphere radius r2 = 0.620 cm is the heating volume; hence, the total heating volume is equal to 1 cm3.
Figure 1.
Geometry of the physical domain.
Moreover, a 2D axisymmetric configuration can be employed as shown in Figure 2; indeed, on the one hand, the computational time is small such as for a 1D case, and therefore, the computational time can be reduced, compared to a 3D configuration. On the other hand, the aim of building a 2D axisymmetric model is to obtain a general model that can be applied to more complicated cases in the future plans, such as irregular tumor shapes, nonuniform properties, the inclusion of the effect of a single large vein near the tumor, etc.
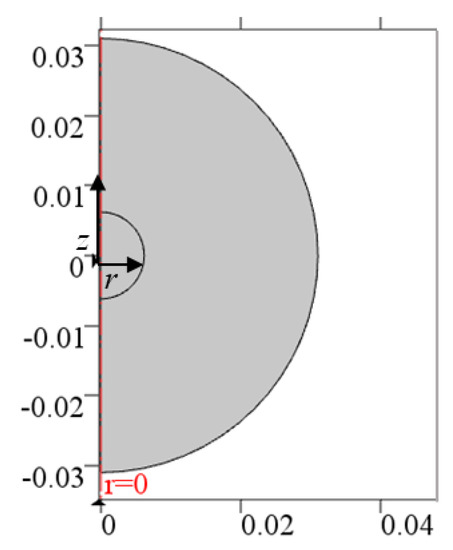
Figure 2.
The 2D axisymmetric computational domain.
A modified porous media model is used to evaluate the heat transfer in the biological domain. This is based on the porous media theory [13], according to which the biological medium can be divided into two different phases coexisting in the same domain. The first one is the tissue phase, which includes cells and interstitial spaces, and the second one is the blood phase, represented by the blood vessels that permeate in the tissue. Moreover, a local thermal nonequilibrium model is implemented and modified to include the vaporization of the two distinct phases water contents separately, as in [23]. Therefore, two different equations can be written for the two phases as follows.
For the blood phase:
For the tissue phase:
where εvar is the variable porosity in the tumoral tissue, namely, the blood volume fraction in the entire tissue volume, and it will be described in the following paragraph, ρ is the density, c the specific heat, Tt and Tb are the tumoral tissue and blood temperatures, respectively, t is the time, u is the blood velocity vector, hc is the interfacial heat transfer coefficient, and a is the volumetric transfer area between tissue and blood, evaluated from the hydraulic diameter definition in porous media as
where d is the blood vessel diameter. In this work, four different blood vessels’ dimensions are considered, using the results from the work of Crezee and Lagendijk [25]. Thus, the focus is on a wide range of diameters and corresponding blood velocities, from capillaries and terminal arteries to terminal branches and tertiary branches.
As regards the porosity, the novelty of the developed model is to consider a variable porosity function that changes from the core to the rim of the tumoral sphere, according to the experimental in vivo measures made by Stewart et al. [24] in a rabbit liver tumor model. The function takes into account the minimum and maximum blood volume fraction measured values in the core and in the rim of tumoral tissue, respectively, 16 days after the initial tumor detection. A quadratic law is assumed to describe the function behavior as follows:
where εmin = 0.07 and εmax = 0.23. In Figure 3 the variable porosity field in a slice of the spherical domain is displayed. From the figure it is clear the increase of porosity from the very small values in the core to the larger values in the rim, highlighting the different vascularization between the two zones. In the next Results Section, the variable porosity case will be compared to uniform porosities set equal to 0.07 and 0.23, and therefore, the minimum and maximum values of the experimental measures range.
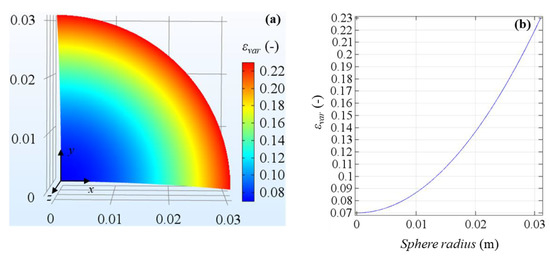
Figure 3.
Variable porosity field in tumoral tissue domain (a) and porosity profile on the sphere radius (b).
As regards the value used for the interfacial heat transfer coefficient hc, it is assumed to be constant and equal to 170 W m−2 K−1, as in Yuan [26]. Table 1 summarizes all the blood velocities with the related investigated blood vessel diameters.

Table 1.
The investigated blood vessel diameters and consequent blood flow velocities.
Furthermore, Qext in Equations (1) and (2) represents a generic external power density applied to the tumoral tissue during the treatment, and the symbol <> means that the volume-averaged quantity of a generic variable is considered. Concerning the fluid phase, a uniform blood velocity is assumed in all directions in order to reproduce a more realistic in vivo vessel network.
Moreover, in order to include the effects of tumoral tissue coagulation as the treatment advances, the blood velocity is assumed to become zero as the tissue is completely damaged, and therefore, the β coefficient is inserted into Equation (1), and it assumes the two values 0 or 1 depending on the thermal damage function Ω defined by using the Arrhenius model [27]. According to this model, the damage is obtained from an exponential relationship between tissue exposure temperature, time, and parameters generally provided by experimental studies on cells survivability as follows:
where A and ΔE are the frequency factor and the activation energy for the irreversible damage reaction, respectively, and R is the universal gas constant. In this work, A = 3247 × 1043 s−1 and ΔE = 2814 × 105 J mol−1, as in [28]. These parameters are available for different tissues, and they have been obtained fitting known exposure times and temperatures with cell surviving probabilities. In the Arrhenius model, if Ω = 1, a 68% of cell death probability is achieved; hence, to have a more accurate prediction of the coagulation zone dimensions, thermal damage is evaluated using the D99 thermal damage contour, considering the isoline at Ω = 4.6, which fits for obtaining the 99% cell death probability. Thus, the β coefficient will be 1 for Ω < 4.6 and 0 for Ω = 4.6.
As previously mentioned, the LTNE model is modified to include the water content vaporization in both blood and tissue phases separately by employing the enthalpy method shown by Abraham and Sparrow [29]. Manipulating the equations, the term (ρc) referred to blood and tissue in Equations (1) and (2) becomes
where the subscript l is used for properties values at the temperature below 100 °C (liquid phase), the subscript g indicates that properties values are referred to as the temperature above 100 °C (gas phase), hfg is the product of water latent heat of vaporization and water density at 100 °C (2.17 × 109 J m−3), and Cw is the water content inside the tumoral liver tissue (81%) or in the blood (79%), as found in the literature [30,31]. The temperature difference ΔTb,t is assumed to be 1 °C [29].
As regards the initial conditions, the temperature value is assumed to be uniform throughout the domain and equal to 37 °C for both tissue and blood. As regards boundary conditions, for t > 0, temperature is fixed at 37 °C on the external contour since the dimensions of the domain are large enough to neglect boundary effects from surroundings, while the adiabatic condition is maintained on the symmetry axis because of the axial symmetry of the model.
Thermal properties are supposed to be isotropic in the domain, and their values are taken from Zhang et al. [28] and Trujillo et al. [32], as shown in Table 2.

Table 2.
Tumoral tissue and blood thermal properties.
The provided power density value is Qext = 5 × 106 W m−3 with a heating time of 100 s, and hence, the resulting total energy provided to the tissue is 500 J.
The LTNE equations are numerically solved employing the finite-element commercial code COMSOL Multiphysics. An 8768-elements triangular mesh is used, and the grid convergence is verified on the maximum temperatures obtained for the lowest porosity and blood velocity in order to consider the highest values of temperature. From Table 3 below, negligible temperature differences are shown. PARDISO direct solver is employed to solve governing equations, and second-order Lagrangian elements are used to discretize equations. Moreover, the absolute tolerance chosen for the transient solver is 0.0001, while the time-stepping method is the intermediate backward differentiation formulas (BDF) with initial and maximum steps of 0.001 s and 0.1 s, respectively. As for the grid convergence, the effect of different time steps is verified on the maximum temperatures achieved for the lowest porosity and blood velocity, and in Table 4, the results confirm the choice made.

Table 3.
Maximum tissue temperatures evaluated for different triangular elements of the mesh.

Table 4.
Maximum tissue temperatures evaluated for different maximum time steps employed.
In order to validate the model, tissue temperature is evaluated at the center of the sphere and compared with results obtained by Yuan [26] for two concentric cubic domains having the same volumes of the used values in this work for the external sphere and internally heated sphere; thus, the external power density does not change. In Figure 4, the validation of the model is displayed, and the tissue temperature profiles are reported for the two extreme heating conditions and porosities used by Yuan [26], taking into account three different blood velocities. It is clear from Figure 4 the agreement between the two models in all the cases.
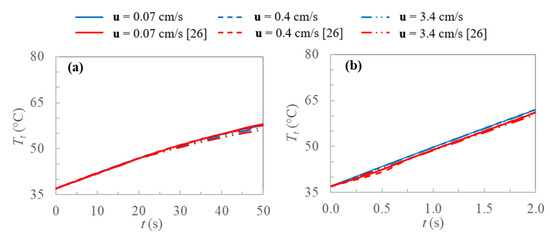
Figure 4.
Tissue temperatures profiles evaluated at the center of the sphere for current work and [26]: (a) ε = 0.005, Qext = 2 × 106 W m−3 and (b) ε = 0.05, Qext = 50 × 106 W m−3.
3. Results and Discussion
The results achieved using a variable porosity function are compared with the results obtained employing two uniform porosity values (ε = 0.07 and ε = 0.23) in terms of coagulation zones at the end of the heating period, maximum temperatures reached in the domain, and temperature fields. Moreover, the outcomes are presented for the different blood vessels previously mentioned, namely, capillaries, terminal arteries, terminal branches, and tertiary branches, which correspond to four different blood velocities and vessel diameters. This kind of evaluation is relevant to investigate different behaviors between small vessels and large vessels. Figure 5 displays the coagulation zones obtained considering the 99% of cell death probability for the variable porosity and the two uniform porosity values.
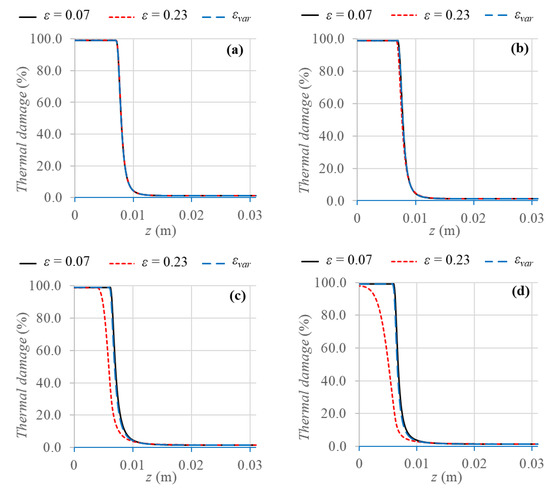
Figure 5.
Axisymmetric view of thermal damage percentage evaluated after 100 s of thermal treatment for the three different porosity models and the four different blood vessels: (a) capillaries, (b) terminal arteries, (c) terminal branches, and (d) tertiary branches.
The first result to highlight is that very similar coagulation zones are achieved for the two smallest blood vessels, namely, capillaries and terminal arteries; indeed, the maximum difference is about 4% for terminal arteries. However, for the two largest vessels, i.e., terminal branches and tertiary branches, the variable porosity model yields about the same results of using the uniform porosity value ε = 0.07, with a maximum percentage difference of about 3% for tertiary branches.
On the other hand, the uniform porosity value ε = 0.23 results in smaller coagulation zones, compared to the other two cases, i.e., from about 3.9 mm smaller for terminal branches to 1.16 cm smaller for tertiary branches, in which the complete cell death is not reached for ε = 0.23.
In this case, indeed, the larger the porosity value, the larger the convective loss contribution of the mass blood flux, and therefore, the removed heat from the tissue is larger as well, and lower tissue temperatures are achieved. Comparing the results at the same porosity values, a gradual decrease of coagulation diameter can be noticed as the vessel diameters increase, due to the larger heat sink effect of blood, which causes temperature decrease and consequently smaller coagulation zones. All the values of coagulation diameters obtained in the different cases are resumed in Table 5.

Table 5.
Coagulation diameters obtained for the different porosity models.
As regards tissue temperature reached, the first result investigated concerns the maximum tissue temperatures obtained in order to have a clear overview of the temperature peaks. This is relevant, indeed, to prevent high-temperature peaks due to the shortcomings that they involve, such as the continuous roll-offs in radiofrequency ablation [32], the steam popping phenomenon [33], and the risk of damaging the surrounding healthy tissue or the medical probes employed.
In Figure 6, the maximum tissue temperatures are displayed for all the cases. As previously happened for the final coagulation diameter obtained, the temperature peaks reached, considering a vascular network made up of capillaries or terminal arteries, i.e., very small vessels, are identical in all the cases. Considering larger blood vessels, instead, the only difference between the variable porosity model and the uniform porosity ε = 0.07 is about 2.6 °C higher temperature for tertiary branches when the uniform porosity is included, confirming the results shown for coagulation zones. Moreover, the uniform porosity ε = 0.23 leads to completely different results, with lower temperature peaks than the variable porosity model, of about 22.6 °C and 41.7 °C for terminal branches and tertiary branches, respectively.
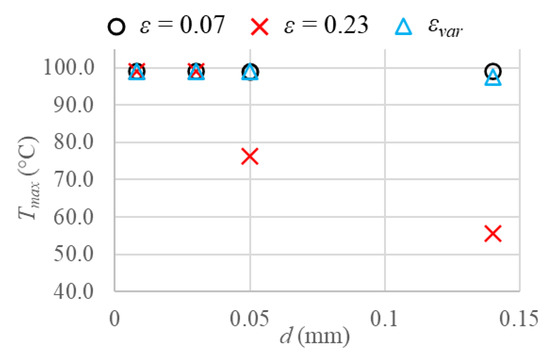
Figure 6.
Maximum tissue temperature values reached considering the three different porosities and the four blood vessels investigated.
In this case, as regards larger blood vessels, the difference between the variable porosity model and the largest porosity yields bigger deviations as larger blood vessels are taken into account. This is because the larger the blood vessels and consequently the blood velocities are, the larger the heat sink effect of blood and the smaller the tissue temperature achieved. In order to have a clear overview of all the aforementioned aspects, in Figure 7, temperature fields obtained at the end of the heating time are shown for all the cases of porosities and blood vessel diameters. From Figure 7, it is clear that the temperature decreases as the blood vessel diameters increase in all the cases. While the same temperature fields and coagulation diameters can be observed for all the cases considering capillaries and terminal arteries, the uniform porosity ε = 0.23 yields very lower temperatures and coagulation zones than uniform porosity ε = 0.07 and variable porosity model when terminal branches and tertiary branches are included. However, the uniform porosity ε = 0.07 results in slightly higher temperatures and coagulation diameters, compared to the variable porosity model for the two largest blood vessels. Furthermore, the symmetry of the coagulation zones along the r and z directions can be observed; therefore, the evaluation of coagulation diameters does not differ in the two directions.
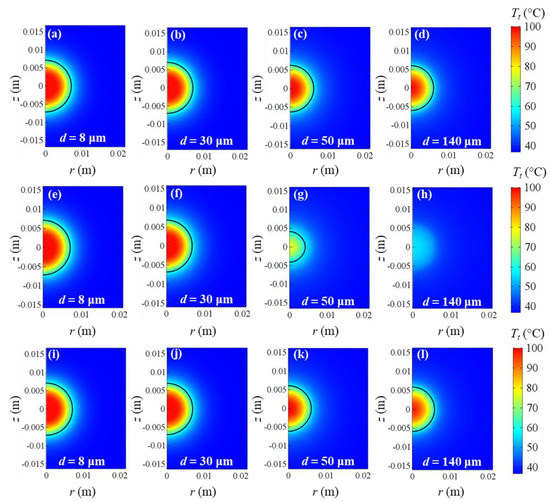
Figure 7.
Tissue temperature fields at the end of heating time for uniform ε = 0.07 (a–d), uniform ε = 0.23 (e–h), and εvar (i–l). Capillaries (d = 8 μm), terminal arteries (d = 30 μm), terminal branches (d = 50 μm), and tertiary branches (d = 140 μm) are taken into account. Coagulation contours delimited by the black lines.
4. Conclusions
A thermal-ablation bioheat model for tumoral tissue was numerically investigated. A modified LTNE model was implemented in order to include the water content vaporization in the two phases separately and to introduce a variable porosity in the domain, described by a quadratic function that changes from the core to the rim of the tumoral sphere. The mathematical model was solved employing the finite-element commercial code COMSOL Multiphysics. The computational domain of tumoral tissue consists of two concentric spheres; the external sphere defines the tissue boundary, while the inner sphere is the heating volume.
Results were compared with the results obtained employing two uniform porosity values (ε = 0.07 and ε = 0.23) in terms of coagulation zones at the end of the heating period, maximum temperatures reached in the domain, and temperature fields and they have been presented for different blood vessels, namely, capillaries, terminal arteries, terminal branches, and tertiary branches, which correspond to four different blood velocities and vessel diameters. Very similar coagulation zones are obtained for the two smallest blood vessels, whereas for the two largest vessels, the variable porosity model produces about the same results of using the uniform porosity value ε = 0.07. As regards the maximum tissue temperature reached, they are identical in all the cases for capillaries or terminal arteries. The only difference between the variable porosity model and the uniform porosity ε = 0.07 is about 2.6 °C higher temperature for tertiary branches when the uniform porosity is included. The uniform porosity ε = 0.23 leads to completely different results, with lower temperature peaks than the variable porosity model. The difference between the variable porosity model and the largest porosity yields bigger deviations as larger blood vessels are taken into account. This is because the larger the blood vessels and consequently the blood velocities are, the larger the heat sink effect of blood and the smaller the tissue temperature achieved. These outcomes highlight the importance of developing increasingly realistic bioheat models in thermal ablation of tumoral tissues in order to predict the coagulation zones achieved accurately. In this way, the main risks of thermal ablations such as incomplete ablation, tumor recurrence, or healthy tissue necrosis can be avoided. Moreover, due to more accurate models, thermal ablation protocols and medical devices can be improved and adapted to different organs and patient profiles.
Author Contributions
Conceptualization, A.A., L.B., M.I., C.T., and G.P.V.; methodology, A.A., L.B., M.I., C.T., and G.P.V.; software, M.I. and C.T.; validation, M.I. and C.T.; formal analysis, A.A., L.B., M.I., C.T., and G.P.V.; investigation, A.A., L.B., M.I., C.T., and G.P.V; resources, A.A., L.B., M.I., C.T., and G.P.V.; data curation, A.A., L.B., M.I., C.T., and G.P.V.; writing—original draft preparation, M.I. and C.T.; writing—review and editing, A.A., M.I., and C.T.; visualization, A.A., L.B., M.I., C.T., and G.P.V.; supervision, A.A., L.B., and G.P.V.; project administration, A.A., L.B., and G.P.V.; funding acquisition, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Italian Government MIUR Grant N° “PRIN-2017F7KZWS”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | Volumetric transfer area (m−1) |
| A | Frequency factor (s−1) |
| c | Specific heat (J kg−1 K−1) |
| Cw | Water content (%) |
| d | Diameter of the blood vessel (m) |
| dc | Coagulation diameter (m) |
| hc | Interfacial heat transfer coefficient(W m−2 K−1) |
| hfg | Product of water latent heat of vaporization and water density at 100 °C(J m−3) |
| k | Thermal conductivity (W m−1 K−1) |
| Qext | External power density (W m−3) |
| r | Radial coordinate (m) |
| r1 | Radius of the external sphere (m) |
| r2 | Radius of the internally heated sphere (m) |
| R | Universal gas constant (J mol−1 K−1) |
| t | Time (s) |
| T | Temperature (K) |
| u | Blood velocity vector (m s−1) |
| x, y, z | Spatial coordinates (m) |
| Greek symbols | |
| β | Coefficient (-) |
| ΔE | Activation energy (J mol−1) |
| ε | Porosity (-) |
| ρ | Density (kg m−3) |
| Ω(t) | Degree of tissue death (-) |
| Subscripts | |
| b | Blood |
| max | Maximum |
| min | Minimum |
| t | Tissue |
| tot | Total |
| var | Variable |
References
- Chu, K.F.; Dupuy, D.E. Thermal ablation of tumours: Biological mechanisms and advances in therapy. Nat. Rev. Cancer 2014, 14, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Brace, C. Thermal Tumor Ablation in Clinical Use. IEEE Pulse 2011, 2, 28–38. [Google Scholar] [CrossRef]
- Diederich, C.J. Thermal ablation and high-temperature thermal therapy: Overview of technology and clinical implementation. Int. J. Hyperth. 2005, 21, 745–753. [Google Scholar] [CrossRef]
- Nikfarjam, M.; Muralidharan, V.; Christophi, C. Mechanisms of Focal Heat Destruction of Liver Tumors. J. Surg. Res. 2005, 127, 208–223. [Google Scholar] [CrossRef] [PubMed]
- Moros, E. (Ed.) Physics of Thermal Therapy: Fundamentals and Clinical Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Berjano, E.J. Theoretical modeling for radiofrequency ablation: State-of-the-art and challenges for the future. Biomed. Eng. Online 2006, 5, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling Heat Transfer in Tumors: A Review of Thermal Therapies. Ann. Biomed. Eng. 2018, 47, 676–693. [Google Scholar] [CrossRef]
- Almekkawy, M.; Chen, J.; Ellis, M.D.; Haemmerich, D.; Holmes, D.R., III; Linte, C.A.; Panescu, D.; Pearce, J.; Prakash, P.; Zderic, V. Therapeutic Systems and Technologies: State-of-the-Art Applications, Opportunities, and Challenges. IEEE Rev. Biomed. Eng. 2019, 13, 325–339. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Bioheat transfer in a spherical biological tissue: A comparison among various models. J. Phys. Conf. Ser. 2019, 1224, 012001. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G. Constructal law and ion transfer in normal and cancer cells. Proc. Rom. Acad. A Spec. Issue 2019, 19, 213–218. [Google Scholar]
- Lucia, U.; Ponzetto, A.; Deisboeck, T.S. Constructal approach to cell membranes transport: Amending the ‘Norton-Simon’ hypothesis for cancer treatment. Sci. Rep. 2016, 6, srep19451. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Melnik, R. Thermal ablation of biological tissues in disease treatment: A review of computational models and future directions. Electromagn. Biol. Med. 2020, 39, 1–40. [Google Scholar] [CrossRef] [PubMed]
- Vafai, K. (Ed.) Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Xuan, Y.; Roetzel, W. Bioheat equation of the human thermal system. Chem. Eng. Technol. 1997, 20, 268–276. [Google Scholar] [CrossRef]
- Khaled, A.-R.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. The role of porous media in biomedical engineering as related to magnetic resonance imaging and drug delivery. Heat Mass Transf. 2006, 42, 939–953. [Google Scholar] [CrossRef]
- Nakayama, A.; Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar] [CrossRef]
- Keangin, P.; Rattanadecho, P. Analysis of heat transport on local thermal non-equilibrium in porous liver during microwave ablation. Int. J. Heat Mass Transf. 2013, 67, 46–60. [Google Scholar] [CrossRef]
- Rattanadecho, P.; Keangin, P. Numerical study of heat transfer and blood flow in two-layered porous liver tissue during microwave ablation process using single and double slot antenna. Int. J. Heat Mass Transf. 2013, 58, 457–470. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Timchenko, V.; Jackson, M.; Yeoh, G.H. A combined transient thermal model for laser hyperthermia of tumors with embedded gold nanoshells. Int. J. Heat Mass Transf. 2011, 54, 5459–5469. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Timchenko, V.; Jackson, M. Indirect heating strategy for laser induced hyperthermia: An advanced thermal model. Int. J. Heat Mass Transf. 2012, 55, 4688–4700. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. A novel local thermal non-equilibrium model for biological tissue applied to multiple-antennas configurations for thermal ablation. Numer. Heat Transf. Part A Appl. 2020, 79, 1–11. [Google Scholar] [CrossRef]
- Stewart, E.E.; Chen, X.; Hadway, J.; Lee, T.Y. Correlation between hepatic tumor blood flow and glucose utilization in a rabbit liver tumor model. Radiology 2006, 239, 740–750. [Google Scholar] [CrossRef] [PubMed]
- Crezee, J.; Lagendijk, J.J.W. Temperature uniformity during hyperthermia: The impact of large vessels. Phys. Med. Biol. 1992, 37, 1321–1337. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P. Numerical analysis of temperature and thermal dose response of biological tissues to thermal non-equilibrium during hyperthermia therapy. Med Eng. Phys. 2008, 30, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.A. Considerations for thermal injury analysis for RF ablation devices. Open Biomed. Eng. J. 2010, 4, 3. [Google Scholar] [CrossRef]
- Zhang, B.; Moser, M.A.; Zhang, E.M.; Luo, Y.; Zhang, W. Numerical analysis of the relationship between the area of target tissue necrosis and the size of target tissue in liver tumours with pulsed radiofrequency ablation. Int. J. Hyperth. 2015, 31, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.; Sparrow, E. A thermal-ablation bioheat model including liquid-to-vapor phase change, pressure- and necrosis-dependent perfusion, and moisture-dependent properties. Int. J. Heat Mass Transf. 2007, 50, 2537–2544. [Google Scholar] [CrossRef]
- Smith, S.R.; Foster, K.R.; Wolf, G.L. Dielectric Properties of VX-2 Carcinoma Versus Normal Liver Tissue. IEEE Trans. Biomed. Eng. 1986, 33, 522–524. [Google Scholar] [CrossRef]
- Woodard, H.Q.; White, D.R. The composition of body tissues. Br. J. Radiol. 1986, 59, 1209–1218. [Google Scholar] [CrossRef]
- Trujillo, M.; Bon, J.; Rivera, M.J.; Burdío, F.; Berjano, E. Computer modelling of an impedance-controlled pulsing protocol for RF tumour ablation with a cooled electrode. Int. J. Hyperth. 2016, 32, 931–939. [Google Scholar] [CrossRef]
- Cooper, J.M.; Sapp, J.L.; Tedrow, U.; Pellegrini, C.P.; Robinson, D.; Epstein, L.M.; Stevenson, W.G. Ablation with an internally irrigated radiofrequency catheter: Learning how to avoid steam pops. Heart Rhythm. 2004, 1, 329–333. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).