Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup
Abstract
1. Introduction
2. Description of the Model
2.1. Governing Equations
2.2. Numerical Formulation
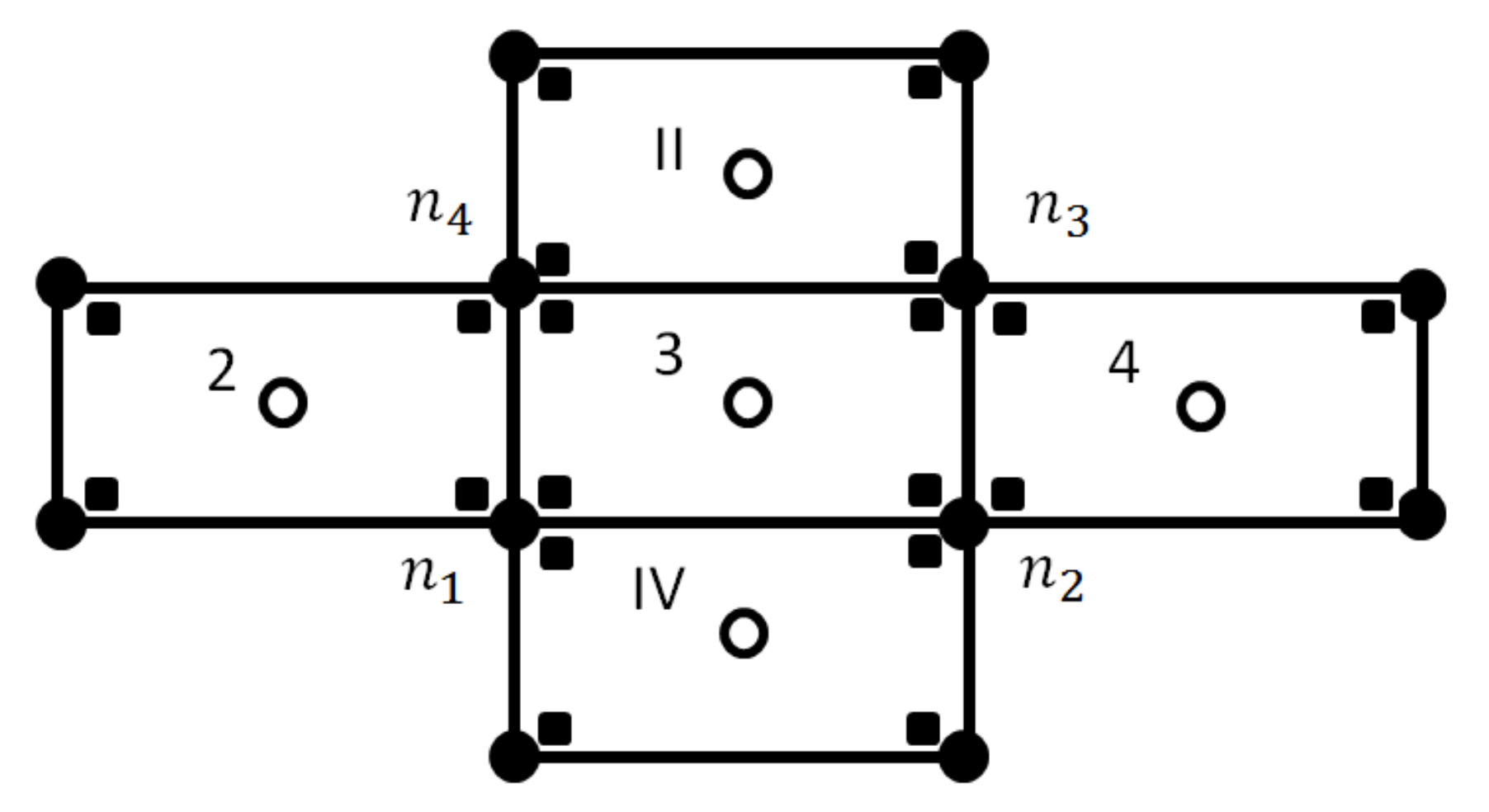
2.2.1. First Step: Discontinuous Galerkin Solution
2.2.2. New Slope Limiter
2.2.3. Second Step: Continuous Galerkin Solution
2.2.4. Third Step
2.2.5. Boundary Conditions
2.2.6. Dry Bed Treatment
2.2.7. Wave Breaking
- The surface variation criterion: a node is flagged if , with ∈ [0.3, 0.65] depending on the type of breaker.
- The local slope angle criterion: a node is flagged if ≥ tan ϕ, with ϕ ∈ [14°, 33°] depending on the flow configuration.
2.2.8. Computational Aspects
3. Model Verification and Validation
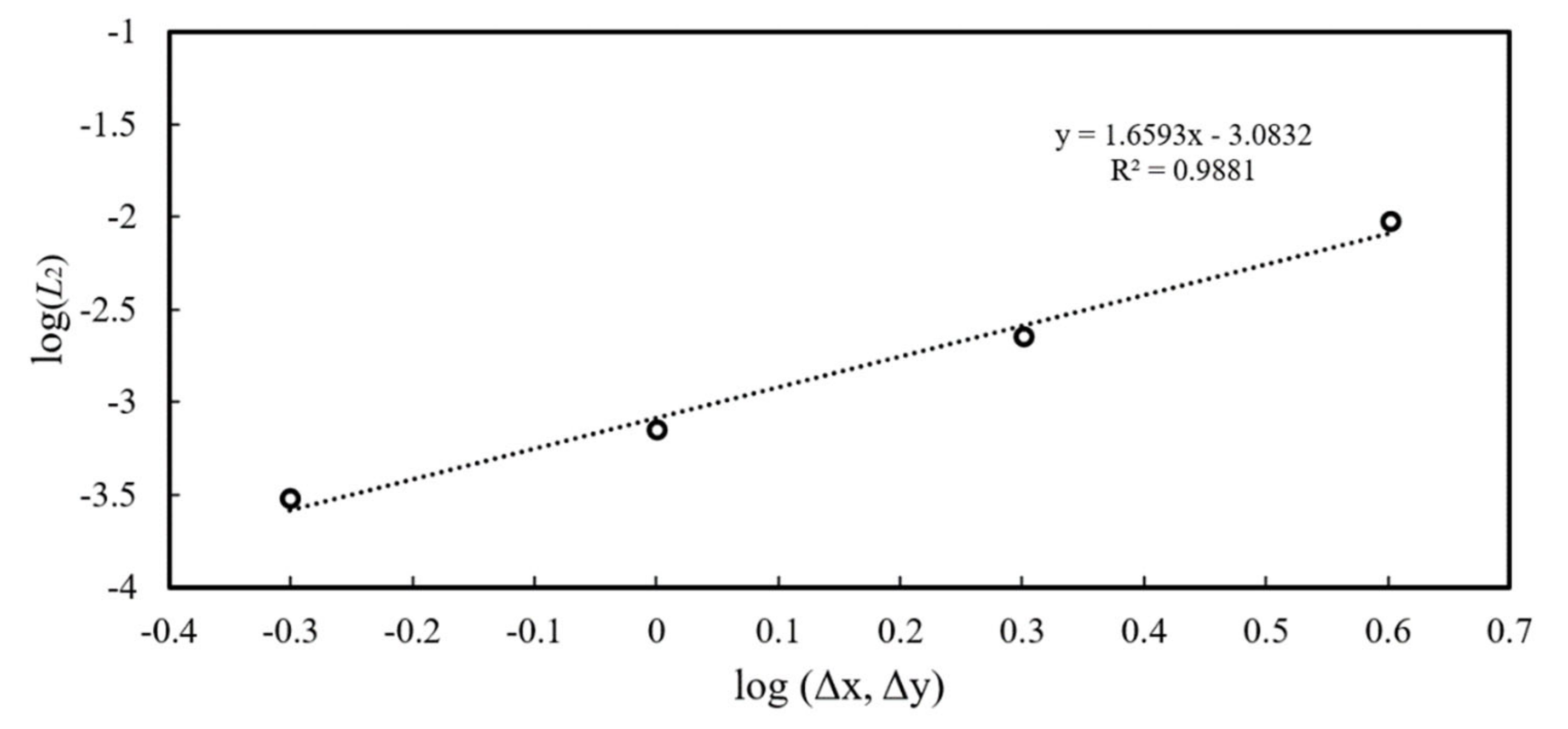
3.1. Solitary Wave Propagation Along a Constant Depth Channel
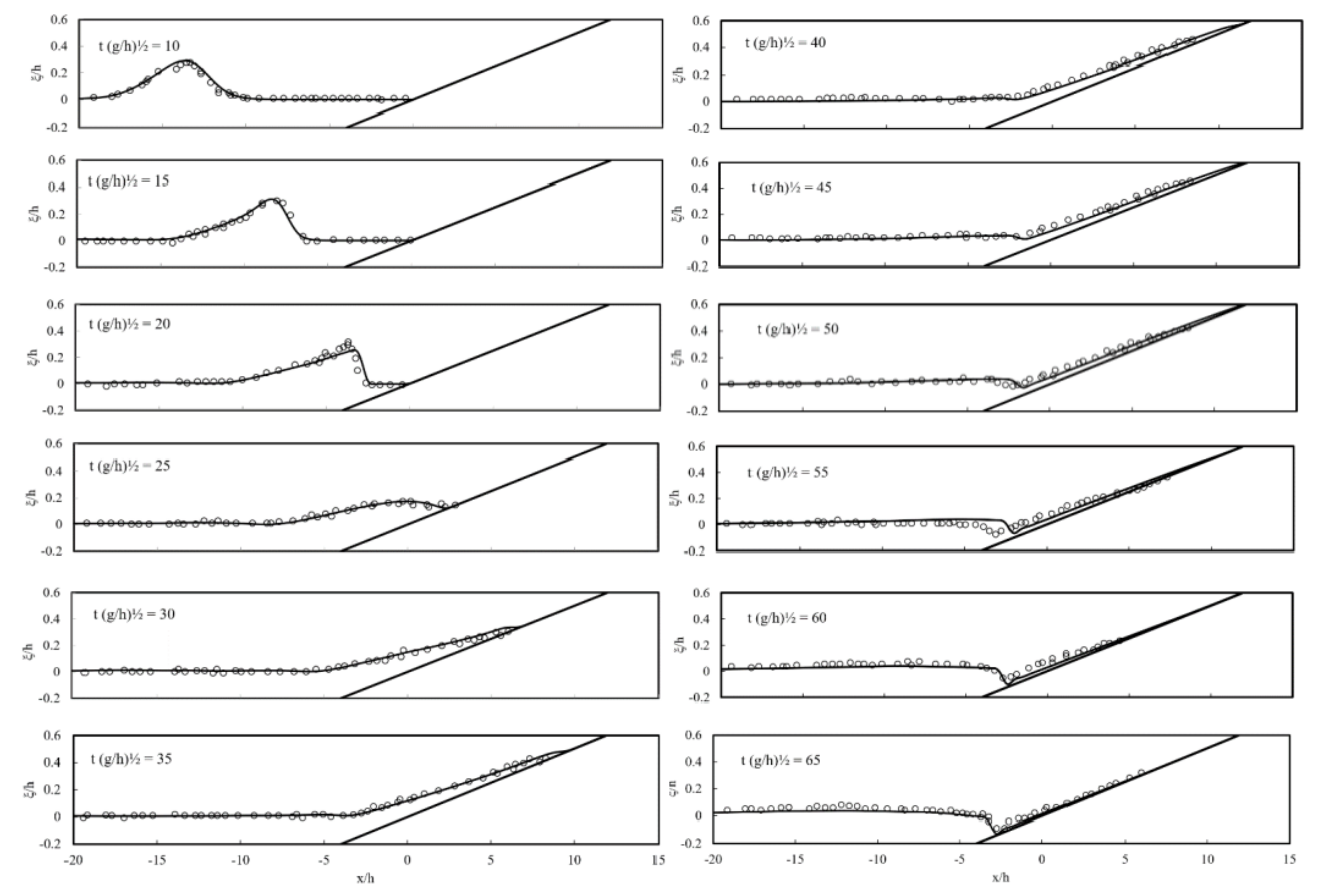
3.2. Solitary Wave Runup on a Plane Beach
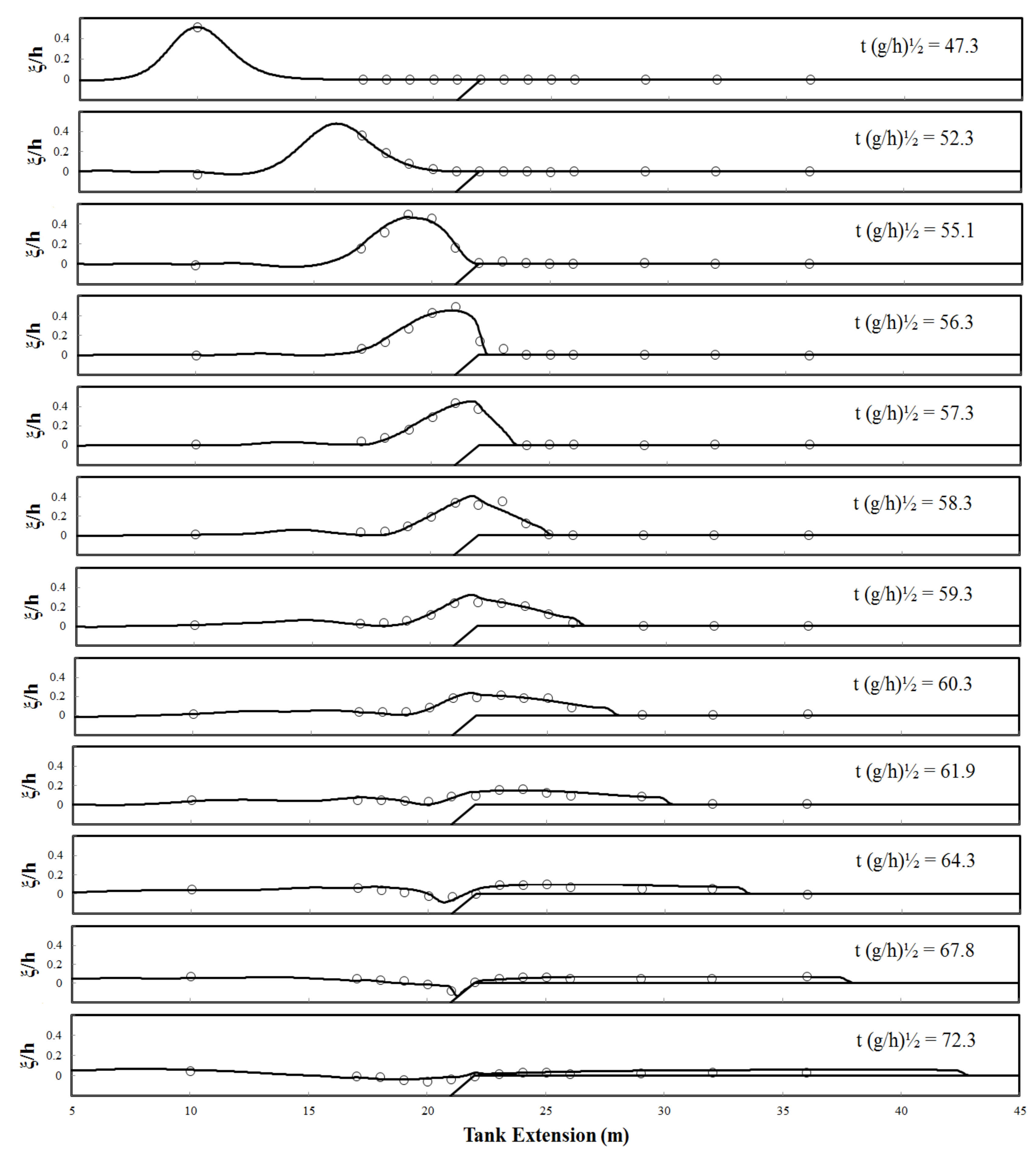
3.3. Solitary Wave Propagation over Fringing Reef
3.4. Series of Regular Waves on a Plane Beach
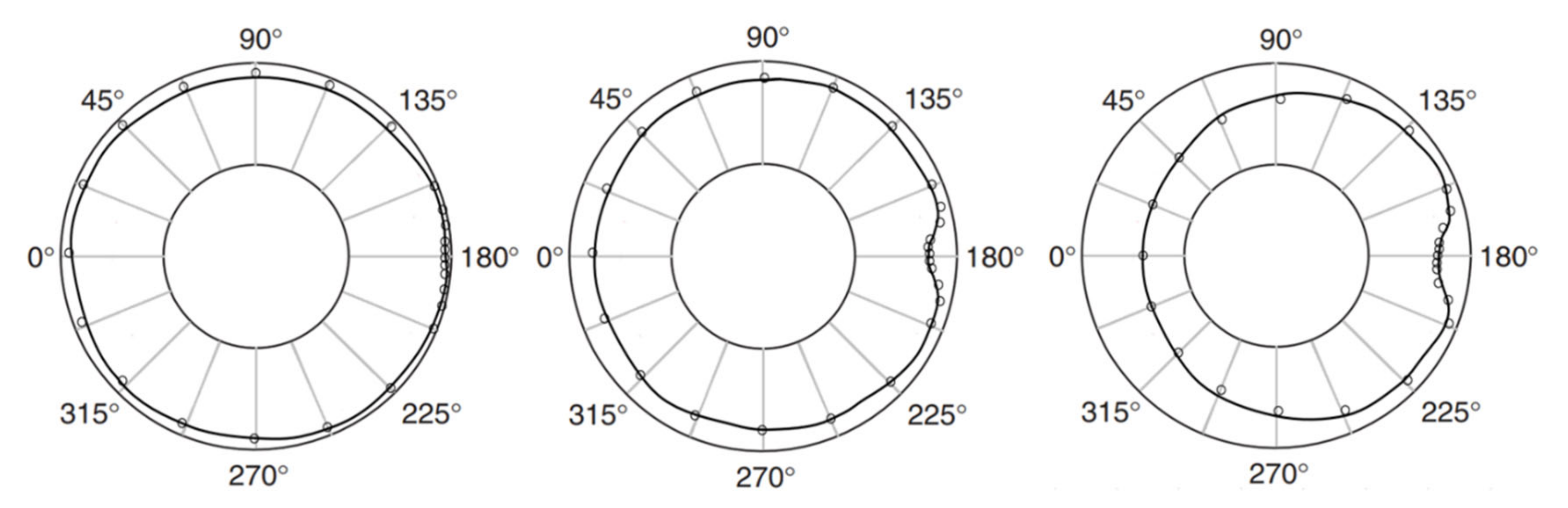
3.5. Solitary Wave Runup on a Conical Island
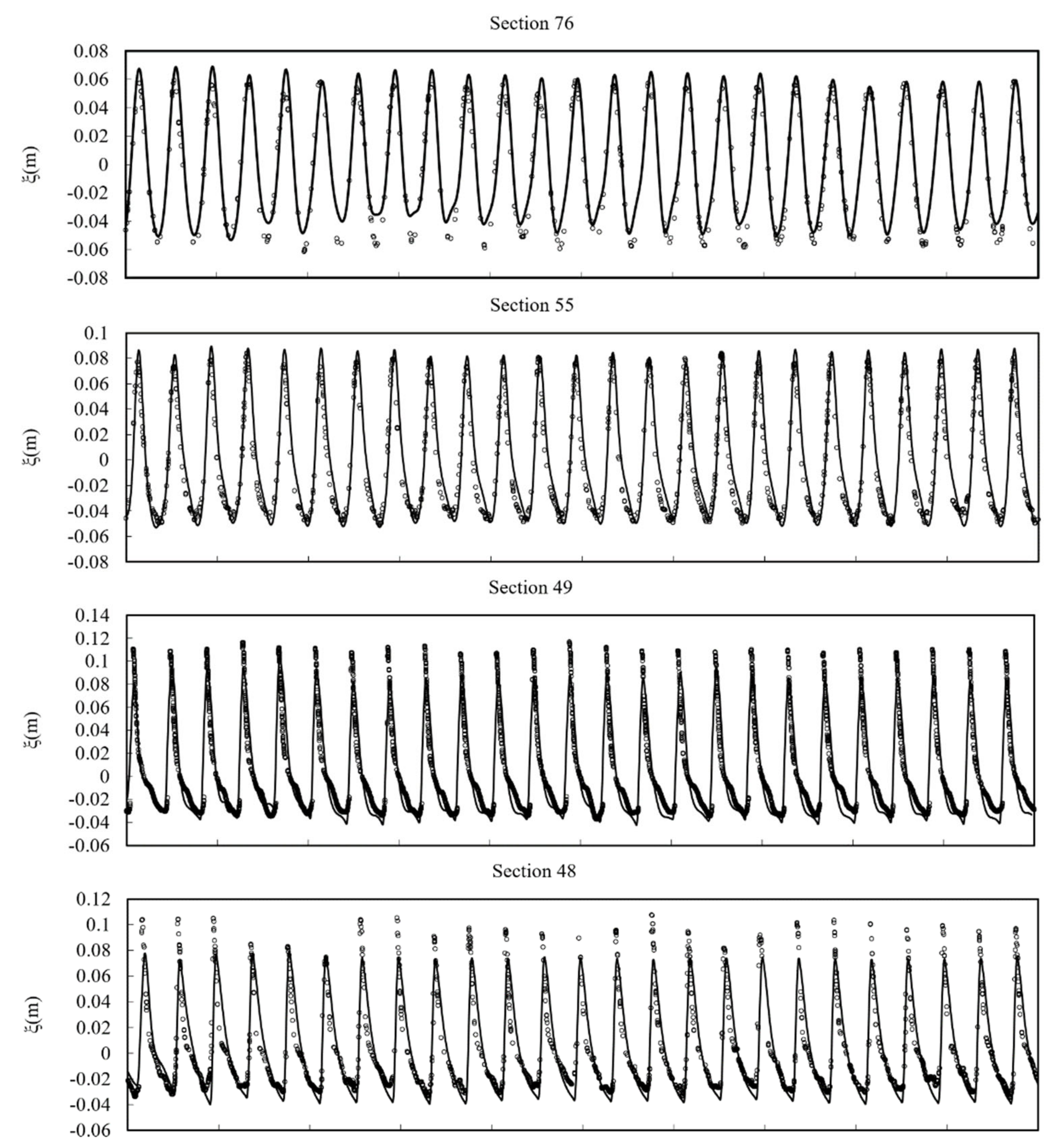
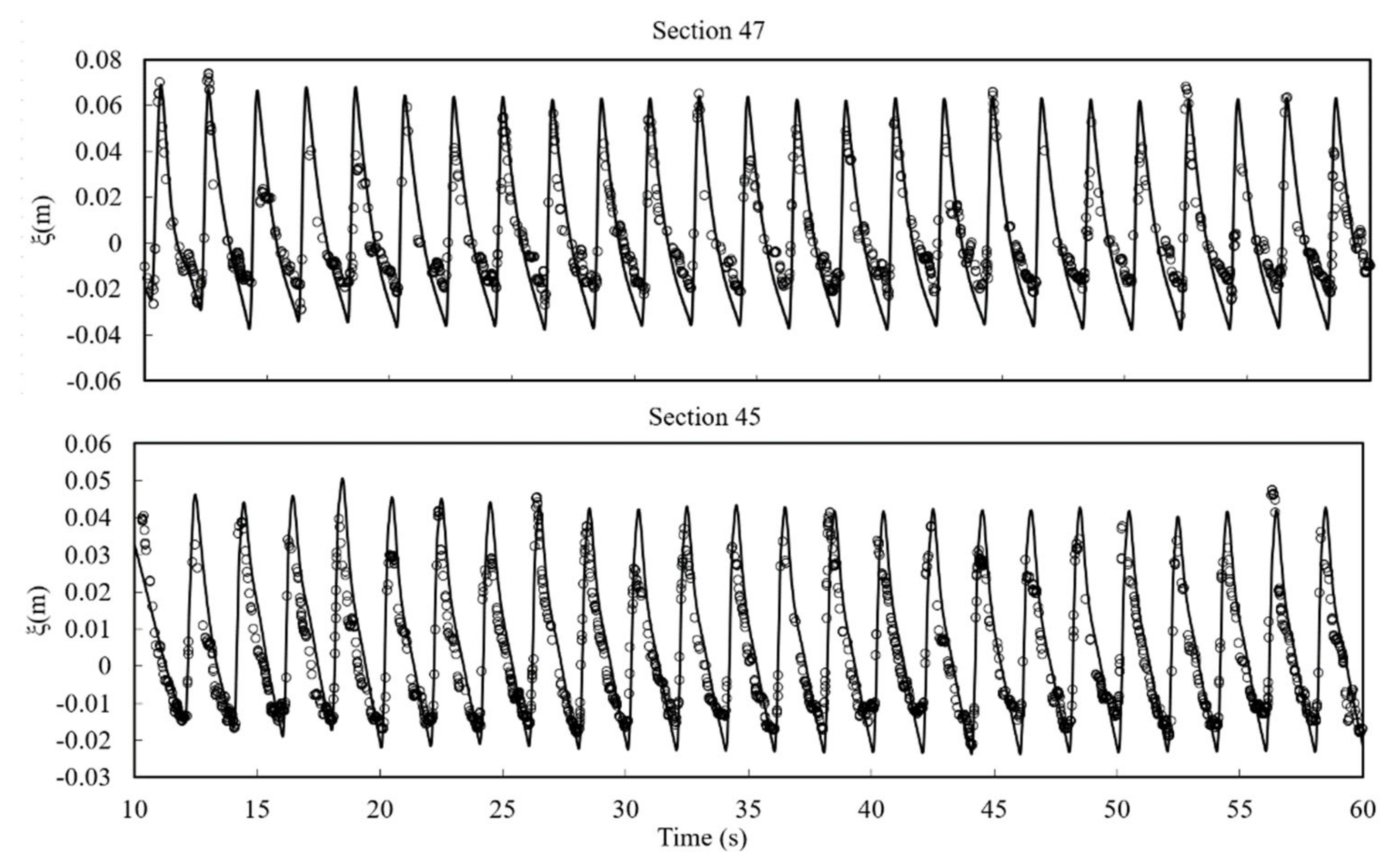
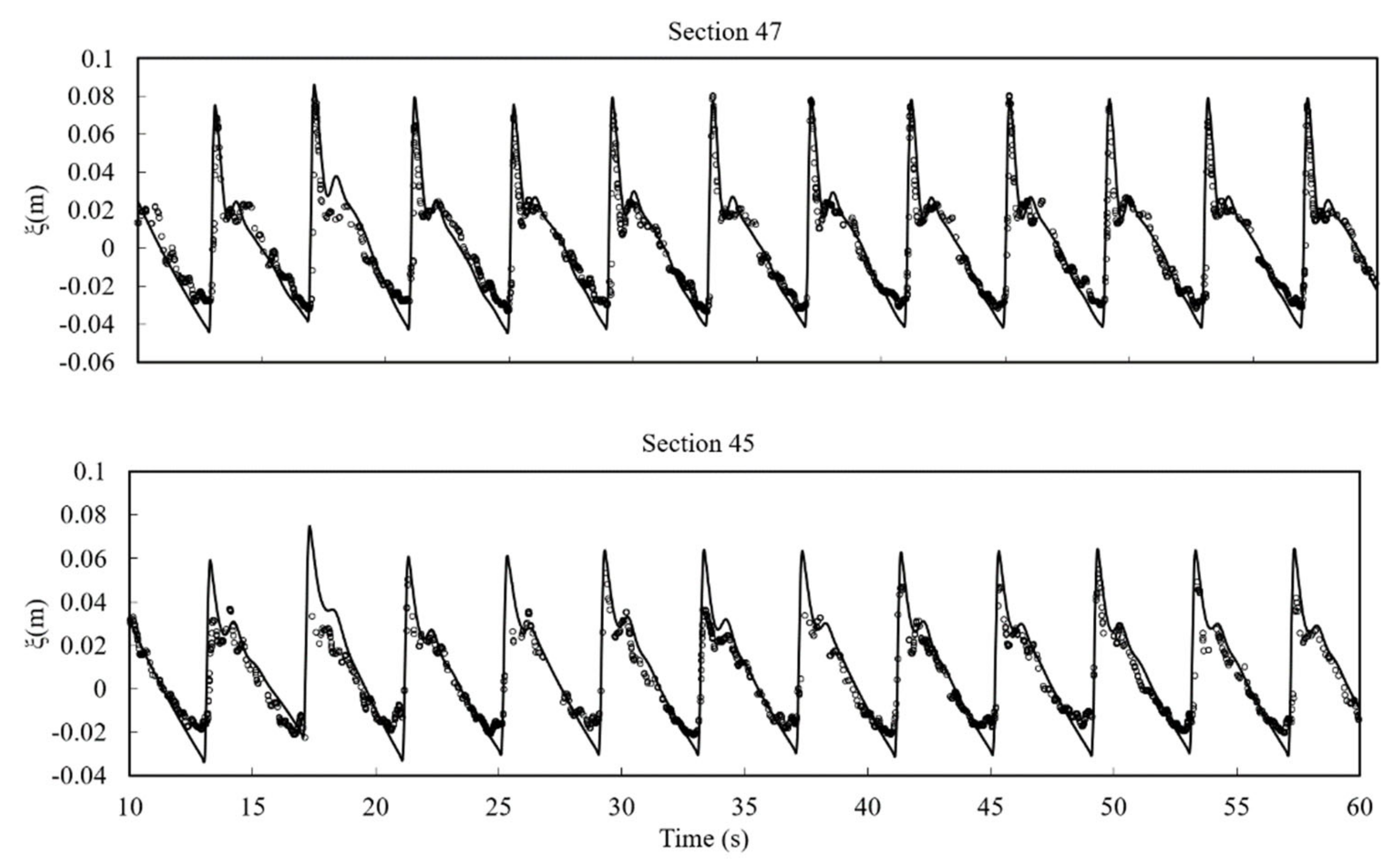
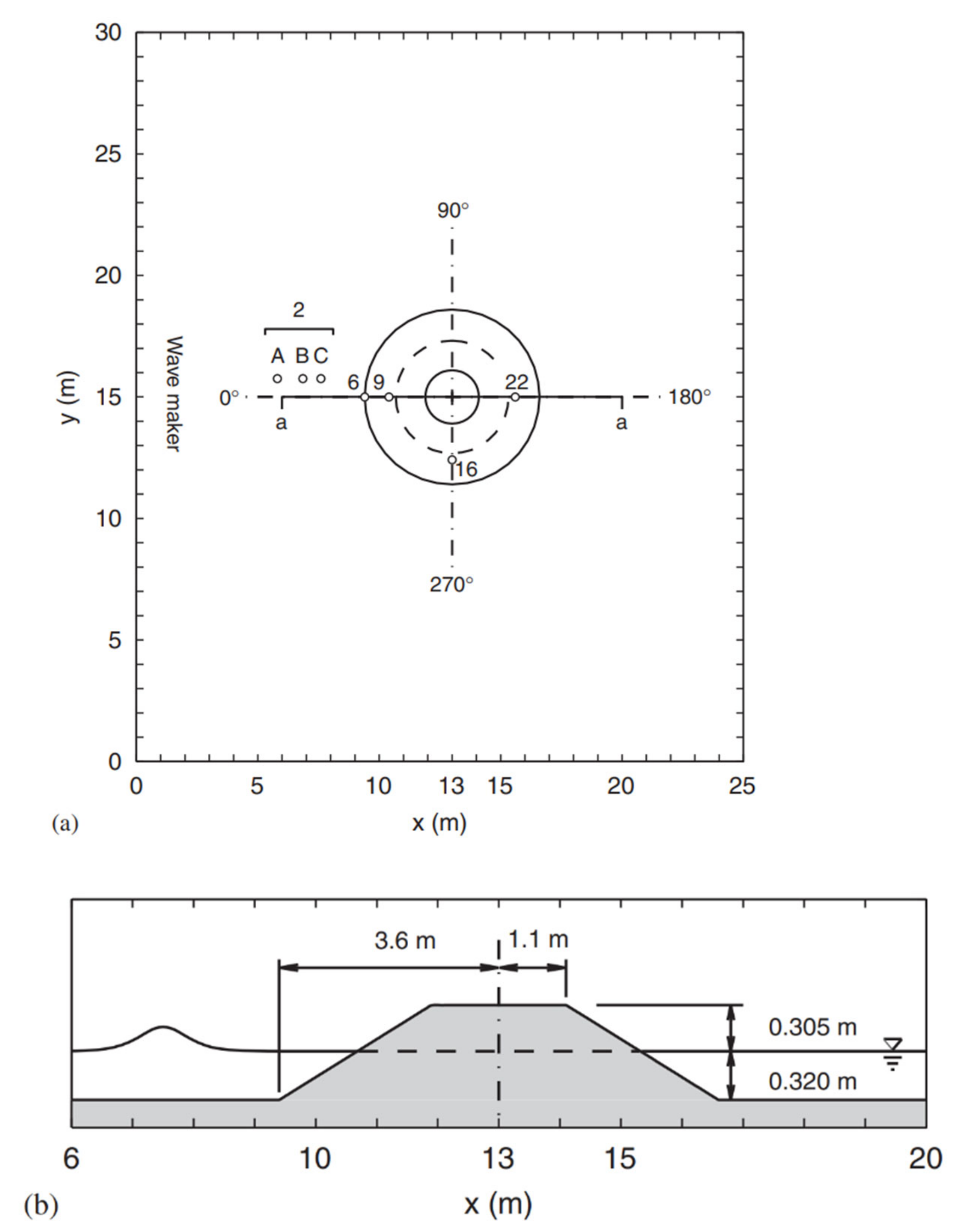
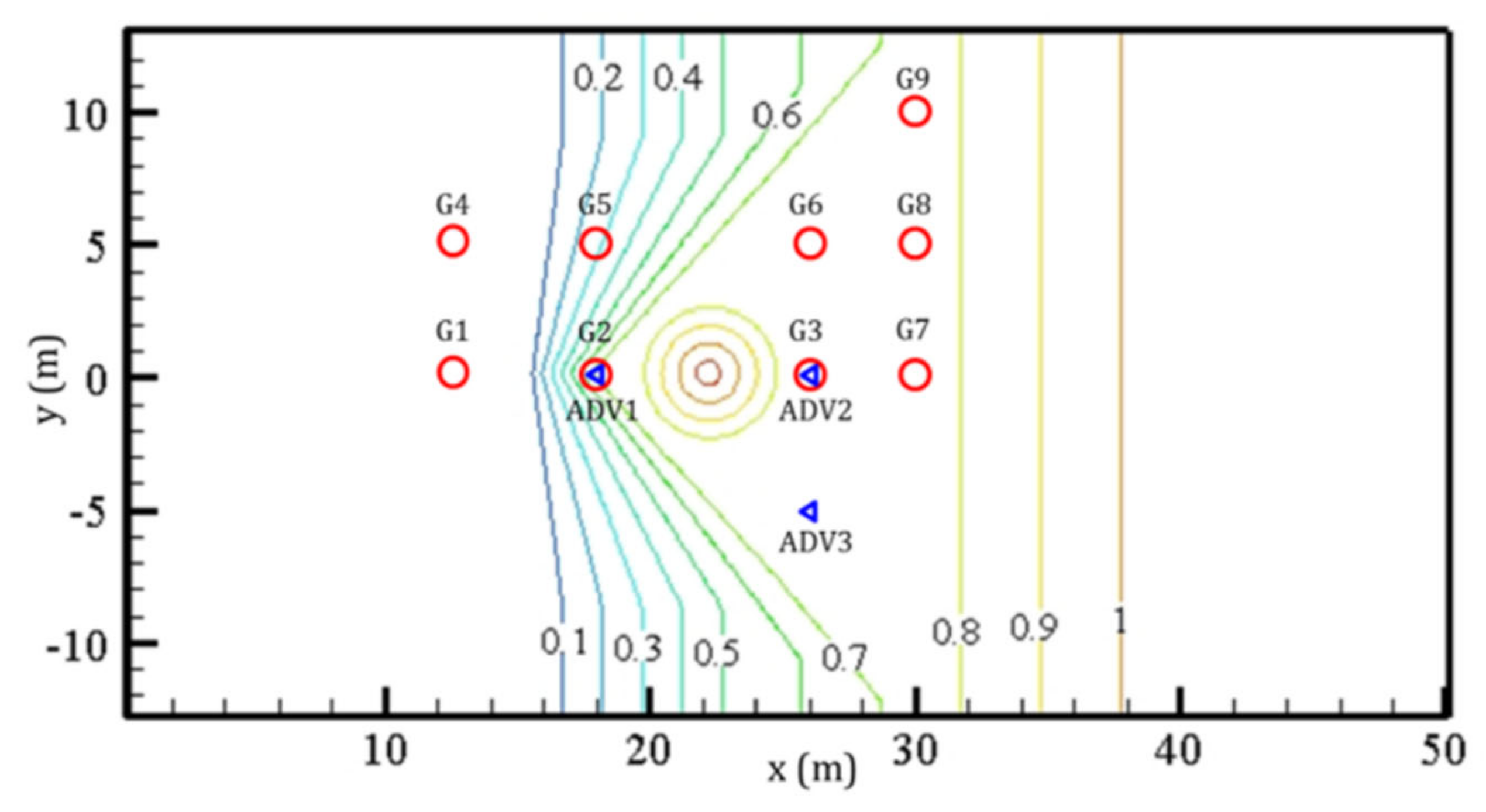
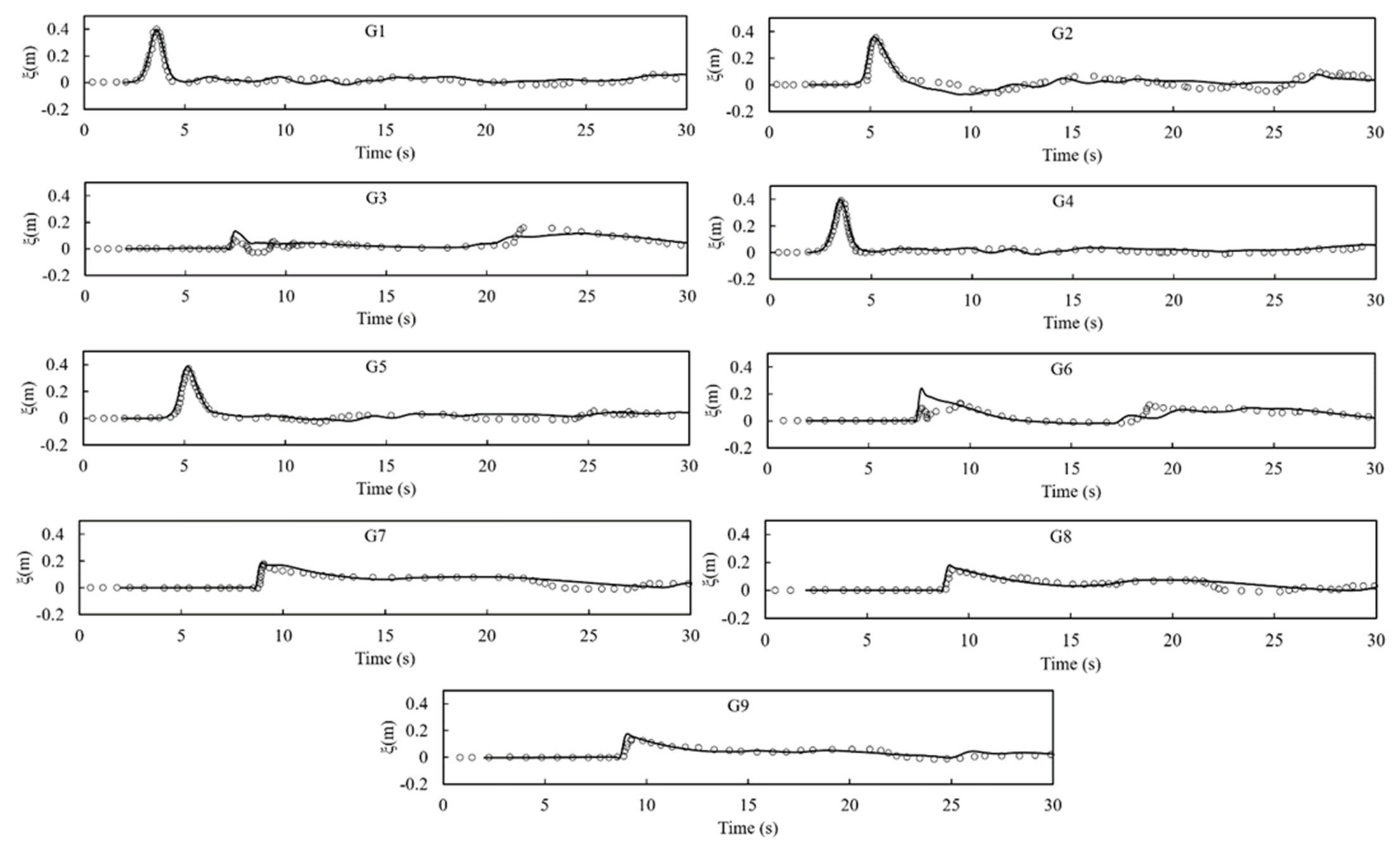
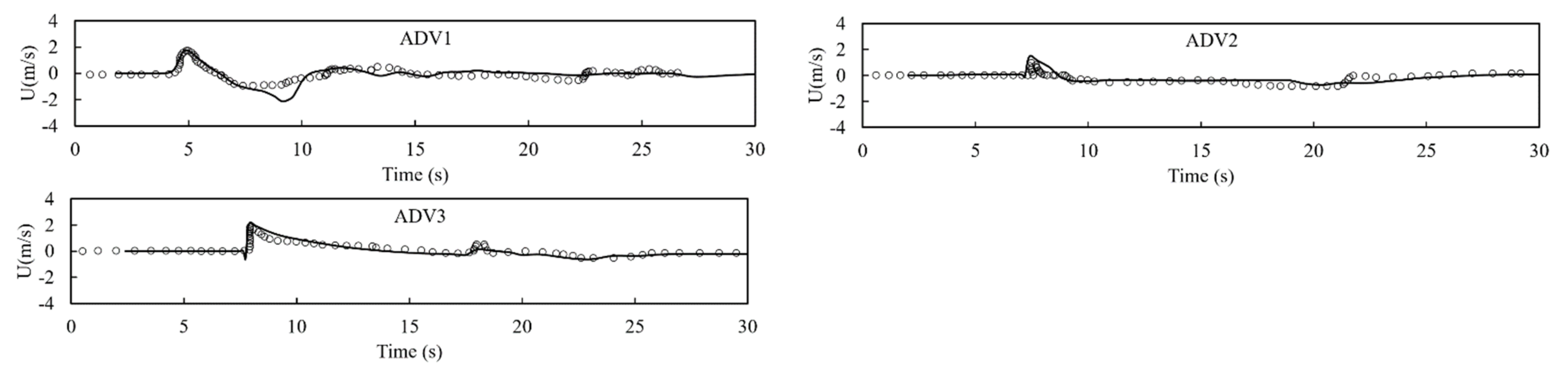
3.6. Solitary Wave Transformation, Breaking and Runup over a Three-Dimensional Complex Bathymetry.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Casulli, V.; Stelling, G.S. Numerical simulation of 3D quasi-hydrostatic, free-surface flows. J. Hydraul. Eng. 1998, 124, 678–686. [Google Scholar] [CrossRef]
- Stansby, P.K.; Zhou, J.G. Shallow-water flow solver with non-hydrostatic pressure: 2D vertical plane problems. Int. J. Numer. Methods Fluids 1998, 28, 541–563. [Google Scholar] [CrossRef]
- Stelling, G.; Zijlema, M. An accurate and efficient finite difference algorithm for non-hydrostatic free surface flow with application to wave propagation. Int. J. Numer. Methods Fluids 2003, 43, 1–23. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Further experiences with computing non-hydrostatic free-surface flows involving water waves. Int. J. Numer. Methods Fluids 2005, 48, 169–197. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure. Coast. Eng. 2008, 55, 780–790. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S.; Smith, P. SWASH: An operational public domain code for simulating wave fiels and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Zijlema, M. Computation of free surface waves in coastal waters with SWASH on unstructured grids. Comp. Fluids 2020, 213, 104751. [Google Scholar] [CrossRef]
- Wu, G.; Lin, Y.; Dong, P.; Zhang, K. Development of two-dimensional non-hydrostatic wave model based on central-upwind scheme. J. Mar. Sci. Eng. 2020, 8, 505. [Google Scholar] [CrossRef]
- Wang, W.; Martin, T.; Kamath, A.; Bihs, H. An improved depth-averaged non-hydrostatic shallow water model with quadratic pressure approximation. Int. J. Numer. Methods Fluids 2020, 92, 803–824. [Google Scholar] [CrossRef]
- Walters, R.A. A semi implicit finite element model for non-hydrostatic (dispersive) surface waves. Int. J. Numer. Methods Fluids 2005, 49, 721–737. [Google Scholar] [CrossRef]
- Wei, Z.; Jia, Y. A depth-integrated non-hydrostatic finite element model for wave propagation. Int. J. Numer. Methods Fluids 2013, 73, 976–1000. [Google Scholar] [CrossRef]
- Wei, Z.; Jia, Y. Simulation of nearshore wave processes by a depth-integrated non-hydrostatic finite element model. Coast. Eng. 2014, 83, 93–107. [Google Scholar] [CrossRef]
- Calvo, L.; Rosman, P.C. Depth Integrated Non Hydrostatic Finite Element Model for Wave Propagation. Revista I+D Tecnológico 2017, 13, 56–66. [Google Scholar]
- Bradford, S. Nonhydrostatic model for surf zone simulation. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 163–174. [Google Scholar] [CrossRef]
- Choi, D.Y.; Wu, C.H.; Young, C. An efficient curvilinear non-hydrostatic model for simulating surface water waves. Int. J. Numer. Methods Fluids 2011, 66, 1093–1115. [Google Scholar] [CrossRef]
- Dawson, C.; Westerink, J.J.; Feyen, J.C.; Pothina, D. Continuous, discontinuous and coupled discontinuous–continuous Galerkin finite element methods for the shallow water equations. Int. J. Numer. Methods Fluids 2006, 52, 63–88. [Google Scholar] [CrossRef]
- Jeschke, A.; Vater, S.; Behrens, J. A discontinuous Galerkin method for non-hydrostatic shallow water flows. In Proceedings of the Conference: Finite Volumes for Complex Applications VIII-Hyperbolic, Elliptic and Parabolic Problems, Lille, France, 12–16 June 2017. [Google Scholar] [CrossRef]
- Rosman, S. Referência Técnica do SisBahia. 2019. Available online: http://www.sisbahia.coppe.ufrj.br/SisBAHIA_RefTec_V10d_.pdf (accessed on 12 April 2021).
- Hoteit, H.; Ackerer, P.; Mosé, R.; Erhel, J.; Philippe, B. New Two-Dimensional Slope Limiters for Discontinuous Galerkin Methods on Arbitrary Meshes; Research Report, RR-4491; Institut National de Recherche en Informatique et en Automatique (Inria): Paris, France, 2002. [Google Scholar]
- Stelling, G.S.; Busnelli, M.M. Numerical simulation of the vertical structure of discontinuous flows. Int. J. Numer. Methods Fluids 2001, 37, 23–43. [Google Scholar] [CrossRef]
- Bai, Y.; Cheung, K.F. Dispersion and nonlinearity of multi-layer non-hydrostatic free-surface flow. J. Fluid Mech. 2013, 726, 226–260. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; van Leer, B. On upstream differencing and Godunov-type schemes for hyperbolic conservations laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Abbot, M.B.; Basco, D.R. Computational Fluid Dynamics, an Introduction for Engineers; Longan Group, UK Limited: London, UK, 1989. [Google Scholar]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coast. Eng. 2013, 76, 1–16. [Google Scholar] [CrossRef]
- Fang, K.Z.; Zou, Z.L.; Dong, P.; Liu, Z.B.; Gui, Q.Q.; Yin, J.W. An efficient shock capturing algorithm to the extended Boussinesq wave equations. Appl. Ocean Res. 2013, 43, 11–20. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geinman, J.D.; Grilli, S.T. A high-order adaptative time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43, 36–51. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Hybrid finite volume-Finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 2009, 56, 609–620. [Google Scholar] [CrossRef]
- Bacigaluppi, P.; Ricchiuto, M.; Bonneton, P. Implementation and Evaluation of Breaking Detection Criteria for a Hybrid Boussinesq Model. Water Waves 2020, 2, 207–241. [Google Scholar] [CrossRef]
- Kazolea, M.; Delis, A.I.; Synolakis, C.E. Numerical treatment of wave breaking on unstructured finite volume approximations for extended Boussinesq-type equations. J. Comput. Phys. 2014, 271, 281–305. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F.; Kobayashi, M.H. Shock-capturing Boussinesq-type model for nearshore wave processes. Coast. Eng. 2010, 57, 407–423. [Google Scholar] [CrossRef]
- Tissier, M.; Bonneton, P.; Marche, F.; Chazel, F.; Lannes, D. A new approach to handle wave breaking in fully non-linear Boussinesq models. Coast. Eng. 2012, 67, 54–66. [Google Scholar] [CrossRef]
- Titov, V.V.; Synolakis, C.E. Modeling of breaking and nonbreaking long-wave evolution and runup using VTCS-2. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 308–316. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kowalik, Z.; Cheung, K.F. Depth-integrated, non-hydrostatic model for wave breaking and run-up. Int. J. Numer. Methods Fluids 2008, 61, 473–497. [Google Scholar] [CrossRef]
- Roeber, V. Boussinesq-Type Model for Nearshore Wave Process in Fringing Reef Environment. Ph.D. Thesis, University Hawaii at Manoa, Honolulu, HI, USA, 2010. [Google Scholar]
- De Serio, F.; Mossa, M. Experimental study on the hydrodynamics of regular breaking waves. Coast. Eng. 2006, 53, 99–113. [Google Scholar] [CrossRef]
- De Padova, D.; Dalrymple, R.A.; Mossa, M. Analysis of the artificial viscosity in the smoothed particle hydrodynamics modelling of regular waves. J. Hydraul. Res. 2014, 52, 836–848. [Google Scholar] [CrossRef]
- De Padova, D.; Mouldi, B.M.; De Serio, F.; Mossa, M.; Sibilla, S. Characteristics of breaking vorticity in spilling and plunging waves investigated numerically by SPH. Environ. Fluid Mech. 2019. [CrossRef]
- Kazolea, M.; Ricchiuto, M. On Wave Breaking for Boussinesq-Type Models; Research Report RR-9092; Institut National de Recherche en Informatique et en Automatique (Inria): Prais, France, 2017. [Google Scholar]
- Hieu, P.D.; Vinh, P.N. A numerical model for simulation of near-shore waves and wave induced currents using the depth-averaged non-hydrostatic shallow water equations with an improvement of wave energy dissipation. Vietnam J. Mar. Sci. Technol. 2020, 20, 155–172. [Google Scholar] [CrossRef]
- Briggs, M.J.; Synolakis, C.E.; Harkins, G.S.; Green, D.R. Laboratory Experiments of Tsunami Runup on a Circular Island. Tsunamis: 1992–1994; Springer: Berlin/Heidelberg, Germany, 1995; pp. 569–593. [Google Scholar]
- Swigler, D.T. Laboratory Study Investigating the Three-Dimensional Turbulence and Kinematic Properties Associated with a Breaking Solitary Wave. Ph.D. Thesis, Texas A & M University, Uvalde, TX, USA, 2010. [Google Scholar]
- Fang, K.; Liu, Z.; Zou, Z. Modelling coastal water waves using a depth-integrated, non-hydrostatic model with shock-capturing ability. J. Hydraul. Res. 2015, 53, 119–133. [Google Scholar] [CrossRef]







| T (sec) | h (m) | Breaking Type | ||||
|---|---|---|---|---|---|---|
| T1 | 11 | 2 | 4.62 | 0.70 | 0.37 | Spilling |
| T2 | 6.5 | 4 | 10.12 | 0.70 | 0.74 | Plunging |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calvo, L.; De Padova, D.; Mossa, M.; Rosman, P. Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup. Computation 2021, 9, 47. https://doi.org/10.3390/computation9040047
Calvo L, De Padova D, Mossa M, Rosman P. Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup. Computation. 2021; 9(4):47. https://doi.org/10.3390/computation9040047
Chicago/Turabian StyleCalvo, Lucas, Diana De Padova, Michele Mossa, and Paulo Rosman. 2021. "Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup" Computation 9, no. 4: 47. https://doi.org/10.3390/computation9040047
APA StyleCalvo, L., De Padova, D., Mossa, M., & Rosman, P. (2021). Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup. Computation, 9(4), 47. https://doi.org/10.3390/computation9040047








