Model and Analysis of Economic- and Risk-Based Objective Optimization Problem for Plant Location within Industrial Estates Using Epsilon-Constraint Algorithms
Abstract
1. Introduction
2. Literature Review
- Plant location decision in industrial estate planning involves various stakeholders with often conflicting requirements. Thus, we develop the bi-objective, mixed-integer linear programming model based on economic and risk criteria to analyze the location decision of industrial factories in the industrial estate in this study.
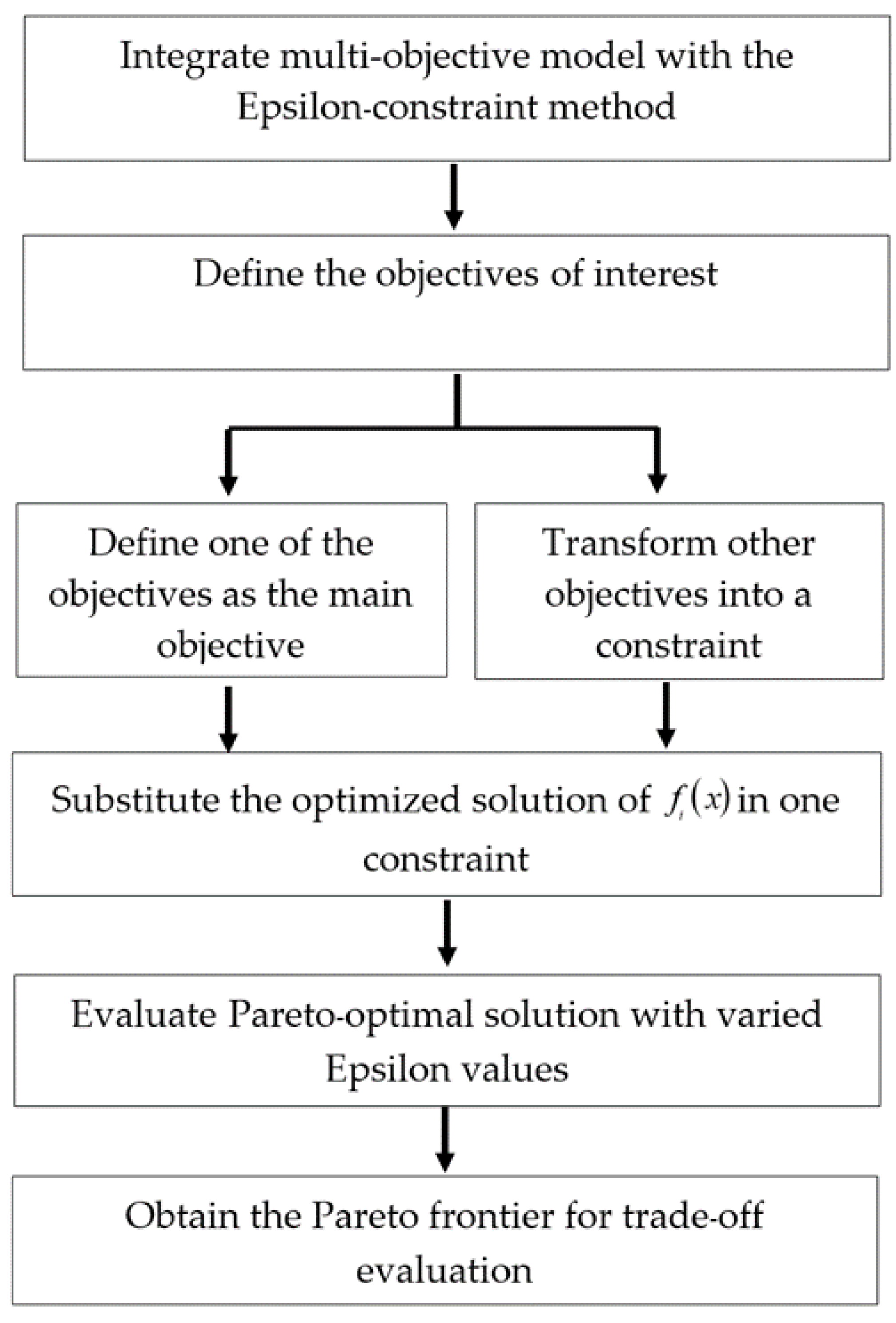
- Given the conflicting nature of bi-objective programming, the Epsilon-constraint method approach is further applied to analyze decision-makers’ preferences and to obtain the Pareto frontier in our analysis.
- In this study, both the bi-objective optimization technique and simulation procedure are used as an integrated tool in which the simulated risk profile obtained from the ALOHA program is used as an input for the developed optimization model in an integrated manner.
- Existing studies focus on developing the optimization model to design the production process of a single plant. In this study, our aim shifts to an analysis of the plant location problem comprising diverse factory classifications in the planned industrial estate.
- The actual case study of the industrial estate located in Thailand is illustrated with actual data in this study. In addition, rather than applying the data to a general plant, we illustrate the model with diverse factory types in this study.
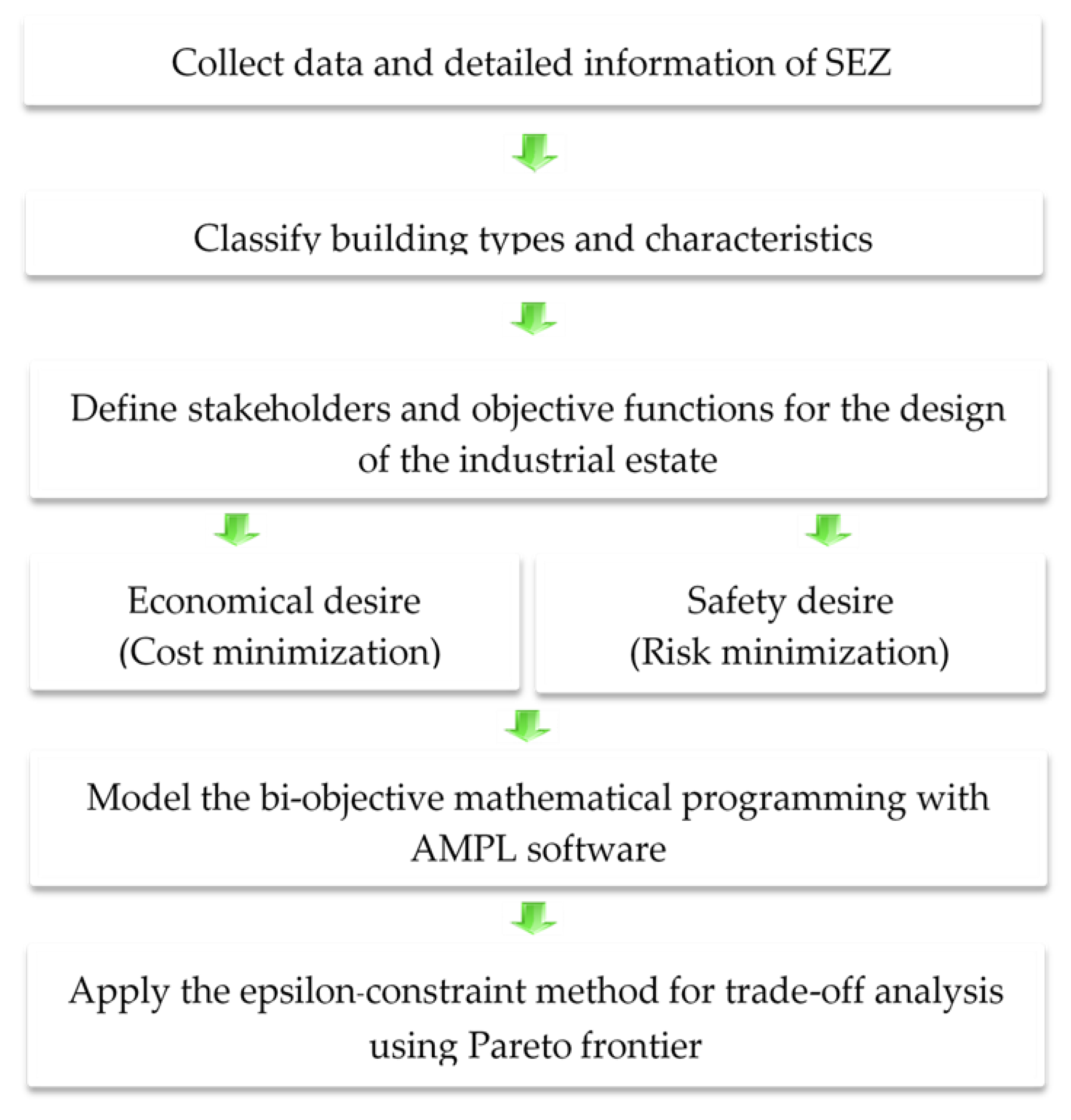
3. Methodology
3.1. Integrated Mathematical and Simulation Modeling
3.2. Assumptions
- The cost of the piping system is approximated based only on the distances between pairs of industrial plants. We assume that the same types of materials are transmitted through the industrial estate with no significant differences.
- The cost from risk is approximated based on an emergency situation that could hypothetically occur in the illustrated industrial estate; this cost is computed using the construction costs of buildings of various sizes. Thus, the cost from risk depends on the size of the area assigned to the industrial plant.
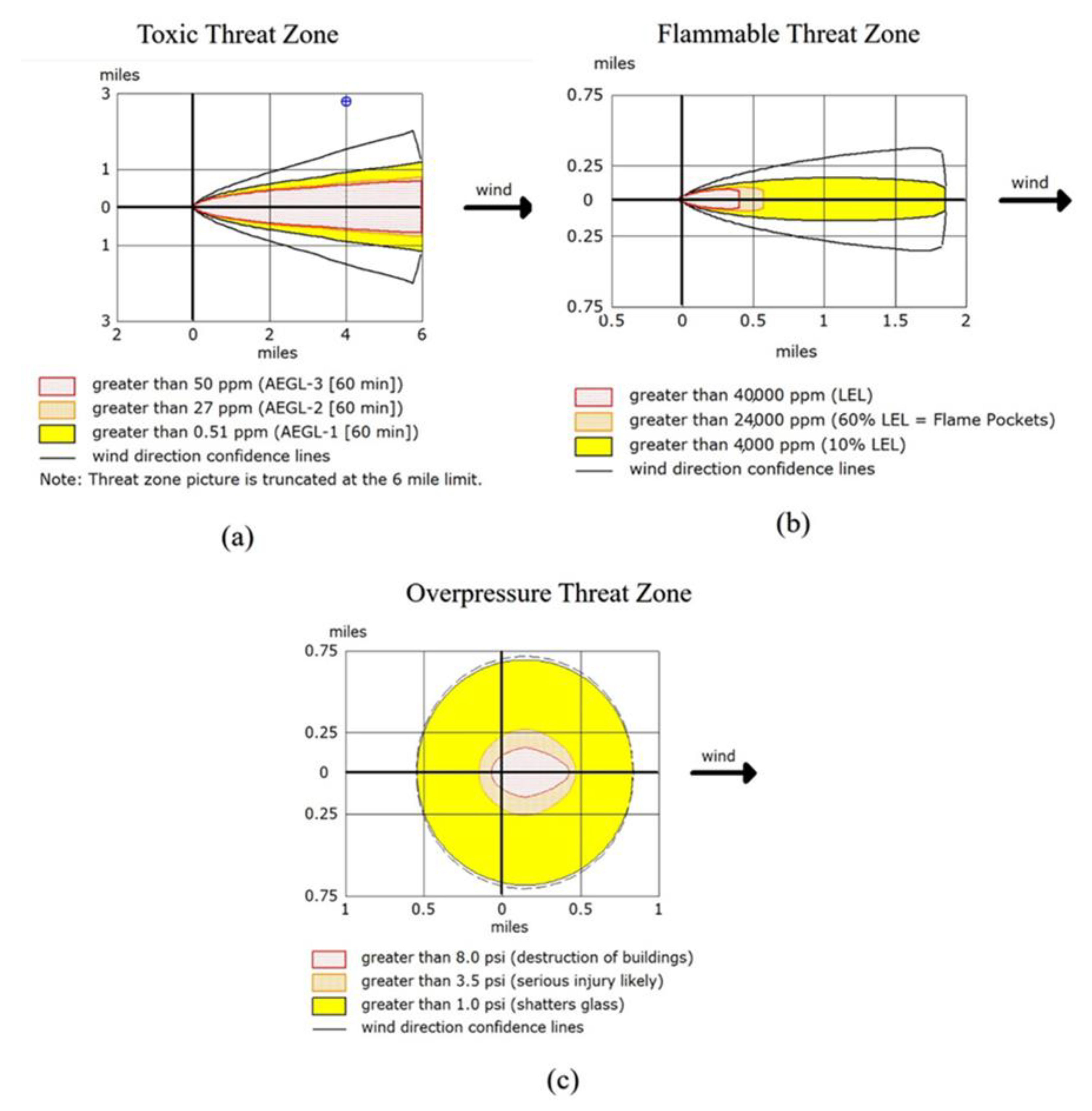
- The hazardous damage considered in this analysis is based on H2S gas approximated via the ALOHA program; this damage hypothetically occurs in the location of the chemical transmission of the pipe system. Although a toxic threat, flammable threat, and overpressure threat were analyzed, only the overpressure threat is used in the analysis of damage in this study.
- Requirements related to the distance data between different plants were obtained from governmental regulations, as well as suggestions from concerned stakeholders of the presented industrial estate.
- The various building types in this study were classified into four categories: hazardous-material factory, warehouse-type building, typical industrial factory, and central office. Thus, the model complexity will depend on the number of building categories used in the analysis.
3.3. Mathematical Notation
- : Set of grids in an industrial estate, indexed by k
- : Set of all plants or buildings to be located, indexed by i
- : Set of hazardous-material plants to be located
- : Set of warehouse-type buildings to be located
- : Set of typical industrial plants to be located
- : Set of central offices to be located
- : The X coordinate of the grid from an office center (meter)
- : The Y coordinate of the grid from an office center (meter)
- : Risk probability for each grid
- : Rectilinear distance of the grid from an office center (meter)
- : Facility cost for each grid (Baht)
- : Unit piping cost of the plant (Baht/meter)
- : An arbitrary number for a fixed upper bound of distance for located plants
- : Minimum separation distance between plants and ,
- : Minimum separation distance between a hazardous-material plant and a central office
- : Minimum separation distance between a hazardous-material plant and a typical industrial plant
- : Minimum separation distance between a hazardous-material plant and a warehouse-type building
- : Minimum separation distance between a warehouse-type building and a central office
- : Minimum separation distance between a warehouse-type building and a typical industrial plant
- : Minimum separation distance between a typical industrial plant and a central office
- : Maximum separation distance between a hazardous-material plant and a central office with four respective parameters
- : Maximum separation distance between a hazardous-material plant and a warehouse-type building with four respective parameters
- : Maximum separation distance between a hazardous-material plant and a typical industrial plant with four respective parameters
- : Maximum separation distance between a warehouse-type building and a central office with four respective parameters
- : Maximum separation distance between a warehouse-type building and a typical industrial plant with four respective parameters
- : Maximum separation distance between a typical industrial plant and a central office with four respective parameters
- : A variable to assign a plant to grid , binary {0, 1}
- : The X coordinate of located plant
- : The Y coordinate of located plant
- : Supporting variable for minimum separation distance between a hazardous-material plant and a central office with four respective variables, binary {0, 1}
- : Supporting variable for minimum separation distance between a hazardous-material plant and a warehouse-type building with four respective variables, binary {0, 1}
- : Supporting variable for minimum separation distance between a hazardous-material plant and a typical industrial plant with four respective variables, binary {0, 1}
- : Supporting variable for minimum separation distance between a warehouse-type building and a central office with four respective variables, binary {0, 1}
- : Supporting variable for minimum separation distance between a warehouse-type building and a typical industrial plant with four respective variables, binary {0, 1}
- : Supporting variable for minimum separation distance between a typical industrial plant and a central office with four respective variables, binary {0, 1}
3.4. Objective Functions
3.5. Constraint Sets
3.5.1. Non-Overlapping Constraint Set
3.5.2. Distance-Related Constraint Set
3.5.3. Separation-Distance Constraint Set for the Minimum Condition
3.5.4. Separation-Distance Constraint Set for the Maximum Condition
3.5.5. Variable-Type Constraint
4. Case Study and Results
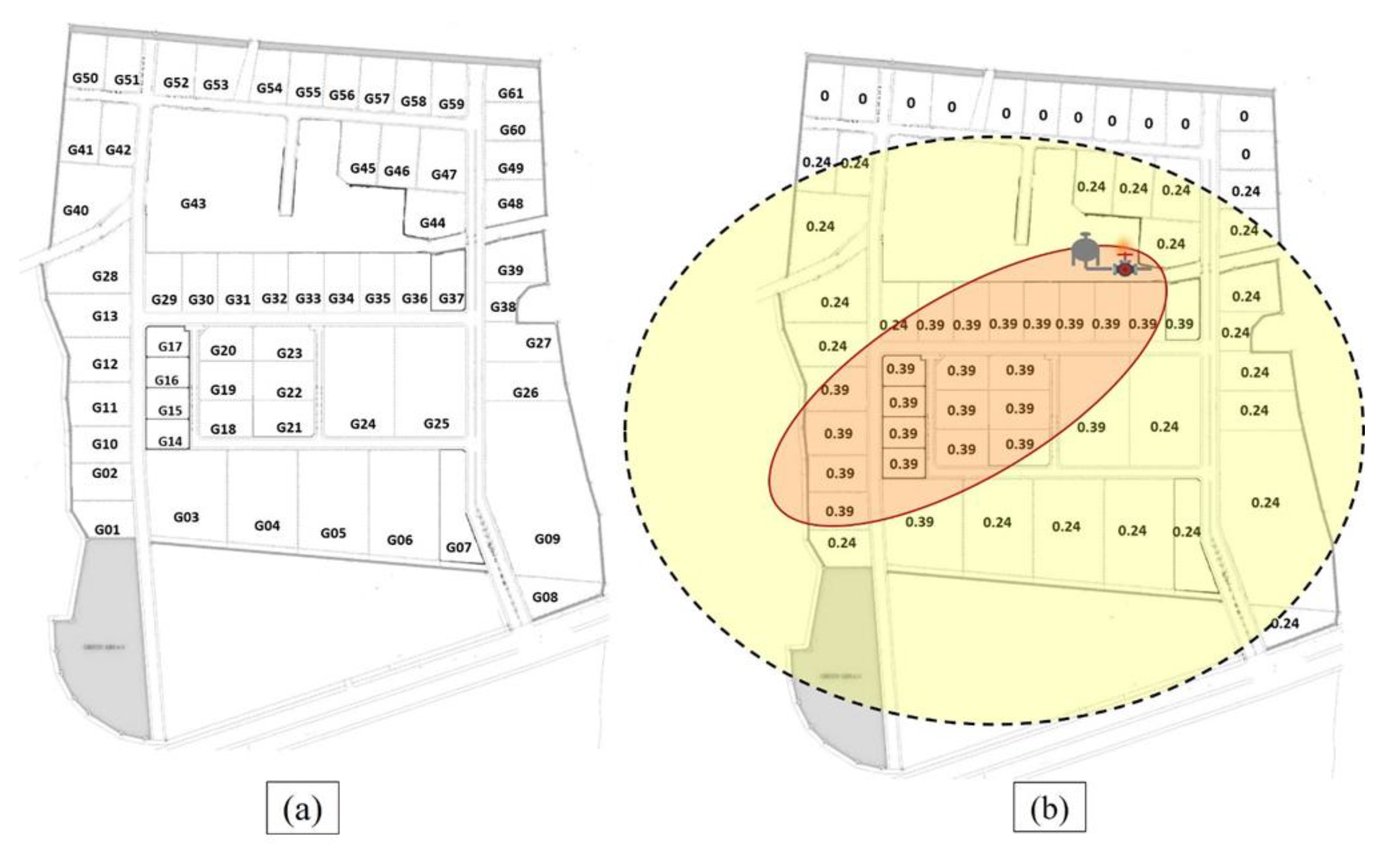
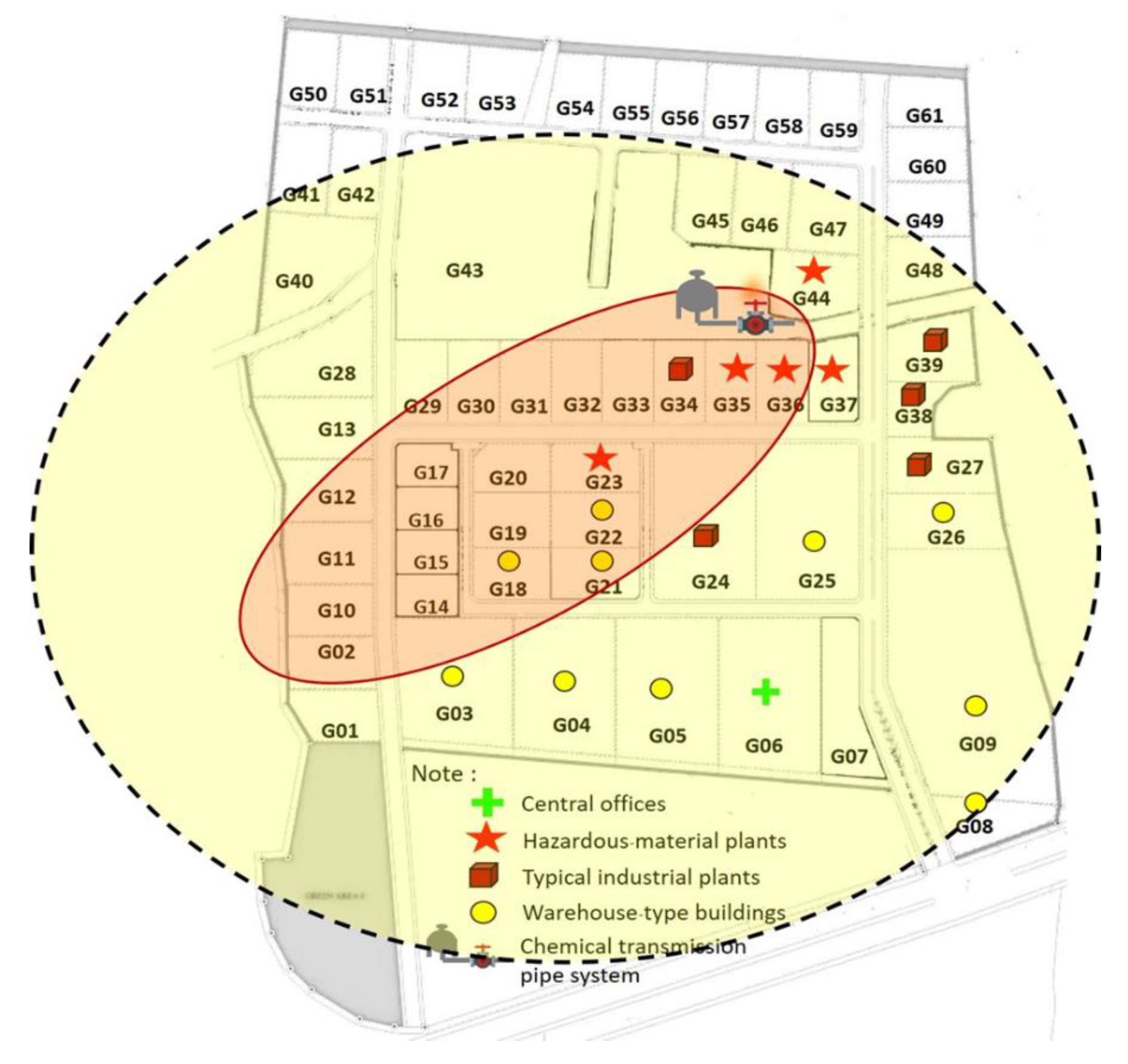
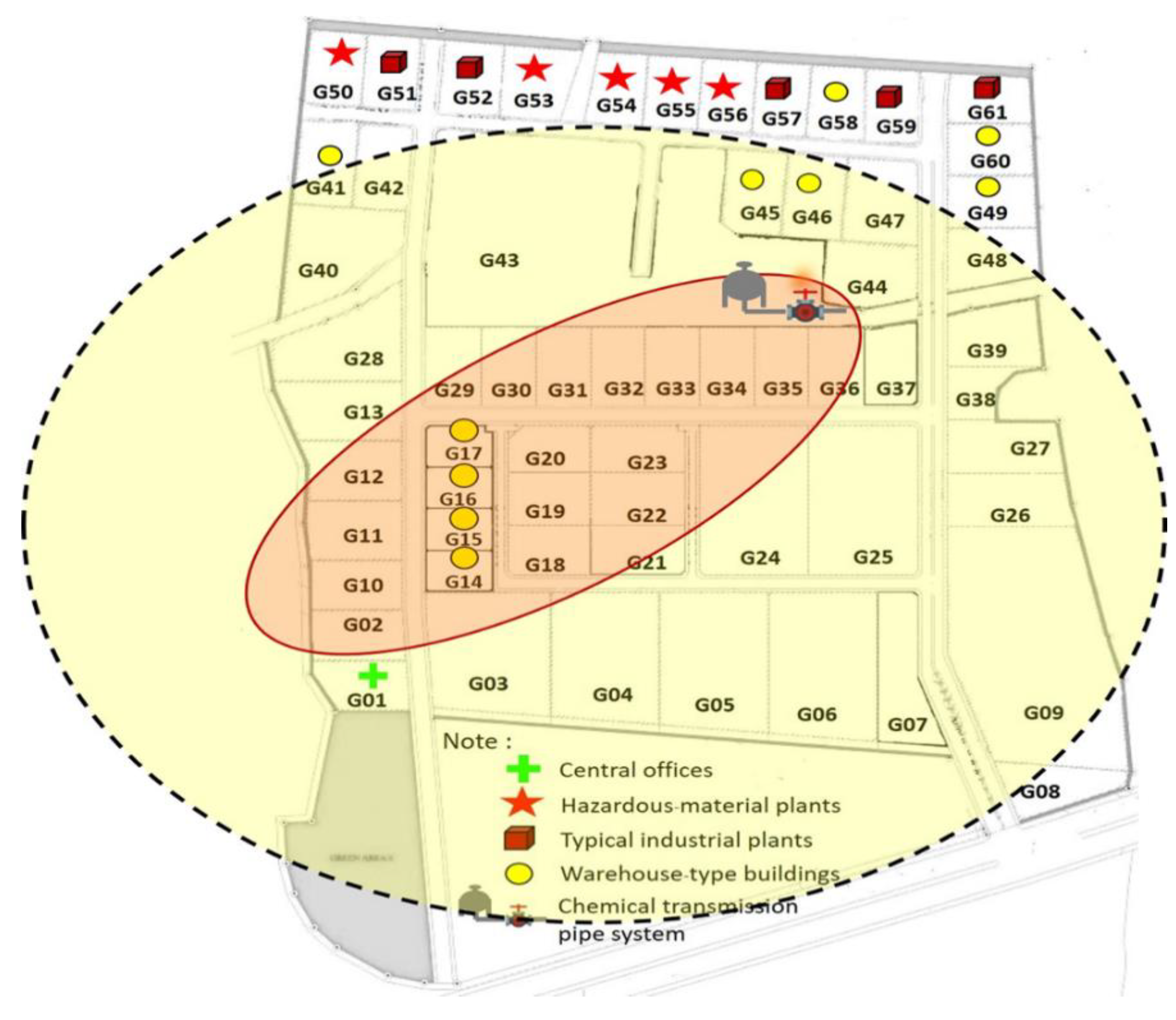
4.1. Case Study
4.2. Results and Discussion
4.2.1. Result from Economic Objective Minimization
4.2.2. Result from Safety Objective Minimization
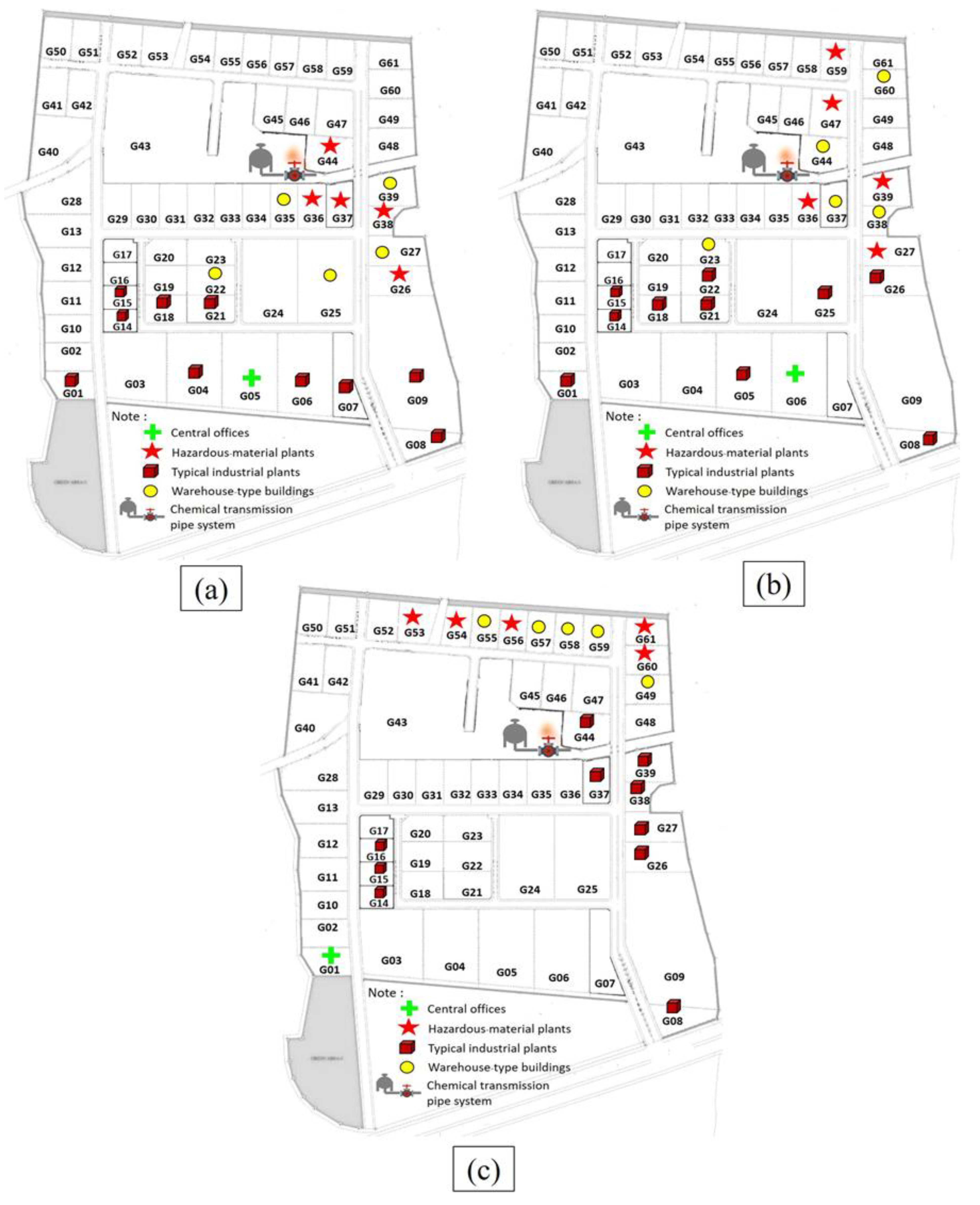
4.2.3. Result from Bi-Objective Optimization
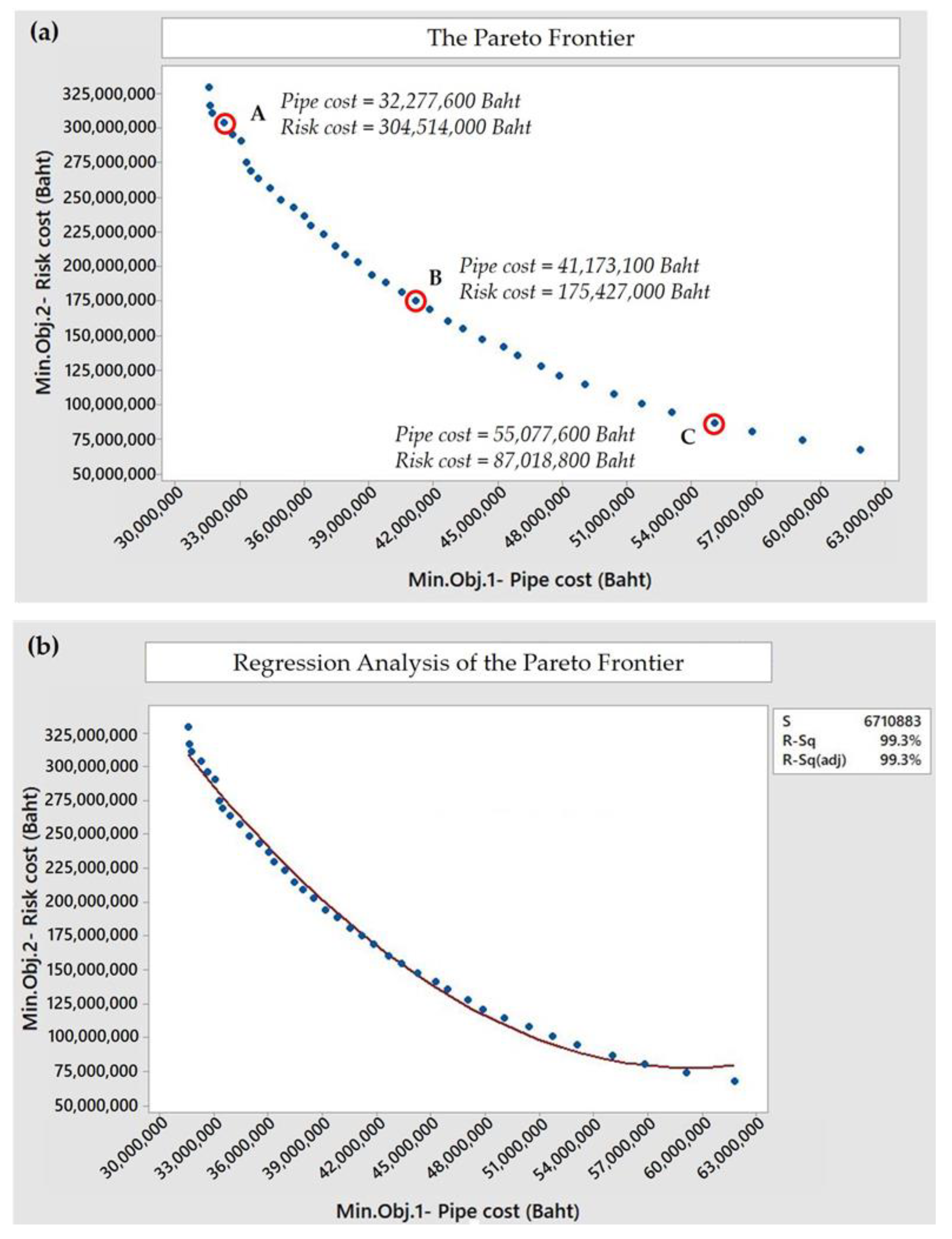
4.2.4. Pareto Frontier Analysis
5. Managerial Insight
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sarkis, J.; Talluri, S. Evaluating and selecting e-commerce software and communication systems for a supply chain. Eur. J. Oper. Res. 2004, 159, 318–329. [Google Scholar] [CrossRef]
- Puchongkawarin, C.; Ransikarbum, K. An Integrative Decision Support System for Improving Tourism Logistics and Public Transportation in Thailand. Tour. Plan. Dev. 2020, 1–16. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Pitakaso, R.; Kim, N. A Decision-Support Model for Additive Manufacturing Scheduling Using an Integrative Analytic Hierarchy Process and Multi-Objective Optimization. Appl. Sci. 2020, 10, 5159. [Google Scholar] [CrossRef]
- Ha, S.; Ransikarbum, K.; Han, H.; Kwon, D.; Kim, H.; Kim, N. A dimensional compensation algorithm for vertical bending deformation of 3D printed parts in selective laser sintering. Rapid Prototyp. J. 2018, 24, 955–963. [Google Scholar] [CrossRef]
- Busogi, M.; Ransikarbum, K.; Oh, Y.G.; Kim, N. Computational modelling of manufacturing choice complexity in a mixed-model assembly line. Int. J. Prod. Res. 2017, 55, 5976–5990. [Google Scholar] [CrossRef]
- Singhal, S.; Kapur, A. Industrial estate planning and management in India—an integrated approach towards industrial ecology. J. Environ. Manag. 2002, 66, 19–29. [Google Scholar] [CrossRef] [PubMed]
- United Nations Conference on Trade and Development (UNCTAD). World Investment Reports 2019: Special Economic Zones; United Nations: Geneva, Switzerland, 2019; Available online: https://unctad.org/ (accessed on 24 February 2020).
- ASEAN Briefing. Special Economic Zones in ASEAN: Opportunities for US Investors. Available online: https://www.aseanbriefing.com/ (accessed on 31 January 2021).
- Industrial Estate Authority of Thailand (IEAT). Annual Report 2018. Available online: https://www.ieat.go.th/ (accessed on 29 December 2019). (In Thai)
- Galbraith, C.; De Noble, A.F. Location decisions by high technology firms: A comparison of firm size, industry type and institutional form. Entrep. Theory Pract. 1989, 13, 31–48. [Google Scholar] [CrossRef]
- Buoro, D.; Casisi, M.; De Nardi, A.; Pinamonti, P.; Reini, M. Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 2013, 58, 128–137. [Google Scholar] [CrossRef]
- Alves, D.T.S.; de Medeiros, J.L.; Ofelia de Queiroz, F.A. Optimal determination of chemical plant layout via minimization of risk to general public using Monte Carlo and Simulated Annealing techniques. J. Loss Prev. Process Ind. 2016, 41, 202–214. [Google Scholar] [CrossRef]
- Hosseinnia, B.; Khakzad, N.; Reniers, G. Multi-plant emergency response for tackling major accidents in chemical industrial areas. Saf. Sci. 2018, 102, 275–289. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Kim, N.; Ha, S.; Wysk, R.A.; Rothrock, L. A highway-driving system design viewpoint using an agent-based modeling of an affordance-based finite state automata. IEEE Access 2017, 6, 2193–2205. [Google Scholar] [CrossRef]
- Chanthakhot, W.; Ransikabum, K. Numerical Simulation for Fire Emergency Planning in a Home Appliances Factory. In Proceedings of the 2019 Research, Invention, and Innovation Congress, Bangkok, Thailand, 11–13 December 2019; pp. 1–5. [Google Scholar]
- Kim, J.; Ransikarbum, K.; Kim, N.; Paik, E. Agent-based simulation modeling of low fertility trap hypothesis. In Proceedings of the 2016 ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, Banff, AB, Canada, 15–18 May 2016; pp. 83–86. [Google Scholar]
- Caputo, A.C.; Pelagagge, P.M.; Palumbo, M.; Salini, P. Safety-based process plant layout using genetic algorithm. J. Loss Prev. Process Ind. 2015, 34, 139–150. [Google Scholar] [CrossRef]
- Chae, J.; Regan, A.C. Layout design problems with heterogeneous area constraints. Comput. Ind. Eng. 2016, 102, 198–207. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Y.; Feng, X. A heuristic approach for petrochemical plant layout considering steam pipeline length. Chin. J. Chem. Eng. 2016, 24, 1032–1037. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Zhu, Q. An improved hybrid genetic algorithm for chemical plant layout optimization with novel non-overlapping and toxic gas dispersion constraints. Chin. J. Chem. Eng. 2013, 21, 412–419. [Google Scholar] [CrossRef]
- Medina-Herrera, N.; Jiménez-Gutiérrez, A.; Grossmann, I.E. A mathematical programming model for optimal layout considering quantitative risk analysis. Comput. Chem. Eng. 2014, 68, 165–181. [Google Scholar] [CrossRef]
- de Lira-Flores, J.A.; Gutierrez-Antonio, C.; Vázquez-Román, R. A MILP approach for optimal storage vessels layout based on the quantitative risk analysis methodology. Process Saf. Environ. Prot. 2018, 120, 1–13. [Google Scholar] [CrossRef]
- Rahman, S.M.T.; Salim, M.T.; Syeda, S.R. Facility layout optimization of an ammonia plant based on risk and economic analysis. Procedia Eng. 2014, 90, 760–765. [Google Scholar] [CrossRef]
- Patsiatzis, D.I.; Knight, G.; Papageorgiou, L.G. An MILP approach to safe process plant layout. Chem. Eng. Res. Des. 2004, 82, 579–586. [Google Scholar] [CrossRef]
- Jung, S.; Ng, D.; Laird, C.D.; Mannan, M.S. A new approach for facility siting using mapping risks on a plant grid area and optimization. J. Loss Prev. Process Ind. 2010, 23, 824–830. [Google Scholar] [CrossRef]
- Han, K.; Cho, S.; Yoon, E.S. Optimal layout of a chemical process plant to minimize the risk to humans. Procedia Comput. Sci. 2013, 22, 1146–1155. [Google Scholar] [CrossRef]
- Ahumada, C.B.; Quddus, N.; Mannan, M.S. A method for facility layout optimization including stochastic risk assessment. Process Saf. Environ. Prot. 2018, 117, 616–628. [Google Scholar] [CrossRef]
- Yoon, K.; Hwang, C.L. Manufacturing plant location analysis by multiple attribute decision making: Part I—Single-plant strategy. Int. J. Prod. Res. 1985, 23, 345–359. [Google Scholar] [CrossRef]
- Wang, R.; Wu, Y.; Wang, Y.; Feng, X. An industrial area layout design methodology considering piping and safety using genetic algorithm. J. Clean. Prod. 2017, 167, 23–31. [Google Scholar] [CrossRef]
- Wattanasaeng, N.; Ransikarbum, K. Cost Optimization Model for Plant Assignment in Industrial Estate Planning. In Proceedings of the 2019 Research, Invention, and Innovation Congress, Bangkok, Thailand, 11–13 December 2019; pp. 1–6. [Google Scholar]
- Wattanaseang, N.; Ransikarbum, K. Sites Selection of industrial estates for Thailand Border’s Special Economic Zones using Data Envelopment Analysis. UBU Eng. J. 2020, 13, 14–26. (In Thai) [Google Scholar]
- Bai, Q.; Labi, S.; Sinha, K.C. Trade-off analysis for multi-objective optimization in transportation asset management by generating Pareto frontiers using extreme points nondominated sorting genetic algorithm II. J. Transp. Eng. 2012, 138, 798–808. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Toro, E.M.; Franco, J.F.; Echeverri, M.G.; Guimarães, F.G. A multi-objective model for the green capacitated location-routing problem considering environmental impact. Comput. Ind. Eng. 2017, 110, 114–125. [Google Scholar] [CrossRef]
- Abounacer, R.; Rekik, M.; Renaud, J. An exact solution approach for multi-objective location–transportation problem for disaster response. Comput. Oper. Res. 2014, 41, 83–93. [Google Scholar] [CrossRef]
- Yu, H.; Solvang, W.D. An improved multi-objective programming with augmented ε-constraint method for hazardous waste location-routing problems. Int. J. Environ. Res. Public Health 2016, 13, 548. [Google Scholar] [CrossRef]
- Ministry of Commerce (MOC). Total Construction Material Price. Available online: http://www.indexpr.moc.go.th/ (accessed on 3 March 2019). (In Thai)
- Thai Appraisal and Estate Agents Foundation (TAEAF). The 2018 Costs of Constructions. Available online: https://www.thaiappraisal.org/ (accessed on 3 March 2019). (In Thai).
- Ransikarbum, K.; Mason, S.J. Multiple-objective analysis of integrated relief supply and network restoration in humanitarian logistics operations. Int. J. Prod. Res. 2016, 54, 49–68. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Mason, S.J. Goal programming-based post-disaster decision making for integrated relief distribution and early-stage network restoration. Int. J. Prod. Econ. 2016, 182, 324–341. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Ha, S.; Ma, J.; Kim, N. Multi-objective optimization analysis for part-to-Printer assignment in a network of 3D fused deposition modeling. J. Manuf. Syst. 2017, 43, 35–46. [Google Scholar] [CrossRef]
- Ransikarbum, K. Decision Analysis for Engineering; Chulalongkorn University Printing House: Bangkok, Thailand, 2021; in press. [Google Scholar]
- Chaiyaphan, C.; Ransikarbum, K. Criteria analysis of food safety using the Analytic Hierarchy Process (AHP)-a case study of Thailand’s fresh markets. In Proceedings of the 2019 Research, Invention, and Innovation Congress, Bangkok, Thailand, 11–13 December 2019; pp. 1–7. [Google Scholar]
- Ransikabum, K.; Yingviwatanapong, C.; Leksomboon, R.; Wajanavisit, T.; Bijaphala, N. Additive Manufacturing-based Healthcare 3D Model for Education: Literature Review and A Feasibility Study. In Proceedings of the 2019 Research, Invention, and Innovation Congress, Bangkok, Thailand, 11–13 December 2019; pp. 1–6. [Google Scholar]
- Xu, J.; Song, X. Multi-objective dynamic layout problem for temporary construction facilities with unequal-area departments under fuzzy random environment. Knowl. Based Syst. 2015, 81, 30–45. [Google Scholar] [CrossRef]
- Tajbakhsh, A.; Shamsi, A. A facility location problem for sustainability-conscious power generation decision makers. J. Environ. Manag. 2019, 230, 319–334. [Google Scholar] [CrossRef] [PubMed]
| Land Category | |||
|---|---|---|---|
| Small | Medium | Large | |
| Land Size | less than 5000 sq.m. | 5001–10,000 sq.m. | more than 10,000 sq.m. |
| Pipe Cost (Baht) [37] | less than 3.5 Million | 3.5–6.0 Million | more than 6.0 Million |
| Risk Cost (Baht) [38] | less than 39.0 Million | 39.0–78.0 Million | more than 78.0 Million |
| Number of Grids | 45 grids | 6 grids | 10 grids |
| Grids | G1, G2, G10, G11, G12, G14, G15, G16, G17, G18, G19, G20, G21, G22, G23, G29, G30, G31, G32, G33, G34, G35, G36, G37, G38, G39, G41, G42, G44, G45, G46, G47, G48, G49, G50, G51, G52, G53, G54, G55, G56, G57, G58, G59, G60, G61 | G7, G8, G13, G26, G27 | G3, G4, G5, G6, G9, G24, G25, G28, G40, G43 |
| Located Plant (Grid) | Pipe Distance (m) | Cost (Baht) | Located Plant (Grid) | Pipe Distance (m) | Cost (Baht) |
|---|---|---|---|---|---|
| P1 (G44) | 400 | 2,078,400 | P12 (G26) | 238 | 1,236,648 |
| P2 (G39) | 388 | 2,016,048 | P13 (G25) | 175 | 909,300 |
| P3 (G35) | 388 | 2,016,048 | P14 (G8) | 276 | 1,434,096 |
| P4 (G34) | 426 | 2,213,496 | P15 (G21) | 326 | 1,693,896 |
| P5 (G37) | 301 | 1,563,996 | P16 (G18) | 388 | 2,016,048 |
| P6 (G36) | 313 | 1,626,348 | P17 (G3) | 351 | 1,823,796 |
| P7 (G38) | 338 | 1,756,248 | P18 (G9) | 126 | 654,696 |
| P8 (G27) | 301 | 1,563,996 | P19 (G4) | 251 | 1,304,196 |
| P9 (G23) | 413 | 2,145,948 | P20 (G5) | 150 | 779,400 |
| P10 (G24) | 276 | 1,434,096 | P21 (G6) | 75 | 389,700 |
| P11 (G22) | 376 | 1,953,696 |
| Plant Located | Risk Probability | Property Damage (Baht) | Plant Located | Risk Probability | Property Damage (Baht) |
|---|---|---|---|---|---|
| P1 (G50) | 0 | 0 | P12 (G60) | 0 | 0 |
| P2 (G51) | 0 | 0 | P13 (G41) | 0.24 | 7,020,000 |
| P3 (G53) | 0 | 0 | P14 (G46) | 0.24 | 7,020,000 |
| P4 (G52) | 0 | 0 | P15 (G49) | 0.24 | 7,020,000 |
| P5 (G54) | 0 | 0 | P16 (G45) | 0.24 | 5,265,000 |
| P6 (G61) | 0 | 0 | P17 (G17) | 0.39 | 5,703,750 |
| P7 (G56) | 0 | 0 | P18 (G16) | 0.39 | 5,703,750 |
| P8 (G57) | 0 | 0 | P19 (G15) | 0.39 | 5,703,750 |
| P9 (G55) | 0 | 0 | P20 (G14) | 0.39 | 5,703,750 |
| P10 (G594) | 0 | 0 | P21 (G1) | 0.24 | 5,850,000 |
| P11 (G58) | 0 | 0 |
| 0% | 25% | 50% | 75% | 100% | |
|---|---|---|---|---|---|
| Z1 value (Baht) | 32,610,100 | 33,509,000 | 38,512,800 | 45,922,200 | 61,827,200 |
| Z2 value (Baht) | 338,386,000 | 269,514,000 | 202,922,000 | 135,354,000 | 67,421,200 |
| Location of hazardous-material plants | P1(G23), P3(G35), P5(G36), P7(G37), P9(G44) | P1(G22), P3(G35), P5(G36), P7(G38), P9(G44) | P1(G27), P3(G36), P5(G39), P7(G47), P9(G57) | P1(G37), P3(G47), P5(G59), P7(G60), P9(G61) | P1(G51), P3(G52), P5(G55), P7(G57), P9(G59) |
| Location of warehouse-type buildings | P2(G24), P4(G27), P6(G34), P8(G38), P10(G39) | P2(G23), P4(G26), P6(G27), P8(G37), P10(G39) | P2(G23), P4(G37), P6(G38), P8(G44), P10(G60) | P2(G36), P4(G39), P6(G44), P8(G57), P10(G58) | P2(G53), P4(G54), P6(G56), P8(G58), P10(G61) |
| Location of typical industrial plants | P11(G3), P12(G4), P13(G5), P14(G8), P15(G9), P16(G18), P17(G21), P18(G22), P19(G25), P20(G26) | P11(G1), P12(G4), P13(G5), P14(G7), P15(G8), P16(G14), P17(G18), P18(G19), P19(G21), P20(G25) | P11(G1), P12(G5), P13(G8), P14(G14), P15(G15), P16(G18), P17(G21), P18(G22), P19(G25), P20(G26) | P11(G8), P12(G14), P13(G15), P14(G18), P15(G21), P16(G22), P17(G23), P18(G26), P19(G27), P20(G38) | P11(G14), P12(G15), P13(G16), P14(G26), P15(G37), P16(G38), P17(G39), P18(G44), P19(G49), P20(G60) |
| Location of a central office | P21(G6) | P21(G6) | P21(G6) | P21(G1) | P21(G1) |
| 20 Plants | ||||
|---|---|---|---|---|
| Epsilon incremental percentage | 25% | 50% | 75% | 100% |
| Computation Time (s) | 5.39 s | 5.53 s | 3.12 s | 2.45 s |
| 40 Plants | ||||
| Epsilon incremental percentage | 25% | 50% | 75% | 100% |
| Computation time (s) | 156.83 s | 225.84 s | 42.93 s | 141.87 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wattanasaeng, N.; Ransikarbum, K. Model and Analysis of Economic- and Risk-Based Objective Optimization Problem for Plant Location within Industrial Estates Using Epsilon-Constraint Algorithms. Computation 2021, 9, 46. https://doi.org/10.3390/computation9040046
Wattanasaeng N, Ransikarbum K. Model and Analysis of Economic- and Risk-Based Objective Optimization Problem for Plant Location within Industrial Estates Using Epsilon-Constraint Algorithms. Computation. 2021; 9(4):46. https://doi.org/10.3390/computation9040046
Chicago/Turabian StyleWattanasaeng, Niroot, and Kasin Ransikarbum. 2021. "Model and Analysis of Economic- and Risk-Based Objective Optimization Problem for Plant Location within Industrial Estates Using Epsilon-Constraint Algorithms" Computation 9, no. 4: 46. https://doi.org/10.3390/computation9040046
APA StyleWattanasaeng, N., & Ransikarbum, K. (2021). Model and Analysis of Economic- and Risk-Based Objective Optimization Problem for Plant Location within Industrial Estates Using Epsilon-Constraint Algorithms. Computation, 9(4), 46. https://doi.org/10.3390/computation9040046






