An Elaborate Preprocessing Phase (p3) in Composition and Optimization of Business Process Models

Abstract

Business process optimization (BPO) has become an increasingly attractive subject in the wider area of business process intelligence and is considered as the problem of composing feasible business process designs with optimal attribute values, such as execution time and cost. Despite the fact that many approaches have produced promising results regarding the enhancement of attribute performance, little has been done to reduce the computational complexity due to the size of the problem. The proposed approach introduces an elaborate preprocessing phase as a component to an established optimization framework (bpoF) that applies evolutionary multi-objective optimization algorithms (EMOAs) to generate a series of diverse optimized business process designs based on specific process requirements. The preprocessing phase follows a systematic rule-based algorithmic procedure for reducing the library size of candidate tasks. The experimental results on synthetic data demonstrate a considerable reduction of the library size and a positive influence on the performance of EMOAs, which is expressed with the generation of an increasing number of nondominated solutions. An important feature of the proposed phase is that the preprocessing effects are explicitly measured before the EMOAs application; thus, the effects on the library reduction size are directly correlated with the improved performance of the EMOAs in terms of average time of execution and nondominated solution generation. The work presented in this paper intends to pave the way for addressing the abiding optimization challenges related to the computational complexity of the search space of the optimization problem by working on the problem specification at an earlier stage.

1. Introduction

A business process is perceived as a collective set of tasks that when properly connected perform a business operation [1]. The composition of candidate tasks—that can be individual web services—in a business process can provide cost saving opportunities as seen in web service mashups, etc., [2,3]. Moreover, the utilization of evolutionary techniques in business processes has shown the potential of generating a population of diverse business process designs based on specific process requirements. A rounded approach in business process redesign should decisively capture the business process (business process modelling), provide all necessary means for bottleneck identification and performance analysis and, finally, generate alternative improved business process models based on specified objectives. Most often, the last part (business process redesign) is overlooked—if not completely neglected [4]. There are only a few approaches in relation to composition and multi-objective optimization of business processes that either use complex mathematical models or assume a fixed design for the process and optimize only the participating tasks. Business process optimization is among the key research areas that provide a formal perspective towards the concept of business processes. The approach presented in this paper builds upon a multi-objective evolutionary framework for business process models [5] and an initial preprocessing approach [6] that demonstrates promising results. This paper introduces an elaborate and improved preprocessing phase (p3) with the aim of further increasing the efficiency of the business process composition and optimization algorithms. The remainder of this paper is structured as follows: Section 2 presents the related work in the field of business process composition and optimization; Section 3 discusses the formulation of the business process optimization problem; Section 4 introduces the p3 preprocessing stage; and Section 5 details the experimental results and measures the effect of the p3 addition compared to the current framework performance.

2. Related Work

Business process optimization (BPO), as a formal approach for improving business processes, has not received the necessary attention in the literature in terms of business process modelling and analysis techniques due to its requirement for formal techniques. On the contrary, soft approaches for restructuring and redesigning business processes are more frequent as they are more straight-forward. In the past decade, businesses have also gradually shifted their interest from obtaining gradual, incremental improvements through BPO to the more radical change and dynamic improvement achieved through business process redesign (BPR) ([7,8]). The emergence of BPR stems from the need to be adaptable to the evolving organizational change by applying various techniques and approaches towards modifying the process design, depending on the feedback of the process run-time, and/or the performance attributes [9]. The prospect of continuously modifying and improving the various business operations highlighted BPR as a central part of business process management (BPM) [10] and is embodied in most BPM lifecycles (e.g., in Mendling et al. [11] and Szelągowski [12]). Regardless of the rigorousness of the process initial design and modeling phase, the need for process refinement stems from the need to (a) cope with the continuously evolving internal and external setting in which an organization operates [1] and (b) keep pace with the changing end-user requirements. Process redesign is not defined explicitly, but through the context it refers to, or its objectives. Brocke and Rosemann [13] assert that process redesign aims at improving nonfunctional requirements, and more specifically, the process performance.

According to Dumas et al. [14], the two methods for systematically redesigning processes are (a) Heuristic Process Redesign, a method that builds upon an extensive set of redesign options, and (b) product-based design, which derives a process design based on the composition of a product. For Heuristic Process Redesign, Dumas et al. [14] identify the full list of twenty nine heuristics from [15] and classify them into seven distinct categories: customers, BP operation, BP behavior, organization, information, technology, and external environment. In a later work, Dumas et al. [16] present the performance criteria of the devil’s quadrangle that each heuristic explicitly targets. Each heuristic can also improve other performance metrics that are not evident because they are not primarily targeted. Although a detailed analysis of a BP typically sparks assorted ideas and perspectives for redesign, it is usually contacted in a nonsystematic way, and is predominantly considered a creative activity [17]. To date, only a few redesign approaches in the literature investigate how the improvement procedure can be methodologically supported or executed to reduce the uncertainty from the AS-IS to the TO-BE process [18]. Moreover, Valiris and Glykas [19] claim that most of the business process re-engineering methodologies lack the formal underpinning to ensure the logical consistency of the generation of improved business process models. With business process redesign projects, the task of developing optimal designs of business processes is left to the designer’s intuition [4]. BPO, on the other hand, lies on the other end of the spectrum and can provide a formal approach towards improving a business process based on predefined criteria. Evolutionary techniques use the principles of evolution to guide the optimization process and have been effectively applied to several combinatorial problems. Genetic algorithms (GAs), have already been used to find solutions to scheduling problems and their variants [4]. According to Moon and Seo [20], the most attractive feature of evolutionary algorithms is the flexibility of handling various kinds of objective functions with a few requirements regarding mathematical properties. Evolutionary optimization has been applied to business processes and has discovered process designs that have been overlooked by a human designer [21]. In addition, these techniques can evaluate a significant number of alternative designs based on the same configuration and determine the fittest based on specific objectives. However, Wang et al. [22] note that process optimization is a difficult task due to the nonlinear, nonconvex, and often discontinuous nature of the mathematical models involved.

Regarding business processes, the evolutionary approaches reported are limited. Hofacker and Vetschera [4] have attempted to transform and optimize a business process model using GAs, but they report unsatisfactory results. Tiwari et al. [23] and Vergidis et al. [24] extended this mathematical model and applied multi-objective optimization algorithms, such as the NSGA-II and SPEA2 and report satisfactory results that provide encouraging opportunities for further investigation. Towards the same direction, Ahmadikatouli and Aboutalebi [25] proposed a novel algorithmic approach to optimize business processes, modelled with Petri-nets, through involving a variety of issues to determine the optimum model, such as cost, time, and quality of products. In a similar approach introduced by Wibig [26] involving Petri-nets, business process scalability and a dynamic programming concept were used to produce measurable results regarding the reduction of necessary computations. The application of such algorithms has further been used in determining the preferable process paths for selected criterions in the course of workflow map evaluation [27]. Vergidis et al. [28] introduced the concept of composite business processes. This approach also involved evolutionary multi-objective optimization and focuses on the tasks that compose a business process rather than the business process design itself.

The business process multi-objective optimization problems belong to the np-hard problems [29]; thus, the efficiency of the optimization algorithms and the quality of the produced results highly depend on the size of the examined problem. Generally, business processes can have too many available alternatives for the participant tasks, and these in turn can involve many different resources as requirements or as products of their utilization. Consequently, the process of seeking for the set of the alternative nondominated optimal business process designs by an algorithm can be extremely difficult because of the vast amount of the combinations that must produce and evaluate. In addition, the solution of np-hard problems, like business process optimization problems, is often approached by heuristic methods that try to find solutions which approximate the optimal ones instead of exact algorithms. Heuristic methods may have a time limit to their execution or a limit to the evaluations that will take part during their execution. When these methods are applied after dataset cleansing, i.e., after the act of removing faulty or unnecessary data, they produce better quality results leading to near-optimal solutions. This procedure is equivalent to data preparation e.g., in process optimization using intelligent process prediction [30] and multi-objective shipment allocation [31], where invalid samples with missing or incorrectly recorded information are excluded from the training samples set. This data preparation procedure involving data preprocessing, cleansing, aggregation, and segmentation is an integral prerequisite—as in most data science and knowledge processes—towards facilitating the execution of algorithms. Most of the algorithms that are considered evolutionary algorithms have limits within their execution related to the number of evaluations or generations that will take part in their execution cycle or with the population size that they manage. An interesting approach focusing on the importance of the population initialization on the solutions resulting from an evolutionary multi-objective optimization (EMOO) is presented in [32]. Mahammed et al. propose the use of a multicriteria decision analysis method and an EMOO framework to sort or classify the initial population. The experimental results are promising in the sense that the proposed framework is capable of producing an acceptable number of optimized design alternatives regarding the problem complexity and in a reasonable period. The benefits of using a multicriteria decision analysis method within a genetic algorithm for BPO are also evident in [33]. The experimental results clearly demonstrated that using a multicriteria decision-analysis method provably facilitates the production of qualitatively interesting alternative solutions in a short period time, a fact that ultimately assists in the decision-making procedure. Current trends in BPM accentuate BPR and BPO as the initiatives for rethinking and re-organizing business processes with the specific purpose of making them perform better. In the light of the aforementioned issues in BPO, the authors attempted to produce business process designs that conform to the problem specification, adding an initial form of preprocessing to investigate whether the task alternatives can provide feasible solutions [6]. The results demonstrate that the framework—with the aid of a preprocessing stage—increased its capability of generating diverse designs and selecting those with optimal objective values for business processes in a reduced amount of time, suggesting a more elaborate investigation. This paper presents the p3 extension of the bpo^F business process optimization framework [21] that includes a more thorough preprocessing stage, as discussed in Section 4. The p3 preprocessing stage builds upon the work in [6] and aims to further enhance the performance of the evolutionary multi-objective optimization algorithms (EMOAs) in relation to the BPO problem.

3. Task Composition and Optimization of Process Designs

This work is built upon the evolutionary multi-objective optimization framework for business process designs (bpo^F) presented in [5] and elaborated in [34,35]. The framework applies state-of-the-art EMOAs to given business process requirements to (i) compose feasible designs utilizing a library that contains a multitude of candidate tasks and (ii) locate the optimal solutions based on multiple criteria. Table 1 shows the main parameters of the business process optimization problem.

Table 1. Parameters of the business process design composition and optimization problem as presented in [5].

Parameter	Description	Parameter	Description
n	No. of candidate tasks in the library	N = {t1, t2, …, tn}	Set of all candidate tasks
nd	No. of tasks in a process design (nd ≤ n)	Nd = {t1, t2, …, tnd}	Set of the nd tasks in a design
rall	No. of available resources	R = {r1, r2, …, rall}	Set of all available resources
rin	No. of process input resources (rin ≤ r)	Rin = {r1, r2, …, rout}	Set of the process input resources
rout	No. of process output resources (rout ≤ r)	Rout = {r1, r2, …, rin}	Set of the process output resources
pall	No. of task/process attributes (pall ≤ 2) *	PAd = {p1, …, pall}	Set of the process attribute values for a particular design
tin	No. of task input resources **	I	Set of the tin resources for a task i
tout	No. of task output resources **	O	Set of the tout resources for a task i
TAnp	Two-dimensional array with the task attribute values **

* at least bi-objective optimization problem; ** for all candidate tasks.

For each candidate task in the library, there are p_all available measurable (quantitative) performance indicators, i.e., task attributes such as task execution cost and task duration. The TA_np task attributes are mapped to corresponding PA_d process attributes (e.g., process cost) using aggregate functions that form the optimization objectives. The available resources (r) are assimilated based the input and output resources of all the candidate tasks in the library. The nature and the type of the resources are not considered in this work. The task resources connect the tasks, forming the process design. Additionally, the resources shape the requirements for a process design by denoting the required process input and expected process output. A feasible business process design is one that starts with the resources in R_in and by properly connecting available tasks produces the requested R_out resources. The composition of a business process design is considered a computationally expensive procedure, especially in the case of increased infeasibility due to constraints [35]. To address this challenge, the Process Composition Algorithm (PCA), described in [34], scrutinizes the task library and attempts to identify and composes feasible process designs, given the problem specification. After producing a set of feasible business process designs, the process attribute values are calculated for each design based on aggregate functions. Each process attribute can either be subjected to maximization or minimization depending on its nature. The bpo^F aims at locating the designs with the optimal process attribute values. To achieve the design composition and optimization, the framework requires four inputs, as shown in Figure 1.

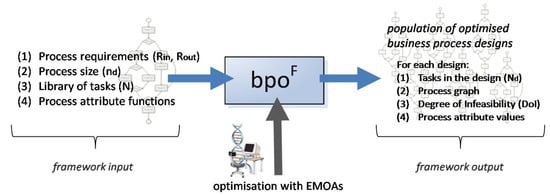
Figure 1. The inputs and outputs of the bpo^F [5].

• The process requirements for the design are the required process inputs (R_in) and process outputs (R_out). All of the generated designs consume the same inputs and produce the same outputs.
• The process size (n_d). The process size denotes the number of participating tasks in the process designs.
• The library of tasks (N). This set contains all of the candidate tasks that can participate in a process design.
• The process attribute functions for each quantitative process attribute. These functions are the optimization objectives.

The outcome of the framework is a population of feasible optimized business process designs. For each design, the framework produces the following (Figure 1):

• The tasks in the design, stored in the N_d set.
• The process graph, which is the diagrammatic representation of the design.
• The degree of infeasibility, a penalty function for infeasible designs (equals to zero for feasible solutions).
• The process attribute values of each feasible optimized design.

Given the problem formulation, design composition and optimization are not structured as a typical optimization problem with a set of objective functions and specific formulated constraints. They represent a discrete problem, as the main variable is a set of tasks (N_d) that form the business process design. In addition to the discrete nature of the problem, the authors assumed a multi-objective nature, and the participating objectives are conflicting; thus, each solution represents a different trade-off between the objectives. For the constrains to be checked, the framework employs an algorithmic procedure (PCA) before the objective functions (i.e., process attribute values) can be calculated for a feasible solution. As a result, the EMOAs employed by the framework have a series of challenges to address when generating the Pareto optimal front of solutions across the objectives. The discrete nature of the problem in conjunction with its multi-objective formulation can make the process of discovering feasible solutions very difficult for the algorithms [35]. During the optimization process, each EMOA has a three-fold task:

• To identify and preserve feasible solutions;
• To converge these solutions towards optimal;
• To maintain diversity of the solutions across the Pareto front.

A strategy to reduce the computational complexity of the problem is to reduce the number of candidate tasks that can participate in a solution by identifying and eliminating those that are redundant given the problem formulation, as demonstrated in the authors’ initial work [6]. The next section introduces the p3 preprocessing phase in an attempt to thoroughly elaborate the above-mentioned strategy and improve the performance and quality of results of the optimization framework.

4. The p3 Preprocessing Phase

When dealing with optimization problems, challenges emerge from the computational complexity, such as the excessive execution time and the high memory usage [36]. A common practice in those situations is the development of a preprocessing stage for the reduction of the amount of data to be processed in the solution through (a) the elimination of unnecessary information that comes from the problem itself or by (b) removing the faulty values of the dataset according to the problem. This section extends and solidifies the preprocessing algorithms for business process design composition and optimization initially presented in [6]. The inputs, outputs, and steps of the p3 preprocessing are shown in Figure 2. The aim of the p3 stage is to increase the efficiency of the composition and optimization algorithms using a two-fold strategy: (i) examination of the scenario validity of a given problem, and, (ii) investigation of the task eligibility for each of the candidate tasks.

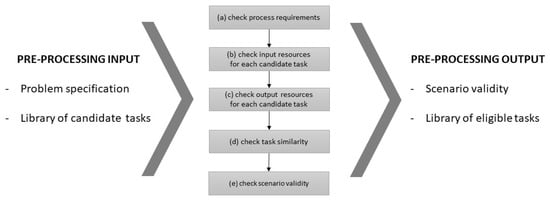
Figure 2. The inputs, outputs, and steps of the preprocessing phase (p3) algorithms.

The scenario validity criterion examines whether a problem specification can generate feasible solutions based on the given dataset (i.e., library of candidate tasks). The process requirements may not be appropriate for the given library of tasks in two cases: (i) the process input resources are not consumed by any task in the library, and/or (ii) at least one process output resource cannot be produced by any task in the library; hence, no feasible designs can be produced. In the case of unsuccessful validation of a particular problem specification, the job of composing and optimizing business process designs is not initiated, thus saving computational resources.

The task eligibility criterion ensures that the dataset contains eligible tasks that can contribute toward a feasible process design by removing redundant tasks following a set of elimination rules:

• Tasks that require input resources that are part of the process output (steps a, e);
• Tasks that produce output resources that are required in the process input (steps a, e);
• Tasks with input resources that are not required in the process input or in any other task output to connect to (step b);
• Tasks with output resources that do not exist in process output or in any other task input to connect to (step c);
• Tasks with identical input and output resources that are dominated in all their attribute values by an equivalent task (step d).

Once redundant tasks are located during one step, they are eliminated from the library so that it contains only eligible tasks at any given time. Initially, all the tasks in library are considered eligible to participate in the process design. The aim of each rule is to locate ineligible tasks and remove them, thus transforming the library of candidate tasks to a smaller and less computationally expensive library of eligible tasks. The steps of the preprocessing phase are shown in Figure 2 and are implemented by the presented algorithms.

4.1. Check Process Requirements (Input and Output Resources)

The first step deals with the scenario validity aspect of the preprocessing phase and compares the process requirements with the available tasks in the library in the following ways: (i) tasks whose set of output resources is a subset of the set of process input resources and (ii) tasks whose set of input resources is a superset of the set of the process output resources, which cannot be part of a feasible process design. This step explores the task library T and removes ineligible tasks creating the T’ library with eligible tasks only, as described by Algorithm 1.

Algorithm 1 Check process requirements

Require: T = {t1, …, tn}, a set of n tasks, Rin, a set of process input resources from the available resources, Rin ⊆ R Rout, a set of process output resources from the available resources, Rout ⊆ R Ensure: T’ ⊆ T, a set that contains eligible tasks based on this step’s requirements 1://Iterate on T 2: For each ti task ∈ T 3:    if Oi ⊄ Rin then insert ti in T’ 4:    else if Rout ⊄ Ii then insert ti in T’ 5: return T’

4.2. Check Individual Task Input Resources

The second step is concerned with task eligibility and seeks to eliminate tasks that have at least one input resource that cannot be matched with a process input resource or connected with an output resource of a previous task in the design. Algorithm 2 demonstrates the transformation of the initial T library of tasks to the new T’ library with eligible tasks. To ensure task connectivity, tasks with interconnecting input and output resources are added to the library, whereas tasks whose input resources cannot be connected are considered ineligible.

4.3. Check Individual Task Output Resources

As the previous step examined the individual input resources of the candidate tasks, this step concerns locating the tasks in the library that have least one output resource that cannot be matched with a process output resource or connected with a subsequent input resource of another task. Candidate tasks whose output resources cannot be connected are considered ineligible (see Algorithm 3). There is a significant difference between steps (b) and (c). For step (b), a single unsatisfied input resource is enough for the task to become ineligible, whereas for step (c), a task is considered ineligible only if all of its output resources cannot be connected. This is due to the hard constraint that all the input resources of task must be available before execution.

Algorithm 2 Check individual task input resources

Require: T = {t1, …, tn}, a set of n tasks, Rin, a set of process input resources from the available resources, Rin ⊆ R Ensure: T’ ⊆ T, a set that contains eligible tasks based on this step’s requirements 1: //Iterate on T 2: For each ti task ∈ T, iterate on its set of input resources Ii 3:    if Ii ⊆ Rin then insert ti in T’ 4:    else for each tj ≠ ti task ∈ T, 5:       iterate on its set of output resources Oj 6:          if Ii ⊆ Oj then insert ti, tj in T’ 7: return T’

Algorithm 3 Check individual task output resources

Require: T = {t1, …, tn}, a set of n tasks, Rout, a set of process output resources from the available resources, Rout ⊆ R Ensure: T’ ⊆ T, a set that contains eligible tasks only 1: //Iterate on T 2: For each ti task ∈ T, iterate on its set of output resources Oi 3:    if Oi ⊆ Rout then insert ti in T’ 4:    else for each tj ≠ ti task ∈ T, 5:       iterate on its set of input resources Ij 6:          if Oi ⊆ Ij then insert ti, tj in T’ 7: return T’

4.4. Check Task Similarity

The aim of this preprocessing step is to locate similar tasks, i.e., tasks with identical input and output resources, and eliminate the suboptimal ones based on task attribute values and the problem specification objectives.

Algorithm 4 showcases the two parts of this procedure. During the first part, similar tasks are classified into distinct categories. The tasks of a specific category have identical sets of input and output resources. Each of these categories is traversed during the second part to locate and remove the suboptimal tasks, i.e., the tasks whose attribute values are dominated by other tasks of the same category considering the problem specification. In cases where two or more tasks have equivalent or competing attribute values, they are preserved in the library of eligible tasks.

Algorithm 4 Check task similarity

Require:    T = {t1, …, tn}, a set of n tasks,    PAnm, a two-dimensional matrix containing for each of the n tasks, their m attribute values Ensure:    T’ ⊆ T, a set that contains eligible tasks only 1: j = 1 2: //Iterate on library of candidate tasks T 3: For each ti task ∈ T 4:    if ti does not belong to an existing category Sj then 5:       create category Sj 6:       j = j + 1 7:    add ti in Sj 8: //Iterate on k task categories 9: For j in (1, k) 10:    For each ti task ∈ Sj 11:     if PAi dominate or are equivalent to the attribute values of other tasks in Sj then 12:          insert ti in T’ 13: return T’

4.5. Check Scenario Validity

The previous preprocessing steps altered the library of the candidate tasks by eliminating those deemed ineligible, but this can also have an effect on whether a scenario can be solved with the reduced task library. The last step performs a final check on whether the library of eligible tasks—as produced by steps (a) through (d)—can lead to feasible process designs. This step can save time and effort by discouraging redundant design composition and optimization attempts in cases of obvious infeasibility. This step (Algorithm 5) checks if the process input resources can be linked to the input resources of the eligible tasks and if the process output resources can be matched to the output resources of the eligible tasks. The result of this step is a Boolean variable denoting whether the optimization phase should be executed or if the library of eligible task cannot produce feasible solution based on the problem specification.

Algorithm 5 Check scenario validity

Require: T = {t1, …, tn}, a set of n tasks, Ι = {r1, …, rn}, a set of m input resources of the n tasks in the library, I ⊆ R O = {r1, …, rk}, a set of k output resources of the n tasks in the library, O ⊆ R Rin, a set of process input resources from the available resources, Rin ⊆ R Rout, a set of process output resources from the available resources, Rout ⊆ R Ensure: return True or False based on whether a scenario is feasible or not 1: Scenario_validity = True 2://Iterate on the process input resources Rin 3: For each ri resource ∈ Rin 4:    if ri ∉ I then 5:       Scenario_validity = False 6://Iterate on the process output resources Rout 7: For each ri resource ∈ Rout 8:    if ri ∉ O then 9:       Scenario_validity = False 10: return Scenario_validity

5. Creating Experimental BP Scenarios

The lack of reference test problems in relation to business process optimization is acknowledged in the relevant literature [37] both in terms of real-life scenarios and also in complex experimental problems that push the boundaries of the optimization algorithms. Due to the fact that there is no established task library from real-life scenarios for the bpoF framework and the specific parameters, the experimentation is performed on synthetic data, i.e., datasets that were created by the authors and were utilized in previous experimentation with the framework. These experimental scenarios were generated as business process optimization problems in terms of problem requirements—composing and optimizing a business process using a library of tasks given the input and output process requirements [35].

The employment of synthetic datasets is a common approach in scientific research, supported by the fact that synthetic datasets have proved to reflect the properties of original datasets in many cases [38,39]. To better manage the generation and validation of these synthetic datasets, previous work by the authors applied the Design of Experiments (DOE) statistical method [40] to systematically investigate the BPO problem variables. Through a series of scalable business process tests, the authors determined (a) the variable values and limits for which the bpoF generates consistent results; (b) the variables bearing a significant influence on the bpoF results; (c) the magnitudes of the biggest influences; and (d) the involvement proportion of n, r, and n_d variables on the bpoF results. This approach proved an effective method to analyze and interpret the optimization results and a valuable strategy to design the experiments and collect data.

Table 2 and Table 3 show the parameters for the scenarios (A, B, C) that the application of the DOE method determined as those bearing a significant influence on the bpoF results, and these were also tested with the original preprocessing stages for comparison. In the current work, the authors provide two additional scenarios (D, E) that further push the limits of the task library—including up to 3000 candidate tasks. For each scenario, we utilized the same dataset (i.e., library of tasks with known attribute values and input and output resources) as in [6]. The dataset is produced by randomly assigning attribute values to each task in the library given their minimum and maximum attribute values (Table 2). Moreover, the input and output resources for each task are randomly assigned to ensure significant number of variations and task combinations. Each scenario has a progressively larger library size to better assess both the p3 effectiveness in library reduction and the EMOAs’ performance. The problem is set up to minimize attribute 1 and maximize attribute 2. These attributes can reflect process cost, time of execution, etc.

Table 2. Problem parameters for the five scenarios.

Parameter	Scenarios A–E
nd	15
nmin	11
r	30
tin/tout	2/2
rin/rout	2/2
p	2
(min) Attribute1	100–200
(max) Attribute2	300–400

Table 3. Size of the task library for the five scenarios.

Parameter	Scenario A	Scenario B	Scenario C	Scenario D	Scenario E
n	100	500	1000	2000	3000

6. Experimental Results

The bpo^F framework is well established and has been utilized both by the authors [5] and [6,35] and other researchers [41,42] with significant findings both for business process optimization and the performance of the EMOAs. The initial addition of preprocessing presented in [6] increased the capability of the framework in generating diverse designs and selecting those with optimal objective values for business processes in reduced time. The original bpo^F framework is programmed using Java [43]; thus, the preprocessing algorithms described in the previous section were also deployed in the existing codebase. Two of the libraries (jMetal and jGraphT) are open-source and available online, and the third was developed for the purpose of the framework including the implementation of the improved (p3) preprocessing algorithms.

6.1. Scenario Validity

Given the dataset for each scenario, we proceeded with an initial scenario validity check to ensure that the problem specifications (Table 2 and Table 3) can generate feasible solutions based on the given libraries of candidate tasks. Initially, all five scenarios passed the validity check, meaning that for each scenario, feasible solutions can be produced by applying the problem parameters to the relevant dataset. Once the library of candidate tasks transforms to library of eligible tasks, the scenario validity algorithm needs to run again prior to applying EMOAs.

6.2. Task Elimination and Library Reduction

A significant limitation in [6] is that the effects of preprocessing stages are not explicitly measured before the EMOA application; thus, the effects on the library reduction size are not directly correlated with the improved performance of the EMOAs in terms of average time of execution and nondominated solution generation. In this work, the authors explicitly measured the size of the task library before and after the p3 application. To validate the results, the p3 algorithms were applied in the respective scenario datasets both in the bpo^F framework and manually in a spreadsheet where all the task attributes and input and output resources are generated. Table 4 shows the results in terms of library size reduction for each of the five scenarios.

Table 4. Measuring the effects of p3 in library sizes.

	Library of Candidate Tasks (before p3)	Library of Eligible Tasks (after p3)	Eliminated Tasks (Absolute/%)
Scenario A	100	78	22/22%
Scenario B	500	396	104/20.8%
Scenario C	1000	746	254/25.4%
Scenario D	2000	1553	447/22.35%
Scenario E	3000	2437	563/18.77%
	average library size reduction (%):		21.86%

On average, more than 20% of the tasks originally in the library were eliminated. This means that the composition algorithm has 20% less workload to take into account. This is considered a significant reduction in the library size, and it is expected to positively influence the performance of the EMOAs as they have less work to do in terms of discovering feasible solutions and maintaining the optimal ones for each scenario. Interestingly, the percentage of eliminated tasks was not linearly increasing with larger library sizes. This suggests that the library tasks remain largely varied and competitive in their attribute values despite the increasing larger library size. In scenarios where the tasks are increasingly similar, p3 can achieve even larger elimination percentages, thus significantly reducing the task library size and producing less computationally challenging optimization problems.

6.3. bpoF Performance

After preprocessing the library of tasks, the optimization framework is expected to increase its performance in terms of quality of solutions. In this work, the framework was operated only with NSGA-II since it appears to provide similar results with the other EMOAs (SPEA2, PESA2, and PAES) [6,35]. To achieve task composition and design optimization, NSGA-II needs to achieve two goals: (i) converge to the Pareto-optimal front (for obtaining optimal business process designs) and (ii) maintain the population diversity across the front (for obtaining a variety of different sizes of business process designs). With the inclusion of the p3 algorithms, the framework is expected to increase the number of nondominated solutions compared to the original bpo^F [35] and the bpo^Fwp [6]. Figure 3 shows the number of nondominated solutions produced by NSGA-II for the different variations of bpo^F. There was a significant increase in the framework performance for the scenarios A, B, and C, while for scenarios D and E, both versions of preprocessing located the exact number of nondominated solutions. Given that most real-life scenarios tend to be closer to scenarios A–C, the results show a respectable shift in the quality and variation of the produced solutions. Regarding the larger library sizes, the framework operated as expected in terms of composition and optimization as previously discussed. It is speculated that for the newly introduced scenarios D and E, despite the 20% reduction in library tasks with the p3, their post-processing size is still computationally expensive for NSGA-II; thus, it cannot operate more efficiently than before.

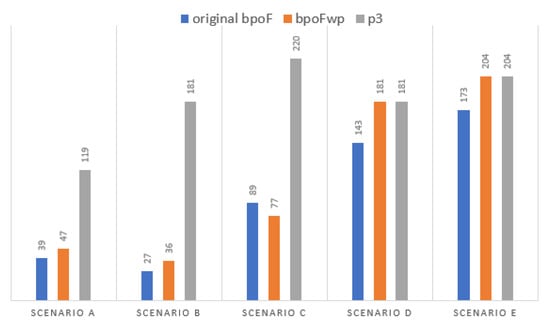
Figure 3. Number of nondominated solutions for different versions of the bpo^F.

In previous works [6], the time required for the preprocessing stage was not taken into account for assessing the overall framework’s performance. Instead, only the time it took EMOAs to produce the results was reported and compared. The authors acknowledge this inaccuracy now that the p3 is embedded into the framework. Figure 4 shows the time it took the framework to generate nondominated solutions with the NSGA-II. However, only in the case of p3 was the time of preprocessing also taken into account, thereby explaining the increased time frames. The p3 algorithms were executed once per scenario but required a fair amount of time before the composition and optimization process. The authors assert that although there is a visible increase in execution time, the overall times are still competitive as they remain well below one minute for their total duration.

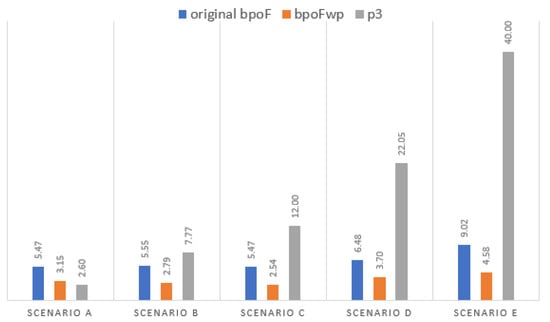
Figure 4. Time (in seconds) for the generation of nondominated solutions.

7. Discussion and Conclusions

This paper presents an elaborate preprocessing phase (p3) for the composition and optimization of business process models that examines the scenario validity of a given problem and the eligibility of candidate tasks. This is achieved in a rule-based and systematic manner with the implementation of a set of algorithms introduced in this work. The purpose of the preprocessing phase was to reduce the amount of data to be processed in the solution through (a) the elimination of unnecessary information that comes from the problem itself and (b) the removal of faulty values of the dataset according to the problem. The results demonstrate an average library size reduction of 21.86% for the five selected scenarios, meaning that the composition algorithm has 20% less workload to take into account and is expected to positively influence the performance of the EMOAs. This expectation is showcased in the experimental results, where the number of nondominated solutions using the p3 version of the optimization framework is significantly larger for the first three scenarios and is relatively stable for the last two scenarios that are still computationally expensive for the NSGA-II. Regarding time for the generation of nondominated solutions, there was an increase in execution time, but the overall times are still competitive as they remain well below one minute of total duration, even for libraries comprised of 3000 candidate tasks. An important contribution of this paper is that it tackles a significant limitation of the preprocessing phase presented in [6], where the effects of preprocessing stages are not explicitly measured before the EMOA application; thus, the effects on the library reduction size are not directly correlated with the improved performance of the EMOAs in terms of average time of execution and nondominated solution generation. In this work, the authors explicitly measure the size of the task library before and after p3 application. A limitation of the presented approach is that the preprocessing phase is applied to a synthetic dataset that emulates real-life business processes. As a future work, the authors intend to use process execution data, particularly records of events corresponding to the execution of activities (event logs), and justify the contribution of preprocessing through extensive experimentation. The authors are also working on even larger library sizes for experimental application to investigate the robustness of the preprocessing phase (p3) in terms of library reduction and performance of EMOAs. Other research works in progress involve the impact analysis of the different preprocessing steps and the investigation of the parameters that affect preprocessing times, e.g., the execution of varying EMOAs. Taking into account the advancements in evolutionary computation, the authors also intend to test the p3 phase and the optimization framework using contemporary EMOAs, such as bat-based algorithms [44], the lion optimization algorithm [45], and the Wolf Search Algorithm [46]. In conclusion, the goal of the work presented in this paper is to pave the way for addressing the abiding optimization challenges related to computation expenses and search space of the optimization problem by working on problem specification at an earlier stage.