Plasma Confined Ground and Excited State Helium Atom: A Comparison Theorem Study Using Variational Monte Carlo and Lagrange Mesh Method
Abstract
:1. Introduction
2. Plasma Model Potentials
3. Variational Monte Carlo Method
4. Theoretical Details
5. Trial Wave Functions for the Low-Lying Excited States of the Helium Atom
- 1.
- For the lowest ortho (space-antisymmetric) state 2, corresponding to the configuration 1s2s, we considered the following simple trial wave function
- 2.
- The state 2 is a para (space-symmetric) state corresponding to the configuration 1s2s and its trial wave function is, then, taken of the form
6. Lagrange Mesh Method
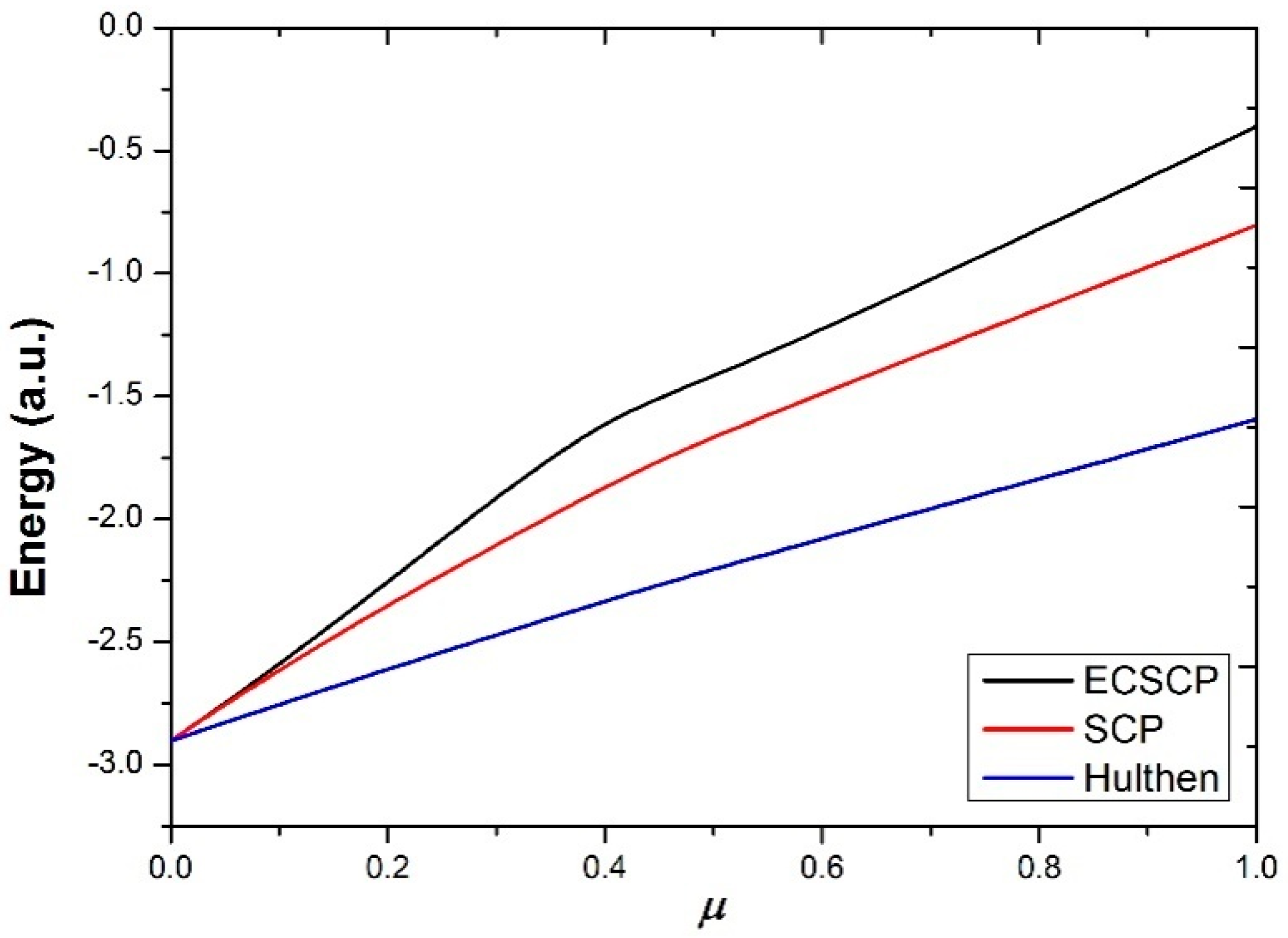
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghoshal, A.; Ho, Y.K. An Investigation on the He−(1s2s2 2S) Resonance in Debye Plasmas. Atoms 2017, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Ning, Y.; Yan, Z.C.; Ho, Y.K. Quantum entanglement for helium atom in the Debye plasmas. Phys. Plasmas 2015, 22, 013302. [Google Scholar] [CrossRef]
- Ning, Y.; Yan, Z.-C.; Ho, Y.K. Natural and Unnatural Parity Resonance States in the Positron-Hydrogen System with Screened Coulomb Interactions. Atoms 2015, 4, 3. [Google Scholar] [CrossRef] [Green Version]
- Kar, S.; Ho, Y.K. Bound states of helium atom in dense plasmas. Int. J. Quantum Chem. 2005, 106, 814–822. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Ground states of helium in exponential-cosine-screened Coulomb potentials. J. Phys. B At. Mol. Opt. Phys. 2009, 42. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K.; Jiang, Z. Dispersion coefficients for interactions between hydrogen and helium atoms with Coulomb and screened Coulomb potentials. J. Phys. B At. Mol. Opt. Phys. 2011, 44. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y. Doubly-excited 2s21Se resonance state of helium embedded in Debye plasmas. Chem. Phys. Lett. 2005, 402, 544–548. [Google Scholar] [CrossRef]
- Janev, R.; Zhang, S.-B.; Wang, J. Review of quantum collision dynamics in Debye plasmas. Matter Radiat. Extrem. 2016, 1, 237–248. [Google Scholar] [CrossRef] [Green Version]
- Margenau, H.; Lewis, M. Structure of Spectral Lines from Plasmas. Rev. Mod. Phys. 1959, 31, 569–615. [Google Scholar] [CrossRef]
- Shukla, P.; Eliasson, B. Screening and wake potentials of a test charge in quantum plasmas. Phys. Lett. A 2008, 372, 2897–2899. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Effects of screened Coulomb (Yukawa) and exponential-cosine-screened Coulomb potentials on photoionization of H and He+. Eur. Phys. J. D 2010, 57, 21–26. [Google Scholar] [CrossRef]
- Soylu, A. Plasma screening effects on the energies of hydrogen atom. Phys. Plasmas 2012, 19, 072701. [Google Scholar] [CrossRef]
- Chang, T.N.; Fang, T.K. Atomic photoionization in a changing plasma environment. Phys. Rev. A 2013, 88. [Google Scholar] [CrossRef] [Green Version]
- Ghoshal, A.; Ho, Y.K. Doubly excited resonance states of helium in exponential cosine-screened Coulomb potentials. Phys. Rev. A 2009, 79, 062514. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Properties of hydrogen molecular ion with static screened coulomb and exponential cosine screened coulomb potentials. Int. J. Quantum Chem. 2011, 111, 4288–4295. [Google Scholar] [CrossRef]
- Ancarani, L.U.; Rodriguez, K.V. Correlated expansions of n1S and n3S states for two-electron atoms in exponential cosine screened potentials. Phys. Rev. A 2014, 89, 012507. [Google Scholar] [CrossRef]
- Fang, T.K.; Wu, C.S.; Gao, X.; Chang, T.N. Redshift of the Heα emission line of He-like ions under a plasma environment. Phys. Rev. A 2017, 96, 052502. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-C.; Lin, C.-Y.; Ho, Y.K. Spectral/structural data of helium atoms with exponential-cosine-screened coulomb potentials. Int. J. Quantum Chem. 2015, 115, 830–836. [Google Scholar] [CrossRef]
- Roy, A.K. Critical parameters and spherical confinement of H atom in screened Coulomb potential. Int. J. Quantum Chem. 2016, 116, 953–960. [Google Scholar] [CrossRef] [Green Version]
- Ghoshal, A.; Ho, Y.K. Two-Electron System in The Field of Generalized Screened PotentiaL. Mod. Phys. Lett. B 2011, 25, 1619–1629. [Google Scholar] [CrossRef]
- Nasser, I.; Zeama, M.; Abdel-Hady, A. The Rényi entropy, a comparative study for He-like atoms using the exponential-cosine screened Coulomb potential. Results Phys. 2017, 7, 3892–3900. [Google Scholar] [CrossRef]
- Nasyrov, V.V. Radial correlation of the helium atom in the ground state. J. Exp. Theor. Phys. 2017, 125, 369–371. [Google Scholar] [CrossRef]
- Bressanini, D.; Morosi, G. A compact boundary-condition- determined wavefunction for two-electron atomic systems. J. Phys. B At. Mol. Opt. Phys. 2008, 41. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, K.V.; Gasaneo, G.; Mitnik, D.M. Accurate and simple wavefunctions for the helium isoelectronic sequence with correct cusp conditions. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 3923–3939. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Jiao, L.G.; Liu, F.; Liu, A.H.; Ho, Y.K. Energy levels of ground and singly excited states of two-electron atoms in dense quantum plasmas. At. Data Nucl. Data Tables 2021, 140, 101420. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Z.; Kar, S.; Ho, Y.K. The 1,3P0 states of exponential cosine-screened helium like atoms. At. Data and Nucl. Data Tables 2021, in press. [Google Scholar]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Doma, S.B.; Abu-Shady, M.; El-Gammal, F.N.; Amer, A.A. Ground states of the hydrogen molecule and its molecular ion in the presence of a magnetic field using the variational Monte Carlo method. Mol. Phys. 2016, 114, 1787–1793. [Google Scholar] [CrossRef]
- Doma, S.; Shaker, M.O.; Farag, A.M.; El-Gammal, F. Ground States of Helium Atom and Hydrogen Negative Ion in the Presence of Magnetic Field Using Variational Monte Carlo Technique. Acta Phys. Pol. A 2014, 126, 700–705. [Google Scholar] [CrossRef]
- Doma, S.B.; Shaker, M.O.; Farag, A.M.; El-Gammal, F.N. Variational Monte Carlo calculations of lithium atom in strong magnetic field. J. Exp. Theor. Phys. 2017, 124, 1–9. [Google Scholar] [CrossRef]
- Baye, D. The Lagrange-mesh method. Phys. Rep. 2014, 565, 1–107. [Google Scholar] [CrossRef] [Green Version]
- Thirring, W. A Course in Mathematical Physics 3: Quantum Mechanics of Atoms and Molecules; Springer: New York, NY, USA, 1981. [Google Scholar]
- Wang, X.R. General theorem on the Schrödinger equation. Phys. Rev. A 1992, 46, 7295–7296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hall, R. Refining the comparison theorem of quantum mechanics. J. Phys. A Math. Gen. 1992, 25, 4459–4469. [Google Scholar] [CrossRef]
- Santos, E.S.; Rivelino, R.; De Montigny, M.; De Melo, G.R. A spin Hamiltonian for non-relativistic electrons and their interaction with an external field. J. Phys. A Math. Theor. 2010, 43. [Google Scholar] [CrossRef]
- Ragusa, M.A.; Tachikawa, A. On continuity of minimizers for certain quadratic growth functionals. J. Math. Soc. Jpn. 2005, 57. [Google Scholar] [CrossRef]
- Fassari, S. On the bound states of non-relativistic Krönig-Penney Hamiltonians with short range impurities. Helv. Phys. Acta 1990, 63, 849–883. [Google Scholar]
- Hall, R.L.; Katatbeh, Q.D. Generalized comparison theorems in quantum mechanics. J. Phys. A Math. Gen. 2002, 35, 8727–8742. [Google Scholar] [CrossRef]
- Chen, G. Spectral comparison theorem for theN-dimensional Dirac equation. Phys. Rev. A 2005, 72, 044102. [Google Scholar] [CrossRef]
- Hall, R.L. Special Comparison Theorem for the Dirac Equation. Phys. Rev. Lett. 2008, 101, 090401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hall, R.L.; Yeşiltaş, Ö. Comparison theorems for the Dirac equation with spin-symmetric and pseudo-spin-symmetric interactions. J. Phys. A Math. Theor. 2010, 43. [Google Scholar] [CrossRef] [Green Version]
- Semay, C. General comparison theorem for eigenvalues of a certain class of Hamiltonians. Phys. Rev. A 2011, 83. [Google Scholar] [CrossRef] [Green Version]
- Ichimaru, S.; Iyetomi, H.; Tanaka, S. Statistical physics of dense plasmas: Thermodynamics, transport coefficients and dynamic correlations. Phys. Rep. 1987, 149, 91–205. [Google Scholar] [CrossRef]
- Hulthén, L. On the characteristic solutions of the Schrödinger deuteron equation. Ark. Met. Astron. Fys. A 1942, 28, 5. [Google Scholar]
- Pottorf, S.; Pudzerd, A.; Choud, M.Y.; Hasbun, J.E. The simple harmonic oscillator ground state using a variational Monte Carlo method. Eur. J. Phys. 1999, 20, 205–212. [Google Scholar] [CrossRef]
- Ruiz, M.B. Hylleraas method for many-electron atoms. I. The Hamiltonian. Int. J. Quantum Chem. 2004, 101, 246–260. [Google Scholar] [CrossRef]
- Turbiner, A.V.; del Valle, J.C.; Vieyra, J.C.L.; Nader, D.J. Ultra-compact accurate wave functions for He-like and Li-like iso-electronic sequences and variational calculus: I. Ground state. Int. J. Quantum Chem. 2021, 121, e26586. [Google Scholar] [CrossRef]
- Filippi, C.; Umrigar, C.J. Multiconfiguration wave functions for quantum Monte Carlo calculations of first-row diatomic molecules. J. Chem. Phys. 1996, 105, 213–226. [Google Scholar] [CrossRef] [Green Version]
- Hesse, M.; Baye, D. Lagrange-mesh calculations of three-body atoms and molecules. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 5605–5617. [Google Scholar] [CrossRef]
- Baye, D.; Sen, K.D. Confined hydrogen atom by the Lagrange-mesh method: Energies, mean radii, and dynamic polarizabilities. Phys. Rev. E 2008, 78, 026701. [Google Scholar] [CrossRef]
- Montgomery, J.H.E.; Sen, K.D.; Katriel, J. Critical screening in the one- and two-electron Yukawa atoms. Phys. Rev. A 2018, 97, 022503. [Google Scholar] [CrossRef]
- Turbiner, A.V.; Vieyra, J.C.L.; Olivares-Pilón, H. Few-electron atomic ions in non-relativistic QED: The ground state. Ann. Phys. 2019, 409, 167908. [Google Scholar] [CrossRef] [Green Version]
- Coolidge, A.S.; James, H.M. On the Convergence of the Hylleraas Variational Method. Phys. Rev. 1937, 51, 855–859. [Google Scholar] [CrossRef]
- Pekeris, C.L. Ground State of Two-Electron Atoms. Phys. Rev. 1958, 112, 1649–1658. [Google Scholar] [CrossRef]
- Bollhöfer, M.; Notay, Y. JADAMILU: A software code for computing selected eigenvalues of large sparse symmetric matrices. Comput. Phys. Commun. 2007, 177, 951–964. [Google Scholar] [CrossRef]
- Sen, K.; Katrielb, J.; Montgomery, H. A comparative study of two-electron systems with screened Coulomb potentials. Ann. Phys. 2018, 397, 192–212. [Google Scholar] [CrossRef]
- Adan, M.; Sanchez, M.; Martinez-Flores, C.; Vargas, R.; Cabera-Trujillo, R.; Garza, J.; Sen, K.D. Ionization of many-electron atoms by the action of two plasma models. Phys. Rev. E 2021, 103, 043202. [Google Scholar]
| 0 | 2.902662 | 2.000000 | 0.902662 |
| 2.9037244 | 2.0000004 | 0.9037244 | |
| 2.9033716 | - | - | |
| 0.01 | 2.872771 | 1.980070 | 0.892701 |
| 2.8738394 | 1.9800754 | 0.8937644 | |
| 0.02 | 2.843117 | 1.960268 | 0.882849 |
| 2.8441814 | 1.9602984 | 0.8838834 | |
| 0.04 | 2.784473 | 1.920408 | 0.864065 |
| 0.05 | 2.755475 | 1.901848 | 0.853627 |
| 2.7565494 | 1.9018454 | 0.8547044 | |
| 0.1 | 2.613758 | 1.807262 | 0.806496 |
| 2.6148534 | 1.8072664 | 0.8075874 | |
| 2.6145116 | - | - | |
| 0.2 | 2.345674 | 1.628183 | 0.717491 |
| 2.3470064 | 1.6282324 | 0.7187744 | |
| 2.3466616 | - | - | |
| 0.4 | 1.864564 | 1.306890 | 0.557674 |
| 1.8684514 | 1.3072344 | 0.5612174 | |
| 0.5 | 1.652445 | 1.162981 | 0.489464 |
| 1.6554014 | 1.1636784 | 0.4917234 | |
| 1.6550416 | - | - | |
| 1 | 0.803519 | 0.585547 | 0.217972 |
| 0.8182144 | 0.5924684 | 0.2257464 | |
| 0.8170416 | - | - |
| 0 | 2.902662 | 2.000000 | 0.902662 |
| 2.9037245 | 2.0000005 | 0.9037245 | |
| 2.9033716 | - | - | |
| 0.01 | 2.872533 | 1.979987 | 0.892546 |
| 2.8737255 | 1.9799885 | 0.8937375 | |
| 0.02 | 2.842163 | 1.959989 | 0.882174 |
| 2.8437305 | 1.9599915 | 0.8837395 | |
| 0.04 | 2.780706 | 1.919235 | 0.861471 |
| 0.05 | 2.749620 | 1.900052 | 0.849568 |
| 2.7538165 | 1.9000485 | 0.8537685 | |
| 0.1 | 2.590905 | 1.800491 | 0.790414 |
| 2.6044365 | 1.8004575] | 0.8039785 | |
| 2.6040916 | - | - | |
| 0.2 | 2.259199 | 1.603504 | 0.655695 |
| 2.3091115 | 1.6035275 | 0.7055875 | |
| 0.4 | 1.770741 | 1.225043 | 0.545698 |
| 0.5 | 1.444394 | 1.046606 | 0.397788 |
| 1.4769585 | 1.0470605 | 0.4298985 | |
| 1.4765316 | - | - | |
| 1 | 0.402097 | 0.296429 | 0.105668 |
| 0.4052615 | 0.3107145 | 0.0945475 |
| 0 | 2.902662 | 2.000000 | 0.902662 |
| 0.01 | 2.887679 | 1.989821 | 0.897858 |
| 0.02 | 2.872731 | 1.979252 | 0.893479 |
| 0.04 | 2.842973 | 1.960275 | 0.882698 |
| 0.05 | 2.828137 | 1.949522 | 0.878615 |
| 0.1 | 2.754565 | 1.900474 | 0.854091 |
| 0.2 | 2.610298 | 1.804300 | 0.805998 |
| 0.4 | 2.333143 | 1.619535 | 0.713608 |
| 0.5 | 2.200208 | 1.530918 | 0.669290 |
| 1 | 1.592340 | 1.124164 | 0.468176 |
| μ | Hulthen (μ) | SCP | Hulthén (2μ) | ECSCP |
|---|---|---|---|---|
| 0 | −2.903724377 (a) | −2.903724377 (a) | −2.903724377 (a) | |
| −2.902662 (b) | −2.902662 (b) | −2.902662 (b) | ||
| 0.01 | −2.888743509 (a) | −2.873838795 (a) | −2.873800905 (a) | −2.873725125 (a) |
| −2.887679 (b) | −2.872771 (b) | −2.872731 (b) | −2.872533 (b) | |
| 0.02 | −2.873800905 (a) | −2.844180576 (a) | −2.84403049 (a) | −2.843730329 (a) |
| −2.872731 (b) | −2.843117 (b) | −2.842973 (b) | −2.842163 (b) | |
| 0.04 | −2.84403049 (a) | −2.785537653 (a) | −2.783771455 (a) | |
| −2.842973 (b) | −2.784473 (b) | −2.780706 (b) | ||
| 0.05 | −2.829202681 (a) | −2.756548811 (a) | −2.755637701 (a) | −2.753815807 (a) |
| −2.828137 (b) | −2.755475 (b) | −2.754565 (b) | −2.749620 (b) | |
| 0.1 | −2.755637701 (a) | −2.614852947 (a) | −2.611379351 (a) | −2.604435567 (a) |
| −2.754565 (b) | −2.613758 (b) | −2.610298 (b) | −2.590905 (b) | |
| 0.2 | −2.611379351 (a) | −2.347006184 (a) | −2.334370372 (a) | −2.309114171 (a) |
| −2.610298 (b) | −2.345674 (b) | −2.333143 (b) | −2.259199 (b) | |
| 0.4 | −2.334370372 (a) | −1.868450546 (a) | −1.742851883 (a) | |
| −2.333143 (b) | −1.864564 (b) | −1.770741 (b) | ||
| 0.5 | −2.201638137 (a) | −1.655401315 (a) | −1.596227498 (a) | −1.47695782 (a) |
| −2.200208 (b) | −1.652445 (b) | −1.592340 (b) | −1.444394 (b) | |
| 1 | −1.596227498 (a) | −0.818214183 (a) | −0.405261234 (a) | |
| −1.592340 (b) | −0.803519 (b) | −0.402097 (b) |
| μ | Hulthen (μ) | SCP | Hulthén (2μ) | ECSCP |
|---|---|---|---|---|
| 0 | −2.14596983 (a) | −2.14596983 (a) | −2.14596983 (a) | |
| −2.145788 (b) | −2.145788 (b) | −2.145788 (b) | ||
| 0.01 | −2.131029234 (a) | −2.116300015 (a) | −2.116194799 (a) | −2.11598439 (a) |
| −2.129545 (b) | −2.115372 (b) | −2.114716 (b) | −2.113992 (b) | |
| 0.02 | −2.116194799 (a) | −2.08725862 (a) | −2.086857072 (a) | −2.08605418 (a) |
| −2.114716 (b) | −2.086387 (b) | −2.085402 (b) | −2.085065 (b) | |
| 0.03 | −2.101470743 (a) | −2.058823511 (a) | −2.05796091 (a) | −2.05623611 (a) |
| −2.100005 (b) | −2.058013 (b) | −2.057528 (b) | −2.055263 (b) | |
| 0.04 | −2.086857072 (a) | −2.030971244 (a) | −2.029506384 (a) | −2.026576457 (a) |
| −2.085402 (b) | −2.028217 (b) | −2.028095 (b) | −2.025621 (b) | |
| 0.05 | −2.072353792 (a) | −2.003680728 (a) | −2.001493594 (a) | −1.99711615 (a) |
| −2.070909 (b) | −2.000982 (b) | −2.000105 (b) | −1.994182 (b) | |
| 0.06 | −2.05796091 (a) | −1.976932817 (a) | −1.967891767 (a) | |
| −2.056528 (b) | −1.974287 (b) | −1.964984 (b) | ||
| 0.08 | −2.029506384 (a) | −1.924996108 (a) | −1.910280654 (a) | |
| −2.028095 (b) | −1.922452 (b) | −1.907431 (b) | ||
| 0.1 | −2.001493594 (a) | −1.875036337 (a) | −1.868060722 (a) | −1.853980921 (a) |
| −2.000105 (b) | −1.872588 (b) | −1.866782 (b) | −1.851209 (b) | |
| 0.2 | −1.868060722 (a) | −1.651488956 (a) | −1.634414579 (a) | −1.601389925 (a) |
| −1.866782 (b) | −1.649457 (b) | −1.633359 (b) | −1.599132 (b) | |
| 0.4 | −1.634414579 (a) | −1.304102639 (a) | −1.275179743 (a) | −1.219166537 (a) |
| −1.633359 (b) | −1.302586 (b) | −1.274386 (b) | −1.217393 (b) | |
| 0.5 | −1.534021688 (a) | −1.158970629 (a) | −1.119597793 (a) | −1.041082207 (a) |
| −1.533064 (b) | −1.157579 (b) | −1.118824 (b) | −1.039325 (b) | |
| 0.8 | −1.275179743 (a) | −0.787833216 (a) | −0.563849944 (a) | |
| −1.274386 (b) | −0.786741 (b) | −0.562433 (b) | ||
| 1 | −1.119597793 (a) | −0.586621163 (a) | −0.304567693 (a) | |
| −1.118824 (b) | −0.585698 (b) | −0.303396 (b) |
| μ | Hulthen (μ) | SCP | Hulthén (2μ) | ECSCP |
|---|---|---|---|---|
| 0 | −2.175228899 (a) | −2.175228899 (a) | −2.175228899 (a) | |
| −2.168892 (b) | −2.168892 (b) | −2.168892 (b) | ||
| 0.01 | −2.160277331 (a) | −2.145513403 (a) | −2.14542119 (a) | −2.145236778 (a) |
| −2.158999 (b) | −2.144725 (b) | −2.143899 (b) | −2.142392 (b) | |
| 0.02 | −2.14542119 (a) | −2.11635153 (a) | −2.115996636 (a) | −2.115287001 (a) |
| −2.143899 (b) | −2.115424 (b) | −2.114533 (b) | −2.112255 (b) | |
| 0.03 | −2.130660957 (a) | −2.08772446 (a) | −2.086955753 (a) | −2.085418757 (a) |
| −2.129201 (b) | −2.086901 (b) | −2.085513 | −2.082449 (b) | |
| 0.04 | −2.115996636 (a) | −2.059614751 (a) | −2.058298598 (a) | −2.05566674 (a) |
| −2.114533 (b) | −2.058829 (b) | −2.056876 (b) | −2.052696 (b) | |
| 0.05 | −2.101428233 (a) | −2.032006504 (a) | −2.030025255 (a) | −2.026062181 (a) |
| −2.099977 (b) | −2.029274 (b) | −2.028622 (b) | −2.023112 (b) | |
| 0.06 | −2.086955753 (a) | −2.004885122 (a) | −1.996633374 (a) | |
| −2.085513 (b) | −2.002199 (b) | −1.993701 (b) | ||
| 0.08 | −2.058298598 (a) | −1.952049995 (a) | −1.938404392 (a) | |
| −2.056876 (b) | −1.949456 (b) | −1.935519 (b) | ||
| 0.1 | −2.030025255 (a) | −1.901012328 (a) | −1.894420022 (a) | −1.88116494 (a) |
| −2.028622 (b) | −1.898506 (b) | −1.893113 (b) | −1.878328 (b) | |
| 0.2 | −1.894420022 (a) | −1.670095721 (a) | −1.652094063 (a) | −1.615667068 (a) |
| −1.893113 (b) | −1.667977 (b) | −1.650979 (b) | −1.613269 (b) | |
| 0.4 | −1.652094063 (a) | −1.307190384 (a) | −1.276412172 (a) | −1.219400057 (a) |
| −1.650979 (b) | −1.305633 (b) | −1.275605 (b) | −1.217612 (b) | |
| 0.5 | −1.54542779 (a) | −1.160139744 (a) | −1.120174566 (a) | −1.041273569 (a) |
| −1.544411 (b) | −1.158742 (b) | −1.119406 (b) | −1.039521 (b) | |
| 0.8 | −1.276412172 (a) | −0.7882615 (a) | −0.564149249 (a) | |
| −1.275605 (b) | −0.7871699 (b) | −0.5627306 (b) | ||
| 1 | −1.120174566 (a) | −0.587027809 (a) | −0.305119077 (a) | |
| −1.119406 (b) | −0.5861029 (b) | −0.3039526 (b) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doma, S.B.; Salem, M.A.; Sen, K.D. Plasma Confined Ground and Excited State Helium Atom: A Comparison Theorem Study Using Variational Monte Carlo and Lagrange Mesh Method. Computation 2021, 9, 138. https://doi.org/10.3390/computation9120138
Doma SB, Salem MA, Sen KD. Plasma Confined Ground and Excited State Helium Atom: A Comparison Theorem Study Using Variational Monte Carlo and Lagrange Mesh Method. Computation. 2021; 9(12):138. https://doi.org/10.3390/computation9120138
Chicago/Turabian StyleDoma, Salah B., Mahmoud A. Salem, and Kalidas D. Sen. 2021. "Plasma Confined Ground and Excited State Helium Atom: A Comparison Theorem Study Using Variational Monte Carlo and Lagrange Mesh Method" Computation 9, no. 12: 138. https://doi.org/10.3390/computation9120138
APA StyleDoma, S. B., Salem, M. A., & Sen, K. D. (2021). Plasma Confined Ground and Excited State Helium Atom: A Comparison Theorem Study Using Variational Monte Carlo and Lagrange Mesh Method. Computation, 9(12), 138. https://doi.org/10.3390/computation9120138





