Abstract
In this work, we present a method to build a first order reduced density matrix (1-RDM) of a molecule from variational Quantum Monte Carlo (VMC) computations by means of a given correlated mapping wave function. Such a wave function is modeled on a Generalized Valence Bond plus Complete Active Space Configuration Interaction form and fits at best the density resulting from the Slater-Jastrow wave function of VMC. The accuracy of the method proposed has been proved by comparing the resulting kinetic energy with the corresponding VMC value. This 1-RDM is used to analyze the amount of correlation eventually captured in Kohn-Sham calculations performed in an unrestricted approach (UKS-DFT) and with different energy functionals. We performed test calculations on a selected set of molecules that show a significant multireference character. In this analysis, we compared both local and global indicators of nondynamic and dynamic correlation. Moreover, following the natural orbital decomposition of the 1-RDM, we also compared the effective temperatures of the corresponding Fermi-like distributions. Although there is a general agreement between UKS-DFT and VMC, we found the best match with the functional LC-BLYP.
1. Introduction
The first measure of electron correlation energy was introduced by Löwdin as the energy difference between the exact solution of the non-relativistic Schrödinger equation and the Hartree-Fock (HF) approximation [1]. Although this is not a rigorous measure, considering that some correlation, namely Fermi correlation, is included in HF theory, it accounts for almost all the so-called Coulomb correlation originated by the two-body electron-electron interaction in the non-relativistic Hamiltonian. The correlation energy can further be decomposed in two terms denoted dynamic and nondynamic (or static) correlation. As the HF description based on a single Slater determinant, the dynamic correlation enters when the ground state of the system is sufficiently well described by a single determinant. On the other hand, nondynamic correlation arises when, in order to reproduce accurately the electronic structure of the system, two or more near degenerate determinants are necessary. Usually, the so-called post Hartree Fock methods (such as perturbation expansions or coupled clusters methods) are able to recover most of the dynamic correlation of the system; however, the recover of nondynamic correlation results more tricky and requires employing multiconfigurational methods. Valence Bond (VB) theory, as well as Multiconfiguration Self Consistent Field (MCSCF) theory, are able to capture the resonance between different configurations and then they can be used to estimate nondynamic correlation. Worth mentioning, in this regard, are the seminal works on the dissociation of the hydrogen molecule of Coulson and Fischer [2] and of Heitler and London [3]. Among the various multiconfiguration techniques, the Complete Active Space SCF (CASSCF) is the most appropriate to fix a reference for the estimate of the nondynamical correlation energy. In such a case, the full valence active space should be taken into account in order to consider all possible arrangements of electrons on the different molecular orbitals. Unfortunately, such large active spaces require computation resources rapidly increasing with the number of active electrons and, consequently, this kind of CASSCF cannot be performed on medium-large molecular systems. Moreover, despite the CASSCF wave function offers a proper treatment of nondynamic correlation, it is usually not able to reproduce dynamic correlation effects unless a large amount of orbitals are included in the calculations. From a computational point of view, density functional theory (DFT) could be an efficient alternative to multiconfigurational methods because it assures a good balance between accuracy and computational cost. However, although DFT usually is considered able to recover most of dynamic correlation, common density functional approximations (DFA) are generally unable to take into account nondynamic correlation effects or they can reproduce them in an unspecified manner [4]. This limitation is related to the intrinsic single determinant shape of the Kohn-Sham (KS) electronic density. Indeed, in order to preserve the spin symmetry of the electronic Hamiltonian, the wave function employed in HF or DFT computations has to be constructed in a restricted framework. However, this formulation results inadequate for the accurate reproduction of ground state energy of systems with a multiconfigurational character. One way to overcome this problem is to relax such restriction by allowing electrons to occupy different orbitals for different spins. Such unrestricted approach allows a lowering of the final energy mimicking in this case the effects of nondynamic correlation. The resulting determinant will not be anymore an eigenfunction of the spin operator . However, it is possible to evaluate the spin contamination between different spin states through the evaluation of the expectation values . It was shown that this approach allows including correlation for some particular systems, but its results are inadequate for others (see, for example, [5,6,7]). In the case of spin contamination we speak of symmetry breaking and in KS theory we can interpret the difference between restricted and unrestricted energy as an estimate of nondynamic correlation energy, namely
To evaluate the extent of correlation that is included in a computational method, several tools based on an analysis of the wave function have been developed. Worth mentioning in this context are the T1 [8,9,10], D1 [11] and D2 [12] diagnostics which were specifically designed to identify nondynamic correlation signatures in Coupled Cluster wave functions. Other indicators of correlation are based on the analysis of the first order reduced density matrix (1-RDM), such for example the ones based on the quantum entanglement and its connection to entropy [13,14,15]. Particularly relevant indicators are the so-called and which are obtained through a decomposition of the Coulomb hole into dynamic and nondynamic contributions [16]. These indicators admit a global [17] and a local [18] expression and can be evaluated by computing the natural orbitals in the framework of the method employed. Therefore these indicators can be easily computed for each method which has a non-diagonal 1-RDM. Further indicators based on natural orbitals have been developed by Tischenko et al. [19] and by Grimme and Hansen [20] in the context of Finite Temperature DFT (FTDFT) [20]. Such a thermal DFT approach treats statistical ensemble of quantum states describing the thermodynamic equilibrium of an electronic system [21]. It has been shown that this approach leads to fractional occupation numbers that can be used to define a sound measure of static electronic correlation. In principle, none of these indicators could be employed in DFT because the corresponding 1-RDM comes from a single determinant wave function and therefore it is diagonal on the basis of the molecular orbitals. On the other hand, if in the unrestricted framework a breaking in the spin symmetry occurs, through the Pulay localization [22] it is possible to recover a non-diagonal 1-RDM for a limited number of orbitals and studying the correlation effects. However, in order to study these effects it is necessary to have a proper reference which appropriately takes into account the correlation. Among all the correlated methods in computational chemistry, the Quantum Monte Carlo (QMC) and in particular its variational variant (VMC) is one of the most efficient for the inclusion of both dynamic and nondynamic correlation effects. VMC is based on a stochastic integration over the expectation value of a many-body wave function, which contains several variational parameters optimized through stochastic techniques. The advantage of this method with respect to standard highly accurate wave function methods, such as Full Configuration Interaction (FCI), is that it guarantees a more favorable computational scaling with respect to the size of the molecule. Indeed it has been largely used in the last 30 years for the evaluation of energies and molecular properties (see, for example, [23]). The correlation effects of a VMC calculation method could be roughly estimated by comparing the energy of the system with the HF and CASSCF results; however, for a deeper analysis, it is necessary to compute the 1-RDM. The direct computation of the 1-RDM needs the performance of N particle integrals (where N is the number of electrons) of the wave function involving non local operators. The peculiar shape of the VMC wave function makes the computations of the 1-RDM by stocastic integration very challenging. In the past, Kent et al. [24] recovered the 1-RDM of silicon by resorting to a QMC wave function in which the determinantal part was a single determinant of local density approximation orbitals.
In this work, we present a route to estimate a correlated 1-RDM from a VMC electronic density through a stochastic fit procedure. The electronic density is one of the most relevant properties which could be reproduced through the VMC method [25], indeed it has been widely shown that accurate electronic densities could be computed by an efficient sampling of the positions of the electrons in the space employing different kinds of density estimators [26,27]. The trial 1-RDM employed for the fit needs to have a proper set of guess orbitals and occupation numbers which are extracted from a test wave function able to preserve the N-representability conditions [28]. Indeed, it has been shown that is fundamental to satisfy this constraint in order to define a functional of 1-RDM [29,30,31]. The reference wave function has the skeleton’s core orbitals coming from a single determinant calculation (DFT/B3LYP), while the highest occupied and the lowest virtual orbitals will be parameterized following different multiconfigurational strategies (GVB and CASSCF like wave functions). This wave function will be proved to be flexible enough to recover most of the correlation (dynamic and nondynamic) effects of the VMC electronic density. Further information on the method proposed will be reported in Section 2.1. The resulting 1-RDM will be used to analyze the correlation effects of some selected systems for which nondynamic correlation is predominant. Once the reliability of this method has been established, the results obtained will be employed as a reference for studying nondynamic correlation of unrestricted DFT computations.
The outline of the paper is as follows. In Section 2, we illustrate the methodology followed in this work based on the construction of the 1-RDM from VMC and from unrestricted Kohn-Sham computations and the subsequent comparison and analysis including a study on nondynamic correlation effects made by finite temperatures extracted from a Fermi-like distribution. In Section 3, we show the details of the calculations performed in this study and, in Section 4, we present the results obtained on a set of illustrative examples with the related discussion. Finally, in Section 5, we discuss the conclusions and possible developments for future work.
2. Methodology
Through the analysis of the one-particle reduced density matrix (1-RDM), it is possible to identify the amount of nondynamic correlation included in the calculation. In this work, we follow two alternative ways to reconstruct a correlated 1-RDM based on different methods which are both able to account for a certain amount of nondynamic correlation effects. In the first of the two routes, we have generated numerically a correlated electronic density by means of a large set of electronic configurations obtained from a VMC sampling. This density has been transcribed in terms of an N-representable 1-RDM that employs both occupied and virtuals KS orbitals through a multi determinantal wave function form. Thanks to the quality of the VMC method, we expect that the resulting 1-RDM includes a considerable amount of both dynamic and nondynamic correlation contributions. The second route explored in this study, instead, involved unrestricted DFT (UDFT) computations. In this case we assumed that it is possible to include nondynamic correlation effects by breaking the spin symmetry of the system. Thus, the projection of the resulting electron density matrix on a natural orbital basis set will allow the study of the effects of correlation. Several density functional approximations (DFAs) have been considered to analyze how nondynamic correlation is treated by unrestricted UDFT in the different rungs of the Jacob’s ladder [32]. The correlation effects have been studied by computing the global indicators of correlation developed by Ramos-Cordoba and coworkers [17], namely
where is the occupation number of the spin-natural orbital i with spin . Finally, the calculated natural orbital occupancies will be related to canonical KS single particle energies through a Fermi-like distribution.
2.1. 1-RDM from a Correlated Electron Density
A correlated electron density can be generated from an accurate wave function obtained through a QMC calculation. In the present study, such a wave function has a multiconfiguration Slater-Jastrow form [33] and has been optimized at VMC level. More informations on the shape of the wave function are reported in Section 1 of the Supporting Information (SI). The optimized wave function , in which is a 3N-dimensional vector which includes the coordinates of the N electrons, is used to efficiently sample the configuration space through the probability density
Through a Metropolis importance sampling [34] it is possible therefore to generate an arbitrary number of electronic configurations. The electron density has been reconstructed on a grid employing an appropriate Gaussian smearing technique applied to a sufficiently large number of such configurations, namely
where M is the number of configurations and is the value of the electron density for the k-th configuration. The expression of has been chosen as a combination of peaked Gaussian functions centered in the position of each electron and simulating as many delta functions, namely
We expect that, with a sufficiently large number of configurations, the electronic density is well reproduced by Equation (6) and that the resulting density brings the information on the correlation effects of the VMC computation.
The Fit Procedure
The information on correlation could be recovered from an appropriate 1-RDM which is able to reproduce the correlated density of Equation (6). Such a 1-RDM has to be flexible enough to capture the basic features of the VMC electron density. We decided to construct a trial N-representable 1-RDM from a multiconfigurational reference wave function. In our construction we used a well given set of orbitals and we varied the coefficients of each determinant of such a function in order to fit the VMC density on diagonal. Therefore, the expression of the trial 1-RDM would be then
where the matrix elements depend on the coefficients of the determinants , namely the parameters of this fit. As many orbitals we include in Equation (8) as more accurate will be the fit itself. In this work, we used orbitals, where is the number of electrons. Finally, the 1-RDM has been parameterized combining a Complete Active Space Configuration Interaction (CASCI) approach for the -orbitals included in the sample and a Generalized Valence Bond (GVB) one for the rest. In principle, several trial wave function could be employed for the parameterization of the 1-RDM; however, we believe that this kind of function is flexible enough to capture the main correlation contributions for the systems considered in this work.
The single particle -orbitals were taken from a CASSCF computation, while the others have been selected from a set of localized orbitals (bonding and antibonding type) obtained from a KS-DFT computation. After the fit of Equation (6) through Equation (8), we diagonalized to obtain a set of natural orbitals and the corresponding occupancies which will be used to analyze nondynamic correlation effects. The details of the procedure are illustrated in Section 3.
2.2. 1-RDM from Unrestricted KS Computations
An unrestricted DFT calculation consists of solving the KS equations using a different set of orbitals for electrons with different spins. Thus, the KS determinant of the model system will not be anymore an eigenfunction of the spin operator bringing, in principle, spin contamination in the calculation. Nevertheless, the resulting electron density should be again an acceptable N-representable density for the real interacting system. Therefore, the unrestricted KS determinant will have enough flexibility to include nondynamic correlation effects which are, otherwise impossible to be treated by restricted DFT. We can analyze the importance of these contributions recovering the 1-RDM of this computation appropriately computed following the Pulay localization scheme. The derivation of this 1-RDM is shown below. The electronic density of the system can be split into the sum of the spin up () and spin down () contributions
where are the orbitals assigned to spin up electrons, while are the corresponding ones with spin down component.
The , as usual, are obtained from the SCF procedure in a basis of atomic orbitals:
To compute the natural orbitals we project this density into the atomic orbital basis orthogonalized by the Löwdin procedure [35] denoted as . The corresponding matrix expression of the 1-RDM would be
Using Equation (10), Equation (11) becomes
where are the elements of the overlap matrix constructed from the initial atomic orbitals, namely . The diagonalization of Equation (12) leads to natural orbitals , and fractional occupation numbers . Thus, the electronic density can be rewritten as
in which the occupation numbers lie between 0 and 2. Because these occupation numbers depend on the amount of spin contamination, we expect to observe different results for different DFAs and we will compare the occupancies with the one obtained through the QMC computations. Concerning the selection of the DFA, it is widely known that hybrid functionals with higher percentage of explicit HF exchange show bigger spin contamination. Indeed GGA functionals and hybrids functionals with a low percentage of explicit exchange are expected to bring less spin contamination with respect to range separated (RS) functionals. On the other hand, UHF calculations tend to largely overestimate symmetry breaking effects. In this work, we tested several density functional approximations focusing in particular on the different percentage of explicit HF exchange.
2.3. Fit of the Fermi Distribution
The occupation numbers previously introduced can be related to the corresponding canonical single particle energies through a Fermi-like distribution. The parameterization of such Fermi distributions should be made, in principle, by resorting to an effective temperature , by taking as chemical potential () the average between the HOMO and LUMO energies, namely . In this work, we decided to include the chemical potential as a further parameter in order to increase the accuracy of the fit. Therefore, the function used for the fit is
and the fit has been carried out on the occupation numbers calculated in both of the two approaches described in the previous sections. The effective temperature resulting from the fit is commonly considered as a further measure of nondynamic correlation.
The single particle energies () have been evaluated as the expectation values of a generalized Fock operator over the set of natural orbitals so far calculated, namely
where the operator is
in which is the monoelectronic operator, containing the kinetic energy and the interaction with the external potential, and and are, respectively, the Coulomb and the exchange operators defined in terms of the 1-RDM. Equation (15) takes the form
in which the integrals are evaluated in the natural orbital basis set and their expressions are:
3. Computational Details
3.1. Construction of the Electronic Density
To fit numerically the electron density, we interpolated the expression of on a regular cubic grid. The value of the density at each point of the grid has been taken as
in which the exponent w of each Gaussian function has been considered as depending on the cell of definition. More precisely, w is proportional to the number of sampled electron positions in the given cell as follows
where is the number of sampled configurations, and d is the side of the cubic cell. To make the electron density profile more homogeneous, the interpolation has been performed a few times up to convergence. At each iteration, the value of the density has been updated through a weighted average. Therefore, the electronic density at the iteration k () will have the following expression
for a density function extracted from a QMC run performed within the iteration itself.
3.2. Description of the Fitting Procedure
The fit has been performed with the least squares method, minimizing the quantity , which is the square of the difference between the VMC electron density interpolated by Equation (19) and the diagonal of the trial 1-RDM () integrated over the whole space, namely
The correct parameterization of the 1-RDM is of paramount importance for an accurate success of this fit. To reproduce appropriate values for the occupation numbers and kinetic energy it is necessary to impose precise N-representability constraints on this 1-RDM. For this reason, we decided to generate the 1-RDM by starting from a GVB wave function and, in a second stage, by modifying the parameterization of a reduced set of orbitals to include some larger active space taken from a CASSCF wave function. The starting 1-RDM has been created using bonding and antibonding orbitals obtained by the localization of B3LYP Kohn-Sham orbitals. We choose B3LYP orbitals for two main reasons, (i) they result from a computation in which electronic correlation is subsumed in the KS potential and (ii) B3LYP is often used to provide orbitals for standard QMC calculations. However, we believe that there is some flexibility in choosing the energy density functional for this purpose.
This picture is appropriate for two-electron two-centre bonds while for the delocalized electrons we improved the description by resorting to a complete active space properly defined. We chose a 1-RDM from a GVB wave function because it has a multiconfigurational character and the density matrix is diagonal for the representation in terms of bonding and anti-bonding orbitals. Moreover, the GVB wave function uses active orbitals, enough to capture the effects of nondynamic correlation. In the case of a perfect pairing, the form chosen in this study, the number of these configuration functions would be where is the number of pairs [36]. When the GVB geminals are written in terms of bonding and antibonding orbitals (see, for example, [37]), the GVB 1-RDM could be expressed in a diagonal form with the occupation numbers which depends strictly on parameters, namely
where the configuration coefficients depend on the order of excitation and the are the bonding and antibonding orbitals. We apply such GVB scheme to the skeleton of the molecules considered in this work while we use a different active space for the remaining electrons. The two relevant subspaces are strong-orthogonal and the final 1-RDM can be written as a sum of two contributions, namely
where is the 1-RDM parameterized as in a CASCI wave function with orbitals, while is the remaining part of the 1-RDM. The expression of is indeed
The 1-RDM has to be diagonalized in order to obtain the set of natural orbitals and occupancies. The minimization of has been achieved by exploring the full space of parameters with a Metropolis sampling in order to find the deepest minimum and finally by a steepest descent to find the minimum.
3.3. Methods and Softwares
In this work, within the QMC method, we used VMC to optimize the wave function taken in a Slater-Jastrow form for all the systems. In all cases we resorted to the Burkatzki, Filippi and Dolg (BFD) pseudopotentials [38] with their associated valence triple-zeta (VTZ) Gaussian basis set. The Jastrow factor included always and two-body terms and three-body terms [33]. The determinantal part of the wave function had a basic CASSCF structure. We used the suite of programs CHAMP [39] for all QMC calculations. The program GAMESS-US [40] is also used for the setup of the QMC wave function. All DFT and UDFT single point calculations have been performed using Gaussian 16 [41] employing the same pseudopotentials and basis sets used for the QMC calculations. Several functionals from the Jacob’s ladder of DFT [32] have been tested, these functionals are: BLYP [42], B3LYP [43], BH&HLYP [44], M06-2X [45], CAM-B3LYP [46] and LC-BLYP [47]. The interpolation of the densities on the grids, the construction of the multiconfigurational parameterization, the numerical fitting of the density as well as the extraction of single particle canonical energies from UKS orbitals have been performed through homemade computer programs.
4. Results
4.1. Fit of the Electronic Density
To test our approach, we considered a set of eight molecules which present a multiconfigurational character. This set includes two triatomic system: the ozone molecule and the complex in its transition state structure. Moreover, we included five cyclic compounds: the cyclobutadiene molecule, studied in both D2h and D4h geometries, the benzyne ortho-, meta- and para-isomers. Finally, we included in this set the retinal protonated Schiff base chromophore with four conjugated bonds (PSB4). A scheme with all the molecules employed in this study has been collected in Figure 1. These molecules display a different multiconfigurational character and therefore a different amount of nondynamic correlation. The geometries for the first seven molecules have been taken from the work of Grimme and Hansen [20] while, for the PSB4, we have taken the geometry from the work of Zulfikri et al. [48].
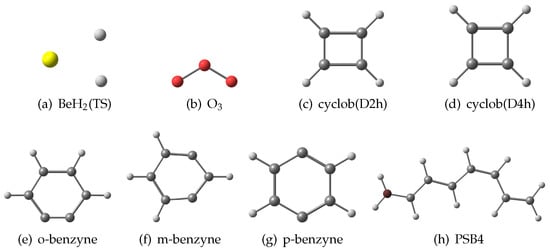
Figure 1.
Collection of the molecules investigated in this study. The geometries of the molecules computed have been reported in Section 1 of the SI.
We report the results of the energies computed with three different wave function methods: HF, CASSCF, in which the active space has been chosen in order to include all the orbitals and electrons of the valence shell, and VMC. These total energies are collected on Table 1.

Table 1.
Ground State electronic energies [a.u.] calculated with the different wave function methods. For the CASSCF calculations m is the number of electrons and n is the number of orbitals of the active space.
From this table, we notice that the CASSCF energy is always between the HF and VMC values recovering from 7 to 18 percent of correlation in all cases except for the transition state of BeH for which, instead, CASSCF and VMC are very close (98 percent). In these cases, the multireference character of the system is strongly related to the fraction of VMC correlation energy recovered by CASSCF. In Figure S1 of the SI we reported the electronic densities resulted from the QMC sampling. In Table 2, we report the results of the density fit in order to assess the reliability of the method presented in this work. In this Table, we compare the kinetic energy derived from the occupation numbers of the fitted one-particle reduced density matrix with the single particle KS kinetic energy and the correlated Pandharipande-Bethe kinetic energy derived from QMC calculation. The expression of the kinetic energy functional is known exactly and it is explicitly written in terms of the 1-RDM. As expected, the value is in between KS and QMC recovering from about 20 to about 90 of the difference. The fit is not able to recover exactly the QMC value but goes beyond the single-particle kinetic energy of KS. This result is not trivial and we believe that it supports the use of the fitted one particle density matrix in the present study. Obviously there is room for improvement especially by switching from GVB to a more flexible functional form for the mapping of the QMC wave function. Finally, in the last column of Table 2 we report the final values of which show that the accuracy is somewhat dependent on the size of the system.

Table 2.
Report on the accuracy of the fit and comparison between the kinetic energies. The number of digits for the kinetic energy depends on the accuracy of the method of calculation and reflects the statistical error of VMC and the standard error of the fit.
At this point, our fitted 1-RDM can be used to compute global and local indicators of correlation introduced by Ramos-Cordoba and Matito [17,18]. The values of global indicators for CASSCF and the fitted occupancies are reported in Table S1. For further information to the reader, we have also calculated the local indicators of correlation, these are displayed in Figures S2 and S3 of the SI. In Figure 2, we show a comparison between the results obtained from the QMC fit and the CASSCF calculations. More precisely, we compare the two fractions and for the two sets of calculations. From this Figure, we can see that the eight systems cover a wide range of the intervals [0:1] of these fractions. Moreover, the QMC fit recovers essentially the nondynamical CASSCF correlation and adds some more dynamical correlation.
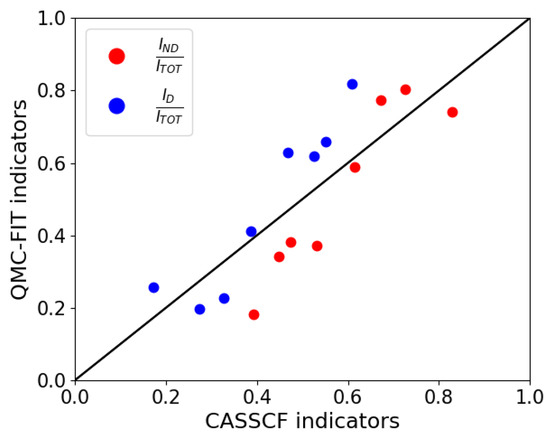
Figure 2.
Comparison of the relative dynamic () and nondynamic () indicators with respect to CASSCF ones.
4.2. Unrestricted Computations
The breaking of the spin symmetry is strongly system and functional dependent. For the systems in which nondynamic correlation is predominant (, cyclobutadiene (D4h), m-benzyne and p-benzyne) all the functionals considered in this study were able to break the spin symmetry leading to a lower unrestricted KS energy. However for systems in which nondynamic correlation effects are moderate (O, cyclobutadiene (D2h), o-benzyne and PSB4) the results differ from case to case. In particular, for O and PSB4 none of the density functionals tested was capable of breaking the spin symmetry. The same happens for the molecules cyclobutadiene (D2h) and o-benzyne employing UBLYP and UM06-2X. Instead, the GGA and RS functionals which have a BLYP core approximation broke the symmetry for all the other six molecular systems. UHF calculations introduced the largest spin contamination for all the systems except for O molecule. Finally, we wanted to compare the correlation indicators of these unrestricted calculations with the corresponding values coming from the QMC fit. Pulay localization can be used to construct the unrestricted natural orbitals (UNO) which can be used to compute . All global indicators relevant to unrestricted computations are reported in Table S3 of the SI. In Table 3, we reported the values of (a) and (b) calculated through UHF, four functionals (UB3LYP, UBH&HLYP, UCAM-B3LYP and ULC-BLYP) and the QMC fit. The values of the corresponding Mean Average Error (MAE) and Mean Absolute Percentage Error (MAPE) with respect to QMC-fit indicators are also reported.

Table 3.
In the table are reported the values of (a) and (b) of each density functional approximation employed plus the UHF values as reference. The MAPE and MAE are computed with respect to the reference QMC-fit which are also reported in the last two lines.
Looking at Table 3 (a), we can observe a general agreement of between the DFAs and the reference while UHF indicators results largely overestimated (MAE[UHF] 0.24 against MAE[UDFT] between 0.05 and 0.08). The largest discrepancies occur with UB3LYP for o- and m-benzyne and it can be traced back to the difficulty of some functionals in breaking symmetry (MAE 0.08 and MAPE 31.08). The other three functionals possess very similar indicators with LC-BLYP slightly outperforming (MAE 0.05 and MAPE 14.22). In Table 3, (b) we confirm what already observed, indeed, also for relative values UB3LYP performs poorly while the other functionals give optimal results. Interestingly, we can observe that for UHF the relative indicators / excellently agree with the reference results even if the global values of are very overestimated. Overall, ULC-BLYP gives the best performance among the cases treated in this work.
4.3. Fit of the Fermi Distribution
We performed the fit of the Fermi distribution of the canonical single particle energies for the QMC results and for the different functionals following Equation (14). The results highlight that there is a good correlation between the energies and the occupation numbers for both the QMC and UDFT calculations. The fitted distributions obtained for the LC-BLYP functional for the molecules o-, m- and p-benzyne have been reported in Figure 3, while the other plots have been reported in in Figures S4–S10 of the SI.
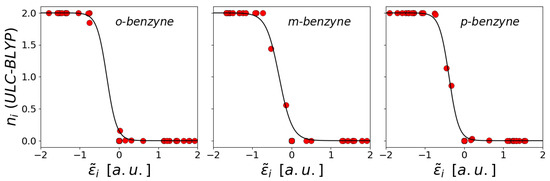
Figure 3.
Fit of the Fermi distribution for the o-, m-, p-benzyne molecules evaluated at ULC-BLYP level. In the figure are the natural occupancies of the UNOs, while are the canonicalized single particle orbitals. In black is reported the Fermi distibution calculated using Equation (14) and the parameters collected in Table S4 of the SI.
The parameters of the fit and the standard deviations have been reported in Table S4 of the SI. In Table 4, we compare the resulting effective temperatures coming from each functional with respect to QMC-fit reference.

Table 4.
Comparison between the obtained with the fit of the Fermi distribution for the different density functional approximations. The corresponding MAE and MAPE are calculated with respect to reference values obtained from the QMC-fit.
All the tested functionals give similar results for the systems for which nondynamic correlation is predominant, with a discrepancy in the range between 0 and 15% with respect to the reference . However these methods differ and give worse results for the systems in which nondynamic correlation is low. In particular, for o-benzyne all the resulting effective temperatures are significantly lower than the reference. UHF generally overestimate for all the systems tested. Furthermore, in this case, the best results are obtained with the ULC-BLYP approach (MAPE 11.1 and MAE 2.9 × 10).
5. Conclusions
The objective of this study has been to present a method able to recover a 1-RDM derived from an accurate wave function and then studying the nondynamic correlation effects included by unrestricted KS-DFT calculations. As accurate wave function, we mean a function of at least multireference configuration interaction quality. For this purpose, we have chosen a VMC wave function which shows a better scaling with the size of the system under study.
We propose a novel method to reconstruct the 1-RDM of a molecule at QMC level avoiding computing the challenging N particle integrals of the QMC wave function. This method consists of fitting the QMC density, properly defined through a large enough number of electronic configurations, using the density produced by a correlated wave function of which the 1-RDM is easily obtainable. In this way, in some sense, we move from the ideal non-interacting KS system toward the physical one along a path in which the density is the same but the reference wave function is modified to include, although not exhaustively, the e-e interaction. As mapping wave function, we chose a function that has a GVB structure for the skeleton of the molecule and a CASCI structure for the electrons. The parameters of this fit are the coefficients of the Slater determinants of the mapping function. The subsequent analysis of the 1-RDM obtained in this way showed that it is possible to capture the main contributions related to both dynamic and nondynamic electronic correlation of the QMC wave function. To assess the reliability of the this procedure, we compared the resulting kinetic energy with the corresponding VMC value.
The 1-RDM extracted from the QMC approach above has been considered as a reference for comparison with the 1-RDM derived from unrestricted KS-DFT calculations. The spin broken symmetry that occurs in unrestricted calculations of an independent particle model system is due in part to static correlation. The associated 1-RDM can thus be obtained from a natural bond analysis such as the one we describe in Section 2.2. We applied this study on a selected set of molecules which have an electronic ground state with a non negligible multireference character. We noticed that broken symmetry KS computations, performed with density functionals with an high percentage of explicit exchange, are able to reproduce the global nondynamic correlation index [17] computed through the QMC fitted 1-RDM. In particular, the best agreement occurs with the functional ULC-BLYP.
As a further test, we reconstructed a Fermi like distribution for each system and approach based on occupation numbers and canonicalized orbital energies. In each one of these distributions we have calibrated the effective temperature and chemical potential needed for the best fit. Although it is necessary a deeper investigation to understand a real meaning of such parameters, we notice that there is a general agreement between the effective temperature resulting from UDFT calculation with the QMC reference for the systems in which nondynamic correlation is important. For the other systems, the discrepancies are more evident. Again, the best functional among the ones included in the set is ULC-BLYP.
As for future work, we intend to improve the form of the mapping function to derive the 1-RDM from the QMC calculation. The need for a large active space, essentially a full valence active space, leads to a method that does not scale exponentially in the computation time with the size of the system under study. In this regard, the Density Matrix Renormalization Group (DMRG) method (see, for example, Ref. [49]) is a valid alternative to our GVB plus CASCI approach. DMRG method, in fact, is able to achieve a polynomial scaling under well defined conditions of calculation. As a final remark, we think that the present suggestion, namely the comparison of QMC and KSDFT through modeled 1-RDM, could be useful in the design of new functionals for DFT and FTDFT calculations.
Supplementary Materials
A Supporting Information file is available online at https://www.mdpi.com/article/10.3390/computation9120135/s1. This file contains detailed information on: (1) The geometries of the molecules in xyz format, (2) The VMC wave function used in this work, (3) The electronic densities computed at QMC level, (4) Tables with the global indicators of correlation for CASSCF and QMC results, (5) The local indicators of correlation calculated with the QMC results, (6) The global indicators of correlation computed at UKS-DFT level as well as the mean values of the S2 operator and the difference between the restricted and unrestricted energies, (7) The results of the fit of the Fermi distribution and the corresponding plots.
Author Contributions
The authors have equally contributed to the work. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, the authors gratefully acknowledge the support of the Donostia International Physics Center (DIPC) and the computer resources and technical support provided by Barcelona Supercomputing Center (BSC). The authors wish to acknowledge also partial financial support from the University of Pisa (Fondi di Ateneo).
Acknowledgments
The authors gratefully acknowledge E. Matito and E. Ramos-Cordoba for the valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Löwdin, P.O. Quantum Theory of Many-Particle Systems. III. Extension of the Hartree-Fock Scheme to Include Degenerate Systems and Correlation Effects. Phys. Rev. 1955, 97, 1509–1520. [Google Scholar] [CrossRef]
- Coulson, P.C.; Fischer, M.I. XXXIV. Notes on the molecular orbital treatment of the hydrogen molecule. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1949, 40, 386–393. [Google Scholar] [CrossRef]
- Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
- Cremer, D. Density functional theory: Coverage of dynamic and non-dynamic electron correlation effects. Mol. Phys. 2001, 99, 1899–1940. [Google Scholar] [CrossRef]
- Garza, A.J.; Jimenez-Hoyos, C.A.; Scuseria, G.E. Capturing static and dynamic correlations by a combination of projected Hartree-Fock and density functional theories. J. Chem. Phys. 2013, 138, 134102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tobola, R. Employing broken symmetry effects from unrestricted coupled cluster wave function to determine dynamic and non-dynamic electron correlation during triple bond breaking in the N2 molecule. Int. J. Quantum Chem. 2019, 119, e25865. [Google Scholar] [CrossRef]
- Zhang, D.; Truhlar, D.G. Unmasking Static Correlation Error in Hybrid Kohn-Sham Density Functional Theory. J. Chem. Theory Comput. 2020, 16, 5432–5440. [Google Scholar] [CrossRef]
- Timothy, J. Lee, Martin Head-Gordon, A.P.R. Investigation of a diagnostic for perturbation theory. Comparison to the T1 diagnostic of coupled-cluster theory. Chem. Phys. Lett. 1995, 243, 402–408. [Google Scholar]
- Lee, T.J.; Taylor, P.R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Fogueri, U.R.; Kozuch, S.; Karton, A.; Martin, J.M.L. A simple DFT-based diagnostic for nondynamical correlation. Theor. Chem. Accounts 2013, 132, 1–9. [Google Scholar] [CrossRef]
- Janssen, C.L.; Nielsen, I.M. New diagnostics for coupled-cluster and Møller–Plesset perturbation theory. Chem. Phys. Lett. 1998, 290, 423–430. [Google Scholar] [CrossRef]
- Nielsen, I.M.; Janssen, C.L. Double-substitution-based diagnostics for coupled-cluster and Møller–Plesset perturbation theory. Chem. Phys. Lett. 1999, 310, 568–576. [Google Scholar] [CrossRef]
- Ziesche, P. Correlation strength and information entropy. Int. J. Quantum Chem. 1995, 56, 363–369. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H.; Kais, S. Entanglement and electron correlation in quantum chemistry calculations. J. Mod. Opt. 2006, 53, 2543–2558. [Google Scholar] [CrossRef]
- Amovilli, C.; Floris, F.M. Shannon Entropy and Correlation Energy for Electrons in Atoms. In Many-Body Approaches at Different Scales: A Tribute to Norman H. March on the Occasion of their 90th Birthday; Angilella, G., Amovilli, C., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 187–198. [Google Scholar]
- Via-Nadal, M.; Rodríguez-Mayorga, M.; Ramos-Cordoba, E.; Matito, E. Singling Out Dynamic and Nondynamic Correlation. J. Phys. Chem. Lett. 2019, 10, 4032–4037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramos-Cordoba, E.; Salvador, P.; Matito, E. Separation of dynamic and nondynamic correlation. Phys. Chem. Chem. Phys. 2016, 18, 24015–24023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramos-Cordoba, E.; Matito, E. Local Descriptors of Dynamic and Nondynamic Correlation. J. Chem. Theory Comput. 2017, 13, 2705–2711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tishchenko, O.; Zheng, J.; Truhlar, D.G. Multireference Model Chemistries for Thermochemical Kinetics. J. Chem. Theory Comput. 2008, 4, 1208–1219. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef] [PubMed]
- Pribram-Jones, A.; Pittalis, S.; Gross, E.K.U.; Burke, K. Thermal Density Functional Theory in Context. In Frontiers and Challenges in Warm Dense Matter; Graziani, F., Desjarlais, M.P., Redmer, R., Trickey, S.B., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Pulay, P. Localizability of dynamic electron correlation. Chem. Phys. Lett. 1983, 100, 151–154. [Google Scholar] [CrossRef]
- Lester, W.A., Jr.; Mitas, L.; Hammond, B. Quantum Monte Carlo for atoms, molecules and solids. Chem. Phys. Lett. 2009, 478, 1–10. [Google Scholar] [CrossRef]
- Kent, P.R.C.; Hood, R.Q.; Towler, M.D.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo calculations of the one-body density matrix and excitation energies of silicon. Phys. Rev. B 1998, 57, 15293–15302. [Google Scholar] [CrossRef] [Green Version]
- Delle Site, L. Levy-Lieb principle: The bridge between the electron density of Density Functional Theory and the wavefunction of Quantum Monte Carlo. Chem. Phys. Lett. 2015, 619, 148–151. [Google Scholar] [CrossRef] [Green Version]
- Assaraf, R.; Caffarel, M.; Scemama, A. Improved Monte Carlo estimators for the one-body density. Phys. Rev. E 2007, 75, 035701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coccia, E.; Chernomor, O.; Barborini, M.; Sorella, S.; Guidoni, L. Molecular Electrical Properties from Quantum Monte Carlo Calculations: Application to Ethyne. J. Chem. Theory Comput. 2012, 8, 1952–1962. [Google Scholar] [CrossRef]
- Coleman, A.J. Structure of Fermion Density Matrices. Rev. Mod. Phys. 1963, 35, 668–686. [Google Scholar] [CrossRef]
- Herbert, J.M.; Harriman, J.E. N-representability and variational stability in natural orbital functional theory. J. Chem. Phys. 2003, 118, 10835–10846. [Google Scholar] [CrossRef] [Green Version]
- Lathiotakis, N.N.; Gidopoulos, N.I.; Helbig, N. Size consistency of explicit functionals of the natural orbitals in reduced density matrix functional theory. J. Chem. Phys. 2010, 132, 084105. [Google Scholar] [CrossRef] [Green Version]
- Mazziotti, D.A. Structure of Fermionic Density Matrices: Complete N-Representability Conditions. Phys. Rev. Lett. 2012, 108, 263002. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. In Proceedings of the International Conference on Density Functional Theory and its Applications to Materials, Antwerp, Belgium, 8–10 June 2000. [Google Scholar]
- Filippi, C.; Umrigar, C.J. Multiconfiguration wave functions for quantum Monte Carlo calculations of first-row diatomic molecules. J. Chem. Phys. 1996, 105, 213–226. [Google Scholar] [CrossRef] [Green Version]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33–83. [Google Scholar] [CrossRef] [Green Version]
- Löwdin, P.O. On the Nonorthogonality Problem. In Advances in Quantum Chemistry; Academic Press: Cambridge, MA, USA, 1970; Volume 5, pp. 185–199. [Google Scholar]
- Goddard, W.A.; Dunning, T.H.; Hunt, W.J.; Hay, P.J. Generalized valence bond description of bonding in low-lying states of molecules. Accounts Chem. Res. 1973, 6, 368–376. [Google Scholar] [CrossRef]
- Fracchia, F.; Filippi, C.; Amovilli, C. Size-Extensive Wave Functions for Quantum Monte Carlo: A Linear Scaling Generalized Valence Bond Approach. J. Chem. Theory Comput. 2012, 8, 1943–1951. [Google Scholar] [CrossRef]
- Burkatzki, M.; Filippi, C.; Dolg, M. Energy-consistent pseudopotentials for quantum Monte Carlo calculations. J. Chem. Phys. 2007, 126, 234105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- CHAMP. A Quantum Monte Carlo Program Written by C. J. Umrigar and C. Filippi; The Code Is Not Freely Distributed, Contact the Authors for More Information. Available online: https://www.utwente.nl/en/tnw/ccp/research/CHAMP.html (accessed on 7 December 2021).
- Schmidt, M.; Baldridge, K.; Boatz, J.; Elbert, S.; Gordon, M.; Jensen, J.; Koseki, S.; Matsunaga, N.; Nguyen, K.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Accounts 2008, 120, 215–241. [Google Scholar]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Iikura, H.; Tsuneda, T.; Yanai, T.; Hirao, K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540–3544. [Google Scholar] [CrossRef]
- Zulfikri, H.; Amovilli, C.; Filippi, C. Multiple-Resonance Local Wave Functions for Accurate Excited States in Quantum Monte Carlo. J. Chem. Theory Comput. 2016, 12, 1157–1168. [Google Scholar] [CrossRef]
- Chan, G.K.L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).