Next Article in Journal
Analytical and Numerical Solutions for the Thermal Problem in a Friction Clutch System
Next Article in Special Issue
Extraction of a One-Particle Reduced Density Matrix from a Quantum Monte Carlo Electronic Density: A New Tool for Studying Nondynamic Correlation
Previous Article in Journal
Direct Sampling for Recovering Sound Soft Scatterers from Point Source Measurements
Previous Article in Special Issue
Is There a Quadruple Fe-C Bond in FeC(CO)3?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Computation
Volume 9
Issue 11
10.3390/computation9110121
computation-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Correlation Effects in Trimeric Acylphloroglucinols

by
Liliana Mammino
School of Mathematical and Natural Science, University of Venda, Thohoyandou 0950, South Africa
Computation 2021, 9(11), 121; https://doi.org/10.3390/computation9110121
Submission received: 31 August 2021 / Revised: 31 October 2021 / Accepted: 2 November 2021 / Published: 15 November 2021
(This article belongs to the Special Issue Electronic Correlation)
Browse Figures
Versions Notes

Abstract

:
Trimeric acylphloroglucinols (T-ACPLs) are a subclass of the large class of acylphloroglucinols—derivatives of 1,3,5-trihydroxybenzene containing an R–C=O group. T-ACPL molecules contain three acylphloroglucinol moieties linked by methylene bridges. Many of them are present in natural sources and exhibit biological activities, often better than the corresponding activities of monomeric acylphloroglucinols. All the stable conformers of T-ACPLs contain seven intramolecular hydrogen bonds, which constitute the dominant stabilising factors. A total of 38 different T-ACPLs, including both naturally occurring and model molecules, have been calculated at the HF and DFT/B3LYP levels. The DFT/B3LYP calculations were carried out both without and with Grimme’s dispersion correction, to highlight the dispersion (and, therefore, also electron correlation) effects for these molecules. The roles of dispersion are evaluated considering the effects of Grimme’s correction on the estimation of the conformers’ energies, the description of the characteristics of the individual hydrogen bonds, the conformers’ geometries and other molecular properties. Overall, the results offer a comprehensive overview of the conformational preferences of T-ACPL molecules, their intramolecular hydrogen bond patterns, and the correlation effects on their properties.

1. Introduction

Acylphloroglucinols (ACPLs, Figure 1, [1]) are a broad class of compounds, structurally derived from phloroglucinol (1,3,5-trihydroxybenzene), and characterised by the presence of at least one R–C=O group (acyl group), where R is more often an alkyl chain. Many ACPLs are of natural origin and show a variety of biological activities, including antibacterial, antiviral, anticancer, antimalarial, antifungal, antioxidant, and antidepressant [1]. They have attracted interest for their pharmaceutical potentialities, spanning a broad range, from earlier considerations of their possible roles as lead compounds in the design of drugs against neurodegenerative diseases [2] to more recent investigations of their potentialities against SARS-CoV-2 [3].
Biologically active molecules of natural origin are particularly interesting for drug development because their activity is already proved, including their ability to reach the relevant biological target within the organism and interact with it. The biological activities of substances depend on the properties of their molecules and may depend on the finest details of these properties [4]. This makes accurate computational studies of biologically active molecules particularly important for subsequent steps of drug design. The present work pertains to a systematic computational study of ACPLs, investigating a number of aspects: the main factors stabilising the molecules of monomeric ACPLs (M-ACPLs) in vacuo [5,6,7,8] and in solution (e.g., [9,10]); the molecular properties of dimeric ACPLs (D-ACPLs, whose molecules contain two ACPL monomers) as a subclass of ACPLs [11]; and the molecular properties of a number of ACPLs with specific activities or specific structural features.
These studies clearly highlighted features related to the acylphloroglucinol unit and, therefore, appearing in all ACPL molecules (besides specific features associated with functions that may be present in the R* or R^ substituents). The general features comprise the dominant role of the intramolecular hydrogen bond (IHB) between the sp2 O of the acyl group and a neighbouring phenol OH (termed ‘first IHB’) [5,6,7,10,11], and the non-negligible influence of the orientation of the phenol OHs [6,7,12] and of the weaker C–H⋅⋅⋅O IHBs [8].
ACPLs in which two or more ACPL monomers are joined by methylene bridges (MB) often exhibit enhanced biological activity with respect to M-ACPLs [1], motivating the interest for specific studies. The study of D-ACPLs [11] highlighted the important role of the hydrogen bonds between monomers (IMHBs, ‘intermonomer hydrogen bonds’) on either side of the MB, turning them into the second stabilising factor for ACPLs consisting of more than one unit.
The present work focuses on trimeric ACPLs (T-ACPLs, Figure 2). It considers naturally occurring and model molecular structures selected in such a way as to provide adequate representativeness of the most common structural features of these compounds, such as the nature of R, R^, and R* and the replacement of one or more phenol OH by OCH3 groups or by keto O. The model structures have been added to highlight the effects of features like the presence of R^ and R* different from H on a given skeleton structure; knowing these effects can be useful both for better understanding of naturally occurring molecules and for better predictions of the properties of derivatives in the process of being designed.
An additional factor influencing the conformational preferences of T-ACPLs is the possibility of two different mutual orientations of the planes of the benzene rings of the three monomers, with all the other features being identical. This doubles the number of possible conformers with respect to an analysis based on the geometries of individual monomers and the associated IHBs (only one mutual orientation of the two planes is possible for each IMHB pair in the case of D-ACPLs).
Both the previous studies of ACPLs and the current one devote particular attention to IHBs. Hydrogen bonds (H-bonds) are often the strongest non-covalent interaction (NCI) between molecules or within a molecule. They play crucial roles in determining the geometries of biomolecules such as proteins and DNA. They may play important roles in determining site-reactivity of biologically active molecules (e.g., [13]), as well as in processes like molecular recognition and the binding of active molecules to their biological targets [14,15,16,17] and references in [17]. Therefore, it is particularly important to study IHBs when studying biologically active molecules, above all when these molecules might be taken into consideration for drug design [18].
Many molecular properties are used as quantum chemical descriptors for the investigation of quantitative structure–activity relationships (QSAR), whose predictive reliability depends on the accuracy of the descriptors-evaluation. The accuracy proved greater when electron-correlation is incorporated in the quantum chemical calculation, and electron-correlation-based QSARs prove satisfactorily predictive [19].
Electron correlation influences many aspects of molecular systems. In particular, dispersion interactions arise from correlation effects [20,21,22]. These interactions can be expected to be significant in T-ACPLs because of the presence of IHBs with different strengths, and the presence of three benzene rings whose planes may be at different angles in different conformers.
While dispersion interactions may not significantly influence strong H-bonds, their influence increases for moderate H-bonds and even more for weaker ones [22]. The first IHB in T-ACPLs (with an sp2 O as acceptor and closing a 6-member ring comprising two double bonds) is moderate-to-strong [6], whereas the IMHBs are significantly weaker; therefore, the inclusion of dispersion interactions can be expected to improve the description of the IHBs in T-ACPLs. Furthermore, a number of C–H⋅⋅⋅O IHBs are present in T-ACPLs; since they are weaker than O–H⋅⋅⋅O IHBs, their description is expected to be considerably sensitive to the inclusion of dispersion interactions.
Stacking interactions between aromatic rings are present in various biomolecules and contribute significantly to their conformational preferences and energetics [23]. They are dispersive in nature and, therefore, they can be taken into account only by computational methods including the consideration of dispersion interactions. The investigation of their effects is relevant for the study of molecules containing two or more benzene rings.
The obtained results highlight the importance of the IHB patterns in determining conformational preferences, and the preference for specific combinations of monomers’ geometries: the only populated conformers of T-ACPLs are those in which each constituting monomer is in one of the lowest energy conformations identified for M-ACPLs (a similar result had been obtained for D-ACPLs [11]). Electron correlation influences the conformers’ energies, their geometries, the characteristics of the IHBs, and the dipole moments; the influence is often more significant for half-bowl-shaped conformers, likely in relation to the mutual orientations of the planes of the three benzene rings.

2. Computational Details

Any investigation of molecular properties requires a prior conformational study, which defines the objects of further investigations. Therefore, a thorough conformational study was performed on the selected T-ACPL molecules, and its results are part of the new information generated by this work.
All the calculations were performed in vacuo, with fully relaxed geometry. An initial set of calculations was performed at the HF/6-31G(d,p) level to enable viable comparisons with the analogous results of M-ACPLs [7]. As noted in [5,6,7], this is the cheapest method capable of providing realistic information about trends across a large family of related compounds, as the errors due to the limitations of the level can be expected to be similar, leading to reasonable trends (also thanks to error cancellation [5]); furthermore, it proved capable of providing realistic information specifically for ACPLs; it is therefore also relevant to assess its performance for multi-unit ACPLs, in view of its possible use for fast preliminary screenings of large numbers of non-small or multi-unit ACPL molecules. A second calculation set utilised the HF/6-31+G(d,p) level to check the effect of the presence of diffuse functions in the basis set for the IHB description with the HF method [24,25,26].
A third calculation set utilised the DFT/B3LYP/6-31+G(d,p) level, to check the effect of the partial consideration of correlation effects in Density Functional Theory (DFT) calculations. The B3LYP functional [27,28,29] and the 6-31+G(d,p) basis set had been used also for M-ACPLs [7] and D-ACPLs [11], as a convenient compromise between results accuracy and computational costs, also in view of the non-small size of many ACPL molecules and of the frequent possibility of a high number of conformers. Their use here was meant to enable meaningful comparisons between the conformational preferences of T-ACPLs and those of M-ACPLs, and between characteristics pertaining to T-ACPLs and those pertaining, or not pertaining, to D-ACPLs.
Given the importance of dispersion effects both for the description of H-bonds [22,30] and for the description of molecules containing aromatic rings, above all when geometries recalling bowl-like shapes [31] are possible (as is the case of half-bowl-shaped T-ACPL conformers), a second set of calculations was performed at the DFT/B3LYP/6-31+G(d,p) level, with the inclusion of a D3-type Grimme’s correction for dispersion [32,33,34,35,36,37,38,39,40,41,42]. The B3LYP-D3 option has already been proved among the best to provide reasonably accurate molecular geometries [40]. This option was here preferred both because the uncorrected B3LYP/6-31+G(d,p) results are necessary for comparisons with all the other results obtained in the overall study of ACPLs and because the comparison between the results obtained with and without the correction provides quantitative information on the effects of the incorporation of correlation effects; this information, in turn, enables comparison of the effects according to the characteristics of the individual molecules and their conformers.
The size of the T-ACPLs molecules made MP2 (second-order Møller-Plesset perturbation theory) calculations largely unaffordable. MP2/6-31+G(d,p) calculations were attempted but proved too costly to be practicable (most of the attempted ones had not reached convergence after calculating for more than two months on a 24-processor cluster). MP2/6-31G(d,p) calculations were performed on the lowest energy conformers of selected comparatively-smaller T-ACPL molecules and managed to converge within 2–3 weeks; their results are used as an additional comparison possibility.
IR vibrational frequencies (harmonic approximation) were calculated at all the utilised calculation levels, except MP2. No imaginary frequency was encountered, confirming that the identified stationary points correspond to minima on the potential energy surfaces of these molecules. Frequency calculations also provide the ZPE (zero-point energy) corrections, thus enabling the evaluation of ZPE-corrected relative energies and of corrected relative free energies.
All the calculations were performed with Gaussian-16 [43]. Visualisation of molecular structures utilised GaussView [44] and Chem3D [45]; the visualisation of bond vibrations utilised Gabedit [46].
For the sake of conciseness, the calculation methods are denoted with the following acronyms in the rest of the text: HF for HF/6-31G(d,p), HF+ for HF/6-31+G(d,p), DFT for DFT/B3LYP/6-31+G(d,p), DFT-D3 for DFT/B3LYP/6-31+G(d,p) with the Grimme’s correction, MP2 for MP2/6-31G(d,p) and MP2+ for MP2/6-31+G(d,p).
Figures showing the conformers of all the calculated T-ACPLs molecules, tables reporting computational results in detail, and tables and graphs carrying out relevant types of comparisons, are included in the Electronic Supporting Information (ESI); they may be cited in the text, and their numbers are preceded by an uppercase S to easily identify them as pertaining to the ESI. Their numbering follows a logic pertaining to the organisation of the ESI and may not be related to the sequence in which they are mentioned in the text.

3. Results

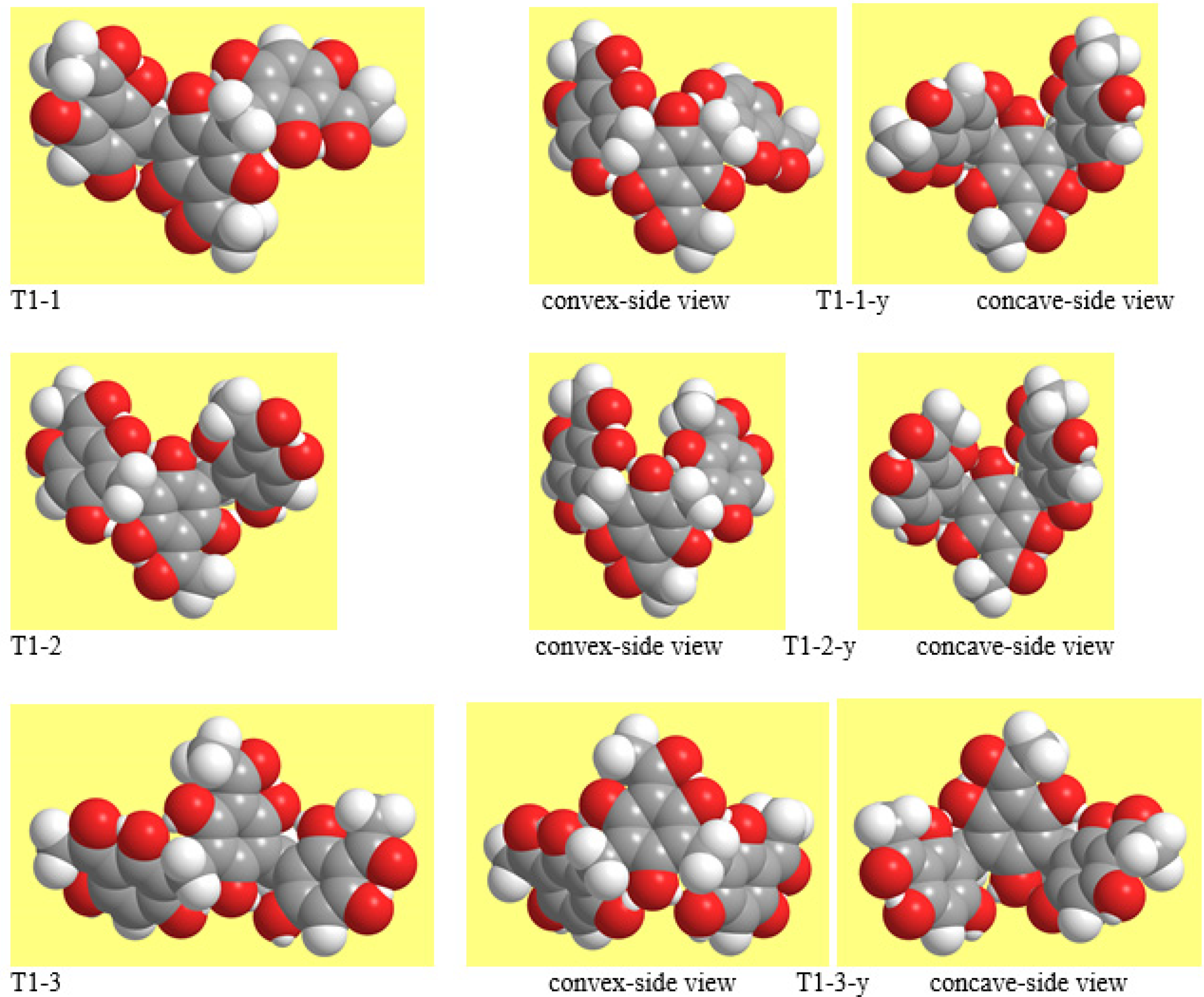
3.1. Selection and Concise Naming of Calculated T-ACPL Molecules

Only T-ACPL molecules in which all the monomers have ACPL moieties were considered. The calculated molecules are denoted with acronyms specifying their characteristics; this follows a practice introduced since the beginning of the study of ACPLs [6,7,8,9,10,11] in the same project and aimed at enabling conciseness and facilitating comparisons through many related molecules. Each acronym starts with an uppercase T (for trimeric) followed by a number that refers to the combination of R chains in the three monomers, as detailed in Table 1. Additional uppercase letters denote substituents in the outer monomers: M for CH3, ET for OCH3, and KT for a keto O replacing a phenol OH; each of these letters is followed by the number/s of the C atom/s of the benzene ring/s to which the given substituent is attached. For instance, T7 denotes a T-ACPL in which R = R′ = CH2CH2CH3 and R″ = CH3; T7-ET6,2″ denotes a T-ACP with the same R, R′, and R″, and with OCH3 groups replacing the OHs at C6 and C2″; T7-KT6″-M5,3″,3″ denotes a T-ACPL with the same R, R′, and R″, and with a keto O replacing the OH at C6″ and two CH3 groups at C3″; and so on.
The atom-numbering selected in this work is shown in Figure 2. It attempts to maintain the numbering of M-ACPLs (Figure 1) for individual monomers utilised in all the previous works on ACPLs within the same project (e.g., [5,6,7,8,9,10,11,31]); the use of consistent atom numbering is meant to facilitate comparisons of molecules and their descriptions across different works. In the case of T-ACPLs, the numbers of the atoms of the inner (second) monomer are primed and the numbers of the atoms of the third monomer are double-primed. When the R chains of the outer monomers have different sizes, the monomer with the longer R is chosen as the first monomer and appears on the left-hand side of the images representing the given molecule and its conformers. Although this convention is basically arbitrary, it is necessary for comparison purposes, to ensure that, for instance, corresponding IHBs are selected for comparisons of their characteristics (in the following text, ‘IHB’ is used both for the first IHB and comprehensively for all the IHBs, and ‘IMHB’ is used when it is important to specify that the given IHB is an intermonomer IHB or that only intermonomer IHBs are being considered).
The selection of molecules to be calculated aimed at representing the features most commonly appearing among T-ACPLs of natural origin, and comprises the simplest model structure (T1, with three identical monomers having R = CH3, that is, the simplest R ≠ H), several of the naturally occurring T-ACPLs reported in [1], and other model structures related to some of the selected natural T-ACPLs and meant to provide indications about the effects of certain substitutions. In terms of their structural features, the selection comprises: molecules in which no OH is replaced by other functions; molecules in which one or more phenol OHs are replaced by OCH3 groups; and molecules in which the OH at C2, or at C6″, or at both C2 and C6″ (i.e., OHs ortho to the acyl groups) are replaced by keto O. The selected molecules are listed in Table 2; the naturally occurring ones are also listed in Table S1, with information on their common names, their natural sources and—where known—also their medicinal properties [1,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]. Table S2 provides the molecular formulas of all the calculated molecules. Some of them are structural isomers, but this does not affect the interest in studying them individually, because structural isomers are different substances with different properties, including different biological activities.
It may also be noted that the way in which acronyms are constructed provides immediate indications about interesting comparisons. For instance, T7 is a T-ACPL in which no OHs are replaced by other functions; the comparison between T7-ET6,2″ and T7 highlights the effects of the replacement of O12–H17 and O8″–H15″ by ether functions (atom numbers shown in Figure 2); the comparison of T7-M5,3″-ET6,2″ with T7 highlights the effects of the replacement of the same two OHs by ether functions and the simultaneous presence of methyls in the remaining available positions (C5 and C3″); the comparison of T7-KT6″-M5,3″,3″ with T7 highlights the effects of the replacement of O12″–H17″ by a keto O; the comparison of T7-KT2,6″-M5,5,3″,3″ with T7 highlights the effects of the replacement of the inward-positioned ortho OH on each outer monomer by keto O, and its comparison with T7-KT6″-M5,3″,3″ highlights the effects-difference of the replacement of one or two of these ortho OHs. In a similar way, one may also choose a specific effect and select all the molecules’ pairs that can highlight that effect. For instance, if one wishes to consider the effect of the presence or absence of methyls at C5 and C3″, one can identify the following pairs from Table 2: T3-ET6,2″ and T3-M5,3″-ET6,2″; T7-ET6,2″ and T7-M5,3″-ET6,2″; T9 and T9-M5,5′; T9-ET6,2″ and T9-M5,3″-ET6,2″; T10-ET6,2″ and T10-M5,3″-ET6,2″; T11-ET6,2″ and T11-M5,3″-ET6,2″; T13-ET6,2″ and T13-M5,3″-ET6,2″; T14-ET6,2″ and T14-M5,3″-ET6,2″.

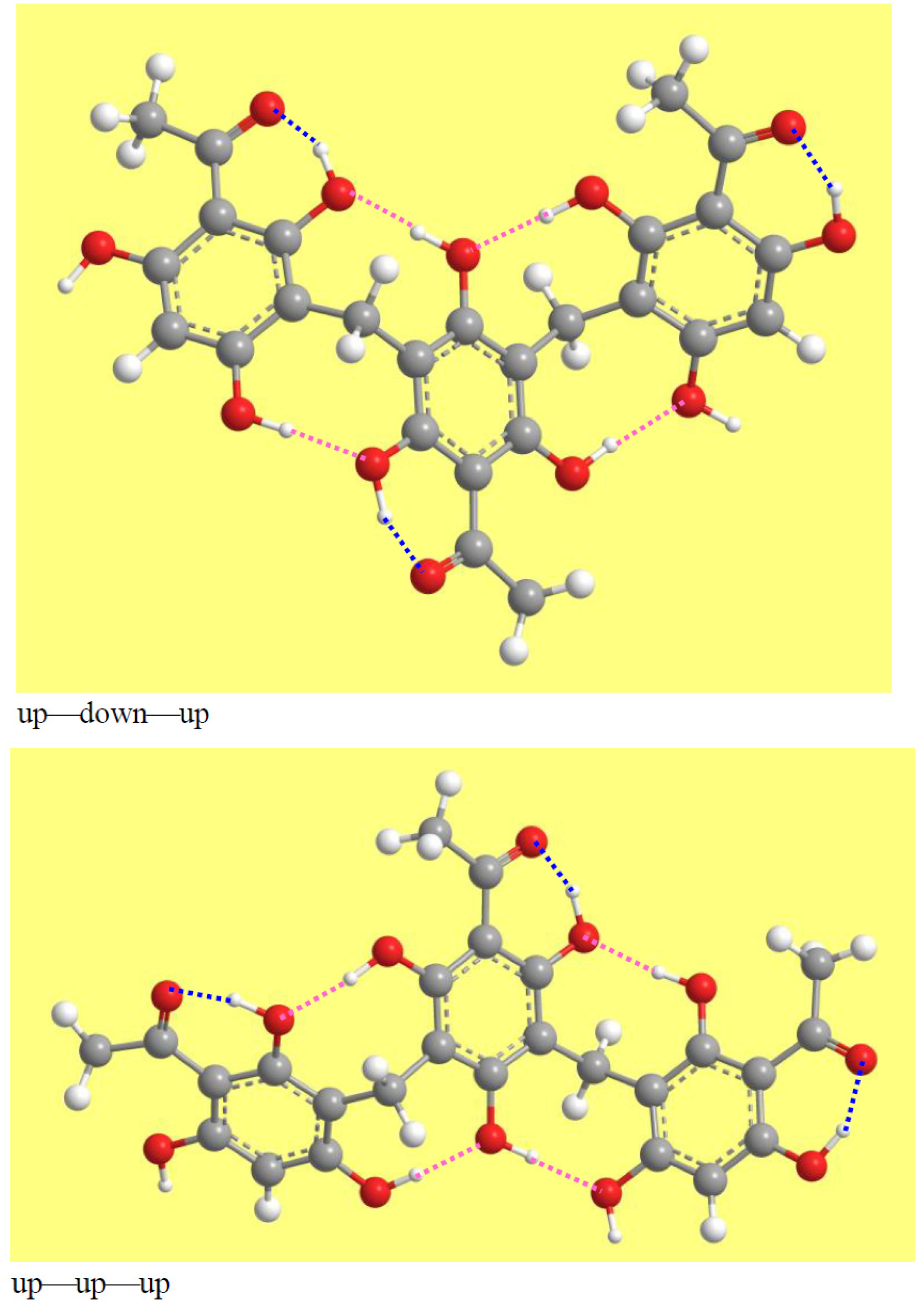
3.2. Conformers’ Geometries and Their Concise Naming

For ACPLs with more than two monomeric units, the investigation of conformational preferences requires attention to three major aspects: the geometry of the individual monomers; the combination of the orientations of the individual monomers; and the combination of the orientations of the two MBs.
The same symbols introduced in previous works on M-ACPLs [5,6,7], and summarised in Figure 3, are utilised in the current analysis to denote the conformer-type of individual monomers; the adaptations of their meaning to the presence of the MBs are explained in the caption of Figure 3 and illustrated in Figure 4. The conformer types are identified on the basis of the position of the first IHB and the orientation of the OHs not engaged in the first IHB. With reference to the atom-numbering in Figure 1 and Figure 2, if the first IHB is of the H15⋅⋅⋅O14 type, the conformer is d and if it is of the H17⋅⋅⋅O14 type, the conformer is s. A d-type conformer is r if H16 is oriented towards the side of the first IHB and w if it is oriented to the other side; an s-type conformer is w if H16 is oriented towards the side of the first IHB and r if it is oriented to the other side.
The mutual orientations of the monomers are more easily identified with reference to their acyl groups. The convention here chosen for both the images and the analysis selects an ‘up’ orientation (orientation for which the acyl group is ‘at the top’ with respect to the image of the ring) for the first monomer; the other monomers are seen as oriented ‘up’ if their acyl groups are on the same side and ‘down’ if the acyl groups are on the other side. Three major combinations of the orientations of individual monomers are possible (Figure 5): two consecutive monomers having the same orientation and the other one having different orientation (e.g., up—down—down); alternating orientations (e.g., up—down—up); and all the three conformers having the same orientation (e.g., up—up—up).
The mutual orientations of the concave side of the C-C-C angles of the two MBs (the C3–C9–C5′ and C3′–C9′–C5″ angles) determine whether the overall geometry is outstretched (opposite orientations) or close to a half-bowl shape (same orientations). This feature is illustrated in Figure 4 and Figure 5. The ‘half-bowl shape’ term is actually rigorous only for the cases in which all the monomers are oriented in the same way, resulting in a clearly identifiable broader upper rim and smaller lower rim of the half-bowl [68,69]; however, the use of the term is here extended to all the geometries in which the C-C-C angles of the two MBs have the same orientation, to avoid unnecessary terms-use complications.
In line with the practice of using acronyms providing concise descriptions, T-ACPL conformers are denoted by acronyms summarising their characteristics. The characteristics are specified by a system of numbers and letters. Different combinations of the geometry-types of the constituting monomers and of the mutual orientations of their R–C=O groups are identified by different numbers, which are based on the most frequent recurrence of the given combination in the increasing relative energy sequences of the conformers of the various molecules. Since a conformer from a given input maintains the same geometry with all the calculation methods utilised (although the values of the geometry parameters may somewhat differ), the same number is apt for the identification of the given conformer in the results of all the methods; thanks to this, the tables reporting calculation results need only one column for the identification of the conformer, and the other columns contain the corresponding values from the four calculation methods.
Previous studies [5,6,7] had shown that M-ACPL conformers without the first IHB have high relative energy (thus being totally unpopulated) both in vacuo and in solution, including water solution; the same proved true for D-ACPLs [11]. Therefore, only conformers in which the first IHB is present in each monomer were considered for the calculated T-ACPLs. All their possible viable combinations of monomer-orientations and IHB patterns have been taken into account in the initial study of model structure T1. Combinations were considered viable if the orientations of the groups at C2, C4, C4″, and C6″ enable the formation of IMHBs on either side of the MBs, because both the study of D-ACPLs [11] and explorative preliminary calculations on T-ACPLs showed that the absence of one or more IMHBs causes an energy increase that makes the given conformer totally unpopulated. Both conformers (outstretched and half-bowl shaped) were calculated for each combination of monomer-orientations and IHB pattern; they are denoted with the same number, adding a y for the half-bowl-shaped one (Figure 4 and Figure 5).
Table S3 lists the viable combinations for the calculated T-ACPLs. The number of viable combinations is greater when no phenol OH is replaced by other functions (Table S3a); they are shown in Figure S1, with the specification of the conformers’ characteristics. The replacement of one or more phenol OH by other functions may restrict the range of possibilities for the formation of IMHBs and exclude some geometries for the individual monomers; the remaining viable combinations are listed in Table S3b–g. The replacement of the OH at C6 or C2″ by OCH3 respectively excludes the s-conformers and d-conformers for the given monomer, and all the combinations involving these conformers; the replacement at C4/C4″ excludes the combinations in which O10–H16 or O10″–H16″ would have been a donor in an IMHB.
The replacement of OHs by OCH3 groups may increase the number of possible half-bowl conformers for the same combination of monomers geometries and IMHBs (i.e., conformers denoted by the same number) when substituents at C5 and C3″ are also present. When such substituents are not present, the OCH3 groups orient themselves in such a way that the C atoms of the methyl groups are approximately co-planar to the benzene ring [7]. When the substituents are present, the methyls of the ether groups become perpendicular to the plane. Three cases become possible for half-bowl conformers: the two methyls are oriented towards the outer part of the bowl (these conformers are denoted simply by the letter y); one of the methyls is oriented towards the internal side of the bowl and the other towards the external one (denoted as y-in-out); or both methyls are oriented towards the internal side of the bowl (denoted as y-in-in). The last case usually corresponds to significantly higher energy when the OCH3 groups are at C4 and C4″, because then the methyls ‘crowd’ in the lower (and narrower) rim of the bowl (Figure 6).
The OHs at C2 and C6″ (O8–H15 and O12″–H17″) are the inward OHs ortho to the acyl group in the outer monomers, i.e., the ortho OHs which can engage in IMHBs with a neighbouring monomer. The replacement of O8–H15 by a keto O excludes the d-conformers for the first monomer, and the replacement of O12″–H17″ excludes the s-conformers for the third monomer; the monomer combinations in which the replaced group is a donor in an IMHB are also excluded. The replacement also enables some combinations that are not present in T-ACPLs in which no OH has been replaced. For this reason, the conformers’ numbering for T-ACPLs with one inward ortho OH replaced by a keto O is independent; it is listed in Table S3e and illustrated in Figure S5. When the OHs at both C2 and C6″ are replaced by keto O, only one conformers-pair is possible for the given molecule (Figure S6). In all the cases in which only one conformers-pair is possible for a given molecule, it is numbered as 1.
Initial explorations also considered exchanging the conformer types of the outer monomers when R ≠ R″ (when R = R″, the exchange would yield the same conformer seen from another perspective). The energy difference was very small in the HF results, became marginal or disappeared in the HF+ results, and completely disappeared in the DFT results. Therefore, conformers resulting from such reversals were not included in the calculations with the dispersion correction, and they are not included in the tables reporting values. Figure S3 illustrates this exchange for a T-ACPL in which the OHs at C6 and C2″ are both replaced by OCH3 groups.

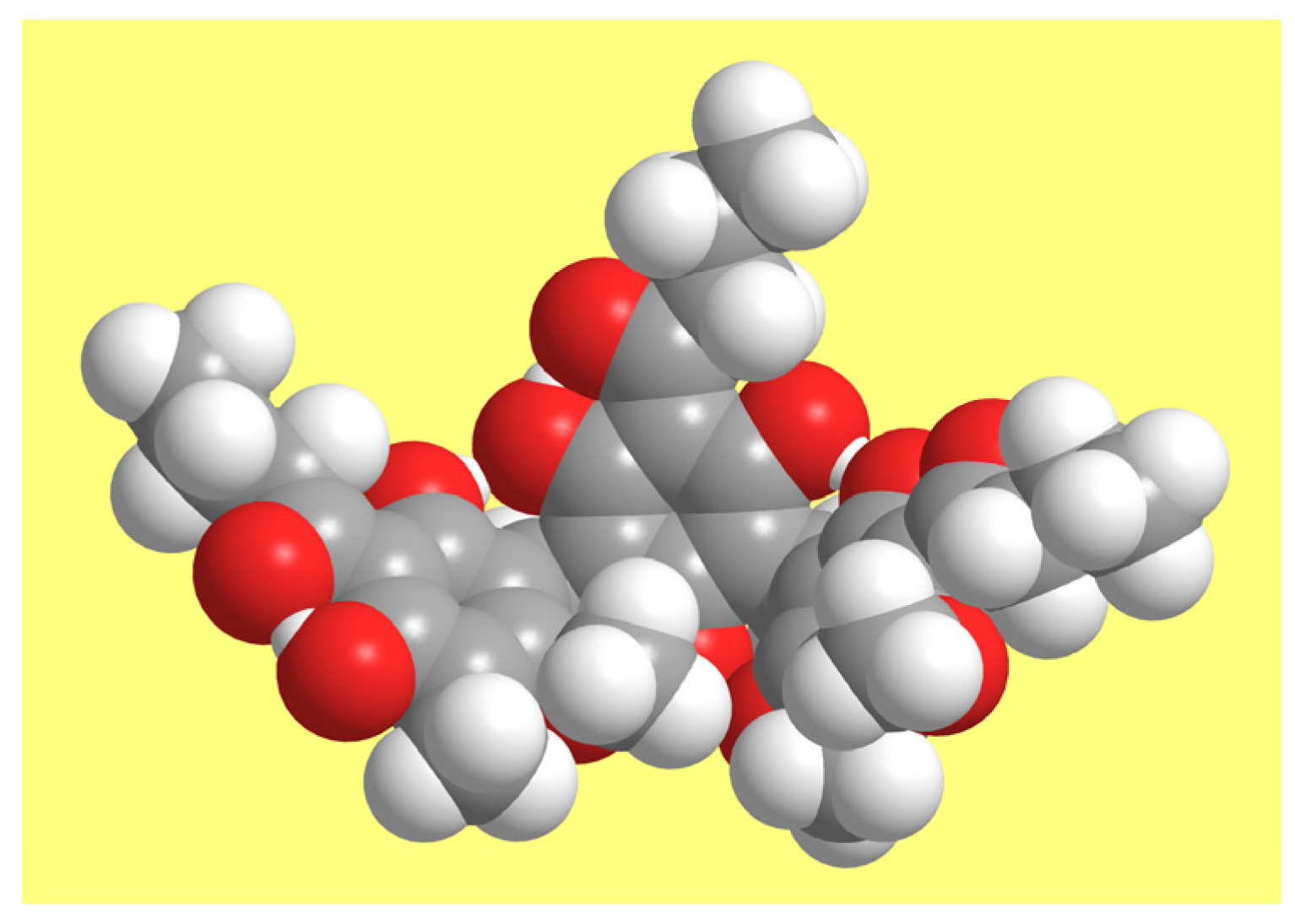
3.3. Conformers’ Geometry Preferences and Energetics

3.3.1. General Features

A preliminary study of T1 calculated all the viable conformers (considering all the possible combinations of orientations of the monomers and of the various OHs, and the consequent IHB patterns) and enabled the selection of the conformers to be calculated for the other molecules, excluding conformers with very high energy to avoid excessive growth in the total number of calculated conformers. Although only conformers with sufficiently low relative energy (lower than 3.5 kcal/mol, as a cautious criterion) may be involved in the biological activity of a molecule, several conformers with higher relative energies were also calculated because their comparison with the lower energy ones is useful for the evaluation of a variety of effects; furthermore, since the biological activity is exerted in a medium, they will also serve for future calculations in suitable solvents, as some of them might have sufficiently low relative energy in a certain solvent (more likely, in water) to be potentially involved in the activity [70].
Table S4 reports the relative energies of the conformers of all the calculated T-ACPLs, in the results of the four calculation methods utilised for all the molecules (HF, HF+, DFT, and DFT-D3); Table S4a groups the molecules according to their acyl groups and Table S4b according to their other substituents. The geometries of the calculated conformers are shown in Figure S2 for the T-ACPLs in which no OH is replaced by other functions, in Figure S4 for the T-ACPLs in which one or more OH groups are replaced by OCH3 groups and no other substitutions occur, and in Figure S6 for the T-ACPLs in which one or two OHs are replaced by keto O.
The results indicate that, in the lower energy conformers, each constituting monomer is in one of the lowest-energy conformations identified for M-ACPLs (d-r or s-w, [7]); a similar result had been obtained for D-ACPLs [11].
Table S5 considers the energy differences between corresponding conformers with outstretched or half-bowl-shaped geometry. The two geometries mostly have very close energies for the lowest energy pairs, while the difference may become significant for higher energy pairs. The difference is often greater in the DFT-D3 results, and the cases in which the half-bowl-shaped conformer has lower energy than the outstretched one are more frequent.
The frequency calculations provide the energies corrected for ZPE (sum of electronic and zero-point energies), the ZPE corrections, and the corrected free energies (sum of electronic and thermal free energies). Table S8 compares the relative energies not corrected for ZPE, those corrected for ZPE and the relative free energies for the two sets of HF results (HF/6-31G(d,p) and HF/6-31+G(d,p)), and Table S9 compares them for the two sets of DFT/B3LYP/6-31+G(d,p) results (without and with the Grimme’s correction). The trends appear largely similar, although some non-marginal reversals of the increasing-energy sequence can be noted. Table S10 reports the ZPE corrections in the results of the four methods. The correction is considerably greater in the HF results than in the DFT results; this may relate to the underestimation of the strength of H-bonds by HF, resulting in a smaller decrease in the vibrational frequencies of the OHs engaged in IHBs with respect to the free ones and, consequently, in an estimation of the vibrational energy partially neglecting the effects of the presence of the IHBs.

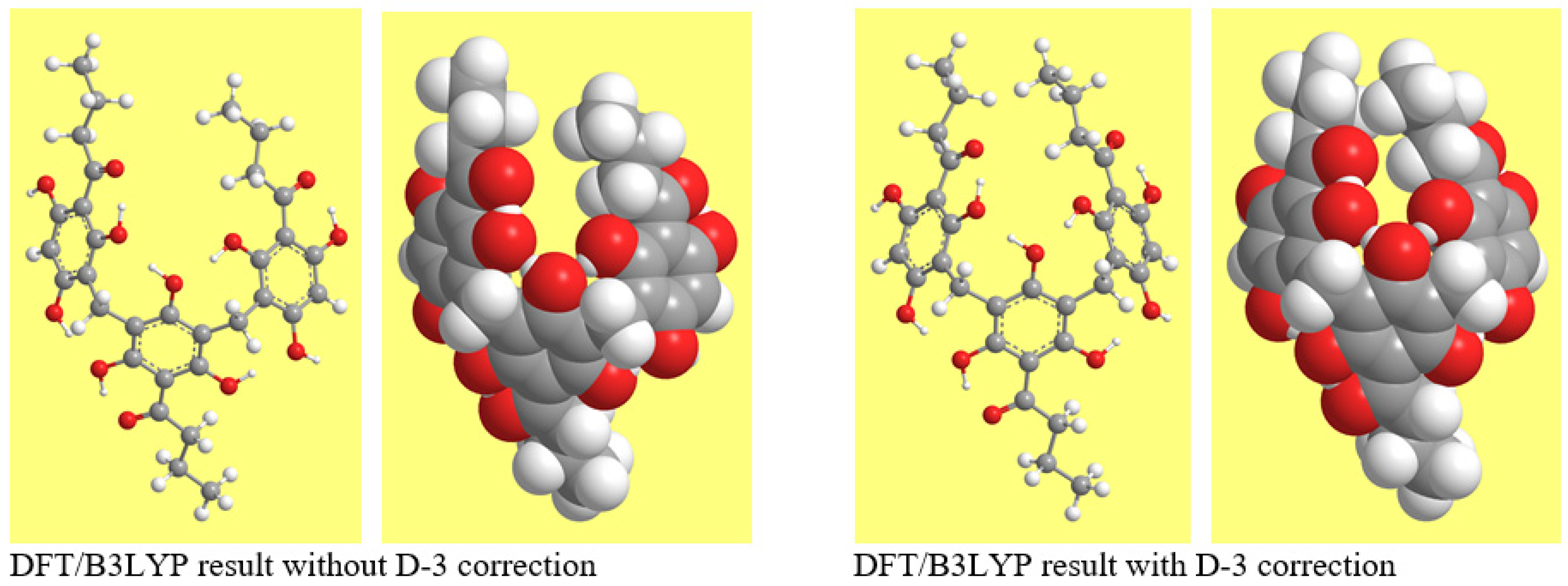
3.3.2. Effects of Grimme’s Correction on Geometries and Energetics

As expected, Grimme’s dispersion correction has a lowering effect on the estimation of the conformers’ energies, because of the largely attractive nature of intramolecular dispersion interactions. Table 3 provides the ranges of this lowering, Table S6 reports the lowerings for individual conformers, and Figure S7 visualises the trends through diagrams.
The lowering depends on the nature of the molecule, being generally greater for larger molecules (molecules with a greater number of electrons). However, it also depends significantly on the details of the molecular structure. Diagram (e) in Figure S7 utilises the smallest values of the energy-lowering for each molecular formula and highlights a general increase for larger molecules. However, the increase is not monotone. Table S7 shows the ranges of the lowering effect by grouping the molecules according to their formulas, thus highlighting the differences related to the individuality of different molecules with the same molecular formula (structural isomers), including the fact that some values may be similar for molecules differing only by two C atoms; this accounts for the discrepancies from a monotone trend revealed by diagram (e) in Figure S7.
The lowering effect of the Grimme’s correction is also slightly greater for half-bowl-shaped conformers (Figure 4 and Figure 5) than for the corresponding outstretched ones, which results in the bowl-shaped conformer having lower energy than the outstretched one considerably more frequently than in the results without dispersion correction. This is likely related to the greater presence of stacking interactions between the benzene rings in the half-bowl-shaped geometries, as the rings of the outer monomers partially ‘face each other’; it also appears that the up—down—up orientation of the monomers favours this effect.
The ranges of the lowering effect (Table 3) are narrower for conformers with outstretched geometry and broader for conformers with half-bowl geometries; this is also likely related to the greater presence of stacking effects in the latter, and to these effects being significantly different for different conformers.
The diagrams in Figure S7 choose different energy scales to better visualise the difference of the effect for the two types of conformers (comparison of the energy scales highlights the different ranges for different molecular sizes). The diagrams of the (a) series (molecules with no OHs replaced by other functions) highlight basically constant trends for corresponding conformers across molecules. The diagrams of the (b) series (molecules with an inward ortho OH replaced by a keto O in one of the outer monomers) highlight analogous patterns for the first five conformer pairs, whereas differences appear for the higher energy conformers. The (c) diagram considers the molecules with the inward ortho OH replaced by a keto O in each of the outer monomers; it highlights close behaviours for the two conformers of each molecule, as well as considerable effect-increase with the size of the molecule. Similarly, the (d) diagram (grouping the molecules in which the OH groups at C6 and at C2″ are replaced by OCH3 ether groups) highlights close behaviours for the two conformers of each molecule and considerable effect-increase with the size of the molecule. Since the molecules considered in diagram (d) constitute seven pairs of corresponding molecules without and with methyl groups at C5 and C3″, the diagram also highlights the increase related to the presence of the two methyls with respect to the corresponding molecules without them.
The ZPE correction in the DFT-D3 results is always greater than in the DFT results, with the difference varying between 0.4 and 1.5 kcal/mol. Figure S8 visualises the trends of the ZPE correction for the DFT and DFT-D3 results, using a layout analogous to that of Figure S7. The diagrams use different scales on the vertical axis because of the different ranges of the ZPE correction for molecules of different sizes. The diagrams of the (a) series (molecules with no OHs replaced by other functions) highlight similar and basically regular trends, despite the large differences in the magnitude of the ZPE correction for different molecules; the value of the half-bowl-shaped conformer is always slightly greater than the value of the corresponding outstretched conformer, and the DFT-D3 values are always greater than the DFT values. The diagrams of the (b) series (molecules with an inward ortho OH replaced by a keto O) highlight some discrepancies with respect to the trend-regularity of series (a), although the discrepancy-magnitudes are small. The (c) diagram considers the molecules with the inward ortho OH replaced by a keto O in each of the outer monomers and the (d) diagram considers molecules in which the OH groups at C6 and C2″ are replaced by OCH3 groups. Both diagrams highlight the considerable increase of the ZPE correction as the size of the molecule increases. Since the molecules in which the OH groups at C6 and C2″ are replaced by OCH3 groups constitute seven pairs of molecules differing only by the absence or presence of methyl groups at C5 and C3″, the (d) diagram also highlights the basically regular increase in the ZPE correction determined by the presence of the two methyls, with respect to the corresponding molecule in which they are not present. The (e) diagram utilises the smallest values for each molecular formula and highlights a general increase as the size of the molecule increases. The increase appears to be practically monotone (the steeper slope between the first two values being determined by the fact that the formulas identified by the numbers 1 and 2 differ by four C atoms, whereas in all the other cases a formula has only two additional C atoms with respect to the previous one). The closeness of the values for molecules with the same formulas is also highlighted by Table S11, showing the ranges of the ZPE correction for the DFT and DFT-D3 results and grouping the molecules in terms of their molecular formulas.
Intramolecular dispersion interactions are mostly attractive; therefore, the dispersion correction yields geometries in which atoms ‘come closer’ where possible [40]. As far as ACPLs are concerned, the phenomenon had already been noted for cavity-containing structures [31]. In the case of T-ACPLs, it is more evident for half-bowl-shaped conformers, because of the greater effect of dispersion in relation to the mutual orientations of the planes of the benzene rings; Figure 7 illustrates it for T9-2-y.

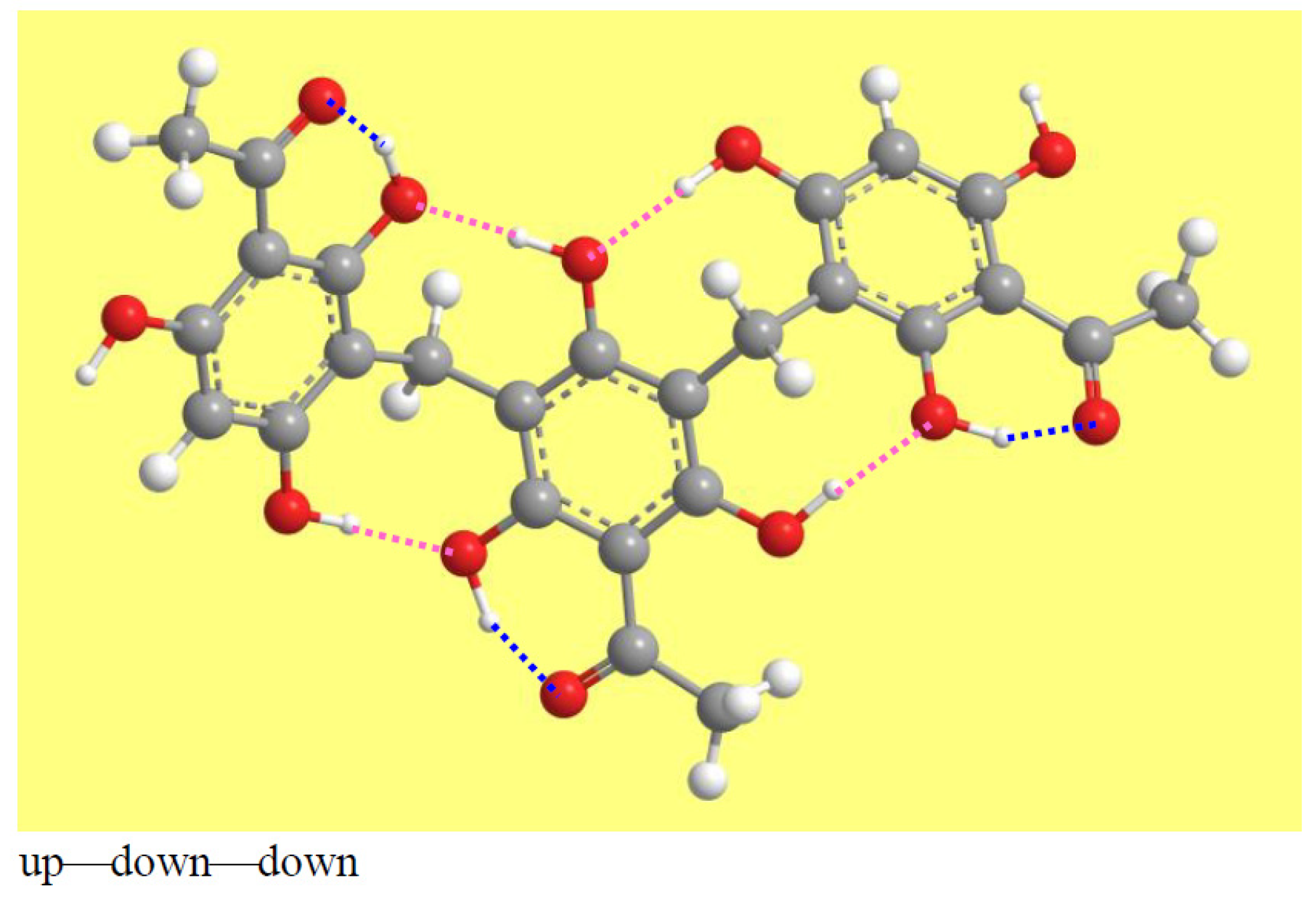
3.4. Characteristics of the Intramolecular Hydrogen Bonds (IHBs)

3.4.1. General Features of the IHBs in Trimeric Acylphloroglucinols

The calculated conformers have seven IHBs: a ‘first IHB’ in each monomer and four IMHBs. The IMHBs depend on the orientations of the OH groups that can form them, i.e., those at C2, C4, C2′, C4′, C6′, C4″, and C6″. Which OHs are available to act as a donor or acceptor depends on the mutual orientations of the monomers and on the orientations of the OHs. Figure 8 shows one possibility for each of the three mutual orientations of the monomers; the other patterns can be easily identified from Figure S1.
An interesting aspect appearing in various manners in all the conformers is the presence of consecutive IHBs, which are likely cooperative. For instance, in the up—down—down model in Figure 8, the H15⋅⋅⋅⋅O14, H16′⋅⋅⋅⋅O8 and H16″⋅⋅⋅⋅O10′ are cooperative in the upper rim, while the lower rim has two pairs of cooperative IHBs: the H16⋅⋅⋅⋅O12′ and H17′⋅⋅⋅⋅O14′ pair and the H15′⋅⋅⋅⋅O12″ and H17″⋅⋅⋅⋅O14″ pair (although the distinction between upper and lower rim is clearly identifiable only for half-bowl conformers, it can be extended to the corresponding outstretched conformers, thanks to the convention adopted for the images and their analysis). In the up—down—up model in Figure 8, H15⋅⋅⋅⋅O14, H16′⋅⋅⋅⋅O8 and H17″⋅⋅⋅⋅O10′ are cooperative in the upper rim, and H16⋅⋅⋅⋅O12′ and H17′⋅⋅⋅⋅O14′ are cooperative in the lower rim. In the up—up—up model in Figure 8, there are two pairs of cooperative IHBs in the upper rim (the H15⋅⋅⋅⋅O14, H17′⋅⋅⋅⋅O8 pair and the H15′⋅⋅⋅⋅O14′, H17″⋅⋅⋅⋅O8′ pair) and one pair in the lower rim (H16⋅⋅⋅⋅O10′, H16′⋅⋅⋅⋅O10″). H-bond cooperativity is important, because it often entails mutual strengthening of the H-bonds, and because it can confer specific properties to the molecule [71,72,73,74,75,76].
It is not easy to evaluate the energy of IHBs, because the removal of an IHB causes major changes in the molecule’s geometry and, therefore, the energy change accompanying the removal cannot be ascribed only to the loss of the IHB. The strengths of IHBs can be compared on the basis of quantities that are intrinsic to the IHB itself, such as its bond length or the lowering in the IR vibrational frequency of the donor that it causes (these quantities are also traditionally utilised in the classification of H-bonds strengths; the comparison of the length with the sum of the van der Waals radii of the H atom and the acceptor atom provides the major criterion to identify H-bonds [77]). Table S12 reports the lengths of all the IHBs present in the calculated conformers, comparing the results of all the calculation methods utilised. The length is shorter for the first IHBs, which are the strongest IHBs present. It can be recalled that the first IHB has an sp2 O as acceptor and closes a 6-member ring containing two double bonds, which is known to stabilise an H-bond (resonance-assisted H-bond, [78,79,80,81]).
An IMHB closes an eight-member ring (which is inherently less favourable than a six-member ring) and is not resonance assisted because there is no alternation of double and single bonds in the ring. IMHBs with an sp2 O as acceptor are present in the conformers of T-ACPL molecules in which one or both inward ortho OHs of the outer monomers are replaced by keto O atoms; the length of these IMHBs is intermediate between that of the first IHB and that of the IMHBs whose acceptor is an sp3 O, although often closer to the latter. IMHBs whose acceptor is an sp3 O are the weakest O–H⋅⋅⋅O IHBs present in these molecules.
On the basis of the bond lengths, it can be inferred that, while the first IHBs in T-ACPLs are on the bordering-on-strong end of the moderate H-bond range [5,6,7], the IMHBs can still be qualified as moderate, but in an intermediate or weaker part of the range.
The trends in the length of the first IHBs are fully consistent with the findings for M-ACPLs [5,6]. The first IHB is shorter when it forms on the same side of a substituent in meta to the acyl chain, leading to considerably greater length for IHBs forming on the outer side of the molecule (H17⋅⋅⋅⋅O14 and H15″⋅⋅⋅⋅O14″), above all when there is no substituent at C5 or C3″, and to shortest length for the first IHB of the central monomer. The first IHB is also longer when the other ortho OH of the same monomer is oriented towards the R chain.
The lengths of the same IHBs in the outstretched and half-bowl geometries are mostly close.
The length differences between the HF and HF+ results are mostly marginal. HF and DFT results show the same considerable difference as for the cases of M-ACPLs [5,6] and D-ACPLs [11], with the HF results underestimating the strength of IHBs (resulting in longer length) and DFT results overestimating it (resulting in shorter length). Comparisons with available experimental results for M-ACPLs had shown that the HF and DFT results often determine an interval within which the actual IHB length lies. The length patterns shown in Table S10 suggest that this is likely the case also for T-ACPLs.

3.4.2. Effects of Grimme’s Correction on the Characteristics of the IHBs

As already mentioned, dispersion components influence H-bonds, and the influence is greater for H-bonds that are not in the strong range. It is therefore expected that the inclusion of the D3 Grimme’s correction influences the estimation of the characteristics of the IHBs in T-ACPLs. Table S13 highlights this effect by considering the changes brought by the D3 correction in the estimation of the IHB lengths obtained from DFT/B3LYP/6-31+G(d,p) calculations. The changes show a frequent slight increase in the length of the first IHB and a frequent slight decrease in the length of the IMHBs. The changes may be similar for the outstretched and half-bowl conformers of the same pair; in a number of cases, however, they have greater magnitude for the half-bowl conformers, which would be consistent with the presence of greater dispersion contributions in these conformers. Figure S9 visualises the comparisons of the lengths of corresponding IHBs obtained with and without Grimme’s correction, in terms of selected comparison criteria. The diagrams comparing the same IHB across different conformers of T1 ((a) series of diagrams) highlight a length increase for the first IHB and more frequent decreases (with few exceptions), for the two IMHBs considered. The diagrams comparing the lengths of the IHBs in the lowest energy conformers (1 and 1-y) across different molecules ((b) series of diagrams) confirm a length increase for the first IHBs, with no exceptions, and a length decrease for the IMHBs, with few exceptions.
The C–H⋅⋅⋅⋅O H-bonds have since long been recognised as true H-bonds [77,82,83]. A considerable number of them are present in the conformers of T-ACPLs and play roles similar to those identified for M-ACPLs—contributing additional stabilisation and influencing the orientation of alkyl groups towards one that enables their formation [8]. Their number in T-ACPLs depends on the presence and nature of the substituents. In order to discuss them, it is necessary to introduce numbering criteria for H atoms in the substituents; it is opted to number these H atoms with the same number of the C atom to which they are attached, distinguishing the ones attached to the same C atom, or to equivalent C atoms, with lowercase subscripts (a, b, c). Figure S10 shows the C–H⋅⋅⋅⋅O IHBs present in the only possible conformer of T4-KT2,6″-M5,5,3″,3″, selecting the outstretched geometry: the R and R′ chains have four H atoms that can act as donors (H13a, H13b, H19a, H19b, H13a′, H13b′, H19a′, H19b′) because the chains orient themselves in such a way that even the H atoms attached to C19 can form C–H⋅⋅⋅⋅O IHBs with lengths shorter than the sum of the van der Waals radii of H and C; the R″ chain, being a methyl, has only three H atoms, and it engages all of them in C–H⋅⋅⋅⋅O IHBs. The two methyls at C5 (with both C atoms numbered as C11) and the two methyls at C3″ ((with both C atoms numbered as C9″) also engage all their H atoms in C–H⋅⋅⋅⋅O IHBs. All this results in the simultaneous presence of twenty C–H⋅⋅⋅⋅O IHBs in the conformer.
Table S14 reports the length of the C–H⋅⋅⋅⋅O IHBs in the lowest energy conformers-pair of representative T-ACPL molecules, comparing the DFT and DFT-D3 results. The inclusion of Grimme’s correction influences the length significantly, as expected for weaker IHBs. Given the total number of molecules and conformers considered, and the number of C–H⋅⋅⋅⋅O IHBs that may present in each conformer, a more complete study of these IHBs will be part of a separate work.

3.5. Other Computable Molecular Properties

Other computable molecular properties may prove significant descriptors for QSAR or QSPR (quantitative structure-properties relationships) analyses. Two such properties are considered in detail in the current study: the HOMO-LUMO energy difference and the dipole moment.
Table S15 reports the HOMO-LUMO energy difference for the calculated conformers in the results of the four calculation methods utilised. The known discrepancy between HF and DFT results is obviously present. The inclusion of Grimme’s correction does not appear to have any significant influence on the estimation of the HOMO-LUMO gap.
Table S16 reports the dipole moments of the calculated conformers. Since the values often differ significantly for the outstretched and bowl-shaped conformers of the same pair, Table S17 reports the differences between conformers of the same pair; the differences are greater for molecules in which one or more OHs are replaced by ether groups and no other substituent is present; they are slightly smaller for molecules in which no OH is replaced by other groups; and smallest for molecules in which one or two inward ortho OHs are replaced by keto O. Since the values in Table S16 show that the inclusion of Grimme’s correction has a significant influence on the estimation of the dipole moment, Table S18 lists its effects. In most cases, the effect is significantly greater for the half-bowl-shaped conformers than for the corresponding outstretched conformers. The effect is greater for molecules in which one or two OHs are replaced by ether groups, followed by molecules in which no OH is replaced by other groups, and is smallest for molecules in which O8–H15 and O12″–H17″ are both replaced by keto O.

3.6. Indications from a Limited Number of MP2 Results

As mentioned in Section 2, MP2 calculations proved mostly unaffordable for T-ACPL molecules. Table S19 reports the results that have been obtained.
The half-bowl-shaped conformer has lower relative energy than the outstretched one in all the cases, which can be ascribed to correlation effects along the previously outlined explanations.
The length of the IHBs is intermediate between the HF values and the DFT values. Since MP2 results are often considered the best benchmarks for H-bond parameters, this supports the inference that the HF and DFT length-values for a given IHB define an interval within which the actual value lies.

4. Discussion and Conclusions

The total number of molecules and conformers calculated in the current study, the use of four calculations methods, and the representativeness of the main features of naturally occurring T-ACPLs ensured by the molecules’ selection, enable a number of realistic inferences.
The lowest energy conformers are those in which each monomer has one of the lowest-energy conformations identified for M-ACPLs. The behaviour of the first IHB of each monomer shows patterns similar to those identified for M-ACPLs (including the energy increase accompanying its removal from one of the outer monomers, verified through calculation of a few randomly selected cases). The IMHBs play important roles in making the overall molecule ‘tightly knit’. Numerous C–H⋅⋅⋅⋅O IHBs are present simultaneously, indicating a significant role for their cumulative stabilising effect.
The set of DFT/B3LYP-D3 results highlights the influence of dispersion interactions on conformational preferences, conformers’ energies, overall geometry aspects (such as the ‘coming closer’ of atoms when possible), characteristics of the IHBs, and dipole moments, and the dependence of these effects on the size and nature of the molecules.
It is interesting to note that the lowering of the energy of individual conformers related to the inclusion of the dispersion correction (Table 3 and Table S6) is comparable with the energy lowering observed for trimeric bowls built from ACPLs [31], which ranges from 46.5 kcal/mol when all the R are methyl groups to 76.2 kcal/mol when all the R are isopropyl groups. The close similarity of these values suggests that the dispersion effects are related more to the presence of the various IHBs and of three benzene rings tightly ‘knit’ to each other by the methylene bridges and the IMHBs than to the fact that the structure in the bowls closes around a cavity, bringing the aromatic rings to ‘face each other’ more extensively.
The observed effects of the inclusion of Grimme’s dispersion correction indicate that it is important to consider electron correlation when evaluating molecular descriptors to be used in QSAR or analogous investigations. The estimation of the dipole moment, which is a relevant descriptor for various classes of molecules [4], is considerably influenced by the inclusion of dispersion. The only descriptor that does not appear to be significantly influenced is the HOMO-LUMO energy gap, but this may be related also to the specificities of the DFT evaluation of the gap; a confirmation of the influence-marginality could come from a study adding the Grimme’s correction to the HF calculations, whose estimation of the gap is substantially different (confirmations are generally more realistic if methods of different nature are used).
The results obtained for T-ACPLs confirm the modelling validity of the M-ACPLs results for the prediction of the behaviour of individual monomers in multi-unit ACPLs. This also suggests that the results obtained for the calculated T-ACPLs can serve as models for other T-ACPL molecules. Furthermore, they indicate that the inclusion of dispersion interactions in the calculation of biologically active molecules containing closely linked benzene rings and several simultaneous IHBs is important to provide more accurate descriptors and a better understanding of the molecular characteristics. Therefore, it will be included also in a planned study of T-ACPLs in a solution—a study that is essential for biologically active molecules because the biological activity is exerted in a medium within a living organism.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/computation9110121/s1, Figure S1: Viable geometries of trimeric acylphloroglucinols in which no phenol OH is replaced by other functions; Figure S2: Geometries of the conformers of the calculated trimeric acylphloroglucinols in which no OH is replaced by a different function; Figure S3: Illustration of the outcome of the reversal of the conformer-types of the two outer monomers in trimeric acylphloroglucinols; Figure S4: Geometries of the conformers of the calculated trimeric acylphloroglucinols in which one or more OH groups are replaced by OCH3 groups, and no other substitutions occur; Figure S5: Viable geometries of trimeric acylphloroglucinols in which an inward OH ortho to the acyl group is replaced by a keto O; Figure S6: Geometries and relative energies of the conformers of the calculated trimeric acylphloroglucinols in which one or two inward OHs ortho to the acyl group are replaced by keto O; Figure S7: Visualisation of relevant trends of the lowering effect of Grimme’s correction on the estimation of the energy of the conformers of the calculated trimeric acylphloroglucinols; Figure S8: Visualisation of relevant trends of the effect of Grimme’s correction on the estimation of the ZPE correction for the conformers of selected trimeric acylphloroglucinols; Figure S9: Comparisons of the lengths of corresponding intramolecular hydrogen bonds (IHBs) in the DFT/B3LYP/6-31+G(d,p) results without and with the Grimme’s correction, for selected trimeric acylphloroglucinol molecules; Figure S10: C–H⋅⋅⋅⋅O intramolecular hydrogen bonds in trimeric acylphloroglucinols; Table S1: Common names, natural occurrence and medicinal properties of the naturally occurring trimeric acylphloroglucinols considered in this study; Table S2: Molecular formulas of the calculated trimeric acylphloroglucinols; Table S3: Viable combinations of monomers’ conformer types in trimeric acylphloroglucinols; Table S4: Relative energies of the calculated conformers of trimeric acylphloroglucinols; Table S5: Energy difference between corresponding conformers with outstretched and half-bowl-shaped geometries, in calculated trimeric acylphloroglucinols; Table S6: Lowering effect of Grimme’s correction on the estimation of the energy of the conformers of the calculated trimeric acylphloroglucinols; Table S7: Ranges of the lowering effect of Grimme’s correction on the estimation of the energy of the conformers of the calculated trimeric acylphloroglucinols, grouping the molecules according to their formulas; Table S8: Relative energies non-corrected (ΔE, kcal/mol) and corrected for ZPE (ΔEcorr, kcal/mol) and relative free energies (sum of electronic and thermal free energies, ΔG, kcal/mol) in the HF results of representative conformers of the calculated trimeric acylphloroglucinols; Table S9: Relative energies non-corrected (ΔE, kcal/mol) and corrected for ZPE (ΔEcorr, kcal/mol) and relative free energies (sum of electronic and thermal free energies, ΔG, kcal/mol) in the DFT results (without and with dispersion correction) of representative conformers of the calculated trimeric acylphloroglucinols; Table S10: ZPE correction for representative conformers of the calculated trimeric acylphloroglucinols; Table S11: Ranges of the ZPE correction for the conformers of the calculated trimeric acylphloroglucinols, grouping the molecules according to their formulas; Table S12: Bond lengths of the intramolecular hydrogen bonds in the calculated trimeric acylphloroglucinols; Table S13: Effect of the inclusion of Grimme’s dispersion correction on the estimation of the length of the intramolecular hydrogen bonds in the calculated trimeric acylphloroglucinols; Table S14: Bond lengths of the C–H⋅⋅⋅⋅O intramolecular hydrogen bonds in selected trimeric acylphloroglucinols; Table S15: HOMO-LUMO energy difference of selected calculated conformers of trimeric acylphloroglucinols; Table S16: Dipole moment of the calculated conformers of trimeric acylphloroglucinols; Table S17: Dipole moment estimation difference between corresponding conformers with outstretched and half-bowl-shaped geometries, in the calculated trimeric acylphloroglucinols; Table S18: Effect of the inclusion of the Grimme’s correction on the estimation of the dipole moment of the conformers of the calculated trimeric acylphloroglucinols; Table S19: Information from the obtained MP2 results for trimeric acylphloroglucinols.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within the article and Supplementary Files.

Acknowledgments

The author expresses her gratitude to the Centre for High Performance Computing (CHPC) in Cape Town (South Africa) for providing the facilities to perform the calculations.

Conflicts of Interest

The author declares that there are no conflicts of interest.

References

  1. Singh, I.P.; Bharate, S.B. Phloroglucinol compounds of natural origin. Nat. Prod. Rep. 2006, 23, 558–591. [Google Scholar] [CrossRef] [PubMed]
  2. Verotta, L. Are acylphloroglucinols lead structures for the treatment of degenerative diseases? Phytochem. Rev. 2002, 1, 389–407. [Google Scholar] [CrossRef]
  3. Kusumaningsih, T.; Prasetyo, W.E.; Wibowo, F.R.; Firdaus, M. Toward an efficient and eco-friendly route for the synthesis of dimeric 2,4-diacetyl phloroglucinol and its potential as a SARS-CoV-2 main protease antagonist: Insight from in silico studies. New J. Chem. 2021, 45, 7830–7843. [Google Scholar] [CrossRef]
  4. Bushelyev, S.N.; Stepanov, N.F. Elektronnaya Struktura y Biologhicheskaya Aktivnost Molecul; Khimiya, Snanye: Moscow, Russia, 1989. [Google Scholar]
  5. Mammino, L.; Kabanda, M.M. Model structures for the study of acylated phloroglucinols and computational study of the caespitate molecule. J. Mol. Struct. (Theochem) 2007, 805, 39–52. [Google Scholar] [CrossRef]
  6. Mammino, L.; Kabanda, M.M. A study of the intramolecular hydrogen bond in acylphloroglucinols. J. Mol. Struct. (Theochem) 2009, 901, 210–219. [Google Scholar] [CrossRef]
  7. Kabanda, M.M.; Mammino, L. The conformational preferences of acylphloroglucinols—A promising class of biologically active compounds. Int. J. Quantum Chem. 2012, 112, 3691–3702. [Google Scholar] [CrossRef]
  8. Mammino, L.; Kabanda, M.M. Computational study of the patterns of weaker intramolecular hydrogen bonds stabilizing acylphloroglucinols. Int. J. Quantum Chem. 2012, 112, 2650–2658. [Google Scholar] [CrossRef]
  9. Mammino, L.; Kabanda, M.M. The role of additional O–H···O intramolecular hydrogen bonds for acylphloroglucinols’ conformational preferences in vacuo and in solution. Mol. Simul. 2013, 39, 1–13. [Google Scholar] [CrossRef]
  10. Mammino, L.; Kabanda, M.M. Adducts of acylphloroglucinols with explicit water molecules: Similarities and differences across a sufficiently representative number of structures. Int. J. Quantum Chem. 2010, 110, 2378–2390. [Google Scholar] [CrossRef]
  11. Mammino, L. Intramolecular hydrogen bonding patterns, conformational preferences and molecular properties of dimeric acylphloroglucinols: An ab initio and DFT study. J. Mol. Struct. 2019, 1176, 488–500. [Google Scholar] [CrossRef]
  12. Rudyk, R.; Molina, M.A.A.; Yurquina, A.; Go’mez, M.I.; Blanco, S.E.; Ferretti, F.H. A theoretical and experimental study on the structure and dipole moment of phloroglucinol in ethanol. J. Mol. Struct. (Theochem) 2004, 673, 231–238. [Google Scholar] [CrossRef]
  13. Hernandez, E.G.; Garza, J. Reactivity sites in dopamine depend on its intramolecular hydrogen bond. J. Mex. Chem. Soc. 2017, 61, 222–228. [Google Scholar]
  14. Fersht, A.R. The hydrogen bond in molecular recognition. Trend. Biochem. Sci. 1987, 12, 301–304. [Google Scholar] [CrossRef]
  15. Desiraju, G.R. Chemistry Beyond the Molecule. Nature 2001, 412, 397–400. [Google Scholar] [CrossRef] [PubMed]
  16. Nguyen, H.P.; Seto, L.O.N.; Cai, Y.; Leinala, E.K.; Borisova, S.N.; Palcic, M.N.; Evans, S.V. The influence of an intramolecular hydrogen bod in a differential recognition of inhibitory acceptor analogs by human ABO(H) blood group A and B glycosyltransferases. J. Biol. Chem. 2003, 49, 4191–4195. [Google Scholar]
  17. Sanchez, G. Introduction to “Intramolecular Hydrogen Bonding 2018”. Molecules 2019, 24, 2858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  18. Yunta, M.J.R. It is important to compute intramolecular hydrogen bonding in drug design? Am. J. Model. Optim. 2017, 5, 24–57. [Google Scholar] [CrossRef] [Green Version]
  19. Reenu, V. Evaluating the role of electron-correlation in the external prediction of the toxicity of nitrobenzenes towards Tetrahymena pyriformis. New J. Chem. 2016, 40, 2343–2353. [Google Scholar]
  20. Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C. Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (bio)organic molecules. Org. Biomol. Chem. 2007, 5, 741–758. [Google Scholar] [CrossRef]
  21. Thirman, J.; Head-Gordon, M. Electrostatic domination of the effect of electron correlation in intermolecular interactions. J. Phys. Chem. Lett. 2014, 5, 1380–1385. [Google Scholar] [CrossRef] [Green Version]
  22. Mcdonagh, J.; Silva, A.F.; Vincent, M.; Popelier, P. Quantifying electron correlation of the chemical bond. J. Phys. Chem. Lett. 2017, 8, 1937–1942. [Google Scholar] [CrossRef] [Green Version]
  23. Hongo, K.; Cuong, N.T.; Maezono, R. The importance of electron correlation on stacking interaction of adenine-thymine base-pair step in B-DNA: A quantum Monte Carlo study. J. Chem. Theory Comput. 2013, 12, 1081–1086. [Google Scholar] [CrossRef]
  24. Vos, R.J.; Hendriks, R.; van Duijneveldt, F.B. SCF, MP2, and CEPA-1 calculations on the OH ‥ O hydrogen bonded complexes (H2O)2 and (H2O-H2CO). J. Comp. Chem. 1990, 11, 1–18. [Google Scholar] [CrossRef]
  25. Mó, O.; Yáñez, M.; Elguero, J. Cooperative (nonpairwise) effects in water trimers: An ab initio molecular orbital study. J. Chem. Phys. 1992, 97, 6628–6638. [Google Scholar] [CrossRef]
  26. Ferrari, A.M.; Garrone, E.; Ugliengo, P. Ab initio study of the gas-phase equilibrium between (H2O) 4 and (H2O) 8. Chem. Phys. Lett. 1993, 212, 644–648. [Google Scholar] [CrossRef]
  27. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1998, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  28. Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
  29. Becke, A.D. Density functional thermochemistry III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  30. Alagona, G.; Ghio, C. Competitive H-bonds in vacuo and in aqueous solution for N-protonated adrenaline and its monohydrated complexes. J. Mol. Struct. (Theochem) 2007, 811, 223–240. [Google Scholar] [CrossRef]
  31. Mammino, L. Stacking interactions in cavity-containing molecular structures built from acylphloroglucinols: A computational study. Mol. Phys. 2020, 119, e1800852. [Google Scholar] [CrossRef]
  32. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
  33. Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef] [PubMed]
  34. Neese, F.; Schwabe, T.; Grimme, S. Analytic derivatives for perturbatively corrected “double hybrid” density functionals: Theory, implementation, and applications. J. Chem. Phys. 2007, 126, 124115. [Google Scholar] [CrossRef]
  35. Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
  36. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  37. Hujo, W.; Grimme, S. Comparison of the performance of dispersion-corrected density functional theory for weak hydrogen bonds. Phys. Chem. Chem. Phys. 2011, 13, 13942–13950. [Google Scholar] [CrossRef] [PubMed]
  38. Grimme, S.; Goerigk, L.; Fink, R.F. Spin-component-scaled electron correlation methods. WIREs Comput. Mol. Sci. 2012, 2, 886–906. [Google Scholar] [CrossRef]
  39. Grimme, S. Supramolecular binding thermodynamics by dispersion-corrected density functional theory. Chem. Eur. J. 2012, 18, 9955–9964. [Google Scholar] [CrossRef]
  40. Grimme, S.; Steinmetz, M. Effects of London dispersion correction in density functional theory on the structures of organic molecules in the gas phase. Phys. Chem. Chem. Phys. 2013, 15, 16031–16042. [Google Scholar] [CrossRef]
  41. Ehrlich, S.; Moellmann, J.; Grimme, S. Dispersion-corrected density functional theory for aromatic interactions in complex systems. Acc. Chem. Res. 2013, 46, 916–926. [Google Scholar] [CrossRef]
  42. Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  44. GaussView 4.1; Gaussian Inc.: Pittsburgh, PA, USA, 2006.
  45. Chem3D; Version 8.0.3; Chemoffice, Cambridge Software: St Neots, UK, 2003.
  46. Allouche, A.R. Gabedit. 2017. Available online: http://gabedit.sourceforge.net/ (accessed on 10 October 2021).
  47. Penttila, A.; Sundman, J. The structures of filixic acid. Acta Chem. Scand. 1963, 17, 191–198. [Google Scholar] [CrossRef]
  48. Penttila, A.; Sundman, J. The chemistry of Dryopteris acylphloroglucinols. J. Pharm. Pharmacol. 1970, 22, 393–404. [Google Scholar] [CrossRef] [PubMed]
  49. Hisada, S.; Shiraishi, K.; Inagaki, I. Phloroglucinol derivatives of Dryoptehs Dicklensi and some related ferns. Phytochemistry 1972, 11, 2881–2882. [Google Scholar] [CrossRef]
  50. Hisada, S.; Inoue, O.; Inagaki, I. Isolation of flavaspidic acid-PB from Dryopteris sieboldii. Phytochemistry 1973, 12, 1493–1494. [Google Scholar] [CrossRef]
  51. Hisada, S.; Inoue, O.; Inagaki, I. Phloroglucinol derivatives of Dryopteris Szeboldzi. Phytochemistry 1973, 12, 2055. [Google Scholar] [CrossRef]
  52. Lounasmaa, M.; Widén, C.J.; Huhtikangas, A. Phloroglucinol derivatives of Hagenia abyssinica. II. The structure determination of kosotoxin and protokosin. Acta Chem. Scand. 1974, 28, 1200–1208. [Google Scholar] [CrossRef] [Green Version]
  53. Puri, H.S.; Widén, C.J.; Lounasmaa, M. Phloroglucinol derivatives in Dryopterzs chrysocoma. Phytochemistry 1976, 15, 343–344. [Google Scholar] [CrossRef]
  54. Coskun, M.; Sakushima, T.A.; Nishibe, S.; Hisada, S.; Tanker, N. A phloroglucinol derivative of Dryopteris Abbreviata. Phytochemistry 1982, 21, 1453–1454. [Google Scholar] [CrossRef]
  55. Patama, T.T.; Widen, C.J. Phloroglucinol derivatives from Dryopteris fusco-atra and d. hawaizensis. Phytochemistry 1991, 30, 3305–3310. [Google Scholar] [CrossRef]
  56. Woldemariam, T.Z.; Fell, A.F.; Linley, P.A.; Bibby, M.C.; Phillips, R.M. Evaluation of the anti-tumour action and acute toxicity of kosins from Hagenia abyssinica. Pharm. Biomed. Anal. 1992, 10, 555–560. [Google Scholar] [CrossRef]
  57. Widen, K.J.; Fraser-Jenkins, C.; Reichstein, T.; Gibby, M.; Sarvela, J. Phloroglucinol derivatives in Driopteris sect Fibrillosae and related taxa (Pteridophyta, Dryopteridaceae). Ann. Bot. Fenn. 1996, 33, 69–100. [Google Scholar]
  58. Katekhaye, S.D.; Shinde, P.B.; Laddha, K.S. Isolation and HPLC method development for filixic acid PBP from Dryopteris filix-mas. Int. J. Phytopharm. 2011, 1, 1–7. [Google Scholar] [CrossRef] [Green Version]
  59. Zhao, D.; Zhao, Q.; Liu, L.; Chen, Z.; Zeng, W.; Lei, H.; Zhang, Y. Compounds from Dryopteris Fragrans (L.) Schott with Cytotoxic Activity. Molecules 2014, 19, 3345–3355. [Google Scholar] [CrossRef] [Green Version]
  60. Wang, Z.; Liu, P.; Liang, P.; Hu, X. Development of a liquid chromatography-mass spectrometry method for determination of agrimol B in rat plasma: Application to preclinical pharmacokinetics. Biomed. Chromatogr. 2015, 29, 481–484. [Google Scholar] [CrossRef] [PubMed]
  61. Han, X.; Li, Z.; Li, C.; Jia, W.; Wang, H.; Wang, C. Phytochemical constituents and biological activities of plants from the genus Dryopteris. Chem. Biodivers. 2015, 12, 1131–1162. [Google Scholar] [CrossRef] [PubMed]
  62. Wang, S.; Zhang, Q.; Zhang, Y.; Shen, C.; Wang, Z.; Wu, Q.; Zhang, Y.; Li, S.; Qiao, Y. Agrimol B suppresses adipogenesis through modulation of SIRT1-PPAR gamma signal pathway. Biochem. Biophys. Res. Commun. 2016, 477, 454–460. [Google Scholar] [CrossRef]
  63. Wang, J.; Yan, Y.; Fu, S.; Peng, B.; Bao, L.; Zhang, Y.; Hu, J.; Zeng, Z.; Geng, D.; Gao, Z. Anti-Influenza Virus (H5N1) Activity Screening on the Phloroglucinols from Rhizomes of Dryopteris crassirhizoma. Molecules 2017, 22, 431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Adamu, M.; Mukandiwa, L.; Awouafack, M.D.; Ahmed, A.S.; Eloff, J.N.; Naidoo, V. Ultrastructure changes induced by the phloroglucinol derivative agrimol G isolated from Leucosidea sericea in Haemonchus contortus. Exp. Parasitol. 2019, 207, 107780. [Google Scholar] [CrossRef]
  65. Garcia-Bustos, J.F.; Sleebs, B.E.; Gasser, R.B. An appraisal of natural products active against parasitic nematodes of animals. Parasites Vectors 2019, 12, 306. [Google Scholar] [CrossRef] [Green Version]
  66. Yim, N.; Lee, J.; Lee, B.H.; Li, W.; Ma, J.Y. Antiplatelet activity of acylphloroglucinol derivatives isolated from Dryopteris crassirhizoma. Molecules 2019, 24, 2212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  67. SHnit, U.S.T.; Ding, R.; Bi, L.; Xie, C.; Yao, M.; de Souza, P.; Xu, L.; Li, Z.; Dong, Q. Agrimol B present in Agrimonia pilosa Ledeb impedes cell cycle progression of cancer cells through G0 state arrest. Biomed. Pharmacother. 2021, 141, 111795. [Google Scholar] [CrossRef]
  68. Mammino, L. Bowl-shaped structures from acylphloroglucinols: An ab initio and DFT study. Mol. Phys. 2017, 115, 2254–2266. [Google Scholar] [CrossRef]
  69. Mammino, L. Five- and six-member bowl-shaped structures from acylphloroglucinols: An ab initio and DFT study. J. Mol. Model. 2020, 26, 13. [Google Scholar] [CrossRef] [PubMed]
  70. Mammino, L. Computational chemistry for green design in chemistry and pharmacy: Building awareness in the classroom. Sustain. Chem. Pharm. 2020, 18, 100283. [Google Scholar] [CrossRef]
  71. Nishiyama, Y.; Langan, P.; Chanzy, H. Crystalstructure and hydrogen-bonding system in cellulose Iβ from synchrotron X-ray and neutron fiber diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. [Google Scholar] [CrossRef] [PubMed]
  72. de la Paz, M.L.; Ellis, G.; Pérez, M.; Perkins, J.; Jiménez-Barbero, J.; Vicent, C. Carbohydrate hydrogen-bonding cooperativity—Intramolecular hydrogen bonds and their cooperative effect on intermolecular processes—Binding to a Hydrogen-bond acceptor molecule. Eur. J. Org. Chem. 2002, 5, 840–855. [Google Scholar] [CrossRef]
  73. Deshmukh, M.M.; Bartolotti, L.J.; Gadre, S.R. Intramolecular Hydrogen bonding and cooperative interactions in carbohydrates via the molecular tailoring approach. J. Chem. Phys. A 2008, 112, 312–321. [Google Scholar] [CrossRef]
  74. Parra, R.D.; Gong, B.; Zeng, X.C. Energetics and cooperativity in three-center hydrogen bonding interactions. II. Intramolecular hydrogen bonding systems. J. Chem. Phys. 2001, 115, 6036–6041. [Google Scholar] [CrossRef] [Green Version]
  75. Xing, B.; Yu, C.W.; Chow, K.H.; Ho, P.L.; Fu, D.; Xu, B. Hydrophobic interaction and hydrogen bonding cooperatively confer a vancomycin hydrogel: A potential candidate for biomaterials. J. Am. Chem. Soc. 2002, 124, 14846–14847. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  76. Dashnau, J.L.; Sharp, K.A.; Vanderkooi, J.M. Carbohydrate intramolecular hydrogen bonding cooperativity and its effect on water structure. J. Phys. Chem. B 2005, 109, 24152–24159. [Google Scholar] [CrossRef] [PubMed]
  77. Horowitz, S.; Trievel, R.C. Carbon-oxygen hydrogen bonding in biological structure and function. J. Biol. Chem. 2012, 287, 41576–41582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  78. Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. Evidence for resonance-assisted hydrogen bonding from crystal-structure correlations on the enol form of the beta-diketone fragment. J. Am. Chem. Soc. 1989, 111, 1023–1028. [Google Scholar] [CrossRef]
  79. Bertolasi, V.; Gilli, P.; Ferretti, V.; Gilli, G. Evidence for resonance-assisted hydrogen bonding. 2. Intercorrelation between crystal structure and spectroscopic parameters in eight intramolecularly hydrogen bonded 1, 3-diaryl-1, 3-propanedione enols. J. Am. Chem. Soc. 1991, 113, 4917–4925. [Google Scholar] [CrossRef]
  80. Guevara-Vela, J.M.; Gallegos, M.; Valentin-Rodriguez, M.A.; Costales, A.; Rocha-Rinza, T.; Pendás, A.M. On the relationships between hydrogen bond strength and the formation energy in resonance-assisted hydrogen bonds. Molecules 2021, 26, 4196. [Google Scholar] [CrossRef]
  81. Grosch, A.A.; van der Lubbe, S.C.C.; Guerra, C.F. Nature of intramolecular resonance assisted hydrogen bonding in malonalehyde and its saturated analogue. J. Phys. Chem. A 2018, 122, 1813–1820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  82. Gu, Y.L.; Kar, T.; Scheiner, S. Fundamental properties of the CH···O interaction: Is it a true hydrogen bond? J. Am. Chem. Soc. 1999, 121, 9411–9422. [Google Scholar] [CrossRef]
  83. Desiraju, G.R. The C-H···O hydrogen bond: Structural implications and supramolecular design. Acc. Chem. Res. 1996, 29, 441–449. [Google Scholar] [CrossRef]
Computation 09 00121 g001 550
Figure 1. General structure of monomeric acylphloroglucinols and atom-numbering utilised for each monomer. R is the alkyl chain of the R–C=O group of the given molecule; R^ and R* denote possible substituents in meta to the R–C=O group. In trimeric acylphloroglucinols (Figure 2), the R^ of the first monomer, the R* of the third monomer, and both R^ and R* of the inner monomer, are replaced by methylene bridges. The first atom of R^ is given the number 9, the first atom of R* is given the number 11, the first atom of R (after C7) is given the number 13, and the second atom of R (if present) is given the number 19.
Figure 1. General structure of monomeric acylphloroglucinols and atom-numbering utilised for each monomer. R is the alkyl chain of the R–C=O group of the given molecule; R^ and R* denote possible substituents in meta to the R–C=O group. In trimeric acylphloroglucinols (Figure 2), the R^ of the first monomer, the R* of the third monomer, and both R^ and R* of the inner monomer, are replaced by methylene bridges. The first atom of R^ is given the number 9, the first atom of R* is given the number 11, the first atom of R (after C7) is given the number 13, and the second atom of R (if present) is given the number 19.
Computation 09 00121 g001
Computation 09 00121 g002 550
Figure 2. General structure of trimeric acylphloroglucinols and atom numbering utilised in this work. The same atom numbering is utilised for corresponding atoms in each monomer and reflects the numbering shown in Figure 1. R is the alkyl chain of the R–C=O group of the given molecule; R^ and R* denote possible substituents in meta to the R–C=O group. The numbers of the atoms of the second monomer (inner monomer) are primed and the numbers of those of the third monomer are double-primed.
Figure 2. General structure of trimeric acylphloroglucinols and atom numbering utilised in this work. The same atom numbering is utilised for corresponding atoms in each monomer and reflects the numbering shown in Figure 1. R is the alkyl chain of the R–C=O group of the given molecule; R^ and R* denote possible substituents in meta to the R–C=O group. The numbers of the atoms of the second monomer (inner monomer) are primed and the numbers of those of the third monomer are double-primed.
Computation 09 00121 g002
Computation 09 00121 g003 550
Figure 3. Symbols utilised to denote relevant geometry features of each monomeric acylphloroglucinol unit. In the above images, R is the alkyl chain of the R–C=O group, R^ denotes the methylene bridge for the first monomer and R* denotes the methylene bridge for the third monomer; both R^ and R* denote methylene bridges for the central monomer. In terms of conformer-types of individual monomers, the letter d informs that the first IHB is of the H15⋅⋅⋅O14 type (atom numbering in Figure 2) and the letter s that it is of the H17⋅⋅⋅O14 type. A d-type conformer is r if H16 is oriented towards the side of the first IHB and w if it is oriented to the other side; an s-type conformer is w if H16 is oriented towards the side of the first IHB and r if it is oriented to the other side. The letter u informs that the OH ortho to the acyl group and not engaged in the first IHB is oriented toward R.
Figure 3. Symbols utilised to denote relevant geometry features of each monomeric acylphloroglucinol unit. In the above images, R is the alkyl chain of the R–C=O group, R^ denotes the methylene bridge for the first monomer and R* denotes the methylene bridge for the third monomer; both R^ and R* denote methylene bridges for the central monomer. In terms of conformer-types of individual monomers, the letter d informs that the first IHB is of the H15⋅⋅⋅O14 type (atom numbering in Figure 2) and the letter s that it is of the H17⋅⋅⋅O14 type. A d-type conformer is r if H16 is oriented towards the side of the first IHB and w if it is oriented to the other side; an s-type conformer is w if H16 is oriented towards the side of the first IHB and r if it is oriented to the other side. The letter u informs that the OH ortho to the acyl group and not engaged in the first IHB is oriented toward R.
Computation 09 00121 g003
Computation 09 00121 g004 550
Figure 4. Monomers’ conformer types and mutual orientations of the methylene bridges, illustrated through the lowest energy conformers of structure T1. Space-filling models are included to better highlight the nature of the geometries and the intramolecular hydrogen bonds (both the first IHB of each monomer and the intermonomer hydrogen bonds). The geometries of individual conformers are identified starting from the left and proceeding to the right. T1-1 and T1-2 have outstretched geometries. The geometry of the first (outer-left) monomer is d-r (H15⋅⋅⋅O14 first IHB) and the geometry of the second monomer is s-w (H17′⋅⋅⋅O14′ first IHB) in both conformers; the geometry of the third monomer is s-w in T1-1 (H17″⋅⋅⋅O14″ first IHB) and d-r in T1-2 (H15″⋅⋅⋅O14″ first IHB). The orientations identified by the acyl groups of the monomers (from left to right) are up—up—down in T1-1 and T1-1-y, and up—up—up in T1-2. T1-1 and T1-1-y differ by the mutual orientations of the two methylene bridges: opposite orientation in T1-1, resulting in an outstretched shape, and same orientations in T1-1-y, resulting in a half-bowl shape.
Figure 4. Monomers’ conformer types and mutual orientations of the methylene bridges, illustrated through the lowest energy conformers of structure T1. Space-filling models are included to better highlight the nature of the geometries and the intramolecular hydrogen bonds (both the first IHB of each monomer and the intermonomer hydrogen bonds). The geometries of individual conformers are identified starting from the left and proceeding to the right. T1-1 and T1-2 have outstretched geometries. The geometry of the first (outer-left) monomer is d-r (H15⋅⋅⋅O14 first IHB) and the geometry of the second monomer is s-w (H17′⋅⋅⋅O14′ first IHB) in both conformers; the geometry of the third monomer is s-w in T1-1 (H17″⋅⋅⋅O14″ first IHB) and d-r in T1-2 (H15″⋅⋅⋅O14″ first IHB). The orientations identified by the acyl groups of the monomers (from left to right) are up—up—down in T1-1 and T1-1-y, and up—up—up in T1-2. T1-1 and T1-1-y differ by the mutual orientations of the two methylene bridges: opposite orientation in T1-1, resulting in an outstretched shape, and same orientations in T1-1-y, resulting in a half-bowl shape.
Computation 09 00121 g004
Computation 09 00121 g005 550
Figure 5. Effect of the monomers’ mutual orientation on the conformer geometry. In T1-1, two consecutive monomers are oriented in the same way (up—down—down orientation). In T1-2, the orientations of the monomers are alternate (up—down—up orientation). In T1-3, the monomers are oriented in the same way (up—up—up orientation). Space-filling models are used to better highlight the mutual orientations of the planes of the three benzene rings.
Figure 5. Effect of the monomers’ mutual orientation on the conformer geometry. In T1-1, two consecutive monomers are oriented in the same way (up—down—down orientation). In T1-2, the orientations of the monomers are alternate (up—down—up orientation). In T1-3, the monomers are oriented in the same way (up—up—up orientation). Space-filling models are used to better highlight the mutual orientations of the planes of the three benzene rings.
Computation 09 00121 g005
Computation 09 00121 g006 550
Figure 6. Illustration of the ‘crowding’ of methyl groups in the lower rim of the half-bowl-shaped conformers of trimeric acylphloroglucinols in which the OHs at C4 and C4″ are replaced by OCH3 groups and methyl groups are present at C5 and C3″. The figure shows the 1-y-in-in conformer of T9-M5,3″-ET6,4″.
Figure 6. Illustration of the ‘crowding’ of methyl groups in the lower rim of the half-bowl-shaped conformers of trimeric acylphloroglucinols in which the OHs at C4 and C4″ are replaced by OCH3 groups and methyl groups are present at C5 and C3″. The figure shows the 1-y-in-in conformer of T9-M5,3″-ET6,4″.
Computation 09 00121 g006
Computation 09 00121 g007 550
Figure 7. Illustration of the geometry changes in terms of ‘coming closer’ of atoms, resulting from the addition of dispersion correction. The T9-2y conformer is selected as example. Distances referred to the upper rim and not depending on the flexibility of the R and R″ chains can be considered as realistic indicators of the phenomenon; for instance, the distances C1----C1″, C13----C13″, O8----O12″ and O12----O8″ respectively have the lengths (Å) 7.477, 7.029, 4.233 and 10.865 in the DFT results and 6.373, 5.487, 3.791 and 9.187 in the DFT-D3 results.
Figure 7. Illustration of the geometry changes in terms of ‘coming closer’ of atoms, resulting from the addition of dispersion correction. The T9-2y conformer is selected as example. Distances referred to the upper rim and not depending on the flexibility of the R and R″ chains can be considered as realistic indicators of the phenomenon; for instance, the distances C1----C1″, C13----C13″, O8----O12″ and O12----O8″ respectively have the lengths (Å) 7.477, 7.029, 4.233 and 10.865 in the DFT results and 6.373, 5.487, 3.791 and 9.187 in the DFT-D3 results.
Computation 09 00121 g007
Computation 09 00121 g008a 550Computation 09 00121 g008b 550
Figure 8. Intramolecular hydrogen bonds (IHBs) in trimeric acylphloroglucinols. The first IHBs of individual monomers are denoted by blue dashed segments and the hydrogen bonds between monomers by purple dashed segments. The three lowest energy conformers of T1 (all with the O8–H15⋅⋅⋅O14 first IHB in the first monomer) are utilised to illustrate the three different combinations of monomers’ orientations and some of the resulting possible IHB and IHB-cooperativity patterns.
Figure 8. Intramolecular hydrogen bonds (IHBs) in trimeric acylphloroglucinols. The first IHBs of individual monomers are denoted by blue dashed segments and the hydrogen bonds between monomers by purple dashed segments. The three lowest energy conformers of T1 (all with the O8–H15⋅⋅⋅O14 first IHB in the first monomer) are utilised to illustrate the three different combinations of monomers’ orientations and some of the resulting possible IHB and IHB-cooperativity patterns.
Computation 09 00121 g008aComputation 09 00121 g008b
Table
Table 1. Symbols (T followed by a number) utilised to denote the different combinations of acyl groups in the calculated trimeric acylphloroglucinols. The same symbol is used in the acronyms denoting different molecules having the same combination of acyl groups.
Table 1. Symbols (T followed by a number) utilised to denote the different combinations of acyl groups in the calculated trimeric acylphloroglucinols. The same symbol is used in the acronyms denoting different molecules having the same combination of acyl groups.
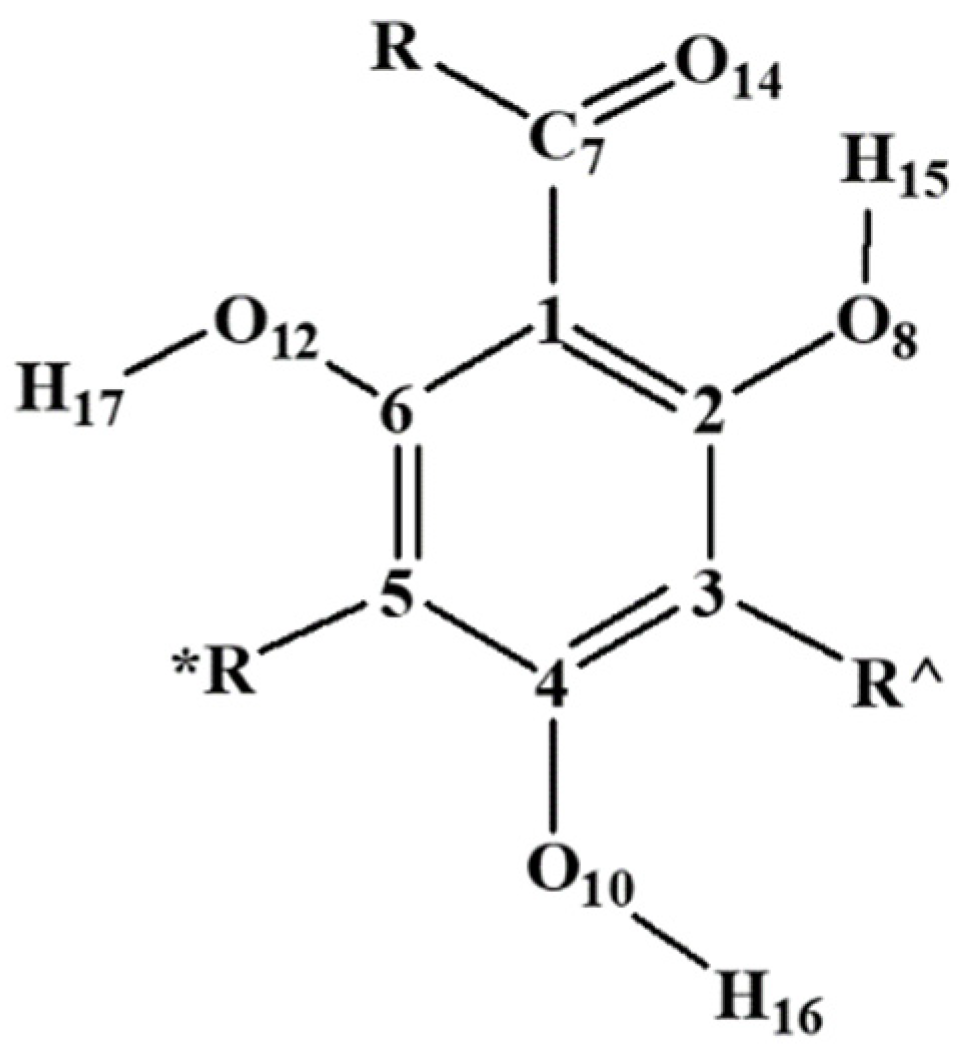
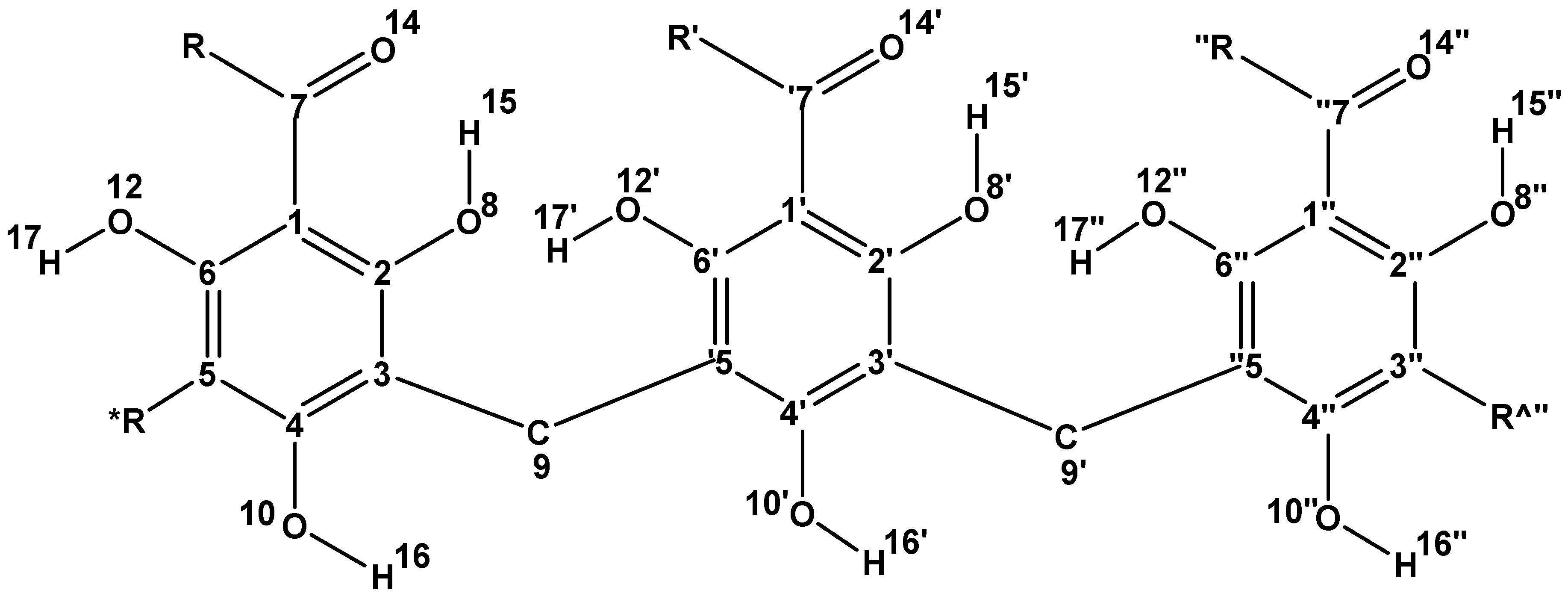
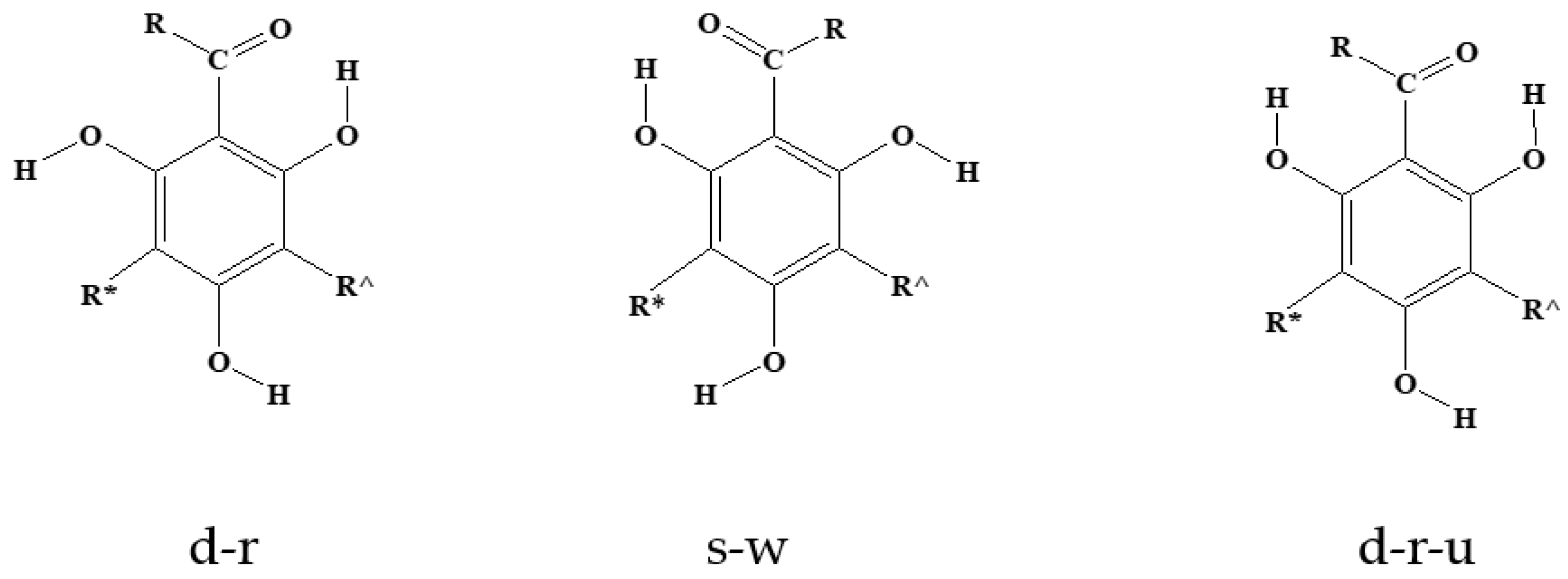
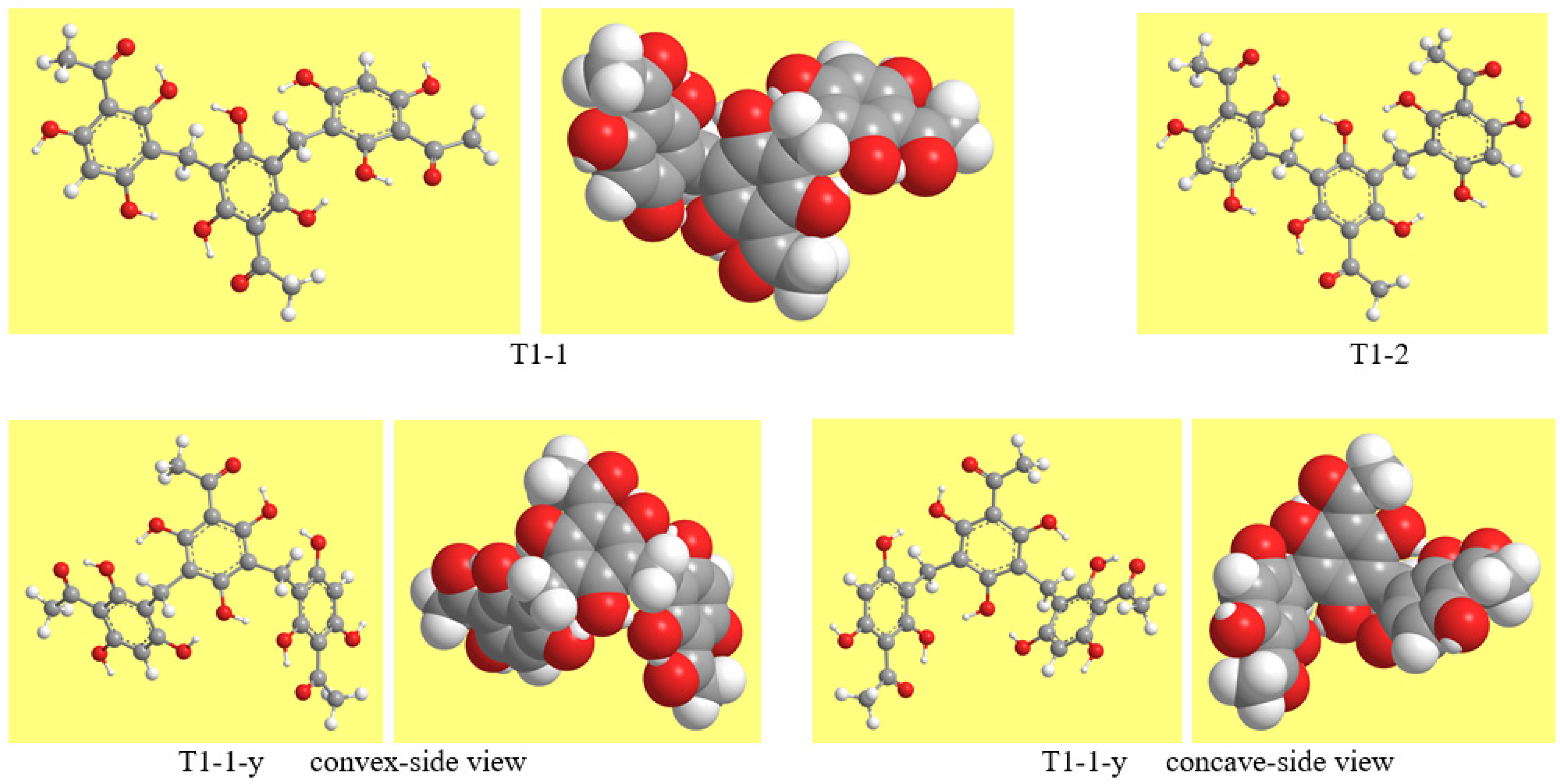
SymbolR, R′ and R″
T1R = R′ = R″ = CH3
T2R = R″ = CH3, R′ = CH2CH2CH3
T3R = R″ = CH3, R′ = CH(CH3)CH2CH3
T4R = CH2CH3, R′ = CH2CH2CH3, R″ = CH3
T5R = R″ = CH2CH3, R′ = CH2CH2CH3
T6R = R″ = CH2CH2CH3, R′ = CH3
T7R = R′ = CH2CH2CH3, R″ = CH3
T8R = R′ = CH2CH2CH3, R″ = CH2CH3
T9R = R′ = R″ = CH2CH2CH3
T10R = R′ = R″ = CH(CH3)2
T11R = CH(CH3)2, R′ = CH(CH3)CH2CH3, R″ = CH3
T12R = CH2CH2CH2CH3, R′ = R″ = CH2CH2CH3
T13R = CH(CH3)CH2CH3, R′ = R″= CH2CH2CH3
T14R = CH(CH3)CH2CH3, R′ = R″= CH(CH3)2
Table
Table 2. List of the calculated trimeric acylphloroglucinols. The molecules are denoted using acronyms. The meaning of the initial components of the acronyms (indicating the nature of the R chains of the three monomeric units) is explained in Table 1. Substituents on the outer rings are denoted by uppercase letters followed by the number of the C atoms to which a given substituent is attached; M denotes a methyl group, ET an OCH3 group, and KT a keto O. The atom numbering is shown in Figure 2.
Table 2. List of the calculated trimeric acylphloroglucinols. The molecules are denoted using acronyms. The meaning of the initial components of the acronyms (indicating the nature of the R chains of the three monomeric units) is explained in Table 1. Substituents on the outer rings are denoted by uppercase letters followed by the number of the C atoms to which a given substituent is attached; M denotes a methyl group, ET an OCH3 group, and KT a keto O. The atom numbering is shown in Figure 2.
Acronyms Denoting the Calculated Trimeric Acylphloroglucinols
T1T8-KT2-M5,5,3″T10
T2-KT2,6″-M5,5,3″,3″T8-KT6″-M5,3″,3″T10-ET6,2″
T3-ET6,2″T8-KT2,6″-M5,5,3″,3″T10-M5,3″-ET6,2″
T3-M5,3″-ET6,2″T9T10-M5,3″-ET6,2″,6″
T4-KT2,6″-M5,5,3″,3″T9-M5,5′T10-KT2,6″-M5,5,3″,3″
T5-KT6″-M3″,3″-ET4T9-ET6,2″T11-ET6,2″
T5-KT2,6″-M5,5,3″,3″T9-M5,3″-ET6,2″T11-M5,3″-ET6,2″
T6-M5,3″-ET6,4″T9-M5,3″-ET6,4″T12-KT2-M5,5,3″
T7T9-KT6″-M5,3″,3″T12-KT6″-M5,3″,3″
T7-ET6,2″T9-KT6″-M3″,3″-ET4T13-ET6,2″
T7-M5,3″-ET6,2″T9-KT6″-M5,3″,3″-ET6T13-M5,3″-ET6,2″
T7-KT6″-M5,3″,3″T9-KT2,6″-M5,5,3″,3″T14-ET6,2″
T7-KT2,6″-M5,5,3″,3″ T14-M5,3″-ET6,2″
Table
Table 3. Ranges of the lowering effect of Grimme’s correction on the estimation of the energy of the conformers of the calculated trimeric acylphloroglucinols. The lowering is evaluated as the magnitude of the difference «energy in the DFT/B3LYP/6-31+G(d,p)/D-3 result minus energy in the DFT/B3LYP/6-31+G(d,p) result». When only one conformers-pair is present for a given molecule, the value for each conformer is reported, and the two values are separated by a comma.
Table 3. Ranges of the lowering effect of Grimme’s correction on the estimation of the energy of the conformers of the calculated trimeric acylphloroglucinols. The lowering is evaluated as the magnitude of the difference «energy in the DFT/B3LYP/6-31+G(d,p)/D-3 result minus energy in the DFT/B3LYP/6-31+G(d,p) result». When only one conformers-pair is present for a given molecule, the value for each conformer is reported, and the two values are separated by a comma.
MoleculeEnergy Difference Range (kcal/mol)
Outstretched GeometryHalf-Bowl Geometry
T147.89–48.0948.24–50.33
T2-KT2,6″-M5,5,3″,3″65.4966.05
T3-ET6,2″59.7360.37
T3-M5,3″-ET6,2″66.9567.31
T4-KT2,6″-M5,5,3″,3″67.5068.06
T5-KT2,6″-M5,5,3″,3″69.5170.21
T5-KT6″-M3″,3″-ET4 65.2265.76
T6-M5,3″-ET6,4″67.4367.77–69.54
T755.68–55.8155.96–57.45
T7-ET6,2″59.9360.23
T7-M5,3″-ET6,2″67.1567.62
T7-KT6″-M5,3″,3″64.83–65.0565.27–67.48
T7-KT2,6″-M5,5,3″,3″69.3669.89
T8-KT6″-M5,3″,3″66.84–67.0867.33–70.52
T8-KT2-M5,5,3″66.89–68.2767.29–71.20
T8-KT2,6″-M5,5,3″,3″71.3872.09
T959.49–59.6759.77–62.44
T9-M5,3″64.21–64.3864.61–67.28
T9-ET6,2″63.8064.12
T9-M5,3″-ET6,2″71.1071.57
T9-M5,3″-ET6,4″71.3171.64–73.42
T9-KT6″-M5,3″,3″68.70–68.9569.15–71.83
T9-KT6″-M3″,3″-ET468.9169.45
T9-KT6″-M5,3″,3″-ET672.1672.65
T9-KT2,6″-M5,5,3″,3″73.2474.59
T1062.98–63.4263.25–65.07
T10-ET6,2″67.5467.81
T10-M5,3″-ET6,2″74.6275.10
T10-M5,3″-ET6,2″,6″79.1679.41
T10-KT2,6″-M5,5,3″,3″78.1377.30
T11-ET6,2″64.6564.98
T11-M5,3″-ET6,2″71.5972.64
T12-KT2-M5,5,3″ 70.46–70.7170.95–75.27
T12-KT6″-M5,3″,3″ 70.46–70.7370.94–74.29
T13-ET6,2″67.2367.56
T13-M5,3″-ET6,2″74.8675.35
T14-ET6,2″70.1170.21
T14-M5,3″-ET6,2″77.1377.31–77.66
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Mammino, L. Correlation Effects in Trimeric Acylphloroglucinols. Computation 2021, 9, 121. https://doi.org/10.3390/computation9110121

AMA Style

Mammino L. Correlation Effects in Trimeric Acylphloroglucinols. Computation. 2021; 9(11):121. https://doi.org/10.3390/computation9110121

Chicago/Turabian Style

Mammino, Liliana. 2021. "Correlation Effects in Trimeric Acylphloroglucinols" Computation 9, no. 11: 121. https://doi.org/10.3390/computation9110121

APA Style

Mammino, L. (2021). Correlation Effects in Trimeric Acylphloroglucinols. Computation, 9(11), 121. https://doi.org/10.3390/computation9110121

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop