TS Fuzzy Robust Sampled-Data Control for Nonlinear Systems with Bounded Disturbances
Abstract
:1. Introduction
- (i)
- Reachable set bounding and fault-tolerant control design are properly considered for the first time in nonlinear fuzzy systems with bounded disturbances and actuator failures.
- (ii)
- On the basis of integral inequality and Lyapunov stability theory, a new set of sufficient conditions is derived to ensure that the proposed TS fuzzy model is asymptotically stable while satisfying the performance index.
- (iii)
- Demonstration and evaluation of effectiveness pertaining to the proposed method with two numerical simulations.
2. Description of Nonlinear Fuzzy System
3. Sampled-Data Control Design
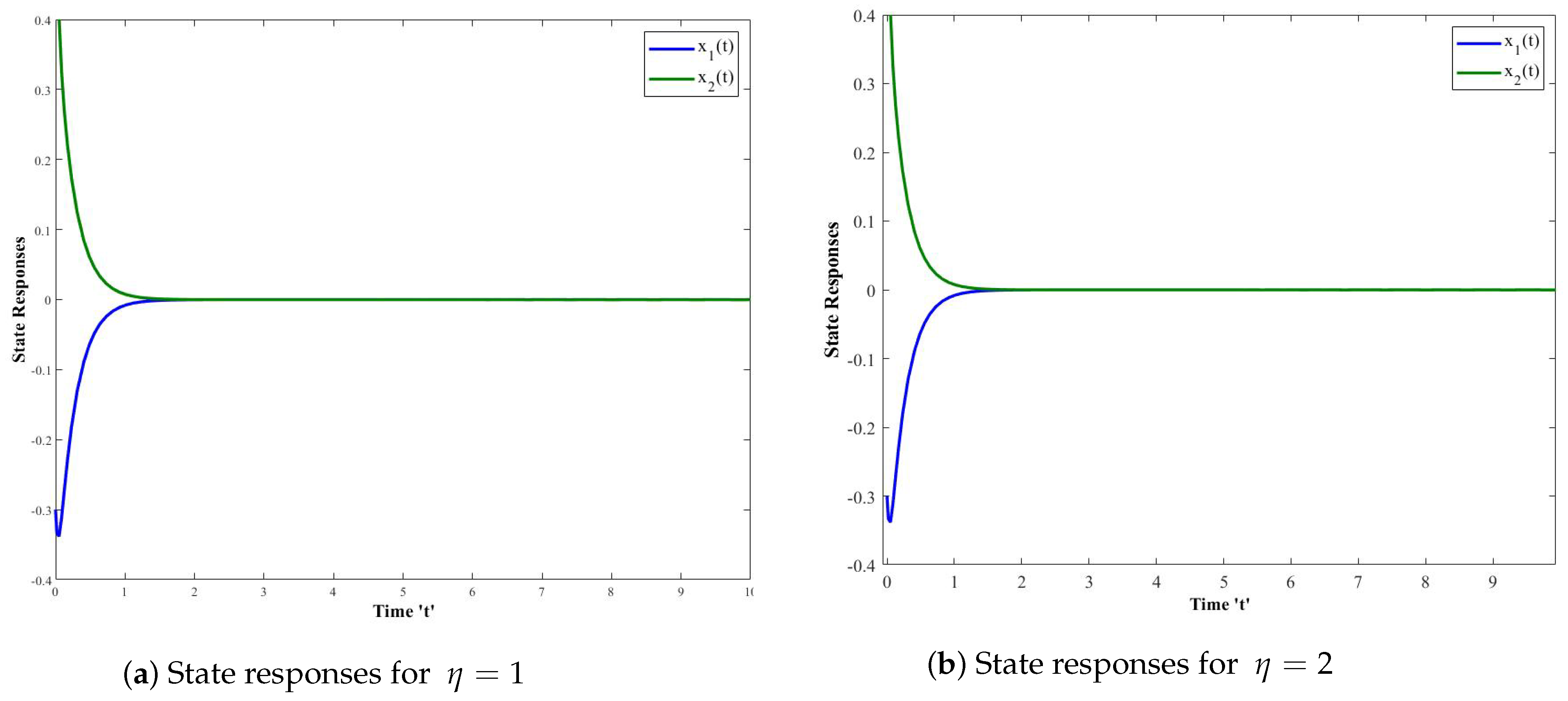
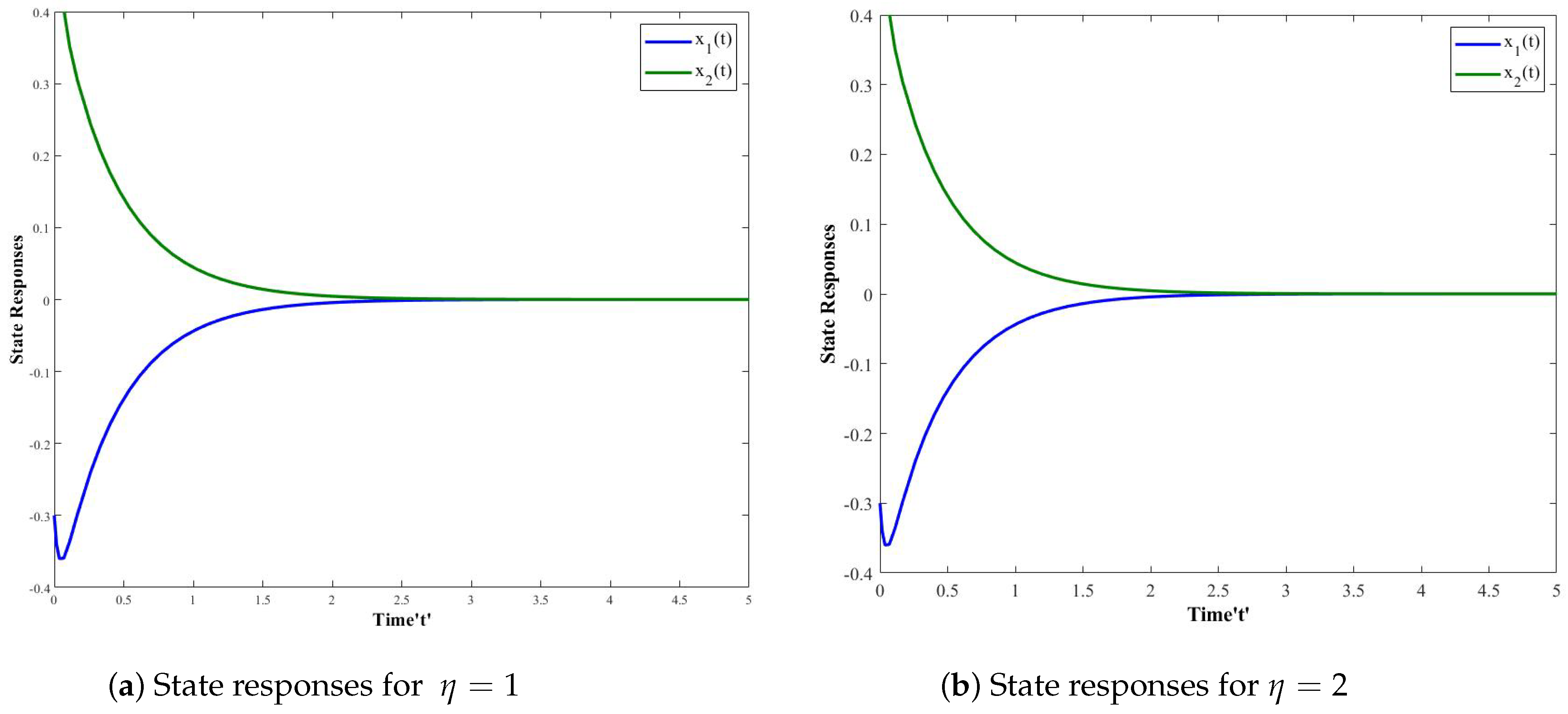
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, X.; Zhong, S.; Wang, J.; Shi, K. Robust H∞ control for uncertain delayed T-S fuzzy systems with stochastic packet dropouts. Appl. Math. Comput. 2020, 385, 125432. [Google Scholar] [CrossRef]
- Senan, S. An Analysis of global stability of Takagi Sugeno fuzzy cohengrossberg neural networks with time delays. Neural Process. Lett. 2018, 10, 1–12. [Google Scholar]
- Senthilraj, S.; Raja, R.; Zhu, Q.; Samidurai, R. Effects of leakage delays and impulsive control in dissipativity analysis of Takagi-Sugeno fuzzy neural networks with randomly occurring uncertainties. J. Frankl. Inst. 2017, 354, 3574–3593. [Google Scholar]
- Shen, H.; Xiang, M.; Huo, S.; Wu, Z.G.; Park, J.H. Finite-time H∞ asynchronous state estimation for discrete-time fuzzy Markov jump neural networks with uncertain measurements. Fuzzy Sets Syst. 2019, 356, 113–128. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, G.H. Event-based output tracking control for fuzzy networked control systems with network-induced delays. Appl. Math. Comput. 2019, 346, 513–530. [Google Scholar] [CrossRef]
- Souza, F.O.; Campos, V.C.S.; Palhares, R.M. On delay-dependent stability conditions for Takagi-Sugeno fuzzy systems. J. Frankl. Inst. 2014, 351, 3707–3718. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, G.; Yan, H.; Chen, Q. Sampled-data control of nonlinear networked systems with time-delay and quantization. Int. J. Robust Nonlinear Control 2016, 26, 919–933. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, B.; Park, J.H.; Kang, W. Sampled-data reliable control for T-S fuzzy semi-Markovian jump system and its application to single link robot arm model. IET Control. Theory Appl. 2017, 11, 1904–1912. [Google Scholar] [CrossRef]
- Liu, W.; Lim, C.C.; Shi, P.; Xu, S. Sampled-data fuzzy control for a class of nonlinear systems with missing data and disturbances. Fuzzy Sets Syst. 2017, 306, 63–86. [Google Scholar] [CrossRef]
- Liu, Y.; Park, J.H.; Guo, B.Z.; Shu, Y. Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans. Fuzzy Syst. 2018, 26, 1040–1045. [Google Scholar] [CrossRef]
- Su, L.; Shen, H. Mixed H∞ and passive synchronization for complex dynamical networks with sampled-data control. Appl. Math. Comput. 2015, 259, 931–942. [Google Scholar]
- Wang, Q.; Zhang, Y.; Dong, C.; Jiang, Y. H∞ output tracking control for flight control systems with time-varying delay. Chin. J. Aeronaut. 2013, 26, 1251–1258. [Google Scholar]
- Wu, Z.G.; Park, J.H.; Su, H.; Song, B.; Chu, J. Mixed H∞ and passive filtering for singular systems with time delays. Signal Process. 2013, 93, 1705–1711. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, Y.; Zou, Y.; Karimi, H.R. Adaptive sliding mode reliable control for switched systems with actuator degradation. IET Control Theory Appl. 2015, 9, 1197–1204. [Google Scholar] [CrossRef]
- Hu, H.; Jiang, B.; Yang, H. Reliable guaranteed-cost control of delta operator switched systems with actuator faults: Mode-dependent average dwell-time approach. IET Control. Theory Appl. 2016, 10, 17–23. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Y.; Xia, J.; Park, J.H.; Wang, Z. Fault-tolerant leader-following consensus for multi-agent systems subject to semi-Markov switching topologies: An event-triggered control scheme. Nonlinear Anal. Syst. 2019, 34, 92–107. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fuzzy adaptive fault-tolerant control of unknown nonlinear systems with time-varying structure. IEEE Trans. Fuzzy Syst. 2019, 27, 1904–1916. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, H.; Wang, Y.; Cai, Y. Dynamic output feedback-based fault-tolerant control design for T-S fuzzy systems with model uncertainties. ISA Trans. 2018, 81, 32–45. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Wang, Y.; Zhang, H.; Xie, X. A new method of fault estimation and tolerant control for fuzzy systems against time-varying delay. Nonlinear Anal. Hybrid Syst. 2020, 38, 100942. [Google Scholar] [CrossRef]
- Feng, Z.; Lam, J. On reachable set estimation of singular systems. Automatica 2015, 52, 146–153. [Google Scholar] [CrossRef]
- Poongodi, T.; Saravanakumar, T.; Mishra, P.P.; Zhu, Q. Extended dissipative control for Markovian jump time-delayed systems with bounded disturbances. Math. Probl. Eng. 2020, 2020, 5685324. [Google Scholar] [CrossRef]
- Feng, Z.; Zheng, W.X. On reachable set estimation of delay Markovian jump systems with partially known transition probabilities. J. Frankl. Inst. 2016, 353, 3835–3856. [Google Scholar] [CrossRef]
- Lam, J.; Zhang, B.; Chen, Y.; Xu, S. Reachable set estimation for discrete-time linear systems with time delays. Int. J. Robust Nonlinear Control 2015, 25, 269–281. [Google Scholar] [CrossRef]
- Sheng, Y.; Shen, Y. Improved reachable set bounding for linear time-delay systems with disturbances. J. Frankl. Inst. 2016, 353, 2708–2721. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Wang, Y.; Yang, G.H. Control synthesis of continuous-time T-S fuzzy systems with local nonlinear models. IEEE Trans. Syst. Man, Cybern. Part B (Cybern.) 2009, 39, 1245–1258. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, J. Robust sampled-data stabilization of uncertain fuzzy systems via input delay approach. Inf. Sci. 2012, 198, 169–176. [Google Scholar] [CrossRef]
- Saravanakumar, T.; Muoi, N.H.; Zhu, Q. Finite-time sampled-data control of switched stochastic model with non-deterministic actuator faults and saturation nonlinearity. J. Frankl. Inst. 2020, 357, 13637–13665. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, J.; Su, C.Y. T-S fuzzy-model-based robust H∞ design for networked control systems with uncertainties. IEEE Trans. Ind. Inform. 2007, 3, 289–301. [Google Scholar] [CrossRef]

| MAUB of | ||
|---|---|---|
| Ref. [28] | 0.2 | 1.2448 |
| Our method | 0.6 | 1.0162 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poongodi, T.; Mishra, P.P.; Lim, C.P.; Saravanakumar, T.; Boonsatit, N.; Hammachukiattikul, P.; Rajchakit, G. TS Fuzzy Robust Sampled-Data Control for Nonlinear Systems with Bounded Disturbances. Computation 2021, 9, 132. https://doi.org/10.3390/computation9120132
Poongodi T, Mishra PP, Lim CP, Saravanakumar T, Boonsatit N, Hammachukiattikul P, Rajchakit G. TS Fuzzy Robust Sampled-Data Control for Nonlinear Systems with Bounded Disturbances. Computation. 2021; 9(12):132. https://doi.org/10.3390/computation9120132
Chicago/Turabian StylePoongodi, Thangavel, Prem Prakash Mishra, Chee Peng Lim, Thangavel Saravanakumar, Nattakan Boonsatit, Porpattama Hammachukiattikul, and Grienggrai Rajchakit. 2021. "TS Fuzzy Robust Sampled-Data Control for Nonlinear Systems with Bounded Disturbances" Computation 9, no. 12: 132. https://doi.org/10.3390/computation9120132
APA StylePoongodi, T., Mishra, P. P., Lim, C. P., Saravanakumar, T., Boonsatit, N., Hammachukiattikul, P., & Rajchakit, G. (2021). TS Fuzzy Robust Sampled-Data Control for Nonlinear Systems with Bounded Disturbances. Computation, 9(12), 132. https://doi.org/10.3390/computation9120132







