Adjustment of Planned Surveying and Geodetic Networks Using Second-Order Nonlinear Programming Methods
Abstract
:1. Introduction
- (1)
- nonlinear programming methods allow the nonlinear and linear conditions that limit the objective function to be taken into account;
- (2)
- these methods allow the solving of large systems of equations using algorithms that are most suitable for implementation on modern computers;
- (3)
- using some nonlinear programming methods (such as second-order Newton’s method) makes it possible to solve nonlinear equations without linearizing the original parametric equations;
- (4)
- using nonlinear programming methods, it is possible to obtain a solution not only using the objective function of the least squares method, which is a classical method in geodesy and surveying, but also in other ways in accordance with the selected criterion function.
- (1)
- a large number of previously developed methods that have clearly formulated algorithms that are easy to implement with a computer;
- (2)
- the ability to use several methods at once at different stages of solving one problem, in order to obtain the best result.
- (1)
- the method has a quadratic convergence rate of the iterative process, in contrast to first-order methods (gradient methods), which have a linear convergence rate;
- (2)
- for any quadratic objective function with a positive definite matrix of second partial derivatives (Hessian matrix), the method gives an exact solution in one iteration;
- (3)
- low sensitivity to the choice of preliminary values of the determined parameters, in comparison with gradient methods.
2. Materials and Methods
2.1. Mathematical Justification for Solving the Task
- (1)
- if the function is quadratic, then to find the minimum of the objective function , when the preliminary values of the determined parameters are close to the true ones, one iteration is required;
- (3)
- the use of the second partial derivatives in the iterative process allows the increase of the convergence rate, and also to increase the accuracy of the results;
- (3)
- this method is less sensitive to the choice of the initial value of the parameter than the first-order methods.
- By the absolute value of the difference between the subsequent and previous values of the determined parameter (7):
- By the absolute value of the difference between the values of the objective function, the next and the previous iteration (8):
- By the absolute value of the derivative of the objective function at the current iteration (9):
2.2. Geodetic Data for Solving the Task
- (1)
- drawing up parametric communication equations;
- (2)
- linearization of these equations by expanding into a Taylor series taking into account only first-order derivatives;
- (3)
- solution of the obtained systems of equations based on the least squares method.
3. Results
4. Discussion
- The objective function , depending on the parameters to be determined, is set.
- The preliminary value of the parameter and the increment step are set.
- The increment is added and subtracted only to the first parameter , the rest of the parameters are also given preliminary values, but they remain unchanged.
- The values of the objective function are calculated with the changed parameters and
- The new value of the determined parameter is calculated by the Formula (18):
- The next parameter is changed and the new value of the function is calculated, only the value is substituted into the target function instead of the parameter .
- Step 1: The user creates an objective function and chooses with what constraint he/she will find the minimum of the objective function (by the method of least squares or by the method of least modules); it is recommended to use the least squares method for solving geodetic tasks;
- Step 2: Sets any preliminary values of the parameters to be determined (it is recommended to set either previously known to true values or accept all parameters as equal to zero);
- Step 3: using the methods of quadratic approximation, namely the Powell–DSK method, in two approximations, the preliminary values are refined according to Formula (18);
- Step 4: The Hessian matrix is created, and its positiveness is checked; if the condition is met, then the revised preliminary values are used in the next step. If the Hessian matrix is not positive, then step 3 is performed again;
- Step 5: The obtained refined preliminary values are used in the second-order Newton’s method, the matrix of the first derivatives and the matrix of the second derivatives are formed;
- Step 6: An iterative process is performed according to Formula (5) until the stopping criterion is met (Formula (7)). The stopping criterion is chosen by the user;
- Step 7: The accuracy of the obtained parameter values is evaluated. To estimate the accuracy of the obtained parameters, an inverse weight matrix is used.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abu, D.I. Mathematical Processing and Analysis of the Accuracy of Ground Spatial Geodetic Networks by Methods of Nonlinear Programming and Linear Algebra. Ph.D. Thesis, Polotsk State University, Novopolotsk, Belarus, 1998; 142p. [Google Scholar]
- Nikonov, A.; Kosarev, N.; Solnyshkova, O.; Makarikhina, I. Geodetic base for the construction of ground-based facilities in a tropical climate. In Proceedings of the E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Volume 91, p. 7019. [Google Scholar] [CrossRef]
- Liu, B.; Wei, Y.; Zhi, S.; Zhao, W.; Lin, J. Optimization of location of robotic total station in 3D deformation monitoring of multiple points. In Information Technology in Geo-Engineering; Springer Series in Geomechanics and Geoengineering; Springer: Cham, Switzerland, 2018; pp. 730–737. [Google Scholar] [CrossRef]
- Liu, G.H. Recovering 3D shape and motion from image sequences using affine approximation. In Proceedings of the 2009 Second International Conference on Information and Computing Science, Manchester, UK, 21–22 May 2009; IEEE: Piscataway, NJ, USA, 2009; Volume 2, pp. 349–352. [Google Scholar] [CrossRef]
- Suzuki, T. Position and attitude estimation by multiple GNSS receivers for 3D mapping. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS + 2016), Portland, OR, USA, 12–16 September 2016; Volume 2, pp. 1455–1464. [Google Scholar]
- Vasilieva, N.V.; Boykov, A.V.; Erokhina, O.O.; Trifonov, A.Y. Automated digitization of radial charts. J. Min. Inst. 2021, 247, 82–87. [Google Scholar] [CrossRef]
- Kopylova, N.S.; Starikov, I.P. Methods of displaying geospatial information using cartographic web technologies for the arctic region and the continental shelf. Geod. Kartogr. 2021, 971, 15–22. [Google Scholar] [CrossRef]
- Kovyazin, V.F.; Lepikhina, O.Y.; Zimin, V.P. Prediction of Cadastral Value of Land in a Single-Industry Town by the Regression Model; Bulletin of the Tomsk Polytechnic University; Kovyazin, V.F., Ed.; Tomsk Polytechnic University, Geo Assets Engineering: Tomsk Oblast, Russia, 2017; Volume 328, pp. 6–13. [Google Scholar]
- Rybkina, A.M.; Demidova, P.M.; Kiselev, V.A. Analysis of the application of deterministic interpolation methods for land cadastral valuation of low-rise residential development of localities. Int. J. Appl. Eng. Res. 2017, 12, 10834–10840. [Google Scholar]
- Rybkina, A.M.; Demidova, P.M.; Kiselev, V. A working-out of the geostatistical model of mass cadastral valuation of urban lands evidence from the city Vsevolozhsk. Int. J. Appl. Eng. Res. 2016, 11, 11631–11638. [Google Scholar]
- Kuzin, A.A.; Kovshov, S.V. Accuracy evaluation of terrain digital models for landslide slopes based on aerial laser scanning results. Ecol. Environ. Conserv. 2017, 23, 908–914. [Google Scholar]
- Pravdina, E.A.; Lepikhina, O.J. Laser scanner data capture time management. ARPN J. Eng. Appl. Sci. 2017, 12, 1649–1661. [Google Scholar]
- Demenkov, P.A.; Goldobina, L.A.; Trushko, O.V. Geotechnical barrier options with changed geometric parameters. Int. J. GEOMATE 2020, 19, 58–65. [Google Scholar] [CrossRef]
- Demenkov, P.A.; Goldobina, L.A.; Trushko, V.L. The implementation of building information modeling technologies in the training of bachelors and masters at Saint Petersburg mining University. ARPN J. Eng. Appl. Sci. 2020, 15, 803–813. [Google Scholar]
- Goldobina, L.A.; Demenkov, P.A.; Trushko, O.V. Ensuring the safety of construction and installation works during the construction of buildings and structures. J. Min. Inst. 2019, 239, 583–595. [Google Scholar] [CrossRef] [Green Version]
- Katuntsov, E.; Kosarev, O. Correlation processing of radar signals with multilevel quantization. Res. J. Appl. Sci. 2016, 11, 624–627. [Google Scholar]
- Kochneva, A.A.; Kazantsev, A.I. Justification of quality estimation method of creation of digital elevation models according to the data of airborne laser scanning when designing the motor ways. J. Ind. Pollut. Control. 2017, 33, 1000–1006. [Google Scholar]
- Karavaichenko, M.G.; Gazaleev, L.I. Numerical modeling of a double-walled spherical reservoir. J. Min. Inst. 2020, 245, 561–568. [Google Scholar] [CrossRef]
- Gusev, V.N.; Maliukhina, E.M.; Volokhov, E.M.; Tyulenev, M.A.; Gubin, M.Y. Assessment of development of water conducting fractures zone in the massif over crown of arch of tunneling (construction) climate. Int. J. Civ. Eng. Technol. 2019, 10, 635–643. [Google Scholar]
- Ivanik, S.A.; Ilyukhin, D.A. Hydrometallurgical technology for gold recovery from refractory gold-bearing raw materials and the solution to problems of subsequent dehydration processes. J. Ind. Pollut. Control. 2017, 33, 891–897. [Google Scholar]
- Pan, G.; Zhou, Y.; Guo, W. Global optimization algorithm in 3D datum transformation of industrial measurement. Geomat. Inf. Sci. Wuhan Univ. 2013, 39, 85–89. [Google Scholar] [CrossRef]
- Kozak, P.M.; Lapchuk, V.P.; Kozak, L.V.; Ivchenko, V.M. Optimization of video camera disposition for the maximum calculation precision of coordinates of natural and artificial atmospheric objects in stereo observations. Kinemat. Phys. Celest. Bodies 2018, 34, 313–326. [Google Scholar] [CrossRef]
- Easa, S.M. Survey review space resection in photogrammetry using collinearity condition without linearization. Surv. Rev. 2010, 42, 40–49. [Google Scholar] [CrossRef]
- Shevchenko, G.G. About adjustment of spatial geodetic networks by the search method. Geod. Cartogr. 2019, 80, 10–20. [Google Scholar] [CrossRef]
- Shevchenko, G.G.; Bryn, M.Y. Adjustments of Correlated Values by Search Method. In IOP Conference Series Materials Science and Engineering; CATPID-2019; IOP Publishing: Kislovodsk, Russia, 2019; Volume 698, p. 44019. [Google Scholar] [CrossRef]
- Maksimov, Y.A.; Fillipovskaya, E.A. Algorithms for Solving Nonlinear Programming Problems; M. MEPhI: Moscow, Russia, 1982; 52p. [Google Scholar]
- Himmelblau, D.M. Applied Nonlinear Programming; McGraw-Hill: New York, NY, USA, 1972; 532p. [Google Scholar]
- Yan, J.; Tiberius, C.; Bellusci, G.; Janssen, G. Feasibility of Gauss-Newton method for indoor positioning. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 6–8 May 2008; pp. 660–670. [Google Scholar]
- Vasil’ev, A.S.; Goncharov, A.A. Special strategy of treatment of difficulty-profile conical screw surfaces of single-screw compressors working bodies. J. Min. Inst. 2019, 235, 60–64. [Google Scholar] [CrossRef]
- Dennis, D. Numerical Methods of Unconstrained Optimization and Solution of Nonlinear Equations; Applied Mathematics: Philadelphia, PA, USA, 1988; 440p. [Google Scholar]
- Kantorovich, L.V. On the Newton’s Method; Works of the V.A. Steklov Mathematic Institute: Moscow, Russia, 1949; Volume 28, pp. 104–144. [Google Scholar]
- Shnitko, S.G. Algorithms for Equalization and Estimating the Accuracy of Geodetic Networks by Nonlinear Methods; PSU Bulletin; State College: Harrisburg, PA, USA, 2012; Volume 8, pp. 133–135. [Google Scholar]
- Ortega, D. Iterative Methods for Solving Nonlinear Systems of Equations with Many Unknowns; Mir: Moscow, Russia, 1975; 558p. [Google Scholar]
- Bykasov, D.A.; Zubov, A.V. Application of Newton’s Method of the Second-Order in Solving Surveying and Geodetic Problems; MineSurveying Bulletin: Moscow, Russia, 2020; Volume 5, pp. 22–26. [Google Scholar]
- Stroner, M.; Michal, O.; Enhanced, R. Maximal precision increment method for network measurement optimization. In Advances and Trends in Geodesy, Cartography and Geoinformatics; CRC Press: Boca Raton, FL, USA, 2018; pp. 101–106. [Google Scholar] [CrossRef]
- Sviridenko, A.B. A priori correction in Newton’s optimization methods. Comput. Res. Model. 2015, 7, 835–863. [Google Scholar] [CrossRef]
- Gubaydullina, R.; Kornilov, Y.N. The application of similarity theory elements in geodesy. In Topical Issues of Rational Use of Natural Resources; CRC Press: Boca Raton, FL, USA, 2019; Volume 1, pp. 183–188. [Google Scholar] [CrossRef]
- Nemirovsky, A.S.; Yudin, D.B. Information Complexity and Efficiency of Optimization Methods; John Wiley and Sons: Hoboken, NJ, USA, 1976; 105p. [Google Scholar]
- Zubov, A.V.; Pavlov, N.S. Assessment of the Stability of Support and Deformation Surveying and Geodetic Networks; Surveyor Bulletin: Moscow, Russia, 2013; Volume 2, pp. 21–23. [Google Scholar]
- Zubov, A.V.; Pavlov, N.S. The use of the gradient method in solving geodetic problems. In Proceedings of the Interuniversity Scientific-Practical Conference. SPb. A.F. Mozhaysky Military Space Academy, Saint Petersburg, Russia, 20 September 2013; pp. 90–93. [Google Scholar]
- Zheltko, C.N. Search Method of Equalization and Estimation of the Accuracy of Unknowns in the Least Squares Method: Monograph; FSBEI HE “KubSTU”: Krasnodar, Russia, 2016; 103p. [Google Scholar]
- Mazurov, B.T. Mathematical Modeling in the Study of Geodynamics; Sibprint Agency: Novosibirsk, Russia, 2019; 360p. [Google Scholar]
- Shu, C.; Li, F.; Wang, S. Improving algorithm to compute geodetic coordinates. In Proceedings of the 2008 International Workshop on Education Technology and Training & 2008 International Workshop on Geoscience and Remote Sensing, Shanghai, China, 21–22 December 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 2, pp. 340–343. [Google Scholar]
- Baran, P.I. Investigation of the accuracy of solving geodetic problems by methods of mathematical programming. Eng. Geod. 1987, 30, 5–8. [Google Scholar]
- Budo, A.Y. Comparative Analysis of the Equalization Results Obtained Using Two Polar Methods when Processing Planned Geodetic Networks; PSU Bulletin; State College: Harrisburg, PA, USA, 2010; Volume 12, pp. 115–122. [Google Scholar]
- Sholomitskii, A.; Lagutina, E. Calculation of the accuracy of special geodetic and mine surveying networks. ISTC Earth Sci. 2019, 272, 10. [Google Scholar] [CrossRef]
- Men’Shikov, S.N.; Dzhaljabov, A.A.; Vasiliev, G.G.; Leonovich, I.A.; Ermilov, O.M. Spatial models developed using laser scanning at gas condensate fields in the northern construction-climatic zone. J. Min. Inst. 2019, 238, 430–437. [Google Scholar] [CrossRef] [Green Version]
- Kougia, V.A.; Kanashin, N.V. Determination of the connection elements between three-dimensional coordinate systems by the gradient method. In News of Higher Educational Institutions; Geodesy and Aerial Photography: Moscow, Russia, 2008; Volume 2, pp. 22–28. [Google Scholar]
- Makarov, G.V.; Khudyakov, G.I. Use of affinne coordinate conversion at the local geodetic surveys with applying of GPS-receivers. J. Min. Inst. 2013, 204, 15–18. [Google Scholar]
- Mitskevich, V.I.; Abu, D.I. Estimation of the accuracy of spatial serifs by nonlinear programming methods. Geod. Cartogr. 1994, 1, 22–24. [Google Scholar]
- Mitskevich, V.I. Mathematical Processing of Geodetic Networks by Nonlinear Programming Methods; PSU: Novopolotsk, Russia, 1997; 64p. [Google Scholar]
- Mitskevich, V.I.; Yaltyhov, V.V. Equalization and assessment of the accuracy of geodetic serifs under various criteria of optimality. Geod. Cartogr. 1994, 7, 14–16. [Google Scholar]
- Shevchenko, G.G. Development of technology for geodetic monitoring of buildings and structures by the method of free stationing using the search method of nonlinear programming. Ph.D. Thesis, Emperor Alexander I St. Petersburg State Transport University SPb, Saint Petersburg, Russia, 2020; 212p. [Google Scholar]
- Eliseeva, N.N. Application of search methods in solving nonlinear optimization problems. In Collection of Materials of the XIV International Scientific-Practical Conference Dedicated to the 25th Anniversary of the Constitution of the Republic of Belarus “Modernization of the Economic Mechanism through the Prism of Economic, Legal, Social and Engineering Approaches”; BSTU: Minsk, Belarus, 2019; pp. 364–369. [Google Scholar]
- Zelenkov, G.A.; Khakimova, A.B. Approach to the development of algorithms for Newton’s optimization methods, software imple-mentation and comparison of efficiency. Comput. Res. Model. 2013, 5, 367–377. [Google Scholar] [CrossRef] [Green Version]
- Mikheev, S.E. Convergence of Newton’s method on various classes of functions. Comput. Technol. 2005, 10, 72–86. [Google Scholar]
- Chen, C.; Bian, S.; Li, S. An Optimized Method to Transform the Cartesian to Geodetic Coordinates on a Triaxial Ellipsoid; Chen, C., Ed.; Studia Geophysica et Geodaetica: Prague, Czech Republic, 2019; Volume 63, pp. 367–389. [Google Scholar]
- Kazantsev, A.I.; Kochneva, A.A. Ground of the geodesic control method of deformations of the land surface when protecting the buildings and structures under the conditions of urban infill. Ecol. Environ. Conserv. 2017, 23, 876–882. [Google Scholar]
- Kuzin, A.A.; Valkov, V.A.; Kazantsev, A.I. Calibration of digital non-metric cameras for measuring works. JP Conf. Ser. 2018, 1118, 012022. [Google Scholar] [CrossRef] [Green Version]
- Mitskevich, V.I.; Yaltyhov, V.V. Peculiarities of equalization of geodetic networks by the method of least modules. Geod. Cartogr. 1997, 5, 23–24. [Google Scholar]
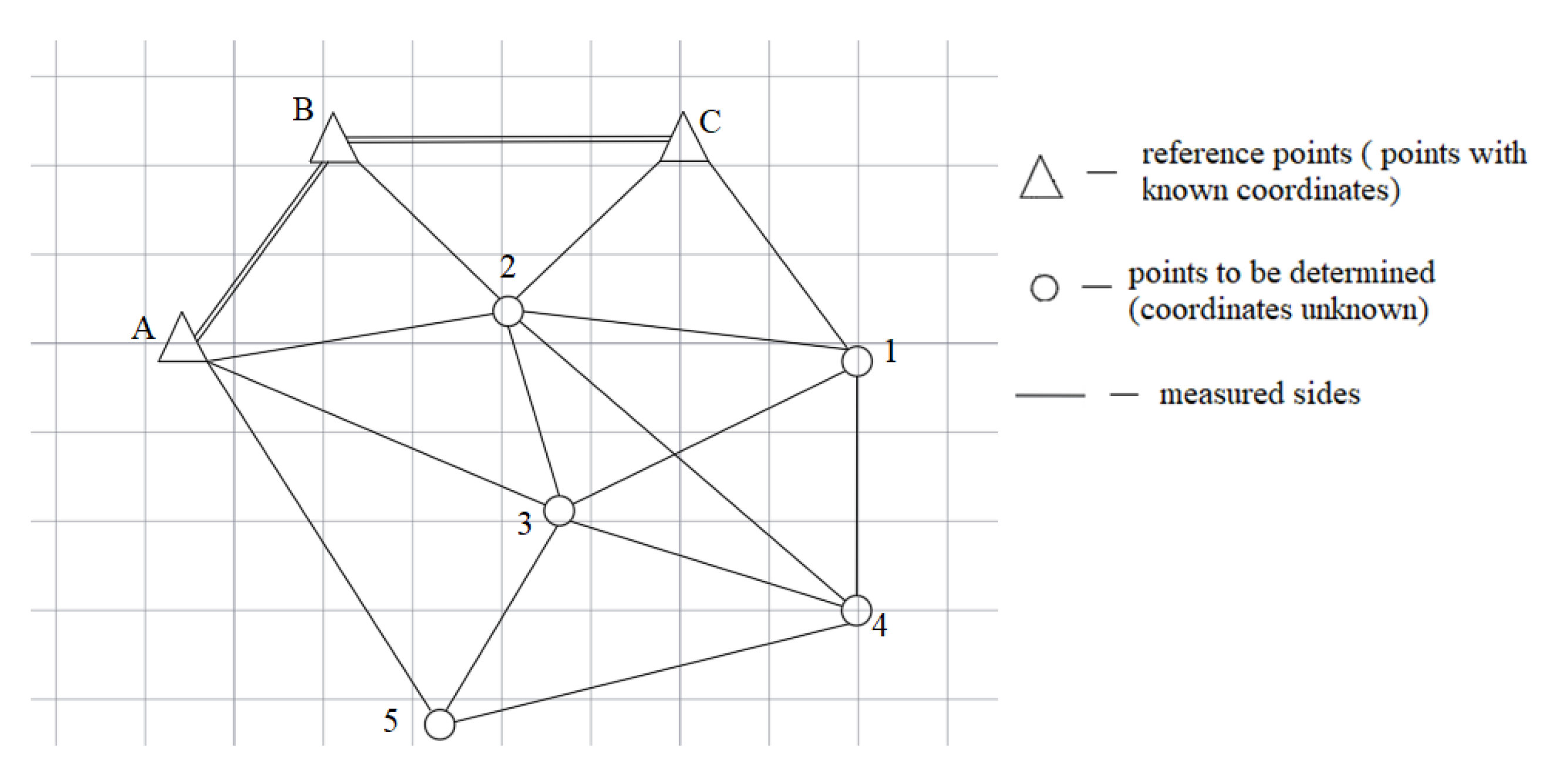

| Item | Coordinates | |
|---|---|---|
| , m | , m | |
| A | 645.112 | 426.229 |
| B | 1028.568 | 857.277 |
| C | 740.339 | 1333.496 |
| No. | Line Name | Length, m |
|---|---|---|
| 1 | C–2 | 492.886 |
| 2 | B–2 | 448.178 |
| 3 | A–2 | 445.726 |
| 4 | A–3 | 512.201 |
| 5 | 3–2 | 504.961 |
| 6 | 2–4 | 733.414 |
| 7 | 2–1 | 523.911 |
| 8 | 1–C | 534.601 |
| 9 | 3–1 | 654.977 |
| 10 | 3–4 | 482.249 |
| 11 | 4–1 | 456.648 |
| 12 | 5–A | 617.706 |
| 13 | 5–3 | 322.978 |
| 14 | 5–4 | 700.240 |
| Item | Preliminary Coordinates | Calculated Coordinates | ||||
|---|---|---|---|---|---|---|
| Second-Order Newton’s Method | Conjugate Gradient Method | |||||
| , m | , m | , m | , m | , m | , m | |
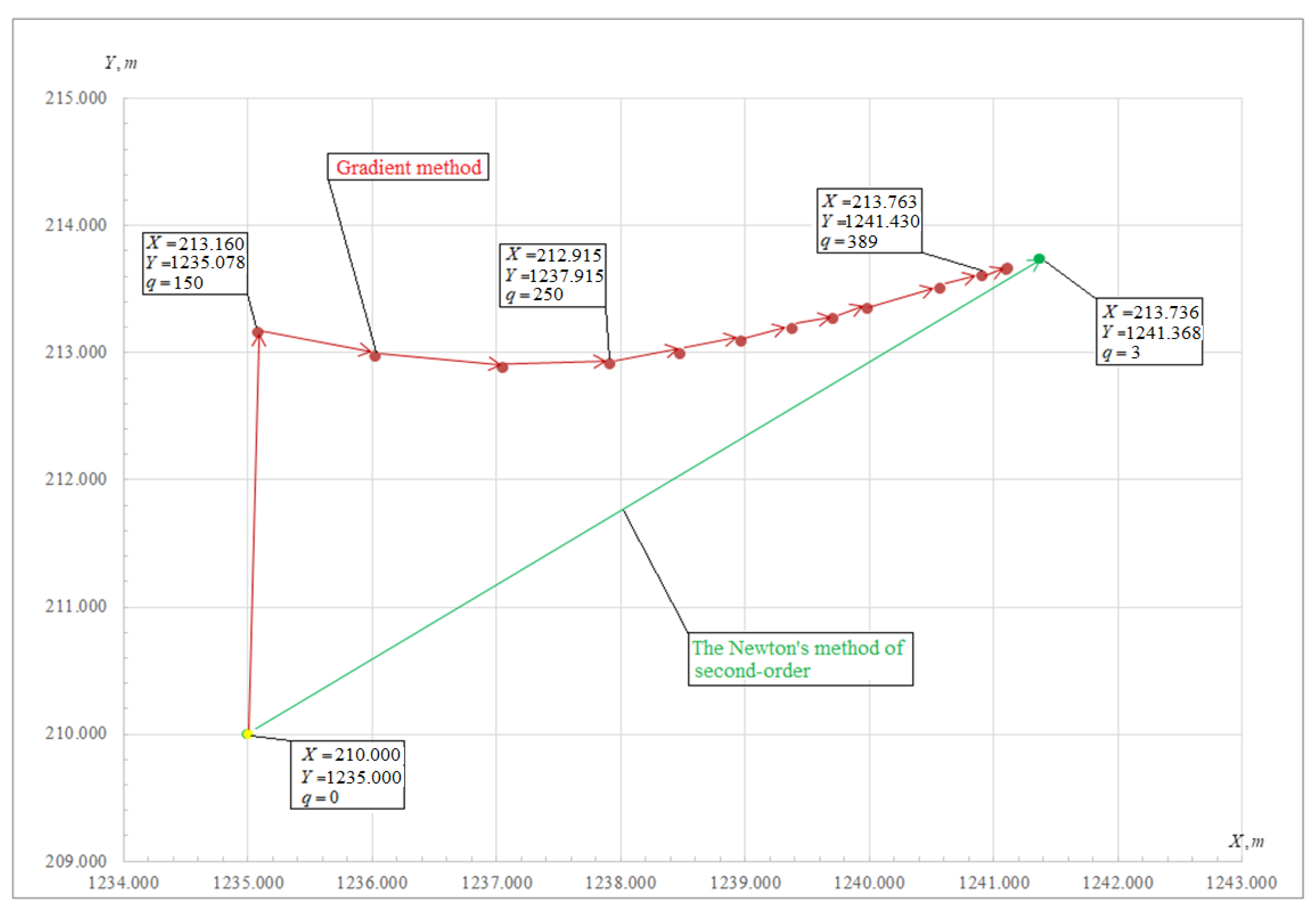
| 1 | 210.000 | 1235.000 | 213.736 | 1241.368 | 213.763 | 1241.430 |
| 2 | 575.000 | 860.000 | 580.501 | 867.247 | 580.515 | 867.261 |
| 3 | 150.000 | 580.000 | 159.346 | 588.653 | 159.363 | 588.730 |
| 4 | −135.000 | 950.000 | −146.870 | 961.206 | −146.851 | 961.283 |
| 5 | 40.000 | 285.000 | 43.240 | 287.266 | 43.042 | 287.478 |
| NoI 1 | 3 | 389 | ||||
| OF 2 | 859.468 | |||||
| CT 3 | 25.5 s | 48.8 s | ||||
| Item | Preliminary Coordinates | Calculated Coordinates | ||||
|---|---|---|---|---|---|---|
| Second-Order Newton’s Method | Conjugate Gradient Method | |||||
| , m | , m | , m | , m | , m | , m | |
| 1 | 10.000 | 10.000 | 213.737 | 1241.370 | 213.517 | 1242.222 |
| 2 | 10.000 | 10.000 | 580.501 | 867.248 | 580.685 | 867.828 |
| 3 | 10.000 | 10.000 | 159.347 | 588.656 | 159.880 | 589.763 |
| 4 | 10.000 | 10.000 | −146.869 | 961.209 | −146.365 | 962.073 |
| 5 | 10.000 | 10.000 | 43.237 | 287.272 | 43.290 | 289.190 |
| NoI 1 | 11 | 586 | ||||
| OF 2 | 859.468 | 2.413 | ||||
| CT 3 | 42.5 s | 59.8 s | ||||
| Item | Preliminary Coordinates | Calculated Coordinates | ||||
|---|---|---|---|---|---|---|
| Second-Order Newton’s Method | Conjugate Gradient Method | |||||
| , m | , m | , m | , m | , m | , m | |
| 1 | 210.000 | 1235.000 | 213.736 | 1241.367 | 213.762 | 1241.379 |
| 2 | 575.000 | 860.000 | 580.500 | 867.246 | 580.515 | 867.246 |
| 3 | 150.000 | 580.000 | 159.346 | 588.652 | 159.352 | 589.665 |
| 4 | −135.000 | 950.000 | −146.869 | 961.205 | −146.406 | 961.591 |
| 5 | 40.000 | 285.000 | 43.231 | 287.275 | 43.300 | 289.085 |
| NoI 1 | 103 | 1233 | ||||
| OF 2 | 859.468 | 1.025 | ||||
| CT 3 | 49.1 s | 100.1 s | ||||
| Item | Preliminary Coordinates | Calculated Coordinates | |||
|---|---|---|---|---|---|
| Modified Second-Order Newton’s Method | |||||
| , m | , m | , m | , m | ||
| 1 | 0.000 | 0.000 | 213.736 | 1241.368 | |
| 2 | 0.000 | 0.000 | 580.501 | 867.247 | |
| 3 | 0.000 | 0.000 | 159.346 | 589.653 | |
| 4 | 0.000 | 0.000 | −146.870 | 961.206 | |
| 5 | 0.000 | 0.000 | 43.240 | 287.266 | |
| NoI 1 | 28 | ||||
| OF 2 | |||||
| CT 3 | 98.7 s | ||||
| RS 4 | / | ||||
| / | |||||
| / | |||||
| / | |||||
| / | |||||
| Item | Preliminary Coordinates | Calculated Coordinates | ||||
|---|---|---|---|---|---|---|
| Second-Order Newton’s Method | BFGS | |||||
| , m | , m | , m | , m | , m | , m | |
| 1 | 0.000 | 0.000 | 213.736 | 1241.368 | 288.806 | 1070.175 |
| 2 | 0.000 | 0.000 | 580.501 | 867.247 | 652.085 | 777.799 |
| 3 | 0.000 | 0.000 | 159.346 | 589.653 | 201.616 | 380.299 |
| 4 | 0.000 | 0.000 | −146.870 | 961.206 | −63.580 | 810.951 |
| 5 | 0.000 | 0.000 | 43.240 | 287.266 | 71.944 | 39.043 |
| NoI 1 | 28 | 144 | ||||
| OF 2 | 859.468 | |||||
| CT 3 | 98.7 s | 122.1 s | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mustafin, M.; Bykasov, D. Adjustment of Planned Surveying and Geodetic Networks Using Second-Order Nonlinear Programming Methods. Computation 2021, 9, 131. https://doi.org/10.3390/computation9120131
Mustafin M, Bykasov D. Adjustment of Planned Surveying and Geodetic Networks Using Second-Order Nonlinear Programming Methods. Computation. 2021; 9(12):131. https://doi.org/10.3390/computation9120131
Chicago/Turabian StyleMustafin, Murat, and Dmitry Bykasov. 2021. "Adjustment of Planned Surveying and Geodetic Networks Using Second-Order Nonlinear Programming Methods" Computation 9, no. 12: 131. https://doi.org/10.3390/computation9120131
APA StyleMustafin, M., & Bykasov, D. (2021). Adjustment of Planned Surveying and Geodetic Networks Using Second-Order Nonlinear Programming Methods. Computation, 9(12), 131. https://doi.org/10.3390/computation9120131






