Abstract
In the current work, we have investigated the flow past a semi-infinite porous solid media, after presenting a similarity transformation, governing equations mapped to a system of non-linear PDE. The flow of a dusty fluid and heat transfer through a porous medium have few applications, viz., the polymer processing unit of a geophysical, allied area, and chemical engineering plant. Further, we had the option to get an exact analytical solution for the velocity to the equation that is non-linear. The highlight of the current work is the flow of hybrid dusty nanofluid due to Darcy porous media through linear thermal radiation with the assistance of an analytical process. The hybrid dusty nanofluid has significant features improving the heat transfer process and is extensively developed in manufacturing industrial uses. It was found that the basic similarity equations admit two phases for both stretching/shrinking surfaces. The existence of computation on velocity and temperature profile is presented graphically for different estimations of various physical parameters.
1. Introduction
The boundary layer flow is studied on continuous moving solid surfaces. Dusty fluid flows have become increasingly important in recent years. Petroleum transportation, wastewater treatment, combustion, and power plant piping are only a few examples. Furthermore, since crude oil is recovered from the pores of reservoir rocks, fluid flow through porous media has become a significant subject. The dusty fluid is a combination of micrometer-sized particles into a base fluid. The latest technical advances necessitate a different revolt in the field of a dusty fluid. The flow happens in numerous engineering and innovative processes. Applications over a wide range of science and design controls, particularly in the expulsion of a polymer in a dissolve turning measure; the expulsion from biting the dust is usually drawn and simultaneously reached out into a stretched sheet, and the boundary layer along with material behavior conveyors, the aerodynamic expulsion extrusion of glass blowing, paper manufacture, plastic sheets, and the boundary layer along with a fluid film are considered in the reduction method.
The desired fluid mechanical properties as a result of such a method would be primarily determined by two factors: the cooling fluid utilized and the rate of stretching. Fluids with non-Newtonian properties that are electrically leading can be used as cooling liquids because the flow and heat transfer can be controlled externally. The level of stretching is crucial because quick stretching induces rapid solidification. Regarding these applications, Sakiadis [1] first talked about boundary layer flow over an insistent, dense surface affected at a consistent speed. Crane [2] stretched out the Sakiadis concern to a stretching sheet and originated a closed-form particular solution. From that point forward, several authors [3,4,5,6,7,8,9,10] generalized the stretching flow problem in different directions, resulting in numerous references. One way to develop the thermal conductivity of conventional coolants is to add nano-sized particles. Furthermore, the nanofluid is referred to as a combination of nano-sized particles, which dissipates extra heat because of its higher thermal conductivity, leading to better device thermal efficiency.
In view of these possibilities, the impact of mass transfer and energy properties concerning the air stream and water surface was investigated by Gu et al. [11]. The thermal conductivity and dynamic viscosity using hybrid nanofluid were calculated experimentally by Esfe et al. [12]. Mahabaleshwar et al. [13,14,15,16] extended his work with heat transfer within the sight of radiation and heat source/sink effects subsequently over the stretching sheet. Nanofluids across a stretching sheet with cross-diffusion impacts of hydromagnetics were investigated by Reddy and Chamkha [17]. Natural convection in a porous media saturated with nanofluid across a non-isothermal vertical plate investigated by Gorla and Chamkha [18]. Further, an extensive and substantial survey of hybrid nanofluids can be perused in the new analysis, see [19,20,21,22]. The equation is widely used in the study of porous media with high porosity. The effective viscosity is the dynamic viscosity that is related with the brinkman term. The magnitude of the viscosity ratio has been studied in the past with different results by Mahabaleshwar et al. [23,24]. The Darcy–Brinkman conditions validity has additionally been explored, especially when it derives solid–fluid interfaces in relation to boundary conditions at the Nield [25]. The research, which addresses the Navier–Stokes conditions instead of the Darcy equation, yields a connection concerning the permeability of the normal exhibit structure and the porosity, showing that the Darcy equation is effective for flow across normal construction across the entire porosity range. Linear stability analysis is used to investigate bio-thermal convection in suspension of gyrotactic microorganisms in a porous media using the Darcy–Brinkman model [26,27,28,29,30]
The main aim of this analysis is to use a proposed convergent analytical technique to examine the features of a hybrid nanofluid due to a Darcy porous medium using nonlinear thermal radiation. An effective resolution is different due to the non-linear nature as well as outline essence of the query. As a consequence, an analytical description of the proposed method is obtained. The governing PDEs are converted into nonlinear ODEs. As a result, the present research will look at the quantitative relationships concerning the wall impacts and the Darcy Brinkman equation in greater detail. To assess the association between flow and temperature, an inventory of equivalent coefficients among the movement aspects, as well as real proportions of the perception model, were calculated. The specifics are described using tables and graphs.
2. Physical Model and Solution
Consider the flow and heat transfer of an incompressible hybrid nanofluid due to a stretching/shrinking sheet in a two-dimensional boundary layer. The velocity of the sheets is assumed to be linear, i.e., with c < 0 for a shrinking sheet and c > 0 for a stretching sheet. The stretching/shrinking sheet is parallel to the y = 0 plane. The flow is produced because of the stretching/shrinking sheet affected by the concurrent utilizations of two equivalents and contrary forces along the x-plane (see Figure 1).
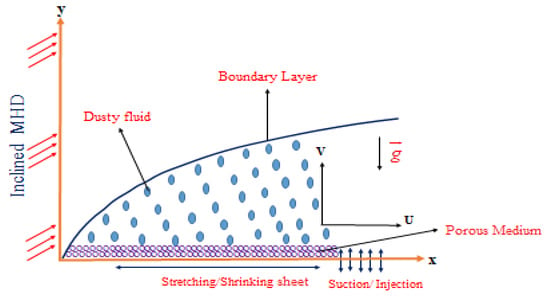
Figure 1.
Physical model for stretching/shrinking boundary.
The governing equations for the boundary layer approximations are:
2.1. Fluid Phase
2.2. Dust Phase
The fluid and dust particle B.C’s are given by.
The radiative heat flux is stated as follows (see Mahabaleshwar et al. [31,32,33,34]) using the Rosseland [35] approximation.
The difference of temperature expressed as linearity function in the fourth power of temperature is an assumption. The Taylor’s series expansion of the term with the value is presented as below; see Mahabaleshwar et al. [36,37]
Ignoring higher-order terms of in the exceeding expression absent from the first degree, can be estimated by:
By employing Equations (8) and (10) substitute in Equation (3) moderates to
Here, the Stefan–Boltzmann constant is σ*, the absorption coefficient is k*, and radiative heat flux is qr. The following is the term for the hybrid nanofluid density, viscosity, thermal conductivity, and specific heat. Anusha et al. [26]
The following are the reduced equations obtained using the similarity transformation:
As a consequence, is the wall mass transfer velocity. The governing equations of motion are then reduced to form.
2.3. Fluid Phase
2.4. Dust Phase
here
The comparative reduced boundary constraints will take the accompanying structure,
Chandrasekhar’s number is ; the density of the particle phase stands for the ; the mass concentration of the dusty particle is ; the Prandtl number is ; the mass transfer strength at the sheet, as determined by the wall mass transfer parameter, is ; the specific heat parameter is ; the velocity fluid particle interaction parameter is ; and the temperature’s fluid-interaction parameter is , the Eckert number is . Furthermore, D is set to such an extent that D = 1 represents the stretching sheet and D = −1 represents the shrinking sheet.
3. Fluid and Dust Phase Flow Fields
The highlights of the solution’s boundary layer estimate are recovered by the accurate solution of exponential form.
where must be strictly positive to match the physical boundary conditions in (18); for , which describes the stretching velocity of dust particles, no such restriction is needed. Both and are real numbers, and at this phase they are unknown. It is easy to demonstrate that the exact solutions satisfy all of the boundary conditions in (18) and (19). The following step is to satisfy the fluid and dust momentum equations given in (14). As a consequence, the fluid phase’s momentum equation yields the following relation.
Solutions are determined by using the cubic formula
When substituting Equation (19) into Equation (16), the momentum equation for the dust phase is obtained, this is as follows:
When Equation (21) is substituted for ,
Furthermore, once the values of and have been determined, the wall shears can be conveniently measured using the formulations:
4. Results and Discussion
The flow of the unique/numerous two-phase dust fluid and temperature solutions due to a stretching/shrinking sheet with the effect of a heat source and heat sink is investigated in the current work. The current segment’s main aim is to investigate the graphical effects of different relevant constraints to temperature profiles and velocity for two distinctive nano fluids. The presence of mass flow transfer constraint is represented by Vc, the Eckert number is Ec, particle parameter is l, is the Darcy porous medium, is the interface parameter for velocity, Pr is the Prandtle number, is the specific heat parameter, is the Brinkmann ratio, the fluid particle interaction parameter of temperature is , and Chandrasekhar’s number is Q.
Figure 2a–d demonstrates the solution domain versus mass transpiration Vc for the varying fluid particle interaction parameter , when considering the stretching surface with l = 0 and l = 1 for different values of the Chandrasekhar’s number Q. The solution domain is a monotonically increasing function of mass transpiration Vc. Figure 3a–d portrays the solution domain as function of mass transpiration Vc in the case of a shrinking surface. For different values of the Chandrasekhar’s number Q, l = 0 and l = 1 for the differing interaction parameter . The estimations of consistent with velocities are monotonically increasing, though the wall suction velocities show both increase and decrease. Figure 4 describes the impact of the stretching sheet on the velocity profile of both nanofluid and dust phases. The physical velocity field of hybrid nanofluid and dust phase will be reduced as the thickness of the momentum boundary layer is also condensed, for the mass flow suction case; there is only a unique solution exit. Figure 5a,b displays the transverse velocity for both two levels in USB. The figure shows that in branch 1, the velocity of the hybrid nanofluid phase is more than the dusty phase, and in branch 2, the velocity of the hybrid nanofluid phase is less than the dusty phase. Chandrasekhar’s number Q increases as the velocity profile decreases.
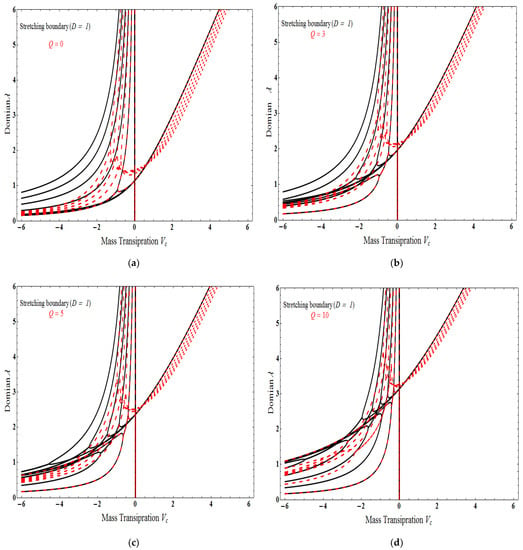
Figure 2.
Influence of domain λ versus mass transpiration Vc for the varying fluid particle interaction parameter . Chandrasekhar’s number is (a) , (b) , (c) , and (d) with = 0.1.
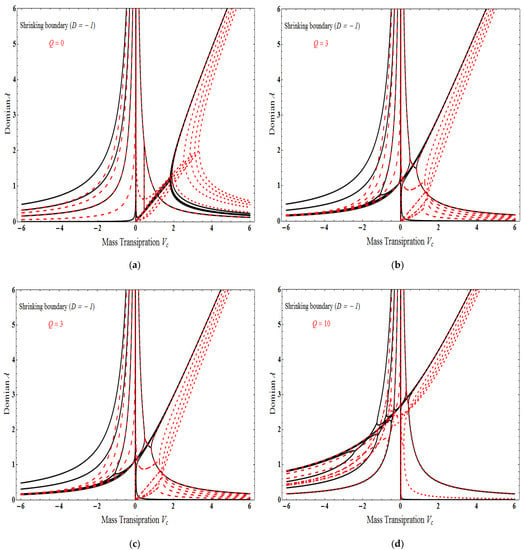
Figure 3.
Influence of domain versus mass transpiration Vc for several values . Chandrasekhar’s number is (a) , (b) , (c) , and (d) with = 0.1.
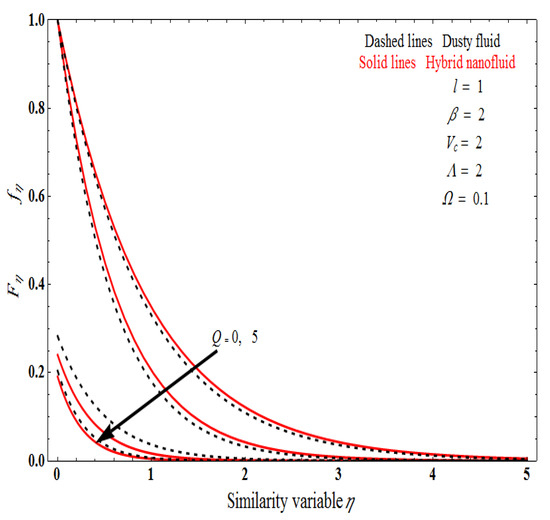
Figure 4.
Influence of fluid velocity and particle velocity for the stretching surface.
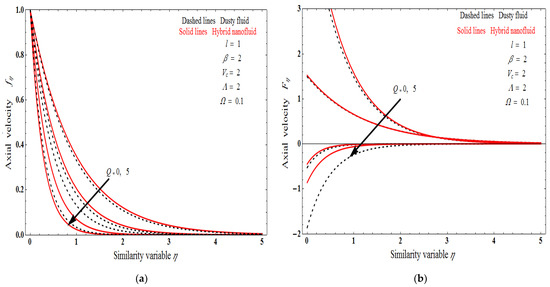
Figure 5.
Influence of fluid velocity (a) and (b) particle velocity for the stretching surface with dual solution.
Figure 6a–d depicts the impact of the stretching sheet on the velocity profile of both fluid and dust fluid. The suction case is illustrated in Figure 6a,b; it is demonstrated that as the suction increases, the velocity profiles of fluid and dust fluid increase. The injection case is shown in Figure 7c,d; as the injection value increases the fluid and dust phases of the velocity profile increase. However, as the injection value increases, the opposite behavior occurs. Subsequently, the magnetic field performances decrease the boundary layer development because of expanding the Lorentz force; the physical validity of this behavior is disputed. Figure 7 portrays the velocity profile under different values of Brinkman numeral; it is observed that Brinkman number increments as velocity profiles are also increased. Figure 8 represents the effect of Darcy number exhibits for both fluid and dusty nanofluids. It is revealed that as the Darcy number increases, the hybrid nanofluid decreases. Since the porosity parameter increases in velocity, as a result, the boundary layer thickness is reduced.
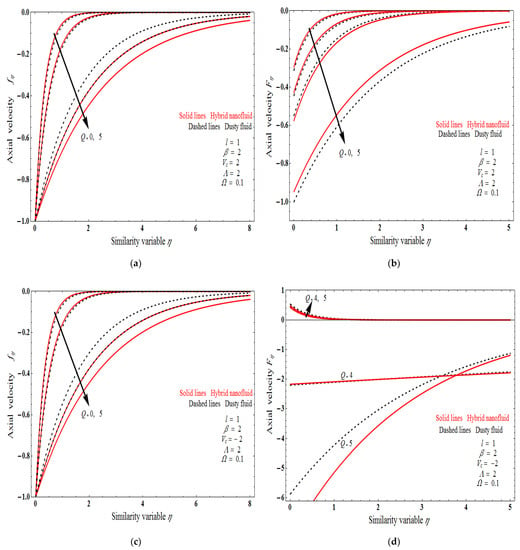
Figure 6.
Influence of fluid velocity and particle velocity for the Shrinking surface: (a) for suction case, (b) for suction case, (c) for injection case and (d) for injection case.
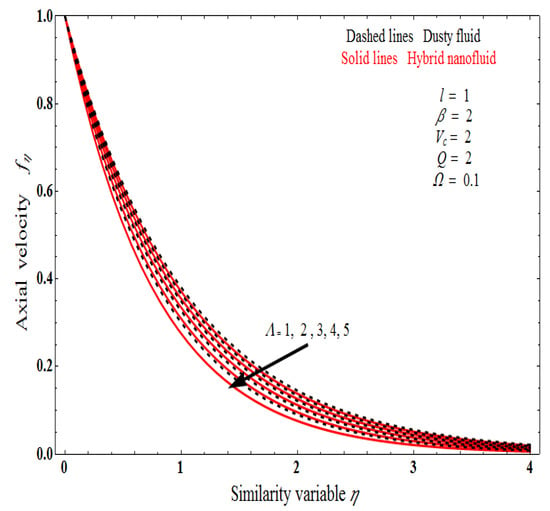
Figure 7.
The impact of velocity profile on Brinkman number .
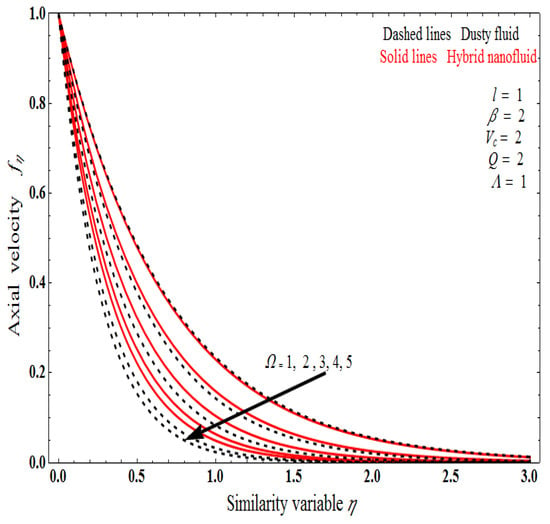
Figure 8.
Impact of Darcy number on velocity profile.
5. Conclusions
In this analytical study, the energy and transfer of momentum of an MHD flow of a hybrid dusty fluid due to a stretching/shrinking sheet are investigated; a set of nonlinear ODEs is attained after applying the appropriate similarity transformations. Also, Darcy–Brinkman ratio and radiation were taken into account and were solved with an analytical method.
- Darcy–Brinkman ratio and radiation were taken into account and were solved by analytical method.
- The velocity profile for two phases reduces when Darcy’s number increases.
- As the Brinkman number increases, the thickness of the momentum boundary layer increases.
- The set of physical parameters under consideration determines if branch 1 or branch 2 arrangements are cooler, which would be important through the cooling method.
Author Contributions
U.S.M. and K.N.S. conceptualized, modeled, and solved the problem, performed formal analysis, contributed to analytical computations, plotted the graphical results, wrote the original draft, and investigated the problem. They also contributed to modeling and solving the problem, and performed programming in Mathematica. R.B. and M.E.G. U.S.M. also contributed to modeling and solving the problem, writing, review & editing, and validation of the results. All authors finalised the manuscript after its internal evaluation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
The author K.N.S. is thankful to National Fellowship and Scholarship for Higher Education for ST (NFST), New Delhi, INDIA for financial support in the form of Junior Research Fellowship: Awardee No. 202021-NFST-KAR-01224, 13 August 2021. U.S.M., R.B. and M.E.G. are acknowledge to the reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | Descriptions | S. I. Units |
| B0 | Magnetic field | (Tesla) |
| d | stretching/shrinking constant | (wm−2) |
| k | thermal conductivity | (m2s−1) |
| k* | absorption constant | (m−2) |
| M | magnetic parameter | (w S Kg−1) |
| N | density number | (-) |
| P | pressure | (-) |
| P | dimensionless pressure | (-) |
| T | temperature | (K) |
| Vw | mass flux | (ms−1) |
| Vc | suction/injection velocity | (-) |
| Vc > 0 | suction velocity | (-) |
| Vc < 0 | injection velocity | (-) |
| u, v | velocities | (m s-1) |
| Greek letters | ||
| constant | (-) | |
| interaction parameter | (-) | |
| Fluid particle for temperature | (-) | |
| Brinkmann ratio | (-) | |
| Darcy model | (-) | |
| limiting viscosity of fluid | (-) | |
| effective dynamic viscosity | (N s m−2) | |
| similarity variable | (-) | |
| electrical conductivity | (S m−1) | |
| Stefan-Boltzmann | (Wm−2K−4) | |
| inclined angle | (-) | |
| relaxation time | (-) | |
| Subscript | ||
| S1 | density of solid fraction of hybrid nanofluid | |
| S2 | density of solid fraction of hybrid nanofluid | |
| P | solid particles | |
| w | wall temperature | |
| ambient fluid | ||
| f | parameter of base fluid | |
| hnf | parameter of hybrid nanofluid | |
References
- Sakiadis, B.C. Boundary-Layer behavior on continuous solid surface, Boundary Layer equation for Two-Dimensional and Axisymmetric Flow. AIChE J. 1961, 7, 26. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew Math. Mech. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- McLeod, B.; Rajagopal, K.R. On the Uniqueness of Flow of a Navier-Stokes Fluid due to a stretching boundary. Arch. Rat. Mech. An. 1987, 98, 385–393. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and Mass Transfer on a stretching sheet with suction and Blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Banks, W.H.H. Similarity solutions of the Boundary-Layer Equation for a stretching wall. J. Mech Theor. Appl. 1988, 13, 568–580. [Google Scholar]
- Dutta, B.K.; Roy, P.; Gupta, A.S. Temperature field in flow over a stretching sheet with uniform heat flux. Int. Commun. Heat Mass Transf. 1985, 12, 88–94. [Google Scholar] [CrossRef]
- Chen, C.K.; Char, M.I. Heat Transfer of a Continuous Stretching Surface with Suction and Blowing. J. Math. An. Appl. 1988, 13, 568–580. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.E. On Thermal Boundary Layer on a Power Law Stretched Surface with Suction or Injection. Int. J. Heat Fluid Flow 1995, 16, 280–290. [Google Scholar] [CrossRef]
- Liao, S.J. A New Branch of Solutions of Boundary-Layer Flows over a Stretching Flat Plate. Int. J. Heat Mass Transf. 2005, 49, 2529–2539. [Google Scholar] [CrossRef]
- Abbas, Z.; Hayat, T. Stagnation Slip Flow and Heat Transfer over a Nonlinear Stretching Sheet. Numer. Meth. Part. Diff. Eqs. 2011, 27, 302–314. [Google Scholar] [CrossRef]
- Gu, L.D.; Min, J.C.; Tang, Y.C. Effects of mass transfer on heat and mass transfer characteristics between water surface and airstream. Int. J. Heat Mass Transf. 2018, 222, 2093–2202. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Sarris, I.E.; Hill, A.A.; Lorenzini, G.; Pop, I. An MHD couple stress fluid due to a perforated sheet undergoing linear stretching with heat transfer. IJHMT 2017, 105, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Astanina, M.; Sheremet, M.; Mahabaleshwar, U.S.; Singh, J. Effect of porous medium and copper heat sink on cooling of heat-generating element. Energies 2020, 13, 2538. [Google Scholar] [CrossRef]
- Xenos, M.A.; Petropoulou, E.N.; Siokis, A.; Mahabaleshwar, U.S. Solving the nonlinear boundary layer flow equation with pressure gradient and radiation. Symmetry 2020, 12, 710. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Nagaraju, K.R.; Sheremet, M.A.; Baleanu, D.; Lorenzini, E. Mass transpiration on Newtonian flow over a porous stretching/shrinking sheet with slip. Chin. J. Phys. 2020, 63, 130–137. [Google Scholar] [CrossRef]
- Reddy, S.; Chamkha, A.J. Soret and Dufour effects on MHD convective flow of Al2O3–water and TiO2–water nanofluids past a stretching sheet in porous media with heat generation/absorption. Adv. Powder Technol. 2016, 27, 93. [Google Scholar] [CrossRef]
- Gorla, R.S.; Chamkha, A. Natural Convective Boundary Layer Flow Over a Non Isothermal Vertical Plate Embedded in a Porous Medium Saturated with a Nanofluid. Nanoscale Microscale Thermophys. Eng. 2011, 15, 81–94. [Google Scholar] [CrossRef]
- Toghraie, D.; Chaharsoghi, V.A.; Afrand, M. Measurement of thermal conductivity of ZnO–TiO2/EG hybrid nanofluid. J. Therm. Anal. Calorim. 2016, 12, 527–535. [Google Scholar] [CrossRef]
- Afrand, M.; Toghraie, D.; Ruhani, B. Effects of temperature and nanoparticles concentration on rheological behavior of Fe3O4–Ag/EG hybrid nanofluid: An experimental study. Exp. Therm Fluid Sci. 2016, 77, 38–44. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Mehryan, S.A.M.; Shafee, A.; Sheremet, M.A. Variable magnetic forces impact on magnetizable hybrid nanofluid heat transfer through a circular cavity. J. Mol. Liq. 2019, 277, 388–396. [Google Scholar] [CrossRef]
- Souayeh, B.; Kumar, K.G.; Reddy, M.G.; Rani, S.; Hdhiri, N.; Alfannakh, H. Slip flow and radiative heat transfer behavior of titanium alloy and ferromagnetic nanoparticles along with suspension of dusty fluid. J. Mol. Liq. 2019, 290, 111223. [Google Scholar] [CrossRef]
- Mastroberardino, A.; Mahabaleshwar, U.S. Mixed convection in viscoelastic flow due to a stretching sheet in a porous medium. J. Porous Media 2013, 16, 483–500. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Sarris, I.E.; Lorenzini, G. Effect of radiation and Navier slip boundary of Walters’ liquid B flow over a stretching sheet in a porous media. Int. J. Heat Mass Transf. 2018, 127, 1327–1337. [Google Scholar] [CrossRef]
- Nield, D.A. The boundary correction for the Rayleigh-Darcy problem: Limitations of the Brinkman equation. J. Fluid Mech. 1983, 128, 37–46. [Google Scholar] [CrossRef]
- Anusha, T.; Mahabaleshwar, U.S.; Sheikhnejad, Y. An MHD of nanofluid flow over a porous stretching/shrinking plate with mass transpiration and Brinkman ratio. Trans. Porous Medium in press. 2021, 1–20. [Google Scholar] [CrossRef]
- Dhananjay, Y.; Mahabaleshwar, U.S.; Abderrahim, W.; Ramesh, C. Significance of the inconstant viscosity and internal heat generation on the occurrence of Darcy-Brinkman convective motion in a couple-stress fluid saturated porous medium: An analytical solution. Int. Commun. Heat Mass Transf. 2021, 122, 105165. [Google Scholar] [CrossRef]
- Moli, Z.; Shaowei, W.; Haibo, W.; Mahabaleshwar, U.S. Darcy–Brinkman bio-thermal convection in a suspension of gyrotactic microorganisms in a porous medium. Neural Comput. Appl. 2019, 31, 1061–1067. [Google Scholar] [CrossRef]
- Moli, Z.; Shaowei, W.; Li, S.C.; Zhang, Q.Y.; Mahabaleshwar, U.S. Chaotic Darcy-Brinkman convection in a fluid saturated porous layer subjected to gravity modulation. Results Phys. 2018, 9, 1468–1480. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Magnetohydrodynamic two-phase dusty fluid flow and heat model over deforming isothermal surfaces. Phys. Fluids 2017, 29, 013302. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Nagaraju, K.R.; Nadagouda, M.N.; Bennacer, R.; Baleanu, D. An MHD viscous liquid stagnation point flow and heat transfer with thermal radiation & transpiration. J. Therm. Sci. Eng. Prog. 2020, 16, 100379. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Nagaraju, K.R.; Vinay Kumar, P.N.; Azese, M.N. Effect of radiation on thermosolutal Marangoni convection in a porous medium with chemical reaction and heat source/sink. Phys. Fluids 2020, 32, 113602. [Google Scholar] [CrossRef]
- Siddheshwar, P.G.; Mahabaleshwar, U.S. Effects of radiation and heat source on MHD flow of a viscoelastic liquid and heat transfer over a stretching sheet. Int. J. Non-Linear Mech. 2005, 40, 807–820. [Google Scholar] [CrossRef] [Green Version]
- Benos, L.T.; Mahabaleshwar, U.S.; Sakanaka, P.H.; Sarris, I.E. Thermal analysis of the unsteady sheet stretching subject to slip and magnetohydrodynamic effects. Therm. Sci. Eng. Prog. 2019, 13, 100367. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik and Atomtheoretische Grundlagen; Springer: Berlin, Germany, 1931. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Nagaraju, K.R.; Vinay Kumar, P.N.; Nadagouda, M.N.; Bennacer, R.; Sheremet, M.A. Effects of Dufour and Sort mechanisms on MHD mixed convective-radiative non-Newtonian liquid flow and heat transfer over a porous sheet. J. Therm. Sci. Eng. Prog. 2020, 16, 100459. [Google Scholar] [CrossRef]
- Xenos, M.A.; Petropoulou, E.N.; Siokis, A.; Mahabaleshwar, U.S. Solving the Nonlinear Boundary Layer Flow Equations with Pressure Gradient and Radiation. J. Therm. Anal. Calorim. 2021, 143, 751–765. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).