Abstract
There is a myriad of career opportunities stemming from science, technology, engineering, and mathematics (STEM) disciplines. In addition to careers in corporate settings, teaching is a viable career option for individuals pursuing degrees in STEM disciplines. With national shortages of secondary STEM teachers, efforts to recruit, train, and retain quality STEM teachers is greatly important. Prior to exploring ways to attract potential STEM teacher candidates to pursue teacher training programs, it is important to understand the perceived value that potential recruits place on STEM careers, disciplines, and the teaching profession. The purpose of this study was to explore students’ perceptions of the usefulness of STEM disciplines and their value in supporting students’ careers. A novel statistical method was utilized, combining exploratory-factor analysis, the analysis of variance, generalized estimating equation evaluations under the framework of a generalized linear model, and quantile regression. Using the outputs from each statistical measure, students’ valuation of each STEM discipline and their interest in pursuing teaching as a career option were assessed. Our results indicate a high correlation of liking and perceived usability of the STE disciplines relative to careers. Conversely, our results also display a low correlation of the liking and perceived usability of mathematics relative to future careers. The significance of these diametrically related results suggests the need for promotion of the interrelatedness of mathematics and STE.
1. Introduction
Since the Great Recession of 1930, the labor market in the United States has been impacted by many factors. The US-based Society for Human Resource Management (SHRM) has reported that technology, globalization, cost containment, speed in market change, and the importance of knowledge capital have reshaped the US workforce and workplace [1]. The shift from the industrial to the postindustrial era created a need for a knowledge-based economy, postsecondary education, and training as a pathway for both individual and company success [2]. Since 2006, the US Congress has emphasized that an increase in STEM majors to meet the 21st century workforce demands [3,4] is inevitable.
The US Bureau of Labor Statistics predicts that there will be an 8.8% gain in STEM employment from 2018 to 2028, as opposed to a 5% gain in non-STEM occupations. Moreover, there is a huge disparity in the median annual wage in 2019 between STEM occupations (USD 86,980) and non-STEM occupations (USD 38,160) (https://www.bls.gov/emp/tables/steml-employment.htm accessed on l September 2019). Of the 1.8 million bachelor’s degrees awarded in 2015–2016, about 18% were in STEM fields [5]. Many researchers have expressed concern about the decline in STEM candidates in the US educational system, which may impact the US economy [6,7]. Evaluating factors underlying the gap between higher-education supply and workforce demand in STEM fields is critical [8].
Attrition from STEM disciplines may be due to many factors. Ref. [9] utilized data from a cohort of students to examine the movement of students entering and then leaving STEM fields. In their report, a multinomial probit (MNP) model revealed that attrition was related to students’ demographics, precollege academic preparedness, type of institutions, STEM course taking, and course intensities. Additionally, [10] reported that 36% of students who initially chose to pursue STEM degrees were no longer in STEM fields 6 years after their initial college entry, according to a longitudinal study following 1530 students in STEM majors. Ref. [3] found that 46% of workers with a bachelor’s degree in STEM left the STEM field within 10 years of entry. Researchers found that students who struggled to complete STEM degrees in 4-year colleges often chose other majors, and nearly 22% of those students ultimately dropped out of college after 5 years [11]. Specifically, 38% of students who started with a STEM major did not graduate [3]. The authors of ref. [3] found that 19% of students who entered postsecondary programs received a bachelor’s in a STEM area. Of that 19%, 10% of STEM graduates at the bachelor’s level actually work in STEM fields, with 8% of STEM bachelor’s graduates still working in STEM fields 10 years after their graduation [3].
Recruiting prospective students into STEM disciplines is a multifaceted but very important factor in understanding the shortage in levels of STEM education [1]. Having STEM educators promote opportunities for students pursing STEM careers is an opportunity for STEM recruitment. Teaching is a valuable and rewarding career [12]. With national declines in the number of individuals entering teaching, particularly in STEM areas, the need to recruit, retain, and promote STEM teaching is increasing. With a critical deficit in the STEM teaching pool, research investigating and seeking opportunities to rectify STEM teacher shortages is needed. Should there be an increase in the amount of STEM activity and training for our students? What is the contribution of mathematics (math) in STEM [13]? Should the curriculum be redesigned for a greater appreciation of math [13,14]? These are very useful questions to answer with data.
Education is an important factor determining the level of a person’s involvement in education and teaching because opportunities often act as a barrier to access to resources that enhance understanding and appreciation of science [14,15]. Studies have also shown that there are multidimensional aspects of sociodemographic factors related to attitudes and behaviors towards teaching and STEM recruitment [14,15,16].
A few recent studies showed that the lack of available teachers in STEM engenders higher risks of poorly educated youth, partly because the probability of participating in STEM educational or recreational activities (such as MathFest, Research America, MATHCOUNTS, or March of Science) decreases. For instance, current trends in US economic development have caused a decrease in the amount of interest in STEM education in general, presenting severe social-policy implications [17,18,19]. The authors reported that the lack in educational STEM training is more important than reported values are; as a barrier to STEM training, they listed the opportunity to participate in one of those activities as early as possible and repetitively. Many empirical studies suggest that STEM activities such as research and mentoring help underserved students’ retention and graduation [20]. Moreover, these students are more likely to be involved in teaching and other academic careers. They demonstrated that students and individuals are less likely to engage in STEM careers using American Survey data. Parents and communities with children are now confronting a lack of STEM appreciation. STEM teacher shortage, a situation in which people can have only insufficient classes and training to engage with students and other basic activities (such as science, mathematics, technology, and engineering), might prevent them from participating actively in STEM careers.
However, few researchers have examined the association between teacher recruitment strategies and STEM interest in the US, although prolonged shortages of STEM teachers is, globally, a central issue [21]. Modeling has faced issues because of the underlying assumptions of normality or homogeneity of variance. Hence, we propose a novel statistical method for the comprehension of needs assessment that educational research has not used before. With this paper, we unfold the ambiguities and gaps that appear in implementing a recruitment intervention.
This study specifically examined relationships between interest in STEM career fields, interest in pursuing teaching as a career, and the perceived usability of school STEM learning by discipline with respect to future career ambitions. Using a regional internet survey distributed to high-school juniors and seniors, and college students in the Hampton Roads region of Virginia, this study examined opportunities for secondary STEM teacher recruitment, STEM career interest, and interest in teaching with respect to STEM disciplines.
To investigate ways of addressing the secondary STEM teacher shortage in the Hampton Roads region of Virginia, a National Science Foundation (NSF) Noyce Capacity Building grant was funded with the goals of (a) enhancing recruitment strategies that target under-represented populations for secondary STEM teacher preparation programs, and (b) revising undergraduate STEM degree programs to include middle-school teacher preparation options. With these goals in mind and using questions from a STEM career interest survey [22] that was validated after being tested for reliability and psychometric properties [23], survey questions were added to customize the survey for the targeted populations. Data outcomes for the assessment were typical in the education system and were based on a proficiency psychometric scale, typically with six points: (1) strongly disagree, (2) disagree, (3) somewhat disagree, (4) somewhat agree, (5) agree, and (6) strongly agree. The instrument consisted of Likert scale responses that asked participants about their liking and understanding of STEM, and plans for future pursuance of STEM careers. For example, in the science cluster, students were asked if they agreed with the following statements:
- Generally speaking, I like doing science activities.
- I understand science concepts in the natural world.
- I plan to use science in my future career.
- If I do well in science classes, it will help me in my future career.
- My parents/guardians would like it if I choose a science related career.
- Someone in my family uses science extensively in their career.
After asking participants about their liking and understanding of each STEM discipline, participants were asked a series of questions about their valuations.
Our study is the first attempt at applying two statistical methods and building recommendations for STEM recruitment and success.
In this study, we proposed to uncover two aspects or hypotheses. The first aspect was that the students generally understand the value of STEM, but do not include math in STEM. In fact, it is questioned whether they associate math to STEM. Once identified, we further sought to discover if there was a relationship between these ideas and other variables by leveraging the impact of variables such as gender, race, and school type. The second aspect related to students’ confidence in liking and using math in STEM.
The remainder of the manuscript is organized as follows. In Section 2, we present a literature review and data background. In Section 3, the hypotheses and proposed methodology are presented. We performed analysis under the generalized and quantile regression models which is reported in Section 4, along with description of the empirical estimates associated with response variables. We end with a conclusion in Section 5.
2. Background Data and Preliminary Findings
As part of the Noyce Capacity Building Grant, the research team conducted a survey to determine potential students’ perspectives about STEM careers in general, and secondary STEM teaching and the teaching profession in particular. The survey was administered at the school level, and targeted high schools and both 2- and 4-year institutions of higher education in the Hampton Road area of Virginia. Baseline covariates included demographic information such as race, gender, type of institution, grade, understanding and perceived usability of science, mathematics, technology, and engineering, career aspiration, and value of teaching. Each survey item response used a Likert scale that was correlated to a scalability score in the range of 1 to 6, with 1 representing the lowest form of agreement and 6 representing the highest form of agreement. We focused on a sample of 316 participants. Four scores were generated to represent values associated with each of the STEM disciplinary categories.
Table 1, Table 2, Table 3 and Table 4 summarize the basic information on gender, race, and schooling level. In Figure, pie charts are displayed for each of the four scores. The same information is again displayed with crosshatched instead of solid pie slices. Figure 1 and Figure 2 evidence that, even though gender was the same, these values dramatically changed the understanding once the averages of Scores 1–4 were included; however, the conclusion is ambiguous. There were subtle changes of which the conditional distribution, associations, and relations among confounders and instruments call for diligent approaches to inferences.

Table 1.
Frequency for gender.

Table 2.
Frequency for race.

Table 3.
Frequency for combined race.

Table 4.
Frequency for schooling.
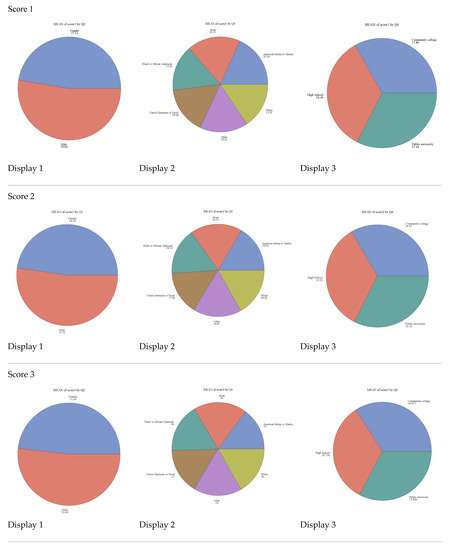
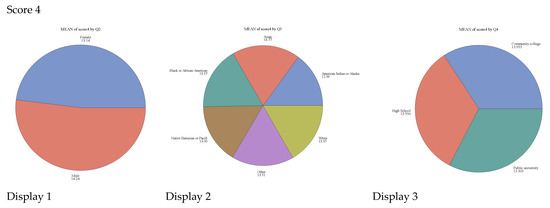
Figure 1.
Pie charts of Scores 1–4 by gender, race, and schooling method.
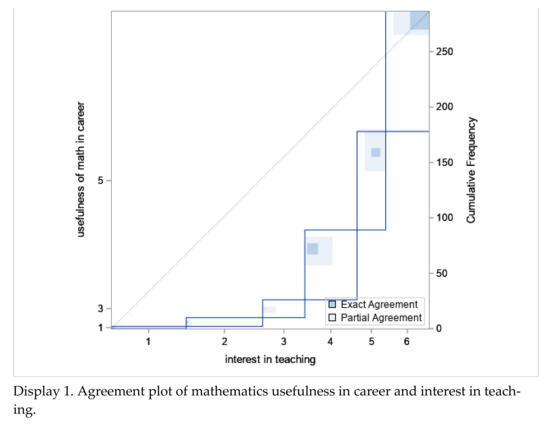
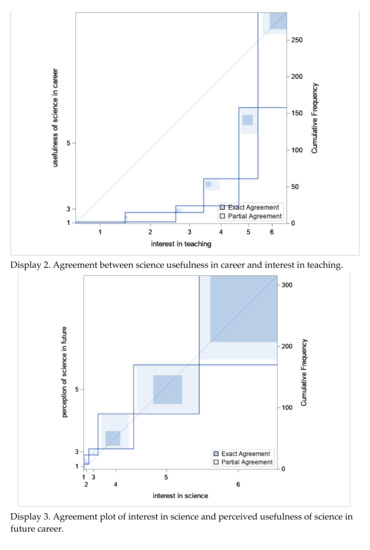
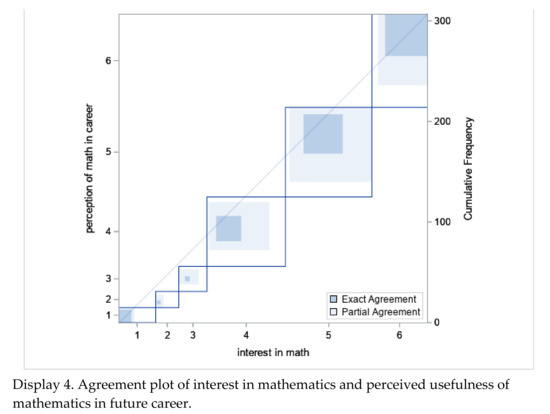
Figure 2.
Agreement plots.
Pioneering research into STEM teacher shortages added the concept of training to the conventional measure of shortages on the basis of sociodemographic factors [17,21]. Since then, several researchers have defined, evaluated, and calculated shortages in various countries. The mathematical concepts and competencies may be a key factor in STEM disciplines [13,24]. They demonstrated that the US government must increase policy support, particularly in engaging students from minority families. They also mentioned that each state has a duty to tailor a policy for their constituents.
In this paper, the concepts of the classification and challenges of STEM teacher recruitment and assessment were applied to examine educational outcomes and related behaviors. We studied multiple dimensions of STEM attitudes (gender, ethnicity, and types of educational institutions) that are most useful to predict individuals’ self-reported STEM interests using a regional survey in the US. In addition, STEM activities may affect individuals’ STEM attitudes, behavior, and future jobs. Nonparametric methods were also explored with the intent of relaxing unrealistic assumptions in the MNP of normality and homogeneous variance.
3. Methodology and Hypotheses of Interests
3.1. Descriptive Statistics
A survey was chosen to answer the research questions and test the hypotheses that the students generally understand the value of STEM, but do not include math in STEM. The survey was sent out to students and to parents if needed for parental consent. Responses were received from 47 high-school students, 65 community-college and 201 public-university students, with 3 missing values. The survey included instruments such as comfort with, projected usability of, and applications of STEM relative to future career aspirations. Respondents selected from gradated agreement options that were then translated into a 6-point Likert scale (1 = strongly disagree to 6 = strongly agree). Demographic information such as gender and race was also included, but provided nominal disparities. Sample size was checked for power analysis, and the computed power was larger than 90%. Assumptions of normality were used for the selected variables and checked for validity.
The gathered data from high-school and college students showed low interest in teaching. Of the respondents, 57% agreed or strongly agreed with the statement, “I believe that teaching is a valued profession in our country”, but only 21% of respondents strongly agreed or agreed with “I can see myself as a middle- or high-school STEM teacher in the future”. Similarly, cross-referencing the students’ responses comparing the usefulness of math in career ambitions with their interest in teaching as a career showed very limited correlation (see Figure 2: Display 1). However, there were small contingents of respondents who agreed that math would support their career ambitions, and they could see themselves teaching (see the shaded squares in Figure 2: Display 2). Similarly, there were slightly larger groups of respondents who strongly agreed that science would support their career ambitions, and they could also see themselves teaching (see Figure 2: Display 2).
With these results, we further investigated participants’ responses about their use, understanding, and liking of math and science, and the connection expressed between math and science and future career ambitions. While interest in teaching math and science was low for both, interest in and the perceived usefulness of science in future career ambitions showed a strong correlation (see Figure 2: Display 3). Similarly, strong correlations were found for both technology and engineering. However, interest in and the perceived usefulness of math in future careers did not show a similar strong correlation (see Figure 2: Display 4). For math, only those who strongly agreed or strongly disagreed showed strong correlations in this comparison.
These findings prompted a focused investigation about why students’ responses about math and their perceptions of the usefulness of math varied so starkly when compared to the other STEM disciplines. To consider liking, understanding, and career implications regarding STEM fields, four new scores were created. Score 1 combined the following statements: (a) “Generally speaking, I like doing science activities”; (b) “Generally speaking, I like doing math; (c) “Generally speaking, I like activities involving technology”; and (d) “Generally speaking, I like activities involving engineering”. The purpose of Score 1 was to compare liking of STEM disciplinary activities with other response areas. Score 2 combined the following statements: (a) “I understand science concepts in the natural world”, (b) “I can use math to solve problems”, (c) “I am able to learn new technologies to solve problems”, and (d) “I can apply engineering design principles to solve problems”. Score 2 was developed to investigate the understanding of STEM disciplinary applications in an effort to compare the understanding and usability of STEM. Score 3 combined the following questions: (a) “I plan to use science in my future career”, (b) “I plan to use math in my future career”, (c) “I plan to use technology in my future career”, and (d) “I plan to use engineering in my future career”. Seeking to pinpoint the impact of math on students’ liking, understanding, and career interests relative to STEM, Score 4 was a replication of Score 3 but with math excluded. Score 4 combined (a) “I plan to use science in my future career”, (b) “I plan to use technology in my future career”, and (c) “I plan to use engineering in my future career”. Score 4 was created to reveal the difference in math responses when compared to the other STEM disciplines.
As the number of covariates increased, it became difficult to find good matches for subjects in their categories or classes. An advantage of introducing a score function is that it provided a data summary related to the participants. Under this framework, a proposed solution was dictated by the liking, understanding, career vision, and perceived usability of the STEM disciplines. These values are described as Scores 1–4.
which describes liking of STEM.
which describes understanding of STEM.
which describes career interest in STEM.
which describes use of STE.
Score1 = Likes Science (Q6) + Likes Math (Q12) + Likes Tech (Q19) + Likes Eng. (Q26)
Score2 = Q7_new + Q13_new + Q20_new + Q27_new
Score3 = Q8_new + Q14_new + Q21_new + Q28_new
Score4 = Q8_new + Q21_new + Q28_new
3.2. Hypotheses of Interests
These findings prompted a focused investigation about why students’ responses about math and their perceptions of the usefulness of math varied so starkly when compared to the other STEM disciplines. To consider liking, understanding, and career implications regarding STEM fields, regression-analysis scores were suggested.
Hypothesis 1 (H1).
Students generally understand the value of STEM, but do not include math in STEM. In fact, it is questioned whether or not they do associate math to STEM.
Hypothesis 2 (H2).
There are questions involving the liking of math and its use. So, the second aspect is the hypothesis that, in their training, students have confidence in using STE but not in using math. The students do not even seem to acknowledge the math influence in STEM careers. Math is in its own bubble. They do not connect math with STEM.
3.3. Variables
The explained variables selected in this questionnaire were as follows:
- Q6: Generally speaking, I like doing science activities.
- Q8: I plan to use science in my future career.
- Q12: Generally speaking, I like doing math.
- Q14: I plan to use math in my future career.
- Q15: If I do well in math classes, it will help me in my future career.
- Q19: Generally speaking, I like activities involving technology.
- Q26: Generally speaking, I like activities involving engineering.
with a 6-point Likert scale, as displayed in Table 5, representing the following alternatives of the measurements of the items as dependent variables: strongly disagree (1), disagree (2), somewhat disagree (3), somewhat agree (4), agree (5), and strongly agree (6).

Table 5.
Percentage of responses of variables.
3.4. Methodology
The seriousness of training future students cannot be overemphasized. By recognizing their perceptions, improved pathways may be recommended in order to promote achievement in math.
This analysis provides a useful link in the sense that it identifies one of the most important effects of math in STEM. It provides a line of reasoning from the contextualization.
Under generalized linear models or, more generally, generalized estimating equations (GEE), statistical methods can be used to analyze data that are either longitudinal or correlated, such as clustered data. They are widely used today, and were first introduced by [25] as a method to estimate the parameters of a generalized linear model with a feasible unknown correlation between outcomes and predictors. Regression analyses with the GEE methodology are, however, a common choice when the outcome measure of interest is discrete (binary or count data, possibly from binomial or Poisson distribution) rather than continuous [26]. The GEE algorithm is available for use in many statistical software programs; in this project, we considered the use in R.
- Objective:
The primary goal was to fit a model for noncontinuous responses, that is, correlated and clustered responses, using GEE methodology.
- Assumptions:
- The responses Y1, Y2, ..., Yn may be correlated or clustered, i.e., cases are not necessarily independent.
- Covariates can be the power terms or some other nonlinear transformations (idea of scaling) of the original independent variables, and can have interaction terms.
- The homogeneity of variance does not need to be satisfied.
- Errors may be correlated.
- It uses quasi-likelihood estimation rather than maximum likelihood estimation (MLE) or ordinary least squares (OLS) to estimate the parameters, but at times these coincide.
- Covariance specification. These are typically four or more correlation structures that are assumed a priori. Four correlation structures are commonly considered:
- Independence (correlation between response points is independent)
- Exchangeable (or compound symmetry)
- Autoregressive of Order 1 (AR1)
- Unstructured
Under such a GLM, the equation can be formulated as follows:
where represents the response of the i-th participant, for , with represent the predictors that could be discrete or continuous, with errors .
Due to the complexity associated with data and the scale method, quantile regression offers techniques of generalized linear regression with no parametric form for the distribution of the response. Quantile regression, as introduced by [27,28], is an alternative and is extensively used, but not in education research data. It fits specified percentiles, and is described as a function of the response variable: y_i represents the response of the i-th participant
where , with representing the predictors which could be discrete or continuous.
In our model formulation, response is the value of the career in STEM (Score 3). We also applied the model for perceived usefulness of STE (Score 4).
4. Data Analysis and Results
Data analysis was conducted in two steps. The first step considered exploratory-factor analysis (EFA): it included the analysis of simple models, multivariate analysis of variance (MANOVA), and GEE or analysis under the framework of the generalized linear model (GLM). The other method was quantile regression.
4.1. Exploratory-Factor Analysis
The objectives of performing EFA were to (1) test and reduce the number of variables used in the assessment, (2) validate the assessment, and (3) modify and prove the theoretical model on the basis of data. Research in [14,15,21] indicated that there were multiple factors associated with STEM recruitment; some of the factors retained after performing EFA are included in Table 1, Table 2, Table 3 and Table 4. Data were summarized for an efficient understanding of the data and building of clauses to answer hypotheses. The subset and filtered data needed further assessment when connected together. In the following sections, the development of the career assessment in STEM and use of math is presented in detail. Underlying factors between latent and measured constructs are difficult to differentiate. Such results prove that factors that influence STEM careers and use of math are interconnected.
4.2. Generalized Linear Analysis
Analysis showed that liking science, math, and technology was highly significant in predicting Score 3. This indicates that science activities, math, and technology greatly impact careers. Math is associated with STEM. In fact, it is a recognized element in the STEM component. This output is given in Display 1. A simple predictor model of Score 3 based on liking engineering and on gender showed that gender was not significant, although females had a slightly higher Score 3 than males. The corresponding estimate of model variance was then = 6.37. Even in the case of mixed-effects models, with gender as random, the variance associated with the model did not change much. Under a Type 1 sum of square, gender (man vs. woman) became significant, but was masked by the liking of engineering. The same remark can be made of gender when the liking of science, technology, engineering, and math were added to the model. The significance of gender was masked once the other variables were present, with Score 3 being lower for females. Score 3 was also highly related to the liking of engineering. Gender and race were not significant. In other words, Hypothesis 1 validated that math is an integral part of STEM, as are engineering and science. The number of females was more than twice that of males (190 vs. 91); see Display 3. Score 3 values showed that gender difference (males and females only) could be removed from the model statement as marginal lines based on gender crossed, although the lines were positive with liking engineering, σ ̂^2 = 6.25. In later models, we included additional predictors and attempted to account for some of the variability in Score 3.
Analysis showed that the liking of science, math, and technology was highly significant in predicting Score 4. However, when the liking of engineering and race were added to the model, the liking of math and gender become nonsignificant in predicting Score 4. This shows that “doing math” was not so well-acknowledged in Score 4 within the use of STEM. This confirmed the second hypothesis. In other words, the second hypothesis was not rejected.
The correlation between Scores 3 and 4 was quite strong and not ignorable. It explained similar results with all the variables, except for the liking of math. In Score 4, the liking of math was not significant. There was a strong correlation between liking of STEM and use of STE.
We interpreted gender as a microunit naturally occurring when the unit groups (Q6, Q12, Q19, and Q26) were not revealed or included. Achievements in Scores 3 and 4 were differentiated by the liking of math.
Score 4 (use of STE) was not significantly related to the liking of math (Q12).
4.3. Quantile Analysis
Although the GLM methods and output are useful in connecting predictors and predicted variables, underlying assumptions may be questionable. Nonparametric methods were explored to relax unrealistic assumptions of normality and homogeneous variance by different groups.
We applied the quantile regression technique proposed by [27,28]. The technique, which is an extension of linear regression, is widely used in finance, economics, and biology. Quantile regression is used when the conditions (linearity, homoscedasticity, independence, or normality assumptions) of linear regression are not met, and offers the option of estimating the relationship between predictors and outcomes at several points in the distribution while minimizing the sum of absolute residuals.
Researchers use multiple strategies to determine if items for scales have convergent validity. First, tests of Kaiser–Meyer–Olkin (KMO) and Bartlett performing exploratory- and confirmatory-factor analysis were conducted where the varimax rotation was indicated by the KMO measure of sampling adequacy. The results of both reliability tests supported convergent validity.
The output in Table 6 for correlations shows that Scores 1–4 were highly correlated (with values of 0.71 and more). The KMO measure of sampling adequacy was 0.781, indicating that the data were suitable to perform quantile-factor analysis [23,29,30,31]. Composite construct reliability and individual item reliability are included in detail. Results from Wilk’s lambda were 0.95 and 0.85, with a p value of 0.0716 and <0.001 for Q4_new and Q2_new, respectively.

Table 6.
The correlation of the scores.
Quantile regression with least absolute shrinkage and selection operator procedure compared and differentiated the students with higher Scores 3 vs. those with lower Scores 3 by considering the sparse model at the 0.05, 0.1, 0.5, and 0.9 quantiles. Of the data, 30% was reserved as validation, which avoided overfitting. The output for quantiles at 0.10, 0.50, and 0.90 is presented in Figure 3. An interesting characteristic is that the AIC had a negative parabola shape. The values of the AIC increased from the 0.05 to the 0.5 quantile, and then decreased from the 0.5 to the 0.9 quantile. This shows that career in STEM was mostly of a better fit at the high and low quantiles of the students that were surveyed. Such a structure would not have been detected by considering GLM analysis. This structure break model revealed an observed effect that could match the critical understanding of the problem. The QA fit and insight can be linked to how STEM is related to the liking of doing science (Q6) and the planning to use of math in the future (Q14). The coefficients for Score 3 (career of STEM) progression plots are displayed in Figure 3. The 95% prediction confidence intervals for the parameters with respect to gender for Score 3 are displayed in Figure 4. This result validated the H1 hypothesis in the sense that the contribution of math in STEM (Q15) was not recognized in almost all percentiles. That means that students’ training could be revaluated to place a clear emphasis on math.
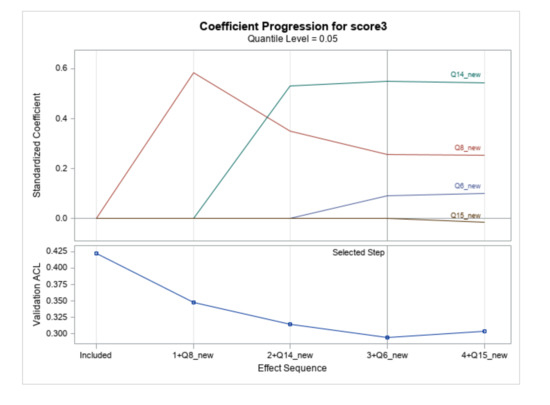
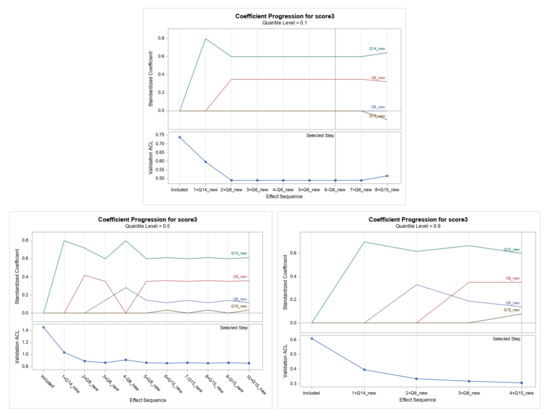
Figure 3.
Plots of coefficient progression plots for Score 3 at 0.05, 0.1, 0.5, and 0.90 quantiles.
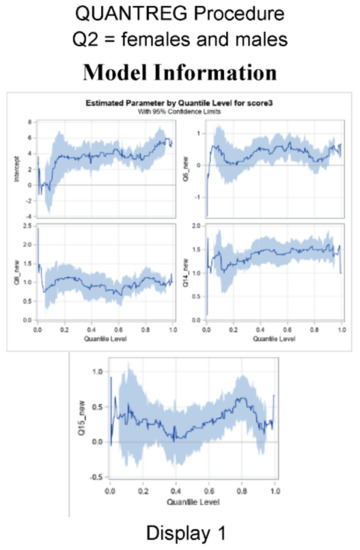
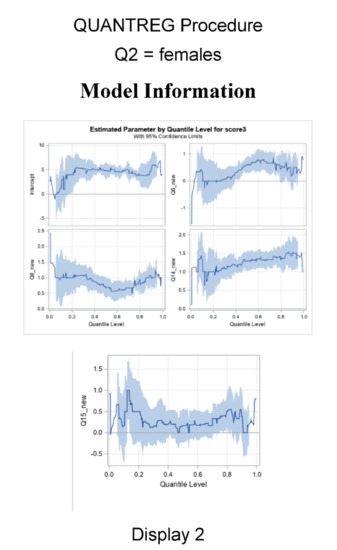
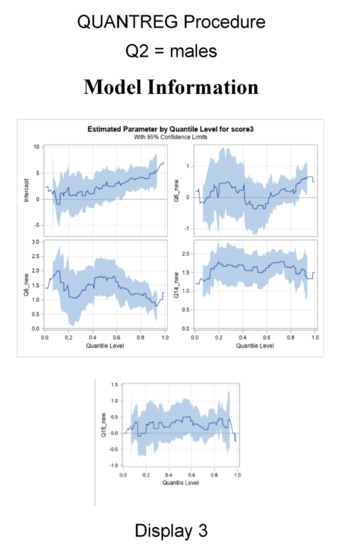
Figure 4.
95% confidence levels for Score 3 with respect to Intercept, Q6_new, Q8_new, Q14_new, and Q15_new for all genders (Display 1), females (Display 2), and males (Display 3).
The coefficient progression plots are displayed in Figure 3. The plots visualize the selection process of the four quantile models, and they all show that the plans to use science and math in career entered the model first and were followed by liking to do science. The plan to use science and liking of science seemed to intersect. They coincided with the assumption that when it comes to science, the liking and the usage/doing are contributing factors in the career. The selection process did not include liking of doing math in most quantiles, which indicates that the liking of math is not a contributing factor in the plans to use math in a career.
Furthermore, quantile plots shown in Figure 4 display the parameter estimates and the 95% confidence intervals for each quantile level. Plots of the quantile regression reveal that all the predictors positively affected the distribution of Score 3 because the confidence limits were positive at all quantiles (greater than 0 or above the x axis).
We compared the results with the GLM output. The results showed the same consistency of math being valued, but not strongly at the 50th percentile. Results were further explored when gender was included. Gender and race were also not significant factors in Score 3. Figure 4 displays cumulative density functions and pdf quantile plots based on females and males, with females outnumbering males. Plots of the single effects under quantile regression are displayed in Figure 4. The confidence bounds were commuted under sparsity with nonindependent and identically distributed assumptions. They also show that the effects of liking science (Q6) fluctuated, with no effect at the lower quantiles. Planning to use math in the future (Q14) affected the STEM career score (Score 3) at the higher quantile levels (Figure 4: Display 1), and more so for females than that for males (Figure 4: Display 2 vs. Figure 4: Display 3).
Schooling environment (community college, high school, or public university: Q4) was then added. The GLM model found no significant difference in Score 3 between the three schooling environments. There were higher variations between high school and public university but, overall, with the variation as shown in the difference plots, there was no difference in Score 3 based on institution once liking science (Q6), the plan to use science (Q8), and the plan to use math (Q14) were included in the model from the GLM to the quantile regressions. This result is somewhat validated in Figure 1 under Score 3. Although public university had more respondents, the mean values of their Score 3 participants were not significantly different than the mean Score 3 values in community college or high school, with a p value of 0.5274.
Planning to use math in a career was the most significant variable in predicting career or Score 3. Our students agreed with using math in their career in STE under the quantile regression model. Planning to use math in the future (Q14) was consistently selected at all quantiles.
The use of STE (Score 4) was highly correlated with a career in STEM (Score 3). The AIC had a negative parabola shape. This shows that using STE was mostly confusing when the middle half of the students were surveyed. The significance of using STE was mainly driven by a plan to use science, and the perception that doing well in math helps to achieve a career in STE (Q15) and technology activities (Q19). The confusion involved how STE is related to liking doing math (Q12) and planning to use math in the future (Q14). This result validated the H2 hypothesis more in the sense that doing math (Q12) in STE was not selected for any of the quantiles. To add to that, planning to use math (Q14) was selected only when we considered the higher percentiles.
The coefficient progression plots are displayed in Figure 5 at the 10th, 50th, and 90th percentiles. The plots visualize the selection process and show that plans to use science (Q8) and technology (Q19) entered the model first. The plans to use science (Q8) and technology activities (Q19) were predominant, whereas liking to do science activities (Q6), liking to do math (Q12), and the perception of math in science (Q15) were not significant and seemed to intersect. They coincided with the assumption that, when it comes to science, liking and use are contributing factors in STE. In particular, the last result indicates that liking math was not a contributing factor in STE, even though it is significant in the use of STE, which explains H2.
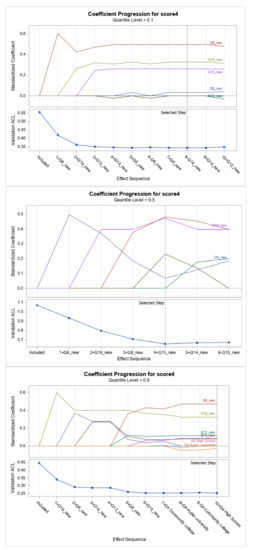
Figure 5.
Plots of coefficient progression plots for Score 4 at 0.1, 0.5, and 0.90 quantiles.
Furthermore, the quantile plots shown in Figure 4 display the parameter estimates and 95% confidence intervals for each quantile level. The plots of the quantile regression reveal that all predictors positively affected the distribution of the use of STE (Score 4) for the plan to use science (Q8) and liking to use technology (Q19) because the confidence limits were positive at all quantiles (greater than 0 or above the x axis).
Thus, both hypotheses were sustained. Students generally understand the value of STEM, but ignore the math component of STEM. They also like and have confidence in using STE (mostly females), but lack confidence in using math. The results are insightful, and can help suggest guidance and training bridges. Indeed, education is a service field, a must for sustainable development, with great rewards. Therefore, a comprehensive assessment should include these findings, which may guide and lead training in being acquainted to such ideas that students have about math. This concept can be described as a function of the understanding that math components play in the curriculum. Connecting training with issues helps students to gain confidence in their abilities to become STEM teachers and influence students in math areas.
5. Conclusions
This study specifically examined relationships in a new methodological analysis to explore the relationships between interest in STEM disciplines, and related interest and competency in secondary STEM teaching. Data were gathered from high-school juniors and seniors, and college students through an Internet survey distributed in the Hampton Roads region of Virginia. Using a novel statistical methodology that had not been proposed for use in educational research, two hypotheses were tested and supported. Students understand the value of STEM, but do not include math, and they have confidence in using STE, but not math. By setting the multidimensionality of STEM, which consists of training and opportunity, and by considering other sociodemographic factors, we analyzed the educational opportunities with associated readiness and training. Although gender was not a significant factor, the implications for this study offer new support for revised or readjusted curricula, and for personal-development opportunities in undergraduate STEM programs to help college students in achieving their career goals in STEM. The impact of mathematics should be re-evaluated. This new assessment integrates the interest in math and science with the perception that math and science are both very useful for future STEM careers, including secondary teaching.
While confident with these results, further work could explore the perceived usability of math in the other STEM disciplines, i.e., science, technology, and engineering. Having a larger and more random sample may be desirable. However, that limitation does not undermine this study, as such findings are fundamental to other studies and training efforts in addressing the STEM recruiting and shortage.
Author Contributions
Conceptualization, M.G., S.F. and N.D.; methodology, N.D. and K.D.; software, N.D.; validation, N.D. and K.D.; formal analysis, N.D.; investigation, M.G.; resources, M.G.; data curation, M.G. and S.F.; writing—original draft preparation, N.D. and K.D.; writing—review and editing, N.D. and K.D.; visualization, N.D.; supervision, N.D., M.G., S.F. and K.D.; project administration, M.G.; funding acquisition, M.G. and N.D. All authors have read and agreed to the published version of the manuscript.
Funding
We gratefully acknowledge the research team at ODU and crew as well as the many scientists participating in the education programs in the Southeast. Funding was provided by NSF’s NOYCE Capacity Building Grant award number 1852813.
Institutional Review Board Statement
Approval from the institutional review board was granted, under Approval Number 18-254.
Informed Consent Statement
The study was conducted anonymously online through voluntary and parental participation. Ethical review and approval were obtained for this study given that some participants were under age and needed parental permission.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rothwell, W.J.; Kolb, J.A. Major workforce and workplace trends influencing the training and development field in the USA. Int. J. Train. Dev. 1999, 3, 44–53. [Google Scholar] [CrossRef]
- Carnevale, A.P.; Desrochers, D.M. Standards for What? The Economic Roots of K-16 Reform; Educational Testing Service: Princeton, NJ, USA, 2003; Available online: https://fordhaminstitute.org/national/commentary/standards-what-economic-roots-k-16-reform (accessed on 10 October 2020).
- Carnevale, A.P.; Smith, N.; Melton, M. STEM: Science Technology Engineering Mathematics; Georgetown University Center on Education and the Work-Force: Washington, DC, USA, 2011; Available online: https://cew.georgetown.edu/cew-reports/stem/ (accessed on 10 October 2020).
- Hanushek, E.A.; Peterson, P.E.; Woessmann, L. Achievement Growth: International and U.S. State Trends in Student Performance; Harvard’s Program on Educa-tion Policy and Governance Institute; SAS/STAT 9.2 User’s Guide. S.A.S.; July 2012. Available online: https://eric.ed.gov/?id=ED534652 (accessed on 10 October 2020).
- NCES National Center for Education Statistics, Indicator 26: STEM Degrees. 2019. Available online: https://nces.ed.gov/programs/raceindicators/indicator_reg.asp (accessed on 10 October 2020).
- Kelic, A.; Zagonel, A. Science, Technology, Engineering, and Mathematics (STEM) Career Attractiveness (Report No. SAND2008-8049); Sandia National Laborato-Ries: Albuquerque, NM, USA, 2009; Available online: http://www.systemdynamics.org/conferences/2009/proceed/papers/P1390.pdf (accessed on 10 October 2020).
- Maltese, A.V.; Tai, R.H. Pipeline persistence: Examining the association of educational experiences. Sci. Educ. 2011, 95, 877–907. [Google Scholar] [CrossRef]
- Lin, Y.-C. Developing a Career Development Assessment for Predicting Young Stem Graduates’ Employability and Career Barriers. Ph.D. Dissertation, STEM Education & Professional Studies, Old Dominion University, Norfolk, VA, USA, 2017. Available online: https://digitalcommons.odu.edu/stemps_etds/21 (accessed on 10 October 2020). [CrossRef]
- Chen, X.; Soldner, M. STEM Attrition: College Students’ Paths into and out of STEM Fields; Statistical Analysis Report; Report NCES 2014–001; U.S. Department of Education: Washington, DC, USA, 2013.
- Chen, X. Students Who Study Science, Technology, Engineering, and Mathematics (STEM) in Postsecondary Education; Stats in Brief. NCES 2009-161; National Center for Education Statistics: Washington, DC, USA, 2009.
- Boundaoui, A. Would-Be Engineers End up as English Majors. 21 May 2011. Available online: http://www.cnn.com/2011/US/05/17/education.stem.graduation/index.html (accessed on 10 October 2020).
- Perrachione, B.A.; Rosser, V.J.; Petersen, G.J. Why Do They Stay? Elementary Teachers’ Perceptions of Job Sat-isfaction and Retention. Prof. Educ. 2008, 32, 1–17. [Google Scholar]
- Fitzallen, N. STEM education: What Does Mathematics Have to Offer? In Mathematics Education in the Margins, Proceedings of the 38th Annual Conference of the Mathematics Education Research Group of Australasi; Marshman, M., Ed.; Mathematics Education Research Group of Australasia (MERGA): Sydney, Australia, 2015; pp. 237–244. Available online: https://acuresearchbank.acu.edu.au/item/884y2/mathematics-education-in-the-margins-proceedings-of-the-38th-annual-conference-of-the-mathematics-education-research-group-of-australasia (accessed on 10 October 2020).
- Roberts, T.; Jackson, C.; Mohr-Schroeder, M.J.; Bush, S.B.; Maiorca, C.; Cavalcanti, M.; Schroeder, D.C.; Delaney, A.; Putnam, L.; Cremeans, C. Students’ per-ceptions of STEM learning after participating in a summer informal learning experience. Int. J. STEM Educ. 2018, 5, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.; Wilton, N. Developing career management competencies among undergraduates and the role of work-integrated learning. Teach. High. Educ. 2016, 21, 266–286. [Google Scholar] [CrossRef]
- van Tuijl, C.; van der Molen, J.H.W. Study choice and career development in STEM fields: An overview and in-tegration of the research. Int. J. Technol. Des. Educ. 2016, 26, 159–183. [Google Scholar] [CrossRef]
- Carnevale, A.P.; Smith, N.; Strohl, J. Recovery: Job Growth and Education Requirements through 2020; Georgetown University Center on Education and the Workforce: Washington, DC, USA, 2013. Available online: https://eric.ed.gov/?id=ED584413 (accessed on 10 October 2020).
- Boston, M.; Henrick, E.; Gibbons, L.; Berebitsky, D.; Colby, G. Investigating How to Support Principals as In-structional Leaders in Mathematics. J. Res. Leadersh. Educ. 2016, 12, 183–214. [Google Scholar] [CrossRef]
- Azano, A.P.; Stewart, T.T. Confronting Challenges at the Intersection of Rurality, Place, and Teacher Preparation: Improving Efforts in Teacher Education to Staff Rural Schools. Glob. Educ. Rev. 2016, 3, 108–128. [Google Scholar]
- Das, K.; Daniel, B.; Andrei, S.; Osborne, L. ASCENT-A Program Designed to Support STEM Students through Undergraduate Research and Mentoring. In Proceedings of the 2016 ASEE Annual Conference & Exposition, New Orleans, LA, USA, 26–29 June 2016; pp. 1–14. [Google Scholar]
- Moakler, M.W.; Kim, M.M. College major choice in stem: Revisiting confidence and demographic factors. Career Dev. Q. 2014, 62, 128–142. [Google Scholar] [CrossRef]
- Pasley, J.D.; Heck, D.J. Identifying, Preparing, and Supporting STEM Master Teachers. (2014); Horizon Research: Washington, DC, USA, 2018. [Google Scholar]
- Kier, M.W.; Blanchard, M.R.; Osborne, J.W.; Albert, J.L. The Development of the STEM Career Interest Survey (STEM-CIS). Res. Sci. Educ. 2013, 44, 461–481. [Google Scholar] [CrossRef]
- English, L.D. Advancing Elementary and Middle School STEM Education. Int. J. Sci. Math. Educ. 2017, 15, 5–24. [Google Scholar] [CrossRef] [Green Version]
- Liang, K.-Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta Regression for Modelling Rates and Proportions. J. Appl. Stat. 2004, 317, 799–815. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G.S. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G.S. Robust Tests for Heteroscedasticity based on Regression Quantiles. Econometrica 1982, 50, 43–61. [Google Scholar] [CrossRef] [Green Version]
- Bruin, J. Newtest: Command to Compute New Test. UCLA: Statistical Consulting Group. Available online: http://stats.idre.ucla.edu/stata/ado/analysis/ (accessed on 18 October 2020).
- Cerny, B.A.; Kaiser, H.F. A study of a measure of sampling adequacy for factor-analytic correlation matrices. Multivar. Behav. Res. 1977, 12, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Xuexia, D. Application of data mining algorithms in the analysis of financial distress early warning model of listed company. In Proceedings of the 2011 3rd International Conference on Computer Research and Development (ICCRD), Shanghai, China, 1–13 March 2011; Volume 4, pp. 287–290. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).