Abstract
Distributed medical, financial, or social databases are analyzed daily for the discovery of patterns and useful information. Privacy concerns have emerged as some database segments contain sensitive data. Data mining techniques are used to parse, process, and manage enormous amounts of data while ensuring the preservation of private information. Cryptography, as shown by previous research, is the most accurate approach to acquiring knowledge while maintaining privacy. In this paper, we present an extension of a privacy-preserving data mining algorithm, thoroughly designed and developed for both horizontally and vertically partitioned databases, which contain either nominal or numeric attribute values. The proposed algorithm exploits the multi-candidate election schema to construct a privacy-preserving tree-augmented naive Bayesian classifier, a more robust variation of the classical naive Bayes classifier. The exploitation of the Paillier cryptosystem and the distinctive homomorphic primitive shows in the security analysis that privacy is ensured and the proposed algorithm provides strong defences against common attacks. Experiments deriving the benefits of real world databases demonstrate the preservation of private data while mining processes occur and the efficient handling of both database partition types.
1. Introduction
In recent years, advances in information and communication technologies have raised deep concerns about how data, and specifically private data, are processed. The development of data mining techniques has attracted considerable attention as the principal goal is to extract knowledge from data and, in the process, discover useful patterns. Useful information can be obtained from data following these steps: (1) data preprocessing, (2) data transformation, (3) data mining, and (4) pattern presentation and evaluation [1]. The information discovered can have incredible value, though serious threats to the security of the individual’s private information must be eliminated. Personal data may be accessed by unauthorized parties and used for different purposes other than the original one for which data were initially collected. The privacy-preserving data mining (PPDM) field has emerged, focusing on solving the privacy issues facing data mining processes. Simultaneously ensuring data accuracy and protecting privacy is the main objective of PPDM.
Public awareness has forced many governments to enforce new privacy protection laws. Regulations are essential to ensure the protection of sensitive information and individual identities. Many countries have established laws on privacy protection. For example, the European Commission released the General Data Protection Regulation (GDPR) [2], which recognizes the need to facilitate the free flow of data, and unifies and promotes the protection of personal data within the European Union. The GDPR requires the implementation of appropriately designed technical measures, and systems should consider data protection to meet the Regulation’s requirements.
Database owners require their data to not be misused by data mining processes and protect their privacy while their data are further analyzed [3,4]. PPDM methods have numerous applications in medical and financial fields. Some companies, for example, aim to extract knowledge on market trends in collaboration with other companies without disclosing their sensitive data due to competition reasons. Consider, for example, several distributed medical institutes desiring to perform medical research while ensuring the privacy of their patients. They wish to run a data mining algorithm on their database union to extract accurate outcomes without revealing private information. The involved parties acknowledge the importance of combining their data, mutually benefiting from their data union but none want to reveal the private data of their patients. Applying PPDM methods, important knowledge is discovered but sensitive information is unable to be extracted by unauthorized parties [5]. Sensitive data are not only limited to financial or medical data, but may also apply to phone calls, buying patterns, and more. Individuals are not interested in sharing personal data without their consent or its sale for various purposes [6].
Databases distributed across several parties may be partitioned either horizontally [7,8,9,10] or vertically [11,12]. In the horizontally partitioned case, each party’s database contains different records with the same set of attributes. The main objective is to mine global information from the data. In the vertically partitioned case, each party’s database contains different sets of attributes for the same record set [13,14] concerning the same identity. The union of vertically partitioned datasets allows the discovery of knowledge that cannot be obtained from each individual database. A horizontally partitioned dataset example is the medical records of a patient, where the attributes associated with the patient are common for all clinics, such as the number of the insurance card, the disease, and so forth. A vertically partitioned dataset example is buying the records of a client, where each store has specific and unique user habits and different patterns are created by each store’s database [15].
Cryptography, randomization, perturbation, and k-anonymity are a few of the various privacy-preserving techniques proposed in the literature. All these methods aim to prevent the possible disclosure of sensitive information to possible adversaries when data mining processes are applied for the extraction of useful information. Numerous data encryption approaches proposed in the PPDM field are based on the idea proposed by Yao [16] and extended by Goldreich [17]. Secure multiparty computation (SMC), a subfield of cryptography [17], aims to mine global information in the form of aggregate statistics. A set of parties wishes to jointly compute a function over the combination of all partitioned private data (input) of each participant. The main aim of this process is to protect local data without revealing the input to other parties. The data collector (miner), a trusted third party, performs all necessary calculations with the input of all the acquired private data of all participants. The miner, who acts as the data collector in the proposed protocol, forwards the final results to each party, with their main concern being the preservation of privacy. This process is secure if, at the end of it, neither of the parties nor the miner can obtain information other than the final outputs [18]. The basic idea is described as follows: “the computation of a function that accepts as input some data is secure if at the end of the calculation process neither party knows anything but their own personal data, which constitute one of the inputs, and the final results” [16,17].
In this paper, we present an extended version of the work originally presented at the SEEDA-CECNSM 2020 conference [19]. The privacy-preserving data mining approach was first introduced in Reference [20] only for horizontally partitioned databases. Here, we exploited the multi-candidate election schema [21] to extract global information from both horizontally and vertically partitioned statistical databases. The traditional naive Bayes classifier has been widely used in privacy preservation techniques, but based on the unrealistic assumption that attributes are independent. Conversely, the tree augmented naive Bayesian (TAN) classifier does not require this assumption and behaves more robustly. In this study, the privacy-preserving version of this classifier was properly designed and developed for the purposes of the proposed implementation. The Paillier cryptosystem [22] was implemented to perform all necessary cryptographic processes to preserve privacy by exploiting the homomorphic primitive, as first proposed by Yang et al. [23]. Based on this, the data collector (miner) and each participant are unable to identify the original data of the shared distributed databases, except for the data owner. In addition, the identity of the database owner is private and unidentifiable by any aggressor. Communication among participants is unfeasible, and the miner is able to continue with the performance of all necessary operations if at least three participants are connected with the data collector.
Most techniques proposed in the literature are empirical or theoretical: they lack implementation of their hypothesis presented in their work. The privacy-preserving algorithms in the literature handle either horizontal or vertical partitioned databases, but not both. In addition, these approaches mainly focus on nominal attribute values. To the best of our knowledge, in the privacy-preserving research field, algorithms that support both horizontally and vertically partitioned databases have never been proposed. In this paper, we present a well-designed and improved privacy-preserving data mining technique, which was originally proposed in References [19,20], which focuses on preserving privacy and aims to obtain useful information from horizontally and vertically partitioned statistical databases, handling both nominal and numeric attributes values (including binary values).
The following section summarizes the PPDM evaluation methods proposed in the literature and briefly reviews some of the proposed privacy-preserving techniques in the field (Section 2). The background of the current approach is presented in Section 3. Section 4 describes the proposed protocol and its security and design requirements. The current protocol in terms of performance and data accuracy is evaluated in Section 5. Section 6 provides an analysis of some possible threats to the proposed method and how they are confronted. Recommendations for future work (Section 7) and our conclusions (Section 8) are presented in the last two sections.
2. Related Work
Privacy-preserving data mining has received extensive attention and has been widely researched in recent years, becoming an important topic in data mining research since the work presented in References [24,25]. Privacy-preserving data mining techniques have several applications in different domains. Some of the domains have raised concerns about the disclosure of sensitive information. The majority of PPDM techniques have been developed to prevent leakage of sensitive information without affecting the extracted knowledge produced by the application of mining processes on the data [26]. The applied methods either modify or remove some original data to achieve privacy preservation. This action creates a trade-off between the data quality and the privacy level, which is known as utility. PPDM techniques should be designed to guarantee the maximum utility of the produced outcomes while ensuring an appropriate level of privacy.
Existing privacy-preserving data mining methodologies, based on Reference [26], can be divided into methodologies that protect the input data in the mining process and methodologies that protect the final results of the mining process. Privacy-preservation techniques (perturbation, generalization, transformation, etc.) in the first type, are applied to the input data to hide any private information and safely distribute the data to other parties. The main goal is the generation of accurate data mining results. SMC methods enable data owners to apply mining methodologies to their data, keeping the datasets private. In the second type of approach, the applied privacy preservation techniques prohibit the disclosure of private information derived through the application of data mining algorithms.
Verykios et al. [12] categorized privacy-preserving data mining algorithms into five segments. The first segment is data distribution, which refers to the division of data, either centralized or distributed. A centralized data set is owned by a single party. Conversely, distributed data sets are divided between two or more parties, who most probably do not trust each other but are interested in performing data mining techniques on their unified data. Distributed data can be classified as horizontally or vertically partitioned. In the former, different database records reside with different parties; in the latter, all values for different attributes reside with different parties. Data modification, the second segment, is used to modify the original database values. The databases may need to be released to the public, so modification ensures the protection of privacy. Modification methods include: perturbation, blocking, aggregation, swapping, and sampling. Perturbation is accomplished by altering an attribute value or adding noise. In blocking methods, an attribute value is replaced by a character; in aggregation, several values are combined. In swapping, the values of individual records are interchanged, and in the sampling method, only a sample of data is released. The data mining algorithm, the third segment, is the algorithm for which the data are modified and the privacy preservation technique is designed. The most important algorithms have been developed for classification, like decision trees, association rule mining algorithms, clustering algorithms, and Bayesian networks. Data or rule hiding, the fourth segment, refers to whether sensitive values should be protected by hiding raw or aggregated data. The complexity of hiding aggregated data is higher; for this reason, mostly heuristics have been developed. In some cases, individual data values are private, but in other cases, individual association or classification rules are considered private. Depending on how privacy is defined, different privacy-preserving techniques are applied. The most important aspect is the privacy preservation technique. These techniques can be categorized as heuristic-, reconstruction-, and cryptography-based techniques. Heuristic techniques modify selected values rather than all available values to minimize information loss. In reconstruction techniques, the original distribution of the data is reconstructed from the randomized data. Data modification results in degradation of the database performance. In cryptographic techniques, that is, SMC, a computation is secure if at the end of it, no one knows the contents except their own input and the final results. These methods are used for preserving privacy in distributed environments using encryption techniques.
Sharma et al. [6] proposed the following classifications of PPDM: (1) data mining scenarios, (2) data mining tasks, (3) data distribution, (4) data types, (5) privacy definitions, and (6) protection methods. Their approach is similar to that of Reference [12], but they added one more extra dimension: the data types. There are two basic data types: numerical and categorical (nominal). Boolean data are a special case of nominal data. The basic difference between the two data types is that categorical data are categorized without a natural rank, whereas numerical data are instantly measured by a number. This difference creates the need to apply different privacy preservation approaches.
An important characteristic in the development of PPDM algorithms is the recognition of appropriate evaluation criteria. The already-developed privacy-preserving algorithms do not outperform all other algorithms on all evaluation criteria. An algorithm may perform better than another one for specific criteria [12]. As such, different sets of metrics for evaluating these algorithms have been proposed over the past years. Quantifying privacy is challenging. Many metrics have been proposed in the literature; however, multiple parameters need to be evaluated. Most of the proposed metrics can be classified into three main categories depending on the aspect being measured:
- Privacy level metrics: the security of the data from a disclosure point of view;
- Data quality metrics: quantify the loss of information/utility;
- Complexity metrics: measure the efficiency and scalability of the different techniques.
Both data quality and privacy level can be further categorized as data metrics and result metrics. Data metrics evaluate the privacy level and data quality by estimating the transformed data resulting from applying a privacy-preserving methodology. Result metrics evaluate the privacy level and data quality by estimating the outcomes of the data mining process having the transformed data as the input [15]. Verykios et al. [12] provided a different list of evaluation criteria to be used for assessing the quality of PPDM algorithms: the performance of the algorithm in terms of time needs to hide sensitive information; the data utility after the PPDM technique is applied, which is equivalent to the minimization of information loss; the level of uncertainty with which the sensitive information hidden can still be discovered; and the resistance accomplished by the privacy algorithm to different data mining techniques. Sharma et al. [6] proposed a different set of evaluation criteria:
- ○
- Versatility: the ability of a technique to serve various data mining tasks, privacy requirements, and data set types. The technique is more useful if it is more versatile.
- ○
- Disclosure risks: the possibility that a malicious party obtains sensitive data. Preservation techniques aim to minimize the risks.
- ○
- Information loss: the decrease in data quality resulting from the noise added to the data and the level of security applied. A privacy-preserving technique is required to maintain the quality of data in the released data sets. If data quality is not maintained, the use of security is purposeless.
- ○
- Cost: the computation and communication costs. The computational cost depends on the processes applied on the data, for example, randomizing the database values, and the cost to run all processes. The higher the cost, the more inefficient the technique.
Qi and Zong [27] described evaluation criteria and reviewed privacy protection algorithms in data mining such as distortion, encryption, privacy, and anonymity. Malik et al. [28] also presented evaluation parameters and discussed the trade-off between privacy and utility. They suggested that practical algorithms need to be developed that balance disclosure, utility, and costs to be accepted by industry. They stated that novel solutions have been developed but product-oriented solutions need to be developed so that real-world problems are efficiently handled.
Different parameters were also defined [29,30] to quantify the trade-off between privacy and utility. The authors created a framework for evaluating privacy-preserving data mining algorithms, indicating the importance of designing adequate metrics that can reflect the properties of a PPDM algorithm, and of developing benchmark databases to test and evaluate all types of PPDM algorithms. They identified a framework based on the following dimensions to evaluate the effectiveness of privacy preserving data mining algorithms: efficiency, scalability, data quality, hiding failure, privacy level, and complexity. Efficiency is the ability of a privacy-preserving algorithm to execute with good performance. Scalability evaluates the efficiency of a PPDM algorithm with increasing data set sizes. Data quality is the quality of both the input data and the final data mining results. Hiding failure is the portion of sensitive data that is not hidden after the PPDM technique is applied. The privacy level, which results from the use of a privacy-preserving technique, indicates how closely the sensitive information can still be estimated. Complexity refers to the execution of an algorithm in terms of performance.
As defined previously [31], every privacy preserving methodology should answer one major question: Do the results violate privacy. In other words, do the results of a data mining process violate privacy by exposing sensitive data and patterns that can be used by attackers? A privacy preservation classification model was proposed by the authors, and they studied the possible ways an attacker can use the classifier and compromise privacy, but they did not provide a solution to prevent an attacker from accessing the mining results and thus violate privacy.
Sweeney [11] proposed a heuristic approach using generalization and suppression techniques to protect raw data and achieve k-anonymity. A database is k-anonymous with respect to some attributes if at least k transactions exist in the database for each combination of the attribute values. The new generated database guarantees k-anonymity by performing generalizations on the values of the target attributes.
Scardapane et al. [32] analyzed medical data distributed amongst multiple parties. Medical environments may forbid, due to privacy restrictions, the disclosure of their locally produced data to a central location.
The most widely studied privacy preservation techniques are cryptography and randomization. A naive Bayes learning technique was applied [33] to construct differentially private protocols to extract knowledge from distributed data. A multiplicative perturbations approach was applied to the data for introducing noise by Liu et al. [34]. However, perturbation techniques decrease the quality of the final results. The authors, in their privacy analysis, did not consider any prior knowledge. Vaidya et al. [35] applied differential privacy to develop a naive Bayes classifier provided as a cloud service, and focused on generating privacy preserving results instead of sharing secure data sets. These techniques mainly focus on publishing useful results and not sanitized data that can be shared. Randomization techniques have been used to build association rules [36] and decision trees [24] for vertically and horizontally partitioned databases, respectively.
The randomization method, even though efficient, can result in inaccurate outcomes. As revealed [37], randomization techniques may compromise privacy. The authors stated that additive noise can be easily filtered out, and special attacks can result in the reconstruction of the original data. A randomization technique that combines data transformation and data hiding was proposed by Zhang et al. [38]. They exploited a modified naive Bayes classifier to predict the class values on the distorted data. Agrawal et al. [24] built a decision tree classifier by applying perturbation techniques on the training data and estimated the distribution probability of numeric values. They proposed a measure and evaluated the privacy offered by their method. The privacy was measured by how closely the original values can be determined through the modified data. The approach presented in Reference [14] is another reconstruction technique based on an expectation maximization algorithm for distribution reconstruction. The authors provided metrics for quantification and privacy and information loss measurement. Unlike the approach in Reference [24], the metric proposed in Reference [14] assumes that the perturbing distribution as well as both the perturbed record and the reconstructed distribution are available to the user.
Cryptographic-based techniques are more secure; they provide accurate results but they lack efficiency. Most cryptographic methods proposed in the literature are based on Yao’s idea [16], and an extension proposed by Goldreich [17], who studied the secure multi-party computation problem. A few proposed privacy preservation techniques apply encryption mechanisms on horizontally partitioned databases for building decision trees [25,39]. A variety of cryptography-based techniques have been applied using naive Bayesian classifiers [8,23,40,41]. Others [7] applied cryptography to build association discovery rules, whereas others [9,42] and References [40,43] benefited from the cryptographic methods and applied them on vertically partitioned databases to create association rules and naive Bayesian classifiers, respectively. Tassa [44] focused on horizontally partitioned databases and proposed a protocol for secure mining of association rules, presenting the protocol’s advantages over existing protocols [7]. Goethals et al. [45] proposed a simple and secure method, applying secure multiplications. Similarly, Keshavamurthy et al. [46] proposed a multi-party approach to calculate the aggregate class for vertically partitioned data applying a naive Bayes classifier. Because of its simplicity and straightforward nature, naive Bayes classification has been used by many researchers [8,23,41,47]. Other data mining methods have been proposed in the PPDM field, such as tree augmented naive Bayes [48] and the K2 algorithm [9].
The authors of Reference [48] proposed a similar approach to ours. However, they applied an algebraic technique to perturb the original data. Instead, our protocol exploits cryptographic-based techniques, assuring privacy and resulting in more accurate outcomes. A comparison of some privacy preserving data mining techniques proposed in the literature are presented in Table 1.

Table 1.
Comparison of privacy-preserving data mining (PPDM) techniques.
3. Background
In machine learning and statistics, classification refers to a supervised predictive learning approach where a class value is predicted from data provided as the input. Classification can be performed on both structured or unstructured data. The main goal of the approach is to identify the class of the new data. Classification algorithms require training data as the input to predict the likelihood that future data will fall into one of the predetermined classes. The learning model is trained using the training data and the performance is measured using test data. Common classification problems are speech recognition, face detection, handwriting recognition, document classification, credit approval, medical diagnosis, target marketing, and so forth.
3.1. Classification of Nominal Attributes
The main objective of classification is the prediction of an attribute value given a training set by estimating the probabilities. Given an attribute X with nominal values , …, , the calculation of the probability of each value is given by applying Equation (1), where n is the total number of training instances for which and is the number of instances that have .
The conditional probability that an instance belongs to a certain class c is calculated by Equation (2), where is the number of instances with class value c and attribute value a, and is the number of instances with attribute value a.
3.2. Classification of Numeric Attributes
The calculations of the classification probabilities differ for numeric and nominal attributes. The mean and variance parameters, for numeric attributes, are calculated for each class and each attribute. The probability that an instance is class can be estimated by substituting in the probability density equation. The conditional probability of a class is calculated for all classes, and the class with the highest relative probability is chosen as the class of the instance. These local sums are added together and divided by the total number of instances having that same class to compute the mean for a class value. Each party, since it is aware of the class of the training instances, can subtract the appropriate mean from an instance having class value y, square the value, and sum all such values together. The required variance is obtained by dividing the global sum by the global number of instances having the same class y.
Equation (3) computes the normal probability distribution, where x is a random variable, is the mean of the distribution, and is the standard deviation ( is the variance); is approximately and e is approximately .
3.3. Tree Augmented Naive Bayesian Classifier
The traditional naive Bayes classification (Figure 1) is a method based on Bayes theorem. Naive Bayes classifiers are simple, easy to build, and useful for very large data sets as they are highly scalable. Naive Bayes classifiers support both nominal and numeric attribute values. These classifiers compute the conditional probability of each attribute value given the class value C. The Bayes theorem is applied to compute the probability of class C given a specific instance vector , given the total number of n attributes.
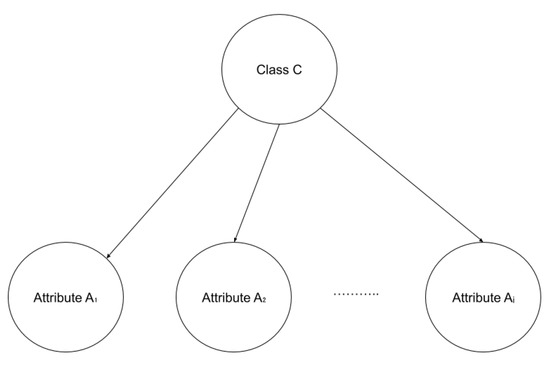
Figure 1.
Bayesian network structure.
These classifiers assume that all attributes are conditionally independent given the value of C, which is a restrictive and oversimplified assumption, reducing the computational cost by only counting the class distribution. However, in most cases, this assumption is unrealistic, as some attributes can be dependent. Since prior knowledge of the class variable C is not considered, a bias in the estimated probabilities is introduced, which leads to poor prediction outcomes in some domains [49]. The performance of such classifiers can be improved by removing this assumption.
One method to reduce the naive Bayes’ bias is to relax the independence assumption using a more complex graph. An interesting variation of Bayesian networks is the tree augmented naive Bayesian (TAN) classifier (Figure 2) [50]. TAN can be viewed as a Bayesian network, a probabilistic graphical model, where each attribute has the class as the parent, and possibly an attribute as a second parent. The existence of additional edges between attributes, which represent the correlation among these attributes, is allowed by the TAN classifier. More specifically, in a TAN network, the class C has no parents and each attribute has the class and at most one other attribute as parents, implying that the assessment of the class of attribute also depends on the value of . For example, in a dataset, the age of an individual and their financial income are two dependent attributes.
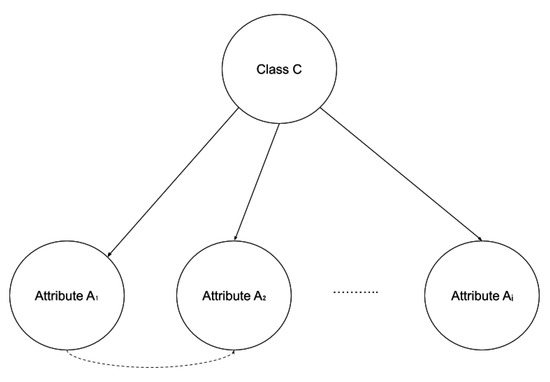
Figure 2.
Tree augmented naive Bayesian (TAN) structure.
The procedure of learning these edges, which is based on a method proposed by Chow and Liu [51], reduces the problem of constructing a maximum likelihood tree to find a maximal weighted spanning tree in a graph. The problem of finding such a tree involves selecting a subset of edges such that the sum of weights attached to the selected edges is maximized. The TAN algorithm consists of four main steps:
- The mutual information for each attribute pair is computed using Equation (4), measuring how much information the attribute y provides about x.
- An undirected graph is built in which the vertices are the variables in x (the weight of an edge connecting two attributes).
- A maximum weighted spanning tree is created.
- The undirected tree is transformed to a directed tree by choosing a root variable and setting the direction of all edges to be outward from it.
The TAN classifier, by removing any independence assumptions, behaves more robustly with regards to classification compared to the classical naive Bayes classifier, since it combines the initial structure of the naive Bayes algorithm with prior knowledge (if available) or obtained knowledge about the correlation of input attributes via a training approach. TAN substantially reduces the zero-one loss of naive Bayes on many data sets and a range of experiments have shown that it outperforms the naive Bayes classifier [50,52]. TAN results are significantly improved compared to those produced by the classical naive Bayes classifier and Bayesian networks. The robustness and computational complexity are also maintained, showing better accuracy.
3.4. The Homomorphic Primitive
Homomorphic encryption is widely used in the literature [45,47,53,54] for approaches implementing cryptography-based techniques. The homomorphic primitive was first used to build a privacy-preserving data mining model in a distributed environment by Yang et al. [23].
This primitive allows the performance of calculations on encrypted data without the need to decrypt these data. Equation (5) describes the operation where the result of encrypting two messages is equal to the sum of the two messages separately encrypted.
3.5. Paillier Cryptosystem
The additive homomorphic primitive is exploited by the Paillier algorithm [22]. Through this primitive, anonymity and unlinkability between parties and personal data are achieved [40].
During the key generation phase of the Paillier cryptosystem, each participant (the miner and all parties involved) generates a key pair 1024 bits in size on their own side. The public key of each party is the product N of two random prime numbers , which are independent and have the same size, and a random number g, which belongs to . The private key is the result of variables shown in Equation (6) and , defined in Equation (7).
Paillier encryption is performed as shown in Equation (8). In the proposed protocol, more specifically, if a participant j is interested in participating in forwarding the frequency i to the miner, then the party needs to encrypt every message sent with the miner’s public key. The cryptosystem is vulnerable to chosen-plaintext attacks. For confronting these types of attacks, a random variable M is computed by the miner, and delivered to each party encrypted with their own public key. The M variable is used for encrypting every transmitted message.
The current approach requires the participation of at least three parties. When all three parties have forwarded their data to the miner, the homomorphic primitive is applied. The miner calculates the total frequencies of each possible attribute value in relation to each class value by decrypting all the received messages simultaneously. The miner is not in a position to associate the received frequencies with the original records and cannot link the data to their owners due to the execution of the decryption process after the participation of at minimum three parties. A decrypted message is presented in Equation (9).
4. Protocol Description
Challenges arise during the execution of data mining processes when preserving privacy, since the collected data being mined often contain sensitive information. Data mining techniques used to derive statistics from distributed databases should ensure that personal data will not be disclosed to unauthorized individuals. Our objective was to develop a privacy-preserving protocol that satisfies the essential security and design requirements, exploiting efficient encryption mechanisms. We use the tree augmented naive Bayesian classification algorithm [51] to extract accurate and global information while preserving privacy.
Encryption processes are applied to a client–server (party–miner) environment ensuring that any message exchanged in a fully distributed environment is not accessible by internal or external attackers, either by the parties involved or the miner. The miner generates the classification model by collecting the frequencies of each attribute value in relation to each class value from at least three horizontally or vertically partitioned databases, which are owned by different parties. In vertically partitioned databases, we assume that every participant is aware of the class value of each record. The proposed protocol was developed for supporting both nominal attribute values (Algorithm 1) and numeric attribute values, including binary data (Algorithm 2). Through the Paillier cryptosystem, all frequencies forwarded are encrypted. The exploitation of the homomorphic primitive ensures that sensitive data remain protected. Communication among parties is prohibited and the only data flow occurs between each party and the miner, making communication among parties infeasible.
As mentioned, the current work is an extension of previous research [19,20]. Notably, some of the features and requirements used arise from the quotations presented by Mangos et al. [53].
4.1. Design and Security Requirements
Each developed protocol must implement appropriate measures and follow data protection principles to safeguard individual rights, as defined by the General Data Protection Regulation (GDPR) [2]. Privacy and data protection must be considered at the design phase and throughout the entire life cycle of any protocol and system, as defined by the Privacy by Design approach. The development and implementation of the current protocol is highly impacted by this approach, and all necessary measures were followed to preserve privacy and the individuals’ identities.
| Algorithm 1: Protocol for nominal attribute values. |
|
| Algorithm 2: Protocol for numeric attribute values. |
|
The proposed protocol satisfies the following main requirements to ensure better performance in scalable and distributed databases:
- Data mining processes extract statistical information.
- Database records are horizontally or vertically partitioned.
- Data can be either nominal or numeric.
- A large number of parties can be handled.
- Only authorized parties can send inputs to the miner.
- The communication among parties is infeasible.
- The miner must be connected with at least three parties before proceeding to the mining process.
- The miner collects all the messages encrypted and performs the mining process.
- Individual records remain secret and only overall results are revealed.
- Any data given as input include the encrypted frequency of each attribute value in relation to any class value and cannot be modified, reduced, or copied.
- A summary is concatenated to each transmitted message as a result of applying the one-way hash function SHA-1.
- It is essential that computation and communication costs are low for each party and the miner.
In a distributed environment, each party is considered either semi-honest or malicious. Semi-honest participants follow the protocol specifications, but are curious to learn more information. However, they do not deviate from the execution of the protocol. Conversely, malicious participants are categorized into internal and external. Internal adversaries deviate from the protocol, for example, by sending specific inputs, with the main purpose of discovering other parties’ private data. External adversaries will try to impersonate a legal participant and then behave as an internal adversary. In the current protocol, both adversary types are considered.
All participants, the miner and each party, undertake the process of authentication, so they can mutually recognize if they are connected to a secure and literal participant. Each participant sends their digital signatures, assuming they were signed by a certification authority (CA), to confront such behaviors. This operation ensures that only authorized parties participate in the protocol and they are assured that a connection with the actual miner was accomplished.
Privacy is preserved only if confidentiality, anonymity, and unlinkability are fulfilled. All transmitted messages between each party and the miner are encrypted, and a message is only decrypted by the party that was supposed to receive the message. The homomorphic primitive ensures that the miner is unable to identify the inputs each party forwards, accomplishing anonymity and unlinkability. Both the identity and the private data of each party remain secret. In the proposed protocol, integrity mechanisms are exploited to identify any modification carried out by active attackers, with the prime goal of diminishing the accuracy of the final outcomes or discovering sensitive data. An SHA-1 digest is concatenated to every transmitted message, prohibiting these behaviors and assuring any altered message will be detected. Section 6 describes in depth the security and threat model of the proposed protocol.
4.2. Protocol Analysis
The protocol presented in the current work follows the classical homomorphic election model, in particular, an extension for supporting the multi-candidate election scheme, where each party has k-out-of-1 selections [21]. The Paillier cryptosystem follows the homomorphic model and preserves privacy while mining operations are applied in a fully distributed environment. A data collector—in the current proposal, the miner—collects and organizes all data forwarded by the participants of the protocol. The miner exploits the homomorphic primitive when all encrypted data are collected, and applies the tree augmented naive Bayesian classification model. Through the classifier, correlations among the attributes are generated, resulting in the creation of a network structure that represents them. Each transmitted message during the execution of the protocol includes an SHA-1 digest to confirm that any modification has not been performed. The miner delivers the final results to each party who contributed to the creation of the mining model. The frequency of each attribute value in relation to each class value, for both horizontally and vertically partitioned databases, constitutes the final results, and we assume that every party is aware of the class value for vertically partitioned database records.
The protocol is divided into six main phases and applied for both horizontally and vertically partitioned databases. The protocol notations are given in Table 2.

Table 2.
Protocol notations.
Phase 1: Key generation.
The miner generates the encryption key pair ( and ) through the Paillier’s cryptosystem key generation phase. The miner produces a 1024 bit digital signature key pair ( and ) with the Rivest–Shamir–Adleman (RSA) cryptosystem using the MD5 hash function. We assume that each party is able to obtain the public keys. The same procedures are followed by each party who also create the encryption key pair / and an RSA key pair /) (Figure 3). We again assume that the miner is as well able to obtain the public keys of all parties. In the key establishment phase, the miner also generates and forwards a random value M.
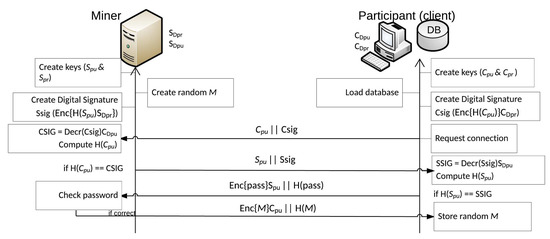
Figure 3.
Key generation and mutual authentication phases.
Phase 2: Mutual authentication.
The miner and each party that participates in the protocol are mutually authenticated by exploiting the digital signature scheme (RSA), as each participant possesses a private and public key pair. This key pair is generated and used only in this phase of the protocol assuming it was signed by a CA. We assume that all parties are able to obtain the public keys of the other participants.
If a party requests to connect with the miner, during the authentication phase, they forward the public key and the digital signature, encrypting the key with the miner’s private key. The miner proceeds to the decryption of the digital signature with the public key of the party and generates a digest of the message. If the miner is able to verify that the party is able to participate in the protocol, responds by sending his public key and digital signature encrypted with the private key. The party continues with the same procedure by decrypting the miner’s digital signature with public key and creates a digest of the message (Figure 3). After these steps are completed, the party is assured that a verified connection with the actual miner is achieved, and both the miner and each party have access to and participate in the protocol, excluding any unauthorized participants. After exchanging all keys, every transmitted message is encrypted. The next step is to send the random variable M, which is used by the Paillier cryptosystem, to confront any chosen-plaintext attacks. This variable is sent encrypted with each party’s public key .
Phase 3: Data collection.
After all the above procedures are performed, the miner is ready to accept the participant’s personal data. A party can participate in the exportation of statistics, providing their own sensitive data. However, the data contained in the database cannot be disclosed in the notion of verbatim records, neither to the miner nor to other participants nor to any attacker not involved in the protocol. Every record is examined for the presence of missing values.
The collection of data begins from the miner. If a party consents to the creation of the classification model, they initially send every possible value of the class and every possible attribute value. All messages sent are encrypted with the miner’s public key . For horizontally partitioned databases, each party sends all possible attribute values. For vertically partitioned databases, each party sends only the values of the attributes that possess the required attribute; if the party does not possess the requested attribute, returns zero. The miner is not aware of the possession of individual values at the end of this step.
The miner requests the frequencies for attribute for each connected party (Figure 4). Using the miner’s public key , each party forwards the frequency of each value for attribute in relation to every class value, encrypted. The only sensitive data sent by all parties are these frequencies, and they are encrypted. Because the homomorphic primitive is applied, the miner remains unaware of the specific frequencies. These procedures are necessary for the miner to initialize the classifier.
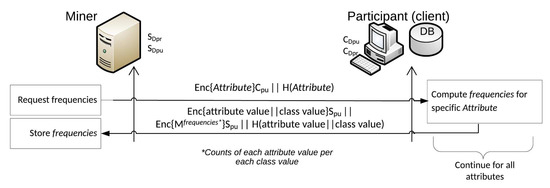
Figure 4.
Data collection phase.
Phase 4: Classifier initialization.
If the Miner has collected the encrypted frequencies related to attribute from all three parties, applies the homomorphic primitive. All encrypted frequencies are decrypted simultaneously, and the miner obtains the overall distributions of each attribute value in relation to each class C value. The process continues with the miner requesting the frequencies for the next attribute. The process is completed after the collection of all frequencies for all attributes . For horizontally partitioned databases, n represents the total number of attributes. For vertically partitioned databases, n refers to the sum of each party’s number of attributes. The classifier initialization is successful when at least three parties cooperate in the implementation of the protocol (Figure 5).

Figure 5.
Classifier initialization phase.
Phase 5: TAN classifier creation.
The miner can proceed to the creation of the TAN classifier after the classifier initialization phase is complete, meaning all frequencies are collected and decrypted for each attribute, from at least three participants. As described in Section 3.3, the miner now is in the position to create the tree augmented naive Bayes model (Figure 6).

Figure 6.
TAN classifier creation and final results phases.
Phase 6: Final results.
When all the above-mentioned phases are complete, the final results of the mining process are delivered by the miner. The miner sends the results to each party involved in the creation of the data mining model, encrypted with their own public key (Figure 6).
After the creation of the mining model and the shipment of the final results, every participant can request that the miner respond with the class value and the corresponding possibility that accrues from a set of possible attribute values, classifying new instances. This process was used to evaluate the performance of the classifier, and the results are presented in the next section.
5. Evaluation
In this section, we evaluate the proposed protocol in terms of security and computational cost. Primarily, the mean Paillier key pair generation time was estimated for both the miner and the party, and compared with El-Gamal key generation. We compared the mean time needed to create the digital signatures in two different systems. The main procedures of the protocol were examined to demonstrate that they have a fast computation time while preserving privacy. Three different scenarios were established for this purpose. The cryptosystem performance was evaluated on encryption and decryption run times. The TAN classifier was evaluated using recall and precision variables as metrics. Expanding upon previous research, we evaluated the classifier using the F1 score.
All experimental results were calculated and are presented in milliseconds (ms). Most experiments were conducted on a modest PC with Intel i5 2.4 GHz with 4 GB of RAM. To extend some experiments, we performed them using a more advanced computer. The purpose of the second system was to evaluate if a more advanced system can decrease the computational cost of specific phases of the proposed protocol, like the key generation phase. The new PC was equipped with Intel Core i7, 2.9 GHz, and 16 GB of RAM, and each phase in which this computer was used is denoted as i7 in contrast to the computer with the i5 processor. For this study, only the key establishment experiments were conducted in both systems. The proposed protocol was implemented in Java programming language, and both the miner and all three participant interfaces were running on the same system.
The experiments showed that the performance of the protocol is mainly shaped by the data collection phase, which is proportional to the number of attributes included in the databases. We conclude that the partition of databases affects the collection of data phase mainly when the amount of instances increases.
5.1. Key Establishment
The key establishment was evaluated on both systems described above. Measurements were collected from 50 runs performed for one participant and the miner to calculate the performance of the key generation, authentication, and login operations. The encryption key pair generation and the RSA digital signature creation were included in the key generation phase. We assumed that each participant knew the miner’s key and the miner was aware of all public keys of the parties involved in the mining process.
From the experiments conducted on the i5 computer system, we found that a party requires 479 ms to create the encryption key pair and 122 ms to generate the digital signature. The miner performs the encryption key pair generation in 433 ms and requires 108 ms to create the digital signature. The random variable M used by the Paillier cryptosystem was produced in 43 ms. When the experiments were conducted on the i7 computer system, the mean times significantly improved, as shown in Figure 7. The Paillier encryption key generation mean time was almost four times faster when the measurements were performed in the i7 system. The El-Gamal key generation was implemented to compare this phase using the two cryptosystems. The Paillier and El-Gamal key generation experiments were performed on the i7 system and we found that the key generation of the El-Gamal cryptosystem was remarkably slower compared to the Paillier cryptosystem. The generation of RSA digital signatures was also compared between the two computer systems, as presented in Figure 7. The digital signatures generation was significantly faster when the computer system was more advanced (i7). As shown by the results, the Paillier asymmetric encryption algorithm is efficient in terms of key establishment.
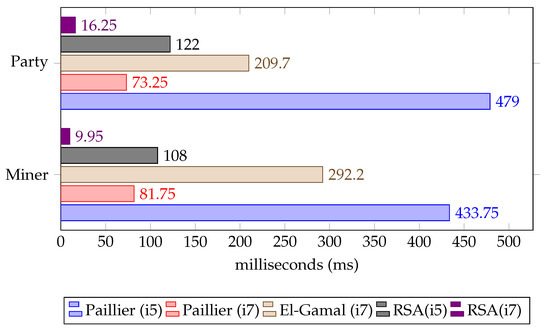
Figure 7.
Comparison of key establishment procedures.
The time needed by the miner and each party to be mutually authenticated is represented by the authentication time. In this phase, each participant sends the public keys and digital signatures created in the key establishment phase. The measurements from the conducted experiments showed that the mutual authentication is achieved in 24 ms. In the login phase, the party sends the miner’s password encrypted with the key and the miner, in return, responds with the correctness of the password received by sending the encrypted random variable M. The mean login time (262 ms) is longer than the mean authentication time as all the messages transmitted are encrypted, meaning decryption and encryption operations are required.
5.2. Experiments
The performance of the proposed protocol was measured by separately examining its main procedures: (1) the collection of data from the miner (DC), (2) the initialization of the classifier (CI), (3) the creation of the TAN classifier (TAN CC), and (4) the delivery of the final results (FR) to each party. Table 3 presents the three customized scenarios used for conducting the experiments based on the database partition. For each scenario, three parties were connected to the miner and participated in the protocol with either horizontally or vertically partitioned databases. These scenarios were evaluated and compared to determine the performance of the protocol when different amounts of records and attributes are involved in the creation of the mining model.

Table 3.
Experiment scenarios.
The experiments were performed using real datasets provided by the UC Irvine Machine Learning Repository [55]. The data were tailored for each scenario, and the training set size was set to 1000, 2000, and 5000 records. A simplified structure of this dataset is displayed in Figure 8. Table 4 provides the mean time to complete each phase of the proposed protocol.
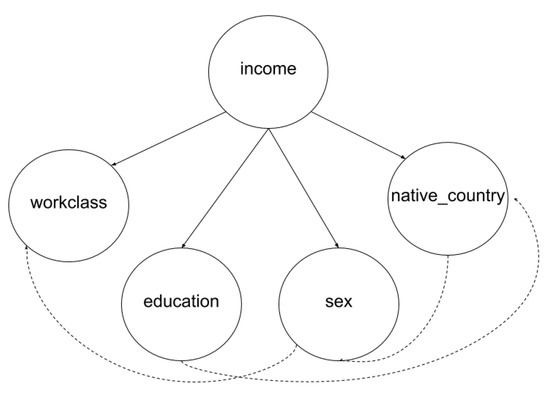
Figure 8.
Simplified TAN structure of the Adult dataset.

Table 4.
Main procedures comparison for each scenario.
The customized scenarios were selected to compare the performance of the protocol depending on the number of attributes and records. From the results, we found that the overall time to complete the main procedures of the protocol is mainly determined by the data collection phase, which mostly increases with increasing number of attributes. Comparing both database cases, we found that the partition affects mainly the data collection phase by doubling the mean time, mostly as the number of instances is increased.
The distributed environment with three parties connected to the miner was selected because we wanted the first evaluation of the protocol to be less ambiguous. If more than three parties are connected with the miner and send their data, the data collection phase is expected to be affected as well. In the future, conducting experiments with more parties involved can prove the scalability and efficiency of the proposed protocol.
5.2.1. Experiments: Horizontally Partitioned Databases
The scenarios used to evaluate the protocol for horizontally partitioned databases are presented in Table 3a. For the first scenario, each database consisted of 50 records and 5 attributes; in the second scenario, it consisted of 100 records and 5 attributes; and in the third scenario, 100 records and 10 attributes. The results showed that the initialization of the classifier has a low mean time, but it is affected when the number of attributes is increased. Conversely, the initialization time is slightly longer as the amount of database instances increases. Similar conclusions were drawn during the data collection phase. However, the data collection process has a long execution time, as each party has to send all their data/frequencies to the miner. The data collection time increases reasonably when the number of instances is higher, but when the database consists of a larger number of attributes, the miner requires more time to collect all the frequencies. The mean time to create the TAN model increases when the quantity of instances increases, unlike the increase in the mean time when the attributes are doubled. Increases in the number of attributes do not influence the mean time. When both the quantity of instances and attributes increase, the mean time to forward the final results to each party also increases.
5.2.2. Experiments: Vertically Partitioned Databases
The scenarios used to evaluate the protocol for vertically partitioned databases are presented in Table 3b. In each customized scenario, we assumed that all parties involved know the class C value. For the first scenario, each database included 50 records and 3 different attributes (plus the class attribute); in the second scenario, the number of records was doubled and the number of attributes remained the same; while in the third scenario, 100 records and 5 different attributes were included in each database. The results showed that all the procedures of the protocol require slightly more time to be completed compared to the corresponding scenario for horizontally partitioned databases. The collection of data requires almost twice the time due to the data partition. Like with horizontally partitioned databases, the creation of the TAN classifier and the data collection phases require more time when the amount of instances increases. When the attributes increase, the data collection time lengthens, but less time is required in comparison to the horizontally partitioned databases. The results showed that the classifier requires more time to be initialized in relation to horizontally partitioned databases. If the number of attributes increases, the TAN classifier behaves similarly for both horizontally and vertically partitioned databases. The delivery of the final results is slower for double the number of attributes for vertically partitioned databases.
5.3. Cryptosystem Performance
The mean encryption and decryption time were calculated to measure the performance of the Paillier cryptosystem. During the execution of the protocol, different messages were transmitted, each one with a different number of characters. From all the above executed scenarios, we measured all the encryption and decryption mean times. The results showed that a message can be encrypted in 51.5 ms on average. The average time needed to decrypt a message was similar, and the measurements revealed that a message can be decrypted in 67 ms. The decryption time slightly increased most probably because of the application of the homomorphic primitive. We conclude that the Paillier cryptosystem is efficient as the mean times are low. In the future, a comparison of the Paillier and El-Gamal cryptosystem would determine the most appropriate algorithm in terms of computational cost.
5.4. Classifier Evaluation
To examine the mining model created by the miner, we calculated the recall, precision, and F1 scores. The percentage of records categorized with the correct class in relation to the number of all records with this class is the recall. The percentage of records that truly have a certain class over all the records that were categorized with this class is the precision. The F1 score is computed using Equation (10). If the F1 score is equal to 1, the precision and recall results are perfect. The lowest possible F1 score is 0 if either the precision or recall is 0.
Three customized datasets with different amounts of instances were used as training sets (1000, 2000, and 5000 records). The databases were obtained from a real dataset [55] and contained 14 attributes. A test set of 100 records (10% of the training records) was used, which was not used in the training phase. The aim of the classifier evaluation is to determine which mining model correctly classified the test set. The evaluation results of the TAN classifier are presented in Table 5. The naive Bayes classifier evaluation results are presented in Table 6.

Table 5.
TAN classifier evaluation results.

Table 6.
Naive Bayes classifier evaluation results.
Comparing the two classifiers, we found that TAN correctly classified more instances compared to the naive Bayes classifier. Analyzing all three measurements mentioned above, we found that the TAN classifier is a more accurate and appropriate method compared to traditional naive Bayes.
6. Threat and Security Analysis
Many serious attacks need to be considered when a protocol is being developed. Distributed environments have to prevent every possible threat on systems designed with privacy preservation as their main concern. A threat is a potential violation of security that exists when an action could breach security and cause harm. A threat can be either intentional (an individual attacker) or accidental (a computer malfunction). Some types of security threats are related to unauthorized access. Services or data becoming unavailable can be considered another security threat. The modification of transmitted data is considered a major threat to the security of a system, as well as the generation of fabricated data [56]. This section presents and discusses the possible threats that can be confronted by the proposed protocol. Table 7 summarizes these attacks and how they are approached and solved using appropriate mechanisms by the presented system.

Table 7.
Possible security threats and their management.
Security in distributed environments is an important concern that needs to be analyzed to discover possible vulnerabilities or threats and avoid information loss. A distributed system must follow some requirements for security enforcement: (1) The sender of a message should be able to know that the message was received by the intended receiver; (2) The receiver of a message should be able to know that the message was sent by the original sender; (3) Both sides should be guaranteed that the contents of the message were not modified while transferring data [56]. There are some broad areas of security in distributed systems: authentication, access control, data confidentiality, data integrity, encryption, digital signature, and nonrepudiation. Authentication is a fundamental concern when developing distributed systems. All entities in a secure system should follow an authentication process assuring the communication is authentic. The authentication service assures the participants that the message received is actually from the stated source. This process occurs the first time a connection is initialized, and assures that all entities involved are authentic. It must also ensure that there is no interference by unauthorized third parties. Access control is the ability to control the access to systems and prevent the unauthorized use of a service. This is achieved by identifying or authenticating each participant that tries to gain access, so that specific access rights are provided to each party. Confidentiality is the protection of data being transmitted from attackers and unauthorized disclosure. There are several levels of protection, both regarding the data content being sent and the data flow. This requires the attacker to not be able to observe the source and destination or other characteristics of the traffic flow. As with confidentiality, data integrity mechanisms can be applied to part of a message or the whole message. The most useful approach is full-message protection, ensuring messages received are not modified. Encryption mechanisms transform data into a form that is not readable without the use of intelligent systems. The transformation and recovery of data depend on the combination of algorithms and encryption keys. Digital signatures allow the recipient of a message to prove the source and integrity of the message and protect against forgery. The digital signature can be signed to produce digital certificates that establish trust among users and organizations. Nonrepudiation prevents users from denying they received or send a transmitted message. In these cases, the messages are registered by a notary so that none of the participants can back out of a transaction and disputes can be resolved by presenting relevant signatures or encrypted text [57]. In the present work, we did not consider nonrepudiation, as these cases fall beyond the scope of the presented protocol.
All parties involved in a distributed environment are considered to be mutually mistrustful and, in some cases, curious to learn information about other participants’ data. Every participant is considered either semi-honest or malicious. Semi-honest adversaries follow the protocol specifications; they do not collude but are curious to discover other party’s data during the execution of the protocol. Malicious adversaries can be internal or external. Internals deviate from the protocol and send specific inputs to infer other participants’ private data. An external adversary tries to impersonate a legal participant and behave as an internal. The miner could be considered an internal adversary. To address such behaviors in our proposal, external adversaries were excluded as they cannot participate, since all parties have to send their digital signatures. We assumed the digital signatures are signed by a certification authority. The mutual authentication provided by the proposed protocol excludes any unauthorized users. Participants with no permission to connect with the miner are not able to participate in the protocol. This means that the Miner cannot be an internal adversary, as all participants are aware if a connection is established with the actual miner. Participants who also behave as internal adversaries are restricted to sending blank inputs or missing values to the system. The only information revealed are the final outcomes; further information is impossible to obtain. By exploiting the digital signatures, man-in-the-middle attacks are not possible.
Several studies have examined the re-identification attack on privacy-preserving data mining algorithms. Many hospitals, for example, are willing to publish their data for research on the condition that any identifier that allows information pertaining to specific patients is removed, either for administrative or commercial reasons. This action, however, may not be enough, as re-identification attacks can lead to different public databases, thus revealing the real names of the referring patients [11]. To reduce re-identification risk, in the proposed method, we consider the privacy of the individuals: the data are anonymized and the final results are published to each participant to prevent any possibility of private and identification data being revealed.
Some security attacks depend on the presence of one or more miners in a distributed environment or personal data being transmitted among two or many parties. In distributed environments with only one miner, the final results can be discovered by the data collector, but if more miners are involved, the protocol is vulnerable to collusion attacks. If parties directly exchange data with each other, in the two-party model, each party can easily determine the other party’s private data. In a model where multiple parties are connected without a miner as the data collector, malicious parties can modify the input data, which can be disastrous if users collaborate. In the proposed protocol, to prevent these behaviors, data are exchanged only between the miner and each party, ensuring there is no collusion among the participants. At least three parties must be involved, preventing any probing attack. This approach establishes a secure protocol and semi-honest adversaries are faced as the only information revealed and sent by the miner is the final outcomes. We did not consider the collaboration of the parties outside of the protocol. Participants in a protocol have a mutual interest to follow the protocol’s principles in real-world applications.
If the requirements of confidentiality, anonymity, and unlinkability are fulfilled, privacy can be preserved. The Paillier cryptosystem ensures that sensitive data remain secret. The asymmetric encryption establishes an environment in which all parties receive the messages that were intended only for them, and they are the only ones that can decrypt these messages. Eavesdropping attacks or data leaking are successfully managed by the proposed protocol. In addition, the Paillier cryptosystem exploits the homomorphic primitive for both nominal and numeric attribute values, which guarantees that the original data will not be revealed to any attacker, the participants, or the miner. This primitive achieves anonymity and unlinkability, two aspects that the proposed system is committed to providing. The Paillier cryptosystem is vulnerable to chosen-plaintext attacks. This type of attack is overcome by the current protocol using a random variable (M).
If active attackers try to modify any message exchanged during the execution of the protocol and alter the final results or disclose sensitive data, they are stopped using integrity mechanisms (SHA-1). The participants in the proposed protocol are unable to resend their data and the protocol can be executed only once per computer system, preventing denial of service attacks. Blank or missing inputs are also excluded. Table 8 summarizes the security requirements and the technique is used in the current protocol.

Table 8.
Security requirements.
7. Future Work
The current work could be expanded in the future by comparing the proposed method with ensemble methods such as random forest or gradient boosting machines. This comparison could lead to the discovery of the most efficient and accurate algorithm. An extended comparison with El-Gamal’s elliptic curve cryptosystem could be conducted in future research to achieve a balance between security and efficiency. The comparison of the computation cost of the main phases of the proposed protocol when either the Paillier or El-Gamal cryptosystem is applied could be examined in the future. The evaluation could be broadened by comparing the proposed method with previous schemes in the literature. Another interesting avenue for future research is the evaluation of the main procedures of the proposed protocol when more than three parties are connected to the miner. Conducting such experiments could prove the scalability and efficiency of the proposed protocol and how the number of participants affects the performance of the protocol. Finally, in the future, larger datasets and training sets from different real data sources could be exploited to evaluate the overall performance of the presented protocol.
8. Conclusions
Voluminous data stored in distributed databases are exchanged daily. Global information can be acquired and important patterns can be detected by applying data mining techniques on statistical databases. Such databases often contain private data, and their disclosure when mining operations are applied could compromise the privacy and the fundamental rights of individuals. In this study, we focused on solving this problem. We presented a properly designed privacy-preserving data mining technique developed for a distributed environment. Participating databases can be horizontally or vertically partitioned, supporting both nominal and numeric attribute values. A data collector, the miner, groups the data received by at least three parties and performs all the operations to generate the mining model. Communication among parties is infeasible and the only workflow is between the trusted data collector (miner) and each participant in the protocol. All messages exchanged during the execution of the proposed protocol are encrypted using the Paillier cryptosystem. The homomorphic primitive ensures that the miner decrypts the messages received all at once, preserving the privacy of data. Cryptography-based techniques, as shown by previous research , are the most appropriate approaches in terms of accuracy, as the original data are not modified or transformed; therefore, the quality of the final results remains high. All transmitted messages are examined for any type of modification, as each message is concatenated with its summary produced by the one-way hash function SHA-1.
The experimental results showed that the proposed protocol is effective and efficient for both database partitions. The performance of the protocol is mainly affected by the increase in database attributes. Yet, given the size of the real dataset, this is considered acceptable.
The contribution of the proposed protocol is significant as, to the best of our knowledge, none of the previously proposed techniques was designed and implemented for both horizontally and vertically partitioned databases while simultaneously providing accurate results and preserving privacy.
Author Contributions
Methodology, M.E.S. and M.M.; Software, M.E.S.; Writing—original draft preparation, M.E.S.; Writing—review and editing, M.M.; Supervision, M.M.; Validation, M.E.S., M.M., S.G., and L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://archive.ics.uci.edu/ml/datasets/Adult.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, L.; Jiang, C.; Wang, J.; Yuan, J.; Ren, Y. Information security in big data: Privacy and data mining. IEEE Access 2014, 2, 1149–1176. [Google Scholar] [CrossRef]
- General Data Protection Regulation (GDPR)—Official Legal Text. Available online: https://gdpr-info.eu/ (accessed on 25 November 2020).
- Clifton, C. Privacy Preserving Distributed Data Mining; Technical Report; Department of Computer Sciences: West Lafayette, IN, USA, 2001; Available online: https://www.cs.purdue.edu/homes/clifton/DistDM/CliftonDDM.pdf (accessed on 25 November 2020).
- Clifton, C.; Marks, D. Security and Privacy Implications of Data Mining. In Proceedings of the ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, Montreal, QC, Canada, 2 June 1996; pp. 15–19. [Google Scholar]
- Srivastava, A. Comparative Study of Privacy Preservation Techniques in Data Mining. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 7280–7287. [Google Scholar]
- Sharma, M.; Chaudhary, A.; Mathuria, M.; Chaudhary, S. A Review Study on the Privacy Preserving Data Mining Techniques and Approaches. Int. J. Comput. Sci. Telecommun. 2013, 4, 42–46. [Google Scholar] [CrossRef]
- Kantarcioglu, M.; Clifton, C. Privacy preserving distributed mining of association rules on horizontally partitioned data. IEEE Trans. Knowl. Data Eng. 2004, 16, 1026–1037. [Google Scholar] [CrossRef]
- Kantarcioglu, M.; Vaidya, J.; Clifton, C. Privacy preserving naive bayes classifier for horizontally partitioned data. In Proceedings of the IEEE ICDM Workshop on Privacy Preserving Data Mining, Melbourne, FL, USA, 19–22 November 2003; pp. 3–9. [Google Scholar]
- Wright, R.; Yang, Z. Privacy-Preserving Bayesian Network Structure Computation on Distributed Heterogeneous Data. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’04), Seattle, WA, USA, 22–25 August 2004; Association for Computing Machinery: New York, NY, USA, 2004; pp. 713–718. [Google Scholar] [CrossRef]
- Zhan, J.; Matwin, S.; Chang, L.W. Privacy-Preserving Naive Bayesian Classification over Horizontally Partitioned Data. In Data Mining: Foundations and Practice; Springer: Berlin/Heidelberg, Germany, 2008; pp. 529–538. [Google Scholar] [CrossRef]
- Sweeney, L. K-Anonymity: A Model for Protecting Privacy. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Verykios, V.S.; Bertino, E.; Fovino, I.N.; Provenza, L.P.; Saygin, Y.; Theodoridis, Y. State-of-the-Art in Privacy Preserving Data Mining. SIGMOD Rec. 2004, 33, 50–57. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Yu, P.S. A General Survey of Privacy-Preserving Data Mining Models and Algorithms. In Advances in Database Systems; Springer: Boston, MA, USA, 2008; pp. 11–52. [Google Scholar] [CrossRef]
- Agrawal, D.; Aggarwal, C.C. On the design and quantification of privacy preserving data mining algorithms. In Proceedings of the ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, Santa Barbara, CA, USA, 21–23 May 2001; Association for Computing Machinery (ACM): New York, NY, USA, 2001; pp. 247–255. [Google Scholar] [CrossRef]
- Mendes, R.; Vilela, J.P. Privacy-Preserving Data Mining: Methods, Metrics, and Applications. IEEE Access 2017, 5, 10562–10582. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to Generate and Exchange Secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (SFCS ’86), Toronto, ON, Canada, 27–29 October 1986; IEEE Computer Society: Washington, DC, USA, 1986; pp. 162–167. [Google Scholar] [CrossRef]
- Goldreich, O. Secure Multi-Party Computation. 1998. Available online: http://www.wisdom.weizmann.ac.il/~oded/PSX/prot.pdf (accessed on 25 November 2020).
- Lindell, Y.; Pinkas, B. Secure Multiparty Computation for Privacy-Preserving Data Mining. IACR Cryptol. ePrint Arch. 2008, 2008, 197. [Google Scholar] [CrossRef]
- Skarkala, M.E.; Maragoudakis, M.; Gritzalis, S.; Mitrou, L. PP-TAN: A Privacy Preserving Multi-party Tree Augmented Naive Bayes Classifier. In Proceedings of the 2020 5th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Corfu, Greece, 25–27 September 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Skarkala, M.E.; Maragoudakis, M.; Gritzalis, S.; Mitrou, L. Privacy Preserving Tree Augmented Naïve Bayesian Multi-party Implementation on Horizontally Partitioned Databases. In Trust, Privacy and Security in Digital Business; Furnell, S., Lambrinoudakis, C., Pernul, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 62–73. [Google Scholar]
- Baudron, O.; Fouque, P.A.; Pointcheval, D.; Stern, J.; Poupard, G. Practical Multi-Candidate Election System. In Proceedings of the Twentieth Annual ACM Symposium on Principles of Distributed Computing (PODC ’01), Newport, RI, USA, 26–29 August 2001; Association for Computing Machinery: New York, NY, USA, 2001; pp. 274–283. [Google Scholar] [CrossRef]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Advances in Cryptology—EUROCRYPT ’99; Stern, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
- Yang, Z.; Zhong, S.; Wright, R.N. Privacy-Preserving Classification of Customer Data without Loss of Accuracy. In Proceedings of the 2005 SIAM International Conference on Data Mining, Newport Beach, CA, USA, 21–23 April 2005; pp. 92–102. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Privacy-preserving data mining. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data (SIGMOD ’00), Dallas, TX, USA, 16–18 May 2000; ACM Press: New York, NY, USA, 2000; pp. 439–450. [Google Scholar] [CrossRef]
- Lindell, Y.; Pinkas, B. Privacy preserving data mining. J. Cryptol. 2003, 15, 177–206. [Google Scholar] [CrossRef]
- Gkoulalas-Divanis, A.; Verykios, V.S. An Overview of Privacy Preserving Data Mining. XRDS 2009, 15, 23–26. [Google Scholar] [CrossRef]
- Qi, X.; Zong, M. An Overview of Privacy Preserving Data Mining. Procedia Environ. Sci. 2012, 12, 1341–1347. [Google Scholar] [CrossRef]
- Malik, M.; Ghazi, M.; Ali, R. Privacy Preserving Data Mining Techniques: Current Scenario and Future Prospects. In Proceedings of the 2012 Third International Conference on Computer and Communication Technology, Allahabad, India, 23–25 November 2012; pp. 26–32. [Google Scholar] [CrossRef]
- Bertino, E.; Nai Fovino, I.; Provenza, L. A Framework for Evaluating Privacy Preserving Data Mining Algorithms. Data Min. Knowl. Discov. 2005, 11, 121–154. [Google Scholar] [CrossRef]
- Bertino, E.; Lin, D.; Jiang, W. A Survey of Quantification of Privacy Preserving Data Mining Algorithms. In Privacy-Preserving Data Mining: Models and Algorithms; Springer: Boston, MA, USA, 2008; pp. 183–205. [Google Scholar] [CrossRef]
- Kantarcioglu, M.; Jin, J.; Clifton, C. When Do Data Mining Results Violate Privacy? In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’04), Seattle, WA, USA, 22–25 August 2004; Association for Computing Machinery: New York, NY, USA, 2004; pp. 599–604. [Google Scholar] [CrossRef]
- Scardapane, S.; Altilio, R.; Ciccarelli, V.; Uncini, A.; Panella, M. Privacy-Preserving Data Mining for Distributed Medical Scenarios. In Multidisciplinary Approaches to Neural Computing; Springer: Cham, Switzerland, 2018; pp. 119–128. [Google Scholar] [CrossRef]
- Huai, M.; Huang, L.; Yang, W.; Li, L.; Qi, M. Privacy-Preserving Naive Bayes Classification. In Knowledge Science, Engineering and Management; Zhang, S., Wirsing, M., Zhang, Z., Eds.; Springer: Cham, Switzerland, 2015; pp. 627–638. [Google Scholar]
- Liu, K.; Kargupta, H.; Ryan, J. Random Projection-Based Multiplicative Data Perturbation for Privacy Preserving Distributed Data Mining. IEEE Trans. Knowl. Data Eng. 2006, 18, 92–106. [Google Scholar] [CrossRef]
- Vaidya, J.; Shafiq, B.; Basu, A.; Hong, Y. Differentially Private Naive Bayes Classification. In Proceedings of the 2013 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT), Atlanta, GA, USA, 17–20 November 2013; Volume 1, pp. 571–576. [Google Scholar] [CrossRef]
- Vaidya, J.; Clifton, C. Privacy Preserving Association Rule Mining in Vertically Partitioned Data. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’02), Edmonton, AB, Canada, 23–26 July 2002; Association for Computing Machinery: New York, NY, USA, 2002; pp. 639–644. [Google Scholar] [CrossRef]
- Kargupta, H.; Datta, S.; Wang, Q.; Sivakumar, K. On the privacy preserving properties of random data perturbation techniques. In Proceedings of the Third IEEE International Conference on Data Mining, Melbourne, FL, USA, 19–22 November 2003; pp. 99–106. [Google Scholar] [CrossRef]
- Zhang, P.; Tong, Y.; Tang, S.; Yang, D. Privacy Preserving Naive Bayes Classification. In Advanced Data Mining and Applications; Li, X., Wang, S., Dong, Z.Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 744–752. [Google Scholar]
- Pinkas, B. Cryptographic Techniques for Privacy-Preserving Data Mining. SIGKDD Explor. Newsl. 2002, 4, 12–19. [Google Scholar] [CrossRef]
- Vaidya, J.; Kantarcioglu, M.; Clifton, C. Privacy-Preserving Naive Bayes Classification. VLDB J. 2008, 17, 879–898. [Google Scholar] [CrossRef]
- Yi, X.; Zhang, Y. Privacy-preserving naive Bayes classification on distributed data via semi-trusted mixers. Inf. Syst. 2009, 34, 371–380. [Google Scholar] [CrossRef]
- Clifton, C.; Kantarcioglu, M.; Vaidya, J.; Lin, X.; Zhu, M.Y. Tools for Privacy Preserving Distributed Data Mining. SIGKDD Explor. Newsl. 2002, 4, 28–34. [Google Scholar] [CrossRef]
- Vaidya, J.; Clifton, C. Privacy Preserving Naïve Bayes Classifier for Vertically Partitioned Data. In Proceedings of the 2004 SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 22–24 April 2004; pp. 522–526. [Google Scholar] [CrossRef]
- Tassa, T. Secure Mining of Association Rules in Horizontally Distributed Databases. IEEE Trans. Knowl. Data Eng. 2011, 26, 970–983. [Google Scholar] [CrossRef]
- Goethals, B.; Laur, S.; Lipmaa, H.; Mielikäinen, T. On Private Scalar Product Computation for Privacy-Preserving Data Mining. In Information Security and Cryptology—ICISC 2004; Park, C.S., Chee, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 104–120. [Google Scholar]
- Keshavamurthy, B.; Sharma, M.; Toshniwal, D. Privacy Preservation Naïve Bayes Classification for a Vertically Distribution Scenario Using Trusted Third Party. In Proceedings of the 2010 International Conference on Advances in Recent Technologies in Communication and Computing, Kottayam, India, 16–17 October 2010; pp. 404–407. [Google Scholar] [CrossRef]
- Gao, C.Z.; Cheng, Q.; He, P.; Susilo, W.; Li, J. Privacy-Preserving Naive Bayes Classifiers Secure against the Substitution-then-Comparison Attack. Inf. Sci. 2018, 444, 72–88. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, S.; Zhao, W. A New Scheme on Privacy-Preserving Data Classification. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining (KDD ’05), Chicago, IL, USA, 21–24 August 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 374–383. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning, 1st ed.; McGraw-Hill, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian Network Classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Chow, C.; Liu, C. Approximating Discrete Probability Distributions with Dependence Trees. IEEE Trans. Inf. Theor. 1968, 14, 462–467. [Google Scholar] [CrossRef]
- Madden, M.G. On the classification performance of TAN and general Bayesian networks. Knowl.-Based Syst. 2009, 22, 489–495. [Google Scholar] [CrossRef]
- Magkos, E.; Maragoudakis, M.; Chrissikopoulos, V.; Gritzalis, S. Accurate and large-scale privacy-preserving data mining using the election paradigm. Data Knowl. Eng. 2009, 68, 1224–1236. [Google Scholar] [CrossRef]
- Takabi, H.; Hesamifard, E.; Ghasemi, M. Preserving Multi-party Machine Learning with Homomorphic Encryption. In Proceedings of the 29th Annual Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 25 November 2020).
- Shadmanov, I.; Shadmanova, K. Summarization of Various Security Aspects and Attacks in Distributed Systems: A Review. Adv. Comput. Sci. 2016, 5, 35–39. [Google Scholar]
- Kantzavelou, I.; Patel, A. Issues of attack in distributed systems—A Generic Attack Model. In Communications and Multimedia Security, Proceedings of the IFIP TC6, TC11 and Austrian Computer Society Joint Working Conference on Communications and Multimedia Security, Graz, Austria, 1995; Springer: Boston, MA, USA, 1995; pp. 1–16. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).