Spatial and Temporal Validation of a CFD Model Using Residence Time Distribution Test in a Tubular Reactor
Abstract
1. Introduction
2. Materials and Methods
2.1. Reactor Setup and Experimental Design
2.2. CFD Modeling
2.2.1. Geometry and Mesh
2.2.2. The Model
2.2.3. Solver, Boundary, and Initial Conditions
2.2.4. Tracer Injection Simulation
2.2.5. Tracer Recirculation
2.3. Validation Technique
3. Results and Discussion
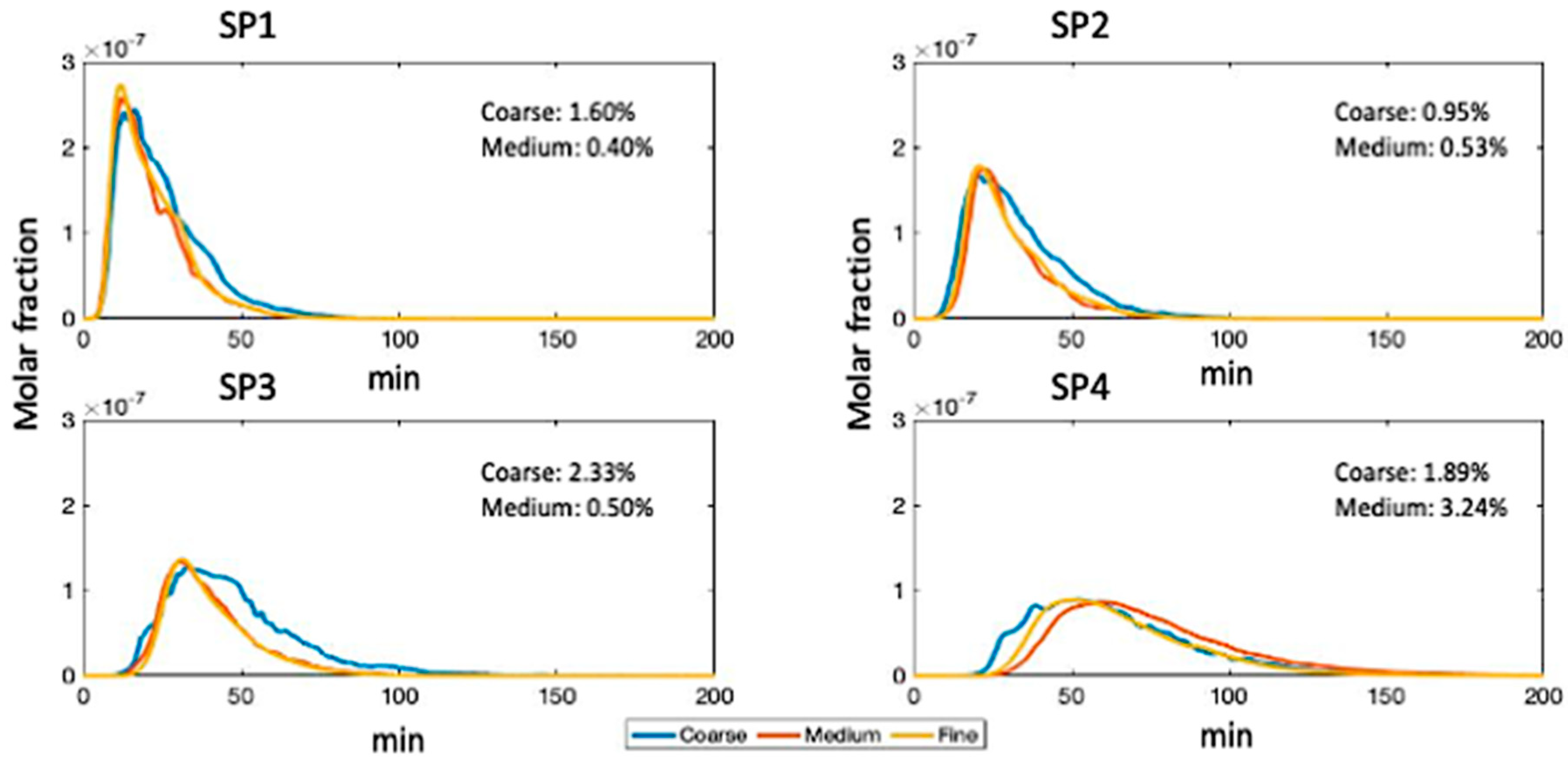
3.1. Mesh Quality and Independence
3.2. Model Validation
3.3. Model Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wicklein, E.; Batstone, D.J.; Ducoste, J.; Laurent, J.; Griborio, A.; Wicks, J.; Saunders, S.; Samstag, R.; Potier, O.; Nopens, I. Good modelling practice in applying computational fluid dynamics for WWTP modelling. Water Sci. Technol. 2015, 73, 969–982. [Google Scholar] [CrossRef] [PubMed]
- Kiared, K.; Larachi, F.; Guy, C.; Chaouki, J. Trajectory length and residence-time distributions of the solids in three-phase fluidized beds. Chem. Eng. Sci. 1997, 52, 3931–3939. [Google Scholar] [CrossRef]
- Arratia, P.E.; Muzzio, F.J. Planar Laser-Induced Fluorescence Method for Analysis of Mixing in Laminar Flows. Ind. Eng. Chem. Res. 2004, 43, 6557–6568. [Google Scholar] [CrossRef]
- Delafosse, A.; Calvo, S.; Collignon, M.-L.; Delvigne, F.; Crine, M.; Toye, D. Euler-Lagrange approach to model heterogeneities in stirred tank bioreactors—Comparison to experimental flow characterization and particle tracking. Chem. Eng. Sci. 2015, 134, 457–466. [Google Scholar] [CrossRef]
- Odeleye, A.O.O.; Marsh, D.T.J.; Osborne, M.D.; Lye, G.J.; Micheletti, M. On the fluid dynamics of a laboratory scale single-use stirred bioreactor. Chem. Eng. Sci. 2014, 111, 299–312. [Google Scholar] [CrossRef]
- Schirmaier, C.; Jossen, V.; Kaiser, S.C.; Jüngerkes, F.; Brill, S.; Safavi-Nab, A.; Siehoff, A.; Bos, C.V.D.; Eibl, D.; Eibl, R. Scale-up of adipose tissue-derived mesenchymal stem cell production in stirred single-use bioreactors under low-serum conditions. Eng. Life Sci. 2014, 14, 292–303. [Google Scholar] [CrossRef]
- Rahimi, M.; Parvareh, A. Experimental and CFD investigation on mixing by a jet in a semi-industrial stirred tank. Chem. Eng. J. 2005, 115, 85–92. [Google Scholar] [CrossRef]
- Pakzad, L.; Ein-Mozaffari, F.; Upreti, S.R.; Lohi, A. Characterisation of the mixing of non-newtonian fluids with a scaba 6SRGT impeller through ert and CFD. Can. J. Chem. Eng. 2013, 91, 90–100. [Google Scholar] [CrossRef]
- Hashemi, N.; Ein-Mozaffari, F.; Upreti, S.R.; Hwang, D.K. Analysis of mixing in an aerated reactor equipped with the coaxial mixer through electrical resistance tomography and response surface method. Chem. Eng. Res. Des. 2016, 109, 734–752. [Google Scholar] [CrossRef]
- Kazemzadeh, A.; Elias, C.; Tamer, M.; Ein-Mozaffari, F. Hydrodynamic performance of a single-use aerated stirred bioreactor in animal cell culture: Applications of tomography, dynamic gas disengagement (DGD), and CFD. Bioprocess Biosyst. Eng. 2018, 41, 679–695. [Google Scholar] [CrossRef]
- Nopens, I.; Sudrawska, D.; Audenaert, W.; del Pozo, D.F.; Rehman, U. Water and wastewater CFD validation: Are we losing the balance? Water Sci. Technol. 2020, 81, 1636–1645. [Google Scholar] [CrossRef]
- Paul, E.L.; Victor, A.; Atiemo, O.; Suzanne, M.K. Handbook of Industrial Mixing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Gunjal, P.R.; Ranade, V.V.; Chaudhari, R.V. Liquid Distribution and RTD in Trickle Bed Reactors: Experiments and CFD Simulations. Can. J. Chem. Eng. 2003, 81, 821–830. [Google Scholar] [CrossRef]
- Kalaga, D.V.; Reddy, R.K.; Joshi, J.B.; Dalvi, S.V.; Nandkumar, K. Liquid phase axial mixing in solid-liquid circulating multistage fluidized bed: CFD modeling and RTD measurements. Chem. Eng. J. 2012, 191, 475–490. [Google Scholar] [CrossRef]
- Alvarado, A.; Vesvikar, M.; Cisneros, J.F.; Maere, T.; Goethals, P.; Nopens, I. CFD study to determine the optimal configuration of aerators in a full-scale waste stabilization pond. Water Res. 2013, 47, 4528–4537. [Google Scholar] [CrossRef]
- Manenti, S.; Todeschini, S.; Collivignarelli, M.C.; Abbà, A. Integrated RTD—CFD Hydrodynamic Analysis for Performance Assessment of Activated Sludge Reactors. Environ. Process. 2018, 5, 23–42. [Google Scholar] [CrossRef]
- Choi, B.S.; Wan, B.; Philyaw, S.; Dhanasekharan, K.; Ring, T.A. Residence time distributions in a stirred tank: Comparison of CFD predictions with experiment. Ind. Eng. Chem. Res. 2004, 43, 6548–6556. [Google Scholar] [CrossRef]
- Ren, T.-T.; Mu, Y.; Ni, B.-J.; Yu, H.-Q. Hydrodynamics of upflow anaerobic sludge blanket reactors. AIChE J. 2009, 55, 516–528. [Google Scholar] [CrossRef]
- Rhee, B.K. Enhancement of Mass Transfer Coefficient in Three-Phase Magnetically Stabilized Fluidized Bed. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 1998. [Google Scholar]
- Sadino-Riquelme, C.; Hayes, R.E.; Jeison, D.; Donoso-Bravo, A. Computational fluid dynamic (CFD) modelling in anaerobic digestion: General application and recent advances. Crit. Rev. Environ. Sci. Technol. 2018, 48, 39–76. [Google Scholar] [CrossRef]
- Kwok, W.; Chen, Z. A Simple and Effective Mesh Quality Metric for Hexahedral and Wedge Elements. In Proceedings of the 9th International Meshing Roundtable, New Orleans, LA, USA, 2–5 October 2000. [Google Scholar]
- Parthasarathy, V.N.; Graichen, C.M.; Hathaway, A.F. A comparison of tetrahedron quality measures. Finite Elem. Anal. Des. 1994, 15, 255–261. [Google Scholar] [CrossRef]
- Liu, M. Prediction of tracer concentration and mixing in CFSTRs with mean age distribution. Ind. Eng. Chem. Res. 2011, 50, 5838–5851. [Google Scholar] [CrossRef]
- Markthaler, S.; Plankenbühler, T.; Weidlich, T.; Neubert, M.; Karl, J. Numerical simulation of trickle bed reactors for biological methanation. Chem. Eng. Sci. 2020, 226, 115847. [Google Scholar] [CrossRef]

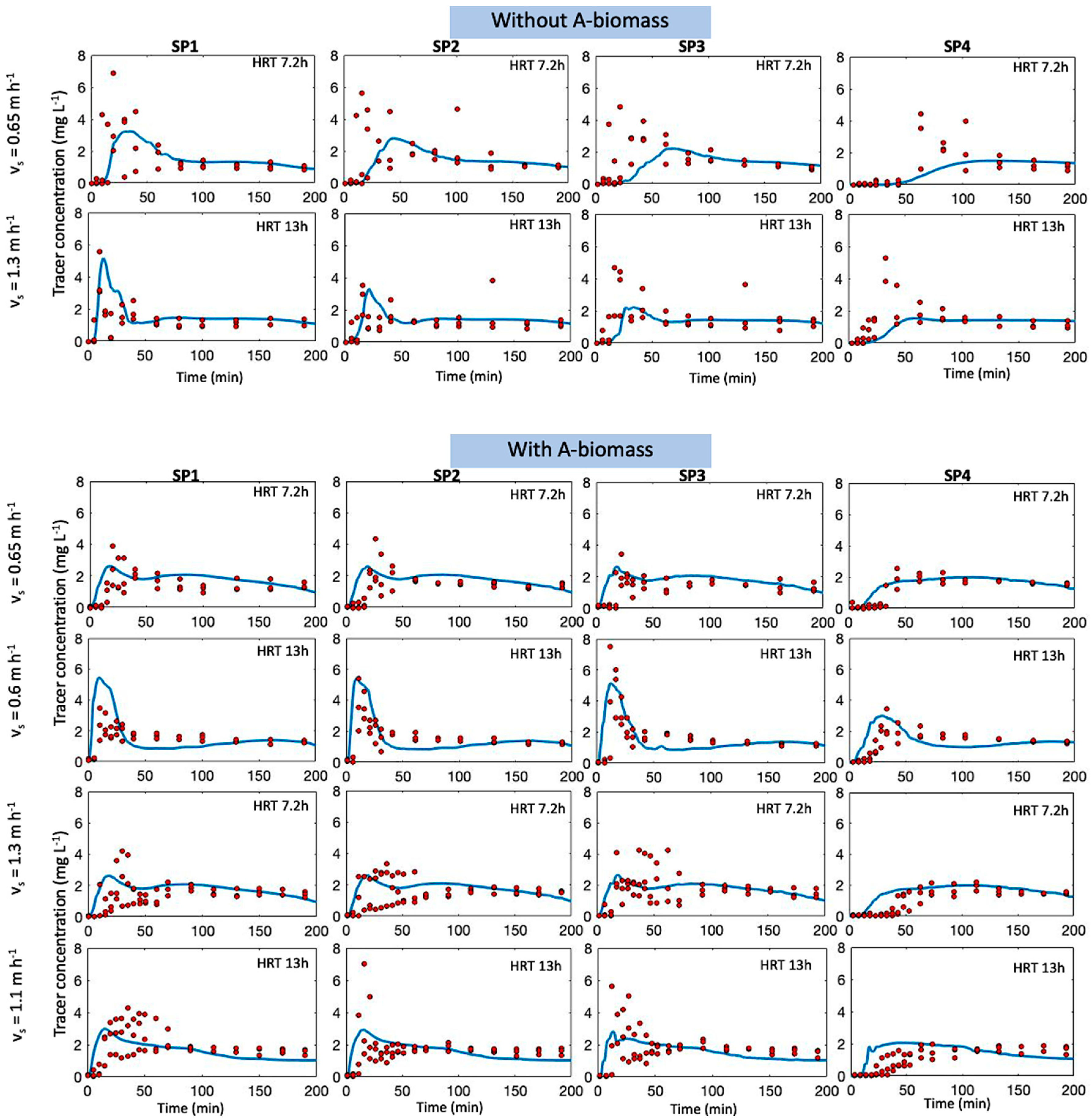

| Without A-Biomass | With A-Biomass | |||||
|---|---|---|---|---|---|---|
| General operational conditions | ||||||
| Hydraulic retention time (h) | 7.2 | 7.2 | 13 | |||
| vs (m h−1) | 0.65 | 1.3 | 0.65 | 1.3 | 0.6 | 1.1 |
| Feed flow (mL s−1) | 0.078 | 0.078 | 0.078 | 0.078 | 0.043 | 0.043 |
| Recirculation flow (mL s−1) | 0.197 | 0.471 | 0.197 | 0.471 | 0.211 | 0.422 |
| Transport lag time of the recirculation loop (h) | 0.085 | 0.036 | 0.085 | 0.036 | 0.079 | 0.040 |
| General boundary conditions | ||||||
| Inlet (m s−1) | 0.0027 | 0.0055 | 0.0027 | 0.0055 | 0.0025 | 0.0046 |
| Recirculation (m s−1) | 0.0039 | 0.0094 | 0.0039 | 0.0094 | 0.0042 | 0.0084 |
| Boundary conditions during tracer injection | ||||||
| Inlet (m s−1) | 0.00572 | 0.0085 | 0.00572 | 0.0085 | 0.0055 | 0.0086 |
| Molar fraction | 2.930 × 10−5 | 1.989 × 10−5 | 1.831 × 10−6 | 4.972 × 10−6 | 1.904 × 10−6 | 5.514 × 10−6 |
| Mesh | Coarse | Medium | Fine |
|---|---|---|---|
| Aspect ratio | |||
| Min | 1.1584 | 1.1585 | 1.0685 |
| Max | 86.5120 | 60.8970 | 55.1290 |
| Average | 2.8538 | 2.7202 | 2.5419 |
| Skewness | |||
| Min | 1.75 × 10−5 | 4.20 × 10−6 | 3.27 × 10−6 |
| Max | 0.9760 | 0.9768 | 0.9157 |
| Average | 0.2183 | 0.2118 | 0.2038 |
| Orthogonal Quality | |||
| Min | 0.0239 | 0.0231 | 0.0842 |
| Max | 0.9953 | 0.9956 | 0.9988 |
| Average | 0.7803 | 0.7867 | 0.7986 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivas, J.; Sadino-Riquelme, M.C.; Garcés, I.; Carvajal, A.; Donoso-Bravo, A. Spatial and Temporal Validation of a CFD Model Using Residence Time Distribution Test in a Tubular Reactor. Computation 2020, 8, 94. https://doi.org/10.3390/computation8040094
Rivas J, Sadino-Riquelme MC, Garcés I, Carvajal A, Donoso-Bravo A. Spatial and Temporal Validation of a CFD Model Using Residence Time Distribution Test in a Tubular Reactor. Computation. 2020; 8(4):94. https://doi.org/10.3390/computation8040094
Chicago/Turabian StyleRivas, José, M. Constanza Sadino-Riquelme, Ignacio Garcés, Andrea Carvajal, and Andrés Donoso-Bravo. 2020. "Spatial and Temporal Validation of a CFD Model Using Residence Time Distribution Test in a Tubular Reactor" Computation 8, no. 4: 94. https://doi.org/10.3390/computation8040094
APA StyleRivas, J., Sadino-Riquelme, M. C., Garcés, I., Carvajal, A., & Donoso-Bravo, A. (2020). Spatial and Temporal Validation of a CFD Model Using Residence Time Distribution Test in a Tubular Reactor. Computation, 8(4), 94. https://doi.org/10.3390/computation8040094






