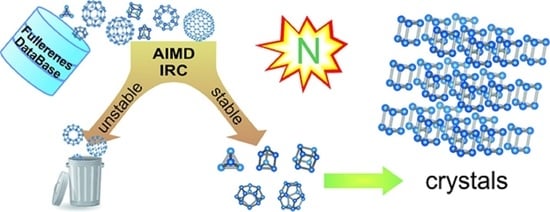
All-Nitrogen Cages and Molecular Crystals: Topological Rules, Stability, and Pyrolysis Paths
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
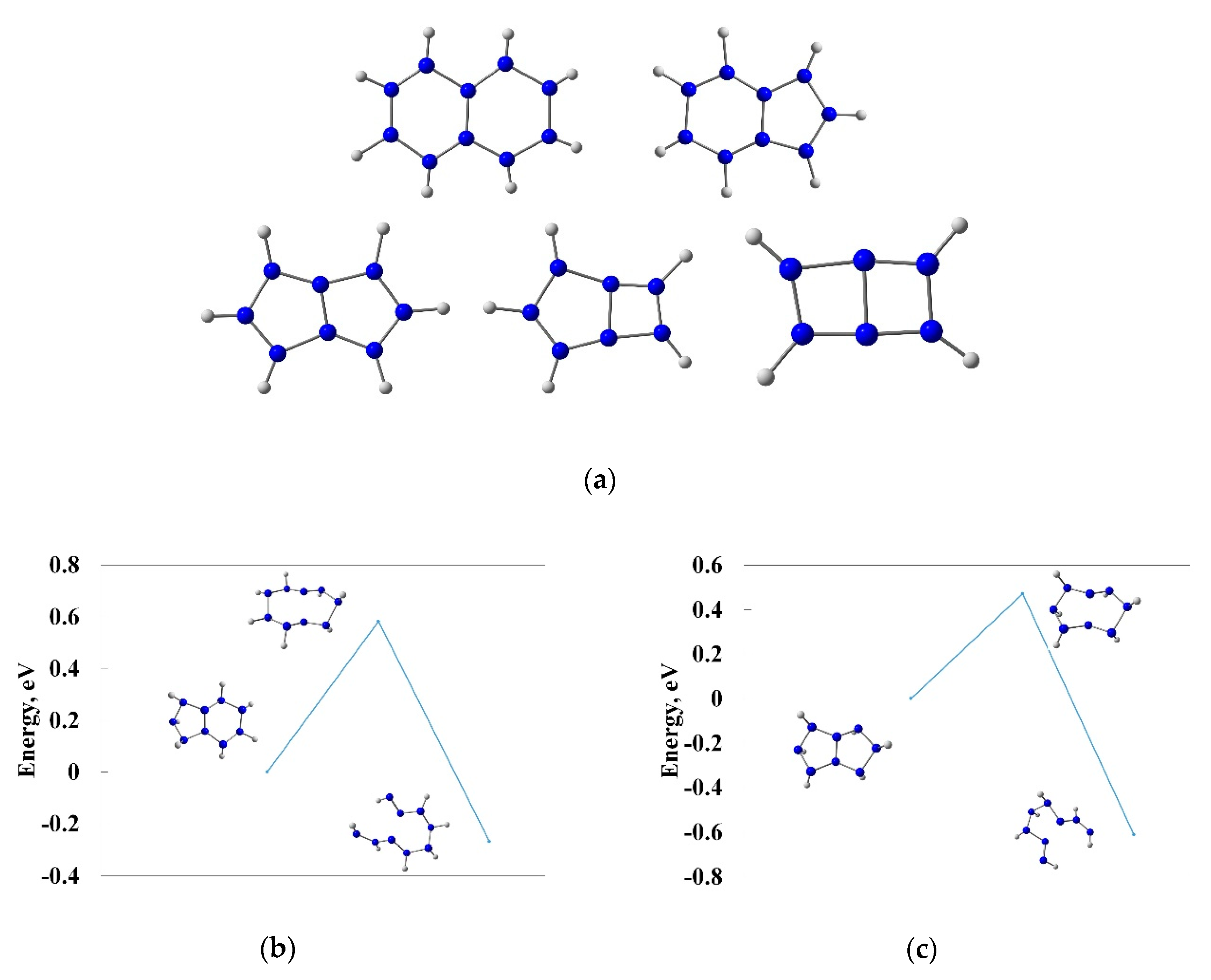
3.1. The First Insight on the Bicyclic Hydronitrogen Molecules
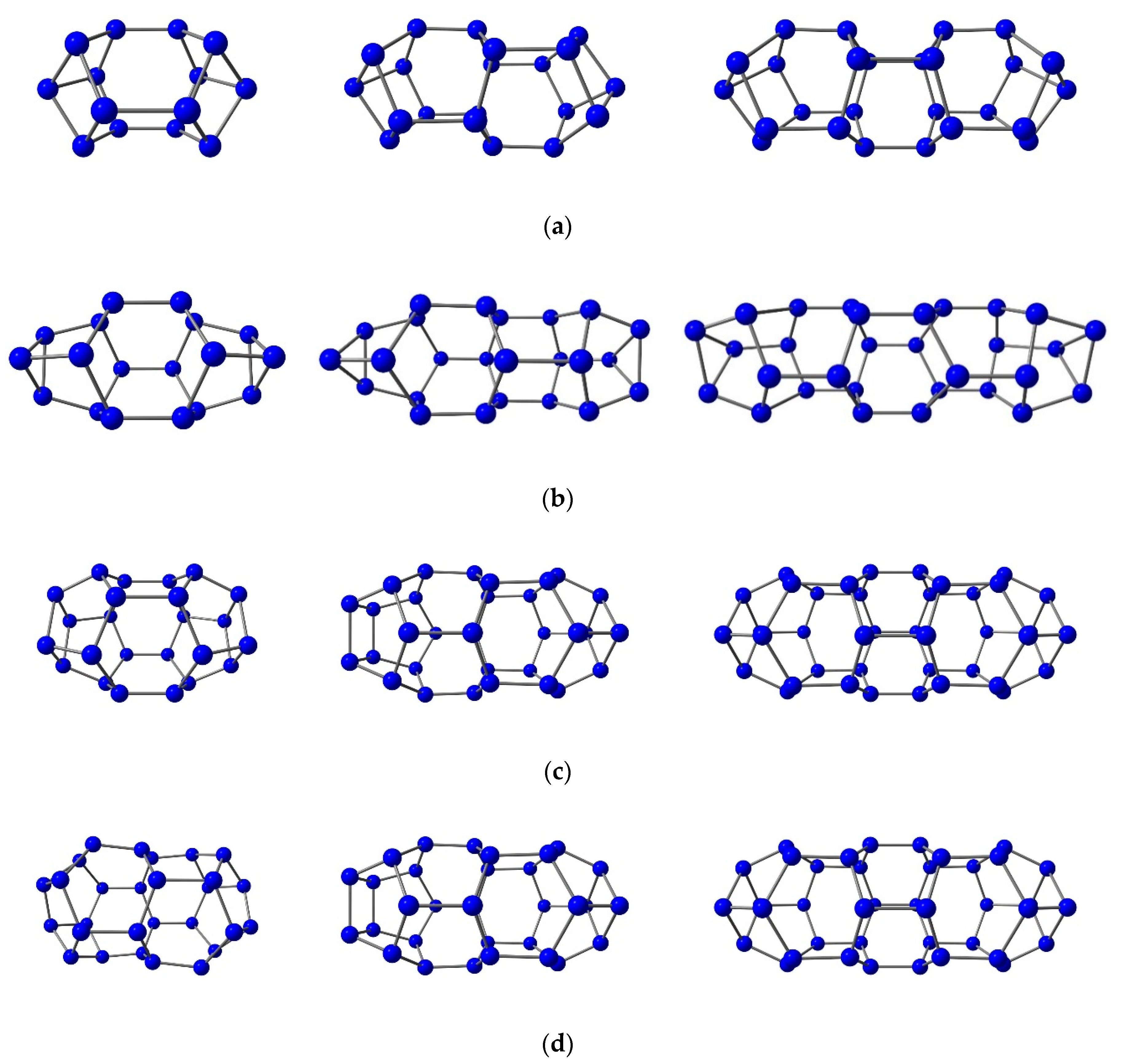
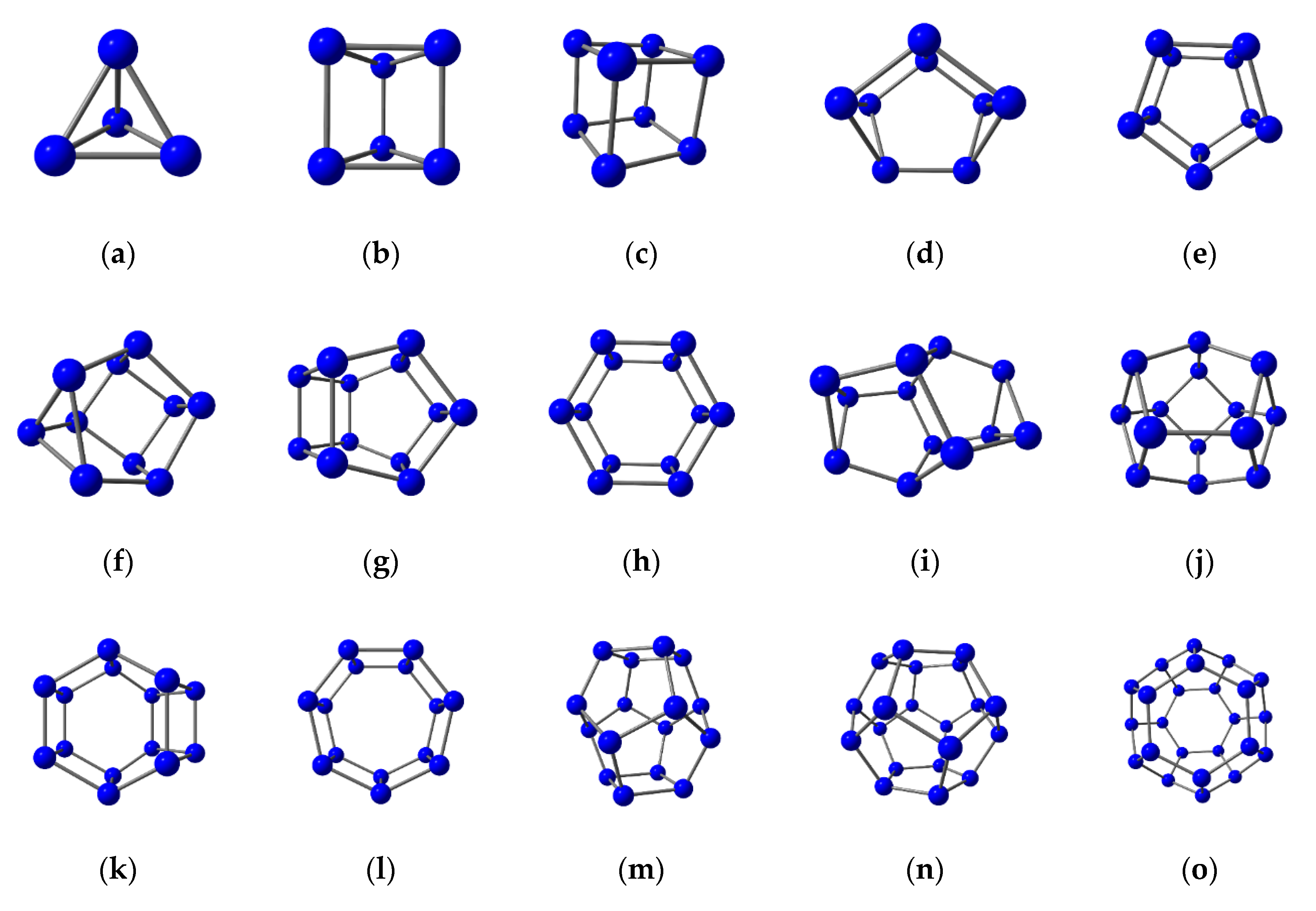
3.2. Nitrogen Cages with Adjacent Hexagons
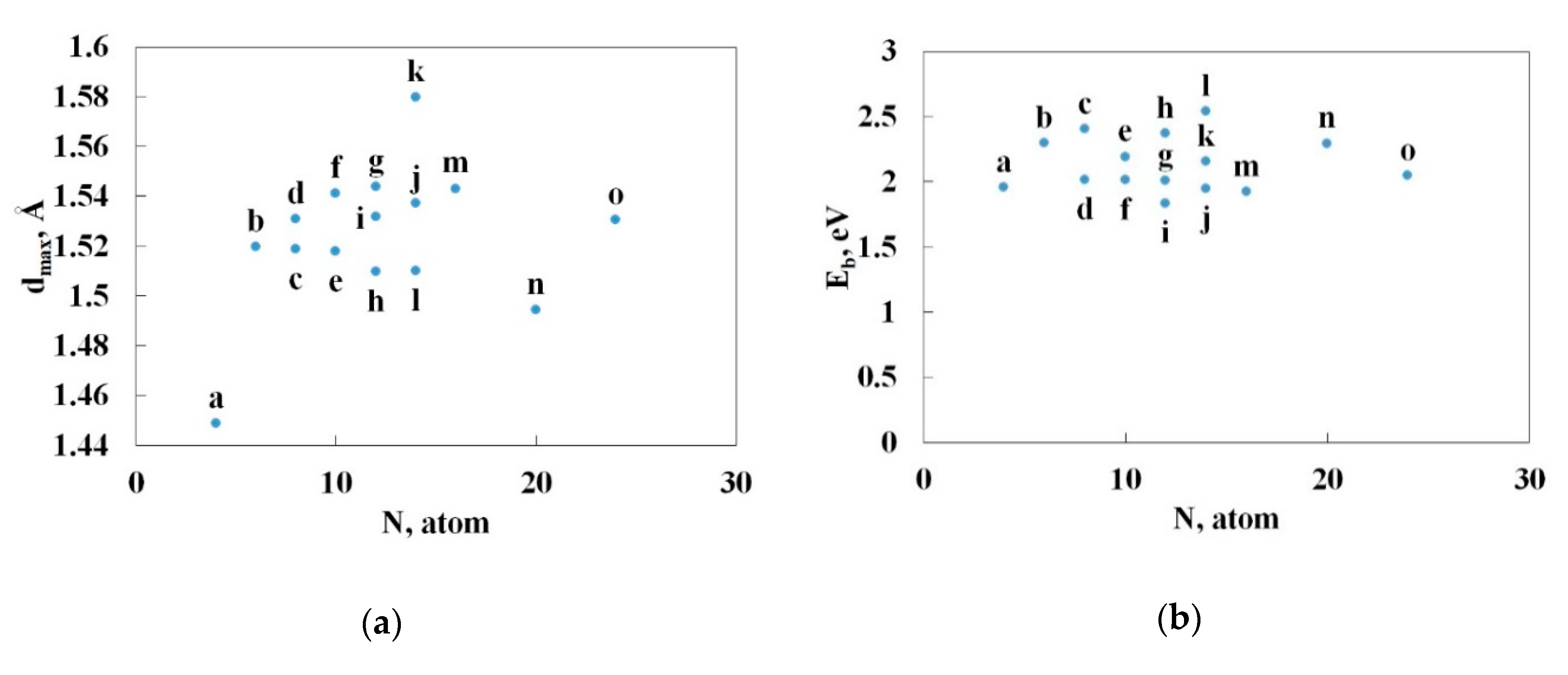
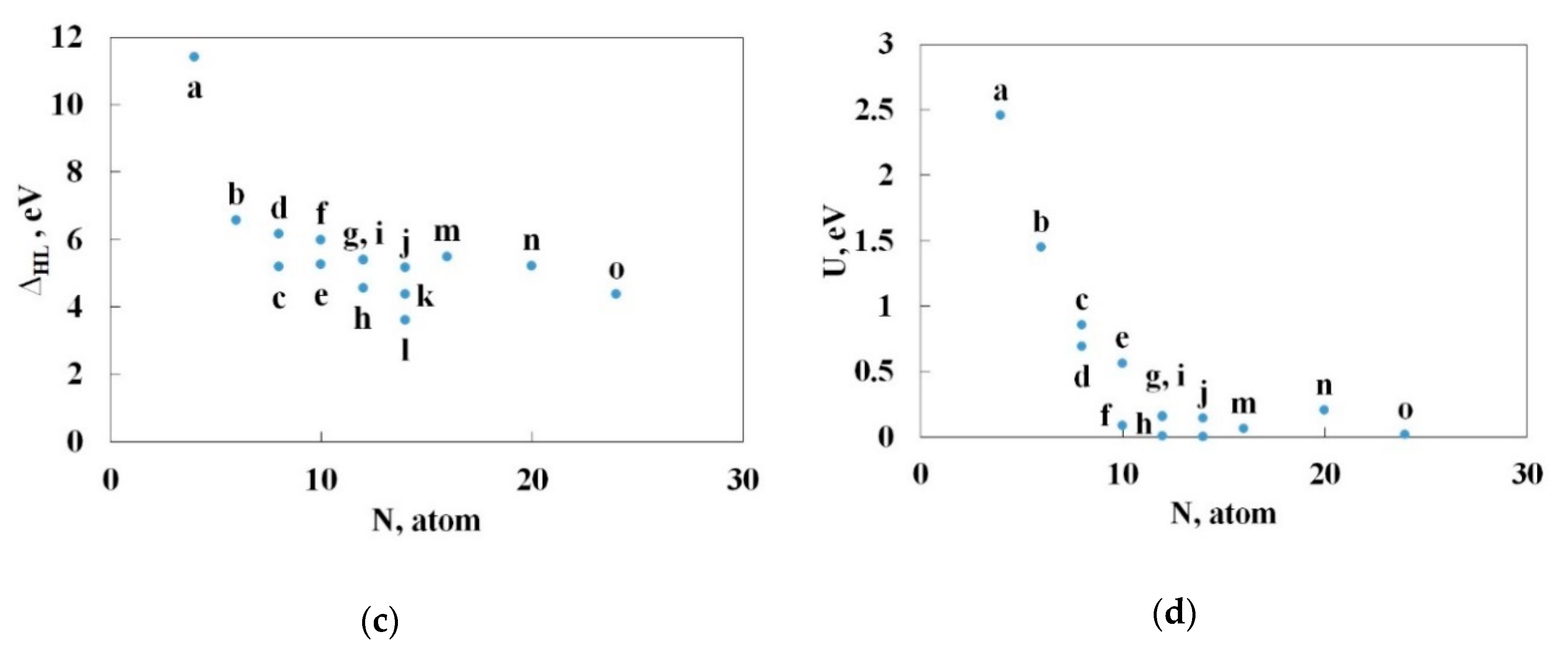
3.3. Nitrogen Cages without Adjacent Hexagons
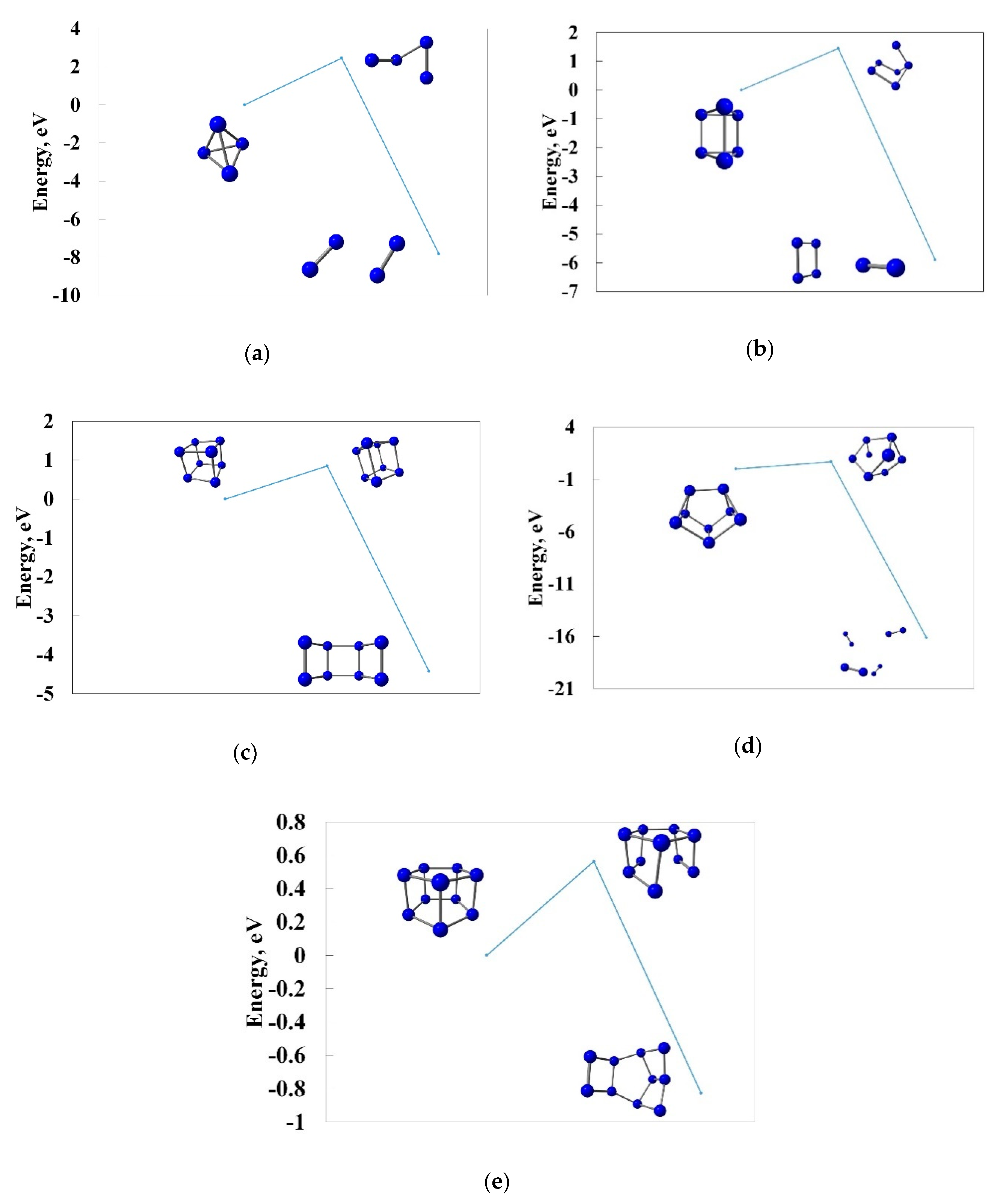
3.4. Pyrolysis of the Most Stable Nitrogen Cages and the Possibility of Further Stabilization
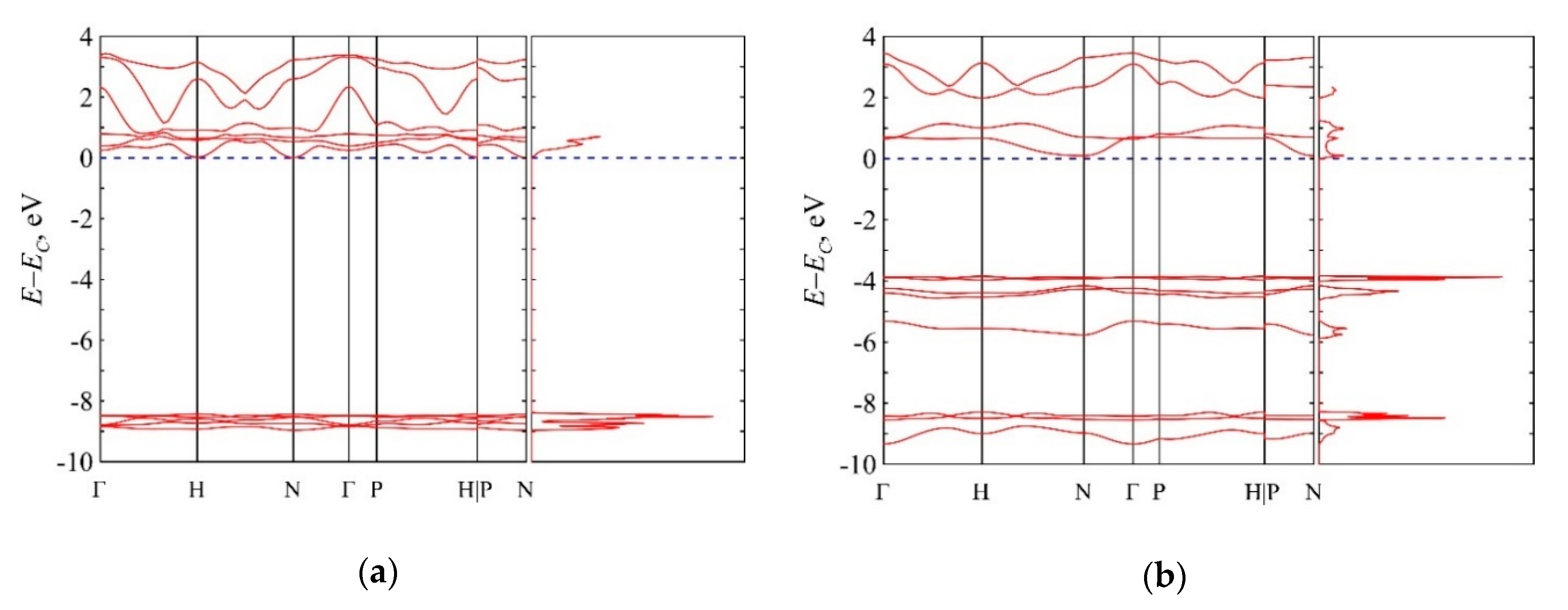
3.5. Van der Waals Nitrogen Crystals
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Samartzis, P.C.; Wodtke, A.M. All-Nitrogen Chemistry: How Far Are We from N60? Int. Rev. Phys. Chem. 2006, 25, 527–552. [Google Scholar] [CrossRef]
- Witkowski, T.G.; Richardson, P.; Gabidullin, B.; Hu, A.; Murugesu, M. Synthesis and Investigation of 2,3,5,6-Tetra-(1H-Tetrazol-5-Yl)Pyrazine Based Energetic Materials. ChemPlusChem 2018, 83, 984–990. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, G.; Gong, X. Screening for Potential Energetic C–N Cages with High Energy and Good Stability: A Theoretical Comparative Study. Mol. Simul. 2018, 45, 129–136. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, J.; Zhou, Q.; Hu, W.; Zhang, X. 2-Fluoro-1,3-Diamino-4,6-Dinitrobenzene (ZXC-7) and 2-Fluoro-1,3,5-Triamino-4,6-Dinitrobenzene (ZXC-8): Thermally Stable Explosives with Outstanding Properties. ChemPlusChem 2019, 84, 119–122. [Google Scholar] [CrossRef] [PubMed]
- Eremets, M.I.; Gavriliuk, A.G.; Serebryanaya, N.R.; Trojan, I.A.; Dzivenko, D.A.; Boehler, R.; Mao, H.K.; Hemley, R.J. Structural Transformation of Molecular Nitrogen to a Single-Bonded Atomic State at High Pressures. J. Chem. Phys. 2004, 121, 11296. [Google Scholar] [CrossRef]
- Tomasino, D.; Kim, M.; Smith, J.; Yoo, C.-S. Pressure-Induced Symmetry-Lowering Transition in Dense Nitrogen to Layered Polymeric Nitrogen (LP-N) with Colossal Raman Intensity. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef]
- Strout, D.L. Stabilization of an All-Nitrogen Molecule by Oxygen Insertion: Dissociation Pathways of N8O6. J. Phys. Chem. A 2003, 107, 1647–1650. [Google Scholar] [CrossRef]
- Chen, J.; Yu, Y.; Li, Y.; Pang, S. Combination High Energy with Stability: Polynitrogen Explosives N14 and N18. Phys. Chem. 2018. [Google Scholar] [CrossRef]
- Owens, F.J. Density Functional Calculation of Structure and Stability of Nitrogen Clusters N10, N12, and N20. J. Mol. Struct. THEOCHEM 2003, 623, 197–201. [Google Scholar] [CrossRef]
- Lee, T.J.; Rice, J.E. Theoretical Characterization of Tetrahedral N4. J. Chem. Phys. 1991, 94, 1215–1221. [Google Scholar] [CrossRef]
- Li, Q.S.; Liu, Y.D. Theoretical Studies of the N6Potential Energy Surface. J. Phys. Chem. A 2002, 106, 9538–9542. [Google Scholar] [CrossRef]
- Chung, G.; Schmidt, M.W.; Gordon, M.S. An Ab Initio Study of Potential Energy Surfaces for N8Isomers. J. Phys. Chem. A 2000, 104, 5647–5650. [Google Scholar] [CrossRef]
- Bruney, L.Y.; Bledson, T.M.; Strout, D.L. What Makes an N12 Cage Stable? Inorg. Chem. 2003, 42, 8117–8120. [Google Scholar] [CrossRef]
- Strout, D.L. Cage Isomers of N14 and N16: Nitrogen Molecules That Are Not a Multiple of Six. J. Phys. Chem. A 2004, 108, 10911–10916. [Google Scholar] [CrossRef]
- Sturdivant, S.E.; Nelson, F.A.; Strout, D.L. Trends in Stability for N18 Cages. J. Phys. Chem. A 2004, 108, 7087–7090. [Google Scholar] [CrossRef]
- Strout, D.L. Why Isn’t the N20 Dodecahedron Ideal for Three-Coordinate Nitrogen? J. Phys. Chem. A 2005, 109, 1478–1480. [Google Scholar] [CrossRef]
- Strout, D.L. Isomer Stability of N24, N30, and N36 Cages: Cylindrical versus Spherical Structure. J. Phys. Chem. A 2004, 108, 2555–2558. [Google Scholar] [CrossRef]
- Silva, M.X.; Silva, F.T.; Galvão, B.R.L.; Braga, J.P.; Belchior, J.C. A Genetic Algorithm Survey on Closed-Shell Atomic Nitrogen Clusters Employing a Quantum Chemical Approach. J. Mol. Modeling 2018, 24. [Google Scholar] [CrossRef]
- Zhou, H.; Beuve, M.; Yang, F.; Wong, N.-B.; Li, W.-K. Theoretical Investigation on the Cylinder-Shaped N66 Cage. Comput. Theor. Chem. 2013, 1005, 68–74. [Google Scholar] [CrossRef]
- Zhou, H.; Wong, N.-B.; Zhou, G.; Tian, A. What Makes the Cylinder-Shaped N72 Cage Stable? J. Phys. Chem. A 2006, 110, 7441–7446. [Google Scholar] [CrossRef]
- Zhou, H.; Wong, N.-B.; Zhou, G.; Tian, A. Theoretical Study on “Multilayer” Nitrogen Cages. J. Phys. Chem. A 2006, 110, 3845–3852. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.J.; Zgierski, M.Z. Super-High Energy-Rich Nitrogen Cluster N60. Chem. Phys. Lett. 2003, 376, 698–703. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Vineyard, G.H. Frequency Factors and Isotope Effects in Solid State Rate Processes. J. Phys. Chem. Solids 1957, 3, 121–127. [Google Scholar] [CrossRef]
- Ufimtsev, I.S.; Martinez, T.J. Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics. J. Chem. Theory Comput. 2009, 5, 2619–2628. [Google Scholar] [CrossRef]
- Titov, A.V.; Ufimtsev, I.S.; Luehr, N.; Martinez, T.J. Generating Efficient Quantum Chemistry Codes for Novel Architectures. J. Chem. Theory Comput. 2012, 9, 213–221. [Google Scholar] [CrossRef]
- Kästner, J.; Carr, J.M.; Keal, T.W.; Thiel, W.; Wander, A.; Sherwood, P. DL-FIND: An Open-Source Geometry Optimizer for Atomistic Simulations†. J. Phys. Chem. A 2009, 113, 11856–11865. [Google Scholar] [CrossRef]
- Goumans, T.P.M.; Catlow, C.R.A.; Brown, W.A.; Kästner, J.; Sherwood, P. An Embedded Cluster Study of the Formation of Water on Interstellar Dust Grains. Phys. Chem. Chem. Phys. 2009, 11, 5431–5436. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University press: New York, NY, USA, 1991; ISBN 978-0198556459. [Google Scholar]
- Chemcraft-Graphical Software for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com (accessed on 12 October 2020).
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 46. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-Precision Sampling for Brillouin-Zone Integration in Metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef] [PubMed]
- Kroto, H.W. The Stability of the Fullerenes Cn, with n = 24, 28, 32, 36, 50, 60 and 70. Nature 1987, 329, 529–531. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Wirz, L.; Avery, J. Program Fullerene: A Software Package for Constructing and Analyzing Structures of Regular Fullerenes. J. Comput. Chem. 2013, 34, 1508–1526. [Google Scholar] [CrossRef]
- Tománek, D. Guide through the Nanocarbon Jungle: Buckyballs, Nanotubes, Graphene, and Beyond; Morgan & Claypool Publishers: San Rafael, CA, USA, 2014. [Google Scholar] [CrossRef]
- Grishakov, K.; Katin, K.; Gimaldinova, M.; Maslov, M. Stability and Energy Characteristics of Extended Nitrogen Nanotubes: Density Functional Theory Study. Lett. Mater. 2019, 9, 366–369. [Google Scholar] [CrossRef]
- Gimaldinova, M.A.; Zemenkov, L.I.; Merinov, V.A. Stabilization of Small Nitrogen Clusters via Spatial Constraint. J. Phys. Conf. Ser. 2020, 1435, 012062. [Google Scholar] [CrossRef]
- Gimaldinova, M.A.; Katin, K.P.; Grishakov, K.S.; Maslov, M.M. Kinetic Stability of Nitrogen Cubane inside the Fullerene Cage: Molecular Dynamics Study. Fuller. Nanotub. Carbon Nanostruct. 2019, 28, 304–308. [Google Scholar] [CrossRef]
- Greschner, M.J.; Zhang, M.; Majumdar, A.; Liu, H.; Peng, F.; Tse, J.S.; Yao, Y. A New Allotrope of Nitrogen as High-Energy Density Material. J. Phys. Chem. A 2016, 120, 2920–2925. [Google Scholar] [CrossRef]
- Li, Y.; Feng, X.; Liu, H.; Hao, J.; Redfern, S.A.T.; Lei, W.; Liu, D.; Ma, Y. Route to High-Energy Density Polymeric Nitrogen t-N via He−N Compounds. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Bondarchuk, S.V.; Minaev, B.F. Super High-Energy Density Single-Bonded Trigonal Nitrogen Allotrope—A Chemical Twin of the Cubic Gauche Form of Nitrogen. Phys. Chem. Chem. Phys. 2017, 19, 6698–6706. [Google Scholar] [CrossRef]
- Adeleke, A.A.; Greschner, M.J.; Majumdar, A.; Wan, B.; Liu, H.; Li, Z.; Gou, H.; Yao, Y. Single-Bonded Allotrope of Nitrogen Predicted at High Pressure. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Maslov, M.M.; Katin, K.P. On the Thermal Stability of Tetrahedrane: Tight-Binding Molecular Dynamics Study. Chem. Phys. 2011, 387, 66–68. [Google Scholar] [CrossRef]
- Katin, K.P.; Prudkovskiy, V.S.; Maslov, M.M. Influence of Methyl Functional Groups on the Stability of Cubane Carbon Cage. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 81, 1–6. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Crystal Structure Prediction Usingab Initioevolutionary Techniques: Principles and Applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A Method for Crystal Structure Prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Xiong, W. A Simole Method for Calculating Detonation Parameters of Explosives. J. Energ. Mater. 1985, 3, 263–277. [Google Scholar] [CrossRef]
- Yan, Q.-L.; Zeman, S. Theoretical Evaluation of Sensitivity and Thermal Stability for High Explosives Based on Quantum Chemistry Methods: A Brief Review. Int. J. Quantum Chem. 2012, 113, 1049–1061. [Google Scholar] [CrossRef]
- Kim, C.; Cho, S.-G.; Kim, C.K.; Lee, H.W. QSPR Studies on Impact Sensitivities of High Energy Density Molecules. Bull. Korean Chem. Soc. 2011, 32, 4341–4346. [Google Scholar] [CrossRef]
- Rice, B.M.; Hare, J.J. A Quantum Mechanical Investigation of the Relation between Impact Sensitivity and the Charge Distribution in Energetic Molecules. J. Phys. Chem. A 2002, 106, 1770–1783. [Google Scholar] [CrossRef]
- Simpson, R.L.; Urtiew, P.A.; Ornellas, D.L.; Moody, G.L.; Scribner, K.J.; Hoffman, D.M. CL-20 Performance Exceeds That of HMX and Its Sensitivity Is Moderate. Propellants Explos. Pyrotech. 1997, 22, 249–255. [Google Scholar] [CrossRef]
| U (eV) | g | ω (cm−1) | ΔH (kJ/mol) | ΔG (kJ/mol) | t (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 300 K | 400 K | 500 K | 300 K | 400 K | 500 K | 300 K | 400 K | 500 K | ||||
| N4 (a) | 2.46 | 4 | 664.1i | 230.5 | 230.5 | 226.1 | 229.1 | 228.7 | 228.3 | 9.6 × 1026 | 4.6 × 1016 | 2.9 × 1010 |
| N6 (b) | 1.45 | 2 | 721.1i | 132.0 | 132.1 | 132.0 | 130.7 | 130.2 | 129.8 | 1.6 × 1010 | 1.3 × 104 | 3.0 |
| N8 (c) | 0.85 | 6 | 1658.4i | 70.6 | 71.4 | 71.7 | 65.8 | 64.1 | 62.3 | 6.1 × 10−2 | 1.6 × 10−5 | 1.2 × 10−7 |
| N8 (d) | 0.69 | 4 | 746.4i | 58.7 | 59.0 | 59.0 | 55.1 | 53.9 | 52.6 | 5.1 × 10−4 | 6.6 × 10−7 | 1.2 × 10−8 |
| N10 (e) | 0.56 | 10 | 566.7i | 47.8 | 47.9 | 47.6 | 46.1 | 45.5 | 45.0 | 4.3 × 10−6 | 1.8 × 10−8 | 6.9 × 10−10 |
| Crystallography Data | p (g/cm3) | Q (cal/g) | D (m/s) | Γ | P (Kbar) | h50% (cm) | |
|---|---|---|---|---|---|---|---|
| N4 | a = 5.3 Å, b = c = 4.6 Å α = 70°, β = γ = 55° | 1.23 | 2679.3 | 7550 | 3.1 | 170.4 | 28.7 |
| N6 | a = 5.7 Å, b = 4.8 Å, c = 6.0 Å α = 67.5°, β = 50.6°, γ = 54.4° | 1.36 | 3219.1 | 8310 | 3.2 | 220.9 | 28.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katin, K.P.; Merinov, V.B.; Kochaev, A.I.; Kaya, S.; Maslov, M.M. All-Nitrogen Cages and Molecular Crystals: Topological Rules, Stability, and Pyrolysis Paths. Computation 2020, 8, 91. https://doi.org/10.3390/computation8040091
Katin KP, Merinov VB, Kochaev AI, Kaya S, Maslov MM. All-Nitrogen Cages and Molecular Crystals: Topological Rules, Stability, and Pyrolysis Paths. Computation. 2020; 8(4):91. https://doi.org/10.3390/computation8040091
Chicago/Turabian StyleKatin, Konstantin P., Valeriy B. Merinov, Alexey I. Kochaev, Savas Kaya, and Mikhail M. Maslov. 2020. "All-Nitrogen Cages and Molecular Crystals: Topological Rules, Stability, and Pyrolysis Paths" Computation 8, no. 4: 91. https://doi.org/10.3390/computation8040091
APA StyleKatin, K. P., Merinov, V. B., Kochaev, A. I., Kaya, S., & Maslov, M. M. (2020). All-Nitrogen Cages and Molecular Crystals: Topological Rules, Stability, and Pyrolysis Paths. Computation, 8(4), 91. https://doi.org/10.3390/computation8040091