Combined Heat and Power Dynamic Economic Emissions Dispatch with Valve Point Effects and Incentive Based Demand Response Programs
Abstract
1. Introduction
2. Combined Heat and Power Dynamic Economic Emission Dispatch Model
2.1. Thermal Units
- , and are the positive fuel cost coefficients of generator i respectively;
- and are the fuel cost coefficients representing valve point effects of generator i, respectively;
- represents the power generated from thermal unit i at time t;
- represents the minimum capacity of thermal unit i;
- represents the fuel cost of producing .
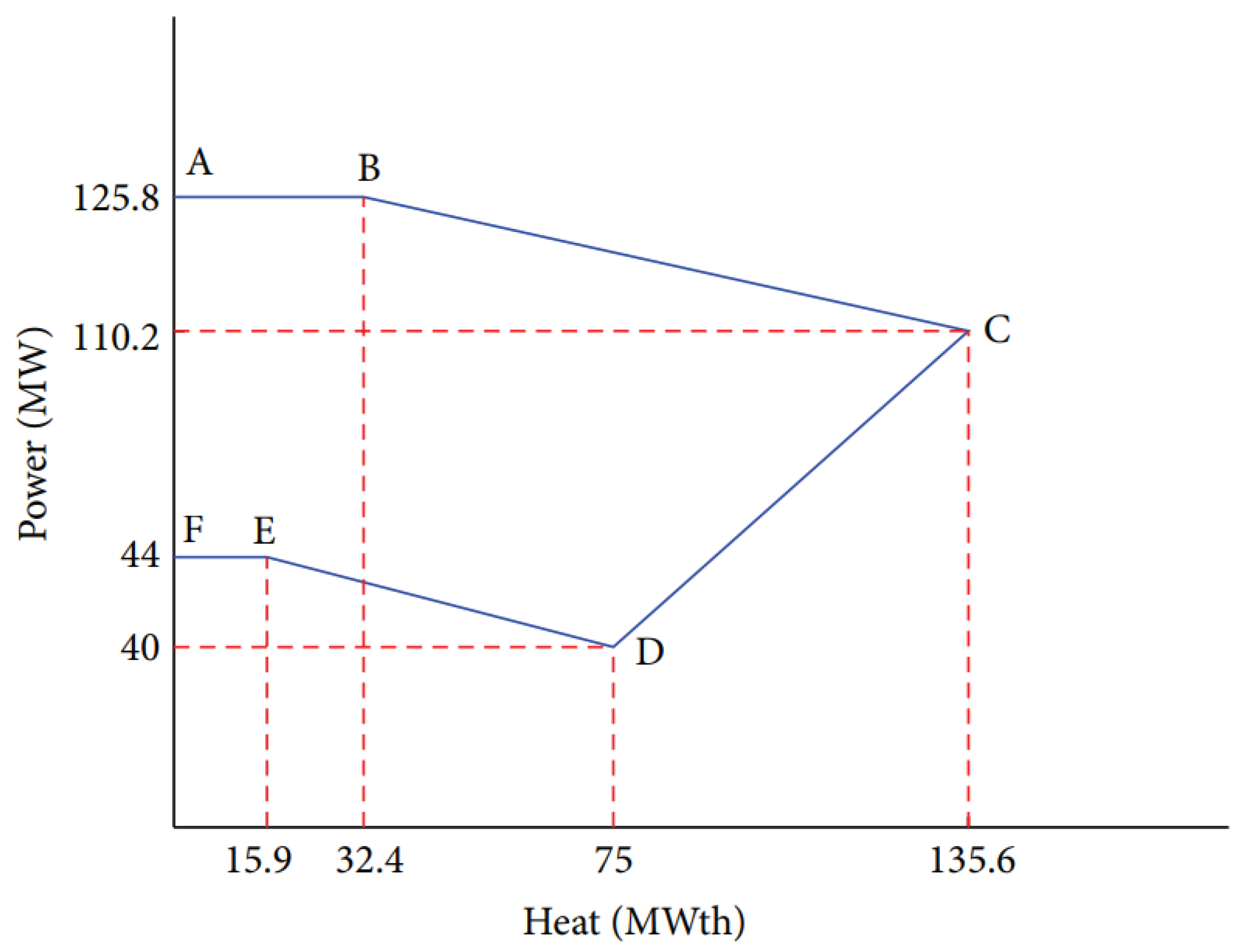
2.2. CHP Units
- , , , and are the fuel cost coefficients of CHP generator l respectively;
- is the fuel cost for CHP generator l to produce heat and power .
2.3. Heat Units
2.4. Objective Functions
2.5. Constraints
- is the power generated from thermal generator i at time t;
- is the power generated from CHP generator k at time t;
- is the heat produced from CHP generator k at time t;
- is the heat produced from heat generator l at time t;
- is the total system power demand at time t;
- is the total system heat demand at time t;
- is the total system losses at time t;
- and are the minimum and maximum power capacity of thermal generator i respectively;
- and are the minimum and maximum heat capacities of generator l respectively;
- and are the minimum and maximum power capacities of CHP generator k, respectively. Both parameters are functions of the heat produced .
- and are the minimum and maximum heat capacities of CHP generator k, respectively. Both parameters are functions of the power produced .
- and are the maximum ramp down and up rates of thermal generator i, respectively;
- and are the maximum ramp down and up rates of CHP generator k, respectively;
- is the th element of the loss coefficient square matrix of size ;
- Constraint (9) is termed the “power balance constraint”. Its role is to compel the total output power from both thermal and CHP units at each scheduling interval to satisfy the load demand and transmission line losses. Transmission line losses are determined by the B-coefficient method [1,2] and is represented mathematically in (17). is the th element of the loss coefficient square matrix B of size . This method has been used in [25,26,27].
- Constraint (10) is termed the “heat balance constraint” and its role is to compel the heat output from both CHP and heat-only units to match heat demand.
- The third constraint is the thermal generation limits constraint (11). It compels the output power from thermal generators to not exceed allowed limits.
- The fourth constraint (12) limits power produced from CHP units within allowable units.
- The fifth constraint (13) limits heat produced from CHP units within allowable limits.
- Constraint (14) ensures that the heat produced from heat only units are within allowable limits.
- Constraint (15) is the “generator ramp rate limits constraint” for thermal generators and compels the thermal generators output power for consecutive scheduling intervals to be within allowable ramp rate limits.
3. Incentive Based Demand Response Model
- is the “customer type”, normalized in .
- x is the amount of power curbed by electric consumer/customer.
- is the cost of reducing x MW by customer of type .
- is the “value of power interruptibility” or LMP.
Customer Cost Function
- Quadratic function:
- term sorts customers by way of .
- Marginal cost decreases with an increase in : Customer (), who is the keenest customer, will therefore have the lowest marginal cost and the largest marginal benefit. Customer (), who is the least keen customer, will have the largest marginal cost and lowest marginal benefit:
- .
- Non-negative marginal cost.
- The marginal cost function is an increasing convex cost function.
- When no power is curtailed, then the customer cost should be zero ().
- Constraint (27) is the “individual rationality constraint” and compels the customer benefit to be greater or at least zero.
- Constraint (28) is the “incentive compatibility constraint” and compels customers to be compensated commensurate to the load they curtail.
- The first constraint (30) makes sure that each customer’s daily incentive is greater than their interruption cost.
- The second constraint (31) makes sure that each customer’s benefit is commensurate with their power curtailment.
- The third constraint (32) compels the total monetary value of incentives paid by the electric utility to be within its budgeted amount.
- The fourth constraint (33) compels the total daily power curbed by each customer to be within its allowable daily limits.
4. Combined Heat and Power Dynamic Economic Emissions Dispatch with Incentive Based Demand Response Model
5. Numerical Simulations, Results, and Discussion
5.1. Numerical Simulations
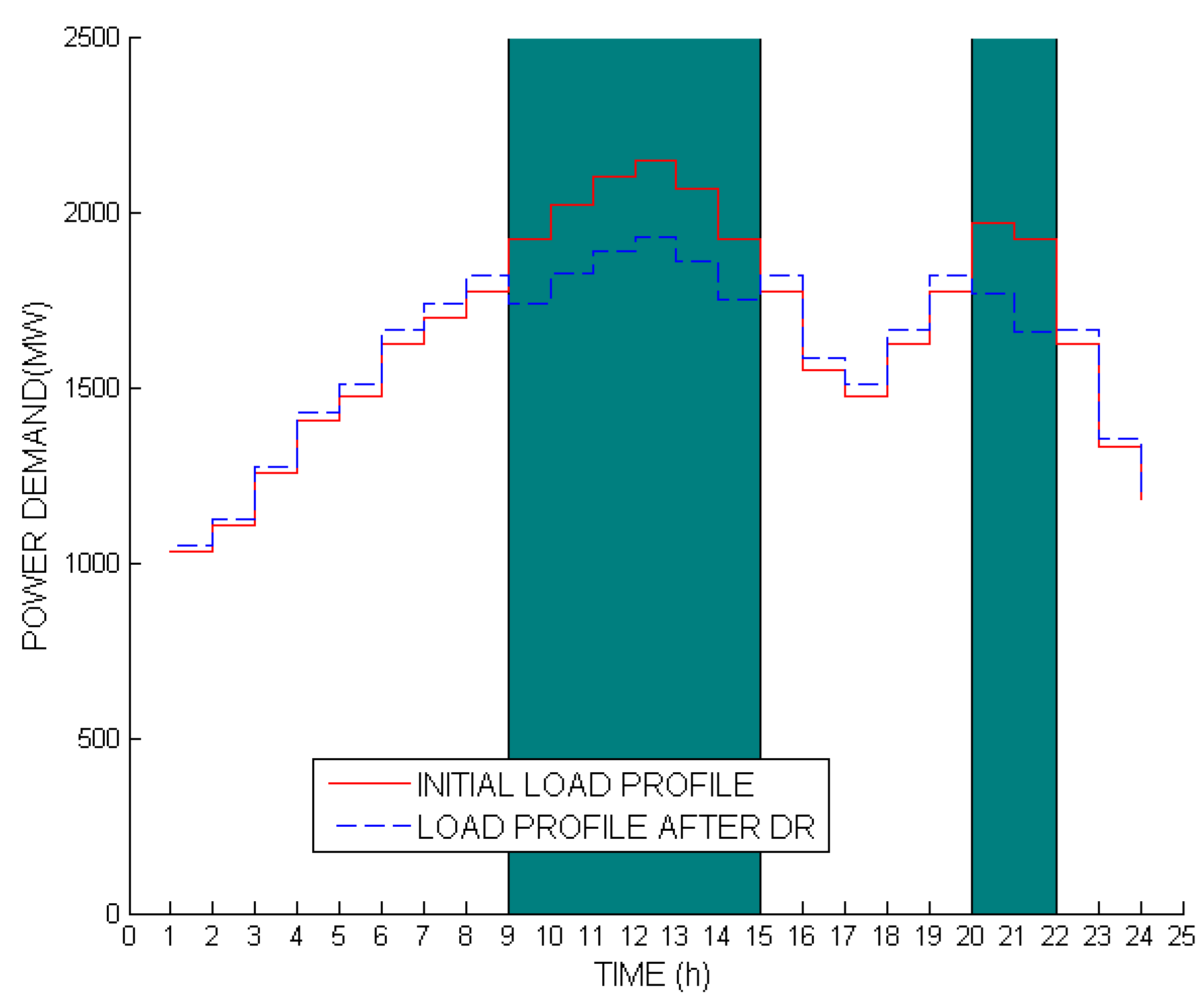
- CHPDEED-IBDR with residential load.
- CHPDEED-IBDR with residential load with restrictions on DR operating hours.
- CHPDEED-IBDR with commercial load.
- CHPDEED-IBDR with commercial load with restrictions on DR operating hours.
5.2. Results and Discussion
6. Conclusions
Funding
Conflicts of Interest
Appendix A
| Hour | Loss | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 150 | 135 | 109.7489 | 89.35082 | 96.82729 | 112.9019 | 36.88607 | 27.59422 | 233.6838 | 39.99988 | 74.90344 | 74.99973 | 240.0968 | 13.09718 |
| 2 | 150 | 136.4462 | 128.1774 | 110.1023 | 110 | 116.1668 | 50 | 29.60287 | 234.4454 | 39.99988 | 70.61991 | 74.99973 | 254.3804 | 15.08474 |
| 3 | 150 | 145.2974 | 137.6983 | 160.1023 | 160 | 118.0521 | 80 | 30.70556 | 234.3518 | 39.99988 | 71.14624 | 74.99973 | 263.854 | 19.844 |
| 4 | 159.1707 | 163.5378 | 182.2429 | 210.1023 | 160 | 130 | 80 | 35.19833 | 236.7834 | 39.99988 | 57.46823 | 74.99973 | 287.532 | 25.11797 |
| 5 | 160.2146 | 164.2684 | 251.412 | 215.2568 | 160 | 130 | 80 | 35.45878 | 234.8311 | 39.99988 | 68.45014 | 74.99973 | 296.5501 | 28.31833 |
| 6 | 169.172 | 171.4428 | 310.4962 | 240.9695 | 160 | 130 | 80 | 55 | 235.5495 | 39.99988 | 64.40885 | 74.99973 | 310.5914 | 33.99743 |
| 7 | 172.0027 | 173.9966 | 317.4051 | 290.9695 | 160 | 130 | 80 | 55 | 236.2106 | 39.99988 | 60.69033 | 74.99973 | 314.3099 | 37.06452 |
| 8 | 181.7142 | 183.6094 | 337.8782 | 300 | 160 | 130 | 80 | 55 | 238.2035 | 39.99988 | 49.48041 | 74.99973 | 330.5199 | 39.74278 |
| 9 | 204.0737 | 241.4617 | 340 | 300 | 160 | 130 | 80 | 55 | 243.7653 | 39.99988 | 18.19526 | 74.99973 | 366.805 | 44.67131 |
| 10 | 206.7852 | 321.4617 | 340 | 300 | 160 | 130 | 80 | 55 | 244.4121 | 39.99988 | 14.557 | 74.99973 | 370.4433 | 50.06188 |
| 11 | 229.0042 | 340.7004 | 340 | 300 | 160 | 130 | 80 | 55 | 246.9001 | 39.99988 | 0.561893 | 74.99973 | 394.4384 | 52.89532 |
| 12 | 305.7668 | 338.6892 | 340 | 300 | 160 | 130 | 80 | 55 | 245.2347 | 39.99988 | 9.929787 | 74.99973 | 395.0705 | 58.09444 |
| 13 | 225.7667 | 332.4944 | 340 | 300 | 160 | 130 | 80 | 55 | 246.2441 | 39.99988 | 4.251684 | 74.99973 | 390.7486 | 52.08944 |
| 14 | 199.4458 | 252.4944 | 340 | 300 | 160 | 130 | 80 | 55 | 242.5867 | 39.99988 | 24.82495 | 74.99973 | 360.1753 | 45.05088 |
| 15 | 181.1145 | 182.9797 | 336.7133 | 300 | 160 | 130 | 80 | 55 | 238.5704 | 39.99988 | 47.41671 | 74.99973 | 327.5836 | 39.61549 |
| 16 | 159.7222 | 163.9207 | 260.8003 | 250 | 160 | 130 | 80 | 35.33374 | 233.6861 | 39.99988 | 74.89069 | 74.99973 | 300.1096 | 30.18157 |
| 17 | 160.5475 | 164.5066 | 209.708 | 215.5181 | 160 | 130 | 80 | 35.5456 | 237.0129 | 39.99988 | 56.17747 | 74.99973 | 288.8228 | 26.58233 |
| 18 | 164.7643 | 167.7247 | 289.708 | 250 | 160 | 130 | 80 | 55 | 236.2032 | 39.99988 | 60.73213 | 74.99973 | 299.2681 | 32.95242 |
| 19 | 180.05 | 182.5306 | 334.6189 | 300 | 160 | 130 | 80 | 55 | 238.8119 | 39.99988 | 46.05784 | 74.99973 | 323.9424 | 39.41853 |
| 20 | 210.148 | 262.5306 | 340 | 300 | 160 | 130 | 80 | 55 | 246.2231 | 39.99988 | 4.370017 | 74.99973 | 370.6303 | 46.40771 |
| 21 | 173.926 | 182.5306 | 321.7879 | 300 | 160 | 130 | 80 | 55 | 237.2134 | 39.99988 | 55.04968 | 74.99973 | 314.9506 | 38.34489 |
| 22 | 174.3208 | 176.1754 | 251.7905 | 250 | 160 | 130 | 80 | 55 | 238.3747 | 39.99988 | 48.51707 | 74.99973 | 311.4832 | 32.07618 |
| 23 | 150 | 144.5724 | 171.7905 | 200 | 160 | 117.8513 | 80 | 30.59099 | 235.3151 | 39.99988 | 65.72751 | 74.99973 | 259.2728 | 22.45059 |
| 24 | 150 | 138.6916 | 130.085 | 150 | 110 | 116.5344 | 80 | 29.82219 | 234.6404 | 39.99988 | 69.52269 | 74.99973 | 255.4776 | 17.36916 |
| Hour | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 6.244155 | 10.86018 | 0 | 0 | 0 | 0 | 0 | 65.34662 | 179.6396 |
| 2 | 0 | 0 | 0 | 0 | 0 | 7.819165 | 12.32473 | 0 | 0 | 0 | 0 | 0 | 98.79992 | 231.3574 |
| 3 | 0 | 0 | 0 | 0 | 0 | 8.565755 | 13.0709 | 0 | 0 | 0 | 0 | 0 | 117.046 | 260.219 |
| 4 | 0 | 0 | 0 | 1.115466 | 3.075355 | 12.91314 | 16.97867 | 0 | 0 | 0 | 9.21682 | 23.83082 | 253.8093 | 439.0722 |
| 5 | 0.008338 | 0 | 0.440804 | 1.84011 | 3.797803 | 13.37419 | 17.41559 | 0.097179 | 0 | 3.902188 | 16.42098 | 31.84187 | 271.3681 | 461.9606 |
| 6 | 3.059928 | 3.919222 | 5.67241 | 8.031704 | 10.19235 | 17.45501 | 21.03695 | 52.91132 | 60.36577 | 82.23481 | 117.047 | 142.771 | 452.3256 | 674.0527 |
| 7 | 4.603666 | 5.544515 | 7.963648 | 10.67522 | 12.96446 | 19.22408 | 22.50458 | 92.7315 | 97.81712 | 135.1397 | 181.3194 | 213.2062 | 545.0333 | 771.3831 |
| 8 | 6.967306 | 8.76888 | 12.12143 | 15.56859 | 18.06104 | 22.47658 | 25.37369 | 170.759 | 193.6635 | 260.0753 | 333.9428 | 377.9704 | 737.9854 | 980.6088 |
| 9 | 13.02001 | 16.87848 | 22.52218 | 27.85431 | 30.80779 | 30.61119 | 32.67679 | 464.6573 | 561.3841 | 735.985 | 909.7012 | 990.0659 | 1348.209 | 1626.324 |
| 10 | 15.01676 | 19.62672 | 25.66872 | 31.64148 | 34.59993 | 33.03122 | 34.8182 | 591.2993 | 727.1192 | 925.9565 | 1142.722 | 1227.318 | 1564.948 | 1846.465 |
| 11 | 18.96843 | 24.85769 | 32.59274 | 39.79202 | 43.06123 | 38.43098 | 39.5876 | 885.3454 | 1100.094 | 1419.23 | 1732.992 | 1847.867 | 2106.736 | 2386.969 |
| 12 | 16.66543 | 21.80212 | 28.75432 | 35.24329 | 38.42017 | 35.46919 | 37.04936 | 706.9649 | 873.0689 | 1132.998 | 1388.62 | 1491.901 | 1799.613 | 2090.692 |
| 13 | 16.84881 | 21.93227 | 28.93649 | 35.45401 | 38.629 | 35.60246 | 37.18125 | 720.4509 | 882.2137 | 1145.864 | 1403.739 | 1507.104 | 1812.912 | 2105.602 |
| 14 | 12.66507 | 16.52778 | 21.66313 | 26.9517 | 29.68029 | 29.89165 | 32.14457 | 443.6879 | 541.7322 | 687.8329 | 858.0268 | 924.4028 | 1286.88 | 1573.779 |
| 15 | 7.200182 | 8.968488 | 12.46018 | 15.96447 | 18.4277 | 22.71057 | 25.50621 | 179.5634 | 200.5388 | 271.8978 | 348.2009 | 391.5854 | 752.9909 | 990.8783 |
| 16 | 3.387038 | 3.895056 | 6.012794 | 8.335103 | 10.52673 | 17.6684 | 20.89348 | 60.61396 | 59.86385 | 89.37781 | 123.7759 | 150.5502 | 463.0507 | 664.8904 |
| 17 | 3.56426 | 4.282629 | 6.523734 | 8.934618 | 11.14874 | 18.06535 | 21.22434 | 64.95217 | 68.10778 | 100.5693 | 137.5658 | 165.5443 | 483.3356 | 686.1147 |
| 18 | 5.078838 | 5.943857 | 8.697197 | 11.50494 | 13.81062 | 19.76408 | 22.75276 | 106.7603 | 108.1332 | 154.4716 | 204.122 | 237.3986 | 575.05 | 788.4906 |
| 19 | 7.429757 | 9.326211 | 12.98489 | 16.58028 | 19.0911 | 23.13393 | 25.86096 | 188.4392 | 213.1349 | 290.6993 | 370.9479 | 416.8202 | 780.5241 | 1018.633 |
| 20 | 14.86784 | 19.24895 | 25.82097 | 31.70823 | 34.85042 | 33.19108 | 34.8186 | 581.3459 | 703.1033 | 935.6907 | 1147.064 | 1243.88 | 1579.832 | 1846.507 |
| 21 | 24.0194 | 30.31808 | 39.82173 | 48.17577 | 51.77917 | 43.99452 | 43.77839 | 1345.179 | 1569.873 | 2044.624 | 2466.627 | 2618.944 | 2749.008 | 2919.094 |
| 22 | 6.628941 | 8.159066 | 11.34263 | 14.6287 | 17.07609 | 21.84801 | 24.73148 | 158.3233 | 173.3393 | 233.834 | 301.2376 | 342.5671 | 698.4232 | 931.5982 |
| 23 | 0 | 0 | 0 | 0 | 0 | 10.03198 | 14.29846 | 0 | 0 | 0 | 0 | 0 | 157.3503 | 311.3917 |
| 24 | 0 | 0 | 0 | 0 | 0 | 8.48332 | 13.11226 | 0 | 0 | 0 | 0 | 0 | 114.9559 | 261.8686 |
| Hour | Loss | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 150 | 135 | 116.9008 | 92.50541 | 100.4869 | 114.1034 | 37.84465 | 28.34338 | 234.3704 | 39.99988 | 71.04158 | 74.99973 | 243.9587 | 13.55487 |
| 2 | 150 | 141.0142 | 132.4188 | 119.5844 | 110.7193 | 116.9911 | 50 | 30.09195 | 234.8788 | 39.99988 | 68.18154 | 74.99973 | 256.8187 | 15.6984 |
| 3 | 150 | 149.3548 | 143.9307 | 169.5844 | 160 | 119.355 | 80 | 31.42898 | 234.9691 | 39.99988 | 67.67405 | 74.99973 | 267.3262 | 20.62276 |
| 4 | 160.8465 | 164.7226 | 189.1882 | 215.7564 | 160 | 130 | 80 | 55 | 237.0645 | 39.99988 | 55.88721 | 74.99973 | 289.1131 | 26.57806 |
| 5 | 159.759 | 163.9465 | 259.5701 | 226.9737 | 160 | 130 | 80 | 55 | 234.7547 | 39.99988 | 68.87959 | 74.99973 | 296.1207 | 30.00393 |
| 6 | 177.455 | 179.2389 | 329.3582 | 276.9737 | 160 | 130 | 80 | 55 | 237.5875 | 39.99988 | 52.94527 | 74.99973 | 322.055 | 37.61319 |
| 7 | 195.7558 | 200.2882 | 340 | 300 | 160 | 130 | 80 | 55 | 242.6572 | 39.99988 | 24.42833 | 74.99973 | 350.5719 | 41.70109 |
| 8 | 195.2703 | 280.2882 | 340 | 300 | 160 | 130 | 80 | 55 | 241.9928 | 39.99988 | 28.16566 | 74.99973 | 351.8346 | 46.55112 |
| 9 | 193.99 | 204.3575 | 340 | 300 | 160 | 130 | 80 | 55 | 241.1081 | 39.99988 | 33.14173 | 74.99973 | 351.8585 | 41.80378 |
| 10 | 198.9531 | 284.3575 | 340 | 300 | 160 | 130 | 80 | 55 | 242.4565 | 39.99988 | 25.55698 | 74.99973 | 359.4433 | 47.05042 |
| 11 | 212.4203 | 332.4949 | 340 | 300 | 160 | 130 | 80 | 55 | 244.5663 | 39.99988 | 13.68941 | 74.99973 | 381.3109 | 51.19031 |
| 12 | 241.5722 | 342.0758 | 340 | 300 | 160 | 130 | 80 | 55 | 246.26 | 39.99988 | 4.162793 | 74.99973 | 400.8375 | 53.82275 |
| 13 | 215.1175 | 300.0821 | 340 | 300 | 160 | 130 | 80 | 55 | 245.0795 | 39.99988 | 10.80276 | 74.99973 | 384.1975 | 49.15255 |
| 14 | 187.5541 | 220.0821 | 340 | 300 | 160 | 130 | 80 | 55 | 239.3024 | 39.99988 | 43.29878 | 74.99973 | 341.7015 | 42.31181 |
| 15 | 214.4817 | 255.7835 | 340 | 300 | 160 | 130 | 80 | 55 | 247 | 39.99988 | 1.23E-07 | 74.99973 | 375.0003 | 46.26504 |
| 16 | 164.6975 | 175.7835 | 297.6536 | 250 | 160 | 130 | 80 | 55 | 234.596 | 39.99988 | 69.7724 | 74.99973 | 305.2279 | 33.73042 |
| 17 | 159.7152 | 163.9158 | 261.0814 | 223.3672 | 160 | 130 | 80 | 55 | 236.8726 | 39.99988 | 56.96685 | 74.99973 | 288.0334 | 29.95209 |
| 18 | 176.6302 | 183.9776 | 327.6358 | 273.3672 | 160 | 130 | 80 | 55 | 238.9655 | 39.99988 | 45.19396 | 74.99973 | 314.8063 | 37.57627 |
| 19 | 207.2303 | 263.9776 | 340 | 300 | 160 | 130 | 80 | 55 | 246.1086 | 39.99988 | 5.01441 | 74.99973 | 364.9859 | 46.31636 |
| 20 | 205.6656 | 215.0327 | 340 | 300 | 160 | 130 | 80 | 55 | 245.2119 | 39.99988 | 10.05784 | 74.99973 | 364.9424 | 43.20015 |
| 21 | 170.9809 | 173.0608 | 314.9828 | 300 | 160 | 130 | 80 | 55 | 236.4985 | 39.99988 | 59.0709 | 74.99973 | 310.9294 | 37.29164 |
| 22 | 190.4652 | 193.37 | 299.4772 | 274.3901 | 160 | 130 | 80 | 55 | 242.7791 | 39.99988 | 23.74276 | 74.99973 | 336.2575 | 37.48144 |
| 23 | 150 | 144.1026 | 219.4772 | 224.3901 | 114.168 | 117.726 | 80 | 30.51909 | 235.2527 | 39.99988 | 66.07878 | 74.99973 | 258.9215 | 23.63544 |
| 24 | 150 | 135 | 139.4772 | 180.5145 | 101.0132 | 114.2708 | 80 | 28.44703 | 233.4024 | 39.99988 | 76.48669 | 74.99973 | 248.5136 | 18.12498 |
| Hour | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 19.64781 | 25.02451 | 26.9937 | 29.52427 | 34.03768 | 41.66656 | 44.4537 | 941.7097 | 1109.822 | 1113.23 | 1256.117 | 1535.217 | 1885.894 | 1962.057 |
| 10 | 21.30725 | 27.29367 | 28.83105 | 31.58829 | 36.70859 | 44.86648 | 47.68799 | 1086.552 | 1266.046 | 1299.519 | 1433.776 | 1761.476 | 2161.72 | 2240.445 |
| 11 | 23.5553 | 30.26581 | 31.54303 | 34.66593 | 40.65654 | 49.5117 | 52.51058 | 1298.995 | 1515.427 | 1564.987 | 1720.486 | 2124.109 | 2595.377 | 2689.713 |
| 12 | 24.08571 | 30.99629 | 32.34531 | 35.45502 | 41.62935 | 50.65624 | 53.74706 | 1351.842 | 1593.497 | 1633.959 | 1798.201 | 2218.631 | 2708.273 | 2811.491 |
| 13 | 22.91612 | 29.35634 | 30.87044 | 33.81703 | 39.54495 | 48.18829 | 51.18037 | 1236.693 | 1451.49 | 1481.17 | 1638.796 | 2018.604 | 2467.818 | 2561.706 |
| 14 | 19.05823 | 24.31241 | 26.21511 | 28.58164 | 32.87127 | 40.35798 | 42.97663 | 892.698 | 1046.723 | 1057.695 | 1178.887 | 1441.237 | 1778.48 | 1841.04 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 21.76798 | 27.79986 | 29.50289 | 32.43051 | 37.75176 | 46.0293 | 49.00772 | 1128.571 | 1325.737 | 1343.011 | 1509.641 | 1854.024 | 2266.581 | 2359.324 |
| 21 | 27.6616 | 34.95112 | 35.31359 | 39.41571 | 46.79987 | 56.6735 | 59.95338 | 1735.239 | 1899.382 | 2032.912 | 2214.203 | 2755.289 | 3341.124 | 3463.357 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Hour | Loss | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 150 | 135 | 79.00656 | 78.37702 | 85.57975 | 108.9882 | 33.73286 | 25.13429 | 231.4204 | 39.99988 | 87.63524 | 74.99973 | 227.365 | 11.5044 |
| 2 | 150 | 137.5371 | 129.0615 | 111.6008 | 110 | 116.3365 | 50 | 29.70436 | 234.5357 | 39.99988 | 70.11144 | 74.99973 | 254.8888 | 15.1985 |
| 3 | 150 | 146.0397 | 138.7456 | 161.6008 | 160 | 118.2672 | 80 | 30.82744 | 234.4569 | 39.99988 | 70.55493 | 74.99973 | 264.4453 | 19.97249 |
| 4 | 160.1769 | 164.2416 | 186.1037 | 211.6008 | 160 | 130 | 80 | 35.44907 | 236.9498 | 39.99988 | 56.53238 | 74.99973 | 288.4679 | 25.4226 |
| 5 | 159.6808 | 163.8917 | 263.0963 | 214.8467 | 160 | 130 | 80 | 35.32342 | 234.7418 | 39.99988 | 68.95243 | 74.99973 | 296.0478 | 28.78274 |
| 6 | 170.4579 | 172.5879 | 313.714 | 250 | 160 | 130 | 80 | 55 | 235.8447 | 39.99988 | 62.74843 | 74.99973 | 312.2518 | 34.71576 |
| 7 | 173.18 | 175.0937 | 320.1129 | 300 | 160 | 130 | 80 | 55 | 236.4972 | 39.99988 | 59.07803 | 74.99973 | 315.9222 | 37.7962 |
| 8 | 184.0877 | 187.1201 | 340 | 300 | 160 | 130 | 80 | 55 | 238.8609 | 39.99988 | 45.78271 | 74.99973 | 334.2176 | 40.20465 |
| 9 | 200.8483 | 267.1201 | 340 | 300 | 160 | 130 | 80 | 55 | 242.9526 | 39.99988 | 22.76644 | 74.99973 | 362.2338 | 46.06511 |
| 10 | 221.9147 | 337.812 | 340 | 300 | 160 | 130 | 80 | 55 | 247 | 39.99988 | 1.04E-07 | 74.99973 | 385.0003 | 52.22524 |
| 11 | 301.9147 | 336.1576 | 340 | 300 | 160 | 130 | 80 | 55 | 245.5656 | 39.99988 | 8.068615 | 74.99973 | 386.9317 | 57.63266 |
| 12 | 321.5741 | 353.1975 | 340 | 300 | 160 | 130 | 80 | 55 | 247 | 39.99988 | 74.99973 | 405.0003 | 60.38091 | |
| 13 | 241.5741 | 335.9406 | 340 | 300 | 160 | 130 | 80 | 55 | 245.5044 | 39.99988 | 8.412973 | 74.99973 | 386.5873 | 53.37156 |
| 14 | 216.6362 | 335.3788 | 340 | 300 | 160 | 130 | 80 | 55 | 246.4095 | 39.99988 | 3.321337 | 74.99973 | 381.6789 | 51.69873 |
| 15 | 212.3928 | 302.7366 | 340 | 300 | 160 | 130 | 80 | 55 | 246.6859 | 39.99988 | 1.766713 | 74.99973 | 373.2336 | 49.18659 |
| 16 | 190.5178 | 222.7366 | 340 | 300 | 160 | 130 | 80 | 55 | 241.2001 | 39.99988 | 32.62473 | 74.99973 | 342.3755 | 42.67793 |
| 17 | 186.3176 | 188.6042 | 340 | 300 | 160 | 130 | 80 | 55 | 243.2045 | 39.99988 | 21.34966 | 74.99973 | 323.6506 | 40.49445 |
| 18 | 182.9296 | 184.9002 | 340 | 300 | 160 | 130 | 80 | 55 | 240.664 | 39.99988 | 35.64024 | 74.99973 | 324.36 | 40.04607 |
| 19 | 182.2847 | 184.2128 | 338.9765 | 300 | 160 | 130 | 80 | 55 | 239.4231 | 39.99988 | 42.62013 | 74.99973 | 327.3801 | 39.89166 |
| 20 | 178.0216 | 179.8066 | 320.6654 | 266.5937 | 160 | 130 | 80 | 55 | 237.7371 | 39.99988 | 52.10383 | 74.99973 | 322.8964 | 36.69988 |
| 21 | 153.1085 | 159.8315 | 240.6654 | 216.5937 | 160 | 125.1189 | 80 | 33.99694 | 233.2824 | 39.99988 | 77.16154 | 74.99973 | 292.8387 | 27.06824 |
| 22 | 177.0002 | 178.7861 | 268.9207 | 235.4927 | 160 | 130 | 80 | 55 | 239.062 | 39.99988 | 44.65116 | 74.99973 | 315.3491 | 32.52098 |
| 23 | 150 | 145.2209 | 188.9207 | 185.4927 | 160 | 118.0305 | 80 | 30.69326 | 235.4037 | 39.99988 | 65.22925 | 74.99973 | 259.771 | 22.59729 |
| 24 | 150 | 143.8448 | 135.7636 | 135.4927 | 113.8196 | 117.6588 | 80 | 30.48042 | 235.219 | 39.99988 | 66.26803 | 74.99973 | 258.7322 | 17.46721 |
| Hour | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 1.073123 | 6.192283 | 0 | 0 | 0 | 0 | 0 | 3.583761 | 58.40231 |
| 2 | 0 | 0 | 0 | 0 | 0 | 5.858739 | 10.56377 | 0 | 0 | 0 | 0 | 0 | 58.20154 | 169.9676 |
| 3 | 0 | 0 | 0 | 0 | 0 | 6.666101 | 11.36882 | 0 | 0 | 0 | 0 | 0 | 73.63834 | 196.8608 |
| 4 | 0 | 0 | 0 | 0 | 0 | 11.33485 | 15.56594 | 0 | 0 | 0 | 0 | 0 | 198.1356 | 369.0446 |
| 5 | 0 | 0 | 0 | 0 | 0 | 11.48207 | 15.72002 | 0 | 0 | 0 | 0 | 0 | 203.0385 | 376.3871 |
| 6 | 1.498326 | 1.851964 | 3.043666 | 5.071154 | 7.344788 | 16.29847 | 20.00298 | 21.58699 | 23.2492 | 35.49193 | 60.20434 | 84.49082 | 396.3801 | 609.4213 |
| 7 | 3.118843 | 3.555658 | 5.446934 | 7.843507 | 10.25219 | 18.15388 | 21.54138 | 54.26944 | 52.98463 | 77.64082 | 112.9576 | 144.1485 | 487.9193 | 706.7658 |
| 8 | 5.980069 | 7.450068 | 10.46264 | 13.75015 | 16.40115 | 22.07798 | 25.01405 | 135.659 | 150.9979 | 205.7582 | 272.1243 | 319.2923 | 712.7711 | 953.0081 |
| 9 | 10.91159 | 14.05672 | 18.94639 | 23.76805 | 26.79498 | 28.71102 | 30.95551 | 346.9197 | 412.8734 | 546.034 | 687.6326 | 766.5508 | 1189.342 | 1459.501 |
| 10 | 16.48708 | 21.60569 | 28.20392 | 34.7857 | 38.08136 | 35.91366 | 37.42125 | 693.9683 | 859.3541 | 1094.561 | 1356.067 | 1467.398 | 1844.16 | 2132.873 |
| 11 | 16.6718 | 21.78401 | 28.68861 | 35.31904 | 38.63988 | 36.2701 | 37.62138 | 707.4316 | 871.7999 | 1128.375 | 1394.046 | 1507.899 | 1880.278 | 2155.747 |
| 12 | 20.18962 | 26.5321 | 34.81982 | 42.55983 | 46.23508 | 41.11713 | 42.15586 | 987.8827 | 1235.415 | 1599.88 | 1961.011 | 2113.111 | 2406.183 | 2706.727 |
| 13 | 15.02397 | 19.48629 | 25.83842 | 31.93347 | 35.19962 | 34.07462 | 35.7962 | 591.7834 | 718.146 | 936.8092 | 1161.775 | 1267.153 | 1663.374 | 1951.652 |
| 14 | 15.12656 | 19.83818 | 25.89607 | 32.10627 | 35.24453 | 34.10328 | 35.9594 | 598.6903 | 740.7343 | 940.5107 | 1173.123 | 1270.161 | 1666.12 | 1969.488 |
| 15 | 13.60996 | 17.55804 | 23.46007 | 29.11587 | 32.29696 | 32.22223 | 34.10834 | 500.5414 | 600.4281 | 790.3748 | 984.4168 | 1080.219 | 1490.698 | 1771.943 |
| 16 | 8.990607 | 11.40608 | 15.63705 | 19.85942 | 22.70867 | 26.10325 | 28.51859 | 253.9455 | 293.3571 | 394.8226 | 503.729 | 568.046 | 987.5143 | 1238.752 |
| 17 | 7.868401 | 10.06025 | 13.93513 | 17.84176 | 20.61529 | 24.76732 | 27.28008 | 205.9392 | 240.0861 | 326.2606 | 419.7064 | 477.7303 | 891.3801 | 1133.496 |
| 18 | 7.752972 | 9.516332 | 13.29525 | 17.08504 | 19.82501 | 24.26298 | 26.81484 | 201.2651 | 219.9729 | 302.0997 | 390.1094 | 445.6386 | 856.3666 | 1095.163 |
| 19 | 6.422297 | 7.97684 | 11.29545 | 14.72507 | 17.39198 | 22.7103 | 25.47274 | 150.9367 | 167.4649 | 232.2865 | 304.5167 | 353.7357 | 752.9734 | 988.2793 |
| 20 | 5.264273 | 6.37521 | 9.422704 | 12.45557 | 15.10451 | 21.2505 | 24.0028 | 112.4613 | 119.77 | 174.7337 | 231.7914 | 276.8264 | 661.8251 | 877.5104 |
| 21 | 19.43101 | 24.10031 | 31.91636 | 38.96182 | 42.44003 | 38.69524 | 38.92623 | 923.5381 | 1041.423 | 1366.485 | 1667.323 | 1798.025 | 2135.313 | 2307.879 |
| 22 | 5.652624 | 6.84626 | 9.691513 | 12.81829 | 15.42399 | 21.45438 | 24.37228 | 124.8122 | 133.0636 | 182.5294 | 242.7837 | 287.0151 | 674.2026 | 904.7335 |
| 23 | 0 | 0 | 0 | 0 | 0 | 8.191343 | 12.64431 | 0 | 0 | 0 | 0 | 0 | 107.7036 | 243.5112 |
| 24 | 0 | 0 | 0 | 0 | 0 | 7.207448 | 11.98094 | 0 | 0 | 0 | 0 | 0 | 84.995 | 218.6304 |
| Hour | Loss | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 150 | 135 | 83.07487 | 79.52765 | 86.65976 | 109.3681 | 34.03976 | 25.37179 | 231.6376 | 39.99988 | 86.41339 | 74.99973 | 228.5869 | 11.67944 |
| 2 | 150 | 141.0142 | 132.4188 | 119.5844 | 110.7193 | 116.9911 | 50 | 30.09195 | 234.8788 | 39.99988 | 68.18154 | 74.99973 | 256.8187 | 15.6984 |
| 3 | 150 | 149.3548 | 143.9307 | 169.5844 | 160 | 119.355 | 80 | 31.42898 | 234.9691 | 39.99988 | 67.67405 | 74.99973 | 267.3262 | 20.62276 |
| 4 | 160.8465 | 164.7226 | 189.1882 | 215.7564 | 160 | 130 | 80 | 55 | 237.0645 | 39.99988 | 55.88721 | 74.99973 | 289.1131 | 26.57806 |
| 5 | 159.759 | 163.9465 | 259.5701 | 226.9737 | 160 | 130 | 80 | 55 | 234.7547 | 39.99988 | 68.87959 | 74.99973 | 296.1207 | 30.00393 |
| 6 | 177.455 | 179.2389 | 329.3582 | 276.9737 | 160 | 130 | 80 | 55 | 237.5875 | 39.99988 | 52.94527 | 74.99973 | 322.055 | 37.61319 |
| 7 | 195.7558 | 200.2882 | 340 | 300 | 160 | 130 | 80 | 55 | 242.6572 | 39.99988 | 24.42833 | 74.99973 | 350.5719 | 41.70109 |
| 8 | 195.2703 | 280.2882 | 340 | 300 | 160 | 130 | 80 | 55 | 241.9928 | 39.99988 | 28.16566 | 74.99973 | 351.8346 | 46.55112 |
| 9 | 187.9204 | 212.5365 | 340 | 300 | 160 | 130 | 80 | 55 | 239.4057 | 39.99988 | 42.71801 | 74.99973 | 342.2823 | 41.89176 |
| 10 | 210.0774 | 292.5365 | 340 | 300 | 160 | 130 | 80 | 55 | 245.1455 | 39.99988 | 10.4315 | 74.99973 | 374.5688 | 48.33105 |
| 11 | 222.4176 | 338.4098 | 340 | 300 | 160 | 130 | 80 | 55 | 246.215 | 39.99988 | 4.415866 | 74.99973 | 390.5844 | 52.2861 |
| 12 | 293.477 | 344.755 | 340 | 300 | 160 | 130 | 80 | 55 | 247 | 39.99988 | 1.02E-07 | 74.99973 | 405.0003 | 57.67062 |
| 13 | 213.477 | 317.9663 | 340 | 300 | 160 | 130 | 80 | 55 | 241.4341 | 39.99988 | 31.30792 | 74.99973 | 363.6923 | 50.19526 |
| 14 | 197.631 | 310.6326 | 340 | 300 | 160 | 130 | 80 | 55 | 242.1036 | 39.99988 | 27.54251 | 74.99973 | 357.4578 | 48.70581 |
| 15 | 207.7126 | 230.6326 | 340 | 300 | 160 | 130 | 80 | 55 | 245.6873 | 39.99988 | 7.383949 | 74.99973 | 367.6163 | 44.26741 |
| 16 | 172.4266 | 197.4764 | 318.3897 | 300 | 160 | 130 | 80 | 55 | 236.3131 | 39.99988 | 60.11399 | 74.99973 | 314.8863 | 38.88871 |
| 17 | 223.7681 | 277.4764 | 340 | 300 | 160 | 130 | 80 | 55 | 247 | 39.99988 | 74.99973 | 345.0003 | 48.2444 | |
| 18 | 192.6148 | 298.6175 | 340 | 300 | 160 | 130 | 80 | 55 | 243.3818 | 39.99988 | 20.35225 | 74.99973 | 339.648 | 47.61405 |
| 19 | 195.3638 | 279.0518 | 340 | 300 | 160 | 130 | 80 | 55 | 243.081 | 39.99988 | 22.04437 | 74.99973 | 347.9559 | 46.49649 |
| 20 | 197.1243 | 201.7175 | 340 | 300 | 160 | 130 | 80 | 55 | 243.0295 | 39.99988 | 22.3343 | 74.99973 | 352.666 | 41.87116 |
| 21 | 177.3621 | 179.1462 | 329.1656 | 300 | 160 | 130 | 80 | 55 | 238.0944 | 39.99988 | 50.0942 | 74.99973 | 319.9061 | 38.7682 |
| 22 | 190.4652 | 193.37 | 299.4772 | 274.3901 | 160 | 130 | 80 | 55 | 242.7791 | 39.99988 | 23.74276 | 74.99973 | 336.2575 | 37.48144 |
| 23 | 150 | 144.1026 | 219.4772 | 224.3901 | 114.168 | 117.726 | 80 | 30.51909 | 235.2527 | 39.99988 | 66.07878 | 74.99973 | 258.9215 | 23.63544 |
| 24 | 150 | 135 | 139.4772 | 180.5145 | 101.0132 | 114.2708 | 80 | 28.44703 | 233.4024 | 39.99988 | 76.48669 | 74.99973 | 248.5136 | 18.12498 |
| Hour | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 19.64362 | 25.00925 | 26.92596 | 29.4655 | 34.04431 | 41.57898 | 44.36162 | 941.357 | 1104.259 | 1112.025 | 1251.231 | 1535.76 | 1878.607 | 1954.4 |
| 10 | 24.06603 | 30.98375 | 32.10609 | 35.22577 | 41.43728 | 50.36501 | 53.38783 | 1349.863 | 1570.013 | 1632.763 | 1775.446 | 2199.807 | 2679.319 | 2775.834 |
| 11 | 25.7766 | 33.23366 | 34.16567 | 37.58586 | 44.46961 | 53.92638 | 57.08604 | 1527.248 | 1777.904 | 1854.365 | 2016.636 | 2506.286 | 3044.005 | 3153.774 |
| 12 | 25.83785 | 33.33616 | 34.40607 | 37.74957 | 44.6422 | 54.12432 | 57.34256 | 1533.8 | 1803.012 | 1864.793 | 2033.935 | 2524.326 | 3064.954 | 3180.881 |
| 13 | 21.86693 | 27.93825 | 29.53163 | 32.3537 | 37.75891 | 45.98109 | 48.88736 | 1137.697 | 1328.322 | 1355.025 | 1502.641 | 1854.667 | 2262.185 | 2348.356 |
| 14 | 21.78599 | 27.96239 | 29.45748 | 32.17789 | 37.54741 | 45.79568 | 48.61187 | 1130.23 | 1321.659 | 1357.125 | 1486.68 | 1835.71 | 2245.315 | 2323.345 |
| 15 | 22.87339 | 29.26686 | 30.76873 | 33.72922 | 39.50779 | 48.04623 | 51.04278 | 1232.582 | 1441.941 | 1473.046 | 1630.46 | 2015.123 | 2454.315 | 2548.644 |
| 16 | 17.63471 | 22.26968 | 24.42338 | 26.75245 | 30.59249 | 37.49995 | 40.11034 | 779.6534 | 908.5317 | 906.1405 | 1036.007 | 1266.103 | 1554.746 | 1617.15 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
References
- Elaiw, A.M.; Xia, X.; Shehata, A.M. Combined Heat and Power Dynamic Economic Dispatch with Emission Limitations Using Hybrid DE-SQP Method. Abstr. Appl. Anal. 2013, 2013, 120849. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Xia, X.; Shehata, A.M. Hybrid DE-SQP Method for Solving Combined Heat and Power Dynamic Economic Dispatch Problem. Math. Probl. Eng. 2013, 2013, 982305. [Google Scholar] [CrossRef]
- Haghrah, A.; Nazari-Heris, M.; Mohammadi-ivatloo, B. Solving combined heat and power economic dispatch problem usingreal coded genetic algorithm with improved Muhlenbein mutation. Appl. Therm. Eng. 2016, 99, 465–475. [Google Scholar] [CrossRef]
- Narang, N.; Sharma, E.; Dhillon, J.S. Combined heat and power economic dispatch using integrated civilized swarm optimization and Powell’s pattern search method. Appl. Soft Comput. 2017, 52, 190–202. [Google Scholar] [CrossRef]
- Paul, C.; Roy, P.K.; Mukherjee, V. Chaotic whale optimization algorithm for optimal solution of combined heat and power economic dispatch problem incorporating wind. Renew. Energy Focus 2020, 35, 56–71. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mehdinejad, M.; Mohammadi-ivatloo, B.; Babamalek-Gharehpetian, G. Combined heat and power economic dispatch problem solution by implementation of whale optimization method. Neural Comput. Appl. 2019, 31, 421–436. [Google Scholar] [CrossRef]
- Basu, M. Squirrel search algorithm for multi-region combined heat and power economic dispatch incorporating renewable energy sources. Energy 2019, 182, 296–305. [Google Scholar] [CrossRef]
- Srivastava, A.; Das, D.K. A new Kho-Kho optimization Algorithm: An application to solve combined emission economic dispatch and combined heat and power economic dispatch problem. Eng. Appl. Artif. Intell. 2020, 94, 103763. [Google Scholar] [CrossRef]
- Sun, J.; Deng, J.; Li, Y. Indicator and crowding distance-based evolutionary algorithm for combined heat and power economic emission dispatch. Appl. Soft Comput. 2020, 90, 106158. [Google Scholar] [CrossRef]
- Nguyen, T.; Vo, D.N.; Dinh, B.H. Cuckoo search algorithm for combined heat and power economic dispatch. Int. J. Electr. Power Energy Syst. 2016, 81, 204–214. [Google Scholar] [CrossRef]
- Mehdinejad, M.; Mohammadi-ivatloo, B.; Dadashzadeh-Bonab, R. Energy production cost minimization in a combined heat and power generation systems using cuckoo optimization algorithm. Energy Effic. 2017, 10, 81–96. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Vo, D.N. An effective cuckoo search algorithm for large-scale combined heat and power economic dispatch problem. Neural Comput. Appl. 2018, 30, 3545–3564. [Google Scholar] [CrossRef]
- Ghorbani, N. Combined Heat and Power Economic Dispatch using Exchange Market Algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 58–66. [Google Scholar] [CrossRef]
- Beigvand, S.D.; Abdi, H.; la Scala, M. Combined heat and power economic dispatch problem using gravitational search algorithm. Electr. Power Syst. Res. 2016, 13, 160–172. [Google Scholar] [CrossRef]
- Basu, M. Group search optimization for combined heat and power economic dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 138–147. [Google Scholar] [CrossRef]
- Davoodi, E.; Zare, K.; Babaei, E. A GSO-based algorithm for combined heat and power dispatch problem with modified scrounger and ranger operators. Appl. Therm. Eng. 2017, 120, 36–48. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-ivatloo, B.; Babamalek-Gharehpetian, G. A comprehensive review of heuristic optimization algorithms for optimal combined heat and power dispatch from economic and environmental perspectives. Renew. Sustain. Energy Rev. 2018, 81, 2128–2143. [Google Scholar] [CrossRef]
- Gislason, G.K. Unit Commitment for Combined Heat and Power Production-Using Tabu Search. Master’s Thesis, Technical University of Denmark, Lynby, Denmark, 2003. [Google Scholar]
- Wu, C.; Jiang, P.; Sun, Y.; Zhang, C.; Gu, W. Economic dispatch with CHP and wind power using probabilistic sequence theory and hybrid heuristic algorithm. J. Renew. Sustain. Energy 2017, 9, 013303. [Google Scholar] [CrossRef]
- Yuan, R.; Ye, J.; Lei, J.; Li, T. Integrated Combined Heat and Power System Dispatch Considering Electrical and Thermal Energy Storage. Energies 2016, 9, 474. [Google Scholar] [CrossRef]
- Lin, X.; Li, P.; Ma, J.; Tian, Y.; Su, D. Dynamic optimal dispatch of combined heating and power microgrid based on leapfrog firefly algorithm. In Proceedings of the 12th IEEE International Conference on Networking, Sensing and Control (ICNSC), Taipei, Taiwan, 9–11 April 2015. [Google Scholar]
- Abarghooee, R.A.; Niknam, T.; Bina, M.A.; Zare, M. Coordination of combined heat and power-thermal- wind-photovoltaic units in economic load dispatch using chance-constrained and jointly distributed random variables methods. Energy 2015, 79, 50–67. [Google Scholar] [CrossRef]
- Niknam, T.; Abarghooee, R.A.; Roosta, A.; Amiri, B. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch. Energy 2012, 42, 530–545. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Agboola, O.P. Modelling and predicting electricity consumption using artificial neural networks. In Proceedings of the 11th International Conference on Environment and Electrical Engineering, EEEIC 2012, Venice, Italy, 18–25 May 2012. [Google Scholar]
- Nwulu, N.I.; Xia, X. A combined dynamic economic emission dispatch and time of use demand response mathematical modelling framework. J. Renew. Sustain. Energy 2015, 7, 043134. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Implementing a model predictive control strategy on the dynamic economic emission dispatch problem with game theory based demand response programs. Energy 2015, 91, 404–419. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Multi-objective dynamic economic emission dispatch of electric power generation integrated with game theory based demand response programs. Energy Convers. Manag. 2015, 89, 963–974. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Optimal dispatch for a microgrid incorporating renewables and demand response. Renew. Energy 2015, 89, 963–974. [Google Scholar] [CrossRef]
- Houwing, M.; Negenborn, R.R.; de Schutter, B. Demand Response With Micro-CHP Systems. Proc. IEEE 2011, 99, 200–213. [Google Scholar] [CrossRef]
- Pazouki, S.; Ardalan, S.; Haghifam, M.R. Demand Response Programs in Optimal Operation of Multi-Carrier Energy Networks. Indian J. Sci. Technol. 2015, 8, 1–7. [Google Scholar] [CrossRef]
- Alipour, M.; Zare, K.; Mohammadi-Ivatloo, B. Short-term scheduling of combined heat and power generation units in the presence of demand response programs. Energy 2014, 71, 289–301. [Google Scholar] [CrossRef]
- Alipour, M.; Zare, K.; Seyedi, H.; Jalali, M. Real-time price-based demand response model for combined heat and power systems. Energy 2019, 168, 1119–1127. [Google Scholar] [CrossRef]
- Majidi, M.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A. Optimal robust operation of combined heat and power systems with demand response programs. Appl. Therm. Eng. 2019, 149, 1359–1369. [Google Scholar] [CrossRef]
- Noreika, M.; Downes, K.; O’Leary, M.; Stitzer, J. CHP Implementation: Designing Combined Heat and Power Financial Incentives and Eligibility Requirements for Non-Residential Demand-Side Management Programs. Available online: https://www.aceee.org/files/proceedings/2013/data/papers/6_202.pdf (accessed on 23 November 2020).
- Gbadamosi, S.L.; Nwulu, N.I.; Sun, Y. Multi-objective optimisation for composite generation and transmission expansion planning considering offshore wind power and feed-in tariffs. IET Renew. Power Gener. 2018, 12, 1687–1697. [Google Scholar] [CrossRef]
- Bisschop, J.; Roelofs, M. AIMMS Language Reference, version 3.12; Paragon Decision Technology: Haarlem, The Netherlands, 2011. [Google Scholar]
- Singal, S.K.; Goel, V.; Singh, R.P. Rural electrification of a remote island by renewable energy sources. Renew. Energy 2007, 32, 2491–2501. [Google Scholar] [CrossRef]





| Thermal Units | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i = 1 | 786.7988 | 38.5397 | 0.1524 | 450 | 0.041 | 103.3908 | 2.4444 | 0.0312 | 0.5035 | 0.0207 | 150 | 470 | 80 |
| i = 2 | 451.3251 | 46.1591 | 0.1058 | 600 | 0.036 | 103.3908 | 2.4444 | 0.0312 | 0.5035 | 0.0207 | 135 | 470 | 80 |
| i = 3 | 1049.998 | 40.3965 | 0.028 | 320 | 0.028 | 300.391 | 4.0695 | 0.0509 | 0.4968 | 0.0202 | 73 | 340 | 80 |
| i = 4 | 1243.531 | 38.3055 | 0.0354 | 260 | 0.052 | 300.391 | 4.0695 | 0.0509 | 0.4968 | 0.0202 | 60 | 300 | 50 |
| i = 5 | 1356.659 | 38.2704 | 0.0179 | 310 | 0.048 | 320.0006 | 3.8132 | 0.0344 | 0.4972 | 0.02 | 57 | 160 | 50 |
| i = 6 | 1450.705 | 36.5104 | 0.0121 | 300 | 0.086 | 330.0056 | 3.9023 | 0.0465 | 0.5163 | 0.0214 | 20 | 130 | 30 |
| i = 7 | 1455.606 | 39.5804 | 0.109 | 270 | 0.098 | 350.0056 | 3.9524 | 0.0465 | 0.5475 | 0.0234 | 20 | 80 | 30 |
| i = 8 | 1469.403 | 40.5407 | 0.1295 | 380 | 0.094 | 360.0012 | 3.9864 | 0.047 | 0.5475 | 0.0234 | 10 | 55 | 30 |
| CHP Units | (MW/h) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| k = 1 | 2650 | 14.5 | 0.0345 | 4.2 | 0.03 | 0.031 | 0.00015 | 0.00015 | 70 |
| k = 2 | 1250 | 36 | 0.0435 | 0.6 | 0.027 | 0.011 | 0.00015 | 0.00015 | 50 |
| Heat Unit | (MW/h) | (MW/h) | |||||
|---|---|---|---|---|---|---|---|
| l = 1 | 950 | 2.0109 | 0.038 | 0.0008 | 0.001 | 0 | 2695.2 |
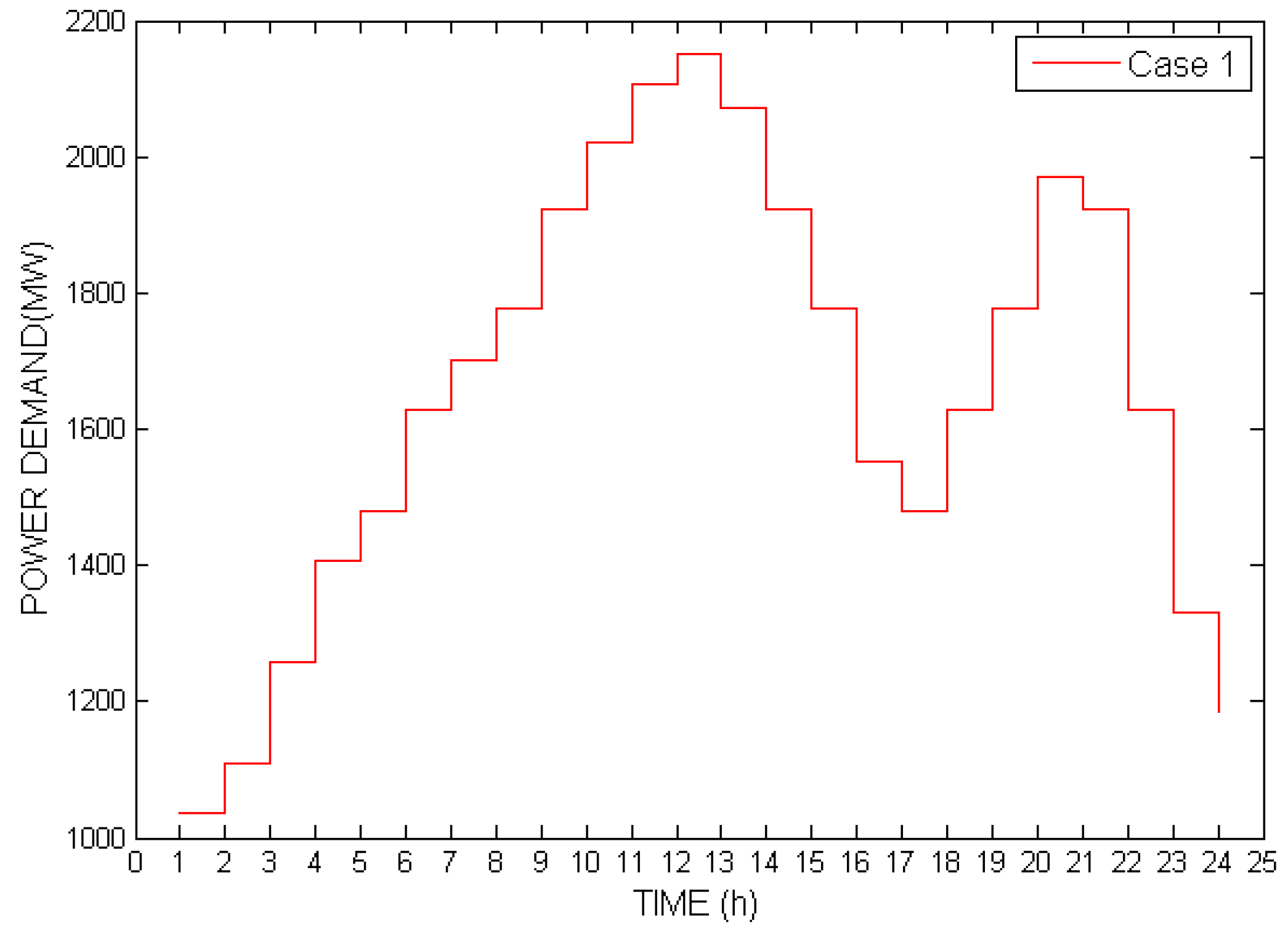
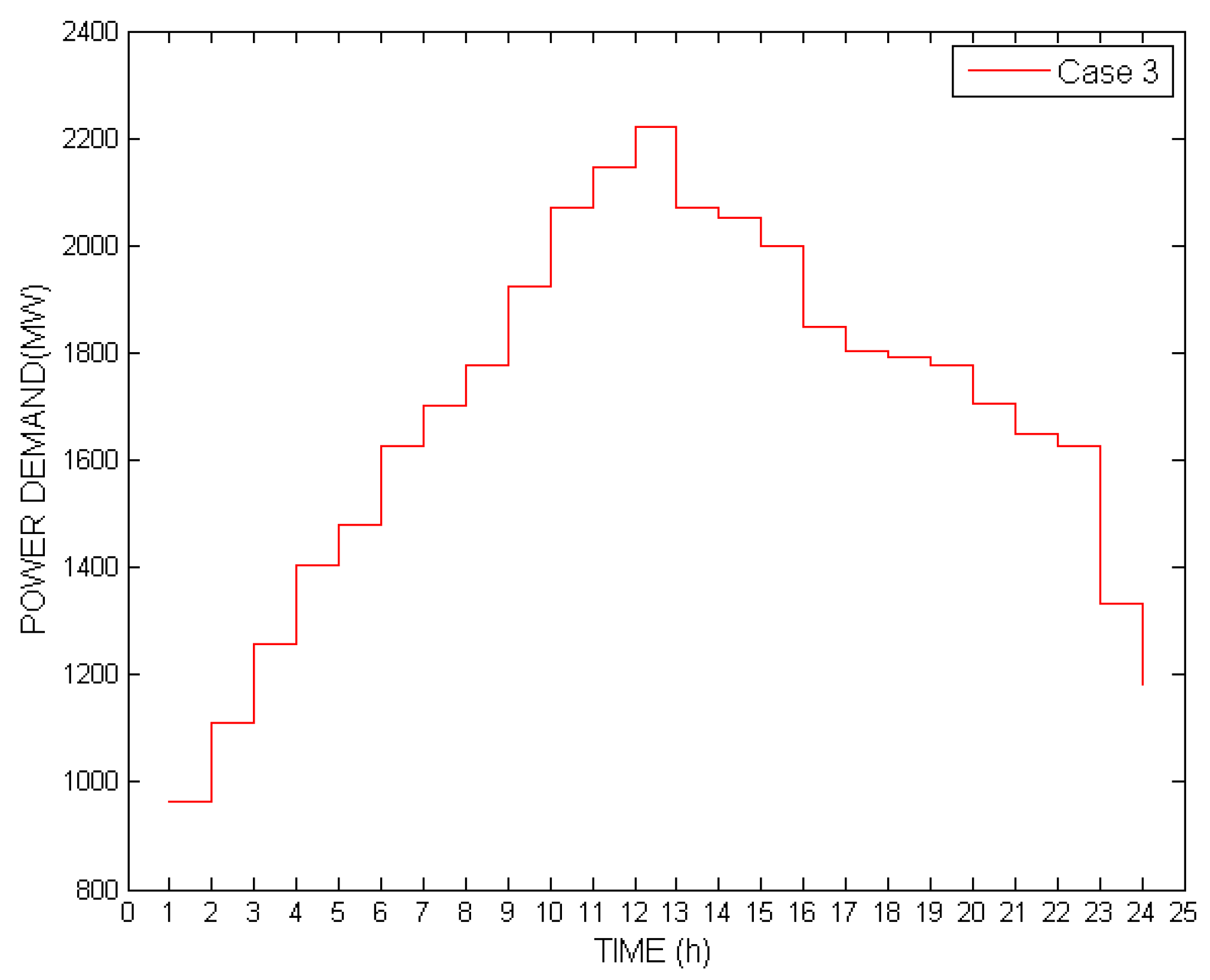
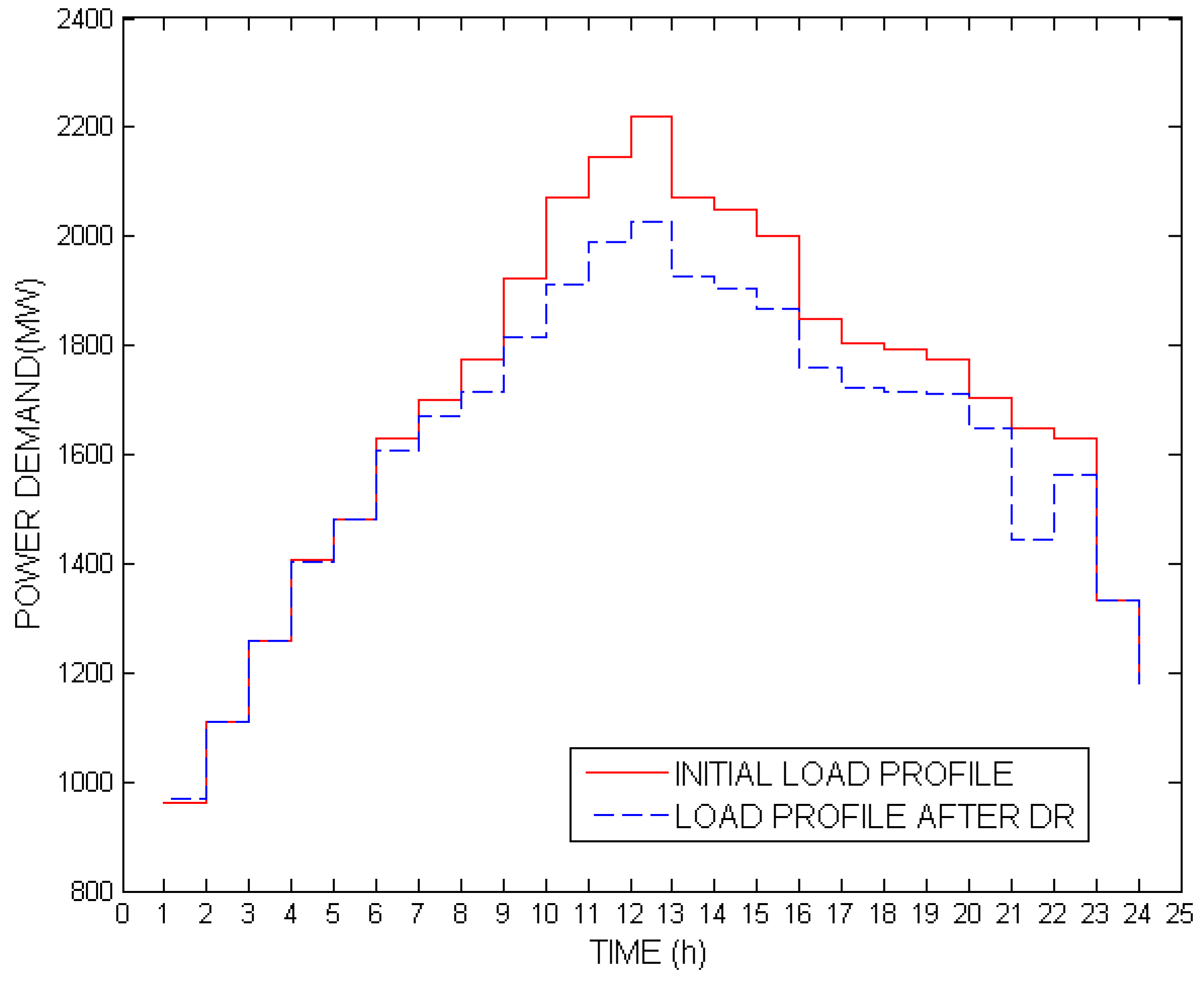
| Hour | Heat Demand (MWth) | Case 1 Demand (MW) | Case 3 Demand (MW) |
|---|---|---|---|
| 1 | 390 | 1036 | 963 |
| 2 | 400 | 1110 | 1110 |
| 3 | 410 | 1258 | 1258 |
| 4 | 420 | 1406 | 1406 |
| 5 | 440 | 1480 | 1480 |
| 6 | 450 | 1628 | 1628 |
| 7 | 450 | 1702 | 1702 |
| 8 | 455 | 1776 | 1776 |
| 9 | 460 | 1924 | 1924 |
| 10 | 460 | 2022 | 2072 |
| 11 | 470 | 2106 | 2146 |
| 12 | 480 | 2150 | 2220 |
| 13 | 470 | 2072 | 2072 |
| 14 | 460 | 1924 | 2050 |
| 15 | 450 | 1776 | 2000 |
| 16 | 450 | 1554 | 1850 |
| 17 | 420 | 1480 | 1805 |
| 18 | 435 | 1628 | 1792 |
| 19 | 445 | 1776 | 1776 |
| 20 | 450 | 1972 | 1705 |
| 21 | 445 | 1924 | 1650 |
| 22 | 435 | 1628 | 1628 |
| 23 | 400 | 1332 | 1332 |
| 24 | 400 | 1184 | 1184 |
| j | (MW/h) | |||
|---|---|---|---|---|
| 1 | 1.847 | 11.64 | 0 | 180 |
| 2 | 1.378 | 11.63 | 0.14 | 230 |
| 3 | 1.079 | 11.32 | 0.26 | 310 |
| 4 | 0.9124 | 11.5 | 0.37 | 390 |
| 5 | 0.8794 | 11.21 | 0.55 | 440 |
| 6 | 1.378 | 11.63 | 0.84 | 530 |
| 7 | 1.5231 | 11.5 | 1 | 600 |
| Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Fuel Cost ($) | 2,266,792 | 2,311,892 | 2,330,577 | 2,376,601 |
| Emissions (lb) | 458,955.4 | 475,320.5 | 478,319 | 494,630.5 |
| Total Energy Generated (MWh) | 38,008.53 | 38,712.67 | 38,732.62 | 39,439.46 |
| Total Heat (MWth) | 10,545 | 10,545 | 10,545 | 10,545 |
| Total Losses (MW) | 840.5291 | 871.2289 | 883.6219 | 914.9209 |
| Total Incentive ($) | 100,000 | 100,000 | 100,000 | 100,000 |
| Total Energy Saved (MWh) | 2680 | 2006.561 | 2680 | 2004.458 |
| Cost of Energy ($/MWh) | 62.27 | 62.30 | 62.75 | 62.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nwulu, N. Combined Heat and Power Dynamic Economic Emissions Dispatch with Valve Point Effects and Incentive Based Demand Response Programs. Computation 2020, 8, 101. https://doi.org/10.3390/computation8040101
Nwulu N. Combined Heat and Power Dynamic Economic Emissions Dispatch with Valve Point Effects and Incentive Based Demand Response Programs. Computation. 2020; 8(4):101. https://doi.org/10.3390/computation8040101
Chicago/Turabian StyleNwulu, Nnamdi. 2020. "Combined Heat and Power Dynamic Economic Emissions Dispatch with Valve Point Effects and Incentive Based Demand Response Programs" Computation 8, no. 4: 101. https://doi.org/10.3390/computation8040101
APA StyleNwulu, N. (2020). Combined Heat and Power Dynamic Economic Emissions Dispatch with Valve Point Effects and Incentive Based Demand Response Programs. Computation, 8(4), 101. https://doi.org/10.3390/computation8040101




