Simulation of Diffusion Bonding of Different Heat Resistant Nickel-Base Alloys
Abstract
1. Introduction
2. Experimental Results and Simulation Setup
2.1. Experimental Results
2.2. Order Parameters for Ternary Alloy
2.3. Vacancy Diffusion Model
2.4. Ternary Alloy Model and Simulation Setup
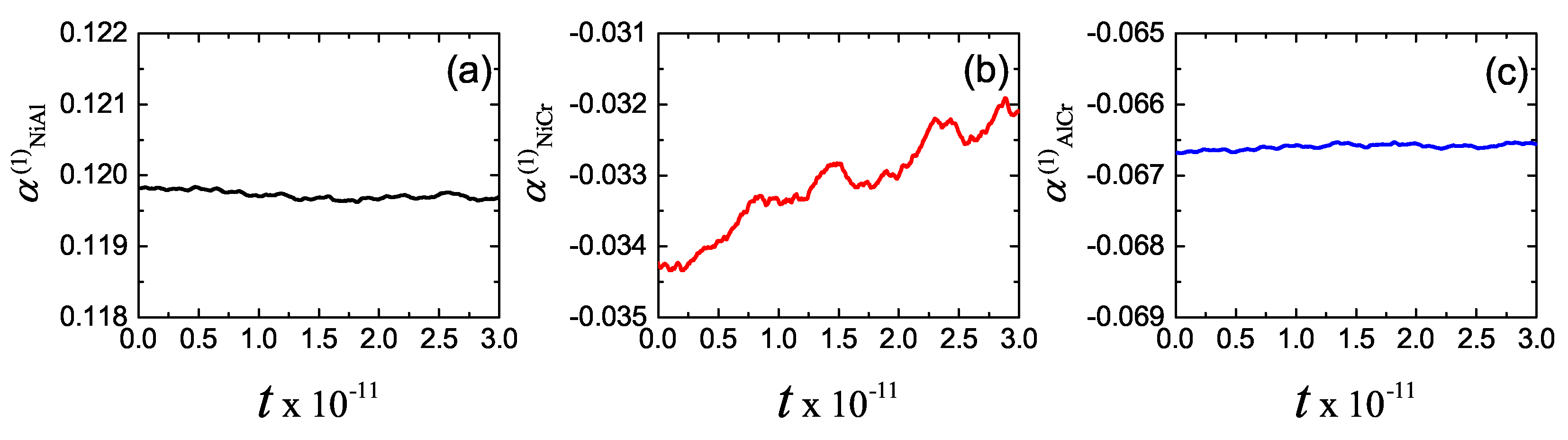
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mendez, P.F.; Eagar, T.W. Welding processes for aeronautics. Adv. Mater. Process. 2008, 159, 39–43. [Google Scholar]
- Tynchenko, V.S. Intellectualization of the technological processes of permanent joints formation at the rocket-space enterprises. IOP Conf. Ser. Mat. Sci. 2019, 537, 032062. [Google Scholar] [CrossRef]
- Jafarian, M.; Khodabandeh, A.; Manafi, S. Evaluation of diffusion welding of 6061 aluminum and AZ31 magnesium alloys without using an interlayer. Mater. Des. 2015, 65, 160–164. [Google Scholar] [CrossRef]
- Bemani, M.; Pouranvari, M. Microstructure and mechanical properties of dissimilar nickel-based superalloys resistance spot welds. Mater. Sci. Eng. A 2020, 773, 138825. [Google Scholar] [CrossRef]
- Avettand-Fènoël, M.-N.; Naji, K.; Pouligny, P. Brazing vs. diffusion welding of graded Fe based matrix composite and yttria stabilized zirconia. J. Manuf. Process. 2019, 45, 557–570. [Google Scholar] [CrossRef]
- Atasoy, E.; Kahraman, N. Diffusion bonding of commercially pure titanium to low carbon steel using a silver interlayer. Mater. Charact. 2008, 59, 1481–1490. [Google Scholar] [CrossRef]
- Yıldız, A.; Kaya, Y.; Kahraman, N. Joint properties and microstructure of diffusion-bonded grade 2 titanium to AISI 430 ferritic stainless steel using pure Ni interlayer. Int. J. Ad. Manuf. Tech. 2016, 86, 1287–1298. [Google Scholar] [CrossRef]
- Cooke, K.O.; Atieh, A.M. Current trends in dissimilar diffusion bonding of titanium alloys to stainless steels, aluminium and magnesium. J. Manuf. Mater. Process. 2020, 4, 39. [Google Scholar] [CrossRef]
- Kundu, S.; Chakraborty, A.; Mishra, B. Interfacial reaction and microstructure study of DSS/Cu/Ti64 diffusion-welded couple. Weld. World 2018, 62, 155–167. [Google Scholar] [CrossRef]
- Torun, O.; Çelikyürek, İ. Boriding of diffusion bonded joints of pure nickel to commercially pure titanium. Mater. Des. 2009, 30, 1830–1834. [Google Scholar] [CrossRef]
- Aydin, K.; Kaya, Y.; Kahraman, N. Experimental study of diffusion welding/bonding of titanium to copper. Mater. Des. 2012, 37, 356–368. [Google Scholar] [CrossRef]
- Aboudi, D.; Lebaili, S.; Taouinet, M.; Zollinger, J. Microstructure evolution of diffusion welded 304L/Zircaloy4 with copper interlayer. Mater. Des. 2017, 116, 386–394. [Google Scholar] [CrossRef]
- Sim, C.T.; Stoloff, N.S.; Hagel, W.C. Superalloys II: High Temperature Materials for Aerospace and Industrial Power; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure, and properties. J. Propul. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Povarova, K.B.; Valitov, V.A.; Obsepyan, S.V.; Drozdov, A.A.; Bazyleva, O.A.; Valitova, E.V. Study of the properties and the choice of alloys for bladed disks (Blisks) and a method for their joining. Russ Metall. 2014, 2014, 733–741. [Google Scholar] [CrossRef]
- Jozwik, P.; Polkowski, W.; Bojar, Z. Applications of Ni3Al based intermetallic alloys-current stage and potential perspectivities. Materials 2015, 8, 2537–2568. [Google Scholar] [CrossRef]
- Siefert, J.A.; Shingledecker, J.P.; DuPont, J.N.; David, S.A. Weldability and weld performance of candidate nickel based superalloys for advanced ultrasupercritical fossil power plants part II: Weldability and cross-weld creep performance. Sci. Technol. Weld. Join. 2016, 21, 397–427. [Google Scholar] [CrossRef]
- Popovich, V.A.; Borisov, E.V.; Popovich, A.A.; Sufiiarov, V.S.; Masaylo, D.V.; Alzina, L. Functionally graded Inconel 718 processed by additive manufacturing: Crystallographic texture, anisotropy of microstructure and mechanical properties. Mater. Des. 2017, 114, 441–449. [Google Scholar] [CrossRef]
- Piasecki, A.; Kotkowiak, M.; Makuch, N.; Kulka, M. Wear behavior of self-lubricating boride layers produced on Inconel 600-alloy by laser alloying. Wear 2019, 426–427, 919–933. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, Y.; Gu, L.; Luo, Y.; Ge, B. Study of microstructure of nickel-based superalloys at high temperatures. Scr. Mater. 2017, 126, 55–57. [Google Scholar] [CrossRef]
- Avtokratova, E.; Sitdikov, O.; Latypova, O.; Markushev, M. Effect of the bimodal structure processed by ECAP and subsequent rolling on static strength and superplasticity of Al-Mg-Sc-Zr alloy. Facta Univ. Ser. Mech. Eng. 2020, 18, 255–267. [Google Scholar] [CrossRef]
- Singh, A.; Ghadai, R.K.; Kalita, K.; Chatterjee, P.; Pamučar, D. EDM process parameter optimization for efficient machining of Inconel-718. Facta Univ. Ser. Mech. Eng. 2020, 18, 473–490. [Google Scholar]
- Kazakov, N.F. Diffusion Bonding of Materials; Pergamon Press: Oxford, UK, 1985. [Google Scholar]
- Huang, Z.W.; Li, H.Y.; Baxter, G.; Bray, S.; Bowen, P. Characterization of the weld line zones of an inertia friction welded superalloy. Adv. Mat. Res. 2011, 278, 440–445. [Google Scholar] [CrossRef]
- Ola, O.T.; Ojo, O.A.; Wanjara, P.; Chaturvedi, M.C. A study of linear friction weld microstructure in single crystal CMSX-486 superalloy. Metall. Mater. Trans. A 2012, 43, 921–933. [Google Scholar] [CrossRef]
- Ma, T.; Yan, M.; Yang, X.; Li, W.; Chao, Y.J. Microstructure evolution in a single crystal nickel-based superalloy joint by linear friction welding. Mater. Des. 2015, 85, 613–617. [Google Scholar] [CrossRef]
- Sopousek, J.; Bursık, J.; Broz, P. Experimental and theoretical study of redistribution of alloying elements in Ni-based weld joints at high temperatures. Intermetallics 2005, 13, 872–878. [Google Scholar] [CrossRef]
- Henderson, M.B.; Arrell, D.; Larsson, R.; Heobel, M.; Marchant, G. Nickel based superalloy welding practices for industrial gas turbine applications. Sci. Technol. Weld. Join. 2004, 9, 13–21. [Google Scholar] [CrossRef]
- Pouranvari, M.; Ekrami, A.; Kokabi, A.H. Microstructure development during transient liquid phase bonding of GTD-111 nickel-based superalloy. J. Alloy. Compd. 2008, 461, 641–647. [Google Scholar] [CrossRef]
- Fan, Y.; Fan, J.; Wang, C. Formation of typical Cu-Ti intermetallic phases via a liquid-solid reaction approach. Intermetallics 2019, 113, 106577. [Google Scholar] [CrossRef]
- Li, P.; Wang, L.; Yan, S.; Meng, M.; Xue, K. Temperature effect on the diffusion welding process and mechanism of B2–O interface in the Ti2AlNb-based alloy: A molecular dynamics simulation. Vacuum 2020, 173, 109118. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Wang, T.; Ardell, A.J.; Zhou, S.H.; Liu, Z.K.; Chen, L.Q. Three-dimensional phase-field simulations of coarsening kinetics of γ’ particles in binary Ni-Al alloys. Acta Mater. 2004, 52, 2837–2845. [Google Scholar] [CrossRef]
- Galieva, E.V.; Lutfullin, R.Y.; Akhunova, A.K.; Valitov, V.A.; Dmitriev, S.V. Effect of surface relief on solid phase joining of heat-resistant nickel superalloys. Sci. Technol. Weld. Join. 2018, 23, 612–618. [Google Scholar] [CrossRef]
- Potekaev, A.I.; Chaplygina, A.A.; Chaplygin, P.A.; Starostenkov, M.D.; Kulagina, V.V.; Klopotov, A.A.; Grinkevich, L.S. The influence of grain size on low-stability pre-transitional structural-phase states of NiAl intermetallide. Russ. Phys. J. 2019, 62, 519–526. [Google Scholar] [CrossRef]
- Potekaev, A.I.; Chaplygina, A.A.; Chaplygin, P.A.; Starostenkov, M.D.; Kulagina, V.V.; Klopotov, A.A.; Grinkevich, L.S. The influence of variations in atomic composition on low-stability pretransitional structural-phase states of a NiAl intermetallic compound. Russ. Phys. J. 2019, 62, 323–332. [Google Scholar] [CrossRef]
- Potekaev, A.I.; Chaplygina, A.A.; Chaplygin, P.A.; Starostenkov, M.D.; Kulagina, V.V.; Klopotov, A.A.; Grinkevich, L.S. The influence of vacancy concentration of low-stability pre-transitional structural-phase states and energy characteristics of NiAl intermetallide. Russ. Phys. J. 2019, 62, 119–126. [Google Scholar] [CrossRef]
- Khalikov, A.R.; Sharapov, E.A.; Korznikova, E.A.; Potekaev, A.I.; Starostenkov, M.D.; Galieva, E.V.; Dmitriev, S.V. Monte Carlo simulation of diffusion processes in three-component alloys. Russ. Phys. J. 2019, 62, 691–697. [Google Scholar] [CrossRef]
- Jaseliunaite, J.; Galdikas, A. Kinetic modeling of grain boundary diffusion: The influence of grain size and surface processes. Materials 2020, 13, 1051. [Google Scholar] [CrossRef] [PubMed]
- Krishna, R.; Wesselingh, J.A. The Maxwell-Stefan approach to mass transfer. Chem. Eng. Sci. 1997, 52, 861–911. [Google Scholar] [CrossRef]
- Drozdov, A.A.; Povarova, K.B.; Valitov, V.A.; Galieva, E.V.; Arginbaeva, E.G.; Bazyleva, O.A.; Bulakhtina, M.A.; Raevskikh, A.N. Effect of the temperature of pressure welding of a wrought EP975 nickel alloy and a single-crystal intermetallic VKNA-25 alloy on the structure and properties of the welded joints. Russ. Metall. (Metally) 2020, 2020, 752–759. [Google Scholar] [CrossRef]




| Atomic Element | VKNA-25 | EP975 |
|---|---|---|
| Al | 8.1–8.6 | 4.5–5.1 |
| Ti | 0.3–0.7 | 2.0–2.7 |
| Cr | 5.6–6.0 | 7.5–9.0 |
| W | 2.5–3.5 | 9.5–11.0 |
| Mo | 4.5–5.5 | 0.8–1.5 |
| Nb | – | 1.0–2.0 |
| Co | 4.0–5.0 | 14.1–17.0 |
| Re | 1.2–1.6 | – |
| C | 0.005–0.02 | 0.1–0.16 |
| Ni | Bal. | Bal. |
|
Group Notation | Group Description | EP975 | VKNA-25 | ||
|---|---|---|---|---|---|
| wt.% | at.% | wt.% | at.% | ||
| Ni | Base (Ni) | 60.04 | 54.8 | 71.185 | 63.7 |
| Al | Intermetallic-forming elements (Al and Ti) | 7.1 | 14.0 | 8.9 | 16.5 |
| Cr | Alloying elements (all other elements) | 32.86 | 31.8 | 19.915 | 19.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalikov, A.R.; Sharapov, E.A.; Valitov, V.A.; Galieva, E.V.; Korznikova, E.A.; Dmitriev, S.V. Simulation of Diffusion Bonding of Different Heat Resistant Nickel-Base Alloys. Computation 2020, 8, 102. https://doi.org/10.3390/computation8040102
Khalikov AR, Sharapov EA, Valitov VA, Galieva EV, Korznikova EA, Dmitriev SV. Simulation of Diffusion Bonding of Different Heat Resistant Nickel-Base Alloys. Computation. 2020; 8(4):102. https://doi.org/10.3390/computation8040102
Chicago/Turabian StyleKhalikov, Albert R., Evgeny A. Sharapov, Vener A. Valitov, Elvina V. Galieva, Elena A. Korznikova, and Sergey V. Dmitriev. 2020. "Simulation of Diffusion Bonding of Different Heat Resistant Nickel-Base Alloys" Computation 8, no. 4: 102. https://doi.org/10.3390/computation8040102
APA StyleKhalikov, A. R., Sharapov, E. A., Valitov, V. A., Galieva, E. V., Korznikova, E. A., & Dmitriev, S. V. (2020). Simulation of Diffusion Bonding of Different Heat Resistant Nickel-Base Alloys. Computation, 8(4), 102. https://doi.org/10.3390/computation8040102






