Abstract
This paper explores the flow structure, mean/turbulent statistical characteristics of the vector field and entrainment of round jets issued from a smooth contracting nozzle at low nozzle exit velocities (1.39–6.44 m/s). The motivation of the study was to increase understand of the near field and get insights on how to control and reduce entrainment, particularly in applications that use jets with low-medium momentum flow like microclimate ventilation systems. Additionally, the near field of free jets with low momentum flow is not extensively covered in literature. Particle image velocimetry (PIV), a whole field vector measurement method, was used for data acquisition of the flow from a 0.025 m smooth contracting nozzle. The results show that at low nozzle exit velocities the jet flow was unstable with oscillations and this increased entrainment, however, increasing the nozzle exit velocity stabilized the jet flow and reduced entrainment. This is linked to the momentum flow of the jet, the structure characteristics of the flow and the type or disintegration distance of vortices created on the shear layer. The study discusses practical implications on microclimate ventilation systems and at the same time contributes data to the development and validation of a planned computational turbulence model for microclimate ventilation.
1. Introduction
Scientific investigation of jets is extensively covered in literature and much has been driven by industrial needs to achieve improvements for specific performance [1,2]. Literature reviews [1,2,3,4] show that the far field of free turbulent jets has been the subject of considerable research curiosity because the region offers useful interrogation of fine scales of turbulence [5,6]. However, little attention has been paid to the near field and transition region despite being the area were highly isotropic turbulent structures are formed, evolve and interact as the flow develops. According to Ball et al. [1] the near to intermediate region should be of interest as it significantly influenced upstream conditions of heat, mass and momentum transfer, which often dominates practical applications of a jet.
Knowledge of the flow structure and the ability to control the flow development in the near field would have a vital impact on many engineering applications. For example, jet applications on ideas of individual air supply to people covered under microclimate ventilation systems (commonly known as personalized ventilation; refer to Appendix A for commonly used types of microclimate ventilation systems), necessitates revisiting jet concepts and theories to assert optimal operational conditions. This is important because: (1) There has not been much interest to investigate flow development in these applications or in the near field and in transitional regions of low exit velocity jets, which can speculatively be linked to lack of industrial application until now. (2) In addition to improved technical processes and performance, economic and ecological implications dictate designing and building devices whose performance is not left to be managed by the whims of the flow but rather controlled for. Fiedler [2] defines flow control as “a process or operation by which certain characteristics of a given flow are manipulated in such a way as to achieve improvements of a specific technical performance”. Regarding flow structures and microclimate ventilation systems, improved technical performance can mean energy efficiency, high delivery capacity of supply air or low entrainment mixing factor and delivery of acceptable thermal comfort. As Fiedler states, this can only be achieved with an adequate level of control that requires a detailed knowledge of the flow structure. Fiedler proposed three principal areas for control applications: Mixing, noise and entrainment. Understanding and controlling for entrainment is of particular interest in ventilation systems, although it is also important in many other engineering applications like quenching and chemical mixing.
Entrainment is an interesting phenomenon and should be one of the main points of focus in microclimate ventilation applications because the phenomenon explains jet behavior (flow structures) and development as a result of its interaction with surrounding space and the ambient fluid [1,3,7]. For example, both transport and mixing in turbulent flows are controlled by entrainment. In ventilation systems, entrainment is desirable in applications requiring mixing between fluids, however it is problematic when mixing is undesirable. Ventilation strategies that employ dilution air distribution concepts illustrates cases were entrainment is a friend, while on the other hand it is a foe for optimal performance of systems that employ delivery air distribution principles as delivered or inhaled air quality is dependent on minimal entrainment of contaminants [8]. Therefore, entrainment under operational or flow conditions in microclimate ventilation systems needs to be understood.
This study aims to contribute to understanding the near-field flow structure and entrainment behavior of jets at low exit velocities, particularly so in relation to microclimate or personalized ventilation systems whose performance depend on their capacity to minimize dilution and deliver as much of the supply conditions to the occupant and desirably at minimal system energy use. The current investigation is one of the planned series of studies aiming to contribute to this understanding [8,9,10]. While the previous studies in the series focused on air distribution concepts and the mean vector and scalar field of jet supply flows in relation to entrainment, the current study focuses on the turbulent flow field. Additionally, this paper lays a foundation and provides data for the development and validation of the computational turbulence model that will investigate airflow dynamics in microclimate ventilation. An approach common in ventilation and other industrial applications [11,12,13]. The overall objective and approach is to develop a hierarchy of entrainment relations consistent with jet flows in microclimate ventilation systems and general jet flows, “… that can be used either in a diagnostic mode, clarifying the physics of turbulent entrainment, or in a prognostic mode, leading to entrainment models that can be used for predictive purposes,” as van Reeuwijk and Craske [14] puts it into perspective.
Herein, the author refrains from indulging in a detailed literature review on entrainment or general jet flow behavior in the near and transition field because a detailed review with respect to this subject was performed in an earlier study [9] and interested readers can also see [1,3,4,15,16,17,18] and the references therein. Additionally, the development of the jet and the consequences thereto when interacting with other indoor air flows or plumes are not considered nor discussed but interested readers can see the discussion in [9]. Owing to limited studies on early development of free shear flows at low nozzle exit velocities, the current study investigates characteristic scales that establish basic jet behavior and development in the initial region. Examples of the characteristic scales are energy-based entrainment relationships with particular focus on mass transfer in and out of the jet which can be established by spanwise and streamwise velocity profiles, mixing characteristics defined by the entrainment mixing factor, and the jet spread.
2. Materials and Methods
2.1. Experimental Setup and Equipment
Jet flow issued from a specially designed smooth contracting nozzle (diameter, D = 0.025 m) was investigated. The nozzle was a 5th polynomial, designed to the specifications similar to the ones by [19,20], with the exit section coinciding with the point where the tangent is parallel to the nozzle axis. Particle image velocimetry (PIV), 2 dimensional–2 components, measurement method was used for data acquisition of the whole flow vector field under isothermal conditions in a climate control chamber with dimensions of 3(W) by 2.5(H) by 4.2(L) [m3] at the University of Gävle; a similar setup and the same room used in an earlier study [9]. The nozzle setup was vertically mounted and installed in the middle of the room at 2 m from the floor, a schematic and plan representation of the setup is shown in Figure 1.
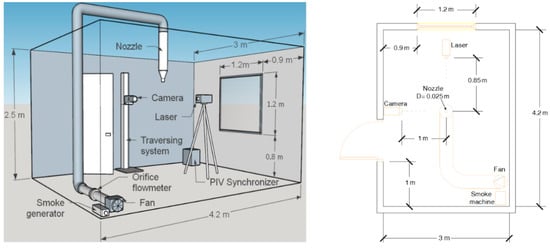
Figure 1.
Experimental setup of particle image velocimetry (PIV) measurements.
All experimental measurements were performed under a closed room setup with air re-circulation in the jet stream to make it possible to achieve a well-distributed global seeding, a prerequisite for high-quality PIV measurements. The PIV system comprised of a 15-Hz New Wave Solo PIV 50-mJ double-pulsed Nd:YAG laser operating at 6 Hz as a light source, and placed at about 0.85 m from the nozzle centerline and at the height of 1.5 m from the floor. The delay between laser pulses was adjusted depending on the flow-field and was optimized for the interrogation region. A double-frame, high-sensitivity 12-bit CCD camera (HiSense MKII) with resolution of 1344 by 1024 pixels mounted with an AF Micro Nikkor objective with a focal length of 60 mm was used for imaging. The camera was installed 1 m away from the nozzle centerline and placed on a traversing system moving perpendicular to the laser sheet and parallel to the jet axial axis. A SAFEX FOG 2001 smoke generator with “normal power mix” as fog generating liquid was used and gave satisfactory measurement results.
2.2. Experimental Conditions
A preliminary study [10] reported challenges of supplying at low exit velocities and illustrated the instability and oscillations resulting hence forth, reproduced herein as Figure 2 with smoke visualization. The instabilities on shear layer structures cause oscillations and consequently reduce the penetration of the jet flow into the ambient fluid, resulting in an asymmetrical jet particularly at lower Reynolds numbers (<3000). The observations from the visualization method showed some form of stability and reduced oscillations at about 2 m/s nozzle exit velocity and the jet developed to about 30D downstream before disintegrating or dying out. No observable differences were made in the form of stability or vortices behavior other than increased penetration into the ambient at Reynolds number ≥3400 (2.34 m/s nozzle exit velocity). Therefore, five experimental conditions were chosen for the present study based on this insight, and on jet exit conditions similar to the range used under microclimate ventilation systems.

Figure 2.
Jet development at different initial conditions.
The investigated experimental cases are listed in Table 1. The cases were defined by the Reynolds number (Re) scaled with a relationship, Re = V0D/v, where V0 is the nozzle bulk exit velocity D is the nozzle diameter and v is the kinematic viscosity of the fluid, v = 14.8 × 10‒6 m2/s [20]. The bulk exit velocity was determined by the relationship V0 = 4/πD2, is the flowrate determined from a 25 mm diameter orifice plate measurement meter.

Table 1.
Experimental conditions.
Data acquisition and pre-processing was done with PIV software packages, Dantec Flow manager and Dantec Dynamic Studio. The whole-field velocity vectors were obtained with three interrogation regions limited to the measurement region 0 < x/D < 14. The cross-correlation was performed with interrogation region of 32 by 32 pixels with a typical overlap of 50%. Peak and range validation were applied to identify spurious vectors respective of the flow field. Overall, spurious vectors were rejected and substituted with interpolated vectors within the spatial region in the mean PIV field. PIV measurements uncertainties are influenced by various error sources, which can either be systematic or statistical errors [21]. Statistical errors are mainly due to random sampling, [22,23,24] while systematic errors relate to the experimental setup and procedure with likely sources of error originating from tracking behavior, seeding density, background noise etc. Indoor airflow measurements with 2 dimensional PIV have systematic errors less 2% [22,25]. For the current study, the statistical errors were <8% in the time averaged velocity field using the central limit theorem [23].
The statistical mean velocity field was obtained with an ensemble of 650 images of instantaneous velocity fields for each experimental case (spanwise (U) and streamwise (V) statistical means). The turbulent velocity field was defined by the root mean square (r.m.s) of the fluctuations of the velocity components (spanwise component u′; streamwise component ′) are compiled based on the equations below, where u and are the spanwise and streamwise mean velocity whereas and are the variance of the velocity, respectively:
Treatment of the mean and turbulent flow field was normalized with the bulk exit velocity for each measurement case. The volumetric flowrate at different axial locations was determined by graphical integration of the local mean streamwise velocity profiles, see [9]. This was used to evaluate the evolution of the volumetric flowrate with downstream distance. The downstream distance x at which the jet is fully mixed can theoretically be determined by the relationship = 0, which is derived based on a hypothetical jet that is supplying clean air into a polluted room or ambient with uniform concentration (Ca). Figure 3 illustrates a schematic representation of this scenario.
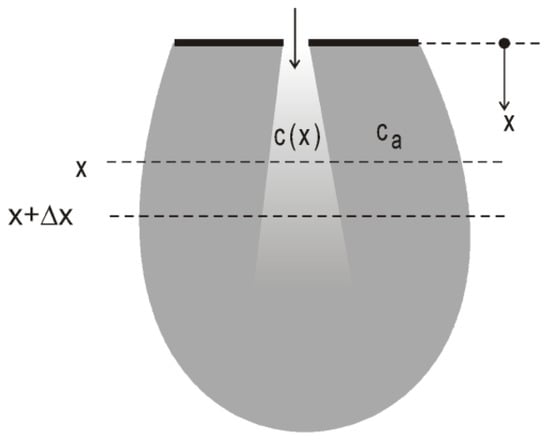
Figure 3.
Schematic representation of jet with clean air is supplied into an ambient with uniform concentration (courtesy of Professor Mats Sandberg).
is the flowrate in the jet and the change in the jets flowrate due to entrainment of ambient air into the jet with downstream distance x is . The inflow of ambient contaminant into the jet is
The change in concentration within the jet due to this inflow is
Therefore, the change in contaminant concentration in the jet flow is determined by the following relationship,
where C is the mean concentration within the jet. The following differential equation for the increase of the concentration within the jet is obtained
After integration of Equation (3) we obtain
The integral is
Assuming that the initial concentration at the exit in the jet in relation to the ambient contaminant is zero, C(0) = 0, Equation (4) is simplified to
Setting the downstream distance x to be the distance where the concentration in the jet has become equal to the concentration in the ambient, C(x) = Ca.
This gives the ratio between the flow rate at location x, where the contaminant concentration in the jet is equal to the concentration of the ambient, and the flowrate at the nozzle exit to be
Thus, if the evolution of the volumetric flowrate with downstream distance is established, one can solve for the hypothetical distance at which the concentration in the jet is equal to that of the room.
3. Results
3.1. Evolution of the Mean Velocity Field
A time averaged quantitative characterization of the streamwise velocity profiles are presented in Figure 4 and, as observed, in all cases a top-hat profile typical of free round jets [26,27,28] was obtained. The exit top-hat velocity profiles diffused out gradually to a Gaussian profile within the first four diameters and with increase in downstream distance the velocity distribution eventually relaxes to bell-shaped profiles [29]. An apparent observation is that the velocity profiles are superimposed on each other up to 4D, with the exception of the case with the lowest nozzle exit velocity (sustains the exit velocity longer than other cases). After the zone of flow establishment, the Reynolds number dependence manifests between six to nine diameters which may be deduced as part of a critical transitional region where the jet changes from laminar to turbulent flow. Here, increase in exit velocities suggest increase in the radial spread (width of the jet) with downstream distance. However, after 10D the profiles exhibit self-similarity as they are superimposed on each other again for the rest of the interrogation region (shown here only up to 12D). This observation is supported by the qualitative representation of the mean flow field shown in Figure 5.
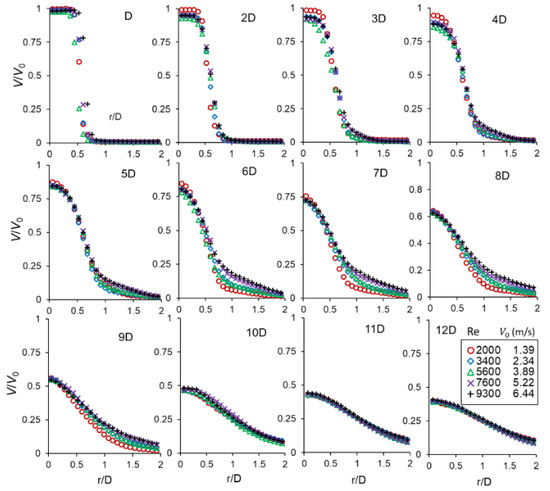
Figure 4.
Normalized streamwise velocity profiles at different downstream distances (half of the profiles is shown).
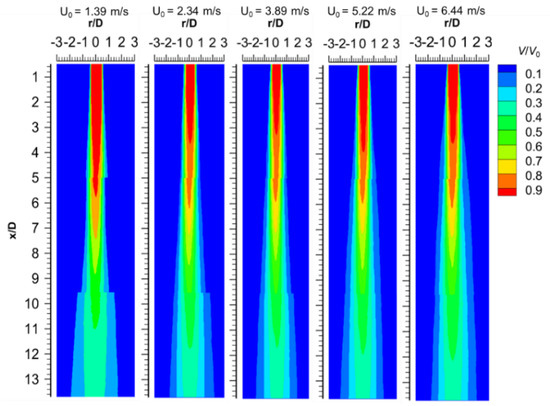
Figure 5.
Normalized contour plots of the mean streamwise velocity component.
The spanwise velocity profile is critical for mass transfer or exchange between the jet and the ambient fluid, thus it is sometimes referred to as the entrainment velocity [30]. Figure 6 shows the statistical spanwise mean velocity distribution that is qualitatively represented by the velocity contours in Figure 5. As shown near the exit (x/D = 1), the spanwise velocity curves are antisymmetric, with r/D = 0 being the radial velocity inversion (the point where turbulent outflow from the jets center equals non-turbulent inflow towards the jet). The inflow and outflow have a maximum/minimum close to the radial location of the nozzle lips. This maximum gradually moves outwards with downstream distance, consequently increasing the spread of the jet. A direct observation is the instability of the mean spanwise velocity component specifically for the case with the lowest nozzle exit velocity. Here, the velocity profile distribution does not match the “double S” reported in literature [31].
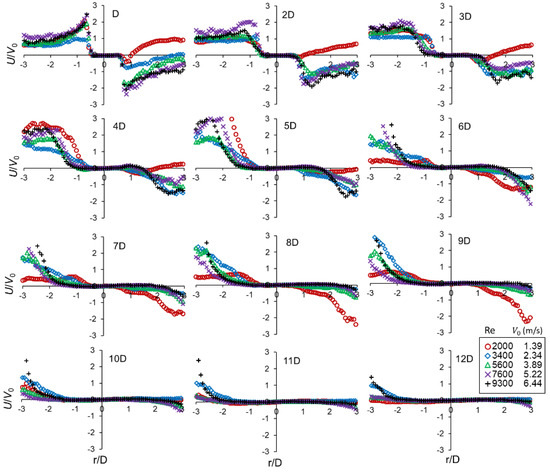
Figure 6.
Normalized spanwise velocity profiles at different downstream distance.
3.2. Evolution of the Turbulent Velocity Field
Figure 7 shows the lateral distribution of the r.m.s fluctuations of the streamwise velocity field A, the spanwise velocity field C and their normalized contour plots B and D, respectively. Near the nozzle exit and in both fluctuating velocity components, the statistical distribution peaks around the points stemming from the nozzle lips (0.5 < r/D < 0.75), indicating the existence of a shear layer or vorticity layer at the nozzle exit. No fluctuations are observed in the initial region (attributed to be the potential core) but there is an increase in fluctuations as the downstream distance increases. Cases with low exit velocities (≤3.89 m/s) exhibit higher fluctuations after three diameters because of the instabilities and oscillatory nature of the jet. The cases with high exit velocities (≥5.22 m/s) has higher fluctuations near the nozzle exit and the observed hump on the nozzle lips diminishes at about 3D and the flow evolves with little distinguishable differences between the cases.
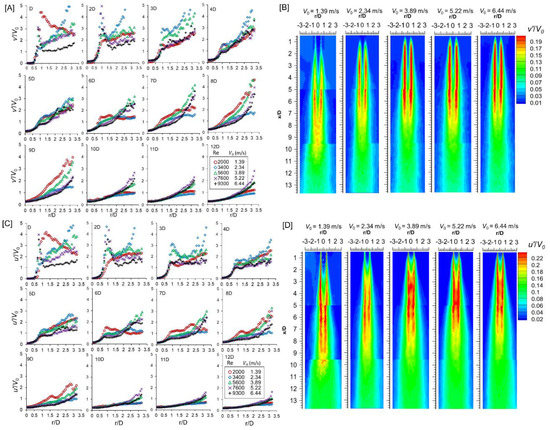
Figure 7.
Lateral distribution of the root mean square (r.m.s) fluctuations of the turbulent velocity component (left; (A) is streamwise component and (C) spanwise component) and the respective contour plots (right; (B) is streamwise component and (D) spanwise component).
The contour plots show that the streamwise r.m.s fluctuations () peaks in the jet mixing layer along the nozzle lips (about r/D ≈ 0.5) and grows stronger towards the nozzle exit with increasing exit velocity. In setups with V0 ≥ 5.22 m/s, a strong jet mixing layer is uniformly sustained downstream up to about x/D = 7 after which it gradually disintegrates to an asymptotic flow. Similarly, the spanwise r.m.s fluctuations (u′) peaks along the nozzle lips but the fluctuations grow inwards towards the jet centerline. In both Figure 7B,D, the inward growth and merging of the shear layer introduce fluctuations along the central portion of the jet consequently increasing entrainment and the mixing processes between the jet and the ambient.
3.3. Characteristics of the Mean and Turbelent Flow on the Jet Centerline
Figure 8 present the centerline characteristics of jet flows. The decay rate of the streamwise mean velocity component is similar for all cases except the case with the low nozzle exit velocity, which has a longer average length of the potential core. However, the spanwise velocity component become chaotic in low nozzle exit velocity conditions after 4D, particularly for V0 = 1.39 m/s. The r.m.s fluctuations of the streamwise component shows a tendency towards similarity by about 3D while this is attained after 8D on spanwise component, except for the low nozzle exit velocity condition (delayed in both cases and seems unstable). While these results are consistent with what is in the literature and they give insight on the flow characteristics and behavior of the jet centerline, it is hard to explain the results influence on entrainment. However, the results suggest that the jet attains self-similarity rather early (conservatively about 10D) and we can deduce that entrainment rate will likely transition from non-linear to linear within this region.
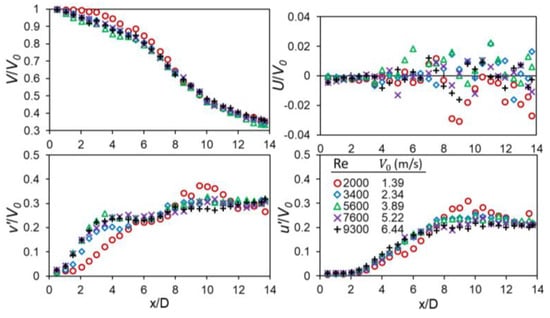
Figure 8.
Centerline characteristics of mean and turbulent flow field.
3.4. Evolution of the Mass Flowrate and Jet Entrainment
When the jet entrains fluid from outside the jet boundaries into the main turbulent stream, the volumetric mass flowrate increases with increasing downstream distance from the jet exit [32]. Figure 9 shows the change of the volumetric flowrate with downstream distance. The volumetric flowrate in the near field develops nonlinearly and depend on the exit velocity reaches a constant within the first 4D. In higher exit velocity flows, there is a sharp increase in volumetric flowrate and quickly reaches a constant as compared to flows with low exit velocities. The general overview shows that conditions with high exit flows have low mass flowrate increase which is a consequence of low entrainment compared to conditions with low nozzle exit velocities.
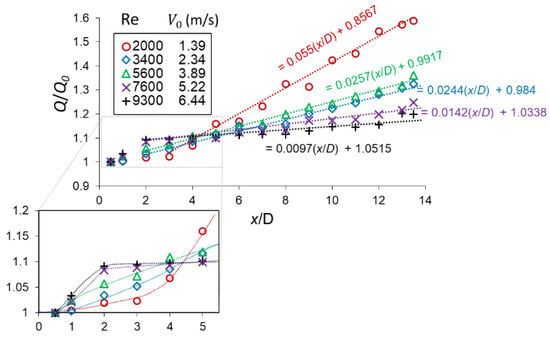
Figure 9.
Volumetric flowrate as a function of downstream distance.
The most effective way to characterize this behavior is to plot the instantaneous vector contour field which characterizes vortex structures. Figure 10 offers a qualitative interpretation of the instantaneous flow field (V0 = 5.22 m/s and V0 = 6.44 m/s had no distinct differences). As comprehensively described by List [33], when a high speed jet interacts with the irrotational ambient fluid, a laminar shear layer is produced. The shear layer is unstable and grows very rapidly, forming coherent structures (ring vortices) that pair and rotate along the jets axis and later break off after a loss of momentum (increased mixing happens after break off). This behavior of coherent structures increases mass exchange of fluids between turbulent jet fluid and the irrotational ambient fluid.
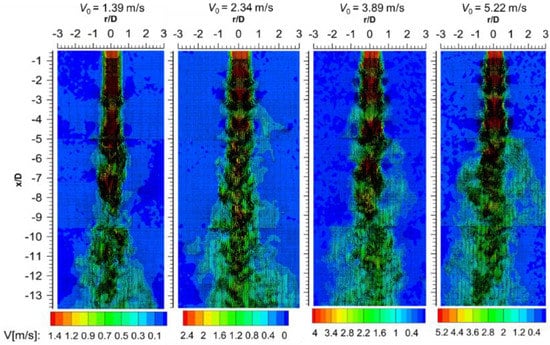
Figure 10.
Instantaneous velocity fields with velocity vectors, streamlines and contours of their magnitudes. These images are selected arbitrarily out of 650 images and presented here as typical flow for each experimental condition.
The main factor governing the resulting nature of the flow is the momentum flow [8]. The instantaneous contour plots show that the conditions with low nozzle exit velocities (V0 = 1.39 m/s and V0 = 2.34 m/s) are oscillatory and with minimal to no coherent structures on the shear layer (particularly for V0 = 1.39 m/s). The oscillating manner of the jet creates flow instabilities as also evidenced in an earlier study [10]. In low nozzle exit velocity cases, the momentum flow is insufficient to generate and sustain the flow of coherent structures, thus any vortices or tendency of formation easily disintegrate within a short downstream distance from the nozzle exit (about x/D = 3). Cases with high nozzle exit velocities are dominated by formation of small-scale vortices close to the nozzle exit (x/D = 1; suggesting early mixing of the jet flow) which later disintegrate downstream at about x/D = 5. This behavior explains the evolution of the volumetric mass flowrate.
As the jet develop downstream, mixing between the ambient and the jet stream occurs. Figure 11 shows the jet and ambient mixing as a function of downstream distance. Logically, as shown, the mixing of the flow follows the evolution of the volumetric flowrate as a function of downstream distance (compare Figure 9). The general observation is that when the profiles attain linearity, mixing reduces with increasing nozzle exit velocities (except for V0 = 3.89 m/s which develops similarly to V0 = 2.34 m/s, no explanation was found for this case).
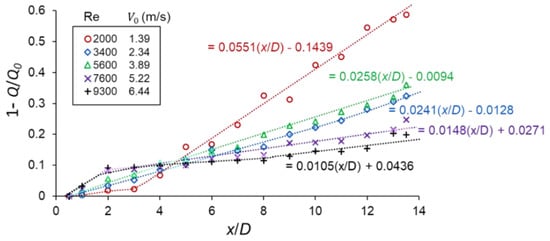
Figure 11.
Jet and ambient mixing as a function of downstream distance.
Hypothetically, if there is no fluid entrained into the jet flow then jet mixing = 0. On the other hand, when the jet mixing = 1, then flow is fully mixed with the surrounding fluid. Table 2 shows a comparison of the estimated downstream distance for fully mixed jet flow: With the graphical method (Figure 11) and the proposed relationship where is the function of the downstream distance from Figure 9.

Table 2.
Downstream distance at which the jet is fully mixed.
4. Discussion
The preceding sections have reported the near-field jet behavior, structure and statistical properties of low velocity round jets from a smooth contracting nozzle. Not only have differences been statistically quantified but also a qualitative structure and explanation given. The momentum flow, F = ρ A (V0)2 where ρ is the fluid density and A is the cross-sectional area of the jet, is the key link to the behavior of the jet and the implications this will have on air supply in microclimate ventilation. The velocity differences between the jet and the quasi-stationary ambient fluid creates a highly unstable thin shear layer that continuously grows downstream accompanied by the generation of strong turbulent fluctuations [33]. This behavior is the driving mechanism for fluid mass transfer or entrainment into the jet. This paper links the momentum flow to the shear stress (S) between the jet flow and the ambient fluid. It is therefore proposed that studies than can focus on defining the range of the shear stress as a gradient of the axial velocity component (S ) within which entrainment is reduce can give a better understanding on how to optimize operation or fresh air supply in microclimate ventilation systems or related applications.
As shown herein, conditions with much lower nozzle exit velocities had an oscillatory jet flow and an early on disintegration of the jet. This increased entrainment of ambient fluid consequently reducing the distance at which the jet gets fully mixed with ambient fluid. Initial conditions with higher exit velocities had a lower entrainment rate and penetration distance, see Figure 10 and Table 2. The results here should be interpreted cautiously as the two methods give very different results and thus further studies are strongly recommended.
The results and findings obtained herein are similar to what was reported in an earlier study [9] that investigated a larger nozzle (D = 0.05 m). In both these two studies the entrainment rate values are lower compared to other previous studies [30]. The study also confirms that entrainment increases nonlinearly in the initial region [18] although as shown in this study, it happens within the first 3D and the nonlinear development region gets smaller with increase in nozzle exit velocity. Overall, the reported results are in agreement with the literature [1] although much of the studies involve jets issued at very high velocities and most predominantly focus on the far field.
The consequence of the observed jet behavior in applications that use jets with low nozzle exit velocities is the increased fluid mass transfer into the jet. First, this is an energy problem because it will redistribute momentum across the jet resulting in gradual decrease of the momentum flow. To avoid jet oscillations or achieve higher penetration distance (depending on application) will require using more fan power to strengthen the jet flow. Second, there is a loss of the initial exit conditions due to entrainment of contaminants. This causes an increased mixing of the jet flow (clean air supply) with the ambient fluid (contains contaminants). Both conditions are undesirable for microclimate ventilation because the desire is to deliver as much clean air as possible (preferably with zero entrainment) to the occupant at a low energy use and flowrate that is deemed comfortable [34].
Entrainment can be reduced by controlling exit conditions to increase the streamwise and reduce the spanwise fluctuations and mean flow. Although, both streamwise and spanwise components have an influence on the development of the core region, it can be seen that evolution of the shear layer towards the central portion of the jet was mostly influenced by the spanwise components. One way to reduce the influence of the spanwise velocity component is by supplying at moderately higher nozzle exit velocities that can overcome jet instabilities and oscillation of the jet flow. As shown in the current study, cases with higher exit velocities had low entrainment of ambient fluid and a high delivery distance (point where the jet is fully mixed). This observation agrees with results from another study on a contracting nozzle [9] and other studies with different types of nozzles [35,36]. Although entrainment is a combined effort of large and small-scale vortices [37], larger scale vortices are dominant entraining flow structures. Therefore, supplying at higher nozzle exit velocities that offer a wider range of small turbulence length scales. Under these initial conditions the natural engulfment of ambient fluid consistent with large scale vortices is depressed and an increased shear layer vortex formation process enhanced, consequently reducing the mixing effect of the jet and the ambient fluid.
The results of the normalized downstream distance at which the jet is fully mixed are not in agreement. First, under the current measurement region it is unclear whether the volumetric flowrate profiles maintain linearity for the rest of the flow development (x/D > 14). The assumption of linearity that is taken can explain the different results. Second, the proposed volumetric flowrate relationship is derived on the concepts and assumptions on uniform contaminant distribution and entrainment rate. Since flow development for each initial condition is different, the proposed relationship may not correctly account for the growth of the volumetric flowrate particularly in the nonlinear region. In this case more experimental work is needed to determine the correction factor for contamination of the jet flow with downstream distance. The author recommends further studies to improve the results and/or correct the relationship between the exit bulk flowrate and the jet stream volumetric flowrate as a function of a downstream distance. Additionally, the reported results are limited to the setup herein and thus further studies are recommended to verify whether they are replicable for other experimental conditions, e.g., different nozzle types, jet initial conditions, direction of the jet flow and the influence of nozzle sizes in microclimate ventilation applications.
Funding
This research received no external funding.
Acknowledgments
The author acknowledges Amir Sattari for the help with PIV measurements and Mats Sandberg for the discussion and suggestions on this topic.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
A common example of microclimate climate ventilation systems are shown in Figure A1. In some cars there are dedicated ventilation air supply diffusers that service individual passengers while on planes there a secondary systems that are personalized to passenger’s. These systems use free turbulent jets whose optimal performance depend on reduced ventilation.

Figure A1.
Examples of common microclimate ventilation nozzle diffusers.
References
- Ball, C.G.; Fellouah, H.; Pollard, A. The flow field in turbulent round free jets. Prog. Aerosp. Sci. 2012, 50, 1–26. [Google Scholar]
- Fiedler, H.E. Control of free turbulent shear flows. In Flowcontrol: Fundamentalsandpractices; Hak, M., Pollard, A., Bonnet, J., Eds.; Springer: Berlin, Germany, 1998; pp. 335–429. [Google Scholar]
- Townsend, A.A. Entrainment in Free Turbulent Flows. In Advances in Turbulence 2; Springer: Berlin, Germany, 1989; pp. 109–112. [Google Scholar]
- Mi, J.; Nathan, G.J.; Nobes, D.S. Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet. J. Fluid Mech. 2001, 432, 91–125. [Google Scholar]
- Sreenivasan, K.R.; Antonia, R.A. The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 1997, 29, 435–472. [Google Scholar]
- George, W.K. The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. Adv Turbul. 1989, 3973, 39–74. [Google Scholar]
- Capp, S.P. Experimental Investigation of the Turbulent Axisymmetric Jet; State Univ. of New York: Albany, NY, USA, 1984. [Google Scholar]
- Sandberg, M.; Kabanshi, A.; Wigö, H. Is building ventilation a process of diluting contaminants or delivering clean air? Indoor Built Environ. 2020, 29, 768–774. [Google Scholar] [CrossRef]
- Kabanshi, A.; Sandberg, M. Entrainment and its implications on microclimate ventilation systems: Scaling the velocity and temperature field of a round free jet. Indoor Air 2019, 29, 331–346. [Google Scholar] [CrossRef]
- Kabanshi, A.; Sattari, A.; Linden, E.; Wigö, H.; Sandberg, M. Experimental study on contaminant entrainment in air distribution systems with free jets. In Proceedings of the Healthy Buildings 2017 Europe, Lublin, Poland, 2–5 July 2017. [Google Scholar]
- Tavangar, T.; Tofighian, H.; Tarokh, A. Investigation of the Horizontal Motion of Particle-Laden Jets. Computation 2020, 8, 23. [Google Scholar]
- Haque, J.N.; Mahmud, T.; Roberts, K.J.; Rhodes, D. Modeling turbulent flows with free-surface in unbaffled agitated vessels. Ind. Eng. Chem. Res. 2006, 45, 2881–2891. [Google Scholar]
- Svensson, K.; Ghahremanian, S.; Moshfegh, B.; Tummers, M. Numerical and experimental investigation of flow behavior in a confluent jet ventilation system for industrial premises. In Proceedings of the The 10th International Conference on Industrial Ventilation, Paris, France, 17–19 September 2012. [Google Scholar]
- van Reeuwijk, M.; Craske, J. Energy-consistent entrainment relations for jets and plumes. J. Fluid Mech. 2015, 782, 333–355. [Google Scholar]
- Viggiano, B.; Dib, T.; Ali, N.; Mastin, L.G.; Cal, R.B.; Solovitz, S.A. Turbulence, entrainment and low-order description of a transitional variable-density jet. J. Fluid Mech. 2018, 836, 1009–1049. [Google Scholar]
- List, E.J.; Imberger, J. Turbulent entrainment in buoyant jets and plumes. J. Hydraul. Div. 1973, 99, 1461–1474. [Google Scholar]
- Ricou, F.P.; Spalding, D.B. Measurement of entrainment by axisymmetric turbulent. J. Fluid Mech. 1961, 11, 21–31. [Google Scholar]
- Hill, B.J. Measurement of local entrainment rate in the initial region of axisymmetric turbulent air jets. J. Fluid Mech. 1972, 51, 773–779. [Google Scholar]
- Todde, V.; Spazzini, P.G.; Sandberg, M. Experimental analysis of low-Reynolds number free jets. Exp. Fluids 2009, 47, 279–294. [Google Scholar]
- Todde, V.; Linden, E.; Sandberg, M. Indoor Low Speed Air Jet Flow: Fibre Film Probe Measurements. In Proceedings of the ROOMVENT’98, Stockholm, Sweden, 14–17 June 1998. [Google Scholar]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Cham, Germany, 2018; ISBN 3319688529. [Google Scholar]
- Feng, L.; Yao, S.; Sun, H.; Jiang, N.; Liu, J. TR-PIV measurement of exhaled flow using a breathing thermal manikin. Build. Environ. 2015, 94, 683–693. [Google Scholar]
- Cao, X.; Liu, J.; Pei, J.; Zhang, Y.; Li, J.; Zhu, X. 2D-PIV measurement of aircraft cabin air distribution with a high spatial resolution. Build. Environ. 2014, 82, 9–19. [Google Scholar]
- Westerweel, J. Theoretical analysis of the measurement precision in particle image velocimetry. Exp. Fluids 2000, 29, S003–S012. [Google Scholar]
- Cao, X.; Liu, J.; Jiang, N.; Chen, Q. Particle image velocimetry measurement of indoor airflow field: A review of the technologies and applications. Energy Build. 2014, 69, 367–380. [Google Scholar]
- Du, Z.; Jin, X.; Fan, B. Evaluation of operation and control in HVAC (heating, ventilation and air conditioning) system using exergy analysis method. Energy 2015, 89, 372–381. [Google Scholar]
- Ferdman, E.; Ötugen, M.V.; Kim, S. Effect of Initial Velocity Profile on the Development of Round Jets. J. Propuls. Power 2000, 16, 676–686. [Google Scholar]
- Etheridge, D.W.; Sandberg, M. Building Ventilation: Theory and Measurement; John Wiley & Sons: Chichester, UK, 1996; ISBN 9780471960874. [Google Scholar]
- New, T.H.; Lim, T.T.; Luo, S.C. Effects of jet velocity profiles on a round jet in cross-flow. Exp. Fluids 2006, 40, 859–875. [Google Scholar]
- Falcone, A.M.; Cataldo, J.C. Entrainment Velocity in an Axisymmetric Turbulent Jet. J. Fluids Eng. 2003, 125, 620–627. [Google Scholar]
- Mih, W.C. Equations for axisymmetric and twodimensional turbulent jets. J. Hydraul. Eng. 1989, 115, 1715–1719. [Google Scholar]
- Morton, B.R.; Taylor, G.I.; Turner, J.S. Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1956, 234, 1–23. [Google Scholar]
- List, E.J. Turbulent jets and plumes. Annu. Rev. Fluid Mech. 1982, 14, 189–212. [Google Scholar]
- Melikov, A.K. Personalized ventilation. Indoor Air 2004, 14, 157–167. [Google Scholar]
- Mi, J.; Kalt, P.; Nathan, G.J.; Wong, C.Y. PIV measurements of a turbulent jet issuing from round sharp-edged plate. Exp. Fluids 2007, 42, 625–637. [Google Scholar]
- Russ, S.; Strykowski, P.J. Turbulent structure and entrainment in heated jets: The effect of initial conditions. Phys. Fluids A Fluid Dyn. 1993, 5, 3216–3225. [Google Scholar]
- Philip, J.; Marusic, I. Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 2012, 24, 55–108. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).