Abstract
Put-away operations typically consist of moving products from depots to allocated storage locations using either operators or Material Handling Equipment (MHE), accounting for important operative costs in warehouses and impacting operations efficiency. Therefore, this paper aims to formulate and solve a Put-away Routing Problem (PRP) in distribution centres (DCs). This PRP formulation represents a novel approach due to the consideration of a fleet of homogeneous Material Handling Equipment (MHE), heterogeneous products linked to a put-away list size, depot location and multi-parallel aisles in a distribution centre. It should be noted that the slotting problem, rather than the PRP, has usually been studied in the literature, whereas the PRP is addressed in this paper. The PRP is solved using a discrete particle swarm optimization (PSO) algorithm that is compared to tabu search approaches (Classical Tabu Search (CTS), Tabu Search (TS) 2-Opt) and an empirical rule. As a result, it was found that a discrete PSO generates the best solutions, as the time savings range from 2 to 13% relative to CTS and TS 2-Opt for different combinations of factor levels evaluated in the experimentation.
1. Introduction
Put-away operations mainly consist of moving products from locations where inventory is stored for later utilization (depots) to assigned storage locations using either operators or Material Handling Equipment (MHE) [1,2]. Put-away also includes order batching and routing to place products in the storage system. The order batching problem consolidates several orders in a batch to place the items of several orders in the storage system in a single tour, generating efficient routes and reducing the travelled distance [3], while the picker routing problem plans the shortest tour to minimize the travelled time and distance to place all items in a batch [4]. The order batching and routing problem should be solve jointly because grouping orders directly affects the sequence of storage positions to visit in picking routing, and produces significant performance benefits compared to the sequential resolution of these problems [5,6]. Therefore, the put-away operation is associated with inbound logistics in a distribution centre (DC) by impacting efficiency and customer satisfaction.
A distribution center is the warehouse facility which holds inventory from manufacturing pending distribution to the appropriate stores [2], and then picks-up and delivers goods to meet stores’ demands later [7]. At the distribution centre level, the main operations include receiving, put-away, order picking, sortation, cross-docking, and shipping [8], and the performance indicators are typically focused on material handling efficiency [9]. From these operations, put-away not only accounts for about 15% of logistics costs in a DC for the distribution of goods for retail stores [1,10], but also can impact efficiency due to the use of resources such as human resources, MHE, information and communication technologies (ICT), amongst others [10]. Therefore, this operation must be planned, executed and controlled effectively.
In a DC with a multi-level storage system, it can be necessary to use multiple MHE that can access the storage locations according to the height of the warehouse and type of products (weight or volume). These characteristics can increase the complexity of the problem formulation, as well as its solution [11]. In addition, this operation is directly linked to the storage location assignment problem, as the products must be allocated to storage locations. For this reason, these decisions should be integrated and synchronized, as they are interdependent [5,12]. Moreover, put-away operations gain importance in logistics processes in which the products must be placed at the assigned storage locations in the shortest time. For instance, products requiring cold chain put-away operations can be classified as critical since these products could be damaged if they are not handled quickly enough. Similarly, dangerous products must be put away quickly and effectively, as those products could generate cross-contamination in a DC [1]. These reasons are some examples noting and justifying the importance of this operation in a DC.
This article therefore formulates and solves a Put-away Routing Problem (PRP) in distribution centres considering multiple MHE and 3D-warehouses using metaheuristics to provide efficient solutions. The remainder of this paper is organized as follows. The second section introduces the literature review about the PRP and the solution approaches for this problem. The third section describes and formulates the PRP. In the fourth section, the discrete PSO algorithm for solving the PRP is represented. In the fifth section, the experimental study is planned. The sixth section shows the results and discussion of the experiments. Finally, in the seventh section, the conclusions and further research are presented.
2. Literature Review
From the results of a literature review, it was discovered that research on put-away operations has been focused only on the assignment of storage locations. The reviewed research used a class-based storage policy to assign storage locations (slotting) within a storage area [13]. Also, slotting methodologies have been used to assign products to storage locations in a DC [14]. Takahama et al. [15] implemented a method to support decision making regarding the assignment of storage locations using simulation-based optimization models. Heragu et al. [16] developed a mathematical model and a heuristic algorithm for solving a slotting problem or product allocation problem for a DC considering storage areas of different sizes. Hou et al. [17] elaborated a model for storage assignment and re-allocation of products in storage locations using a Warehouse Management System (WMS) in order to execute the put-away operation effectively, although unlike our proposal, this method did not consider put-away routing. Later, Kutzelnigg [18] implemented a mixed integer programming formulation and heuristics for solving a slotting problem in a DC. An order batching problem for put-away was represented and solved using heuristics [19], but the routing problem was not integrated with the put-away order batching problem in this study. Likewise, a basic put-away routing problem was solved using a classical tabu search [20], however, this paper did not consider a fleet of Material Handling Equipment (MHE), multiple products and a multi-parallel racking system with different height levels.
Regarding solution approaches for the PRP, particle swarm optimization (PSO) approaches emerge as an appropriate optimization algorithm for many optimization problems due to its quick development, its easy implementation, fast convergence and few particles required to be tuned [21]. In addition, it is more appropriate to deal with several optimization problems than other metaheuristics such as a genetic algorithm (GA), ant colony optimization (ACO) or tabu search (TS) [21,22,23,24]. In fact, PSO has been successfully implemented to solve complex optimization problems, such as combinatorial and assignment problems in different fields including logistics and warehousing processes. Compared to other approaches, there is no overlapping and mutation calculation when implementing discrete PSO for solving PRP, which could be considered as an advantage. Bai [21] described how discrete PSO could suffer from partial optimism, which makes it difficult to regulate the speed and position of the particles. This last issue is appreciated as a disadvantage of discrete PSO, but its advantage is the ease of representation and computational efficiency regarding other metaheuristics.
There are relevant papers that provide literature reviews of discrete PSO implementations in Vehicle Routing Problems (VRP). Chen et al. [25] developed a discrete PSO for solving a Capacitated Vehicle Routing Problem (CVRP) using global search and local search considering a fleet of trucks to minimize total transporting cost. Goksal et al. [22] describe how a discrete PSO was implemented for solving combinatorial optimization problems in supply chains, such as the Travelling Sales Problem (TSP), scheduling problems and VRP; even a discrete PSO for the VRP with simultaneous pickup and delivery (VRPSPD) was developed. Moreover, a permutation encoding was implemented to represent the solutions of the VRPSPD problem, considering constraints regarding the load capacity of truck fleets. Gong et al. [26] developed a set-based PSO to solve the discrete combinatorial optimization problem regarding VRP Time Windows (VRPTW), and real-value positions in continuous space for classical PSO are converted to integer values to represent routes for discrete PSO. On the other hand, Gong et al. [26] described an approach whereby discrete PSO generated the best-known results for Solomon’s VRPTW benchmarks, which proved able to achieve high performance to solve this kind of routing problem. Wo et al. [27] implemented a discrete PSO for solving a VRPWT using techniques such as initializing the population using a Push Forward Insertion Heuristic (PFIH), velocity and position updating, redefinition of the past best position (pbest) updating operation as well as using an objective function for measuring the total cost of routing the vehicles. As a result, the discrete PSO generated an increased efficiency of 30.9% compared to Ant Colony Optimization (ACO) to solve the routing problem.
Likewise, Alinaghian et al. [28] implemented a discrete PSO to solve a Time Dependent VRP (TDVRP) within a city logistics system considering traffic conditions. Discrete PSO provided the best solutions for the VRP problem by the cooperation of the particles, and it generated good performance compared to a branch and bound (method) since time differences were between 0 and 8%. Gómez et al. [11] developed a comparative analysis of the order batching and routing problem in the picking operation, regarding the classical Heterogeneous Vehicle Routing Problem (HVRP), which tackled this kind of problem in the warehouse and DC. These previous results guarantee that discrete PSO produces satisfactory results for VRP problems and its variants, advancing a promising approach for this kind of problems. Zhu and Hu [29] modelled a green TSP to minimize fuel consumption costs; they considered traffic congestion, and by combining a genetic algorithm and PSO, the authors greatly reduced fuel consumption. Dridi et al. [30] proposed an algorithm based on PSO to solve the VRP considering multiple vehicles, multiple depots, and the pickup and delivery problem with time windows, aiming to minimize the total travelled distance; they obtained better results by decreasing the travelled distance for several studied instances.
On the other hand, solving the PRP can support decision-makers in determining the best way to batch orders and perform routing for put-away operations in warehouses. The PRP solution would be expected to decrease travel times, MHE usage time, and work hours required to serve a given volume of work, therefore improving the economic, environmental, and social dimensions in warehouse management and supporting the achievement of sustainable supply chains [31]. Even the PRP solution algorithms can be integrated into flexible inventory management, warehouse management, and operations management systems to optimize the flow in the supply chain [32], and can become the input for cyber-physical systems such as augmented reality, with which operators can easily locate the items and storage positions involved in put-away operations [33].
From the literature review, it is noted that papers regarding discrete PSO to solve the PRP have not been identified, since the detected studies were focused on VRP and their different variants, and they were mainly applied to transport and distribution systems within supply chains rather than put-away operations in warehouses. Therefore, our paper covers some gaps in the literature by proposing a Put-away Routing Problem (PRP) for DCs considering a non-palletized racking system (3D warehouses), multiple homogeneous Material Handling Equipment (MHE) and multiple products to be processed. This approach for the PRP has not been found in the literature as presented above. Furthermore, the proposed PRP is solved using a discrete PSO algorithm that is compared to several tabu search approaches (Classical Tabu Search (CTS), Tabu Search (TS) 2-Opt) and an empirical rule. These metaheuristics and the empirical rule have not been found in the literature to address PRP. To the best of our knowledge, this paper is one of the first in addressing the PRP in the literature.
3. Problem Description and Modelling
In this section, the problem description and its mathematical modelling are presented.
3.1. Problem Description
The put-away routing problem (PRP) is formulated for a conventional multi-parallel aisle warehouse layout with two cross-aisles. This type of warehouse is classified as a non-palletized racking system (3D warehouse) since the logistic items to be stored are boxes, packages and so on, and they are managed manually. Each aisle has multiple storage locations in multiple height levels (see Figure 1).
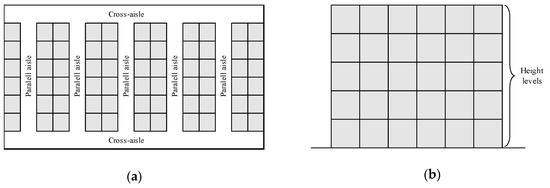
Figure 1.
(a) Superior view of the warehouse and (b) front view of a parallel aisle.
The products are put at the pre-allocated storage locations using Material Handling Equipment. The received products to be put away are linked to an arrival document. Each arrival document is formed by product identification codes and the number of products to be stored as well as specific characteristics such as temperature, nature of the product, relative humidity, expiration date, among others. The products are allocated using a put-away list, where a put-away list is created by the WMS based on the information of a set of arrival documents.
A put-away route is formed by a sequence of storage locations to be visited. The products of each arrival document or put-away list must be assigned to one route. Usually, a set of put-away routes are generated based on the load and volume capacity constraints of a homogeneous MHE and the number of products to be allocated. Moreover, costly and limited logistic resources such as MHE, intensive labour force, and ICT are usually used to execute put-away operations (unloading, inspection, handling and so on). Therefore, PRP must be performed in the minimum time and with an efficiency-based approach. An agile put-away operation improves replenishment of storage locations, which impacts positively on the effective inventory management and the performance of DCs. For this reason, the minimum operation time is set as the objective function of the problem.
The PRP allows assignment of any possible storage location for each product, representing a random storage policy. The WMS is the information system used to state the location for the product, attending to availability and logistic constraints (e.g., load capacity, volume, non-cross-contamination between products). The WMS output is considered as a known input for the PRP. It has to be noted that put-away time will depend on the storage location allocated to each product. On the other hand, a fleet of homogenous MHE is considered for this PRP. The fleet is composed by homogeneous MHE with the same load and volume capacity, travel speed, and maximum lift height. Additionally, MHE execute vertical and horizontal movements in a DC and only one MHE is assigned to a put-away route.
The problem is complex because multiple products linked to an arrival document must be allocated to the assigned storage locations in each work shift for a DC. Therefore, a set of put-away routes must be created using metaheuristics to perform the operation in the shortest time. A slotting method must be implemented to assign storage locations in a multilevel rack storage system, which directly impacts put-away routes. Finally, this problem is approached using a product portfolio, which is formed by products with different weights, volumes, and sizes.
Although the PRP presents some similarities with picking operations, they have differences in their objective function, decision variables, and constraints. Regarding the objective function and decision variables in the picking routing problem, these functions aim to find the shortest possible operation time, minimum tardiness and maximum level of customer service since they are oriented to outbound logistics in supply chains [34,35,36]. The order picking is constrained by the availability of inventory while the operation is executed, while the PRP is constrained by storage locations in the rack system. In addition, as the PRP considers simultaneously slotting and routing problems, the structures of the search spaces and the set of routes are different from those of order picking problems such as order batching, sequencing, and routing [3,37].
3.2. Problem Formulation
We define the following assumptions for the PRP model formulation:
- Every product is allocated to a storage location. This allocation is made following storage compatibility among products based on the type of product, volume, weight, fragility, etc.
- There is a set of homogeneous vehicles (MHE) with the same characteristics of speed and available load capacity and each of them will be assigned to a specific route. In the case that some MHE were not used, the idle MHE would be assigned to fictitious routes with the depot as origin and destination.
The indices, sets, data, variables and mathematical model formulation to optimize the put-away routing problem (PRP) are as follows.
Indices and sets:
| e, fN | Storage locations. This set includes the depot that acts as the origin and destination of the route (first and final node for every route) |
| N | Storage subset of locations |
| c C | Put-away routes. The set of candidate routes are associated with the number of available MHE. Therefore, there are as many candidate routes as MHE in the depot plus a fictitious route with the depot as origin and destination to represent the case of a MHE not being used. |
| i I | Product i received to be put-away. |
Data:
| def | Distance between storage locations e and f. |
| Travel speed (m/s) of each MHE. | |
| Available load capacity of each MHE. | |
| bi | Quantity of product expressed in units for the product i to be put away. In manual picking warehouses bi < LC to allow handling product boxes manually. |
| Product i is assigned to storage location e. Note that this allocation is predefined and it is done as a function of the product characteristics (weight, volume, etc.). |
Variables:
Model:
The objective function in Equation (1) aims to minimize the total put-away time for the set of designed routes measured as the travel time to the storage locations since the handling time at the location is a constant value given the pre-allocation . Constraints in Equation (2) ensure the assignment of each product i to only one route cC, which will be associated with one of the MHE. Constraints in Equation (3) ensure that the load capacity of the MHE is not being exceeded by the number of products allocated to the vehicle in the route cC. Constraints in Equations (4) and (5) ensure that each storage location has one predecessor and one successor within a put-away route. Note that the first node of the route will have the depot as the predecessor and the last node will have the depot as successor. Constraints in Equation (6) avoid sub-tours in the set of G storage locations that will give place to disconnected routes. This is a common and mandatory constraint in every vehicle routing problem. Constraints in Equation (7) ensure that the storage location e is visited within the put-away route c if a set of products i with this storage location is allocated to route c. Constraints in Equation (8) ensure that the variables of the problem are binary.
4. Approaches for Solving the Put-Away Routing Problem (PRP)
The mathematical model formulated in the previous section can be a large scale optimization problem with binary decision variables. This fact leads to the implementation of computational intelligence approaches with more efficiency than exact mathematical methods. In this line, this section shows a discrete PSO that is formulated and implemented for solving the PRP. Benchmark methods named Tabu Search metaheuristic (Classical Tabu Search (CTS), Tabu Search (TS) 2-Opt) and empirical rule are proposed for evaluating the performance of the discrete PSO.
4.1. Subsection
PSO is a metaheuristic approach based on evolutionary techniques, which uses a population-based swarm intelligence algorithm [38,39]. Discrete PSO is established to appropriately represent the structure of the solution space and set of put-away routes, as well as the position and velocity operators, because a classical PSO metaheuristic is used for problems with continuous solutions spaces and continuous encoding schemes for the particles. The approach we followed by implementing a discrete PSO algorithm for solving the proposed PRP is presented in Figure 2.
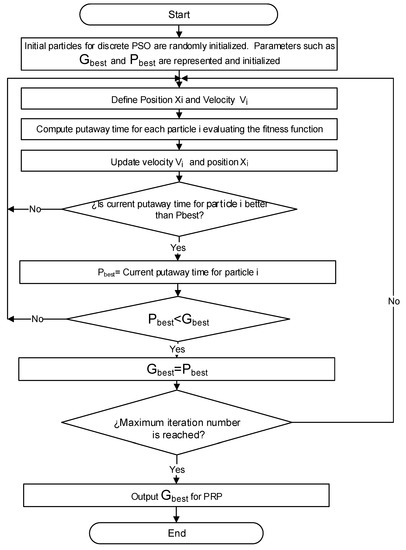
Figure 2.
Flowchart of the discrete particle swarm optimization (PSO) for the Put-away Routing Problem (PRP).
4.1.1. Generation of the Initial Set of Particles for PSO
An initial set of put-away routes is created by implementing a FIFO priority rule that considers the availability and capacity of K homogenous MHE, as well as products to be allocated at the storage locations. Note that a put-away route cC is composed of a sequence of storage locations eN to be visited to place an amount (bi) of products i using MHE.
Discrete PSO has particles, which are formed by a set of put-away routes (SPR). Each route of the set SPR has an MHE that is assigned to serve N storage locations to put away the allocated products. Each storage location is a named discrete point, which is encoded with a value of 0 or 1. If the value is 1 then that storage location is assigned to a route cC belonging to SPR, otherwise the value is 0. An example of a particle for a set of 12 storage locations to be visited to perform the put-away operation is shown in Figure 3. Put-away routes cC start and finish at the same place named Depot (D) in the DC.
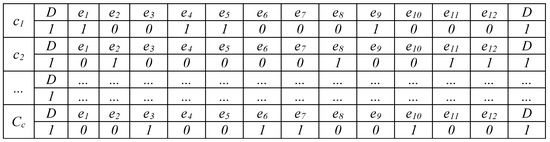
Figure 3.
Encoding scheme of a particle for a discrete PSO.
Additionally, each particle has a position Xi, and a velocity Vi, linked to a storage location eN belonging to each route c C. In this step, the parameters Gbest, Pbest, the position Xi, and the Vi velocity are determined to initialize the discrete PSO metaheuristic.
4.1.2. Definition of the Position of the Particles
The position of each particle i (Xi) is represented using the following expressions (Equations (9) and (10)).
where:
: Position of the product i in dimension l (storage location). This dimension is formed by arcs adjacent to the current storage location l.
l: Current storage location (node) to be visited within the put-away route.
e: Previous storage location of location l.
f: Subsequent storage location of location l.
n: Number of storage positions (node) of the (DC).
4.1.3. Definition of the Velocity of the Particles
The velocity of a particle i (Vi) is defined using expressions (Equations (11) and (12))
where:
a: An arc which links two storage locations within storage locations.
p(a): Probability of a component a ∈ A in the dth dimension, which is measured as a proportion of the distance between storage locations and total distance.
d: Dimension dth is a set of adjacent arcs to the specific storage location l (current node) associated with the position of a particle .
: Search space formed by the arc set associated with dimension d.
4.1.4. Put-Away Time for Each Particle r (Fitness Function)
Put-away times are calculated for each particle r linked to a route c ∈ C by implementing the objective function (Equation (1)). Then, the put-away time is calculated for each route c ∈ C and then added to compute the total put-away time of the set of routes. Put-away times are expressed in minutes.
4.1.5. Velocity Updating for Discrete PSO
Velocity updating is executed using Equations (13)–(18), following the proposal provided by [26,27].
where:
i and h: Index of particles i and h in the dth dimension.
a: An arc which links two storage locations within storage locations.
p(a): Probability of a component a ∈ A in the dth dimension, which is used to represents a proportion of the distance between storage locations and total distance.
p′(a): Probability of a component a ∈ A in the dth dimension for updating velocity.
: Substraction of positions of particles i and h in the dth dimension for discrete PSO.
: Parameter implemented to update velocity for discrete PSO with a range from 0 to 1 [0, 1].
: Sum of velocities of particles i and h in the dth dimension for discrete PSO.
: Arc set used to update velocity in the dth dimension, which is associated with particles defined for discrete PSO.
Velocity updating (Equations (13)–(18)) is calculated based on velocity ) and position ) of a particle i in a dth dimension. In the discrete PSO, the velocity updating is represented by operators with a factor and velocity for particle i ), named )), the addition of velocities (), and the subtraction of positions () associated to the storage locations that form a particle i in the dth dimension. Therefore, position updating is directly associated with the velocity of a particle i for discrete PSO. Equation (19) is used for position updating:
where:
P (random): Random number with a range from 0 to 1 [0, 1].
: Velocity of a particle i in a dth dimension is transformed into a temporal set for updating the position for the discrete PSO.
4.1.6. Stopping Criteria
The algorithm ends when the maximum number of iterations has been met. If this condition has been reached, then the PSO metaheuristic is ended and Gbest is stated as the solution for the PRP.
4.2. Tabu Search Metaheuristic Approach
A Classical Tabu Search and a hybrid approach combining the Tabu Search and the 2-Opt operator, known as TS 2-Opt, are used for sorting out the PRP. These metaheuristics are selected because they allow dealing with NP-hard problems such as the PRP. The TS metaheuristic proved to be a good method to solve picker routing problems in DCs [40].
The CTS metaheuristic implements classic components such as the solution structure (put-away routes), the tabu list, the objective function, the swap and shift movements, and the stopping criteria for the PRP. Meanwhile, the main difference between TS 2-Opt and CTS is the implementation of the double swap and shift movements, which are designed to improve the efficiency of exploration of the solution space, generating minimum time put-away routes. CTS and TS-2-Opt are novel approaches for solving the PRP since metaheuristics were not found for tackling this problem in the literature for put-away operation. In addition, CTS and TS-2-Opt were also used as benchmark metaheuristics for solving the picking routing problem since they proved to have good performance for this class problem [40]. However, note that order picking and put-away operations have differences regarding the objective functions and their constraints (MHE, multiple products, non-pallet racking system).
4.3. Empirical Rule FPNP
In addition to tabu search approaches, an empirical rule called Farthest Position and Nearest Position (FPNP) was implemented for solving the PRP in the business environment [23,40,41]. This routing rule starts putting the products at the allocated storage locations farthest from the depot and continues to put away the products up to the ones nearest to the depot. This routing rule generates only one solution, which is created using the logic described above.
5. Experimental Study
In this section, we present the experimental study; it allows comparing the performances of the PSO against other metaheuristics and the FPNP heuristic. The total put-away routing time is set as the response variable.
The put-away routing problem is formulated for a conventional multi-parallel aisle layout classified as a medium-sized warehouse. This layout is formed by 400 storage locations, and 6 parallel aisles, and each aisle has storage locations with different height levels. The products are put at an allocated storage location using Material Handling Equipment. A fleet of homogenous MHE is represented in this problem. A fleet is formed by several MHE with the same load capacity, travel speed, and maximum lift height.
A full factorial design 4 × 4 × 3 × 2 is planned to perform the experimental analysis. This design of experiment (DOE) is chosen since the combination of factor levels are randomly executed. The combination of factor levels generates the set of problems to study the performance of metaheuristics (discrete PSO, CTS, and TS 2-Opt) and the empirical rule (FPNP). Experimental conditions for the developed metaheuristics, factor levels and response variables for this experimental study are represented in Table 1 and Table 2.

Table 1.
Experimental study for PRP.

Table 2.
Experimental factors for the PRP.
Metaheuristics and the FPNP rule are encoded using JAVA®. The tenure list for CTS and TS 2-Opt was equal to 7. Parameter ω was equal to 0.7 (ω = 0.7) for the discrete PSO. Other factors, such as a, p(a), p′(a), and Td were set according to the set of arcs of the storage locations for the PRP. The parameters for the metaheuristics were determined based on an analysis of 1000 experimental tests for CTS, TS 2-Opt and discrete PSO; they were selected according to those tests that produced the best results for the PRP using the total put-away time as the response variable. The differences between the selected parameters and the other implemented ones were around 5 and 7% for total put-away times, respectively. Experimental runs were performed on a PC with a Pentium VII processor with 2 GB RAM.
Four benchmark treatments are set up for evaluating the performance of CTS, TS 2-Opt and discrete PSO. The difference between the benchmarks is the put-away list size.
- Benchmark treatment 1: FPNP (routing strategy), one MHE and Centre (depot) and 100 products (put-away list size)
- Benchmark treatment 2: FPNP (routing strategy), one MHE and Centre (depot) and 250 products (put-away list size)
- Benchmark treatment 3: FPNP (routing strategy), one MHE and Centre (depot) and 400 products (put-away list size)
- Benchmark treatment 4: FPNP (routing strategy), one MHE and Centre (depot) and 600 products (Put-away list size)
6. Results and Discussion
The results of the experimental scenarios are presented in Table 3. The experiments are formed by four factors including the routing method, put-away list size, depot and number of MHE. Additionally, the total average put-away routing times (minutes) and performance savings are used as response variables for this problem. Note that 20 replicates for each of the 96 problems are performed, providing 1920 runs (total replicates) to ensure the statistical validity to implement the Analysis of Variance (ANOVA) for the full factorial design 4 × 4 × 3 × 2.

Table 3.
Results of the experiments for the PRP.
Based on the results of 1920 experimental runs, it is found that the discrete PSO generates the best set of put-away routes for the PRP since it decreases the total average put-away time by 30 to 81% when compared to FPNP empirical rule. The time difference between discrete PSO and TS 2-Opt is smaller since it varies between 3.2 and 3.5%, generating a good performance to solve the PRP. Meanwhile, the time difference between discrete PSO and CTS was higher since it differs from 5.8 to 8.2%.
The Analysis of Variance (ANOVA) obtained for the full factorial design 4 × 4 × 3 × 2 is examined to detect significant main effects and two-way interaction effects for the response variable (Table 4). Three main effects and two two-way interaction effects are identified to be statistically significant in the ANOVA because the p-values are less than 0.05. Note that significant effects with a higher Mean Square (MS) usually generate a shorter total average put-away time. Therefore, the combinations of factor levels of these significant effects are set as the solution for the PRP. If a factor is significant within a two-way interaction effect, it must be analysed instead of its main effect. Therefore, there is a hierarchy of importance between the main effects and interactions effects for analysing the statistical results for the PRP.

Table 4.
ANOVA of full factorial design for the PRP.
The two-way interaction effects of fleet size (FMHE) by routing method (RM), fleet size (FMHE) by put-away list size (PLS), and routing method (RM) by put-away list size (PLS) are statistically significant at an alpha value of 0.05. Therefore, these interactions have a significant effect on the response variable, and they are analysed to evaluate the differences and impacts of the factors and their levels on total average put-away times. Additionally, the significant interaction effects for the PRP are evaluated to determine the combination of factor levels that generates the shortest possible put-away times in a DC. The two-way interaction effect plots are represented in Figure 4.
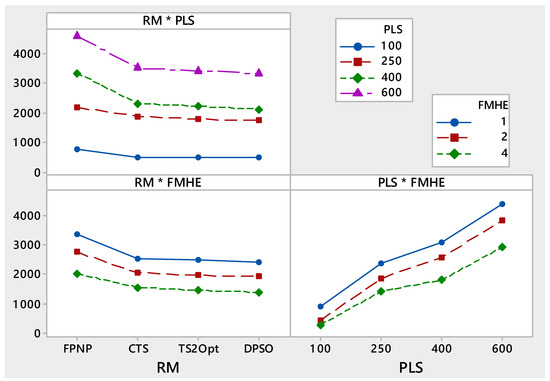
Figure 4.
Two-way interaction effects for the PRP.
The results in Figure 4 show that discrete PSO (method routing) produces the best solution for the PRP compared to the CTS and TS 2-Opt metaheuristics. The difference between the total put-away times generated by the three-way interaction effects is explained by the levels of the fleet size of MHE and list size put-away factors. This occurs because a larger list size generates longer total put-away times due to the distance to be travelled to put away the products at assigned storage locations.
On the other hand, Table 5 presents the time reduction provided by discrete PSO when compared to CTS, TS 2-Opt, and the FPNP empirical rule for the two-way interaction effects of RM by FMHE. Table 5 shows that discrete PSO generates the greatest reduction in put-away time relative to FPNP, which varies between 41.8% and 43.9% according to the level of FMHE. Moreover, the time difference between discrete PSO and TS 2-Opt is small and varies from 3.2% to 3.5%.

Table 5.
Time savings (seconds) and percentage savings (%) of discrete PSO by FMHE.
Meanwhile, Table 6 describes the time reduction provided by discrete PSO relative to CTS, TS 2-Opt and the FPNP empirical rule for the two-way interaction effects RM by PLS. Table 6 shows that discrete PSO produces a greater reduction of put-away time compared to FPNP, which varies between 25.2% and 65.6% according to the level of PLS. In addition, PSO outperforms tabu approaches, although the time reduction between discrete PSO and TS 2-Opt (the best tabu) is smaller, and varies from 2.4% to 4.7%.

Table 6.
Time savings (seconds) and percentage savings (%) by PLS.
The discrete PSO metaheuristic (routing method) and its two-way effect interactions formed by the number of MHE and put-away list size have the greater statistical significance on the total average put-away times for solving the PRP due to their high values of MS, as explained above. The discrete PSO metaheuristic decreases the total put-away time relative to the CTS and TS 2-Opt metaheuristics by 2.4 to 8.9%. Finally, these results prove the relevance of the PSO approach for solving the PRP.
7. Conclusions
This paper addresses the relevance of put-away operations in DCs; it aims to improve the planning, execution, and efficiency of the put-away of products at storage locations. This paper reveals that the routing activity has a significant impact on put-away time, which in turn affects the operational efficiency of this process. These findings are supported by the results of the experimental study performed for the middle size DC represented in this paper.
A PSO algorithm was developed and compared to other tabu approaches (TS 2-Opt and CTS), as well as a FPNP rule for the PRP. It should be noted that both the formulated problem and metaheuristics constitute novel approaches since they represent one of the first approaches to tackle the put-away routing problem in the literature. The discrete PSO approach generated the best solution for solving the PRP relative to TS 2-Opt and CTS, as well as the FPNP rule. Furthermore, it was detected that discrete PSO produced the largest reduction of the put-away time relative to the FPNP, which was between 41.8% and 43.9% according to the FMHE. The time difference between discrete PSO and TS 2-Opt was smaller since it varied between 3.2% and 3.5%. On the other hand, it was found that discrete PSO provided the greatest put-away time reduction compared to the FPNP (between 25.2% and 65.6%), according to the level of PLS. Additionally, the time difference between discrete PSO and TS 2-Opt is smaller since it varies from 2.4% and 8.9%.
These results showed that the discrete PSO metaheuristic routing method generates the best solutions for the PRP, outperforming other approaches, and advancing as a very promising solution method for this kind of problems. Therefore, this study allows reducing travel times for the PRP, which implies a reduction in operating costs, a reduction in energy consumption by the MHE in a work shift, and the reduction in operating hours, supporting the achievement of sustainable warehousing.
As further research, we suggest considering heterogeneous MHE to address real environments in put-away operations. Likewise, future research should address the integration of PRP solution algorithms with inventory management systems and WMS, and the integration of these traditional systems with cyber-physical systems that facilitate the interaction between operators and optimization methods. Finally, novel formulations and metaheuristic approaches can be considered regarding this issue.
Author Contributions
R.A.G.-M. and P.C. contributed in this work in the formulation of the mathematical model, the process of experimentation, and they analyzed and interpreted the results. J.A.C. and F.S. participated in the editing and writing of the document; they conducted a literature review based on the importance of the put-away routing problem; and in addition they analyzed the state-of-the art of the models applied to the solutions of these problems. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bartholdi, J.J.; Hackman, S.T. Warehouse & Distribution Science; The Supply Chain and Logistics Institute: Atlanta, GA, USA, 2014. [Google Scholar]
- CSCMP Supply Chain Management: Terms and Glossary. Available online: https://bit.ly/2e3NMGE (accessed on 8 November 2016).
- Cano, J.A.; Correa-Espinal, A.; Gómez-Montoya, R.A. Solving the Order Batching Problem in Warehouses using Genetic Algorithms. Inf. Tecnol. 2018, 29, 235–244. [Google Scholar] [CrossRef]
- Cano, J.A. Order Picking Optimization Based on a Picker Routing Heuristic: Minimizing Total Traveled Distance in Warehouses. In Handbook of Research on the Applications of International Transportation and Logistics for World Trade; Ceyhun, G.Ç., Ed.; IGI Global: Hershey, PA, USA, 2020; pp. 74–96. [Google Scholar]
- Van Gils, T.; Ramaekers, K.; Caris, A.; de Koster, R.B.M. Designing Efficient Order Picking Systems by Combining Planning Problems: State-of-the-art Classification and Review. Eur. J. Oper. Res. 2018, 267, 1–15. [Google Scholar] [CrossRef]
- Cano, J.A. Formulations for joint order picking problems in low-level picker-to-part systems. Bull. Electr. Eng. Inform. 2020, 9, 836–844. [Google Scholar] [CrossRef]
- Yan, H.; Tang, S.-L. Pre-distribution and post-distribution cross-docking operations. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 843–859. [Google Scholar] [CrossRef]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Buijs, P.; Danhof, H.W.; Wortmann, J.H.C. Just-in-Time Retail Distribution: A Systems Perspective on Cross-Docking. J. Bus. Logist. 2016, 37, 213–230. [Google Scholar] [CrossRef]
- Frazelle, E.H. World-Class Warehousing and Material Handling, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2016; ISBN 9780071842822. [Google Scholar]
- Gómez, R.A.; Correa, A.; Muñuzuri, J.; Cortes, P. Comparative analysis of order batching and routing problem in the picking regarding classical HVRP (heterogeneous vehicle routing problem) [Análisis comparativo del problema de conformación de lotes con ruteo en la preparación de pedidos respecto al HVRP]. Dir. Organ. 2016, 59, 49–60. [Google Scholar]
- Chan, F.T.S.; Chan, H.K. Improving the productivity of order picking of a manual-pick and multi-level rack distribution warehouse through the implementation of class-based storage. Expert Syst. Appl. 2011, 38, 2686–2700. [Google Scholar] [CrossRef]
- Muppani, V.R.; Adil, G.K. Efficient formation of storage classes for warehouse storage location assignment: A simulated annealing approach. Omega 2008, 36, 609–618. [Google Scholar] [CrossRef]
- Kim, B.S.; Smith, J.S. Slotting methodology using correlated improvement for a zone-based carton picking distribution system. Comput. Ind. Eng. 2012, 62, 286–295. [Google Scholar] [CrossRef]
- Takahama, H.; Nishi, T.; Konishi, M.; Imai, J. A determination method of product allocation schedule for warehouse management. In Proceedings of the 41st SICE Annual Conference, SICE 2002, Osaka, Japan, 5–7 August 2002; pp. 1004–1007. [Google Scholar]
- Heragu, S.S.; Du, L.; Mantel, R.J.; Schuur, P.C. Mathematical model for warehouse design and product allocation. Int. J. Prod. Res. 2005, 43, 327–350. [Google Scholar] [CrossRef]
- Hou, J.L.; Wu, Y.J.; Yang, Y.J. A model for storage arrangement and re-allocation for storage management operations. Int. J. Comput. Integr. Manuf. 2010, 23, 369–390. [Google Scholar] [CrossRef]
- Kutzelnigg, R. Optimal allocation of goods in a warehouse: Minimizing the order picking costs under real-life constraints. In Proceedings of the LINDI 2011—3rd IEEE International Symposium on Logistics and Industrial Informatics, Budapest, Hungary, 25–27 August 2011; pp. 65–70. [Google Scholar]
- Gómez, R.A.; Giraldo, O.G.; Campo, E.A. Conformación de Lotes Mínimo Tiempo en la Operación de Acomodo Considerando k Equipos Homogéneos usando Metaheurísticos. Inf. Tecnol. 2016, 27, 53–62. [Google Scholar] [CrossRef][Green Version]
- Correa, A.; Rodríguez, E.; Gómez, R. Modelamiento del ruteo del acomodo de tiempo mínimo en centros de distribución (CEDI) usando búsqueda tabú. Rev. Soluc. Postgrado EIA 2014, 6, 15–28. [Google Scholar]
- Bai, Q. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180–184. [Google Scholar] [CrossRef]
- Goksal, F.; Karaoglan, I.; Altiparmak, F. A Hybrid Discrete Particle Swarm Optimization for Vehicle Routing Problem with Simultaneous Pickup and Delivery. Comput. Ind. Eng. 2013, 65, 39–53. [Google Scholar] [CrossRef]
- Chen, F.; Wang, H.; Xie, Y.; Qi, C. An ACO-based online routing method for multiple order pickers with congestion consideration in warehouse. J. Intell. Manuf. 2016, 27, 389–408. [Google Scholar] [CrossRef]
- Masae, M.; Glock, C.H.; Grosse, E.H. Order picker routing in warehouses: A systematic literature review. Int. J. Prod. Econ. 2020, 224, 107564. [Google Scholar] [CrossRef]
- Chen, A.L.; Yang, G.K.; Wu, Z.M. Hybrid Discrete Particle Swarm Optimization Algorithm for Capacitated Vehicle Routing Problem. J. Zhejiang Univ. Sci. A 2006, 7, 607–614. [Google Scholar] [CrossRef]
- Gong, Y.J.; Zhang, J.; Liu, O.; Huang, R.Z.; Chung, H.S.H.; Shi, Y.H. Optimizing the Vehicle Routing Problem with Time Windows: A Discrete Particle Swarm Optimization Approach. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2011, 42, 254–267. [Google Scholar] [CrossRef]
- Wu, D.; Dong, M.; Li, M.; Li, F. Vehicle routing problem with time windows using multi-objective co-evolutionary approach. Int. J. Simul. Model. 2016, 15, 742–753. [Google Scholar] [CrossRef]
- Alinaghian, M.; Ghazanfari, M.; Norouzi, N.; Nouralizadeh, H. A Novel Model for the Time Dependent Competitive Vehicle Routing Problem: Modified Random Topology Particle Swarm Optimization. Netw. Spat. Econ. 2017, 17, 1185–1211. [Google Scholar] [CrossRef]
- Zhu, L.; Hu, D. Study on the vehicle routing problem considering congestion and emission factors. Int. J. Prod. Res. 2019, 57, 6115–6129. [Google Scholar] [CrossRef]
- Harbaoui Dridi, I.; Ben Alaïa, E.; Borne, P.; Bouchriha, H. Optimisation of the multi-depots pick-up and delivery problems with time windows and multi-vehicles using PSO algorithm. Int. J. Prod. Res. 2020, 58, 4201–4214. [Google Scholar] [CrossRef]
- Tebaldi, L.; Bigliardi, B.; Bottani, E. Sustainable supply chain and innovation: A review of the recent literature. Sustainability 2018, 10, 3946. [Google Scholar] [CrossRef]
- Di Nardo, M.; Clericuzio, M.; Murino, T.; Sepe, C. An economic order quantity stochastic dynamic optimization model in a logistic 4.0 environment. Sustainability 2020, 12, 4075. [Google Scholar] [CrossRef]
- Di Nardo, M.; Forino, D.; Murino, T. The evolution of man–machine interaction: The role of human in Industry 4.0 paradigm. Prod. Manuf. Res. 2020, 8, 20–34. [Google Scholar] [CrossRef]
- Lu, W.; McFarlane, D.; Giannikas, V.; Zhang, Q. An algorithm for dynamic order-picking in warehouse operations. Eur. J. Oper. Res. 2016, 248, 107–122. [Google Scholar] [CrossRef]
- Schrotenboer, A.H.; Wruck, S.; Roodbergen, K.J.; Veenstra, M.; Dijkstra, A.S. Order picker routing with product returns and interaction delays. Int. J. Prod. Res. 2017, 55, 6394–6406. [Google Scholar] [CrossRef]
- Cano, J.A.; Correa-Espinal, A.A.; Gómez-Montoya, R.A. Mathematical programming modeling for joint order batching, sequencing and picker routing problems in manual order picking systems. J. King Saud Univ. Eng. Sci. 2019, 32, 219–228. [Google Scholar] [CrossRef]
- De Vries, J.; de Koster, R.; Stam, D. Exploring the Role of Picker Personality in Predicting Picking Performance with Pick by Voice, Pick to Light and RF-Terminal Picking. Int. J. Prod. Res. 2015, 54, 2260–2274. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar]
- Lin, M.Y.; Chin, K.S.; Tsui, K.L.; Wong, T.C. Genetic based discrete particle swarm optimization for Elderly Day Care Center timetabling. Comput. Oper. Res. 2016, 65, 125–138. [Google Scholar] [CrossRef]
- Cortés, P.; Gómez-Montoya, R.A.; Muñuzuri, J.; Correa-Espinal, A. A tabu search approach to solving the picking routing problem for large- and medium-size distribution centres considering the availability of inventory and K heterogeneous material handling equipment. Appl. Soft Comput. 2017, 53, 61–73. [Google Scholar] [CrossRef]
- Henn, S. Algorithms for on-line order batching in an order picking warehouse. Comput. Oper. Res. 2012, 39, 2549–2563. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).