An Operational Matrix Method Based on Poly-Bernoulli Polynomials for Solving Fractional Delay Differential Equations
Abstract
1. Introduction
2. Preliminaries
2.1. The Atangana–Baleanu Derivative
2.2. The Properties of Poly-Bernoulli Polynomials
2.3. The Poly-Bernoulli Delay Operational Matrix
3. An Operational Matrix Based on Poly-Bernoulli Polynomials for an ABC-Fractional Derivative
Error Bound
4. An Application to Solving Variable Coefficients of Fractional Delay Differential Equations in the ABC-Derivative
4.1. Collocation Scheme
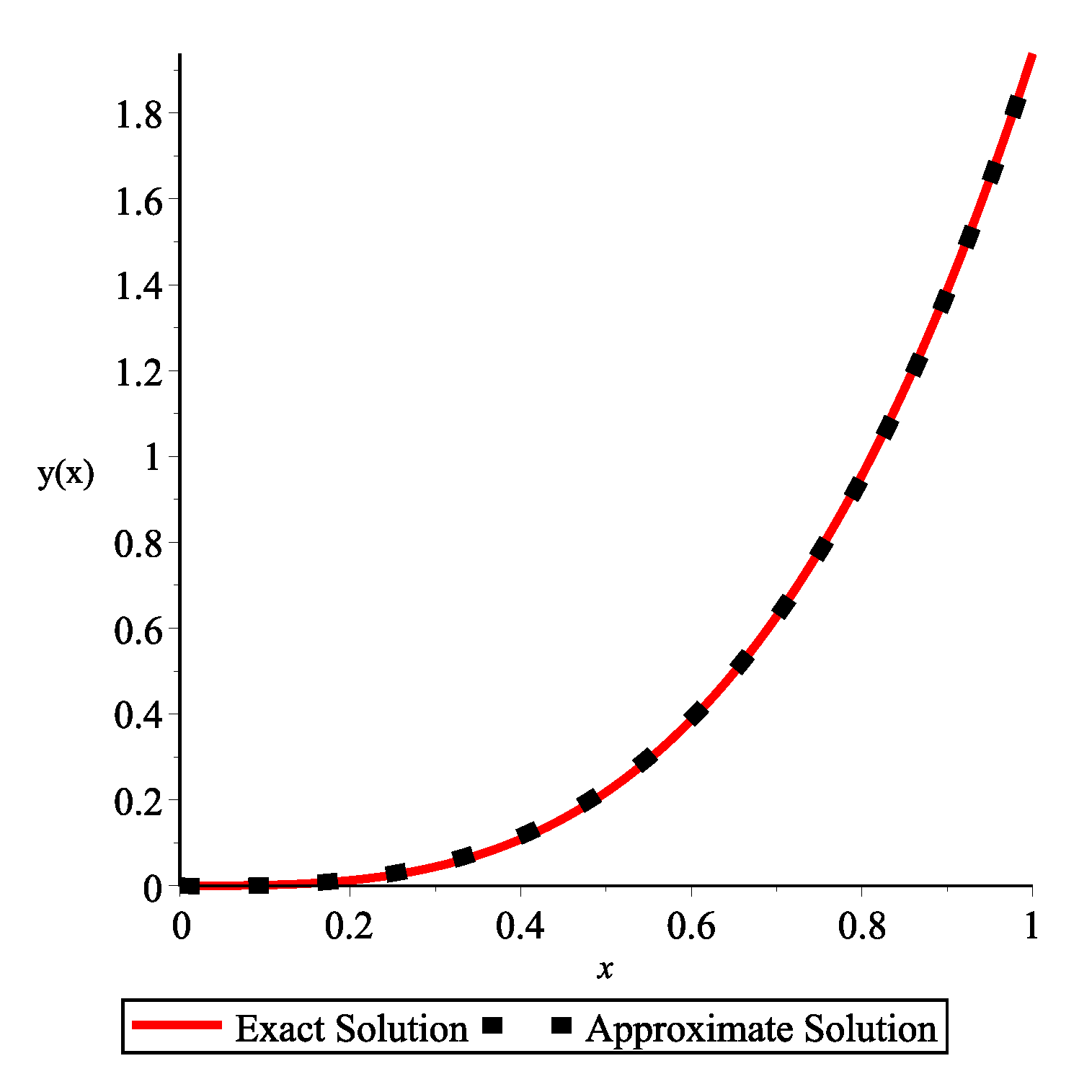
4.2. Numerical Examples
5. Conclusions
- A new operational matrix based on poly-Bernoulli polynomials for ABC-derivative.
- A new delay operational matrix based on poly-Bernoulli polynomials.
- A collocation scheme via operational matrix and delay operational matrix based on poly-Bernoulli polynomials for fractional differential equations in an ABC-sense.
- The proposed scheme can be modified to solve various other problems that use an ABC-derivative.
- The operational matrix can be extend to other poly-type polynomials.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017, 143, D4016005. [Google Scholar]
- Abdulhameed, M.; Vieru, D.; Roslan, R. Magnetohydrodynamic electroosmotic flow of Maxwell fluids with Caputo–Fabrizio derivatives through circular tubes. Comput. Math. Appl. 2017, 74, 2503–2519. [Google Scholar]
- Al-khedhairi, A. Dynamical analysis and chaos synchronization of a fractional-order novel financial model based on Caputo-Fabrizio derivative. Eur. Phys. J. Plus 2019, 134, 532. [Google Scholar]
- Atangana, A.; Khan, M.A. Modeling and analysis of competition model of bank data with fractal-fractional Caputo-Fabrizio operator. Alex. Eng. J. 2020, 59, 1985–1998. [Google Scholar]
- Ullah, S.; Khan, M.A.; Farooq, M. Modeling and analysis of the fractional HBV model with Atangana-Baleanu derivative. Eur. Phys. J. Plus 2018, 133, 313. [Google Scholar]
- Aliyu, A.I.; Alshomrani, A.S.; Li, Y.; Baleanu, D. Existence theory and numerical simulation of HIV-I cure model with new fractional derivative possessing a non-singular kernel. Adv. Differ. Equ. 2019, 2019, 408. [Google Scholar]
- Prakasha, D.; Veeresha, P.; Baskonus, H.M. Analysis of the dynamics of Hepatitis E virus using the Atangana-Baleanu fractional derivative. Eur. Phys. J. Plus 2019, 134, 241. [Google Scholar]
- Gómez-Aguilar, J.; Abro, K.A.; Kolebaje, O.; Yildirim, A. Chaos in a calcium oscillation model via Atangana-Baleanu operator with strong memory. Eur. Phys. J. Plus 2019, 134, 140. [Google Scholar]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Appl. 2020, 542, 123516. [Google Scholar]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar]
- Akgül, A.; Modanli, M. Crank–Nicholson difference method and reproducing kernel function for third order fractional differential equations in the sense of Atangana–Baleanu Caputo derivative. Chaos Solitons Fractals 2019, 127, 10–16. [Google Scholar]
- Yadav, S.; Pandey, R.K. Numerical approximation of fractional Burgers equation with Atangana–Baleanu derivative in Caputo sense. Chaos Solitons Fractals 2020, 133, 109630. [Google Scholar]
- Kumar, S.; Pandey, P. Quasi wavelet numerical approach of non-linear reaction diffusion and integro reaction-diffusion equation with Atangana–Baleanu time fractional derivative. Chaos Solitons Fractals 2020, 130, 109456. [Google Scholar]
- Kumar, S.; Kumar, A.; Nieto, J.; Sharma, B. Atangana–Baleanu derivative with fractional order applied to the gas dynamics equations. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Berlin/Heidelberg, Germany, 2019; pp. 235–251. [Google Scholar]
- Li, X.; Gao, Y.; Wu, B. Approximate solutions of Atangana-Baleanu variable order fractional problems. AIMS Math. 2020, 5, 2285–2294. [Google Scholar]
- Loh, J.R.; Isah, A.; Phang, C.; Toh, Y.T. On the new properties of Caputo–Fabrizio operator and its application in deriving shifted Legendre operational matrix. Appl. Numer. Math. 2018, 132, 138–153. [Google Scholar]
- Ganji, R.; Jafari, H.; Baleanu, D. A new approach for solving multi variable orders differential equations with Mittag–Leffler kernel. Chaos Solitons Fractals 2020, 130, 109405. [Google Scholar]
- Heydari, M.; Atangana, A. A cardinal approach for nonlinear variable-order time fractional Schrödinger equation defined by Atangana–Baleanu–Caputo derivative. Chaos Solitons Fractals 2019, 128, 339–348. [Google Scholar]
- Loh, J.R.; Phang, C. Numerical Solution of Fredholm Fractional Integro-differential Equation with Right-Sided Caputo’s Derivative Using Bernoulli Polynomials Operational Matrix of Fractional Derivative. Mediterr. J. Math. 2019, 16, 28. [Google Scholar]
- Rabiei, K.; Ordokhani, Y.; Babolian, E. Numerical Solution of 1D and 2D fractional optimal control of system via Bernoulli polynomials. Int. J. Appl. Comput. Math. 2018, 4, 7. [Google Scholar]
- Dehestani, H.; Ordokhani, Y.; Razzaghi, M. A numerical technique for solving various kinds of fractional partial differential equations via Genocchi hybrid functions. Rev. Real Acad. Cienc. Exactas Físicas Nat. Ser. A Mat. 2019, 113, 3297–3321. [Google Scholar]
- Loh, J.R.; Phang, C. A new numerical scheme for solving system of Volterra integro-differential equation. Alex. Eng. J. 2018, 57, 1117–1124. [Google Scholar]
- Kanwal, A.; Phang, C.; Iqbal, U. Numerical solution of fractional diffusion wave equation and fractional Klein–Gordon equation via two-dimensional Genocchi polynomials with a Ritz–Galerkin method. Computation 2018, 6, 40. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar]
- Baleanu, D.; Shiri, B.; Srivastava, H.; Al Qurashi, M. A Chebyshev spectral method based on operational matrix for fractional differential equations involving non-singular Mittag-Leffler kernel. Adv. Differ. Equ. 2018, 2018, 353. [Google Scholar]
- Ryoo, C.S.; Khan, W.A. On two bivariate kinds of poly-Bernoulli and poly-Genocchi polynomials. Mathematics 2020, 8, 417. [Google Scholar] [CrossRef]
- San Kim, D.; Kim, T. A note on degenerate poly-Bernoulli numbers and polynomials. Adv. Differ. Equ. 2015, 2015, 1–8. [Google Scholar]
- Kim, D.; Kim, T. A note on poly-Bernoulli and higher-order poly-Bernoulli polynomials. Russ. J. Math. Phys. 2015, 22, 26–33. [Google Scholar]
- Kaharuddin, L.N.; Phang, C.; Jamaian, S.S. Solution to the fractional logistic equation by modified Eulerian numbers. Eur. Phys. J. Plus 2020, 135, 229. [Google Scholar] [CrossRef]
- Sadeghi, S.; Jafari, H.; Nemati, S. Operational matrix for Atangana–Baleanu derivative based on Genocchi polynomials for solving FDEs. Chaos Solitons Fractals 2020, 135, 109736. [Google Scholar] [CrossRef]
- Saad, K.M. New fractional derivative with non-singular kernel for deriving Legendre spectral collocation method. Alex. Eng. J. 2020, 59, 1909–1917. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
| x | Exact Solution | Propose Method, | Propose Method, |
|---|---|---|---|
| 0 | 0 | 8.80000 × 10 | 2.01000 × 10 |
| 0.1 | 0.0076097334 | 1.72599 × 10 | 1.90269 × 10 |
| 0.2 | 0.0324547395 | 2.67576 × 10 | 4.08169 × 10 |
| 0.3 | 0.0765034239 | 4.61467 × 10 | 4.46544 × 10 |
| 0.4 | 0.1412220778 | 1.64420 × 10 | 2.74740 × 10 |
| 0.5 | 0.2278397784 | 4.87371 × 10 | 3.09000 × 10 |
| 0.6 | 0.3374369990 | 7.40603 × 10 | 5.74909 × 10 |
| 0.7 | 0.4709895148 | 1.99067 × 10 | 1.17086 × 10 |
| 0.8 | 0.6293940988 | 9.19385 × 10 | 8.89538 × 10 |
| 0.9 | 0.8134851328 | 1.61673 × 10 | 1.52310 × 10 |
| 1.0 | 1.0240460870 | 0.00000 × 10 | 0.00000 × 10 |
| x | Exact Solution | Propose Method, | Propose Method, |
|---|---|---|---|
| 0 | 0 | 2.00000 × 10 | 3.00000 × 10 |
| 0.1 | 0.0028633363 | 4.328440 × 10 | 3.34223 × 10 |
| 0.2 | 0.0132584457 | 3.51223 × 10 | 4.63151 × 10 |
| 0.3 | 0.0334875577 | 4.19672 × 10 | 4.52455 × 10 |
| 0.4 | 0.0656052327 | 1.97477 × 10 | 4.43244 × 10 |
| 0.5 | 0.1115273498 | 1.68033 × 10 | 5.43080 × 10 |
| 0.6 | 0.1730740180 | 1.88093 × 10 | 7.83066 × 10 |
| 0.7 | 0.2519928613 | 7.64132 × 10 | 1.09456 × 10 |
| 0.8 | 0.3499735921 | 1.27417 × 10 | 1.29460 × 10 |
| 0.9 | 0.4686579538 | 1.24322 × 10 | 1.07597 × 10 |
| 1.0 | 0.6096469123 | 4.00000 × 10 | 8.00000 × 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phang, C.; Toh, Y.T.; Md Nasrudin, F.S. An Operational Matrix Method Based on Poly-Bernoulli Polynomials for Solving Fractional Delay Differential Equations. Computation 2020, 8, 82. https://doi.org/10.3390/computation8030082
Phang C, Toh YT, Md Nasrudin FS. An Operational Matrix Method Based on Poly-Bernoulli Polynomials for Solving Fractional Delay Differential Equations. Computation. 2020; 8(3):82. https://doi.org/10.3390/computation8030082
Chicago/Turabian StylePhang, Chang, Yoke Teng Toh, and Farah Suraya Md Nasrudin. 2020. "An Operational Matrix Method Based on Poly-Bernoulli Polynomials for Solving Fractional Delay Differential Equations" Computation 8, no. 3: 82. https://doi.org/10.3390/computation8030082
APA StylePhang, C., Toh, Y. T., & Md Nasrudin, F. S. (2020). An Operational Matrix Method Based on Poly-Bernoulli Polynomials for Solving Fractional Delay Differential Equations. Computation, 8(3), 82. https://doi.org/10.3390/computation8030082





