A Modification of Gradient Descent Method for Solving Coefficient Inverse Problem for Acoustics Equations
Abstract
1. Introduction
2. Direct Problem
2.1. Governing Equations
2.2. Brief Introduction to Godunov Finite-Difference Scheme
3. Inverse Problem of Recovering the Density
4. Modification of Gradient Descent Method
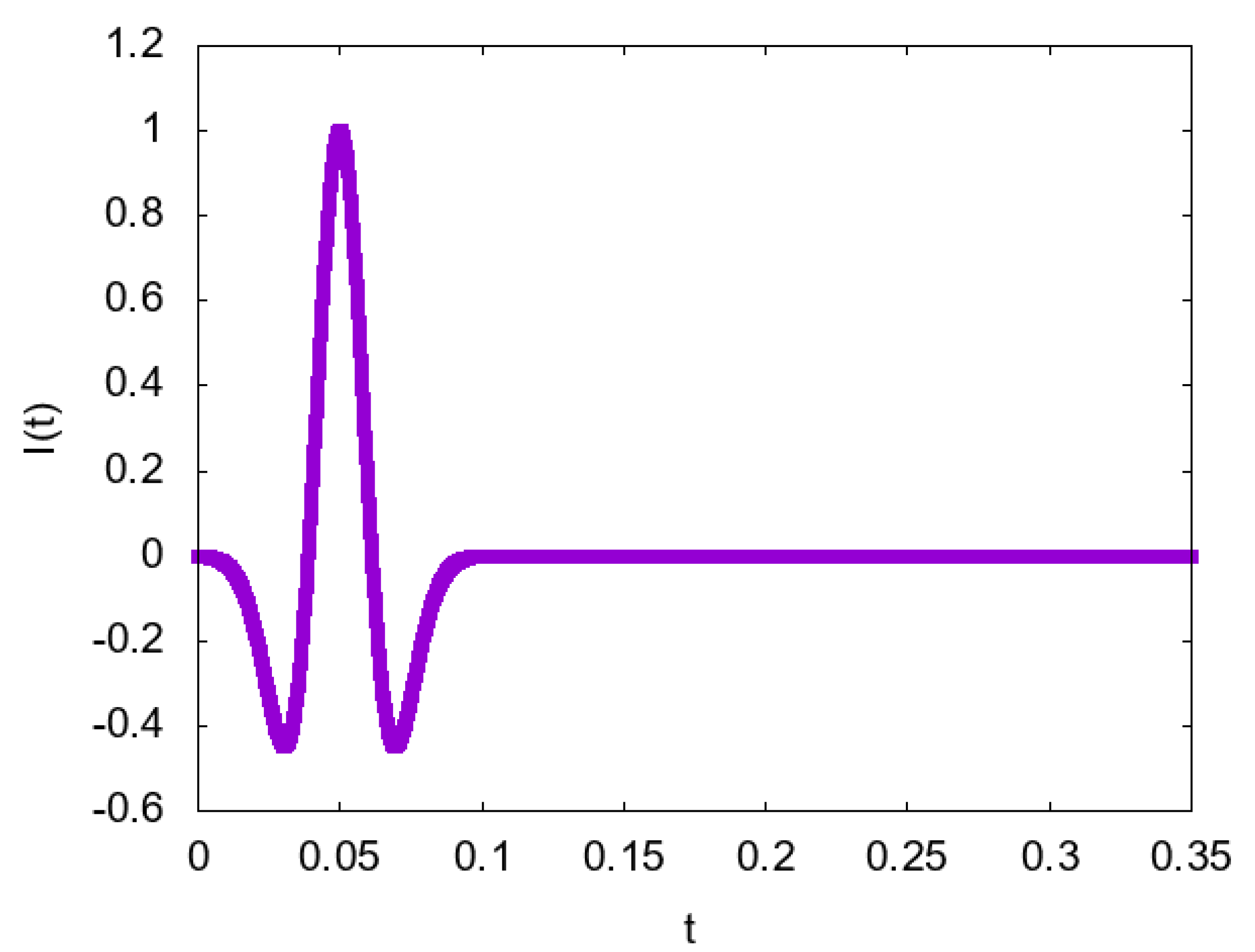
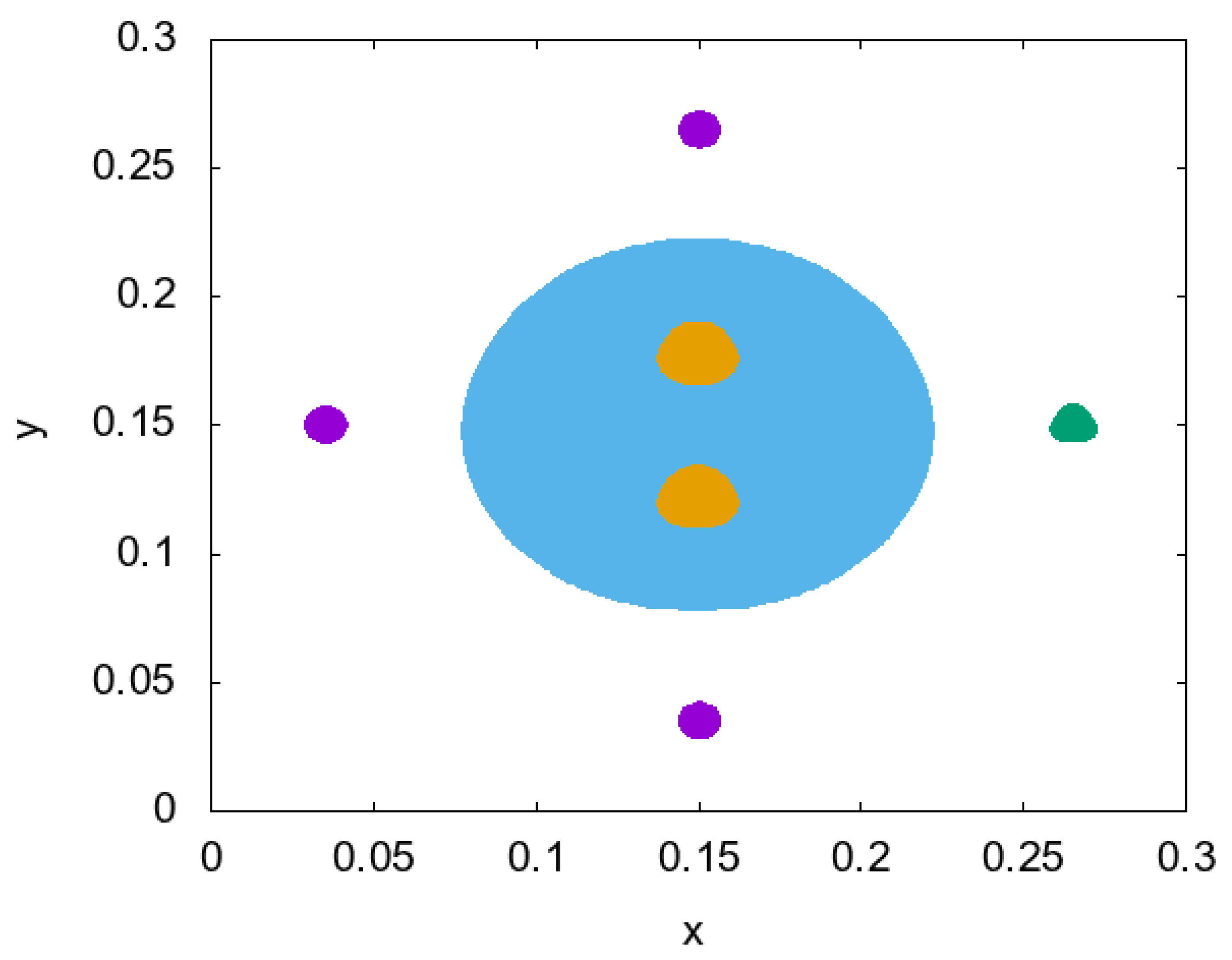
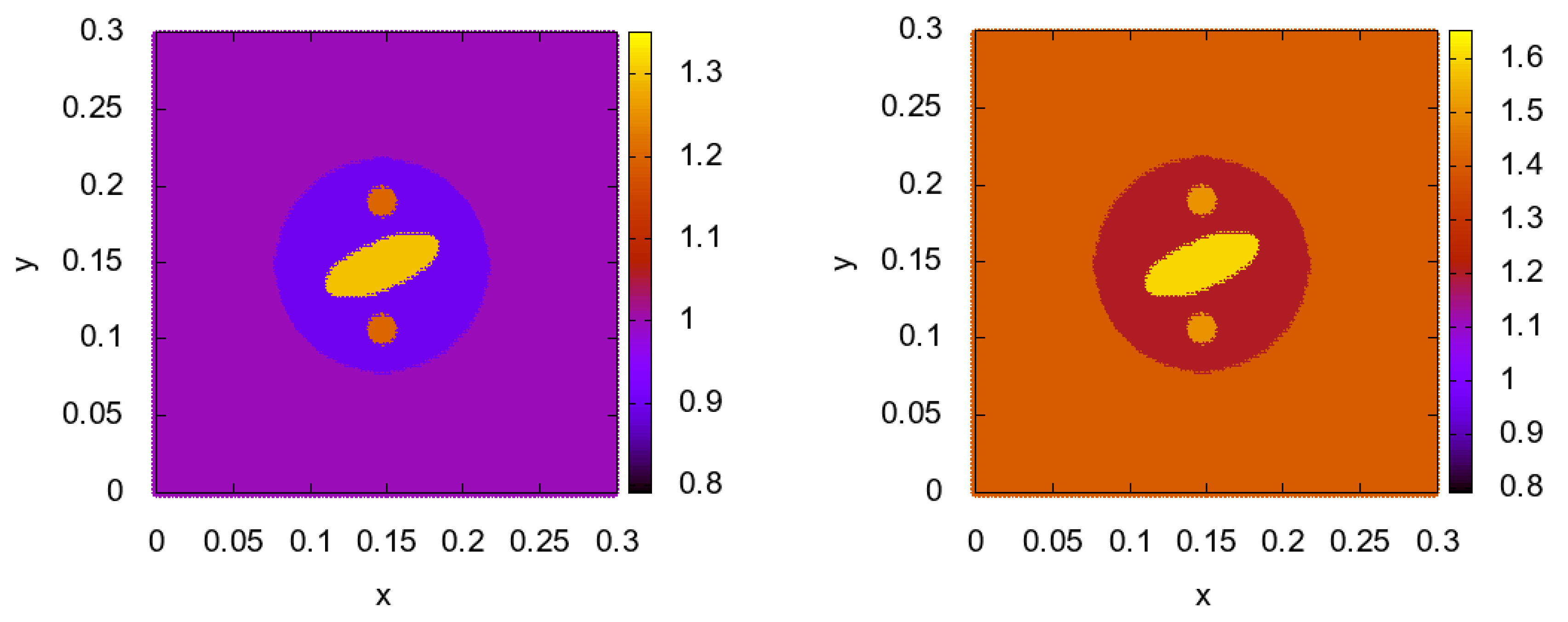
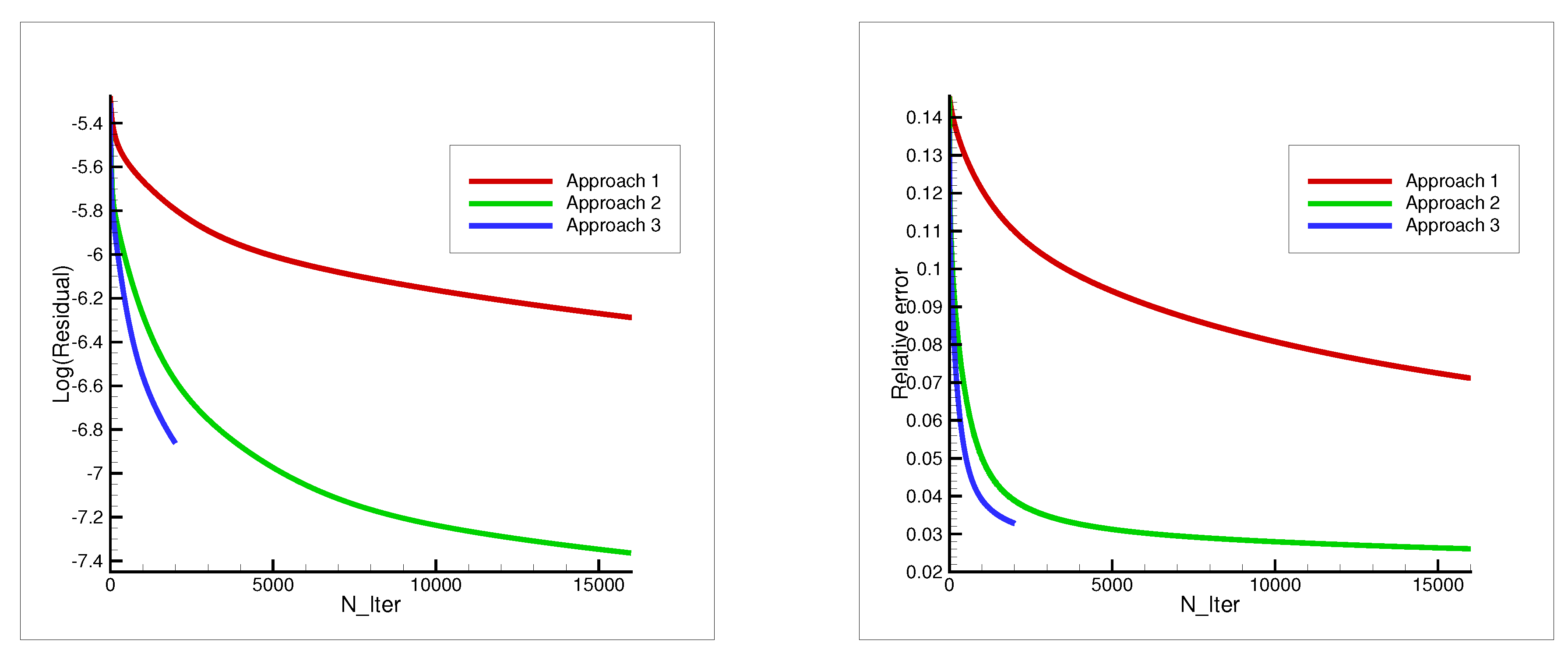
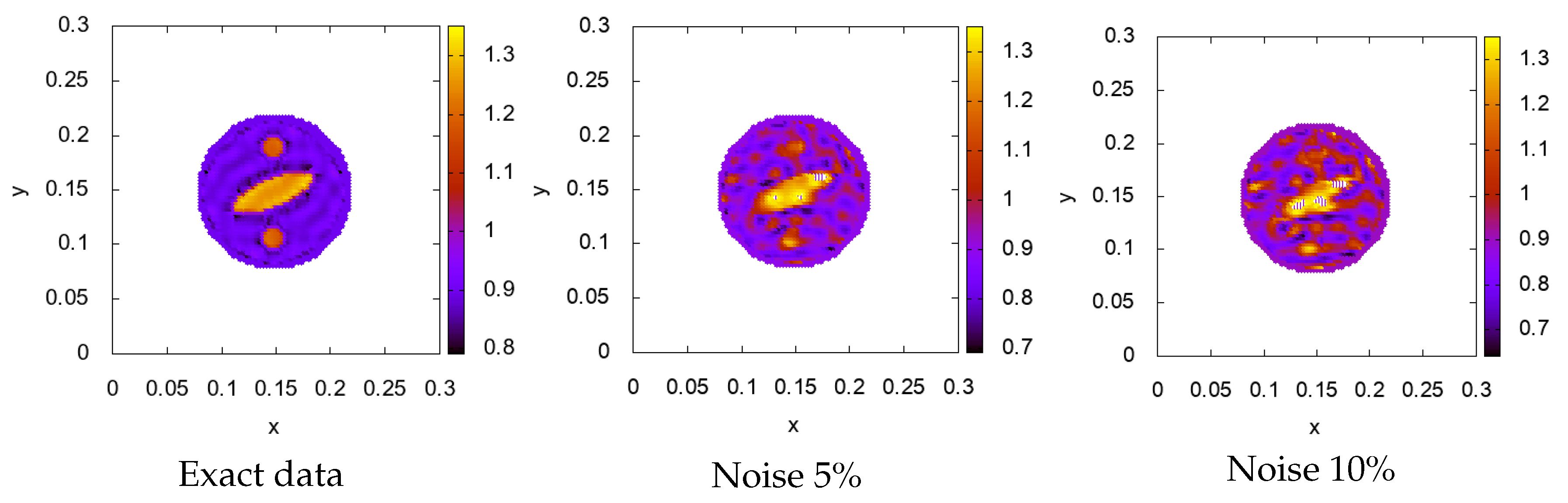
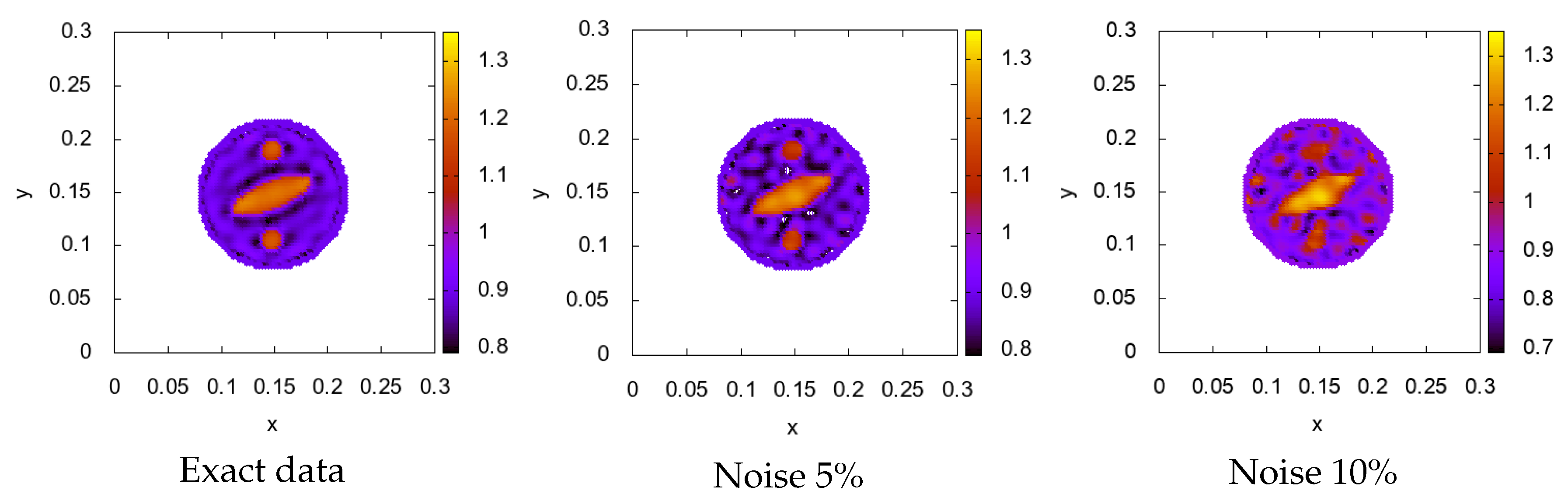
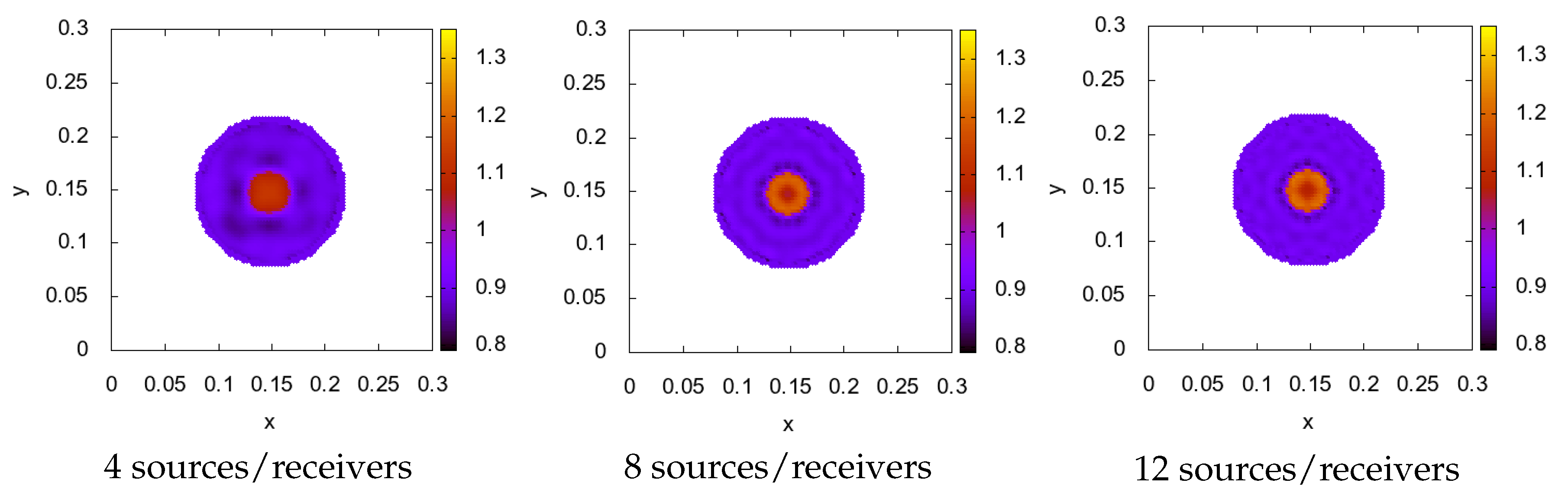
5. Numerical Results
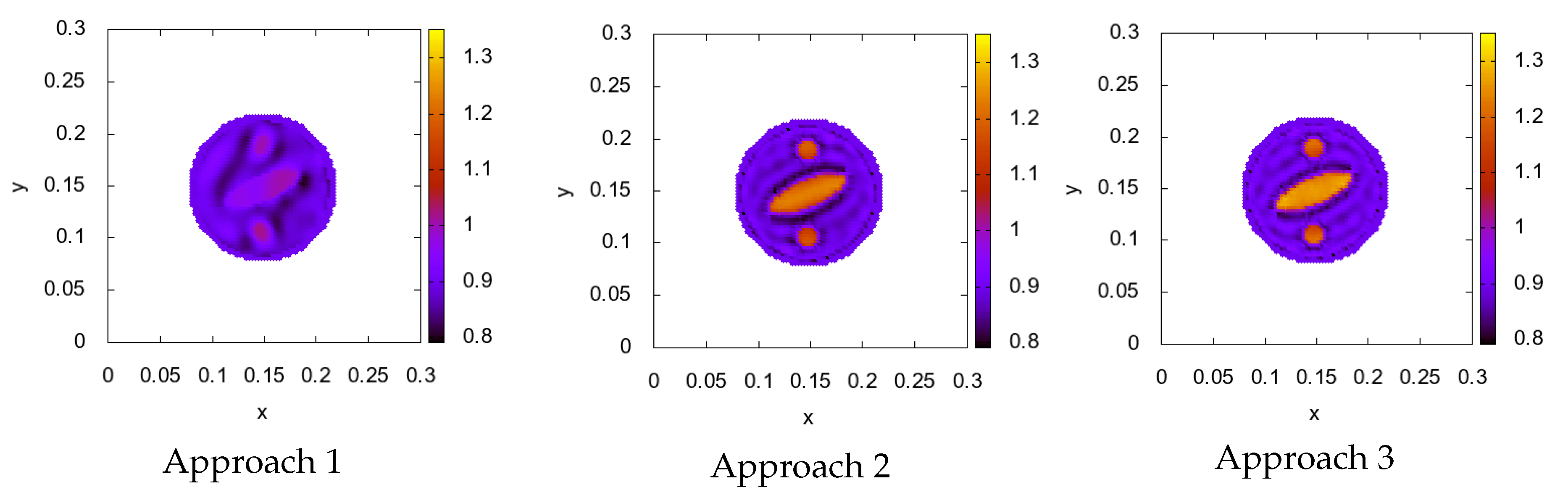
- Gradient constructed of 1 source, fixed in position (Figure 2). The formula of gradient descent is
- Gradient constructed of 1 source, but its location was changed on each iteration through positions , that are located uniformly on the circle of the radius m. The formula is in the next view
- Gradient constructed of 16 sources from positions with each iteration in a cyclic manner. The final formula is
6. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IP | Inverse problem |
| DP | Direct problem |
References
- Burov, V.A.; Voloshinov, V.B.; Dmitriev, K.V.; Polikarpova, N.V. Acoustic waves in metamaterials, crystals, and anomalously refracting structures. Adv. Phys. Sci. 2011, 54, 1165–1170. [Google Scholar]
- Burov, V.A.; Zotov, D.I.; Rumyantseva, O.D. Reconstruction of spatial distributions of sound velocity and absorption in soft biological tissues using model ultrasonic tomographic data. Acoust. Phys. 2014, 60, 479–491. [Google Scholar] [CrossRef]
- Burov, V.A.; Zotov, D.I.; Rumyantseva, O.D. Reconstruction of the sound velocity and absorption spatial distributions in soft biological tissue phantoms from experimental ultrasound tomography data. Acoust. Phys. 2015, 61, 231–248. [Google Scholar] [CrossRef]
- Duric, N.; Littrup, P.; Poulo, L.; Babkin, A.; Pevzner, R.; Holsapple, E.; Rama, O.; Glide, C. Detection of breast cancer with ultrasound tomography: First results with the computed ultrasound risk evaluation (CURE) prototype. Med. Phys. 2007, 34, 773–785. [Google Scholar] [CrossRef]
- Duric, N.; Littrup, P.; Li, C.; Roy, O.; Schmidt, S.; Janer, R.; Cheng, X.; Goll, J.; Rama, O.; Bey-Knight, L.; et al. Breast ultrasound tomography: Bridging the gap to clinical practice. Proc. SPIE 2012, 8320, 83200O. [Google Scholar]
- Jirik, R.; Peterlik, I.; Ruiter, N.; Fousek, J.; Dapp, R.; Zapf, M.; Jan, J. Sound-speed image reconstruction in sparse-aperture 3D ultrasound transmission tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 254–264. [Google Scholar] [CrossRef]
- Wiskin, J.; Borup, D.; Andre, M.; Johnson, S.; Greenleaf, J.; Parisky, Y.; Klock, J. Three dimensional nonlinear inverse scattering: Quantitative transmission algorithms, refraction corrected reflection, scanner design, and clinical results. Proc. Meet. Acoust. 2013, 19, 075001. [Google Scholar]
- Wiskin, J.; Borup, D.; Iuanow, E.; Klock, J.; Lenox, M. 3-D nonlinear acoustic inverse scattering: Algorithm and quantitative results. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1161–1174. [Google Scholar] [CrossRef]
- Wiskin, J.; Malik, B.; Natesan, R.; Lenox, M. Quantitative assessment of breast density using transmission ultrasound tomography. Med. Phys. 2019, 46, 2610–2620. [Google Scholar] [CrossRef]
- Wiskin, J.; Malik, B.; Natesan, R.; Borup, D.; Pirshafiey, N.; Lenox, M.; Klock, J. Full Wave 3D Inverse Scattering Transmission Ultrasound Tomography: Breast and Whole Body Imaging. In Proceedings of the IUS—IEEE International Ultrasonics Symposium, Glasgow, UK, 6–9 October 2019; pp. 951–958. [Google Scholar] [CrossRef]
- Filatova, V.; Danilin, A.; Nosikova, V.; Pestov, L. Supercomputer Simulations of the Medical Ultrasound Tomography Problem. Commun. Comput. Inf. Sci. 2019, 1063, 297–308. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. Synthesis of global convergence and adaptivity for a hyperbolic coefficient inverse problem in 3D. J. Inverse Ill-Posed Probl. 2010, 18, 85–132. [Google Scholar] [CrossRef]
- Klibanov, M.V. Travel time tomography with formally determined incomplete data in 3D. Inverse Probl. Imaging 2019, 13, 1367–1393. [Google Scholar] [CrossRef]
- Klibanov, M.V. On the travel time tomography problem in 3D. J. Inverse Ill-Posed Probl. 2019, 27, 591–607. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Kulikov, I.M.; Shishlenin, M.A. An Algorithm for Recovering the Characteristics of the Initial State of Supernova. Comput. Math. Math. Phys. 2020, 60, 1008–1016. [Google Scholar] [CrossRef]
- Godunov, S.K. Differential method for numerical computation of noncontinuous solutions of hydrodynamics equations. Matematicheskiy Sbornik 1959, 47, 271–306. (In Russian) [Google Scholar]
- Godunov, S.K.; Zabrodin, A.V.; Ivanov, M.Y.; Kraikov, A.N.; Prokopov, G.P. Numerical Solution for Multidimensional Problems of Gas Mechanics; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Samarskii, A.A. The Theory of Difference Schemes; Marcel Dekker Inc.: New York, NY, USA; Basel, Switzerland, 2001. [Google Scholar]
- Bastin, G.; Coron, J.-M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. In Progress in Nonlinear Differential Equations and Their Applications; Birkhauser: Boston, MA, USA, 2016. [Google Scholar]
- Blokhin, A.M.; Trakhinin, Y.L. Well-Posedness of Linear Hyperbolic Problems: Theory and Applications; Nova Publishers: Hauppauge, NY, USA, 2006. [Google Scholar]
- Kaltenbacher, B.; Nikolic, V.; Thalhammer, M. Efficient time integration methods based on operator splitting and application to the Westervelt equation. IMA J. Numer. Anal. 2014, 35, 1092–1124. [Google Scholar] [CrossRef]
- Secchi, P. Linear Symmetric Hyperbolic Systems with Characteristic Boundary. Math. Methods Appl. Sci. 1995, 18, 855–870. [Google Scholar] [CrossRef]
- Morando, A.; Secchi, P. regularity of weakly well posed hyperbolic mixed problems with characteristic boundary. J. Hyperbol. Differ. Equat. 2011, 8, 37–99. [Google Scholar] [CrossRef]
- Peralta, G.; Propst, G. Well-posedness and regularity of linear hyperbolic systems with dynamic boundary conditions. Proc. R. Soc. Edinb. Sec. A Math. 2016, 146, 1047–1080. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Novikov, N.S.; Oseledets, I.V.; Shishlenin, M.A. Fast Toeplitz linear system inversion for solving two-dimensional acoustic inverse problem. J. Inverse Ill-Posed Probl. 2015, 23, 687–700. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Sabelfeld, K.K.; Novikov, N.S.; Shishlenin, M.A. Numerical solution of an inverse problem of coefficient recovering for a wave equation by a stochastic projection methods. Monte Carlo Methods Appl. 2015, 21, 189–203. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Sabelfeld, K.K.; Novikov, N.S.; Shishlenin, M.A. Numerical solution of the multidimensional Gelfand–Levitan equation. J. Inverse Ill-Posed Probl. 2015, 23, 439–450. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Shishlenin, M.A. Numerical algorithm for two-dimensional inverse acoustic problem based on Gel’fand–Levitan–Krein equation. J. Inverse Ill-Posed Probl. 2011, 18, 979–995. [Google Scholar] [CrossRef]
- Baev, A.V. Numerical Solution of the Inverse Scattering Problem for the Acoustic Equation in an Absorptive Layered Medium. Comput. Math. Model. 2018, 29, 83–95. [Google Scholar] [CrossRef]
- Baev, A.V. Imaging of Layered Media in Inverse Scattering Problems for an Acoustic Wave Equation. Math. Models Comput. Simul. 2016, 8, 689–702. [Google Scholar] [CrossRef]
- Belishev, M.I.; Ivanov, I.B.; Kubyshkin, I.V.; Semenov, V.S. Numerical testing in determination of sound speed from a part of boundary by the BC-method. J. Inverse Ill-Posed Probl. 2016, 24, 59–180. [Google Scholar] [CrossRef]
- Belishev, M.I.; Vakulenko, A.F. On characterization of inverse data in the boundary control method. Rendiconti dell’Istituto di Matematica dell’Universita di Trieste 2016, 48, 49–77. [Google Scholar]
- Kabanikhin, S.I.; Shishlenin, M.A. Comparative analysis of boundary control and Gel’fand-Levitan methods of solving inverse acoustic problem. In Inverse Problems in Engineering Mechanics IV; Elsevier: Amsterdam, The Netherlands, 2003; pp. 503–512. [Google Scholar]
- Kabanikhin, S.I.; Shishlenin, M.A. Boundary control and Gel’fand-Levitan-Krein methods in inverse acoustic problem. J. Inverse Ill-Posed Probl. 2004, 12, 125–144. [Google Scholar] [CrossRef]
- He, S.; Kabanikhin, S.I. An optimization approach to a three-dimensional acoustic inverse problem in the time domain. J. Math. Phys. 1995, 36, 4028–4043. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Nurseitov, D.B.; Shishlenin, M.A.; Sholpanbaev, B.B. Inverse problems for the ground penetrating radar. J. Inverse Ill-Posed Probl. 2013, 21, 885–892. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Scherzer, O.; Shishlenin, M.A. Iteration methods for solving a two dimensional inverse problem for a hyperbolic equation. J. Inverse Ill-Posed Probl. 2011, 11, 87–109. [Google Scholar] [CrossRef]
- Beilina, L. Adaptive Finite Element Method for a coefficient inverse problem for the Maxwell’s system. Appl. Anal. 2011, 90, 1461–1479. [Google Scholar] [CrossRef]
- Beilina, L.; Hosseinzadegan, S. An adaptive finite element method in reconstruction of coefficients in Maxwell’s equations from limited observations. Appl. Math. 2016, 61, 253–286. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. A posteriori error estimates for the adaptivity technique for the Tikhonov functional and global convergence for a coefficient inverse problem. Inverse Probl. 2010, 26, 045012. [Google Scholar] [CrossRef][Green Version]
- Xin, J.; Beilina, L.; Klibanov, M. Globally convergent numerical methods for some coefficient inverse problems. Comput. Sci. Eng. 2010, 12, 64–76. [Google Scholar]
- Beilina, L.; Klibanov, M.V. Globally strongly convex cost functional for a coefficient inverse problem. Nonlinear Anal. Real World Appl. 2015, 22, 272–288. [Google Scholar] [CrossRef]
- Klibanov, M.V. Carleman estimates for global uniqueness, stability and numerical methods for coefficient inverse problems. J. Inverse Ill-Posed Probl. 2013, 21, 477–560. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Klyuchinskiy, D.V.; Novikov, N.S.; Shishlenin, M.A. Numerics of acoustical 2D tomography based on the conservation laws. J. Inverse Ill-Posed Probl. 2020, 28, 287–297. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Klychinskiy, D.V.; Kulikov, I.M.; Novikov, N.S.; Shishlenin, M.A. Direct and Inverse Problems for Conservation Laws. In Continuum Mechanics, Applied Mathematics and Scientific Computing: Godunov’s Legacy; Demidenko, G., Romenski, E., Toro, E., Dumbser, M., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Romanov, V.G.; Kabanikhin, S.I. Inverse Problems for Maxwell’s Equations; VSP: Utrecht, The Netherlands, 1994. [Google Scholar]
- Kabanikhin, S.I.; Shishlenin, M.A. Quasi-solution in inverse coefficient problems. J. Inverse Ill-Posed Probl. 2008, 16, 705–713. [Google Scholar] [CrossRef]
- Dvinskikh, D.; Ogaltsov, A.; Gasnikov, A.; Dvurechensky, P.; Tyrin, A.; Spokoiny, V. Adaptive Gradient Descent for Convex and Non-Convex Stochastic Optimization. arXiv 2019, arXiv:1911.08380. [Google Scholar]
- Kabanikhin, S.I.; Gasimov, Y.S.; Nurseitov, D.B.; Shishlenin, M.A.; Sholpanbaev, B.B.; Kasenov, S. Regularization of the continuation problem for elliptic equations. J. Inverse Ill-Posed Probl. 2013, 21, 871–884. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Shishlenin, M.A.; Nurseitov, D.B.; Nurseitova, A.T.; Kasenov, S.E. Comparative Analysis of Methods for Regularizing an Initial Boundary Value Problem for the Helmholtz Equation. J. Appl. Math. 2014, 2014, 786326. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Shishlenin, M.A. Regularization of the decision prolongation problem for parabolic and elliptic elliptic equations from border part. Eurasian J. Math. Comput. Appl. 2014, 2, 81–91. [Google Scholar]




| Approach 1 | Approach 2 | Approach 3 | |
|---|---|---|---|
| Relative error | 0.121 | 0.050 | 0.039 |
| Elapsed time | 40 s | 40 s | 480 s |
| Approach 1 | Approach 2 | Approach 3 | |
|---|---|---|---|
| Relative error | 0.071 | 0.026 | 0.032 |
| Elapsed time | 15 min | 15 min | 17 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klyuchinskiy, D.; Novikov, N.; Shishlenin, M. A Modification of Gradient Descent Method for Solving Coefficient Inverse Problem for Acoustics Equations. Computation 2020, 8, 73. https://doi.org/10.3390/computation8030073
Klyuchinskiy D, Novikov N, Shishlenin M. A Modification of Gradient Descent Method for Solving Coefficient Inverse Problem for Acoustics Equations. Computation. 2020; 8(3):73. https://doi.org/10.3390/computation8030073
Chicago/Turabian StyleKlyuchinskiy, Dmitriy, Nikita Novikov, and Maxim Shishlenin. 2020. "A Modification of Gradient Descent Method for Solving Coefficient Inverse Problem for Acoustics Equations" Computation 8, no. 3: 73. https://doi.org/10.3390/computation8030073
APA StyleKlyuchinskiy, D., Novikov, N., & Shishlenin, M. (2020). A Modification of Gradient Descent Method for Solving Coefficient Inverse Problem for Acoustics Equations. Computation, 8(3), 73. https://doi.org/10.3390/computation8030073





