1. Introduction
In the last decade, the emergence of Bitcoin [
1] and other cryptocurrencies has revolutionized many sectors of modern society, as reported in [
2], which provides a systematic review of the literature on major topics related to the cryptocurrencies market: firstly, the financial one, as they represent innovative assets, characterized by the concept of scarcity [
3], and elusive to traditional market logics; then, of course, the IT sector, since these technologies introduced, for the first time on a large scale, the concept of the blockchain, a decentralized and secure data structure for the certification of information (initially, payment transactions), immutable, and that does not require the intervention of a central control authority such as a bank or a government; and last, but not least, the legal sphere, where this lack of central control makes these instruments difficult to regulate, but at the same time attractive, thanks to the collateral opportunities they offer.
The system is designed to be anonymous; hence, each user receives a digital identity. The underlying idea is then to create a virtual currency, the Bitcoins, and use the blockchain as a public record of payment transactions, in order to uniquely determine how many Bitcoins are owned and transferred by each user. Indeed, once a certain amount of time has elapsed after the publication of the transaction on the blockchain, it becomes no longer possible to change its content or delete it, permanently.
Adding new transactions on the blockchain is the job of a peer-to-peer network of nodes, called miners, through a distributed consensus protocol. Roughly, transactions are organized into blocks: to publish a new block, the protocol requires solving a moderately difficult cryptographic puzzle. The first miner who solves the puzzle earns some fresh coins for the mined block, plus a small fee for each transaction included therein. Such a process is based on the fact that a cryptographic puzzle is really hard to solve, but is very easy to prove [
4,
5]. In contrast, removing or modifying existing blocks is computationally unfeasible: this would require an adversary with more computational power than the rest of all the other nodes. According to its promoters, Bitcoin will resist attacks unless the adversaries control the majority of total computing power of the Bitcoin network. In fact, even though some vulnerabilities have been reported in the literature [
6,
7], the most known successful attacks of Bitcoin are standard hacks or frauds [
8], unrelated to the Bitcoin protocol. In [
9], the authors discussed the different types of attacks related to Bitcoin and other cryptocurrencies, whereas in [
10,
11], the authors introduced and discussed, respectively, the security and privacy issues related to Bitcoin and to the blockchain technology.
Additionally, Bitcoin transactions may also include some bytes of metadata, through the
OP_RETURN instruction, as reported in the study performed in [
12], where the authors identified and classified real-life blockchain transactions embedding metadata, with regard to several major protocols that operate over the Bitcoin blockchain. Recently, this led to an increase in the number of third-party services that take advantage of this possibility, in order to permanently store messages, digests, or information generated by their execution. This is the case, for example, of miscellaneous decentralized applications, systems for the certification of documents and production chains, smart contracts, distributed computing services, and tokenization platforms. In such a context, a sequence of messages, embedded in the blockchain and related to the same decentralized application or service, can therefore be abstractly interpreted as an independent subchain, meaningless for Bitcoin nodes, but incremental and ideally contiguous for nodes running such an application.
However, since subchains often need to preserve the order of the messages they contain (mainly to guarantee an agreement, between the distributed participants, on the application execution), it is important to ensure that their contents are unambiguous and consistent. This would require, e.g., a protocol for managing the simultaneous publication of (potentially conflicting) new messages, as well as the possibility of recognizing invalid or fraudulent sequences. Nonetheless, the majority of third-party applications that exploit the blockchain to store their messages do not use a secure protocol to establish if their subchain is consistent. This is a serious issue, since it either limits the expressiveness of the features offered by these applications (i.e., they must consider all messages as consistent, then losing the notion of state) or, conversely, degrades their security level (because adversaries can manage to publish inconsistent messages).
To cope with this issue, our protocol, based on proof-of-stake [
13,
14], requires providing a money deposit in order to earn the right to extend the current subchain. Intuitively, a node that publishes a consistent message gets back its deposit once the message is confirmed by the rest of the network, while behaving dishonestly is discouraged and disincentivized.
In light of the above, the main original contributions of this work are:
a broad revision and extension of our protocol [
15] that allows third-party decentralized applications to maintain consistent subchains on Bitcoin;
a detailed analysis of the security properties and guarantees offered by the protocol, through the definition of multiple attack scenarios and adversarial strategies;
a description of how to concretely implement in Bitcoin this revised protocol, adapted from its original formulation.
The remainder of the paper is organized as follows.
Section 2 introduces the background and related work of the scenario taken into account.
Section 3 formalizes the proposed consensus protocol for Bitcoin subchains.
Section 4 evaluates the security of such a protocol, whereas
Section 5 describes a possible implementation in Bitcoin. Some concluding remarks and future work are finally given in
Section 6.
2. Background and Related Work
To better present the rest of our work, we start by giving a general overview on Bitcoin and how it works, along the lines of our conference paper in [
15]. Basically, Bitcoin is a cryptocurrency and a digital open-source payment infrastructure, conceived of by an anonymous inventor, known under the pseudonym Satoshi Nakamoto, and launched for the first time on 3 January 2009. This cryptocurrency gave rise to an exponentially growing number of applications, representing the basis of many other cryptocurrencies, as highlighted in the bibliometric analysis of the literature on Bitcoin performed in [
16]. Moreover, an overarching in-depth study of the phenomenon originated from Bitcoin itself was instead made in [
17].
The main peculiarity of Bitcoin lies in the fact that it does not require the control of any central authority, relying instead on a peer-to-peer network of nodes called miners that are responsible for maintaining a public ledger called the blockchain [
1]. The advantages and disadvantages of this decentralized scheme were discussed in [
18], where the authors evaluated the benefits of decentralized finance, identifying the existing business models, and evaluating the potential limits.
The underlying intuition is that, compared to a conventional payment intermediary, in Bitcoin, all currency transfers are permanently stored in this public ledger, through which it is possible to reconstruct, at any time and in a deterministic way, the balance held by each Bitcoin owner. Indeed, the virtual currency exchanged in such an infrastructure is the Bitcoin (
). Each Bitcoin user owns one or more personal wallets, which essentially consist of pairs of asymmetric cryptographic keys: the public key uniquely identifies the user address, to receive funds, while the private key is used to authorize payments. To do so, they attest to their transfer of Bitcoins with digital transactions, validated through cryptographic methods, and registered on the blockchain, neatly organized into blocks. A simplified scheme of a Bitcoin transaction is shown in
Figure 1.
The transaction
enables a transfer of
, which are redeemed from a previous transaction by referring to
in the infield. To prove that
is the rightful recipient of
, its
scriptSig field contains a witness value that makes the
scriptPubKey of
, a Boolean programmable function, evaluate to true. If
respects this condition and is published in the blockchain, the value of
is transferred to
, and
is no longer redeemable. Similarly, a new transaction can then redeem
by satisfying its respective
scriptPubKey.
Figure 1 shows the standard form of
scriptPubKey: it essentially evaluates to true when the redeeming transaction (e.g.,
) provides a valid digital signature
. In particular,
denotes the signature verification with the public part of the key pair
k, while
denotes the signature itself, performed with the private part of
k, on the body (i.e., all parts except its
scriptSig) of the redeeming transaction.
However, Bitcoin transactions may be more general than those illustrated by the previous example: first, they may contain multiple inputs and outputs (we denote them with the array notation). In particular, each output has its own scriptPubKey and value and can be redeemed independently of the others. Consequently, in fields must specify which output of a transaction they are redeeming ( in the figure), and each must be associated with a scriptSig that satisfies the corresponding scriptPubKey. The values of the inputs are aggregated and can be distributed freely among the outputs, with the condition that the sum of the values of all the inputs must be greater than or equal to the sum of the values of all outputs. As a side effect, it is therefore possible to spend only part of the value associated with the transaction, with the difference still redeemable by the owner.
More thoroughly, scriptPubKey describes a Boolean function, expressed in a not Turing-complete scripting language, and featuring a limited set of logic, arithmetic, and cryptographic operators. Finally, the lockTime field specifies the earliest moment in time (block number or timestamp) when the transaction can appear on the blockchain.
To reach a consensus on new blocks of transaction to be published, Bitcoin implements a proof-of-work system [
19]. It consists of a protocol that essentially pushes miners to compete with each other for the right to add these blocks to the blockchain: indeed, to append a new block
to the blockchain, each miner has to solve a cryptographic challenge, which requires a high consumption of computational resources. This challenge involves the hash
of the last published block
, the sequence of unconfirmed transactions
contained in
, and some salt
R. As soon as a miner finds a solution to the current challenge, it can add
to the blockchain, obtain a reward in Bitcoins, and start mining a new block on top of
. In this way, the other miners are incentivized to discard their attempts, update their local copies of the blockchain with the new block
, and start over with new transactions. The PoWprotocol ensures each new block is mined every ∼10 min, on average.
Finally, note that when two or more miners solve the current challenge simultaneously, they generate a fork in the blockchain (i.e., two or more parallel valid branches). When such a fork happens, miners must choose a branch wherein the mining process is carried out; roughly, the divergence is resolved once one of the branches becomes longer than the others. In this case, the other branches are discarded, and all the orphan transactions contained therein are nullified. As a side effect, this mechanism encourages miners to properly verify the validity of blocks and transactions, since an honest majority of miners will discard branches containing invalid transactions, causing their respective miners to lose the associated fees and rewards.
2.1. Smart Contracts and Decentralized Applications
As previously mentioned, one of the most interesting features of Bitcoin and other cryptocurrencies is the possibility, beyond the exchange of digital currency, to deploy so-called smart contracts. This concept was introduced for the first time, at the beginning of the 1990s, by Nick Szabo [
20], which defines them as agreements between two or more entities, which can be applied automatically without the need for a trusted intermediary. In other words, a smart contract represents a self-executing contract with the terms of the agreement between entities (e.g., buyer and seller), which have been defined in lines of code in the context of a distributed, decentralized blockchain network [
21].
The cryptocurrencies scenario has provided a first concrete example of this intuition, since in this context, actors operate in a decentralized way, in order both to create and transfer crypto-assets [
22]. Indeed, the blockchain and its protocol can enforce the contract execution, since each transaction is traceable and irreversible. In particular, Bitcoin offers the possibility to specify some simple contracts in transactions through short programs expressed in a Forth-like scripting language. These contracts are evaluated by the miners before the respective transactions are appended to the blockchain and often contain clauses that involve the transfer of some Bitcoins among nodes.
The idea of using the blockchain and its consensus protocol as foundations for a decentralized contract-oriented interaction has been explored by several recent works. For instance, References [
23,
24,
25,
26,
27,
28,
29,
30] proposed protocols for secure multiparty computations, fair lotteries, and (decentralized) role-based access control; Reference [
31] implemented decentralized authorization systems on Bitcoin; Reference [
32,
33] allowed users to log statements on the blockchain; Reference [
34] was a key-value database with get/set operations; Reference [
35] extended Bitcoin with advanced financial operations (like, e.g., the creation of virtual assets, payment of dividends, etc.), by embedding its own messages in Bitcoin transactions.
Later approaches, such as that of Ethereum [
36], have been developed, by-design, to be natively oriented to the implementation of smart contracts and decentralized applications in a more general sense [
37], rather than payments. For instance, in [
38], the authors proposed a security framework that integrates the blockchain technology with smart devices to provide a secure communication platform in a smart city; Reference [
39] discussed a blockchain application developed for the energy sector that enables distributed market coordination for decentralized energy systems; Reference [
40] presented a survey on couponing platforms where coupons are implemented as smart contracts; and in [
41], the authors introduced a novel blockchain-based distributed paradigm for data exchange between wireless-based devices. Overall, since this technology grants the security and immutability of the involved data, it is suitable for the smart contract implementation. However, in addition to creating new opportunities, this novel form of smart contract implementation generates also new types of fraud [
42], which effectively circumvent the canonical fraud detection approaches [
43,
44,
45], making it necessary to develop new targeted countermeasures [
46,
47]. Since smart contracts usually handle crucial data, their implementation should be secure against attacks that aim at stealing or tampering with the data [
48]. This aspect has been faced by an increasing number of literature works, such as [
49], where the authors proposed a survey on the attacks related to the Ethereum smart contracts; or [
50], which aims to develop secure Bitcoin contracts; or more generally, in [
51,
52], the authors, respectively, provided a systematic survey about the security, performance, and applications of smart contracts and presented a study about their formal verification.
However, specifically for Bitcoin, the possible contracts that are natively supported by this platform are very limited, since its language is not Turing-complete, an aspect investigated by the authors in [
53].
Nonetheless, its protocol allows clients to embed a few extra bytes as metadata in transactions, and many third-party decentralized applications (or smart contracts) exploit these metadata to store a persistent, timestamped, and tamper-proof historical record of all their execution messages [
54,
55]. Usually, metadata are stored in transactions by using the
OP_RETURN field [
56], making them meaningless to the Bitcoin network. With this approach, the sequence of application-dependent messages forms a subchain, whose content can only be interpreted by the nodes that execute that application, thus potentially extending the decentralization power of Bitcoin to more complex computational models.
2.2. Subchains and Consistency
To formally describe the concept of a Bitcoin subchain and, more specifically, of a consistent subchain, we now briefly recall a set of definitions, previously introduced in [
15]. To do so, let us define a set
of participants, who want to extend the subchain by appending messages
to it. We call a label a pair consisting of a participant
and a message
, written
. In such a context, subchains can be considered as finite sequences of labels, written
, embedded in the Bitcoin blockchain. This can be interpreted as the participant
that embedded the message
in some transaction of the blockchain, and subsequently, the participant
appended a new transaction that embeds
, and so on. We also alternatively denote (long) sequences of labels with
, thus writing, e.g.,
for the subchain obtained by appending
to
.
To be more general, we model subchains as traces of Labeled Transition Systems (LTS). An LTS is a tuple , where: (i) Q is a set of states (ranging over ); (ii) L is a set of labels (in our case, of the form ); (iii) is the initial state; and (iv) is a transition relation. In particular, we write when , and we require the relation → to be deterministic, i.e., if and , then it must be .
Given this model, we then assume that the subchain has a state, and each subsequent message (appended to it) updates its state according to the transition relation. More formally, if the current subchain state is q, then a participant who sends a message makes the state evolve to , only if: is a transition of the LTS. However, it can be observed that for some state q and label , it may happen that no state exists such that . The goal is that, in this case, it would be hard for a participant to append such a message. Indeed, it could be the case of an adversary who tries to subvert the messages produced by the (decentralized) application execution. Therefore, we informally say that a subchain is consistent if, starting from the initial state , there exist the states such that, from each , there is a transition labeled to .
We also notice that, in general, application messages—since they are embedded in Bitcoin transactions—can also produce side effects on the Bitcoin blockchain. Thus, we indicate with a message that, besides updating the subchain, also transfers (i.e., v Bitcoins) from a participant to a participant . In other words, when this message is on the subchain, it also makes in a transaction of redeemable by , acting as a money transfer, and therefore, making it possible to potentially define smart contracts external to the native Bitcoin protocol. Finally, note that, for the sake of clarity, if the value v is zero, we simply write rather than .
Below, we now formalize some of the intuitions previously described.
Definition 1 (Consistent subchain). A subchain is consistent if and only if there exists such that: .
We also observe that, whenever a subchain is consistent, the required property of determinism enforces the existence of and its uniqueness. Consequently, a consistent sequence of messages uniquely identifies the state of the subchain, and a node can reconstruct the application computation as .
Following the same approach, we assume that an adversary can append a label
such that
, so making the subchain inconsistent. However, upon receiving such a label, honest nodes will discard it. To do so, they apply a function
that, given a subchain
(possibly inconsistent), filters all the invalid messages. The function
is defined as follows:
with
.
Finally, to model labels that are appended to the subchain without breaking its consistency, we recall below the auxiliary relation ⊧. Informally, given a consistent subchain , the relation holds whenever the subchain is consistent.
Definition 2 (Consistent update). A label is a consistent update of a subchain η, written , if and only if the subchain built by extending with is still consistent.
Given the above definitions, we can now introduce the description and properties of our protocol to incentivize mutually distrusted participants to consistently extend a subchain embedded in the Bitcoin blockchain.
3. Overview of the Extended Protocol
Hereafter, we present an extended and revised version of the protocol preliminarily described in [
15]. It introduces several new elements, such as the refund policies, which, as will be shown in following
Section 4, have an important impact in limiting or preventing certain types of attack to which the simplified version of the protocol could be subject.
This protocol relies on a Proof-of-Stake (PoS) consensus mechanism, built on top of Bitcoin’s native proof-of-work and handled by a set of nodes , called meta-nodes to distinguish them from the nodes of the Bitcoin network. The intuition is that such nodes would ensure that any client of a decentralized application, which (abstractly) stores its execution data on a Bitcoin subchain, can trust the consistency and reliability of these data.
The protocol’s main assumption is that the overall stake retained by honest meta-nodes of a certain application is greater than the stake owned by dishonest ones. Note that an equivalent hypothesis, but related to computational power rather than stake, also holds in Bitcoin, where honest miners are supposed to control more computational power than dishonest ones. On the other hand, the main purpose of the protocol is to allow honest participants (i.e., those who follow the protocol) to perform consistent updates of the subchain, while disincentivizing adversaries who attempt to make the subchain inconsistent.
Meta-nodes use their stake to vote for approving messages sent by participants. These messages are embedded into Bitcoin transactions and called update requests. We indicate with the update request issued by to extend the subchain with the message . To vote for such an update request, a meta-node essentially puts a deposit of on it, where is a constant specified by the protocol.
Each message, encoded as an update request, needs the vote of a meta-node in order to be appended to the subchain; otherwise, this message will be ignored by the other participants. Therefore, meta-nodes are strictly required to vote for a request only if is a consistent update of the current subchain , i.e., if . To incentivize meta-nodes to vote, then approve, their update requests, participants must pay them a constant fee f that can be redeemed by the respective meta-nodes only after the request is published on the Bitcoin blockchain.
The protocol is organized into rounds, and it ensures that exactly one label is appended to the subchain for each round
i. To guarantee this uniqueness, the protocol exploits an arbiter
, a distinguished node of the network that is assumed to be honest (this hypothesis is discussed in
Section 3.4).
The main steps of the protocol, for each round i, are summarized as follows:
A meta-node receives an update request from the client ;
checks the consistency of the message, i.e., whether the relation holds; if true, it proceeds with Step 3, otherwise it discards the request and goes back to Step 1;
votes for the request during a voting phase of duration and adds it to the request pool;
When expires, the arbiter signs all the well-formed s in the request pool;
All the requests signed by the arbiter are sent to the Bitcoin miners, to be published on the blockchain. The first to be mined, indicated with , extends the subchain with its i-th message.
To vote for an update request, as indicated in Step 3,
must confirm some of the past
C updates (where
is the cutoff window, a constant fixed by the protocol and described in
Section 3.1). To confirm an update,
uses the
to pay the meta-nodes who respectively appended each chosen update
(with
) to the subchain. The way to choose the updates
to be confirmed is called the refund policy and is deepened in
Section 3.1. In particular, the request pool is the set of all voted requests of the current round, which is emptied at the beginning of each round. Finally, the choice of
(the duration of the voting phase) is discussed in
Section 5.
Note also that, in Step 4, the arbiter
signs all well-formed request transactions: such transactions are those that correctly adhere to the format specified in
Section 5. In the same section, we also describe the mechanism to ensure that, at each round
i, exactly one transaction
, in Step 5, is published on the Bitcoin blockchain. When this happens, the label
is appended to the subchain.
Overall, the protocol depends on the parameters , which are, respectively, the cutoff window size, the amount required to vote an update request, the fee payed by the client, and the maximum transferable amount in special updates in the form (where, by definition, ).
3.1. Refund Policies
A refund policy can be formally defined as a function that, given a subchain and the protocol parameters , outputs a sequence of refunds , where:
represents, at each round i of the protocol, the amount to pay to the meta-node who voted , for every j s.t. (only updates inside the current cutoff window can be refunded);
(the policy specifies how to split the vote and the fee among the voters of the updates inside the cutoff window).
To enforce good behavior, updates whose voters did not follow the prescribed policy are considered not refundable. This means honest meta-nodes penalize not only inconsistent labels, but also illegal refunds.
Definition 3 (Refundable update). Let be the subchain after the completion of the k-th protocol round, be a published update, and be the refund made by its voter. Then, we say is refundable if and only if it is consistent () and it follows the refund policy ().
Thus, at each round
i, we can define the set of indexes of refundable updates in the current cutoff window. Suppose that the subchain starts with
C predetermined and consistent updates
, then:
since all initial updates are considered refundable. Then, for
:
Note that checking if the voter of the j-th update (with ) has followed the refund policy just requires examining the updates with index . Thus, this check may depend only on and never on .
As an example, some possible refund policies are now presented.
- newest-first
This policy refunds only the newest refundable update in the cutoff window (if any), the newest in general otherwise:
- oldest-first
This policy refunds the oldest consistent update (if any), the oldest in general otherwise (note that it coincides with the
newest-firstif
):
3.2. Proof-of-Burn
To expand the possibilities for meta-nodes and increase the security of the protocol, as will be discussed in depth in
Section 3.3, the sequence of refunds
can be extended to include a special value
. This value represents the amount that should be paid to a pre-set fictional address (e.g., an all-zero address). Refunding such an address effectively corresponds to burning the money sent, making it unspendable.
With this enhancement, the policies defined previously can be improved, removing the case
and adding:
which can be interpreted as follows: if no update in the cutoff window is refundable, burn vote and fee. The variants of the previous policies, after the inclusion of the proof-of-burn condition, are called
newest-first-pburn and
oldest-first-pburn. This change avoids the (forced) confirmation of a non-refundable update that is allowed in the previous definitions of the
newest-first and
oldest-first policies.
Now, recall that in
Section 3, the condition
is provided. However, the choice
makes sense only if there is the possibility of burning the vote. On the contrary, voters would have no other choice besides confirming the previous update (refundable or not). Introducing the proof-of-burn, instead, the following policy for
can be defined and used.
- harsh policy
This policy refunds the previous update if refundable, burns the money otherwise:
3.3. Properties of the Protocol
Our extended protocol provides some properties, which in part differ from those presented in its original formulation. Nonetheless, both versions rely on the same underlying assumptions. In detail:
Assumption 1. The honest meta-nodes control the majority of the total stake of the network, and this amount is denoted by S.
Assumption 2. The overall stake needed to vote on pending update requests is greater than the overall stake detained by honest meta-nodes.
Assumption 3. Each honest meta-node votes for as many requests as is allowed by its stake.
Hence, if its stake is
h, any honest meta-nodes votes on
requests per round. Consequently, the rest of the network—which may include dishonest meta-nodes not following the protocol—can vote on at most
. In this regard, note that assuming the ability of the adversary to delay some messages (as in the Dolev–Yao model [
57]), and thus reducing the honest meta-nodes’ actual voting power (since their voted requests might not reach the request pool), is equivalent to considering an adversary with a higher stake.
From these assumptions, it follows that:
Lemma 1. The probability that an honest meta-node with stake h updates the subchain is at least at each round.
Lemma 1 is a direct consequence of Assumptions 2 and 3. Moreover, since in Assumption 1, we assume that honest meta-nodes control the majority of the stake, Lemma 1 also limits the capabilities of the adversary, leading to the following:
Lemma 2. If the global stake of honest meta-nodes is , then dishonest ones update the subchain with probability at most at each round.
However, note that although inconsistent updates are ignored by honest meta-nodes, their side effects as standard Bitcoin transactions (i.e., transfers of from to in labels ) cannot be revoked once they are included in the Bitcoin blockchain. Indeed, even though the goal of the protocol is to let meta-nodes get revenues proportionate to their probability of updating the subchain (as defined in Lemmas 1 and 2), the adversary might exploit these side effects to earn more than it is due by publishing inconsistent updates. Therefore, we show how the incentive system in our protocol reduces the feasibility of such inconsistent updates.
In light of the above, according to Lemma 2, if has stake m, and the other meta-nodes are honest, then has probability at most of extending the subchain in a given round of the protocol. Since rounds can be seen as independent events, we obtain the following:
Lemma 3. The probability that an adversary with stake m saturates a cutoff window with its updates only (consistent or not) is , where C is the cutoff window size, and .
Since Lemma 3 represents the core property of the described protocol, the demonstration of its validity will be the full subject of the discussion in
Section 4.
Finally, note that, to simplify the terminology, hereafter, we consider a consistent update to be also refundable. Indeed, publishing a consistent update that is not refundable does not break the consistency of the subchain, but it causes the meta-node who voted for the update to be (eventually) not refunded for its effort. Therefore, this behavior cannot be considered an attack.
3.4. Honesty of the Arbiter
The protocol exploits a distinguished meta-node, the arbiter , to ensure that only one transaction per round is appended to the blockchain, and that its choice is random as well. In order to simplify the description of the protocol, the arbiter is assumed to behave honestly. However, if this prerequisite proves to be false, the main properties of the protocol would be preserved, but at the cost of a deterioration in its execution performance.
To clarify this point, observe that although the arbiter introduces a point of centralization, it does not play the role of a trusted authority. Indeed, recall that the update requests to be voted on are chosen by the meta-nodes, and once they are added to the request pool, the arbiter is expected to sign all of them, without taking part in the validation, nor in the voting. Transactions are first signed by clients and voters; thus, neither the arbiter, nor other nodes can modify their content once sent to the request pool. This means that a dishonest arbiter can only refuse to add its signature to a subset of them, i.e., prevent their publication (which corresponds to isolating some meta-nodes in the network or, in other words, amplifying the voting power of malicious nodes). However, since everyone can inspect the request pool, any misbehavior of the arbiter can be easily detected by the meta-nodes, which can proceed to replace it. For these reasons, the presence of the arbiter cannot affect the decentralization of the approach, but without the assumption of its honesty, it would be necessary to take into consideration some possible performance attacks like, e.g., temporary denial-of-service attacks performed by the arbiter. This is still an open issue, and in this regard,
Section 6 presents our future research directions on algorithms that allow meta-nodes to safely replace the arbiter when misbehavior is detected.
4. Analysis of the Protocol
In this section, we evaluate the security of the protocol, providing some analytical results. In particular, we illustrate some realistic attack scenarios and investigate how the choice of protocol parameters and the refund policy can disincentivize adversaries from behaving dishonestly. We also examine how possible attacks to Bitcoin may affect subchains built on top of its blockchain.
4.1. Self-Compensation and Reversed Self-Compensation Attacks
To start our analysis, we start by illustrating two attacks that could potentially compromise the effectiveness of the protocol. Let us assume an adversary that manages to publish C consecutive updates (consistent or inconsistent) starting from index j, with the probability given by Lemma 3. can use each update at index to recover its vote and eventually the fee f for its previous update at index , such that only the last update at index remains unrefunded.
In particular, if the protocol specifies a refund policy that does not admit the proof-of-burn described in
Section 3.2, at least one honest update at index
has to necessarily refund
of
, since
saturated the cutoff window with its updates only. Consequently, following this strategy, the attacker does not lose any deposit and possibly earns an additional extra revenue
r for each inconsistent update published, if any. This extra revenue
r models the case where
induces a victim
to publish an inconsistent update in the form
.
Note also that, if cannot manage to saturate the cutoff window immediately, it can delay the completion of the attack by publishing at least one inconsistent update every C ones on the subchain (to keep refunding itself the vote and the fee). We call the above behavior of (and all its variants) the self-compensation attack.
Now, we slightly change the attack scenario, assuming an adversary that manages to append two updates on the subchain, the first with index i and the second with index . Suppose that the update at index i is consistent, then the honest meta-node that publishes the update at index (recall that the considered refund policy is newest-first) refunds to . can use these funds again to publish a new inconsistent update at index j, refunding its update again at index i (thus, also violating the refund policy). Therefore, manages to earn the undeserved extra revenue r without having lost neither , nor f, therefore performing a special case of the self-compensation attack.
Hence, consider a conservative strategy where the attacker at first tries to publish consistent updates only. When manages to publish a few, it tries to publish just one inconsistent update until the last consistent update published is beyond the cutoff window, then reverses again to consistent updates.
Let
be the probability
has of successfully publishing an update, and suppose it published the latest (consistent) update. We show that the expected payoff
of
, when it follows the described dishonest strategy, is always greater than the expected payoff
can get if it follows the honest strategy. The analysis is limited to the subsequent
C updates, since the two strategies coincide afterwards, and holds only for
(with
, meta-nodes have no choice of refunding the last update, so an inconsistent update is always more profitable than a consistent one). From the hypothesis, it follows that:
In Equation (
7),
describes the payoff of
for the first update it publishes, while the rest denote the sum of the revenues obtained by publishing one or more updates in the subsequent cutoff window, weighted for the respective probabilities to occur. Then, the gain
obtained by following the dishonest strategy is:
The result of Equation (
9) is justified by the following Lemma 4. Since
,
, we get
. This means that, independently of the chosen protocol parameters
, a protocol that uses the refund policy
newest-first admits at least one dishonest strategy, which is always more profitable than the honest one. Note also that a similar result can be obtained for the
oldest-first policy.
Proof. From the following Lemma 5, it follows that the coefficients of the polynomial in Equation (
11) are all zero, thus proving the above Lemma 4. □
Proof. We prove it by induction over
n. The base case is
; therefore,
.
To conclude, the results of the following Lemma 6 are needed. □
Proof. The proof is again by induction over
n. The base case is
; thus,
.
For the inductive step:
□
In the aforementioned scenario, we showed a dishonest strategy that exploits a variant of the self-compensation attack (which we call reversed self-compensation attack), and through Equation (
9), we proved that it is always more profitable than the honest strategy whether the chosen refund policy is
newest-first. This led us to conclude that the choice of the protocol parameters and, in particular, the refund policy is crucial to force the honest strategy to be more profitable than any dishonest one.
4.2. General Attacker Model
To analyze other possible attacks, we now define a more general attacking strategy, which considers an adversary who can craft any update (consistent or not) and controls one meta-node with stake ratio , where , m is the stake controlled by the adversary, and S is the total stake of the network (assuming a single adversary is not less general than having many non-colluding meta-nodes that carry out individual attacks. Indeed, in this setting, meta-nodes do not join their funds to increase the stake ratio ). Suppose that each meta-node can vote on as many update requests as possible, spending all its stake, and that the network is always saturated with pending updates, which globally amount to the entire stake of honest meta-nodes (note that saying the update queue is not always saturated is equivalent to modeling an adversary with a stronger : this is because honest meta-nodes cannot spend all their stake in a single protocol round, i.e., reducing their actual power. Thus, studying this particular case will not give any additional contribution to the analysis).
To evaluate its security, we model the protocol as a game, in which the attacker is a player that adopts a possibly dishonest strategy, thus trying to publish either consistent or inconsistent updates. Conversely, the other players are the honest meta-nodes, which follow the protocol and therefore adopt a honest strategy, trying to publish consistent updates only. Suppose also that follows an optimal strategy, i.e., according to the current state, the choice of voting for a consistent or inconsistent update—at each protocol round—is made with the goal of maximizing its final revenue. In particular, the current state depends on the content of the current cutoff window, and not on the full history of the subchain:
Lemma 7. The revenue of an update published by an adversary , at the protocol round i, depends only on the state of the cutoff window in that round (i.e., ), on the protocol parameters Π, on the refund policy Θ, and on the adversary ratio μ.
To justify Lemma 7, observe that, by the definition of refund policy , no update with index can be refunded, neither of the vote , nor the fee f, in a protocol round with index i. Thus, no matter what chooses at the current round, there is no additional revenue (but also no loss) for any update outside the cutoff window.
Now, let G be a function that maps a subchain into a sequence of labels . A label can assume one of the following values: Inc, which indicates an inconsistent update published by ; Con, which represents a consistent update published by , and Ext, which denotes a (consistent) external update published by the rest of the network, assumed to be honest.
Furthermore, let be the sequence that represents the cutoff window state at round k This sequence is used to generate two new sequences and that represent the possible continuations of the chain if the adversary manages to publish the next update.
We also need a function that, given the protocol parameters and the refund policy , takes a sequence s as input and computes the a posteriori attacker revenue associated with s. Moreover, let be a variant of that, in addition, takes into account the possible refunds generated appending C updates at the end of s (this models the case of an attack that terminates).
Through
and
and given the attacker’s ratio
, it is possible to define a payoff function
with depth
d. Let
be a sequence of length
N and
be the same sequence of
s, where the first label is elided. The payoff function is defined recursively as:
With all these ingredients, we can formulate the following:
Definition 4 (Optimal choice). Given a sequence that represents the state of the current cutoff window, the optimal choice with depth d for the adversary is to try to publish a consistent update if , an inconsistent one otherwise.
In particular, consider an adversary that plans to meddle with the protocol for a limited amount of time, say for d rounds, starting at round n. In this scenario, the optimal strategy for the adversary would require, at each round , making the optimal choice with depth .
This guarantees , to get the maximum possible revenue at the end of the attack: in fact, the optimal choice of depth d (i.e., the initial choice) takes into account every possible evolution of the protocol for the duration of the attack, weighted for its probability to occur, and considers the best outcome at every step. At last, note that the optimal strategy cannot be well defined for an adversary that plans to attack the protocol for an indefinite number of rounds; however, it can be effectively approximated by considering—at each step—making the optimal choice of fixed depth d, for a big enough d.
4.3. Analytical Results
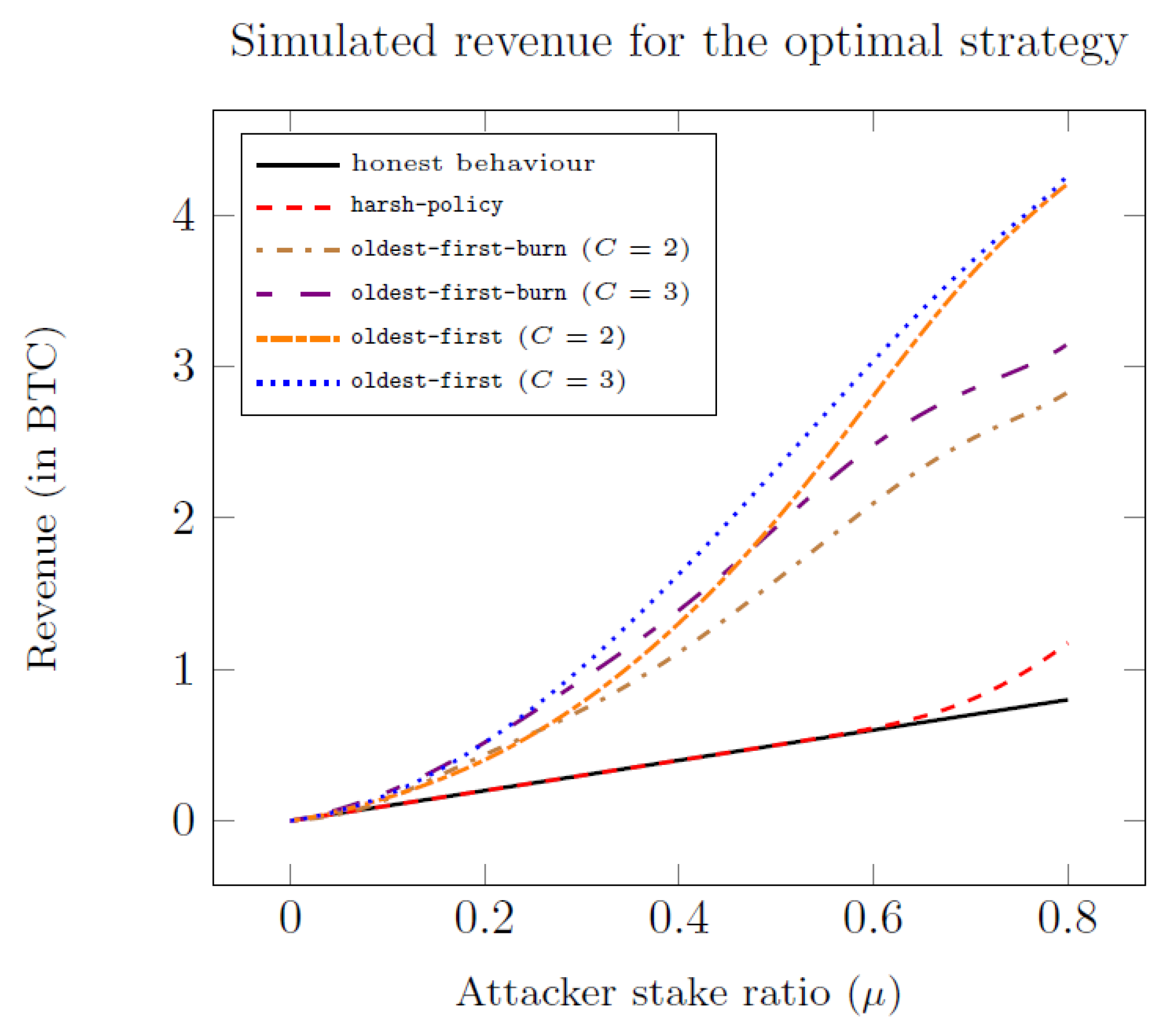
In what follows, we show the results of the security analysis of the protocol, under the attack scenario in which the adversary adopts an optimal strategy, and only for the
policy, which provides the best security performance among the policies shown in
Section 3.1 (according to some simulated preliminary experiments shown in
Figure 2). The results are summarized by the following:
Lemma 8. If the protocol prescribes to use the harsh policy, an adversary with stake ratio μ, who adopts an optimal strategy in pursuing an attack of arbitrary length, behaves necessarily honest iff .
Proof. Note that, if the prescribed policy is the harsh-policy, any update after a must necessarily refund the vote and the fee to the adversary, independently of its type. Thus, this additional gain can be included in the revenue, having:
where the symbol “−” indicates an indifference condition.
On the other side, the revenue for an inconsistent update can be quantified in:
(vote and fee are self-refunded)
(the refund of f and has already been counted for )
Note that, when considering to publish an inconsistent update, a cutoff that contains is equivalent to one with . Finally, observe that computing the revenue in this way gives , and therefore, .
Now, note that, at the terminal rounds of the attack, the adversary is encouraged to publish consistent updates, since it has to publish at least two consecutive to outdo the honest behavior (because ) and the chances to do so decrease. The only exceptions are the rare cases in which a streak of consecutive occurs in the terminal rounds: here, the adversary is motivated to continue publishing inconsistent updates. However, as soon as an attempt fails (an breaks the sequence) and if the end is near enough, the adversary switches to the honest behavior. On the contrary, at the early rounds, a high enough ensures that, on average, a sufficient number of consecutive will be published to gain an advantage over the honest behavior. In this case, since , it follows that if publishing an inconsistent update is the optimal choice at the step k, then it was the optimal choice at the step as well.
Under these assumptions, we can conclude that the optimal strategy can be either completely honest or starting dishonest (always trying to publish
items) and then switching to the honest one as the end of the attack approaches. Thus, for our analysis, we can only consider the early rounds, in which publishing inconsistent updates can be more profitable than publishing consistent ones. Here, the adversary that publishes
gains
with probability
and
with probability
(recall that
is the probability that the adversary manages to publish an update in a given round). Therefore, the adversary chooses the honest strategy right from the start if and only if:
□
The value of f is assumed to be strictly smaller than , in order to incentivize the participation of meta-nodes in the protocol. In fact, with f very close to (or even greater than) , clients have no evident benefit from delegating meta-nodes to vote on their updates (since the required economical effort does not change significantly). This is similar to providing a protocol with no fees, in which it is less attractive for meta-nodes to participate. However, a large participation in the protocol reduces the possibility that single or colluding entities control the majority of the stake.
Under this assumption, Equation (
17) shows that the security of the protocol is essentially proportional to the ratio
: the higher this ratio, the more convenient an honest behavior becomes.
Figure 3 finally illustrates how the switch point (i.e.,
such that
) varies for different combinations of
and
r, with a small fixed fee (
).
5. Implementation Concept in Bitcoin
We describe now how the extended version of the protocol can be implemented in Bitcoin. Note that this implementation, which differs in some aspects from the original one, is conceptual, although the validity of the transactions has been tested using BitMLcalculus [
50], and a preliminary implementation is under development.
Specifically, a label at position i of the subchain is implemented as the Bitcoin transaction . In order to generate it, clients produce an incomplete form of such a transaction, consisting only of the following input and output fields:
the input , which redeems funds from some client’s previous transaction . These funds are used to charge the participant fee for the update request (and the value v, if applicable);
scriptPubKey at Index 0, which embeds the label
, properly binary encoded through a custom
function, through the
instruction [
55].
scriptPubKey of Index 3, which is only required for messages of the type where , i.e., those that also transfer funds between participants. In this case, participant can redeem from this output script by providing its signature.
Then, the incomplete transaction is sent to a meta-node, which respectively adds:
the input , to put the required (from some transaction that in a stage of the protocol must be different for every vote, to prevent attackers to vote for more s with the same funds);
the input , to declare they want to extend the last published update ;
scriptPubKey at Index 1, which links the transaction to the previous confirmed request of the subchain, pointed to by . This link requires the arbiter signature. Note that this field always points to the element immediately preceding it, regardless of whether it is consistent or not;
scriptPubKey of Index 2, which implements the incentive mechanism, i.e., the explicit confirmation of the last consistent of the subchain. Thus, the script rewards the meta-node that has voted for by plus the participant fee.
All transactions also specify a
lockTime , where
n is the current Bitcoin block number and
k is a positive constant. This ensures that a transaction can be mined only after
k blocks. In this way, even if a transaction is signed by the arbiter and sent to miners before the others, it has the same probability as the others of being appended to the blockchain. The overall general scheme of such a transaction is finally depicted in
Figure 4.
To initialize the subchain, the arbiter puts a special
transaction on the Bitcoin blockchain, formed as in
Figure 5. This transaction secures a very small fraction of Bitcoins, which can be redeemed by
through the arbiter signature. This value is then transferred to each subsequent update of the subchain. In particular, observe that, since all the update requests in the same stage redeem the same output (i.e., the arbiter’s one), exactly one of them can be mined, thus avoiding forks.
As seen in
Section 3, the protocol runs in rounds of fixed duration
, where
is the time length of the voting phase. Due to the mechanism for choosing the message to append to the subchain among all the ones in the request pool, the protocol allows each application to publish at most one transaction per Bitcoin block. This means that the Bitcoin block interval time (
min) necessarily represents a lower bound for
. Furthermore, to monitor the arbiter behavior during protocol rounds, all meta-nodes should share a coherent view of the request pool: a naive solution to achieve this goal, similar to that used by Bitcoin, requires meta-nodes to broadcast their request pool lists at each stage. For these reasons,
needs to be large enough to let each node synchronize the request pool with the rest of the network. This leads to some minor issues, which will be discussed in
Section 6.
Note also that, since Bitcoin limits the size of such metadata to 80 bytes, this might not be enough to store the data needed by platforms. To overcome this issue, meta-nodes can maintain a parallel Distributed Hash Table (DHT), like, for instance, Kademlia [
58]. Therefore, message data are not stored in the blockchain:
OP_RETURN scripts would contain only the corresponding message digests, while the full content is stored in the DHT. The unique identifier of the Bitcoin transaction can then be used as the key to retrieve such a message.
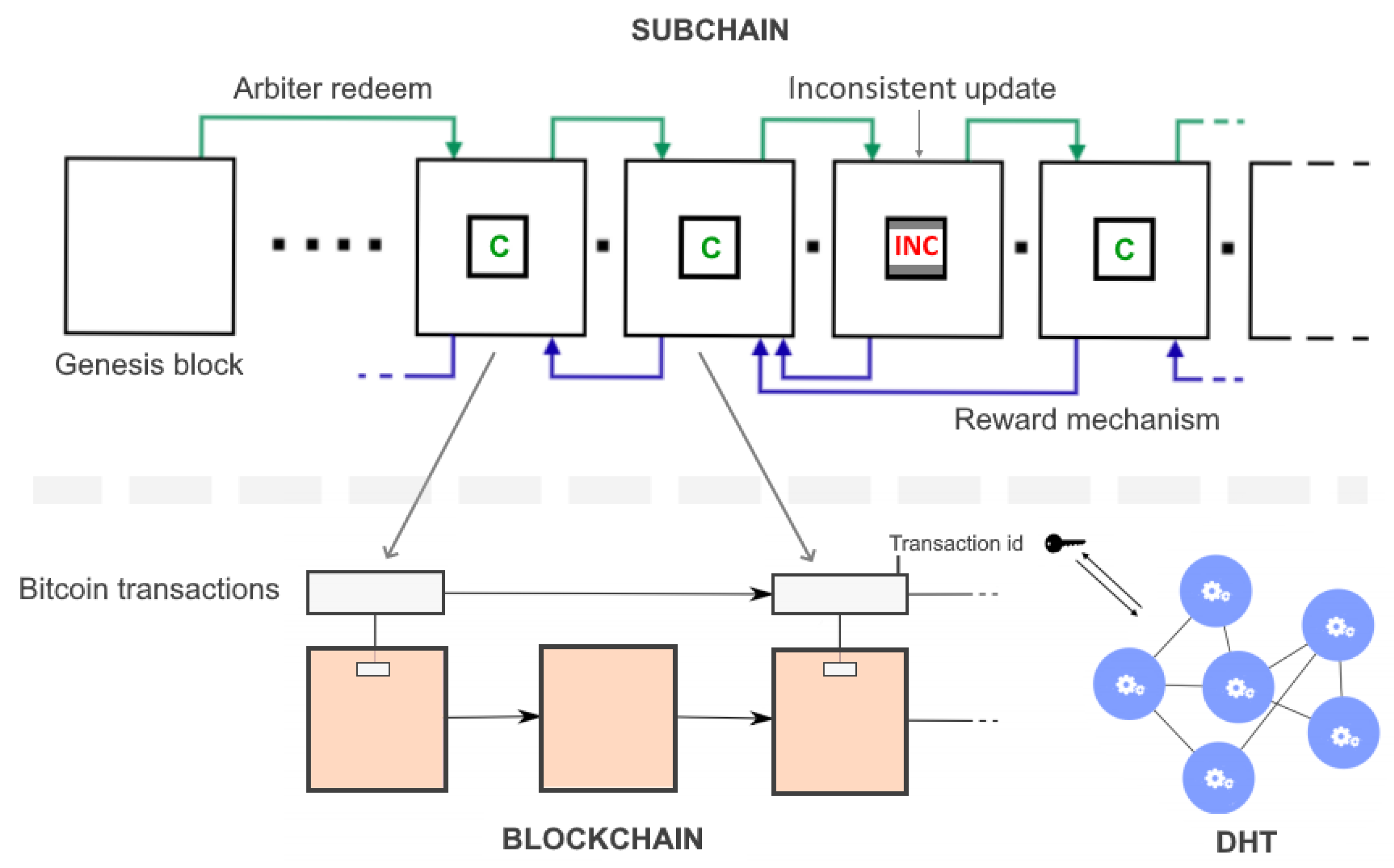
Finally, a subchain implemented through our protocol can be then summarized as in
Figure 6.
6. Conclusions and Further Research
In this work, we proposed an extended version of our protocol for consistently extending subchains embedded in the Bitcoin blockchain. The main scientific contributions of this protocol are: (i) a detailed overview of the context in which this research falls, as well as an extensive review of the state-of-the-art in blockchain and smart contracts, with particular attention on Bitcoin; (ii) a formal definition of the problem we addressed, where peer nodes running decentralized third-party applications or smart contracts want to achieve consensus on the data produced by their execution, hence consistently and permanently storing the outputs of this execution on the blockchain; (iii) a description of the proposed protocol to cope with this issue, largely revised with respect to its original version, along with the definition of its basic properties and peculiarities, and a concept implementation in Bitcoin; and (iv) an in-depth analysis of the security and limitations of our protocol, carried out by defining multiple real-world attack scenarios, as well as the ideal configuration of parameters necessary to prevent adversaries from subverting its correct execution.
However, as outlined in previous sections, some aspects of the proposed protocol have limitations that need to be further investigated. One interesting open problem concerns the role of the arbiter, which, as said in
Section 3.4, does not play the role of a trusted authority. Indeed, it is only required to sign voted updates, while it would participate in the consensus mechanism (i.e., voting and validating update requests) if it were a trusted authority. Since the request pool is public, meta-nodes can verify that the arbiter actually signs all and only the voted for updates, thus detecting any misbehavior. Moreover, we assumed the arbiter to be honest, to simplify our presentation. Nevertheless, if the arbiter stops behaving honestly, nodes can easily fork the subchain and elect a new arbiter, but this could cause a significant overhead in the execution of the protocol, opening the way to potential denial-of-service attacks. For this reasons, we are currently working on an extension of the protocol in which the arbiter can be safely and quickly replaced in case of misbehaviors. The extension relies on some properties of Elliptic-Curve Cryptography (ECC) [
59], and its intuition consists essentially of rotating the key used by the arbiter to sign transactions, through a secret sharing mechanism that involves the nodes of the network. Since this extension introduces additional points of vulnerability in the protocol, a wider security analysis is needed.
A second open issue concerns the synchronization time of the request pool between nodes. This is crucial, since a too high latency could slow down the protocol execution time, which may be a limitation for some categories of decentralized applications (e.g., real-time ones). A possible approach to cope with this issue is to make meta-nodes broadcast their voted updates and to keep a list of the other ones (considering only those that satisfy the format of transactions, as in
Section 5). A clear drawback of this solution is that it can cause a significant increase in the number of packets exchanged by the network. Our future research direction is focused on finding a more efficient alternative, and approaches based on distributed shared memories [
60,
61] seem promising.
Overall, as far as we know, most third-party services that store data on the Bitcoin blockchain do not adopt truly secure solutions for maintaining their subchain. Therefore, our protocol, widely revised compared to its initial version, can represent a starting point for those applications that want to offer a better level of reliability to their users, taking full advantage of the potential offered by the Bitcoin blockchain.