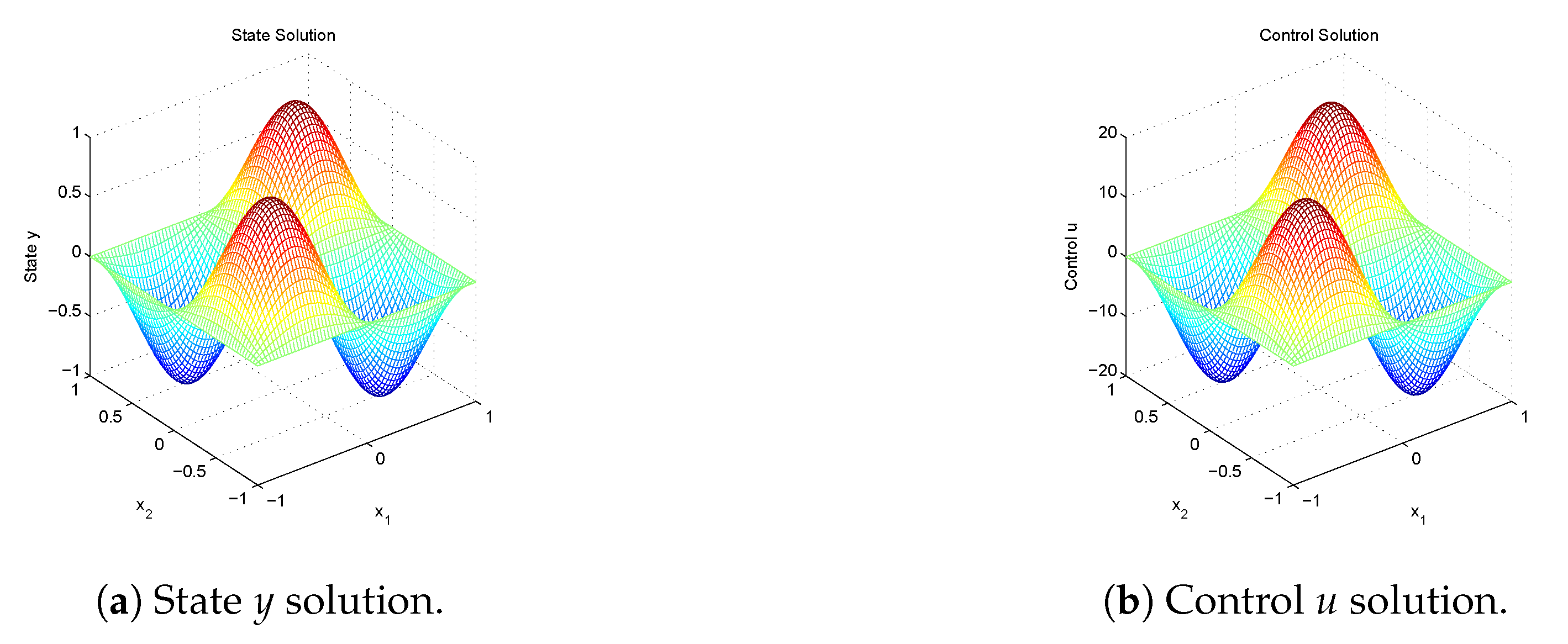A Robust Approximation of the Schur Complement Preconditioner for an Efficient Numerical Solution of the Elliptic Optimal Control Problems

Abstract

In this paper, we consider the numerical solution of the optimal control problems of the elliptic partial differential equation. Numerically tackling these problems using the finite element method produces a large block coupled algebraic system of equations of saddle point form. These systems are of large dimension, block, sparse, indefinite and ill conditioned. The solution of such systems is a major computational task and poses a greater challenge for iterative techniques. Thus they require specialised methods which involve some preconditioning strategies. The preconditioned solvers must have nice convergence properties independent of the changes in discretisation and problem parameters. Most well known preconditioned solvers converge independently of mesh size but not for the decreasing regularisation parameter. This work proposes and extends the work for the formulation of preconditioners which results in the optimal performances of the iterative solvers independent of both the decreasing mesh size and the regulation parameter. In this paper we solve the indefinite system using the preconditioned minimum residual method. The main task in this work was to analyse the 3 × 3 block diagonal preconditioner that is based on the approximation of the Schur complement form obtained from the matrix system. The eigenvalue distribution of both the proposed Schur complement approximate and the preconditioned system will be investigated since the clustering of eigenvalues points to the effectiveness of the preconditioner in accelerating an iterative solver. This is done in order to create fast, efficient solvers for such problems. Numerical experiments demonstrate the effectiveness and performance of the proposed approximation compared to the other approximations and demonstrate that it can be used in practice. The numerical experiments confirm the effectiveness of the proposed preconditioner. The solver used is robust and optimal with respect to the changes in both mesh size and the regularisation parameter.

1. Introduction

The partial differential equation constrained optimisation problems have over the years become an active research area that has arisen in many application areas that include finance, medicine, modern science and engineering. We refer to [1,2] on their theoretical and also to [3,4,5] on their numerical developments. These problems are numerically and analytically challenging to solve. The most clear challenge is that the resulting linear algebraic system is very large such that the only viable way is to get the solution iteratively using specialised methods. The formulation of the linear optimisation problem involves the objective function to minimise subject to the constraints defined by the underlying modelling partial differential equation in a bounded domain $\Omega \subset {\mathcal{R}}^2$ with boundary $\partial \Omega$. Consider the following elliptic distributed PDE-optimal control problem

$${\displaystyle {\min }_{(u,y)}J(y,u):=\frac{1}{2}\Vert y-y_d{\Vert }_{L^2(\Omega )}^2+\frac{\delta }{2}{\Vert u\Vert }_{L^2(\Omega )}^2}$$

(1)

subject to the constraints

$$\begin{array}{ccc}\hfill -\Delta y& =\hfill & f+u\mathrm{in}\Omega \hfill \\ \hfill y& =\hfill & g\mathrm{on}\partial \Omega \hfill \end{array}$$

(2)

with y the state variable, $y_d$ the desired state known over the domain $\overline{\Omega }$ and u the control variable on the right hand side. The parameter $\delta$ is called the regularisation parameter which measures the cost of the control and is supplied and positive. The size of the regularisation parameter is important in the performances of the iterative solvers. The optimal value of the regularisation parameter $\delta$ is ${10}^{-2}$; see [6,7]. The performance of iterative solvers with the decreasing parameter is the central theme of this study. The solution of the state variable y must satisfy the PDE over $\Omega$ and must be as close as possible to the desired state $y_d$ so that the objective function can be minimised.

The optimal control problem Equations (1) and (2) has a unique solution $(y,u)$ characterised by the following optimality system called the Karush–Kuhn–Tucker (KKT) system [8,9]. The first order optimality system of the PDE-optimal control problems consists of a state equation, an adjoint equation and the control equation which is a saddle point problem as given below

$$\begin{array}{ccc}\hfill -\Delta p& =& y-y_d,\mathrm{in}\Omega p=0\mathrm{on}\partial \Omega \mathrm{adjoint} \mathrm{equation}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill -\Delta y& =& f+u,\mathrm{in}\Omega y=g\mathrm{on}\partial \Omega \mathrm{state} \mathrm{equation}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill -\delta u& =& p\mathrm{in}\Omega \mathrm{control} \mathrm{equation}\hfill \end{array}$$

(5)

The optimality system is achieved through the Lagrange multiplier method which partitions the model problem into three equations, namely, the state y, control u and the adjoint, p which form the saddle point problem. For the numerical solution of the elliptic optimal control problem we apply the finite element method to the system ((3)–(5)) to get the linear saddle point problem. The finite element method is the most popular technique for the numerical solution of the PDE-constrained optimisation problems; see [5,6,7] and many more. The finite element method results in the coupled linear algebraic system which has to be solved by the appropriate solvers. The resulting discrete KKT system is

$$\left(\begin{array}{ccc}M& O& K\\ O& \delta M& -M\\ K& -M& O\end{array}\right)\left(\begin{array}{c}\mathbf{y}\\ \mathbf{u}\\ \mathbf{p}\end{array}\right)=\left(\begin{array}{c}\mathbf{b}\\ \mathbf{0}\\ \mathbf{d}\end{array}\right)$$

(6)

where $K\in {\mathcal{R}}^{n\times n}$ is a stiffness matrix, and that and the mass matrix $M\in {\mathcal{R}}^{n\times n}$ are both symmetric and positive definite. The vector $\mathbf{b}=M{\mathbf{y}}_d\in {\mathcal{R}}^n$ is the finite element projection of the desired state $y_d$, and $\mathbf{d}\in {\mathcal{R}}^n$ contains the terms arising from the boundaries of the finite element of the state y.

The finite element discretisation produces a large scale linear algebraic system of Equation (6) which is indefinite and has poor spectral properties. The numerical solution of such problems is a computational uphill task and has a lot of challenges such that constructing robust and efficient solvers has preoccupied the computational scientific community for decades. The linear algebraic indefinite system is parameter dependent such that the condition number grows when the mesh size and the regularisation parameter approach zero. The well known Krylov and multigrid iterative solvers perform poorly for such systems. In recent years, much effort has been devoted in developing specialised iterative solvers using suitable preconditioners [3,6,7,10,11,12] and appropriate smoothers for the multigrid solvers [8,9,13,14,15,16,17]. For the development of the efficient multigrid solvers for the distributed optimal control problems, we refer to ([8,9,15,16,18,19]. Several preconditioned strategies have been developed and evolved that accelerate the iterative solvers. These are the block diagonal preconditioner [6,20,21,22] for the minimum residual (MINRES) solver [23,24], and for the generalised minimal residual (GMRES) method, block triangular preconditioners with nonstandard inner products for the conjugate gradient method [7,10,21,22,25] and the constraint preconditioner [7,11,21]. The preconditioners were also developed for the two by two reduced block linear system and three by three block system to solve the optimal control problems of the Stokes [10,26,27], parabolic [28,29] and convection diffusion [30] equations. In most cases the application of preconditioners shows robustness and efficiency with the decreasing mesh size but not with the decreasing regularisation parameter. In this study, we focus on the improvement of the block diagonal preconditioner to enhance the performance of the MINRES solver. The MINRES was developed by [31] and widely used for PDE-constrained optimisation problems. The aim of this paper is to present preconditioners based on the Schur complement approach that seek to achieve an efficient solution of the linear system arising from the discretisation of the PDE- optimal control problems. We give particular attention to preconditioning techniques that achieve robust performances in the MINRES solver with respect to both decreasing mesh size and the regularisation parameter. As the mesh size approaches zero, the dimensions of the problem increase. A mesh-independent performance is always achieved for such systems, but the small values of the regularisation parameter pose a great challenge to the iterative solvers. As the regularisation parameter decreases, the performance of the iterative solver deteriorates, but it improves for large values.

The optimal performance of the preconditioner depends on applying an appropriate approximation of the (1,1) and (3,3)-block entries of the preconditioner. For the preconditioners based on the Schur complement, the (3,3) Schur complement remains one of the challenges to finding a suitable approximation to achieve robustness in terms of parameter changes. The Schur complement approximation developed in [6] and widely used in literature displays optimal performance for large values of the regularisation parameter, but the performance of it deteriorates as the parameter approaches zero. In [21,23] another Schur complement approximation was developed for PDE-constrained optimisation problems which gives convergence of the appropriate iterative method in a number of steps which are independent of the value of the regularisation parameter. The preconditioned iterative solver displays optimal performance for small values of the regularisation parameter. The main contribution of this work is to present a different form of the Schur compliment approximation to achieve an optimal performance of the MINRES solver in terms of iterative counts that are independent of the decreasing mesh size and the regularisation parameter. The clustering of the eigenvalues points to the good convergence properties of the preconditioned solver. We remove the dependency on the regularisation parameters within the preconditioned matrix as in [21]. We derive and investigate the clustering of the eigenvalues for the Schur compliment approximate and the preconditioned system. The numerical experiments’ outcomes of the proposed approximation are compared with the existing approximations of the Schur complement preconditioner to show its efficiency.

This paper is organised as follows. In Section 2 we preview the block diagonal preconditioner and investigate the eigenvalue distribution. In Section 3, we discuss our proposed approximation for the Schur complement and investigate the eigenvalue distribution of the preconditioned system. In Section 4 we present the numerical experiments to demonstrate how well the proposed approximation works and the conclusion is given.

2. Analysis of the Block Diagonal Preconditioner

We consider the preconditioning strategies for solving the saddle point problem, Equation (6). The optimal performance of the preconditioned Krylov subspace methods such as MINRES, GMRES and conjugate gradient rely more on the distribution of the eigenvalues of the coefficient matrix. It is well known in numerical analysis that the spectral radius must be bounded by one to guarantee convergence of the iterative solvers. The coefficient matrix of the system (6) is known to be large, sparse and indefinite with poor spectral properties. This section aims to outline the block diagonal preconditioner that involves the mass matrix and a Schur complement form. We consider a block diagonal preconditioner for the $3\times 3$ block coefficient matrix of the Equation (6). For the $2\times 2$ block preconditioners we refer to [7,22] and the references therein. The block diagonal preconditioner is given by

$$\mathcal{Q}:=\left(\begin{array}{ccc}M& O& O\\ O& \delta M& O\\ O& O& S\end{array}\right)$$

(7)

where $S:=K{M}^{-1}K+\frac{1}{\delta }M$ is the Schur complement form. A good preconditioner must fulfil the assumptions that it is easy to invert, and the linear system $\mathcal{Q}\mathbf{x}=\mathbf{b}$ associated with it is easy to solve for any vector $\mathbf{b}$. The approximation of the (3,3) block entry poses more challenges and difficulties. One possible widely used approach as in [6,21,24] is to get the approximation of S by discarding the term $\frac{1}{\delta }M$ to obtain $Q_{S_1}=K{M}^{-1}K$ by dropping a term with ${\delta }^{-1}M$ with an argument such that for all very small values of $\delta$ the term $K{M}^{-1}K$ will be dominating. The application of the preconditioner with the approximation $Q_{S_1}=K{M}^{-1}K$ has the shortfall that the iterative solver converges independently of the decreasing mesh size only but not in the decreasing regularisation parameter $\delta$. To demonstrate this we need to give the eigenvalue bounds for $Q_{S_1}^{-1}S$ as derived in [6,21]. We now use the following results, which are Theorems (3.4) and (3.5) in [6] and used by [21,24].

Theorem 1

([6]). For the problem Equation (6) in $\Omega \in {\mathcal{R}}^2$ with the degree of approximation ${\mathbf{Q}}_{\mathbf{m}}$ or ${\mathbf{P}}_{\mathbf{m}}$ with $\mathbf{m}\ge 1$ the following bounds hold:

$${\alpha }_1{h}^2\le \frac{{\mathbf{v}}^{T}M\mathbf{v}}{{\mathbf{v}}^T\mathbf{v}}\le {\alpha }_2{h}^2$$

(8)

where ${\alpha }_1$ and ${\alpha }_2$ are real constants independent of h but dependent on $\mathbf{m}$.

Theorem 2

([6]). For the problem Equation (6) in $\Omega \in {\mathcal{R}}^2$ with the degree of approximation ${\mathbf{Q}}_{\mathbf{m}}$ or ${\mathbf{P}}_{\mathbf{m}}$ with $\mathbf{m}\ge 1$ the following bounds hold:

$${\theta }_1{h}^2\le \frac{{\mathbf{v}}^{T}K\mathbf{v}}{{\mathbf{v}}^T\mathbf{v}}\le {\theta }_2$$

(9)

where ${\theta }_1$ and ${\theta }_2$ are real constants independent of h but dependent on $\mathbf{m}$.

Theorem 3.

The eigenvalues of $Q_{S_1}^{-1}S$ are bounded as $\lambda \left(Q_{S_1}^{-1}S\right)\in [\frac{1}{\delta }\tilde{\alpha }{h}^4+1,\frac{1}{\delta }\tilde{\theta }{h}^4+1]$ where $\tilde{\alpha }$ and $\tilde{\theta }$ are independent of h and but dependent on δ.

Proof of Theorem 3

To find the eigenvalue distribution of $Q_{S_1}^{-1}S$, let $\omega$ be the eigenvalue, and then

$$\begin{array}{ccc}\hfill Q_{S_1}^{-1}S\mathbf{y}& =& \omega \mathbf{y}\hfill \\ \hfill {\left(K{M}^{-1}K\right)}^{-1}(K{M}^{-1}K+\frac{1}{\delta }M)\mathbf{y}& =& \omega \mathbf{y}\hfill \\ \hfill (I\delta +K^{-1}M{K}^{-1}M)\mathbf{y}& =& \omega \delta \mathbf{y}\hfill \\ \hfill {\left(K^{-1}M\right)}^2\mathbf{y}& =& \delta (\omega -1)\mathbf{y}\hfill \end{array}$$

Let $\upsilon$ be an eigenvalue of $K^{-1}M$ then the eigenvalue of ${\left(K^{-1}M\right)}^2$ is ${\upsilon }^2$. This means that ${\upsilon }^2=\delta (\omega -1)$

$$\begin{array}{ccc}\hfill {\left(K^{-1}M\right)}^2\mathbf{y}& =& {\upsilon }^2\mathbf{y}\hfill \\ \hfill \left(K^{-1}M\right)\mathbf{y}& =& \upsilon \mathbf{y}\hfill \\ \hfill M\mathbf{y}& =& \upsilon K\mathbf{y}\hfill \end{array}$$

$\Rightarrow \upsilon =\frac{{\mathbf{y}}^{T}M\mathbf{y}}{{\mathbf{y}}^{T}K\mathbf{y}}=\frac{{\mathbf{y}}^{T}M\mathbf{y}}{{\mathbf{y}}^T\mathbf{y}}·\frac{{\mathbf{y}}^T\mathbf{y}}{{\mathbf{y}}^{T}K\mathbf{y}}$. By using Theorems 1 and 2, there exist positive constants $\tilde{\alpha }$ and $\tilde{\theta }$ independent of mesh size; we have

$$\tilde{\alpha }{h}^2\le \frac{{\mathbf{y}}^{T}M\mathbf{y}}{{\mathbf{y}}^{T}K\mathbf{y}}\le \tilde{\theta }$$

This implies that we have

$$\begin{array}{ccc}\hfill \tilde{\alpha }{h}^4\le & \delta (\omega -1)& \le \tilde{\theta }\hfill \\ \hfill \frac{1}{\delta }\tilde{\alpha }{h}^4\le & \omega -1& \le \frac{1}{\delta }\tilde{\theta }\hfill \\ \hfill \frac{1}{\delta }\tilde{\alpha }{h}^4+1\le & \omega & \le \frac{1}{\delta }\tilde{\theta }+1\hfill \end{array}$$

Thus, it follows that there exist constants $\tilde{\alpha }$ and $\tilde{\theta }$ independent of the mesh size such that

$$\frac{1}{\delta }\tilde{\alpha }{h}^4+1\le \frac{{\mathbf{y}}^{T}S\mathbf{y}}{{\mathbf{y}}^T{Q}_{S_1}\mathbf{y}}\le \frac{1}{\delta }\tilde{\theta }+1$$

□

It is clear that $Q_{S_1}$ has no dependence on $\delta$ but the eigenvalue lower and upper bounds are dependent on $\delta$. The eigenvalue bounds demonstrated by the Theorem 3 above show that the parameter $\delta$ determines the clustering and distribution of eigenvalues. This clearly shows that if $\delta$ is too small the eigenvalues are not clustered and $Q_{S_1}$ will not be a better approximation. This entails that large values of $\delta$, $Q_{S_1}$ are a perfect approximation. The current research seeks to construct an approximation whose performance does not rely on both the mesh size and the regularisation parameter. The following theorem in [6] gives the eigenvalue distribution of the preconditioned coefficient matrix with preconditioner ${\mathcal{Q}}_1$ with the approximation for the Schur complement form $Q_{S_1}$ where

$${\mathcal{Q}}_1:=\left(\begin{array}{ccc}M& O& O\\ O& \delta M& O\\ O& O& K{M}^{-1}K\end{array}\right)$$

(10)

Theorem 4

([7,24]). For ${\mathbf{Q}}_{\mathbf{1}}$ approximation, let the preconditioner ${\mathcal{Q}}_1$ be defined by Equation (10). Assume that λ is an eigenvalue of the preconditioned matrix ${\mathcal{Q}}_1^{-1}\mathcal{K}$. Then $\lambda =1$ or λ satisfies the following bound:

$$1+\frac{1}{2\delta }\frac{{\alpha }_1^2}{{\theta }_2^2}{h}^4\le \lambda \le 1+\frac{1}{2\delta }\frac{{\alpha }_1^2}{{\theta }_2^2}$$

For the proof and details we refer to [7,24] and references therein.

3. Proposed Schur Complement Preconditioner Approximation

The above Theorem 4 has demonstrated that applying the preconditioner with the Schur complement approximation $Q_{S_1}$ results in performance and convergence of the preconditioned iterative solver that are independent of the discretisation mesh size and dependent on the regularisation parameter. It is expected that the convergences of the Krylov methods such as MINRES and GMRES are independent of the mesh size. The crucial task is to develop an efficient preconditioner that gives close eigenvalue bounds of the preconditioned system. The scientific literature on preconditioning optimal control systems includes classical Schur complement based approximations. In [21] we see the extension of the preconditioner whose effects are independent of the regularisation parameter. This was also used in [24]. The main task of this section is to briefly discuss the approximation in [21] and the one we propose in this work, which has the same clustering and distribution of eigenvalues and produces a preconditioned iterative solver that is not sensitive to the changes and decreasing regularisation parameter. The following approximation for S was developed in [21]

$$S=(K+\frac{1}{\sqrt{\delta }}M)M^{-1}(K+\frac{1}{\sqrt{\delta }}M)-\frac{2}{\sqrt{\delta }}K$$

which reduces to

$$S=(K+\frac{1}{\sqrt{\delta }}M)M^{-1}(K+\frac{1}{\sqrt{\delta }}M)-\frac{2}{\sqrt{\delta }}K\approx (K+\frac{1}{\sqrt{\delta }}M)M^{-1}(K+\frac{1}{\sqrt{\delta }}M):=Q_{S_2}$$

by discarding the much smaller term $\frac{2}{\sqrt{\delta }}K$ which is a smaller $O\left({\delta }^{\frac{-1}{2}}\right)$ term than $O\left({\delta }^{-1}\right)$ shown Section 2 above. To get eigenvalue bounds for $Q_{S_2}^{-1}S$, we follow the same derivation and use the Theorems 1–3 above. The preconditioner involving the Schur complement approximation $Q_{S_2}$ is given as follows

$${\mathcal{Q}}_2:=\left(\begin{array}{ccc}M& O& O\\ O& \delta M& O\\ O& O& (K+\frac{1}{\sqrt{\delta }}M)M^{-1}(K+\frac{1}{\sqrt{\delta }}M)\end{array}\right)$$

(11)

There has been development of similarly structured Schur complement approximations to $Q_{S_2}$ whose eigenvalue bounds are the same but differ in computational complexities. We have $Q_{S_c}=(K+\frac{1}{i\sqrt{\delta }}M)M^{-1}(K-\frac{1}{i\sqrt{\delta }}M)$ which is complex based developed by Choi and others in [32]. In this paper we propose and analyse a robust approximation for S which has the same eigenvalue bounds but a different eigenvalue distribution within the interval for $Q_{S_2}$ as the approximation $Q_{S_3}$ which is expected to accelerate the numerical solution. Our proposed approximation for the Schur complement is also derived from $Q_{S_1}$ by writing

$$\begin{array}{ccc}\hfill S& =& K{M}^{-1}K+{\delta }^{-1}M\hfill \\ & =& \left(\sqrt{\delta }K\right){\left(\delta M\right)}^{-1}\left(\sqrt{\delta }K\right)+{\left(\delta M\right)}^{-1}+2{\sqrt{\delta }}^{-1}K-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& [\left(\sqrt{\delta }K\right){\left(\delta M\right)}^{-1}\left(\sqrt{\delta }K\right)+{\delta }^{-1}K]+[{\left(\delta M\right)}^{-1}+{\delta }^{-1}K]-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& \sqrt{\delta }K[{\left(\delta M\right)}^{-1}\left(\sqrt{\delta }K\right)+{\delta }^{-1}I]+{\delta }^{-1}[\sqrt{\delta }K+M]-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& \sqrt{\delta }K[({\left(\delta M\right)}^{-1}\left(\sqrt{\delta }K\right)+{\delta }^{-1}{M}^{-1}M]+{\delta }^{-1}[\sqrt{\delta }K+M]-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& \sqrt{\delta }K{\left(\delta M\right)}^{-1}[\sqrt{\delta }K+M]+{\delta }^{-1}[\sqrt{\delta }K+M]-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& [\sqrt{\delta }K{\left(\delta M\right)}^{-1}+{\delta }^{-1}I][\sqrt{\delta }K+M]-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& [\sqrt{\delta }K{\left(\delta M\right)}^{-1}+{\delta }^{-1}M{M}^{-1}][\sqrt{\delta }K+M]-2{\sqrt{\delta }}^{-1}K\hfill \\ & =& [\sqrt{\delta }K+M]{\left(\delta M\right)}^{-1}[\sqrt{\delta }K+M]-2{\sqrt{\delta }}^{-1}K\hfill \end{array}$$

which similarly reduces to

$$S=(\sqrt{\delta }K+M){\left(\delta M\right)}^{-1}(\sqrt{\delta }K+M)-\frac{2}{\sqrt{\delta }}K\approx (\sqrt{\delta }K+M){\left(\delta M\right)}^{-1}(\sqrt{\delta }K+M)=Q_{S_3}$$

by discarding a $O\left({\delta }^{-\frac{1}{2}}\right)$ term this means that the error committed grows much slower. To motivate our choice of the Schur complement approximation, we illustrate the properties of the preconditioned Schur complement and the preconditioned system. We now discuss the derivation of the eigenvalue distribution of $Q_{S_3}^{-1}S$ by following the same derivation in [21].

Theorem 5.

The eigenvalues of $Q_{S_3}^{-1}S$ satisfy the following bounds $\sigma \left(Q_{S_3}^{-1}S\right)\in [\frac{1}{2},1]$ independent of both mesh size h and regularisation parameter δ

Proof of Theorem 5

$Q_{S_3}$ is invertible since M is symmetric and positive definite. Let $\sigma$ be an eigenvalue of $Q_{S_3}^{-1}S$ corresponding to eigenvector $\mathbf{y}$; then

$$\begin{array}{ccc}\hfill Q_{S_3}^{-1}S\mathbf{y}& =& \sigma \mathbf{y}\hfill \\ \hfill S\mathbf{y}& =& \sigma Q_{S_3}\mathbf{y}\hfill \\ \hfill (K{M}^{-1}K+\frac{1}{\delta }M)\mathbf{y}& =& \sigma (\sqrt{\delta }K+M){\left(\delta M\right)}^{-1}(\sqrt{\delta }K+M)\mathbf{y}\hfill \\ \hfill (K{M}^{-1}K+\frac{1}{\delta }M)\mathbf{y}& =& \sigma (K{M}^{-1}K+\frac{1}{\delta }M+\frac{2}{\sqrt{\delta }}K)\mathbf{y}\hfill \\ \hfill (I+\frac{1}{\delta }{K}^{-1}M{K}^{-1}M)\mathbf{y}& =& \sigma (I+\frac{1}{\delta }{K}^{-1}M{K}^{-1}M+\frac{2}{\sqrt{\delta }}{K}^{-1}M)\mathbf{y}\hfill \\ \hfill (\delta I+K^{-1}M{K}^{-1}M)\mathbf{y}& =& \sigma (\delta I+K^{-1}M{K}^{-1}M+2\sqrt{\delta }{K}^{-1}M)\mathbf{y}\hfill \\ \hfill (\delta I+{\left(K^{-1}M\right)}^2)\mathbf{y}& =& \sigma {(\sqrt{\delta }I+K^{-1}M)}^2\mathbf{y}\hfill \\ \hfill {(\sqrt{\delta }I+K^{-1}M)}^{-2}(\delta I+{\left(K^{-1}M\right)}^2)\mathbf{y}& =& \sigma \mathbf{y}\hfill \end{array}$$

Let $\nu$ be the eigenvalue of $K^{-1}M$; then

$${(\sqrt{\delta }+\nu )}^{-2}(\delta +{\nu }^2)\mathbf{y}=\sigma \mathbf{y}$$

This means that $\sigma =\frac{(\delta +{\nu }^2)}{{(\nu +\sqrt{\delta })}^2}$ is an eigenvalue of $Q_{S_3}^{-1}S$. Now since $K^{-1}M$ is similar to the real and symmetric matrix $M^{\frac{1}{2}}{K}^{-1}{M}^{\frac{1}{2}}$, it is diagonalisable; this means that it describes all the eigenvalues of $Q_{S_3}^{-1}S$. It is known that a fraction of the form $\frac{v^2+w^2}{{(v+w)}^2}$ is bounded between $\frac{1}{2}$ and 1. Hence, $\upsilon =\frac{(\delta +{\nu }^2)}{{(\nu +\sqrt{\delta })}^{-2}}=\frac{({\sqrt{\delta }}^2+{\nu }^2)}{{(\nu +\sqrt{\delta }I)}^{-2}}$ which takes the form $\frac{v^2+w^2}{{(v+w)}^2}$. Thus, $\frac{1}{2}\le \sigma \le 1$. By this we conclude that $\sigma \left({\widehat{Q}}_{S_3}^{-1}S\right)\in [\frac{1}{2},1]$ is clustered and not dependent on the mesh size h and the regularisation parameter $\delta$. □

The actual application of the preconditioner $Q_{S_3}$ in actual computations involving solving two subsystems to accelerate the convergence of Krylov subspace iteration process can be implemented as: Application of Preconditioner $Q_{S_3}$.

Algorithm 1.Application of Preconditioner$Q_{S_3}$

Let $L=\sqrt{\delta }K+M$ and $\mathbf{w}$ be any given vector; we can compute the vector $\mathbf{v}$ and $Q_{S_3}\mathbf{v}=\mathbf{w}$, that is, $L{M}^{-1}L\mathbf{v}=\mathbf{w}$, using the following procedures:

• $L\mathbf{y}=\mathbf{w}$ solve for $\mathbf{y}$;
• $M^{-1}L\mathbf{v}=\mathbf{y}$; we have $M\mathbf{y}=\mathbf{u}$;
• $L\mathbf{v}=\mathbf{u}$ solve for $\mathbf{v}$.

Since M and K are sparse, L is sparse too, and an added bonus for $Q_{S_3}$ and $Q_{S_2}$ is that they maintain $\delta$-dependency and their bounds are fairly good. The preconditioner involving the Schur complement approximation $Q_{S_3}$ is given as follows.

$${\mathcal{Q}}_3:=\left(\begin{array}{ccc}M& O& O\\ O& \delta M& O\\ O& O& (\sqrt{\delta }K+M){\left(\delta M\right)}^{-1}(\sqrt{\delta }K+M)\end{array}\right)$$

(12)

We now derive the eigenvalues distribution of the preconditioned coefficient matrix ${\mathcal{Q}}_3^{-1}\mathcal{K}$ with the modified approximation for the Schur complement form. We will use Proposition (2) in [7] which extends Theorem 4.

Theorem 6

([7]). The eigenvalues of the preconditioned system ${\mathcal{Q}}_3^{-1}\mathcal{K}$ where $\mathcal{K}:=\left(\begin{array}{ccc}M& O& K\\ O& \delta M& -M\\ K& -M& O\end{array}\right)$ and ${\mathcal{Q}}_3=\left(\begin{array}{ccc}M& O& O\\ O& \delta M& O\\ O& O& Q_{S_3}^{-1}\end{array}\right)$ are in the interval $\mu \left({\mathcal{Q}}_3^{-1}\mathcal{K}\right)\in [\frac{1-\sqrt{5}}{2},\frac{1-\sqrt{3}}{2}]\cup 1\cup [\frac{1+\sqrt{3}}{2},\frac{1+\sqrt{5}}{2}]$

Proof of Theorem 5

Let $\sigma$ be the eigenvalue of $Q_{S_3}^{-1}S$ and $\mu$ be an eigenvalue of ${\mathcal{Q}}_3^{-1}\mathcal{K}$ corresponding to the eigenvector $\mathbf{v}=\{v_1,v_2,v_3\}$. We want to find the eigenvalues bounds for ${\mathcal{Q}}_3^{-1}\mathcal{K}$. We use a different approach from the one in [21]. We have

$${\mathcal{Q}}_3^{-1}=\left(\begin{array}{ccc}{M}^{-1}& O& O\\ O& {\left(\delta M\right)}^{-1}& O\\ O& O& Q_{S_3}^{-1}\end{array}\right)$$

The preconditioned coefficient matrix

$$\begin{array}{ccc}\hfill {\mathcal{Q}}_3^{-1}\mathcal{K}& =& \left(\begin{array}{ccc}{M}^{-1}& O& O\\ O& {\left(\delta M\right)}^{-1}& O\\ O& O& Q_{S_3}^{-1}\end{array}\right)\left(\begin{array}{ccc}M& O& K\\ O& \delta M& -M\\ K& -M& O\end{array}\right)\hfill \\ & =& \left(\begin{array}{ccc}I& O& M^{-1}K\\ O& I& -{\left(\delta \right)}^{-1}I\\ Q_{S_3}^{-1}K& -Q_{S_3}^{-1}M& O\end{array}\right)\hfill \end{array}$$

We consider the eigenvalue problem

$$\begin{array}{ccc}\hfill {\mathcal{Q}}_3^{-1}K\mathbf{v}& =& \mu \mathbf{v}\hfill \\ \hfill \left(\begin{array}{ccc}I& O& M^{-1}K\\ O& I& -{\left(\delta \right)}^{-1}I\\ Q_{S_3}^{-1}K& -Q_{S_3}^{-1}M& O\end{array}\right)\left(\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right)& =& \mu \left(\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right)\hfill \end{array}$$

It follows that,

$$\begin{array}{ccc}\hfill v_1+M^{-1}K{v}_3& =& \mu v_1\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill v_2+\frac{1}{\delta }I{v}_3& =& \mu v_2\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill Q_{S_3}^{-1}K{v}_1-Q_{S_3}^{-1}M{v}_2& =& \mu v_3\hfill \end{array}$$

(15)

• If $\mu =1$ from Equations (13) and () we have $M^{-1}K{v}_3=0$ and $\frac{1}{\delta }I{v}_3=0$, then $v_3=0$. Therefore, the corresponding eigenvector is

  $$\mathbf{v}=\left(\begin{array}{c}{v}_1\\ v_2\\ 0\end{array}\right),\forall \left(\begin{array}{c}{v}_1\\ v_2\end{array}\right)\ne \mathbf{0}$$
• If $\mu \ne 1$ from Equations (13) and () we have

  $$\begin{array}{ccc}\hfill v_1& =& \frac{1}{\mu -1}{M}^{-1}K{v}_3\hfill \end{array}$$

  (16)

  $$\begin{array}{ccc}\hfill v_3& =& \frac{1}{\delta (\mu -1)}{v}_3\hfill \end{array}$$

  (17)

  Substituting Equations (16) and () into Equation (), we get

  $$\begin{array}{ccc}\hfill Q_{S_3}^{-1}K\left(\frac{1}{\mu -1}{M}^{-1}K{v}_3\right)-Q_{S_3}^{-1}M\left(\frac{1}{\delta (\mu -1)}{v}_3\right)& =& \mu v_3\hfill \\ \hfill Q_{S_3}^{-1}K{M}^{-1}K{v}_3-\frac{1}{\delta }{Q}_{S_3}^{-1}M{v}_3& =& \mu (\mu -1)v_3\hfill \\ \hfill Q_{S_3}^{-1}(K{M}^{-1}K{v}_3-\frac{1}{\delta }M)v_3& =& \mu (\mu -1)v_3\hfill \\ \hfill Q_{S_3}^{-1}S{v}_3& =& \mu (\mu -1)v_3\hfill \end{array}$$

  Therefore $\mu$ satisfies $Q_{S_3}^{-1}S{v}_3=\mu (\mu -1)v_3$ with the corresponding eigenvector

  $$\mathbf{v}=\left(\begin{array}{c}\frac{1}{\mu -1}{M}^{-1}K{v}_3\\ \frac{1}{\delta (\mu -1)}{v}_3\\ v_3\end{array}\right),\forall v_3\ne 0$$

Since $\sigma$ is the eigenvalue of $Q_{S_3}^{-1}S$, then we have $\mu (\mu -1)=\sigma$ which is

$${\mu }^2-\mu -\sigma =0$$

(18)

Solving Equation (18) we get

$$\mu =\frac{1\pm \sqrt{1+4\sigma }}{2}$$

The values of $\mu$ derived above agree with the Proposition (2) in [6] which gives the bounds $\mu \left({\mathcal{Q}}_3^{-1}\mathcal{K}\right)\in \left[\frac{1-\sqrt{1+4{\sigma }_m}}{2},\frac{1-\sqrt{1+4{\sigma }_1}}{2}\right]\cup 1\cup \left[\frac{1+\sqrt{1+4{\sigma }_1}}{2},\frac{1+\sqrt{1+4{\sigma }_m}}{2}\right]$. We have that if $0\le {\sigma }_1\le {\sigma }_2\le ···\le {\sigma }_m$ are eigenvalues of $Q_{S_3}^{-1}K{M}^{-1}K+\frac{1}{\delta }{Q}_{S_3}^{-1}M$ then the other eigenvalues of ${\mathcal{Q}}_3^{-1}\mathcal{K}$ are

$$\begin{array}{ccc}\hfill \frac{1+\sqrt{1+4{\sigma }_1}}{2}\le & \mu & \le \frac{1+\sqrt{1+4{\sigma }_m}}{2}or\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill \frac{1-\sqrt{1+4{\sigma }_m}}{2}\le & \mu & \le \frac{1-\sqrt{1+4{\sigma }_1}}{2}.\hfill \end{array}$$

(20)

Now we have

$$Q_{S_3}^{-1}K{M}^{-1}K-\frac{1}{\delta }{Q}_{S_3}^{-1}M=Q_{S_3}^{-1}(K{M}^{-1}K+\frac{1}{\delta }M)=Q_{S_3}^{-1}S$$

This means that the eigenvalues of $Q_{S_3}^{-1}K{M}^{-1}K-\frac{1}{\delta }{Q}_{S_3}^{-1}M$ are the eigenvalues of $Q_{S_3}^{-1}S$. From Theorem 5 we have $\sigma \left(Q_{S_3}^{-1}S\right)\in [\frac{1}{2},1]$. Let ${\sigma }_1=\frac{1}{2}$ and ${\sigma }_m=1$; substituting in Equations (19) and () we get

$$\begin{array}{ccc}\hfill \frac{1+\sqrt{1+4{\sigma }_1}}{2}& \le \mu \le & \frac{1+\sqrt{1+4{\sigma }_m}}{2}\hfill \\ \hfill \frac{1+\sqrt{1+4\left(\frac{1}{2}\right)}}{2}& \le \mu \le & \frac{1+\sqrt{1+4\left(1\right)}}{2}\hfill \\ \hfill \frac{1+\sqrt{3}}{2}& \le \mu \le & \frac{1+\sqrt{5}}{2}\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \frac{1-\sqrt{1+4{\sigma }_m}}{2}\le \mu \le \frac{1-\sqrt{1+4{\sigma }_1}}{2}\\ \hfill \frac{1-\sqrt{1+4\left(1\right)}}{2}\le \mu \le \frac{1-\sqrt{1+4\left(\frac{1}{2}\right)}}{2}\\ \hfill \frac{1-\sqrt{5}}{2}\le \mu \le \frac{1-\sqrt{3}}{2}\end{array}$$

Therefore the eigenvalues of the preconditioned coefficient matrix are

$$\begin{array}{ccc}\hfill \mu & =& 1\hfill \\ \hfill \frac{1+\sqrt{3}}{2}\le & \mu & \le \frac{1+\sqrt{5}}{2}\hfill \\ \hfill \frac{1-\sqrt{5}}{2}\le & \mu & \le \frac{1-\sqrt{3}}{2}\hfill \end{array}$$

□

The Theorem 6 above clearly shows that the eigenvalues of the preconditioned coefficient matrix are clustered and are independent of both the mesh size and the regularisation parameter. The iterative solver is expected to converge with changes in the problem parameters and discretisation parameter. In the next section we carry out numerical tests to verify the theoretical findings and compare the performance of the MINRES solver with the block diagonal preconditioner associated with the three approximations for the Schur complement form.

4. Numerical Results

In this section we present the results of the numerical experiments for solving the problem (Equation (6)) using the block diagonal preconditioned MINRES method. The main task here is to demonstrate the effectiveness of preconditioner in accelerating the MINRES solver. In this study the numerical experiments began with the ${\mathbf{Q}}_{\mathbf{1}}$ finite element discretisation of the state y, the adjoint p and the control u equations using uniform grids. All simulations and implementations were performed on a Windows 10 platform with Intel^® Core™ i5-3230M [email protected] GHz 6.00 GB speed Intel^® using Matlab 7 programming language. We used the IFISS matlab package developed in [33] to generate a discrete linear algebraic system. The values of the mesh size h and the dimensions of M, K and $\mathcal{K}$ are shown in

Table 1. Mesh sizes and corresponding sizes of the matrices.

Mesh Size (h)	$2^{-3}$	$2^{-4}$	$2^{-5}$	$2^{-6}$	$2^{-7}$	$2^{-8}$	$2^{-9}$
size of $M\left(n\right)$	81	289	1089	4225	16,641	66,049	26,3169
size of $K\left(n\right)$	81	289	1089	4225	16,641	66,049	263,169
size of $\mathcal{K}\left(3n\right)$	243	867	3267	12,675	49,923	198,147	789,507

below

The exact solutions for the distributed optimality system and $\overline{\Omega }={(-1,1)}^2\subset {\mathcal{R}}^2$ are

$$\begin{array}{ccc}\hfill y_{\mathit{exact}}& =& \frac{1}{1+4\delta {\pi }^4}sin\left(\pi x_1\right)sin\left(\pi x_2\right)\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill u_{\mathit{exact}}& =& 2{\pi }^2{y}_{\mathit{exact}}\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill y_d& =& sin\left(\pi x_1\right)sin\left(\pi x_2\right)\hfill \end{array}$$

(23)

We give a thumbnail outline of the main task of the paper in the application of the approximation of the Schur complement preconditioner $Q_{S_3}$. The main dominant operations in the application of our proposed block diagonal preconditioner ${\mathcal{Q}}_3$ are 10 fixed Chebyshev semi iterations [6,12,29] for the mass matrix M in the (1,1) and (2,2) blocks; the (3,3) block is approximated by two cycles of the algebraic multigrid methods for $\sqrt{\delta }K+M$. This means in total we have two Chebyshev and two algebraic multigrid iterations with two pre and post-smoothing steps of the Jacobi method; similarly for $Q_{S_1}$ and $Q_{S_2}$. We test for four regularisation parameters $\delta ={10}^{-3},\delta ={10}^{-5},\delta ={10}^{-7}$ and $\delta ={10}^{-9}$.

We solve the linear algebraic system of saddle point form Equation (6) using the MINRES with the block diagonal preconditioners ${\mathcal{Q}}_1$ (Equation (10)), ${\mathcal{Q}}_2$ (Equation (11)) and ${\mathcal{Q}}_3$ (Equation (12)) with the three different preconditioner approximations for the Schur complement form S. Then we compare the performance of the block diagonal preconditioned MINRES method with the three preconditioner approximations for the Schur complement in terms of the number of iterations, CPU time, $L^2$ error and the value of the objective function. The numerical solution produced by the MINRES with the preconditioner associated with the three Schur complement approximations is the same. Figure 1 gives the snapshots of the numerical solution,

We now present the eigenvalue distribution of the $Q_{S_1}^{-1}S,Q_{S_2}^{-1}S,Q_{S_3}^{-1}S$.

The

Table 2. Maximum and minimum eigenvalues for the Schur complement S and preconditioned Schur complement with preconditioners $Q_{S_1},Q_{S_2},Q_{S_3}$ for different values of $\delta$ at $h=2^{-4}$.

	S		${\mathit{Q}}_{{\mathit{S}}_1}^{-1}\mathit{S}$		${\mathit{Q}}_{{\mathit{S}}_2}^{-1}\mathit{S}$		${\mathit{Q}}_{{\mathit{S}}_3}^{-1}\mathit{S}$
$\mathbf{\delta }$	min	max	min	max	min	max	min	max
${10}^{-3}$	15.8	4.03 × 10${}^3$	1.004	1001	0.5002	0.9594	0.5002	0.9594
${10}^{-5}$	1.3 × 10${}^3$	1 × 10${}^5$	1.005	1 × 10${}^5$	0.5000	0.9937	0.500	0.9979
${10}^{-7}$	2.21 × 10${}^4$	1 × 10${}^7$	5.49	1 × 10${}^7$	0.5643	0.9940	0.7740	1
${10}^{-9}$	1.8 × 10${}^6$	1 × 10${}^9$	449.9	1 × 10${}^9$	0.9139	0.9979	1	1
${10}^{-15}$	1.8 × 10${}^{12}$	1 × 10${}^{15}$	4.5e+8	1 × 10${}^{15}$	0.9999	1	1	1

shows the largest and the smallest eigenvalues of the Schur complement $S,Q_{S_1}^{-1}S,Q_{S_2}^{-1}S,Q_{S_3}^{-1}S$. The values in Table 2 clearly show the effects of the preconditioner approximation on the spectral properties of the Schur complement. The eigenvalues of $Q_{S_1}^{-1}S$ are clearly dependent on the parameter $\delta$; and the eigenvalues of $Q_{S_2}^{-1}S,Q_{S_3}^{-1}S$ are bounded between $\frac{1}{2}$ and 1 though their distribution and are different independent of the parameter $\delta$. This confirms the theoretical results and is clearly shown on the figures below. Figure 2 shows the distribution of eigenvalues for different values of regularisation parameter.

Figure 2 gives the eigenvalue distribution of $Q_{S_1}^{-1}S,Q_{S_2}^{-1}S,Q_{S_2}^{-1}S$ for different values of the regularisation parameter at $h=2^{-4}$. Figure 2a,d,g gives the eigenvalue distribution of $Q_{S_1}^{-1}S$; Figure 2b,e,h shows the eigenvalue distribution of $Q_{S_2}^{-1}S$; and Figure 2c,f,i shows the eigenvalue distribution of $Q_{S_3}^{-1}S$ for different values of $\delta$ at $h=2^{-4}$. The eigenvalues are sorted form the smallest to the largest. The most important observation is that the eigenvalue distribution of $Q_{S_1}^{-1}S$ is widely spread out as the regularisation parameter decreases. This agrees with the theoretical findings that the eigenvalues depends on the regularisation parameter. Hence the preconditioner approximation performance is not independent of $\delta$ and deteriorates for small values of $\delta$. We also observe that for the approximations $Q_{S_2}$ and $Q_{S_3}$ the eigenvalue distribution falls with the interval that is given theoretically for the different values of the regularisation parameter. This entails that the clustering of the eigenvalues shown in the Figure 2 above points to the fast convergence of the iterative solver for all the values of the regularisation parameter.

We now give the numerical experiment results from our MINRES iterative solver preconditioned with the block diagonal preconditioner associated with the three approximations. Since the numerical solutions are the same, we concentrate on the performance in terms of the number of iterations and the CPU time in seconds for comparison purposes.

It is clear from

Table 3. Number of iterations made by MINRES solver with the block diagonal preconditioners ${\mathcal{Q}}_1,{\mathcal{Q}}_2,{\mathcal{Q}}_3$ with Schur compliment approximated by $Q_{S_1},Q_{S_2},Q_{S_3}$ for different values of h and $\delta$, tolerance = ${10}^{-6}$.

	Approximation ${\mathit{Q}}_{{\mathit{S}}_1}$				Approximation ${\mathit{Q}}_{{\mathit{S}}_2}$				Approximation ${\mathit{Q}}_{{\mathit{S}}_3}$
h	$\mathbf{\delta }$				$\mathbf{\delta }$				$\mathbf{\delta }$
	${\mathbf{10}}^{-\mathbf{3}}$	${\mathbf{10}}^{-\mathbf{5}}$	${\mathbf{10}}^{-\mathbf{7}}$	${\mathbf{10}}^{-\mathbf{9}}$	${\mathbf{10}}^{-\mathbf{3}}$	${\mathbf{10}}^{-\mathbf{5}}$	${\mathbf{10}}^{-\mathbf{7}}$	${\mathbf{10}}^{-\mathbf{9}}$	${\mathbf{10}}^{-\mathbf{3}}$	${\mathbf{10}}^{-\mathbf{5}}$	${\mathbf{10}}^{-\mathbf{7}}$	${\mathbf{10}}^{-\mathbf{9}}$
$2^{-4}$	9	23	35	35	13	5	3	3	13	5	3	3
$2^{-5}$	11	29	71	99	13	9	3	3	13	9	3	3
$2^{-6}$	11	33	111	101	13	11	5	3	13	10	5	3
$2^{-7}$	13	33	133	107	15	11	7	5	15	10	5	3
$2^{-8}$	17	33	139	103	15	11	7	5	15	10	5	3
$2^{-9}$	17	39	147	191	17	11	11	7	17	11	5	5

that all these preconditioners associated with the approximations $Q_{S_1},Q_{S_2},Q_{S_3}$ are robust with respect to mesh size h, but the approximation $Q_{S_1}$ is not robust with respect to the regularisation parameter. The preconditioners associated with approximations $Q_{S_2},Q_{S_3}$ performed efficiently for all the values of h and $\delta$, with $Q_{S_3}$ performing slightly better.

The results in Table 3 and

Table 4. CPU time taken by MINRES solver with the block diagonal preconditioners ${\mathcal{Q}}_1,{\mathcal{Q}}_2,{\mathcal{Q}}_3$ with Schur complement approximated by $Q_{S_1},Q_{S_2},Q_{S_3}$ for different values of h and $\delta$, tolerance = ${10}^{-6}$.

	Approximation ${\mathit{Q}}_{{\mathit{S}}_1}$				Approximation ${\mathit{Q}}_{{\mathit{S}}_2}$				Approximation ${\mathit{Q}}_{{\mathit{S}}_3}$
h	$\mathbf{\delta }$				$\mathbf{\delta }$				$\mathbf{\delta }$
	${\mathbf{10}}^{-\mathbf{3}}$	${\mathbf{10}}^{-\mathbf{5}}$	${\mathbf{10}}^{-\mathbf{7}}$	${\mathbf{10}}^{-\mathbf{9}}$	${\mathbf{10}}^{-\mathbf{3}}$	${\mathbf{10}}^{-\mathbf{5}}$	${\mathbf{10}}^{-\mathbf{7}}$	${\mathbf{10}}^{-\mathbf{9}}$	${\mathbf{10}}^{-\mathbf{3}}$	${\mathbf{10}}^{-\mathbf{5}}$	${\mathbf{10}}^{-\mathbf{7}}$	${\mathbf{10}}^{-\mathbf{9}}$
$2^{-4}$	0.14	0.266	0.297	0.166	0.188	0.109	0.078	0.078	0.081	0.063	0.078	0.047
$2^{-5}$	0.283	0.581	1.317	1.457	0.312	0.25	0.141	0.156	0.297	0.325	0.11	0.109
$2^{-6}$	0.594	1.297	4.168	3.579	0.625	0.530	0.500	0.556	0.510	0.381	0.272	0.532
$2^{-7}$	2.169	5.171	17.27	15.59	2.54	2.00	1.48	1.64	2.42	2.05	1.45	1.531
$2^{-8}$	10.58	21.79	78.92	60.50	10.59	8.43	5.97	5.54	8.64	7.47	4.95	4.02
$2^{-9}$	47.4	100.2	220	347.8	46.7	35.5	33.3	25.1	46.8	35.2	30.1	21.2

demonstrate the practical applicability of the preconditioners explained theoretically in Section 2 and Section 3 and the theoretical prowess of the three approximations of the Schur complement form using the eigenvalue distribution. Table 3 and Table 4 give the number of iterations and the CPU time taken by the MINRES preconditioned by block diagonal preconditioners Equations (10)–(12) with different values of mesh size and the regularisation parameter, and we compare the effectiveness of the three preconditioners with approximations for the Schur compliment preconditioner. The results clearly show that the preconditioner with $Q_{S_1}$ displays mesh-independent convergence but fails on the decreasing values of the regularisation parameter $\delta$. The number of iterations and CPU time increase as $\delta \to 0$. This agrees with the poor eigenvalue distribution of $Q_{S_1}^{-1}S$ and that of ${\mathcal{Q}}_1\mathcal{K}$. The number of iterations and CPU times produced by the preconditioners associated with $Q_{S_2}$ and $Q_{S_3}$ are competitive and exhibited parameters h and $\delta$ independent of convergence, while both h and $\delta$ approached zero. The number of iterations of $Q_{S_2}$ and $Q_{S_3}$ decreased by the decrease of $\delta$, as expected, and those of $Q_{S_3}$ decreased further. The results show that these preconditioners are also robust to the mesh size h and the regularisation parameter $\delta$. This agrees with the theoretical results that the eigenvalues are more clustered and distributed more independently of the parameters h and $\delta$ than those of $Q_{S_1}^{-1}S$; see Figure 2. The results of our numerical experiments clearly show that the preconditioners with the approximations $Q_{S_3}$ and $Q_{S_2}$ are very effective in improving the MINRES in solving elliptic control problems. When compared to other preconditioner approximations in terms of iteration count and computational time, $Q_{S_3}$ slightly outperformed them. The preconditioners are more effective with our new approximation, producing more favourable results. We now give the results including the cost functional at $2^{-6}$ for different values of the objective function for the approximation $Q_{S_3}$ and there are the same outputs with the other approximations.

The results in

Table 5. Numerical results using preconditioner with approximation $Q_{S_3}$ with $h=2^{-6}$.

$\mathit{\delta }$	$\Vert {\mathit{u}}_{\mathit{h}}{\Vert }_2$	$\Vert {\mathit{u}}_{\mathit{h}}{-\mathit{u}\Vert }_2$	$\Vert {\mathit{y}}_{\mathit{h}}{-\mathit{y}\Vert }_2$	$\Vert \mathit{y}-{\mathit{y}}_{\mathit{d}}{\Vert }_2$	$\mathit{J}({\mathit{u}}_{\mathit{h}},{\mathit{y}}_{\mathit{h}})$
${10}^{-1}$	1.58 × ${10}^1$	7.63 × ${10}^{-4}$	1.56 × ${10}^{-3}$	3.13 × ${10}^1$	4.07 × ${10}^2$
${10}^{-2}$	1.29 × ${10}^2$	4.75 × ${10}^{-4}$	1.28 × ${10}^{-3}$	2.55 × ${10}^1$	4.07 × ${10}^2$
${10}^{-3}$	4.56 × ${10}^2$	3.53 × ${10}^{-4}$	4.50 × ${10}^{-4}$	8.98 × ${10}^0$	1.44 × ${10}^2$
${10}^{-4}$	6.08 × ${10}^2$	7.43 × ${10}^{-4}$	6.03 × ${10}^{-5}$	1.20 × ${10}^0$	1.92 × ${10}^1$
${10}^{-5}$	6.29 × ${10}^2$	7.98 × ${10}^{-4}$	6.30 × ${10}^{-6}$	1.24 × ${10}^{-1}$	1.98 × ${10}^{-1}$
${10}^{-6}$	6.32 × ${10}^2$	8.03 × ${10}^{-4}$	6.29 × ${10}^{-7}$	1.25 × ${10}^{-2}$	2.0 × ${10}^{-2}$
${10}^{-7}$	6.32 × ${10}^2$	8.03 × ${10}^{-4}$	6.26× ${10}^{-8}$	1.24 × ${10}^{-3}$	2.0 × ${10}^{-3}$
${10}^{-8}$	6.32 × ${10}^2$	8.03 × ${10}^{-4}$	6.32× ${10}^{-9}$	1.24 × ${10}^{-4}$	2.0 × ${10}^{-4}$
${10}^{-9}$	6.32 × ${10}^2$	8.03 × ${10}^{-4}$	6.32× ${10}^{-10}$	1.24 × ${10}^{-5}$	2.0 × ${10}^{-5}$

show the behaviour of the cost functional for different values of the regularisation parameter $\delta$. It is well known that the $\delta$ determines how close the state approaches the desired state $y_d$. The results provide an interesting observations that ${\Vert u\Vert }_2$ stops increasing at ${10}^{-6}$ with $J(y,u)$ and $\Vert y-y_d{\Vert }_2$ decreases with the decrease by a constant factor of the decrease of $\delta$. This means that the optimal value of $\delta$ for the problem is ${10}^{-6}$, becoming very close to the desired state, and also that the control variable $\Vert u\Vert$ increases as $\delta$ decreases. This is clear indication that the cost functional will be insensitive to the control variable as $\delta$ decreases.

5. Conclusions

The finite element discretisation of the elliptic PDE-constrained optimisation problem produces a large block $3\times 3$ linear algebraic system of saddle point form. The main task of this paper was to present a different approach for the approximation of the Schur complement in the preconditioning strategies to get a robust and efficient numerical solver. This was done to achieve the MINRES solver whose performance is independent of the mesh size h and the regularisation parameter $\delta$. We have demonstrated both theoretically and numerically that the eigenvalues of both the the preconditioned Schur complement and the preconditioned system involving the proposed approximation are independent of the changes in the mesh size and the regularisation parameter. This gives a robust numerical scheme that is independent of h and $\delta$. We have compared numerically the results of the preconditioners involving the proposed approximation of the Schur complement with those that are found in the literature. Numerical results have confirmed the theoretical results and have demonstrated that the proposed preconditioner in this paper can be used practically and can be considered as a viable preconditioner for the problem under investigation.