Mixed Generalized Multiscale Finite Element Method for a Simplified Magnetohydrodynamics Problem in Perforated Domains
Abstract
1. Introduction
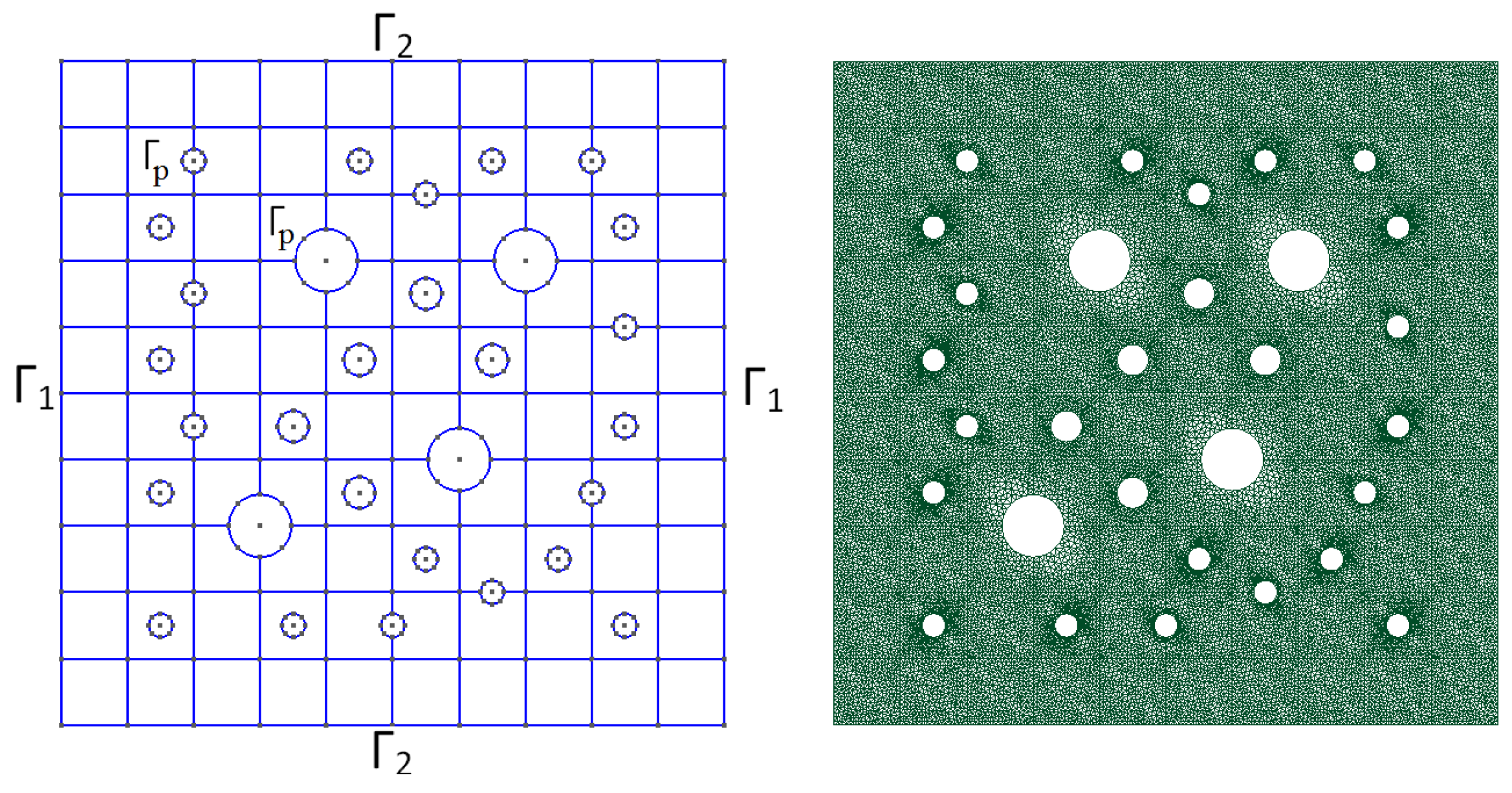
2. Problem Formulation
- Find from
- Find from
3. Magnetic Field Problem
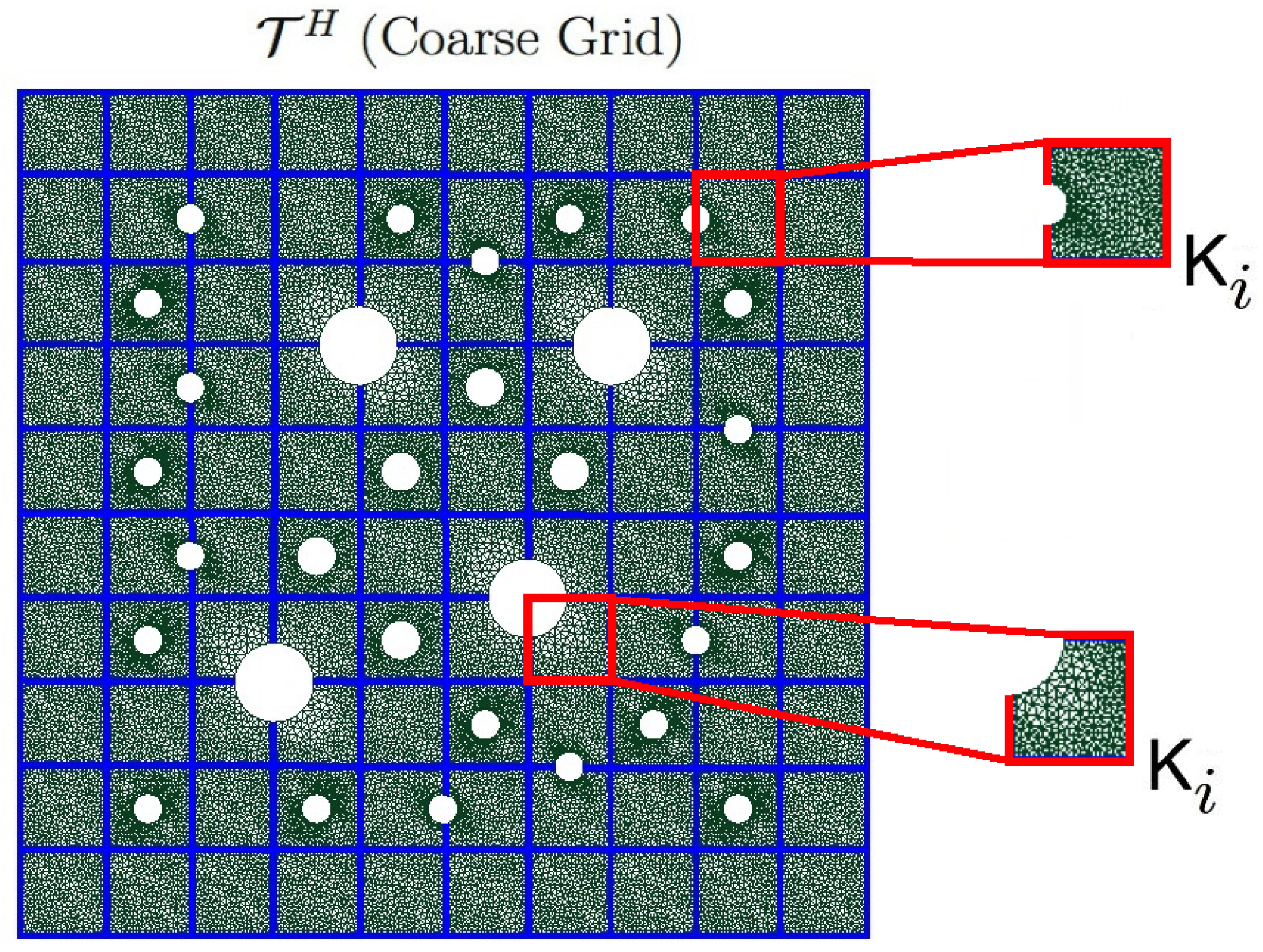
Multiscale Approximation
4. Flow Problem
Multiscale Approximation
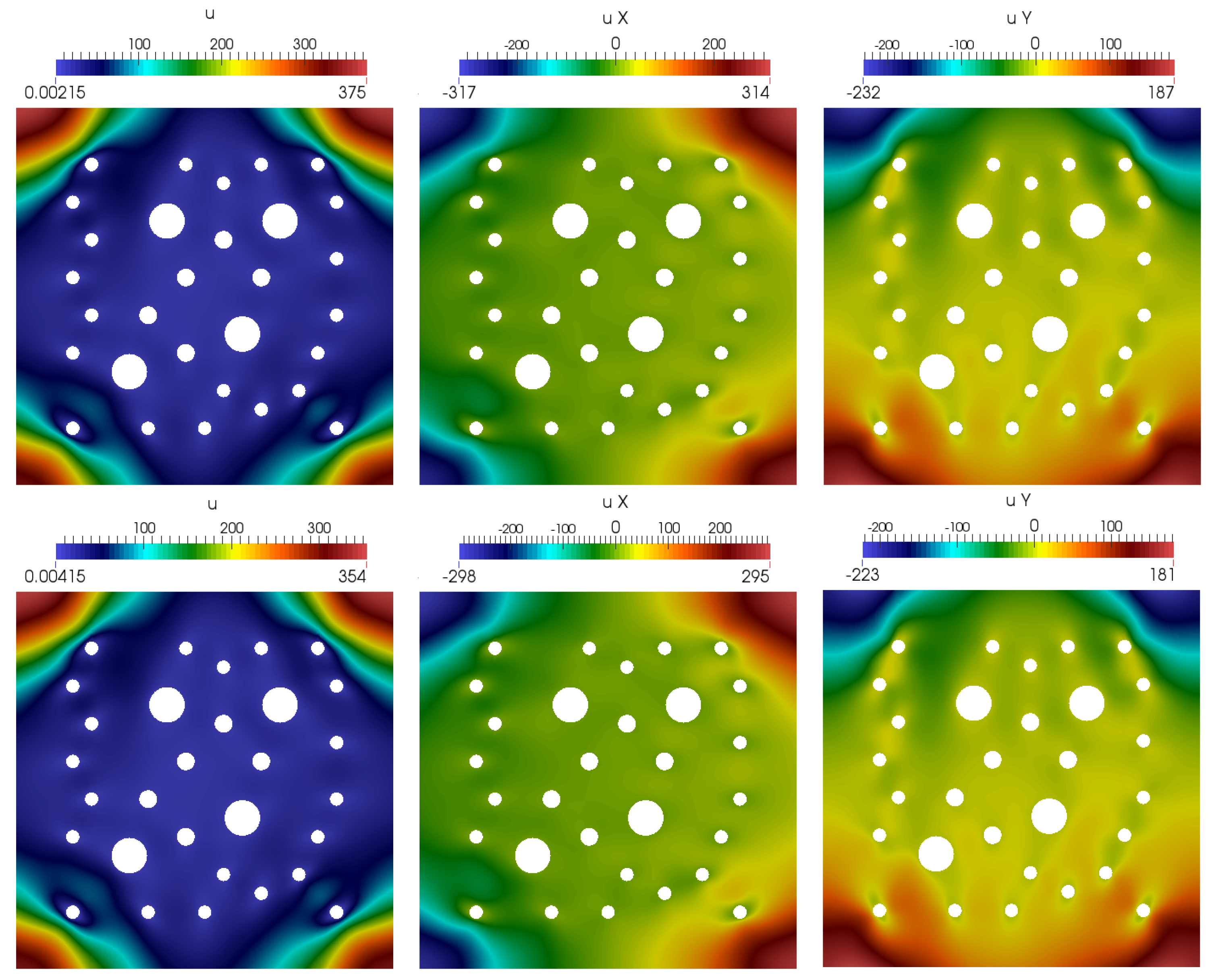
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moreau, R.J. Magnetohydrodynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2013; Volume 3. [Google Scholar]
- Davidson, P.A. An Introduction to Magnetohydrodynamics. Am. J. Phys. 2002, 70, 781. [Google Scholar] [CrossRef]
- Gerbeau, J.F.; Le Bris, C.; Lelièvre, T. Mathematical Methods for the Magnetohydrodynamics of Liquid Metals; Clarendon Press: London, UK, 2006. [Google Scholar]
- Dong, X.; He, Y.; Zhang, Y. Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 2014, 276, 287–311. [Google Scholar] [CrossRef]
- Dong, X.; He, Y. Convergence of some finite element iterative methods related to different Reynolds numbers for the 2D/3D stationary incompressible magnetohydrodynamics. Sci. China Math. 2016, 59, 589–608. [Google Scholar] [CrossRef]
- Dong, X.; He, Y. The Oseen Type Finite Element Iterative Method for the Stationary Incompressible Magnetohydrodynamics. Adv. Appl. Math. Mech. 2017, 9, 775–794. [Google Scholar] [CrossRef]
- Dong, X.; He, Y.; Wei, H.; Zhang, Y. Local and parallel finite element algorithm based on the partition of unity method for the incompressible MHD flow. Adv. Comput. Math. 2018, 44, 1295–1319. [Google Scholar] [CrossRef]
- Tang, Q.; Huang, Y. Local and parallel finite element algorithm based on Oseen-type iteration for the stationary incompressible MHD flow. J. Sci. Comput. 2017, 70, 149–174. [Google Scholar] [CrossRef]
- Tang, Q.; Huang, Y. Analysis of Local and Parallel Algorithm for Incompressible Magnetohydrodynamics Flows by Finite Element Iterative Method. Commun. Comput. Phys. 2019, 25, 729–751. [Google Scholar] [CrossRef]
- Badia, S.; Codina, R.; Planas, R. On an unconditionally convergent stabilized finite element approximation of resistive magnetohydrodynamics. J. Comput. Phys. 2013, 234, 399–416. [Google Scholar] [CrossRef]
- Greif, C.; Li, D.; Schötzau, D.; Wei, X. A mixed finite element method with exactly divergence-free velocities for incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 2010, 199, 2840–2855. [Google Scholar] [CrossRef]
- Hiptmair, R.; Li, L.; Mao, S.; Zheng, W. A fully divergence-free finite element method for magnetohydrodynamic equations. Math. Models Methods Appl. Sci. 2018, 28, 659–695. [Google Scholar] [CrossRef]
- Hu, K.; Ma, Y.; Xu, J. Stable finite element methods preserving ∇ · {B} = 0 exactly for MHD models. Numer. Math. 2017, 135, 371–396. [Google Scholar] [CrossRef]
- Jikov, V.V.; Kozlov, S.M.; Oleinik, O.A. Homogenization of Differential Operators and Integral Functionals; Springer: Berlin, Germany, 1991. [Google Scholar]
- Bakhvalov, N.; Panasenko, G. Homogenization in Periodic Media, Mathematical Problems of the Mechanics of Composite Materials; Nauka: Moscow, Russia, 1984. [Google Scholar]
- Allaire, G.; Brizzi, R. A multiscale finite element method for numerical homogenization. SIAM J. Multiscale Modeling Simul. 2005, 4, 790–812. [Google Scholar] [CrossRef]
- Efendiev, Y.; Hou, T. Multiscale Finite Element Methods: Theory and Applications. In Surveys and Tutorials in the Applied Mathematical Sciences; Springer: New York, NY, USA, 2009; Volume 4. [Google Scholar]
- Efendiev, Y.; Galvis, J.; Hou, T.Y. Generalized multiscale finite element methods (GMsFEM). J. Comput. Phys. 2013, 251, 116–135. [Google Scholar] [CrossRef]
- Ohlberger, M.; Schindler, F. Error control for the localized reduced basis multi-scale method with adaptive on-line enrichment. arXiv 2015, arXiv:1501.05202. [Google Scholar]
- Muljadi, B.; Narski, J.; Lozinski, A.; Degond, P. Non-conforming multiscale finite element method for Stokes flows in heterogeneous media. Part I: Methodologies and numerical experiments. arXiv 2014, arXiv:1404.2837. [Google Scholar]
- Le Bris, L.; Legoll, F.; Lozinski, A. An MsFEM type approach for perforated domains. Multiscale Model. Simul. 2014, 12, 1046–1077. [Google Scholar] [CrossRef]
- Henning, P.; Ohlberger, M. The heterogeneous multiscale finite element method for elliptic homogenization problems in perforated domains. Numer. Math. 2009, 113, 601–629. [Google Scholar] [CrossRef]
- Chen, Z.; Hou, T. A mixed multiscale finite element method for elliptic problems with oscillating coefficients. Math. Comput. 2002, 72, 541–576. [Google Scholar] [CrossRef]
- Brown, D.L.; Peterseim, D. A multiscale method for porous microstructures. arXiv 2014, arXiv:1411.1944. [Google Scholar] [CrossRef][Green Version]
- Efendiev, Y.; Galvis, J.; Wu, X.H. Multiscale finite element methods for high-contrast problems using local spectral basis functions. J. Comput. Phys. 2011, 230, 937–955. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Li, G.; Vasilyeva, M. Generalized multiscale finite element methods for problems in perforated heterogeneous domains. Appl. Analys. 2016, 95, 2254–2279. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Vasilyeva, M.; Wang, Y. A multiscale discontinuous Galerkin method in perforated domains. In Proceedings of the Institute of Mathematics and Mechanics, Maringá, Brazil, 22–23 September 2016; Volume 42, pp. 212–229. [Google Scholar]
- Chung, E.T.; Efendiev, Y.; Lee, C.S. Mixed generalized multiscale finite element methods and applications. Multiscale Model. Simul. 2015, 13, 338–366. [Google Scholar] [CrossRef]
- Chan, H.Y.; Chung, E.; Efendiev, Y. Adaptive mixed GMsFEM for flows in heterogeneous media. Numer. Math. Theory Methods Appl. 2016, 9, 497–527. [Google Scholar] [CrossRef]
- Chung, E.T.; Leung, W.T.; Vasilyeva, M. Mixed GMsFEM for second order elliptic problem in perforated domains. J. Comput. Appl. Math. 2016, 304, 84–99. [Google Scholar] [CrossRef]
- Chung, E.T.; Leung, W.T.; Vasilyeva, M.; Wang, Y. Multiscale model reduction for transport and flow problems in perforated domains. J. Comput. Appl. Math. 2018, 330, 519–535. [Google Scholar] [CrossRef]
- Gunzburger, M.D.; Meir, A.J.; Peterson, J.S. On the existence, uniqueness, and finite element approximation of solutions of the equations of stationary, incompressible magnetohydrodynamics. Math. Comput. 1991, 56, 523–563. [Google Scholar] [CrossRef]
- Arnold, D.; Brezzi, F.; Cockburn, B.; Marini, L. Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 2002, 39, 1749–1779. [Google Scholar] [CrossRef]
- Ewing, R.; Wang, J.; Yang, Y. A stabilized discontinuous finite element method for elliptic problems. Numer. Linear Algebra Appl. 2003, 10, 83–104. [Google Scholar] [CrossRef]
- Lazarov, R.; Pasciak, J.; Schöberl, J.; Vassilevski, P. Almost optimal interior penalty discontinuous approximations of symmetric elliptic problems on non-matching grids. Numer. Math. 2003, 96, 295–315. [Google Scholar] [CrossRef]
- Lazarov, R.; Tomov, S.; Vassilevski, P. Interior penalty discontinuous approximations of elliptic problems. Comput. Methods Appl. Math. 2001, 1, 367–382. [Google Scholar] [CrossRef][Green Version]
- Riviere, B. Discontinuous Galerkin Methods for Solving Elliptic And Parabolic Equations: Theory and Implementation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Girault, V.; Riviére, B.; Wheeler, M. A discontinuous Galerkin method with nonoverlapping domain decomposition for the Stokes and Navier-Stokes problems. Math. Comput. 2005, 74, 53–84. [Google Scholar] [CrossRef]
- Chung, E.T.; Vasilyeva, M.; Wang, Y. A conservative local multiscale model reduction technique for Stokes flows in heterogeneous perforated domains. J. Comput. Appl. Math. 2017, 321, 389–405. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. An adaptive generalized multiscale discontinuous Galerkin method for high-contrast flow problems. Multiscale Model. Simul. 2018, 16, 1227–1257. [Google Scholar] [CrossRef]
- Chung, E.; Leung, W.T. A sub-grid structure enhanced discontinuous Galerkin method for multiscale diffusion and convection-diffusion problems. Commun. Comput. Phys. 2013, 14, 370–392. [Google Scholar] [CrossRef]



| Flux, (%) | Magnetic Field, (%) | |
|---|---|---|
| u-multiscale solution with | ||
| 320 | 4.170 | 1.690 |
| 540 | 1.181 | 1.578 |
| 760 | 0.958 | 1.578 |
| 980 | 0.835 | 1.578 |
| u-multiscale solution with | ||
| 320 | 4.165 | 1.688 |
| 540 | 1.176 | 1.577 |
| 760 | 0.953 | 1.577 |
| 980 | 0.831 | 1.577 |
| u-multiscale solution with | ||
| 320 | 4.164 | 1.688 |
| 540 | 1.176 | 1.577 |
| 760 | 0.953 | 1.577 |
| 980 | 0.830 | 1.577 |
| u-multiscale solution with | ||
| 320 | 4.164 | 1.688 |
| 540 | 1.176 | 1.577 |
| 760 | 0.952 | 1.577 |
| 980 | 0.830 | 1.577 |
| u-multiscale solution with | ||
| 320 | 4.163 | 1.688 |
| 540 | 1.176 | 1.577 |
| 760 | 0.952 | 1.577 |
| 980 | 0.830 | 1.577 |
| u-fine-scale solution with = 433,384 | ||
| 320 | 4.161 | 1.688 |
| 540 | 1.174 | 1.577 |
| 760 | 0.954 | 1.577 |
| 980 | 0.832 | 1.577 |
| Velocity, (%) | Pressure, (%) | |
|---|---|---|
| B-multiscale solution with | ||
| 1100 | 60.501 | 25.800 |
| 2100 | 16.689 | 2.005 |
| 3100 | 11.281 | 1.226 |
| 4100 | 9.792 | 1.138 |
| 6100 | 8.843 | 1.078 |
| B-multiscale solution with | ||
| 1100 | 60.477 | 25.798 |
| 2100 | 16.694 | 1.996 |
| 3100 | 11.282 | 1.225 |
| 4100 | 9.792 | 1.138 |
| 6100 | 8.843 | 1.078 |
| B-multiscale solution with | ||
| 1100 | 60.473 | 25.797 |
| 2100 | 16.695 | 1.997 |
| 3100 | 11.282 | 1.225 |
| 4100 | 9.792 | 1.138 |
| 6100 | 8.843 | 1.078 |
| B-multiscale solution with | ||
| 1100 | 60.472 | 25.797 |
| 2100 | 16.694 | 1.997 |
| 3100 | 11.282 | 1.225 |
| 4100 | 9.792 | 1.138 |
| 6100 | 8.843 | 1.078 |
| B-fine-scale solution with = 155,580 | ||
| 1100 | 59.420 | 25.300 |
| 2100 | 16.615 | 1.878 |
| 3100 | 11.238 | 1.199 |
| 4100 | 9.754 | 1.112 |
| 6100 | 8.809 | 1.055 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alekseev, V.; Tang, Q.; Vasilyeva, M.; Chung, E.T.; Efendiev, Y. Mixed Generalized Multiscale Finite Element Method for a Simplified Magnetohydrodynamics Problem in Perforated Domains. Computation 2020, 8, 58. https://doi.org/10.3390/computation8020058
Alekseev V, Tang Q, Vasilyeva M, Chung ET, Efendiev Y. Mixed Generalized Multiscale Finite Element Method for a Simplified Magnetohydrodynamics Problem in Perforated Domains. Computation. 2020; 8(2):58. https://doi.org/10.3390/computation8020058
Chicago/Turabian StyleAlekseev, Valentin, Qili Tang, Maria Vasilyeva, Eric T. Chung, and Yalchin Efendiev. 2020. "Mixed Generalized Multiscale Finite Element Method for a Simplified Magnetohydrodynamics Problem in Perforated Domains" Computation 8, no. 2: 58. https://doi.org/10.3390/computation8020058
APA StyleAlekseev, V., Tang, Q., Vasilyeva, M., Chung, E. T., & Efendiev, Y. (2020). Mixed Generalized Multiscale Finite Element Method for a Simplified Magnetohydrodynamics Problem in Perforated Domains. Computation, 8(2), 58. https://doi.org/10.3390/computation8020058





