Effect of Structure on the Thermal-Mechanical Performance of Fully Ceramic Microencapsulated Fuel
Abstract
1. Introduction
2. Materials
2.1. Uranium Nitride
2.2. Buffer Layer
2.3. PyCLayer
2.4. Silicon Carbide
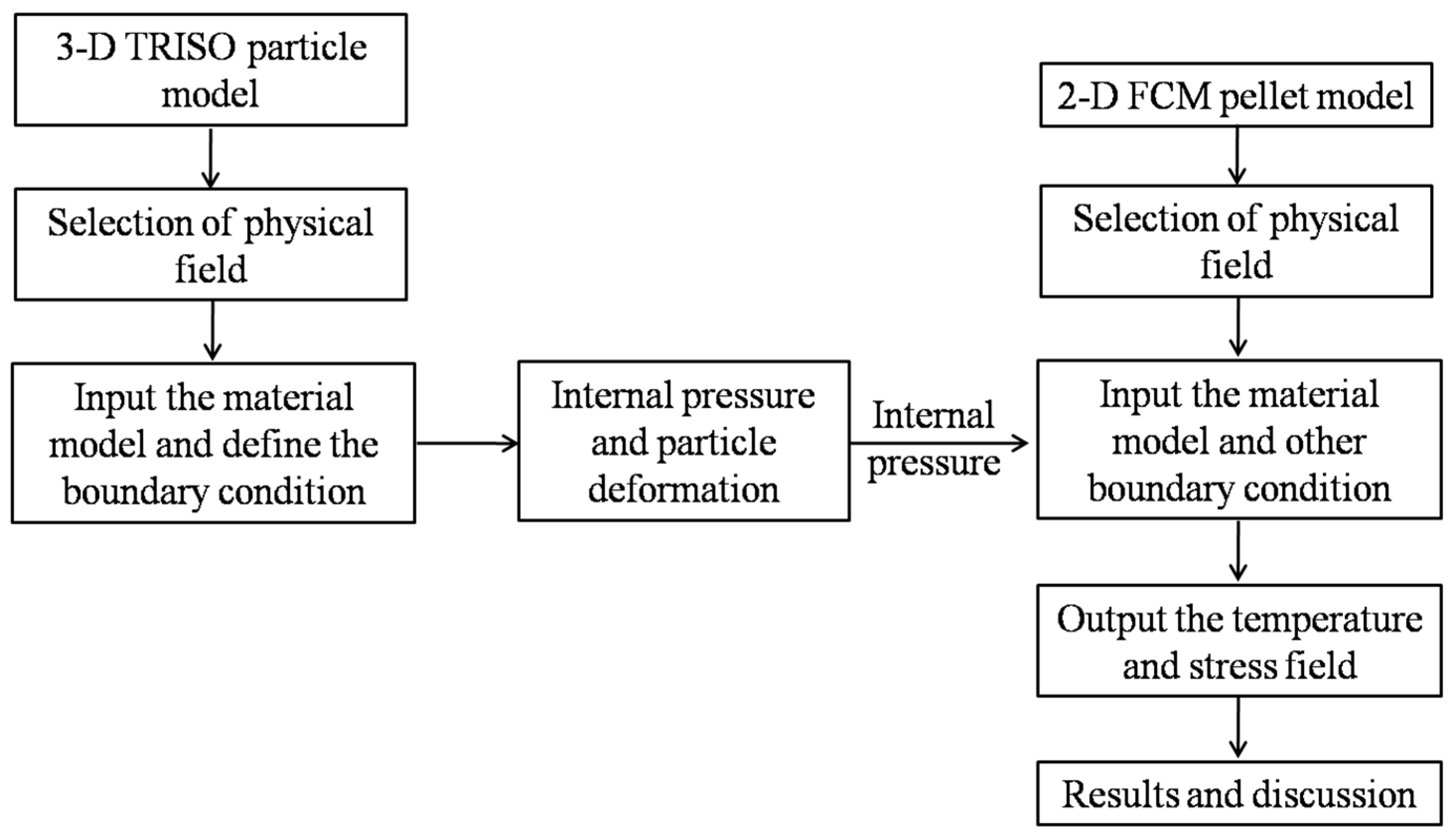
3. Geometry Parameters and Modeling Approach
4. Results and Discussion
4.1. Deformation and Fission Gas Release
4.2. Matrix Temperature
4.3. Stress Distribution of SiCMatrix
4.4. Performance of the SiC Layer
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Snead, L.K.; Terrani, A.; Venneri, F.; Kim, Y. Fully Ceramic Microencapsulated Fuels: A Transformational technology for Present and Next Generation Reactors-Properties and Fabrication of FCM Fuel. Trans. Am. Nucl. Soc. 2011, 104, 1–5. [Google Scholar]
- Nicholas, R.B.; Ludewig, H.; Arnold, A. Neutronic Evaluation of a PWR with Fully Ceramic Microencapsulated Fuel. Part II: Nodal Core Calculations and Preliminary Study of Thermal Hydraulic Feedback. Ann. Nucl. Energy 2013, 62, 548–557. [Google Scholar] [CrossRef]
- Terrani, K.A.; Snead, L.L.; Gehin, C. Microencapsulated Fuel Technology for Commercial Light Water and Advanced Reactor Application. J. Nucl. Mater. 2012, 427, 209–224. [Google Scholar] [CrossRef]
- Snead, L.L.; Terrani, K.A.; Katoh, Y. Stability of SiC-Matrix Microencapsulated Fuel Constituents at Relevant LWR Conditions. J. Nucl. Mater. 2014, 448, 389–398. [Google Scholar] [CrossRef]
- Chun, J.H.; Lim, S.W.; Chung, B.D. Safety Evaluation of Accident-Tolerant FCM Fueled Core with SiC-Coated Zircalloy Cladding for Design-Basis-Accidents and Beyond DBAs. Nucl. Eng. Des. 2015, 289, 287–295. [Google Scholar] [CrossRef]
- Huang, J.F.; Li, N.; Zhang, Y.L.; Guo, Q.X. The Safety Analysis of a Small Pressurized Water Reactor Utilizing Fully Ceramic Microencapsulated. Fuel. Nucl. Eng. Des. 2017, 320, 250–257. [Google Scholar] [CrossRef]
- Sarah, K.; Salehi, A.A. The Potential Impact of Fully Ceramic Microencapsulated (FCM) Fuel on Thermal Hydraulic Performance of SMART Reactor. Nucl. Eng. Des. 2018, 339, 39–52. [Google Scholar] [CrossRef]
- Lindemer, T.B.; Silva, C.M.; Henry, J.J. Quantification of Process Variables for Carbothermic Synthesis of UC1-xNx Fuel Microspheres. J. Nucl. Mater. 2017, 483, 176–191. [Google Scholar] [CrossRef]
- Silva, C.; Rodney, D.H.; Kurt, A.T. UN Kernel Development for Fully Ceramic Microencapsulated Fuels for LWRs. Trans. Am. Nucl. Soc. 2014, 110, 831–833. [Google Scholar]
- Hunt, R.D.; Silva, C.M.; Lindemer, T.B. Preparation of UC0.07–0.10N0.90–0.93 Spheres for TRISO Coated Fuel Particles. J. Nucl. Mater. 2014, 448, 399–403. [Google Scholar] [CrossRef]
- Besmann, T.M.; Shin, D.; Lindemer, T.B. Uranium Nitride as LWR TRISO Fuel: Thermodynamic Modeling of U-C-N. J. Nucl. Mater. 2012, 427, 162–168. [Google Scholar] [CrossRef]
- Besmann, T.M.; Ferber, M.K.; Lin, H.; Collin, B.P. Fission Product Release and Survivability of UN-Kernel LWR TRISO Fuel. J. Nucl. Mater. 2014, 448, 412–419. [Google Scholar] [CrossRef]
- Hayes, S.L.; Thomas, J.K. Material Property Correlation for Uranium Mono Nitride, I: Physique Properties. J. Nucl. Mater. 1990, 171, 262–270. [Google Scholar] [CrossRef]
- Nicholas, R.B.; Hans, L.; Arnold, A.; Gilad, R. Neutronic Evaluation of a PWR with Fully Ceramic Microencapsulated Fuel. Part I: Lattice Benchmarking, Cycle Length, and Reactivity Coefficients. Ann. Nucl. Energy 2013, 62, 538–547. [Google Scholar] [CrossRef]
- Boer, B.; Sen, R.S.; Pope, A.M. Material Performance of Fully-Ceramic Micro-Encapsulated Fuel under Selected LWR Design Basis Scenarios: Final Report; INL/EXT-11-23313; Idaho National Laboratory: Idaho Falls, ID, USA, 2011. [Google Scholar] [CrossRef]
- Powers, J.J.; Wirth, B.D. A review of TRISO fuel performance models. J. Nucl. Mater. 2010, 405, 74–82. [Google Scholar] [CrossRef]
- Chen, P.; Qiu, S.; Liu, S.; Zhou, Y. Preliminary Analysis of a Fully Ceramic Microencapsulated Fuel Thermal-Mechanical Performance. Mathematics 2019, 7, 448. [Google Scholar] [CrossRef]
- Schapple, D.; Terrani, K.; Powers, J.J. Modeling the Performance of TRISO-Based Fully Ceramic Matrix (FCM) Fuel in an LWR Environment Using BISON. Nucl. Eng. Des. 2018, 355, 116–127. [Google Scholar] [CrossRef]
- Ougouag, A.M.; Kloosterman, J.L. Investigation of Bounds on Particle Packing in Pebble-Bed High Temperature Reactors. Nucl. Eng. Des. 2006, 236, 669–676. [Google Scholar] [CrossRef]
- Collin, B.P. Modeling and Analysis of UN TRISO Fuel for LWR Application Using the PARFUME Code. J. Nucl. Mater. 2014, 451, 65–77. [Google Scholar] [CrossRef]
- Ross, S.R.; Matthews, R.B. Thermal Conductivity Correlation for Uranium Nitride Fuel between 10 and 1923 K. J. Nucl. Mater. 1988, 151, 313–317. [Google Scholar] [CrossRef]
- Li, W.; Wu, X.; Liu, S. Performance Analysis of TRISO Coated Fuel Particle with UN Kernel. Atom. Energy Sci. Technol. 2018, 52, 283–289. (In Chinese) [Google Scholar] [CrossRef]
- Katoh, Y.; Ozawa, K.; Shih, C. Continuous SiC Fiber, CVI SiC Matrix Composites for Nuclear Applications: Properties and Irradiation Effects. J. Nucl. Mater. 2014, 448, 448–476. [Google Scholar] [CrossRef]
- Schappel, D.P. Improvements to the Predictive Capability of FCM Fuel Performance Modeling. Ph.D. Thesis, University of Tennessee, Knoxville, Tennessee, 2017. [Google Scholar]
- Hales, J.D.; Williamson, R.L. Multidimensional Multiphysics Simulation of TRISO Particle Fuel. J. Nucl. Mater. 2013, 443, 531–543. [Google Scholar] [CrossRef]
- Ben-Belgacem, M.; Richet, V.; Terrani, K.A. Thermo-Mechanical Analysis of LWR SiC/SiC Composite Cladding. J. Nucl. Mater. 2014, 447, 125–142. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Xiao, Z.; Liu, S.; Chen, P.; Pang, H.; Xin, Y.; Jiao, Y.; Gao, S.; Zhang, K.; Li, W.; et al. Effect of Structure on the Thermal-Mechanical Performance of Fully Ceramic Microencapsulated Fuel. Computation 2020, 8, 13. https://doi.org/10.3390/computation8010013
Zhou Y, Xiao Z, Liu S, Chen P, Pang H, Xin Y, Jiao Y, Gao S, Zhang K, Li W, et al. Effect of Structure on the Thermal-Mechanical Performance of Fully Ceramic Microencapsulated Fuel. Computation. 2020; 8(1):13. https://doi.org/10.3390/computation8010013
Chicago/Turabian StyleZhou, Yi, Zhong Xiao, Shichao Liu, Ping Chen, Hua Pang, Yong Xin, Yongjun Jiao, Shixin Gao, Kun Zhang, Wenjie Li, and et al. 2020. "Effect of Structure on the Thermal-Mechanical Performance of Fully Ceramic Microencapsulated Fuel" Computation 8, no. 1: 13. https://doi.org/10.3390/computation8010013
APA StyleZhou, Y., Xiao, Z., Liu, S., Chen, P., Pang, H., Xin, Y., Jiao, Y., Gao, S., Zhang, K., Li, W., & Yu, J. (2020). Effect of Structure on the Thermal-Mechanical Performance of Fully Ceramic Microencapsulated Fuel. Computation, 8(1), 13. https://doi.org/10.3390/computation8010013



