Configuration and Registration of Multi-Camera Spectral Image Database of Icon Paintings
Abstract
1. Introduction
2. Theory
2.1. The Challenge of Imaging the Icons
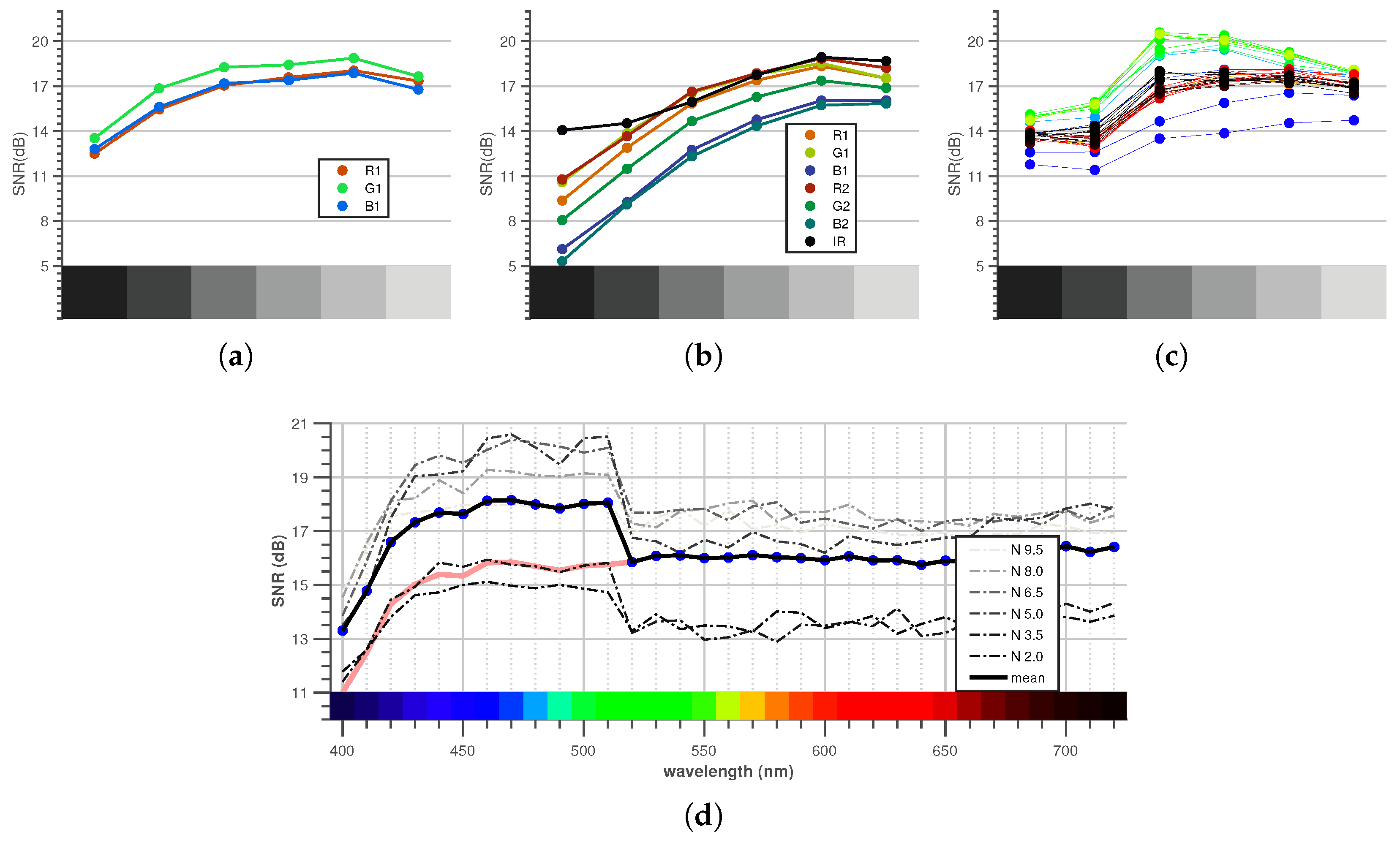
2.2. Signal-To-Noise Ratio and Dynamic Range
3. Methods
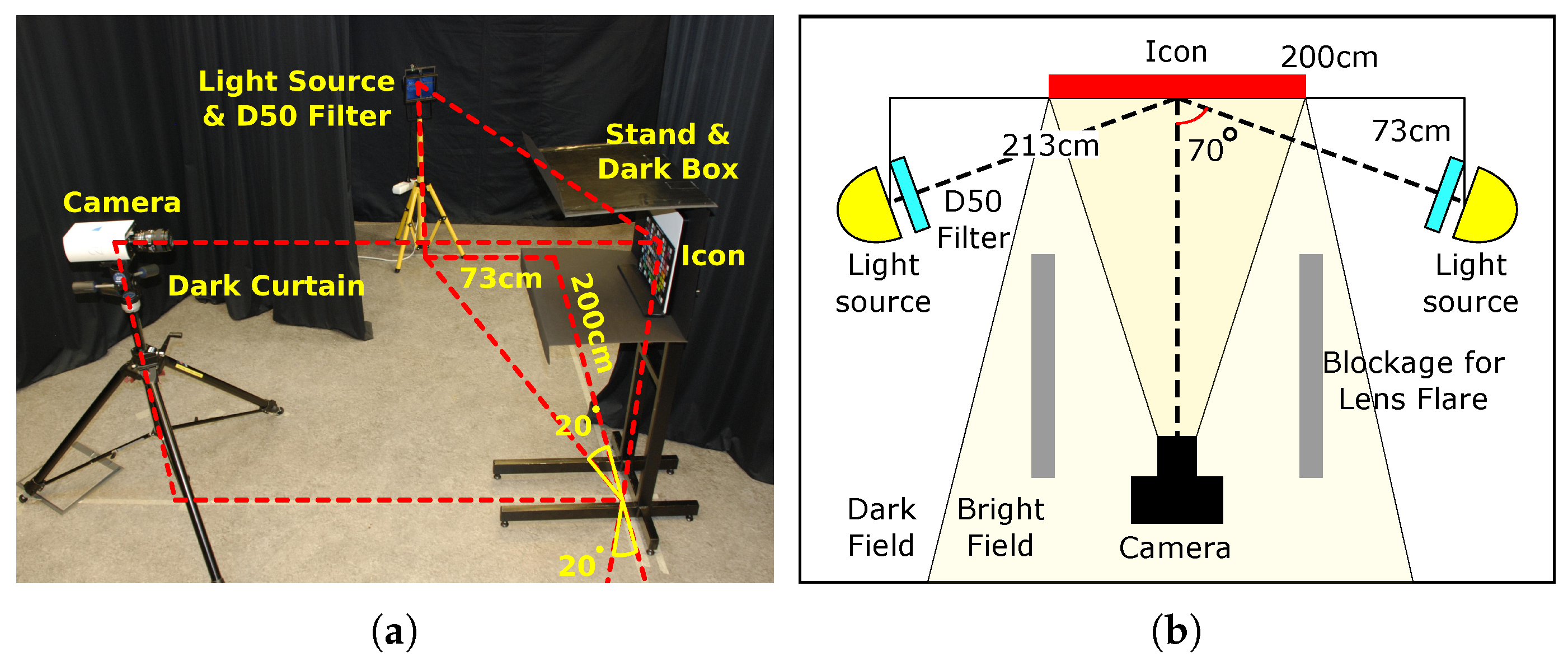
3.1. The Imaging Setup
3.2. The Camera Systems
3.3. The Camera Setup
3.4. Data Collection and Processing
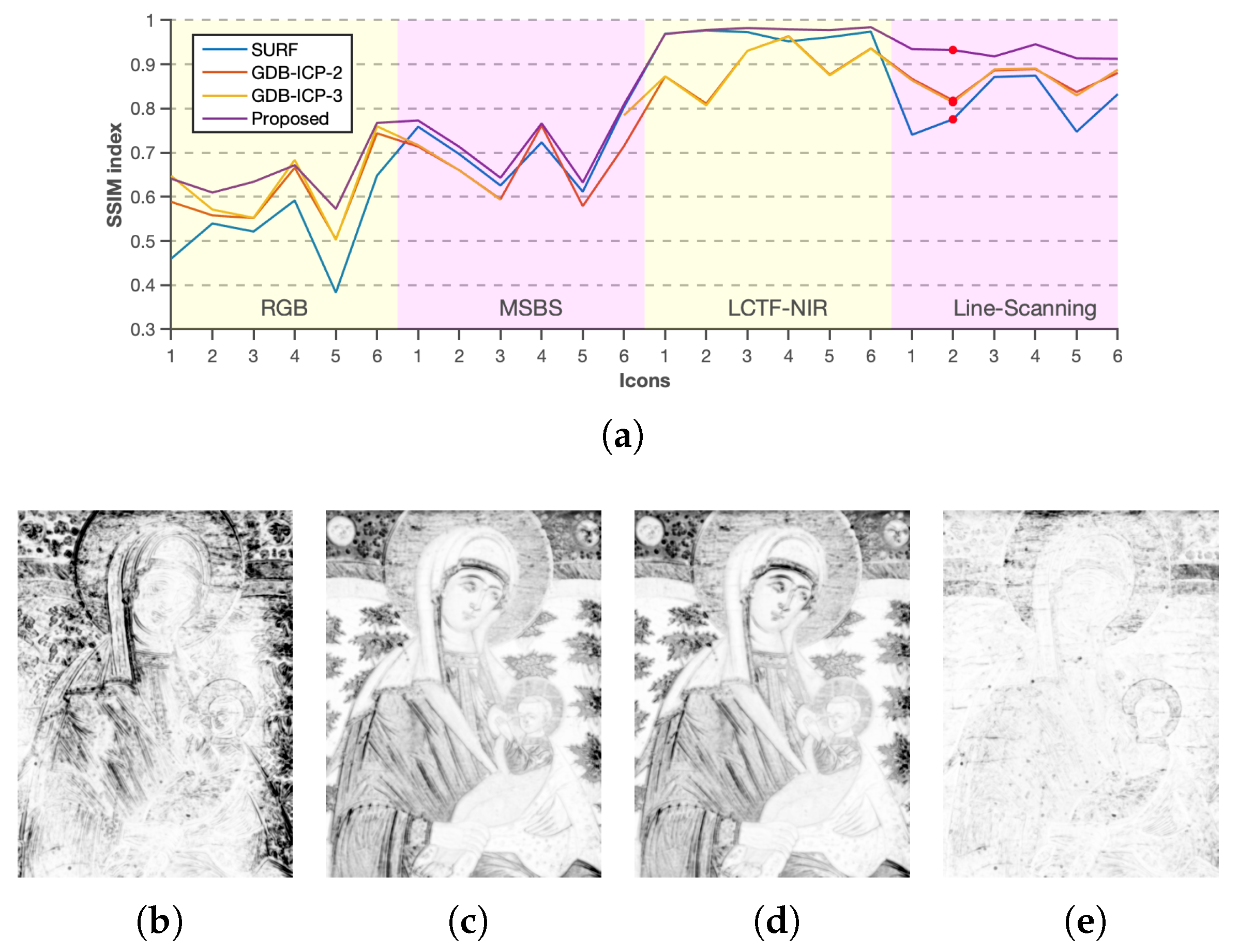
3.5. Multi-Camera Registration
4. Results
5. Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Cucci, C.; Delaney, J.K.; Picollo, M. Reflectance hyperspectral imaging for investigation of works of art: Old master paintings and illuminated manuscripts. Acc. Chem. Res. 2016, 49, 2070–2079. [Google Scholar] [CrossRef] [PubMed]
- Daniel, F.; Mounier, A.; Pérez-Arantegui, J.; Pardos, C.; Prieto-Taboada, N.; de Vallejuelo, S.F.O.; Castro, K. Comparison between non-invasive methods used on paintings by Goya and his contemporaries: Hyperspectral imaging vs. point-by-point spectroscopic analysis. Anal. Bioanal. Chem. 2017, 409, 4047–4056. [Google Scholar] [CrossRef] [PubMed]
- Martinez, K.; Cupitt, J.; Saunders, D.; Pillay, R. Ten years of art imaging research. Proc. IEEE 2002, 90, 28–41. [Google Scholar] [CrossRef]
- Hagen, N.A.; Kudenov, M.W. Review of snapshot spectral imaging technologies. Opt. Eng. 2013, 52, 090901. [Google Scholar] [CrossRef]
- Ni, C.; Jia, J.; Howard, M.; Hirakawa, K.; Sarangan, A. Single-shot multispectral imager using spatially multiplexed fourier spectral filters. JOSA B 2018, 35, 1072–1079. [Google Scholar] [CrossRef]
- Nahavandi, A.M. Metric for evaluation of filter efficiency in spectral cameras. Appl. Opt. 2016, 55, 9193–9204. [Google Scholar] [CrossRef] [PubMed]
- Lapray, P.J.; Wang, X.; Thomas, J.B.; Gouton, P. Multispectral filter arrays: Recent advances and practical implementation. Sensors 2014, 14, 21626–21659. [Google Scholar] [CrossRef] [PubMed]
- Martínez, M.A.; Valero, E.M.; Hernández-Andrés, J.; Romero, J.; Langfelder, G. Combining transverse field detectors and color filter arrays to improve multispectral imaging systems. Appl. Opt. 2014, 53, C14–C24. [Google Scholar] [CrossRef] [PubMed]
- Murakami, Y.; Fukura, K.; Yamaguchi, M.; Ohyama, N. Color reproduction from low-SNR multispectral images using spatio-spectral Wiener estimation. Opt. Express 2008, 16, 4106–4120. [Google Scholar] [CrossRef] [PubMed]
- Imai, F.H.; Berns, R.S. Spectral estimation of artist oil paints using multi-filter trichromatic imaging. In Proceedings of the 9th Congress of the International Colour Association, Rocheste, NY, USA, 24–29 June 2001; SPIE: Bellingham, WA, USA, 2002; Volume 4421, pp. 504–508. [Google Scholar]
- Heikkinen, V.; Lenz, R.; Jetsu, T.; Parkkinen, J.; Hauta-Kasari, M.; Jääskeläinen, T. Evaluation and unification of some methods for estimating reflectance spectra from RGB images. JOSA A 2008, 25, 2444–2458. [Google Scholar] [CrossRef] [PubMed]
- Heikkinen, V.; Mirhashemi, A.; Alho, J. Link functions and Matérn kernel in the estimation of reflectance spectra from RGB responses. JOSA A 2013, 30, 2444–2454. [Google Scholar] [CrossRef] [PubMed]
- Heikkinen, V. Spectral Reflectance Estimation Using Gaussian Processes and Combination Kernels. IEEE Trans. Image Process. 2018, 27, 3358–3373. [Google Scholar] [CrossRef] [PubMed]
- Cuan, K.; Lu, D.; Zhang, W. Spectral reflectance reconstruction with the locally weighted linear model. Opt. Quantum Electron. 2019, 51, 175. [Google Scholar] [CrossRef]
- Ribés, A. Image Spectrometers, Color High Fidelity, and Fine-Art Paintings. In Advanced Color Image Processing and Analysis; Springer: New York, NY, USA, 2013; pp. 449–483. [Google Scholar]
- Mihoubi, S.; Losson, O.; Mathon, B.; Macaire, L. Multispectral demosaicing using pseudo-panchromatic image. IEEE Trans. Comput. Imaging 2017, 3, 982–995. [Google Scholar] [CrossRef]
- Konnik, M.; Welsh, J. High-level numerical simulations of noise in CCD and CMOS photosensors: Review and tutorial. arXiv 2014, arXiv:1412.4031. [Google Scholar]
- Martinec, E. Noise, Dynamic Range and Bit Depth in Digital SLRs; The University of Chicago: Chicago, IL, USA, 2008. [Google Scholar]
- Eckhard, T.; Eckhard, J.; Valero, E.M.; Nieves, J.L. Nonrigid registration with free-form deformation model of multilevel uniform cubic B-splines: Application to image registration and distortion correction of spectral image cubes. Appl. Opt. 2014, 53, 3764–3772. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.L.; Zou, Z.; Zhu, Y.; Li, S. Block-based multispectral image registration with application to spectral color measurement. Opt. Commun. 2019, 451, 46–54. [Google Scholar] [CrossRef]
- Zacharopoulos, A.; Hatzigiannakis, K.; Karamaoynas, P.; Papadakis, V.M.; Andrianakis, M.; Melessanaki, K.; Zabulis, X. A method for the registration of spectral images of paintings and its evaluation. J. Cult. Herit. 2018, 29, 10–18. [Google Scholar] [CrossRef]
- Aguilera, C.A.; Aguilera, F.J.; Sappa, A.D.; Aguilera, C.; Toledo, R. Learning cross-spectral similarity measures with deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1–9. [Google Scholar]
- Hirai, K.; Osawa, N.; Horiuchi, T.; Tominaga, S. An HDR spectral imaging system for time-varying omnidirectional scene. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2059–2064. [Google Scholar]
- Chen, S.J.; Shen, H.L.; Li, C.; Xin, J.H. Normalized total gradient: A new measure for multispectral image registration. IEEE Trans. Image Process. 2017, 27, 1297–1310. [Google Scholar] [CrossRef]
- Brauers, J.; Aach, T. Geometric calibration of lens and filter distortions for multispectral filter-wheel cameras. IEEE Trans. Image Process. 2010, 20, 496–505. [Google Scholar] [CrossRef]
- Martínez, M.Á.; Valero, E.M.; Nieves, J.L.; Blanc, R.; Manzano, E.; Vílchez, J.L. Multifocus HDR VIS/NIR hyperspectral imaging and its application to works of art. Opt. Express 2019, 27, 11323–11338. [Google Scholar] [CrossRef] [PubMed]
- Al-khafaji, S.L.; Zhou, J.; Zia, A.; Liew, A.W. Spectral-spatial scale invariant feature transform for hyperspectral images. IEEE Trans. Image Process. 2017, 27, 837–850. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Zhang, W.; Shi, Y.; Wang, X.; Cao, W. GA-ORB: A New Efficient Feature Extraction Algorithm for Multispectral Images Based on Geometric Algebra. IEEE Access 2019, 7, 71235–71244. [Google Scholar] [CrossRef]
- Ordóñez, Á.; Argüello, F.; Heras, D. Alignment of Hyperspectral Images Using KAZE Features. Remote Sens. 2018, 10, 756. [Google Scholar]
- Dorado-Munoz, L.P.; Velez-Reyes, M.; Mukherjee, A.; Roysam, B. A vector SIFT detector for interest point detection in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4521–4533. [Google Scholar] [CrossRef]
- Hasan, M.; Pickering, M.R.; Jia, X. Modified SIFT for multi-modal remote sensing image registration. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2348–2351. [Google Scholar]
- Mansouri, A.; Marzani, F.; Gouton, P. Development of a protocol for CCD calibration: Application to a multispectral imaging system. Int. J. Robot. Autom. 2005, 20, 94–100. [Google Scholar] [CrossRef]
- MacDonald, L.W.; Vitorino, T.; Picollo, M.; Pillay, R.; Obarzanowski, M.; Sobczyk, J.; Nascimento, S.; Linhares, J. Assessment of multispectral and hyperspectral imaging systems for digitisation of a Russian icon. Herit. Sci. 2017, 5, 41. [Google Scholar] [CrossRef]
- Shrestha, R.; Hardeberg, J.Y. Assessment of Two Fast Multispectral Systems for Imaging of a Cultural Heritage Artifact-A Russian Icon. In Proceedings of the 14th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Las Palmas de Gran Canaria, Spain, 26–29 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 645–650. [Google Scholar]
- Pillay, R.; Hardeberg, J.Y.; George, S. Hyperspectral Calibration of Art: Acquisition and Calibration Workflows. arXiv 2019, arXiv:1903.04651. [Google Scholar]
- Flier, M.S. The Icon, Image of the Invisible: Elements of Theology, Aesthetics, and Technique; Oakwood Publications: Redondo Beach, CA, USA, 1992. [Google Scholar]
- Espinola, V.B.B. Russian Icons: Spiritual and Material Aspects. J. Am. Inst. Conserv. 1992, 31, 17–22. [Google Scholar] [CrossRef]
- Evseeva, L.M. A History of Icon Painting: Sources, Traditions, Present Day; Grand-Holding Publishers: Moscow, Russia, 2005. [Google Scholar]
- Cormack, R. Icons; Harvard University Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Gillooly, T.; Deborah, H.; Hardeberg, J.Y. Path opening for hyperspectral crack detection of cultural heritage paintings. In Proceedings of the 14th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Las Palmas de Gran Canaria, Spain, 26–29 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 651–657. [Google Scholar]
- Biver, S.; Fuqua, P.; Hunter, F. Light Science and Magic: An Introduction to Photographic Lighting; Routledge: London, UK, 2012. [Google Scholar]
- Hirvonen, T.; Penttinen, N.; Hauta-Kasari, M.; Sorjonen, M.; Kai-Erik, P. A wide spectral range reflectance and luminescence imaging system. Sensors 2013, 23, 14500–14510. [Google Scholar] [CrossRef]
- Heikkinen, V.; Cámara, C.; Hirvonen, T.; Penttinen, N. Spectral imaging using consumer-level devices and kernel-based regression. JOSA A 2016, 33, 1095–1110. [Google Scholar] [CrossRef] [PubMed]
- Frey, F.; Heller, D. The AIC Guide to Digital Photography and Conservation Documentation; American Institute for Conservation of Historic and Artistic Works: Washington, DC, USA, 2008. [Google Scholar]
- Walter, B.; Marschner, S.R.; Li, H.; Torrance, K.E. Microfacet models for refraction through rough surfaces. In Proceedings of the 18th Eurographics conference on Rendering Techniques, Grenoble, France, 25–27 June 2007; Eurographics Association: Aire-la-Ville, Switzerland, 2007; pp. 195–206. [Google Scholar]
- Lehman, B.; Wilkins, A.; Berman, S.; Poplawski, M.; Miller, N.J. Proposing measures of flicker in the low frequencies for lighting applications. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2865–2872. [Google Scholar]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Malvar, H.S.; He, L.W.; Cutler, R. High-quality linear interpolation for demosaicing of Bayer-patterned color images. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 485–488. [Google Scholar]
- Vedaldi, A.; Fulkerson, B. VLFeat: An Open and Portable Library of Computer Vision Algorithms. 2008. Available online: http://www.vlfeat.org/ (accessed on 19 August 2019).
- Mirhashemi, A. Spectral Image Database of Religious Icons (SIDRI). 2019. Available online: www.uef.fi/web/spectral/sidri/ (accessed on 19 August 2019).
- Mirhashemi, A. Introducing spectral moment features in analyzing the SpecTex hyperspectral texture database. Mach. Vis. Appl. 2018, 29, 415–432. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Stewart, C.V.; Sofka, M.; Tsai, C. Registration of challenging image pairs: Initialization, estimation, and decision. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 11, 1973–1989. [Google Scholar] [CrossRef]
- Lapray, P.J.; Thomas, J.B.; Gouton, P. High dynamic range spectral imaging pipeline for multispectral filter array cameras. Sensors 2017, 17, 1281. [Google Scholar] [CrossRef] [PubMed]
- Brauers, J.; Schulte, N.; Bell, A.A.; Aach, T. Multispectral high dynamic range imaging. In Proceedings of the Color Imaging XIII: Processing, Hardcopy, and Applications, San Jose, CA, USA, 29–31 January 2008; SPIE: Bellingham, WA, USA, 2008; Volume 6807, p. 680704. [Google Scholar]
- Tsuchida, M.; Sakai, S.; Miura, M.; Ito, K.; Kawanishi, T.; Kunio, K.; Yamato, J.; Aoki, T. Stereo one-shot six-band camera system for accurate color reproduction. J. Electron. Imaging 2013, 22, 033025. [Google Scholar] [CrossRef]













© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirhashemi, A. Configuration and Registration of Multi-Camera Spectral Image Database of Icon Paintings. Computation 2019, 7, 47. https://doi.org/10.3390/computation7030047
Mirhashemi A. Configuration and Registration of Multi-Camera Spectral Image Database of Icon Paintings. Computation. 2019; 7(3):47. https://doi.org/10.3390/computation7030047
Chicago/Turabian StyleMirhashemi, Arash. 2019. "Configuration and Registration of Multi-Camera Spectral Image Database of Icon Paintings" Computation 7, no. 3: 47. https://doi.org/10.3390/computation7030047
APA StyleMirhashemi, A. (2019). Configuration and Registration of Multi-Camera Spectral Image Database of Icon Paintings. Computation, 7(3), 47. https://doi.org/10.3390/computation7030047




