Serial DF Relayed FSO Links over Mixture Gamma Turbulence Channels and Nonzero Boresight Spatial Jitter
Abstract
1. Introduction
2. Channel Model
2.1. Scintillation Model
2.2. Scintillation Model through the MG Distribution
2.3. NZB-PE Model
2.4. The Composite Irradiance Model
3. Performance of the Link
3.1. OP of the Composite FSO System
3.2. ABER of the Composite FSO System
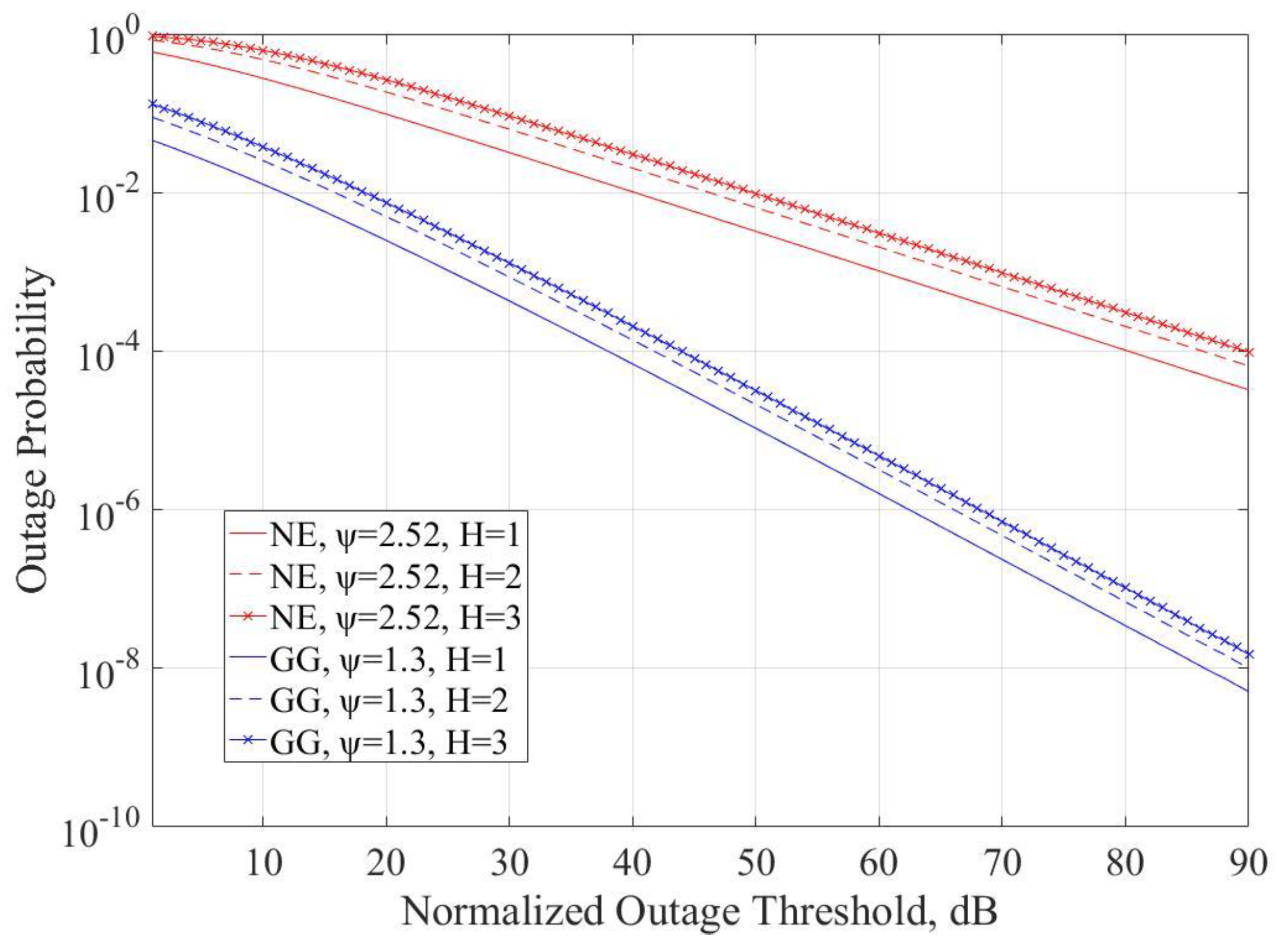
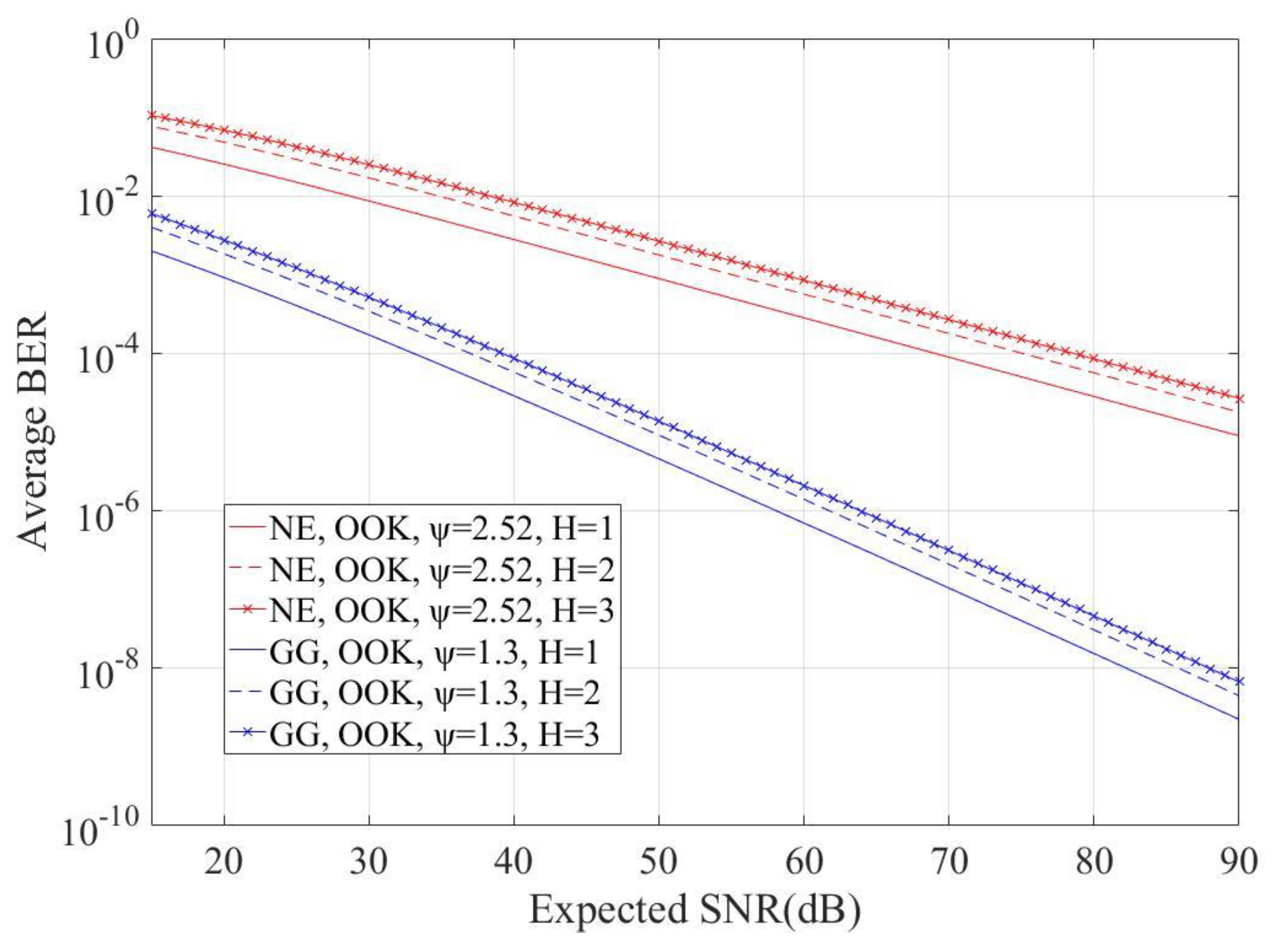
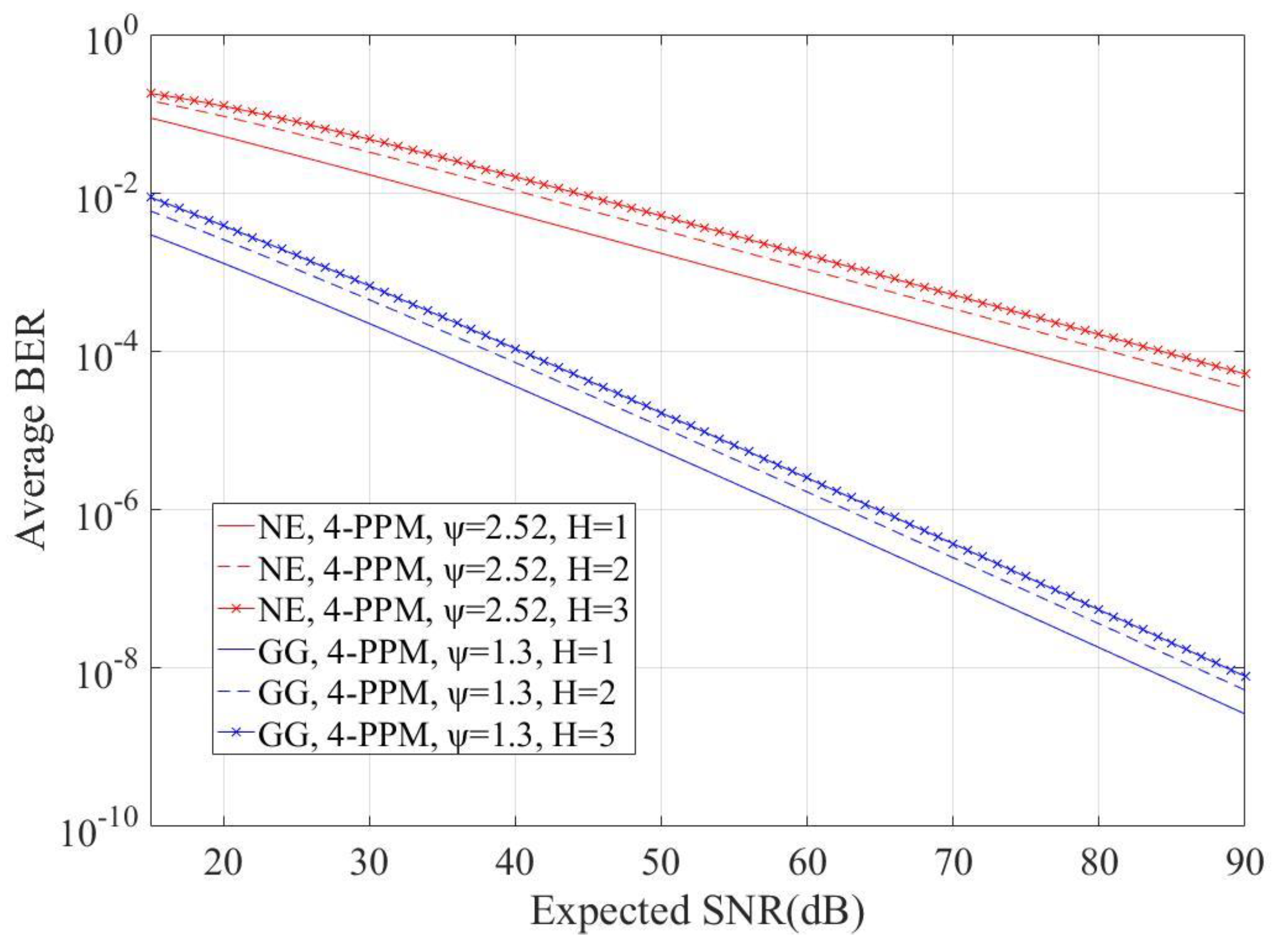
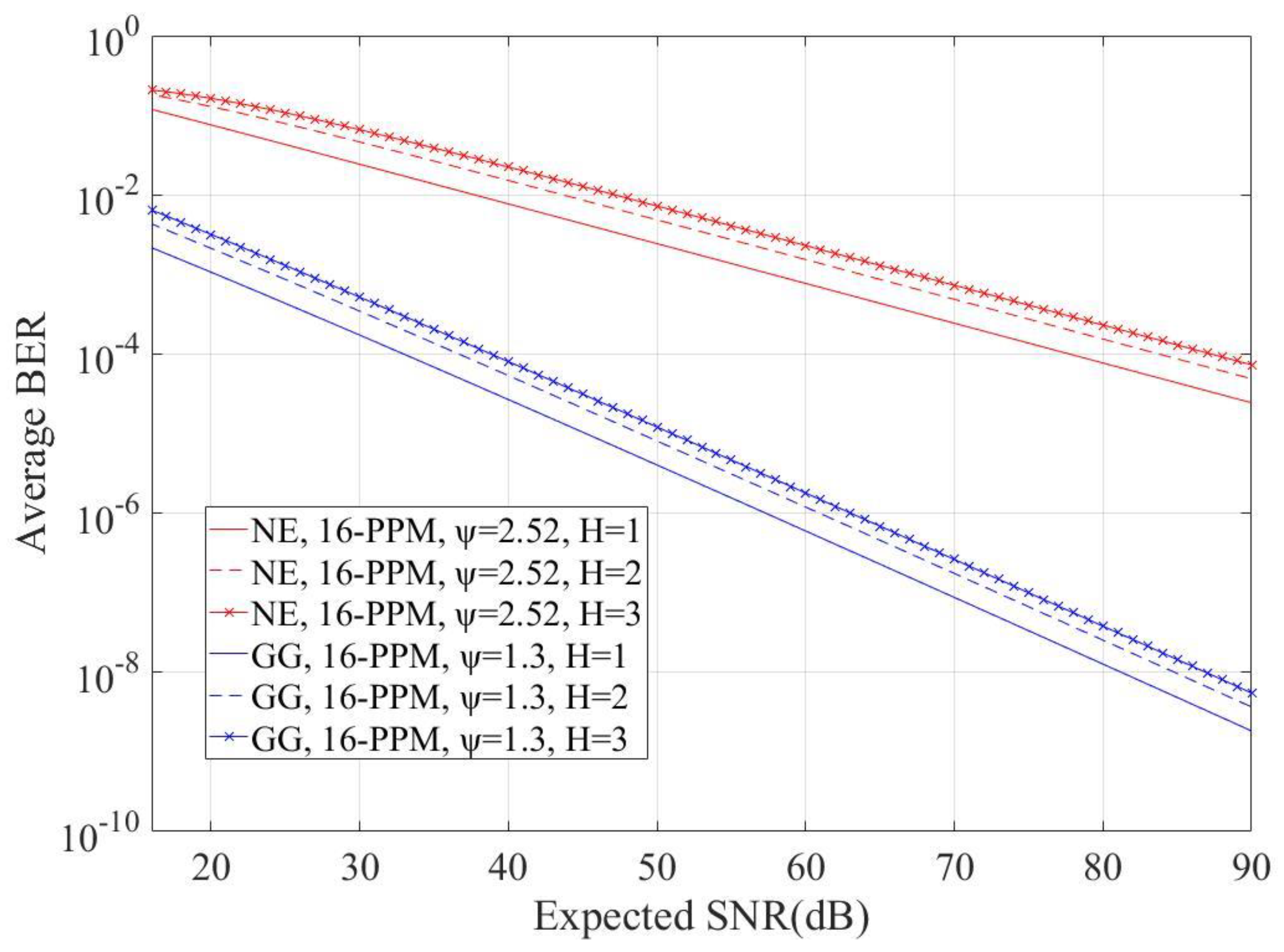
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghassemlooy, Z.; Popoola, W.O. Terrestrial Free-Space Optical Communications. In Mobile and Wireless Communications Network Layer and Circuit Level Design; InTech: London, UK, 2010. [Google Scholar] [CrossRef]
- Majumdar, A.K. Fundamentals of Free-Space Optical (FSO) Communication System. In Advanced Free Space Optics (FSO): A Systems Approach; Springer Series in Optical Sciences: New York, NY, USA, 2015; pp. 1–20. [Google Scholar]
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging Optical Wireless Communications-Advances and Challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Djordjevic, G.; Petkovic, M.; Cvetkovic, A.; Karagiannidis, G. Mixed RF/FSO Relaying with Outdated Channel State Information. IEEE J. Sel. Areas Commun. 2015, 33, 1935–1948. [Google Scholar] [CrossRef]
- Djordjevic, G.T.; Petkovic, M.I.; Spasic, M.; Antic, D.S. Outage Capacity of FSO Link with Pointing Errors and Link Blockage. Opt. Express 2016, 24, 219–230. [Google Scholar] [CrossRef]
- Tsonev, D.; Sinanovic, S.; Haas, H. Complete Modeling of Nonlinear Distortion in OFDM-Based Optical Wireless Communication. J. Light. Technol. 2013, 31, 3064–3076. [Google Scholar] [CrossRef]
- Dimitrov, S.; Sinanovic, S.; Haas, H. Clipping Noise in OFDM-Based Optical Wireless Communication Systems. IEEE Trans. Commun. 2012, 60, 1072–1081. [Google Scholar] [CrossRef]
- Leitgeb, E.; Gebhart, M.; Birnbacher, U. Optical Networks, Last Mile Access and Applications. J. Opt. Fiber Commun. Rep. 2005, 2, 56–85. [Google Scholar] [CrossRef]
- Gappmair, W.; Hranilovic, S.; Leitgeb, E. OOK Performance for Terrestrial FSO Links in Turbulent Atmosphere with Pointing Errors Modeled by Hoyt Distributions. IEEE Commun. Lett. 2011, 15, 875–877. [Google Scholar] [CrossRef]
- Epple, B. Simplified Channel Model for Simulation of Free-Space Optical Communications. J. Opt. Commun. Netw. 2010, 2, 293. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO Optical Wireless Links with Nonzero Boresight Pointing Errors over M Modeled Turbulence Channels. Opt. Commun. 2017, 403, 391–400. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Classical Theory for Propagation Through Random Media. In Laser Beam Propagation through Random Media, 2nd ed.; SPIE—The International Society for Optical Engineering: Washington, DC, USA, 2005; pp. 135–177. [Google Scholar]
- Nistazakis, H.E. A Time-Diversity Scheme for Wireless Optical Links over Exponentially Modeled Turbulence Channels. Optik 2013, 124, 1386–1391. [Google Scholar] [CrossRef]
- Varotsos, G.; Nistazakis, H.E.; Stassinakis, A.N.; Volos, C.K.; Christofilakis, V.; Tombras, G.S. Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels. Technologies 2018, 6, 121. [Google Scholar] [CrossRef]
- Ninos, M.P.; Nistazakis, H.E.; Tombras, G.S. On the BER Performance of FSO Links with Multiple Receivers and Spatial Jitter over Gamma-Gamma or Exponential Turbulence Channels. Optik 2017, 138, 269–279. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Castillo-Vazquez, M.; Puerta-Notario, A. Further Insights onMálaga Distribution for Atmospheric Optical Communications. In Proceedings of the 2012 International Workshop on Optical Wireless Communications (IWOW), Pisa, Italy, 22 October 2012; pp. 5–7. [Google Scholar] [CrossRef]
- Ninos, M.P.; Nistazakis, H.E.; Sandalidis, H.; Tombras, G.S. CDMA RoFSO Links with Nonzero Boresight Pointing Errors over M Turbulence Channels. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Sandalidis, H.G.; Chatzidiamantis, N.D.; Karagiannidis, G.K. A Tractable Model for Turbulence- and Misalignment-Induced Fading in Optical Wireless Systems. IEEE Commun. Lett. 2016, 20, 1904–1907. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. A Mixture Gamma Distribution to Model the SNR of Wireless Channels. IEEE Trans. Wirel. Commun. 2011, 10, 4193–4203. [Google Scholar] [CrossRef]
- Bhatnagar, M.R.; Ghassemlooy, Z. Performance Analysis of Gamma–Gamma Fading FSO MIMO Links With Pointing Errors. J. Light. Technol. 2016, 34, 2158–2169. [Google Scholar] [CrossRef]
- Bhatnagar, M.R. A One Bit Feedback Based Beamforming Scheme for FSO MISO System Over Gamma-Gamma Fading. IEEE Trans. Commun. 2015, 63, 1306–1318. [Google Scholar] [CrossRef]
- Sandalidis, H.G.; Tsiftsis, T.A.; Karagiannidis, G.K. Optical Wireless Communications With Heterodyne Detection Over Turbulence Channels With Pointing Errors. J. Light. Technol. 2009, 27, 4440–4445. [Google Scholar] [CrossRef]
- Sandalidis, H.G.; Chatzidiamantis, N.D.; Ntouni, G.D.; Karagiannidis, G.K. Performance of Free-Space Optical Communications over a Mixture Composite Irradiance Channel. Electron. Lett. 2017, 53, 260–262. [Google Scholar] [CrossRef]
- Gappmair, W.; Nistazakis, H.E. Subcarrier PSK Performance in Terrestrial FSO Links Impaired by Gamma-Gamma Fading, Pointing Errors, and Phase Noise. J. Light. Technol. 2017, 35, 1624–1632. [Google Scholar] [CrossRef]
- Gappmair, W.; Hranilovic, S.; Leitgeb, E. Performance of PPM on Terrestrial FSO Links with Turbulence and Pointing Errors. IEEE Commun. Lett. 2010, 14, 468–470. [Google Scholar] [CrossRef]
- Laourine, A.; Stephenne, A.; Affes, S. Estimating the Ergodic Capacity of Log-Normal Channels. IEEE Commun. Lett. 2007, 11, 568–570. [Google Scholar] [CrossRef]
- Gappmair, W.; Flohberger, M. Error Performance of Coded FSO Links in Turbulent Atmosphere Modeled by Gamma-Gamma Distributions. IEEE Trans. Wirel. Commun. 2009, 8, 2209–2213. [Google Scholar] [CrossRef]
- Al-Habash, M.A. Mathematical Model for the Irradiance Probability Density Function of a Laser Beam Propagating through Turbulent Media. Opt. Eng. 2001, 40, 1554. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Maria, J.; Francisco, J.; Puerta-Notario, A. A Unifying Statistical Model for Atmospheric Optical Scintillation. In Numerical Simulations of Physical and Engineering Processes; InTech: London, UK, 2011. [Google Scholar] [CrossRef]
- Arnon, S. Effects of Atmospheric Turbulence and Building Sway on Optical Wireless-Communication Systems. Opt. Lett. 2003, 28, 129–131. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Outage Capacity Optimization for Free-Space Optical Links with Pointing Errors. J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; García-Zambrana, A.; Castillo-Vázquez, C.; Castillo-Vázquez, B. Novel Approximation of Misalignment Fading Modeled by Beckmann Distribution on Free-Space Optical Links. Opt. Express 2016, 24, 22635. [Google Scholar] [CrossRef]
- Miridakis, N.I.; Tsiftsis, T.A. EGC Reception for FSO Systems under Mixture-Gamma Fading Channels and Pointing Errors. IEEE Commun. Lett. 2017, 21, 1441–1444. [Google Scholar] [CrossRef]
- Prabu, K.; Kumar, D.S. Outage Analysis of Relay-Assisted BPSK-SIM Based FSO Systems over Strong Atmospheric Turbulence with Pointing Errors. IJCCE 2014, 3, 3–6. [Google Scholar] [CrossRef]
- Androutsos, N.A.; Nistazakis, H.E.; Stassinakis, A.N.; Sandalidis, H.G.; Tombras, G.S. Performance of SIMO FSO Links over Mixture Composite Irradiance Channels. Appl. Sci. 2019, 9, 2072. [Google Scholar] [CrossRef]
- Elganimi, Y.T. Performance Comparison between OOK, PPM and PAM Modulation Schemes for Free Space Optical (FSO) Communication Systems: Analytical Study. Int. J. Comput. Appl. 2013, 79, 22–27. [Google Scholar] [CrossRef]
- Feng, M.; Wang, J.; Sheng, M.; Cao, L.; Chen, X.X.M. Outage Performance for Parallel Relay-Assisted Free-Space Optical Communications in Strong Turbulence with Pointing Errors. In Proceedings of the 2011 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 9–11 November 2011; pp. 7–11. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Volos, C.K.; Tombras, G.S. FSO Links with Diversity Pointing Errors and Temporal Broadening of the Pulses over Weak to Strong Atmospheric Turbulence Channels. Optik 2016, 127, 3402–3409. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Special Functions. In Table of Integrals, Series, and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Eds.; Elsevier (Academic Press): New York, NY, USA, 2008; pp. 859–1046. [Google Scholar]
- Boluda-Ruiz, R.; García-Zambrana, A.; Castillo-Vázquez, B.; Castillo-Vázquez, C. Impact of Nonzero Boresight Pointing Error on Ergodic Capacity of MIMO FSO Communication Systems. Opt. Express 2016, 24, 3513. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Cheng, J.; Tsiftsis, T.A. Free-Space Optical Communication with Nonzero Boresight Pointing Errors. IEEE Trans. Commun. 2014, 62, 713–725. [Google Scholar] [CrossRef]
- The Wolfarm Functions Site. Available online: http://functions.wolfarm.com (accessed on 10 April 2019).
- Katsis, A.; Nistazakis, H.E.; Tombras, G.S. Bayesian and Frequentist Estimation of the Performance of Free Space Optical Channels under Weak Turbulence Conditions. J. Frankl. Inst. 2009, 346, 315–327. [Google Scholar] [CrossRef]
- AlQuwaiee, H.; Ansari, I.S.; Alouini, M.-S. On the Performance of Free-Space Optical Communication Systems Over Double Generalized Gamma Channel. IEEE J. Sel. Areas Commun. 2015, 33, 1829–1840. [Google Scholar] [CrossRef]
- Chiani, M.; Dardari, D.; Simon, M.K. New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels. IEEE Trans. Wirel. Commun. 2003, 24, 840–845. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Definite Integrals. In Integrals and Series: Special Functions; Gordon and Breach Science Publishers: Glasgow, UK, 1992; Volume 2, pp. 55–612. [Google Scholar]
- Sheng, M.; Jiang, P.; Hu, Q.; Su, Q.; Xie, X. End-to-End Average BER Analysis for Multihop Free-Space Optical Communications with Pointing Errors. J. Opt. 2013, 15. [Google Scholar] [CrossRef]
- Morgado, E.; Mora-jiménez, I.; Vinagre, J.J.; Ramos, J.; Caamaño, A.J. End-to-End Average BER in Multihop Wireless Networks over Fading Channels. IEEE Trans. Wirel. Commun. 2010, 9, 2478–2487. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Stassinakis, A.N.; Sheikh Muhammad, S.; Tombras, G.S. BER Estimation for Multi-Hop RoFSO QAM or PSK OFDM Communication Systems over Gamma Gamma or Exponentially Modeled Turbulence Channels. Opt. Laser Technol. 2014, 64, 106–112. [Google Scholar] [CrossRef]
| Distributions | α | β | ψ | A0 | g |
|---|---|---|---|---|---|
| NE | - | - | 2.52 | 0.04 | 0.79 |
| GG | 2 | 5 | 1.3 | 0.04 | 1.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Androutsos, N.A.; Nistazakis, H.E.; Khalid, H.; Muhammad, S.S.; Tombras, G.S. Serial DF Relayed FSO Links over Mixture Gamma Turbulence Channels and Nonzero Boresight Spatial Jitter. Computation 2019, 7, 34. https://doi.org/10.3390/computation7030034
Androutsos NA, Nistazakis HE, Khalid H, Muhammad SS, Tombras GS. Serial DF Relayed FSO Links over Mixture Gamma Turbulence Channels and Nonzero Boresight Spatial Jitter. Computation. 2019; 7(3):34. https://doi.org/10.3390/computation7030034
Chicago/Turabian StyleAndroutsos, Nikolaos A., Hector E. Nistazakis, Hira Khalid, Sajid S. Muhammad, and George S. Tombras. 2019. "Serial DF Relayed FSO Links over Mixture Gamma Turbulence Channels and Nonzero Boresight Spatial Jitter" Computation 7, no. 3: 34. https://doi.org/10.3390/computation7030034
APA StyleAndroutsos, N. A., Nistazakis, H. E., Khalid, H., Muhammad, S. S., & Tombras, G. S. (2019). Serial DF Relayed FSO Links over Mixture Gamma Turbulence Channels and Nonzero Boresight Spatial Jitter. Computation, 7(3), 34. https://doi.org/10.3390/computation7030034






