Mode Pressure Coefficient Maps as an Alternative to Mean Pressure Coefficient Maps for Non-Gaussian Processes: Hyperbolic Paraboloid Roofs as Cases of Study
Abstract
1. Introduction
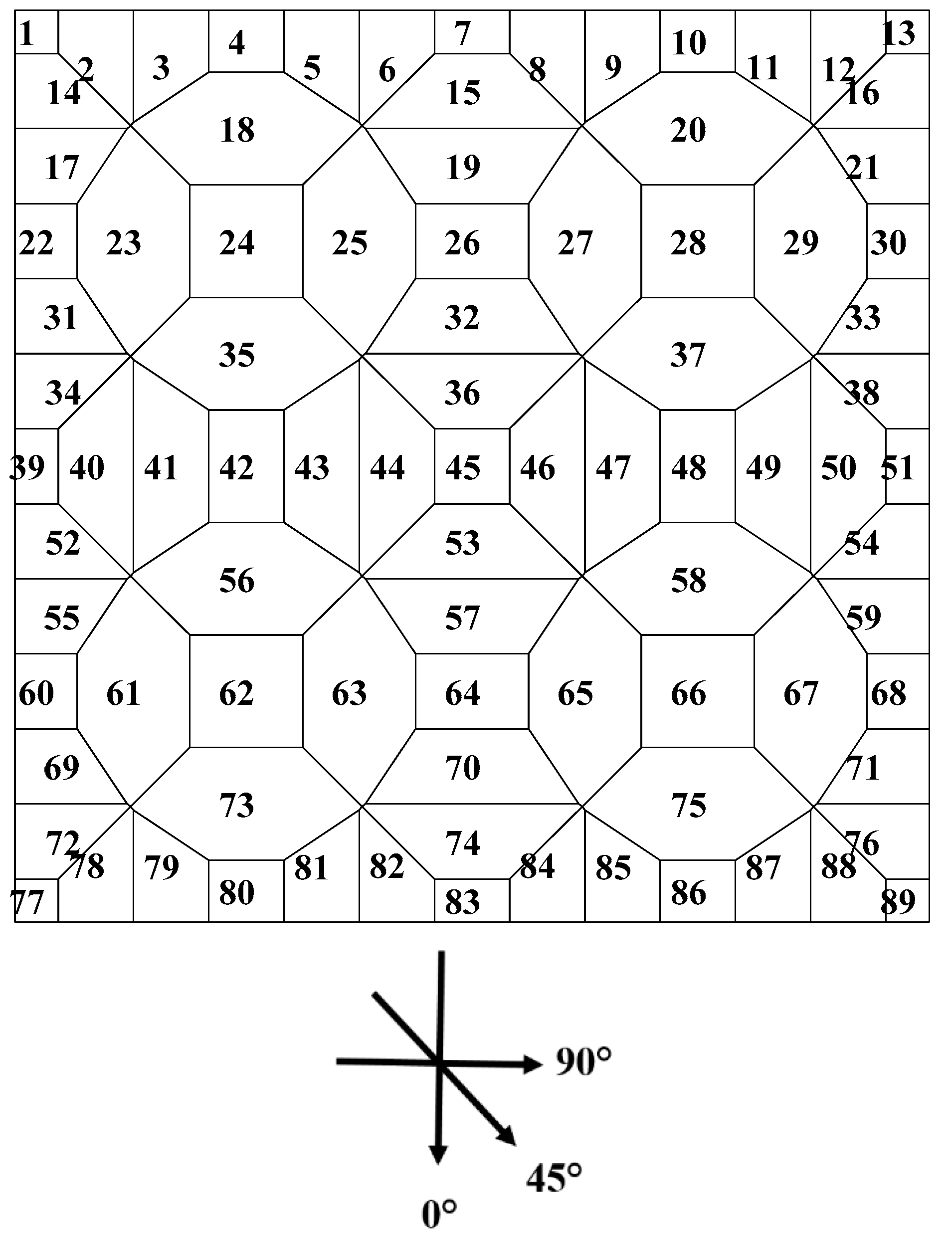
2. Geometrical Sample and Experimental Setup
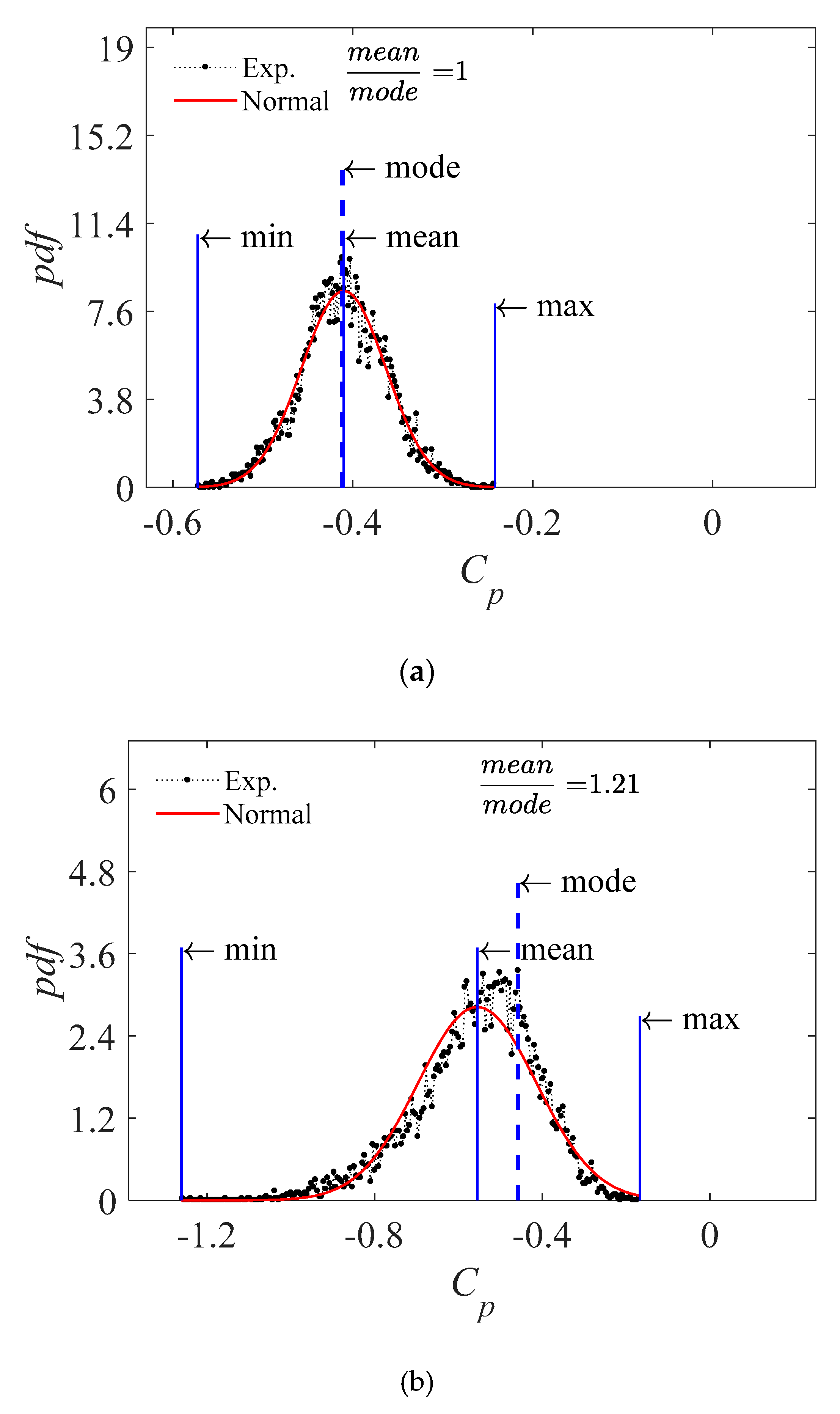
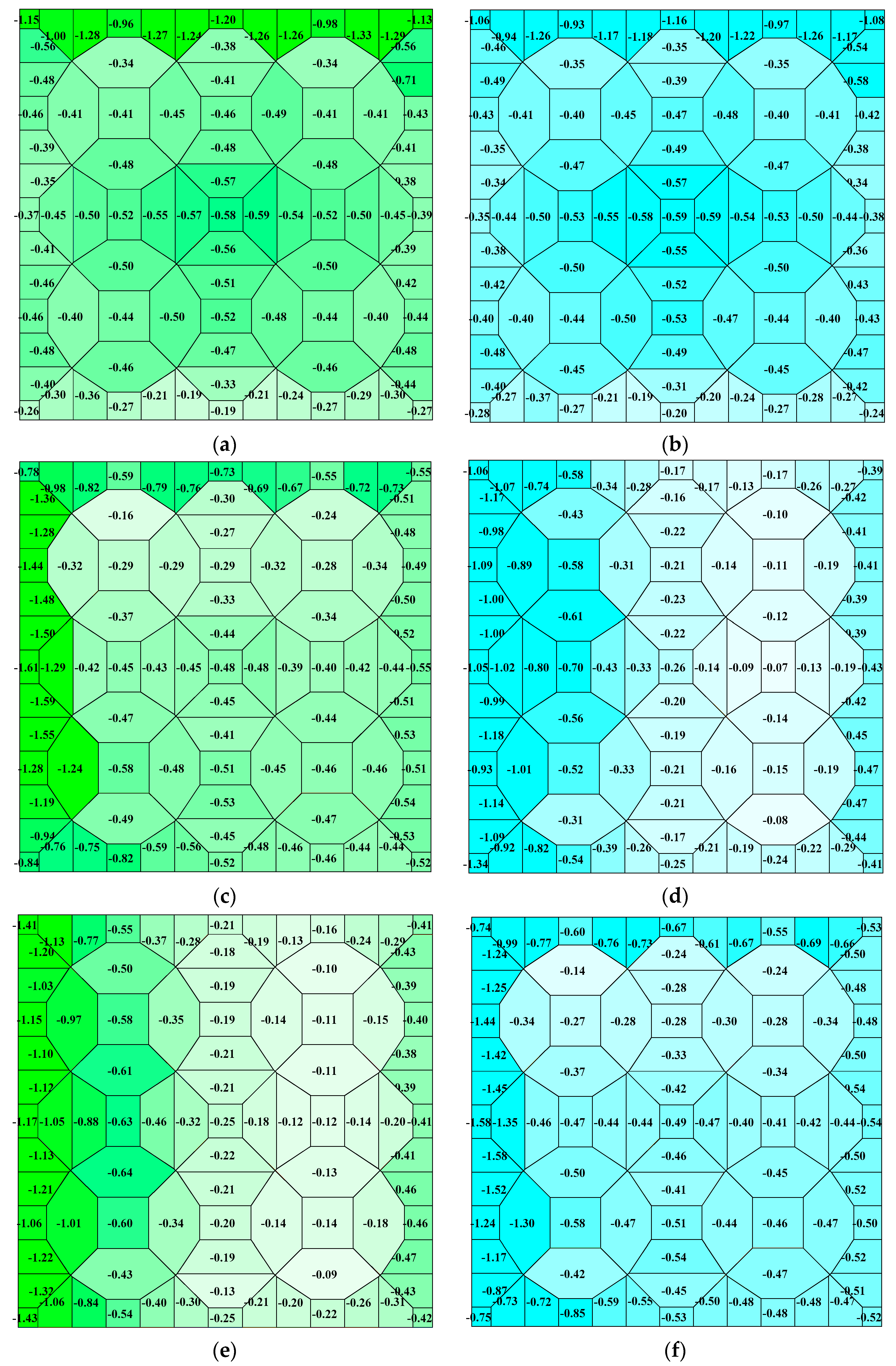
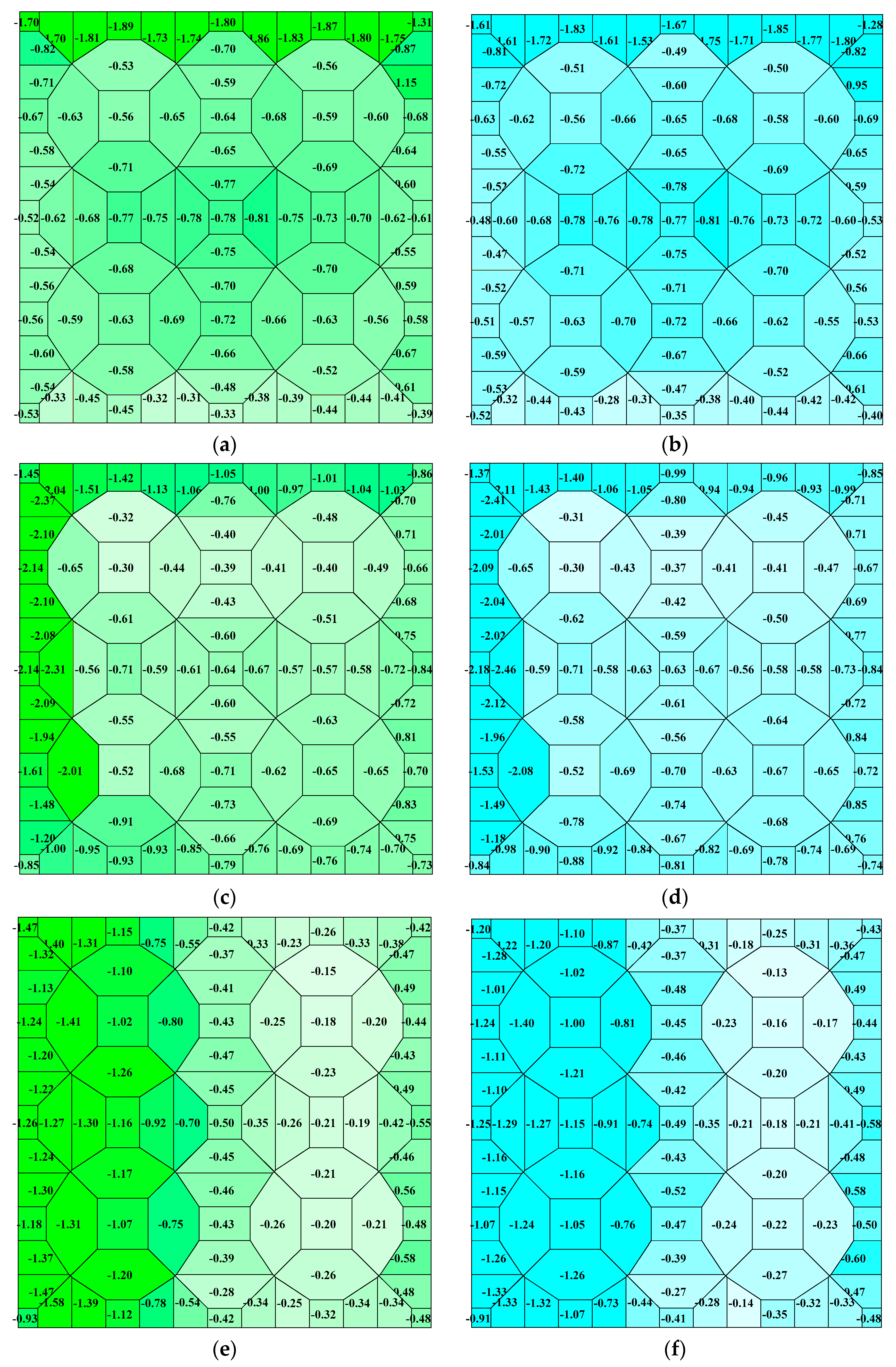
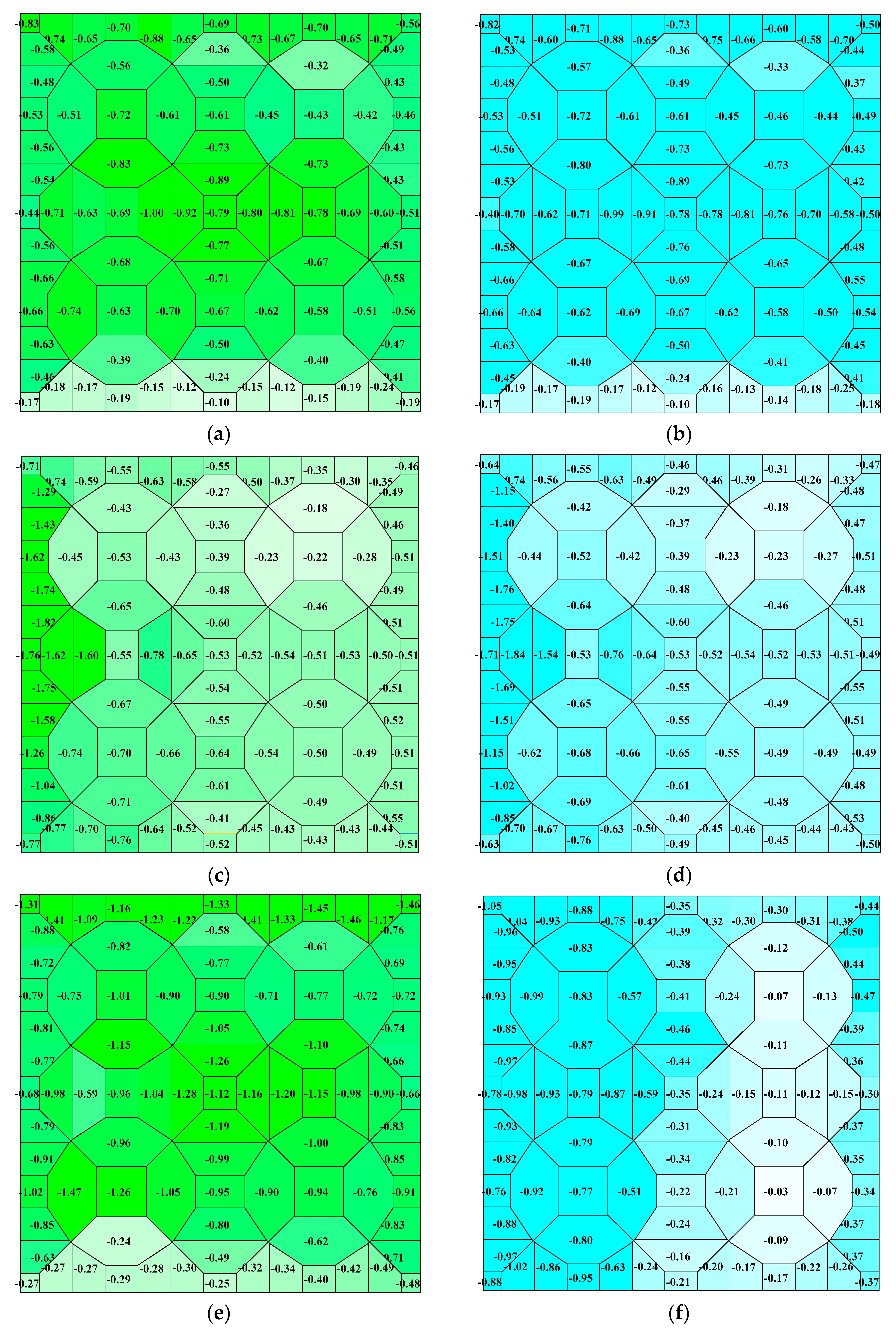
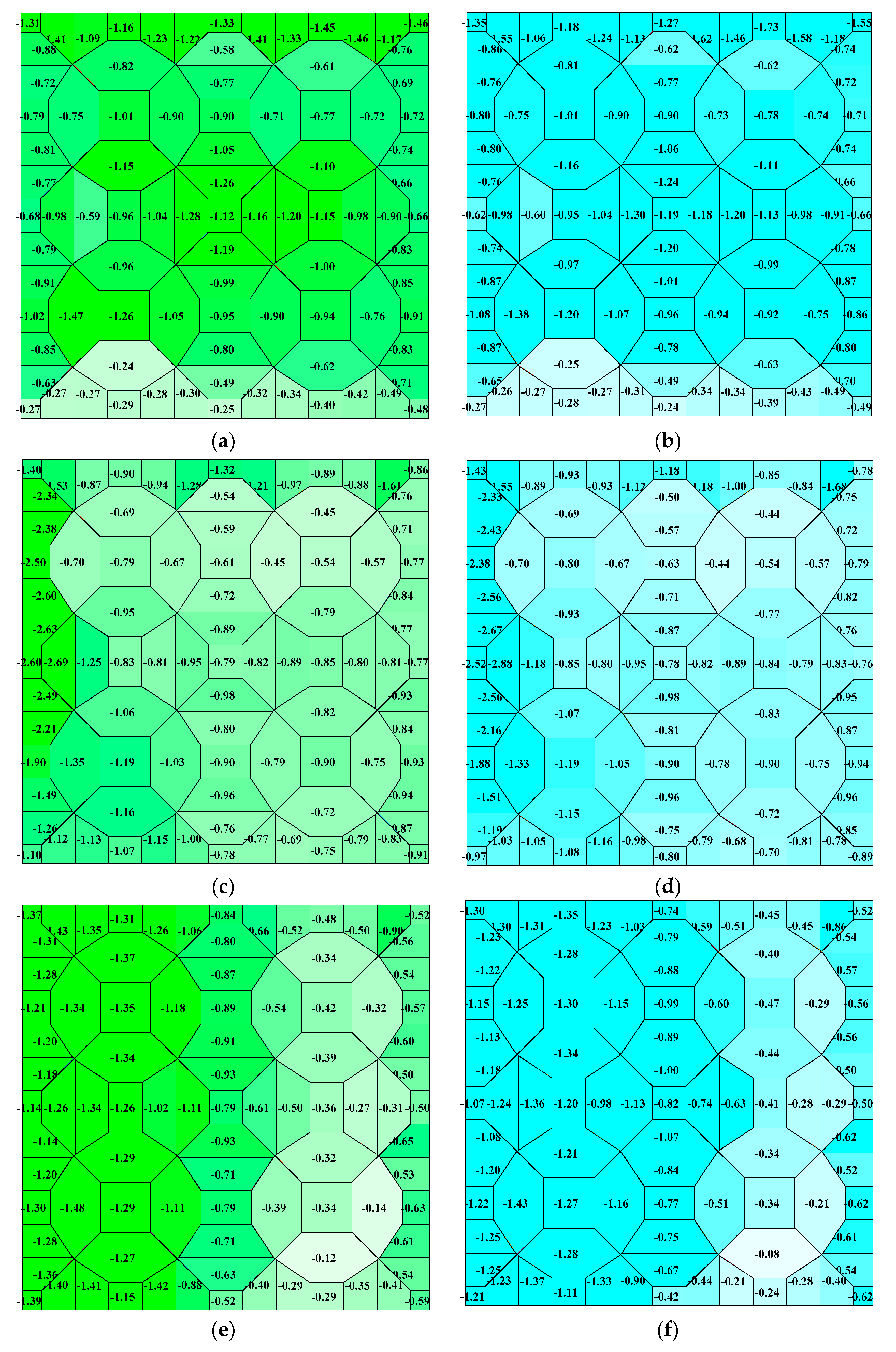
3. Experimental Data
4. Conclusions
Funding
Conflicts of Interest
References
- Lewis, W.J. Tension Structures: Form and Behavior; Thomas Telford: London, UK, 2003. [Google Scholar]
- Majowiecki, M. Tensostrutture: Progetto e Verifica; Edizioni Crea: Massa, Italy, 1994. [Google Scholar]
- Rizzo, F.; Zazzini, P. Improving the acoustical properties of an elliptical plan space with a cable net membrane roof. J. Acoust. Aust. 2016, 44, 449–456. [Google Scholar] [CrossRef]
- Rizzo, F.; Zazzini, P. Shape dependence of acoustic performances in buildings with a Hyperbolic Paraboloid cable net membrane roof. J. Acoust. Aust. 2017, 45, 421–443. [Google Scholar] [CrossRef]
- AIJ (Architectural Institute of Japan). Recommendations for Loads on Buildings; AIJ: Tokyo, Japan, 2004; Chapter 6: Wind Loads. [Google Scholar]
- ASCE (American Society of Civil Engineering). Wind Tunnel Studies of Buildings and Structures; Manuals of Practice (MOP); Isyumov, N., Ed.; ASCE: Reston, VA, USA, 1999; Volume 67. [Google Scholar]
- ASCE (American Society of Civil Engineering). Minimum Design Loads for Buildings and Other Structures; ASCE: Reston, VA, USA, 2010; Volume 7. [Google Scholar]
- AS/NZS (Standards Australia/Standards New Zealand). Structural Design Actions; Part 2: Wind Actions; AS/NZS 1170.2:2002; AS/NZS: Sydney, Australia, 2011. [Google Scholar]
- CEN (Comité Européen de Normalization). Eurocode 1: Actions on Structures—Part 1–4: General actions—Wind Actions; EN-1991-1-4; CEN: European Union, 2005. [Google Scholar]
- CNR (National Research Council of Italy). Guide for the Assessment of Wind Actions and Effects on Structures; CNR-DT 207/2008; CNR: Rome, Italy, 2008. [Google Scholar]
- Krishna, P.; Kumar, K.; Bhandari, N.M. Wind Loads on Buildings and Structures; Indian Standard IS:875, Part 3, Proposed Draft & Commentary; Wiley: New York, NY, USA, 2012. [Google Scholar]
- ISO (International Standards Organization). Wind Action on Structures—D.3 Wind Tunnel Testing Procedures; 4354:2012(E); ISO: Geneva, Switzerland, 2012. [Google Scholar]
- NRC/CNRC (National Research Council/Conseil National de Recherches Canada). Commentary to the National Building Code of Canada, Commentary I: Wind Load and Effects; NRC/CNRC: Ottawa, ON, Canada, 2010. [Google Scholar]
- SIA (Swiss Society of Engineers and Architects). Action on Structures—Appendix C: Force and Pressure Factors for Wind; SIA 261:2003; SIA: Zurich, Switzerland, 2003. [Google Scholar]
- Biagini, P.; Borri, C.; Facchini, L. Wind response of large roofs of stadiums and arena. J. Wind Eng. Ind. Aerodyn. 2007, 95, 9–11. [Google Scholar] [CrossRef]
- Dong, X.; Ye, J.H. Development and verification of a flow model of conical vortices on saddle roofs. J. Eng. Mech. 2015, 141, 04014127. [Google Scholar] [CrossRef]
- Elashkar, I.; Novak, M. Wind tunnel studies of cable roofs. J. Wind Eng. Ind. Aerodyn. 1983, 13, 407–419. [Google Scholar] [CrossRef]
- Kawai, H.; Yoshie, R. Wind-induced response of a large cantilevered roof. J. Wind Eng. Ind. Aerodyn. 1999, 83, 263–275. [Google Scholar] [CrossRef]
- Kawakita, S.; Bienkiewicz, B.; Cermak, J.E. Aeroelastic Model Study of Suspended Cable Roof; Fluid Mechanics and Wind Engineering Program, Department of Civil Engineering, Colorado State University: Fort Collins, CO, USA, 1992. [Google Scholar]
- Killen, G.P.; Letchford, C.W. A parametric study of wind loads on grandstand roofs. Eng. Struct. 2001, 23, 725–735. [Google Scholar] [CrossRef]
- Kimoto, E.; Kawamura, S. Aerodynamic criteria of hanging roofs for structural Design. In Proceedings of the IASS Symposium on Membrane Structures and Space Frames, Osaka, Japan, 15–19 September 1986. [Google Scholar]
- Irwin, H.P.A.H.; Wardlaw, R.L.A. Wind tunnel investigation of a retractable fabric roof for the Montreal Olympic stadium. In Proceedings of the 5th International Conference on Wind Engineering, Fort Collins, CO, USA, 8–14 July 1979; pp. 925–938. [Google Scholar]
- Letchford, C.W.; Killen, G.P. Equivalent static wind loads for cantilevered grandstand roofs. Eng. Struct. 2002, 24, 207–217. [Google Scholar] [CrossRef]
- Vitale, A.; Letchford, C.W. Full-scale wind loads on a porous canopy roof. In Proceedings of the Australasian Structural Engineering Conference, Auckland, New Zealand, 30 September–2 October 1998. [Google Scholar]
- Letchford, C.W.; Denoon, R.O.; Johnson, G.; Mallam, A. Dynamic characteristics of cantilever grandstand roofs. Eng. Struct. 2002, 24, 1085–1090. [Google Scholar] [CrossRef]
- Rizzo, F.; Sepe, V.; Vasta, V. Correlation structure of wind-tunnel pressure fields for a hyperbolic paraboloid roof. In Proceedings of the Italian Association of Theoretical and Applied Mechanics (AIMETA 2017), Salerno, Italy, 4–7 September 2017; Gechi Edizioni: Salerno, Italy, 2017; ISBN 978-889-42484-7-0. [Google Scholar]
- Rizzo, F. Wind tunnel tests on hyperbolic paraboloid roofs with elliptical plane shapes. Eng. Struct. 2012, 45, 536–558. [Google Scholar] [CrossRef]
- Rizzo, F.; D’Asdia, P.; Lazzari, M.; Procino, L. Wind action evaluation on tension roofs of hyperbolic paraboloid shape. Eng. Struct. 2011, 33, 445–461. [Google Scholar] [CrossRef]
- Rizzo, F.; D’Asdia, P.; Procino, L.; Lazzari, M.; Olivato, G. Aerodynamic behavior of hyperbolic parabolic shaped roofs: Wind tunnel test, POD and CFD analysis. In Proceedings of the 12th International Conference on Civil, Structural and Environmental Engineering Computing (CC 2009), Madeira, Portugal, 1–4 September 2009. [Google Scholar]
- Rizzo, F.; D’Asdia, P.; Lazzari, M.; Olivato, G. Aerodynamic behavior of hyperbolic paraboloid shaped roofs: POD and CFD analysis. In Proceedings of the 5th European & African Conference on Wind Engineering (EACWE 5 2009), Florence, Italy, 19–23 July 2009. [Google Scholar]
- Rizzo, F.; D’Asdia, P.; Lazzari, M. Aerodynamic behavior of hyperbolic paraboloid shaped roofs: Wind tunnel tests. In Proceedings of the 5th European & African Conference on Wind Engineering (EACWE 5 2009), Florence, Italy, 19–23 July 2009. [Google Scholar]
- Sykes, D.M. Wind loading tests on models of two tension structures for EXPO’92, Seville. J. Wind Eng. Ind. Aerodyn. 1994, 52, 371–383. [Google Scholar] [CrossRef]
- Sun, X.; Wu, Y.; Yang, Q.; Shen, S. Wind tunnel tests on the aeroelastic behaviors of tension structures. In Proceedings of the VI International Colloquium on Bluff Bodies Aerodynamics & Applications, BBAA VI, Milan, Italy, 20–24 July 2008. [Google Scholar]
- Rizzo, F.; Ricciardelli, F. Design pressure coefficients for circular and elliptical plan structures with hyperbolic paraboloid roof. J. Eng. Struct. 2017, 139, 153–169. [Google Scholar] [CrossRef]
- Rizzo, F.; D’Asdia, P.; Ricciardelli, F.; Bartoli, G. Characterization of pressure coefficients on hyperbolic paraboloid roofs. J. Wind Eng. Ind. Aerodyn. 2012, 102, 61–71. [Google Scholar] [CrossRef]
- Rizzo, F.; Barbato, M.; Sepe, V. Peak factor statistics of wind effects for hyperbolic paraboloid roofs. Eng. Struct. 2018, 173, 313–330. [Google Scholar] [CrossRef]
- Liu, M.; Chen, X.; Yang, Q. Characteristics of dynamic pressures on a saddle type roof in various boundary layer flows. J. Wind Eng. Ind. Aerodyn. 2016, 150, 1–14. [Google Scholar] [CrossRef]
- Brito, R.; Caracoglia, L. Extraction of flutter derivatives from small scale wind tunnel experiments. In Proceedings of the 11th Americas Conference on Wind Engineering, American Association for Wind Engineering (AAWE), San Juan, Puerto Rico, 22–26 June 2009. [Google Scholar]
- Rizzo, F.; Caracoglia, L.; Montelpare, S. Predicting the flutter speed of a pedestrian suspension bridge through examination of laboratory experimental errors. Eng. Struct. 2018, 172, 589–613. [Google Scholar] [CrossRef]
- Rizzo, F.; Caracoglia, L. Examining wind tunnel errors in Scanlan derivatives and flutter speed of a closed-box. J. Wind Struct. 2018, 26, 231–251. [Google Scholar]
- Avossa, A.M.; Di Giacinto, D.; Malangone, P.; Rizzo, F. Seismic Retrofit of a Multi-Span Prestressed Concrete Girder Bridge with Friction Pendulum Devices. Shock Vib. 2018. [Google Scholar] [CrossRef]
- Daw, D.J.; Davenport, A.G. Aerodynamic damping and stiffness of a semi-circular roof in turbulent wind. J. Wind Eng. Ind. Aerodyn. 1989, 32, 83–92. [Google Scholar] [CrossRef]
- Forster, B. Cable and membrane roofs, a historical survey. Struct. Eng. Rev. 1994, 6, 3–5. [Google Scholar]
- Kassem, M.; Novak, M. Wind-Induced response of hemispherical air-supported Structures. J. Wind Eng. Ind. Aerodyn. 1992, 41, 177–178. [Google Scholar] [CrossRef]
- Knudson, W.C. Recent advances in the field of long span tension structures. Eng. Struct. 1991, 13, 174–193. [Google Scholar] [CrossRef]
- Pun, P.K.F.; Letchford, C.W. Analysis of a tension membrane HYPAR roof subjected to fluctuating wind loads. In Proceedings of the 3rd Asia-Pacific Symposium on Wind Engineering, Hong Kong, 13–15 December 1993; pp. 741–746. [Google Scholar]
- Rizzo, F.; Sepe, V. Static loads to simulate dynamic effects of wind on hyperbolic paraboloid roofs with square plan. J. Wind Eng. Ind. Aerodyn. 2015, 137, 46–57. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Q. Wind-induced response analysis and wind-resistant design of hyperbolic paraboloid cable net structures. Int. J. Space Struct. 1999, 14, 57–65. [Google Scholar] [CrossRef]
- Vassilopoulou, I.; Gantes, C.J. Nonlinear dynamic behavior of saddle form cable nets under uniform harmonic load. Eng. Struct. 2011, 33, 2762–2771. [Google Scholar] [CrossRef]
- Vassilopoulou, I.; Gantes, C.J. Vibration modes and natural frequencies of saddle form cable nets. Comput. Struct. 2012, 88, 105–119. [Google Scholar] [CrossRef]
- Vassilopoulou, I.; Petrini, F.; Gantes, C.J. Nonlinear dynamic behavior of cable nets subjected to wind loading. Structures 2017, 10, 170–183. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, R. On Aerodynamic Stability of Membrane Structures. Int. J. Space Struct. 2005, 20, 181–188. [Google Scholar] [CrossRef]
- Suresh Kumar, K.; Stathopoulos, T. Wind loads on low building roofs: A stochastic perspective. J. Struct. Eng. 2000, 126, 944–956. [Google Scholar] [CrossRef]




| Model | l1 [cm] | l2 [cm] | f1 [cm] | f2 [cm] | H [cm] | HB [cm] |
|---|---|---|---|---|---|---|
| 1 | 80.00 | 80.00 | 2.67 | 5.33 | 8.00 | 13.33 |
| 2 | 80.00 | 80.00 | 2.67 | 5.33 | 8.00 | 26.66 |
| 3 | 80.00 | 80.00 | 4.44 | 8.89 | 13.33 | 13.33 |
| 4 | 80.00 | 80.00 | 4.44 | 8.89 | 13.33 | 26.66 |
| Model | α = 0° | α = 45° | α = 90° |
|---|---|---|---|
| 1 | 44.9 | 27.0 | 32.6 |
| 2 | 29.2 | 40.4 | 28.1 |
| 3 | 41.6 | 41.6 | 21.3 |
| 4 | 34.8 | 46.1 | 16.9 |
| Model | α = 0° | α = 45° | α = 90° |
| Mean of ratio | |||
| 1 | 1.03 | 1.01 | 1.05 |
| 2 | 1.03 | 1.01 | 1.05 |
| 3 | 1.02 | 1.02 | 1.01 |
| 4 | 1.00 | 1.01 | 1.02 |
| Percentage of cases where | |||
| (%) | |||
| Value in parenthesis is the mean value of the ratio restricted to cases where ratio <1 | |||
| 1 | 30.3 | 41.6 | 32.6 |
| (0.98) | (0.97) | (0.94) | |
| 2 | 36.0 | 46.1 | 28.1 |
| (0.99) | (0.98) | (0.95) | |
| 3 | 34.8 | 28.1 | 38.2 |
| (0.98) | (0.97) | (0.87) | |
| 4 | 56.2 | 41.6 | 38.2 |
| (0.97) | (0.98) | (0.92) | |
| Percentage of cases where | |||
| (%) | |||
| Value in parenthesis is the mean value of the ratio restricted to cases where ratio >1 | |||
| 1 | 69.7 | 58.4 | 67.4 |
| (1.05) | (1.04) | (1.10) | |
| 2 | 64.0 | 53.9 | 71.9 |
| (1.05) | (1.03) | (1.09) | |
| 3 | 65.2 | 71.9 | 61.8 |
| (1.04) | (1.04) | (1.10) | |
| 4 | 43.8 | 58.4 | 61.8 |
| (1.03) | (1.03) | (1.08) | |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viskovic, A. Mode Pressure Coefficient Maps as an Alternative to Mean Pressure Coefficient Maps for Non-Gaussian Processes: Hyperbolic Paraboloid Roofs as Cases of Study. Computation 2018, 6, 64. https://doi.org/10.3390/computation6040064
Viskovic A. Mode Pressure Coefficient Maps as an Alternative to Mean Pressure Coefficient Maps for Non-Gaussian Processes: Hyperbolic Paraboloid Roofs as Cases of Study. Computation. 2018; 6(4):64. https://doi.org/10.3390/computation6040064
Chicago/Turabian StyleViskovic, Alberto. 2018. "Mode Pressure Coefficient Maps as an Alternative to Mean Pressure Coefficient Maps for Non-Gaussian Processes: Hyperbolic Paraboloid Roofs as Cases of Study" Computation 6, no. 4: 64. https://doi.org/10.3390/computation6040064
APA StyleViskovic, A. (2018). Mode Pressure Coefficient Maps as an Alternative to Mean Pressure Coefficient Maps for Non-Gaussian Processes: Hyperbolic Paraboloid Roofs as Cases of Study. Computation, 6(4), 64. https://doi.org/10.3390/computation6040064




