Abstract
The divergence of fluorine-based systems and significance of their nascent non-covalent chemistry in molecular assemblies are presented in a brief review of the field. Emphasis has been placed to show that type-I and -II halogen-centered F···F long-ranged intermolecular distances viable between the entirely negative fluorine atoms in some fluoro-substituted dimers of C6H6 can be regarded as the consequence of significant non-covalent attractive interactions. Such attractive interactions observed in the solid-state structures of C6F6 and other similar fluorine-substituted aromatic compounds have frequently been underappreciated. While these are often ascribed to crystal packing effects, we show using first-principles level calculations that these are much more fundamental in nature. The stability and reliability of these interactions are supported by their negative binding energies that emerge from a supermolecular procedure using MP2 (second-order Møller-Plesset perturbation theory), and from the Symmetry Adapted Perturbation Theory, in which the latter does not determine the interaction energy by computing the total energy of the monomers or dimer. Quantum Theory of Atoms in Molecules and Reduced Density Gradient Non-Covalent Index charge-density-based approaches confirm the F···F contacts are a consequence of attraction by their unified bond path (and bond critical point) and isosurface charge density topologies, respectively. These interactions can be explained neither by the so-called molecular electrostatic surface potential (MESP) model approach that often demonstrates attraction between sites of opposite electrostatic surface potential by means of Coulomb’s law of electrostatics, nor purely by the effect of electrostatic polarization. We provide evidence against the standalone use of this approach and the overlooking of other approaches, as the former does not allow for the calculation of the electrostatic potential on the surfaces of the overlapping atoms on the monomers as in the equilibrium geometry of a complex. This study thus provides unequivocal evidence of the limitation of the MESP approach for its use in gaining insight into the nature of reactivity of overlapped interacting atoms and the intermolecular interactions involved.
1. Introduction
Fluorine, the first member of the halogen family, has an exceptionally interesting, almost magical, chemistry. Some models of Big Bang nucleosynthesis suggest very high baryon density regions were formed in the early Universe [1]. This generated the production of heavy elements other than lithium, such as F, which have therefore been present from the time of the Dark Age. Species, such as HF (hydrogen fluoride), affect the enhancement of the emission line intensity from proto-objects and could produce spectral-spatial fluctuations [1].
Fluorine has been used innovatively, sometimes spectacularly, in molecular design and in controlling the chemistry of the resulting materials. The importance of fluorine in natural surfactants is currently of great interest. The research focuses on two main application areas: (i) fluorous oil-in-water emulsions and gas microbubbles for biomedical imaging and drug delivery, and (ii) coating and functionalization of solid fluorinated surfaces [2]. The widespread application of fluorine in drug design benefits from its distinctive properties because it can positively modulate several pharmacokinetics properties, inter alia, lipophilicity, eletrophilicity, metabolic stability, and chemical stability [3]. These attributes are of significant interest to medicinal chemists due to their possible application in anticancer, antimicrobial, anti-inflammatory and antiviral activity. This is understandably due to the fact that the judicious introduction of fluorine into molecules could productively influence conformation, pKa, intrinsic potency, membrane permeability, metabolic pathways, and pharmacokinetic properties of drugs [4]. The wide ranging applications of fluorine in drug design can be a strong stimulus for the development of new synthetic methodologies, thereby allowing more facile access to a wide range of fluorinated compounds [4].
Fluorine has been used in the preparation of numerous organic compounds including materials such as Teflon that are temperature-resistant. Its use in the production of cooling fluids, pharmacological products, aerosol products (e.g., freon) and toothpastes, among others, is impressive. Equally impressive is its importance in improving the bioavailability, and even the efficacy, of drug molecules. Zhang et al. [5] have found a beneficial site for fluorination in inhibitors targeting methionyl-tRNA synthetase of Trypanosoma brucei; incorporation of 5-fluoroimidazo[4-b]pyridine into inhibitors leads to central nervous system bioavailability and maintained or even improved efficacy.
By using a model system of fluorine-passivated silicon nanocrystals (SiNCs) in the framework of density functional theory, Ma et al. [6] demonstrated that the effect of surface chemistry on both the excitation energy and emission energy of a SiNC becomes more significant as F coverage at the nanocrystal surface increases. On changing the size of a SiNC from 1.7 to 1.4 nm in both the ground state and the excited state, high F coverage (>50%) increasingly enables the effect of surface chemistry to prevail over that of quantum confinement. For a very small sized SiNC (<1.4 nm) in the ground state, the quantum confinement effect is dominant regardless of the nature of F coverage. In the excited state of the SiNC, F coverage helps to confine excitons inside the very small SiNC. It was found that medium F coverage leads to enhanced radiative recombination for SiNCs, whereas 100% F coverage weakens the radiative recombination of SiNCs.
Despite its importance in many areas of chemistry, it has been said that very few people will use elemental fluorine other than at near-gunpoint, and some of the other classic reagents are still quite unfriendly, tending to leave cursing chemists swearing never to touch them again [7].
By contrast, Menaa and coworkers have suggested that fluorohydrocarbons can serve as a molecular tag for a variety of applications in medicinal chemistry and oncology, including screening, imaging and analytical characterization [8]. The C–F bond in fluorine-substituted molecules is more stable than a typical fluorescent dye, less toxic than fluorine radioisotopes, and less harmful than radio-waves. In their review [8], these authors have discussed the major physical-chemical properties of C–F bond, and its applications in fluorocarbons, as well as the state-of-art imaging technologies that use fluorine for clinical and research and development and for oncology purposes (e.g., drug design, drug discovery, drug delivery and molecular imaging).
Much exciting chemistry has appeared on the reactivity of fluorine through the study of diverse fluorine-substituted molecules. For instance, decades ago it was believed that fluorine in molecules is always negative. It was also believed that fluorine in molecules hardly acts as a hydrogen bond acceptor, despite it being highly electronegative compared to the other members of the halogen family. Some have purported to show that fluorine is not polarizable and that it is not dispersive. By contrast, there have been several studies that report that fluorine in molecules can be a good hydrogen bond acceptor; that it is both polarizable and dispersive, despite it being tiny; this means it is not necessarily negative when incorporated in molecules. This is perhaps not unrealistic given that the charge density distribution on fluorine in an R–F molecule is actually controlled by the fragment/group/atom R to which it is covalently bonded. For instance, the fluorine atom in F2, FCN, and FCCCN is not entirely negative. In these systems, it conceives two regions on its surface that are dissimilar in the distribution of electron density: one, axial, is along the outermost extension of the R–F covalent σ-bond and the other, equatorial, is around the lateral portion of the R–F covalent σ-bond. Because the latter portions of fluorine in molecules are equipped with lone-pair electron densities, these are generally negative, yet more negative than the axial site. In essence, the axial site can be negative or positive depending on the electron-withdrawing and polarizing capacity of R. The same is applicable to the equatorial sites, although the former occasion is by far more evident in molecules.
The anisotropic distribution of charge density on the surface of the bonded halogen in molecules has led to the development of the concept of the “σ-hole” theory. A σ-hole on a halogen atom X along the outermost extension of a R–X covalent bond can be positive, negative, or even neutral [9,10,11,12,13,14]. Its nature and strength are generally judged by the local (surface) maximum of electrostatic surface potential, Vs,max, along the outer extension of the R–X bond; this is generally calculated on the 0.0010 a.u. isodensity surface of the molecule [14]; there are other views that recommend using higher isodensity for mapping of the potential to avoid misleading conclusions to be drawn on a novel system. In either case, if Vs,max < 0, the σ-hole bears a negative electrostatic potential, and is referred to as a negative σ-hole; if Vs,max > 0, it bears a positive electrostatic potential. The latter attribute (which is what has been found in most of the halogenated hydrocarbon compounds with X = Cl, Br and I), in fact, has led to the belief that a σ-hole is always positive (although this is misleading!); and, if there is no local maximum of electrostatic potential (Vs,max = 0) on the surface of the halogen along the R–X bond extension, then the σ-hole could be regarded as neutral, meaning there is no σ-hole.
Is a σ-hole understandable using molecular orbital theory? The answer is “yes”. The term “σ-hole” has originally referred to the electron-deficient outer lobe of a half-filled orbital of predominantly p character involved in forming a covalent bond [15,16]. For instance, the electronic configuration of Cl is [Ne] 3s2 3p5. When this atom replaces a hydrogen atom in CH4, the resulting compound would be H3C–Cl. In this, the Cl atom shares the pz orbital electron density with the C atom to form the C–Cl covalent bond. Although the –CH3 group is weakly electron-withdrawing, it can still pull towards it the electron density of the pz orbital of the Cl atom in H3C–Cl, leaving an electron-deficient region on the outermost extension of the C–Cl covalent bond. Since this deficient region is along the outer extension of the C–Cl covalent σ-bond, it could be termed a “σ-hole”. However, when the electron deficiency on the covalently bound atom in molecules is sufficiently large, a region of positive electrostatic potential results, which can interact attractively (non-covalently) with a negative site [14]. It was shown in several occasions that the strength of the inter- or intramolecular interaction does correlate with the magnitudes of the positive and negative electrostatic potentials of the σ-hole and the negative site (such as N in NH3) [13], although this is not always true. Positive σ-holes can also be found on covalently bonded Group IV-VI atoms and can interact electrostatically with a negative site.
Numerous reports have discussed σ-hole-centered halogen bonding; however, there has been disagreement about its underlying concept. As indicated above, some believe a σ-hole is always positive. For instance, Bauzá and coworkers view a σ-hole as a region of positive electrostatic potential in an unpopulated σ* orbital, which is thus capable of interacting with some electron dense region [17]. However, as delineated above, the nature of the σ-hole on X in R–X molecule can be positive, negative or absent, but its strength depends on the electron-withdrawing capacity of R, as well as the polarizing capability and electronegativity of X. Note that the character of the σ-hole can be s-, p-, or d-type depending on the nature of the valence orbital and of the atom involved in the formation of a covalent bond. For example, the σ-hole on the H atom in a H2 molecule comprises s-character, whereas that of H3C–X (X = Cl, Br, I) is of π-character. It has been recognized that larger the electron deficiency on the atom X in a molecule, the greater the strength of the σ-hole on it, and hence the greater its ability to form a non-covalent interaction with a negative site. For instance, the electron deficiency on atom X in the halobenzenes, F5C6X, is in the order Cl > Br > I; hence the strength of the positive σ-hole on X is in the order σπ (Cl) < σπ (Br) < σπ (I), in inverse order to the polarizability of X. This ordering in the strength of the σ-hole might explain why F5C6I compared to F5C6Br and F5C6Cl forms relatively stronger non-covalent bond with a negative site. However, as indicated already above, this is not always the case, since the surrounding species, as well as the deviation of the location of the σ-hole from the covalent bond axis, impacts the strength of the σ-hole interaction with the negative site. Further details can be gleaned from a recent study of Politzer and coworkers [18].
We note that Kawai and coworkers [19] advance several ideas on fluorine-centered in-plane F···F type-I and type-II non-covalent bonding formed by 1,2-bis[2,3,5,6-tetrafluoro-4-[(2,3,4,5,6-pentafluoro-phenyl)ethynyl]phenyl]ethyne (BPEPE-F18); this was observed using high resolution atomic force microscopy. The study has rapidly attracted considerable attention because it displayed attraction between negative sites centered on the axial and equatorial sites on F, leading to unusual bonding topologies that might be useful for the design of ordered supramolecular architectures on a metal surface. Interactions of this type, in fact, are not just limited to fluorine atoms in molecules, but are also exhibited by other halogens [20,21]. While these authors claimed they were the first to show the occurrence of this kind of non-covalent bonding between fluorinated aromatics, which they called halogen bonding, these interactions have in fact been known since the 1970s (the C6F6 crystal (Cambridge Structure Database (CSD) ref. code: HFBENZ11), for example) but were not fully appreciated. According to these authors, fluorine, because of its high electronegativity and low polarizability, usually has no σ-hole. The manifestation of a σ-hole on X in R–X is strongly affected by the electron attracting power or R; so, for instance, the cyano moiety in FCN and the oxygen in hypofluorite can induce a σ-hole. However, if the electron extraction is not large enough, F has an intrinsic negative electrostatic potential. Simple fluoro-substituted hydrocarbons, such as C6F6 and CF4, are characteristic of this. The halogen bond in such molecules is rarely seen in analyses of crystal structure databases and the stronger C–F···π interaction generally dominates. Therefore, analyses of bulk crystal structures do not usually reveal the F···F contact. Since, however, the freedom of molecules on a surface is restricted, the in-plane intermolecular interaction at the F···F contact can be examined.
Several believe that the F···F contacts found in many crystals are a consequence of close packing rather than intermolecular forces [22,23,24,25,26,27]. Others claim that this view is incorrect as interactions of this and similar type involving the fluorine atom can be stable even in the gas phase, and that the C–F···F–C bonding interaction formed between the negative sites is not a consequence of solid-state and surface effects [10]. It is rather the result of the nature of fluorinated aromatic compounds since they mimic the observations in the solid state and are driven by the combined effects of polarization and dispersion. To provide an example, Baker et al. [28] have examined the solid-state structures of three compounds that contain a perfluorinated chain, viz., CF3(CF2)5CH2CH(CH3)CO2H, CF3(CF2)5(CH2)4(CF2)5CF3 and (CF3(CF2)5CH2CH2)3P=O. They have identified several C–F···F–C and C–F···H–C interactions in these systems, in which the intermolecular distances were closer than the sum of the van der Waals radii of the two fluorine atoms. They then undertook a comprehensive computational chemistry investigation using Quantum Theory of Atoms in Molecules (QTAIM) [29], and confirmed that the specific C–F···F–C interactions they identified are certainly not due simply to crystal packing.
Kawai et al. [19] have claimed that fully fluoro-substituted aromatic molecules … are generally believed not to form halogen bonds due to the absence of a σ-hole. To us, this view is perversely counterintuitive and refers to the traditional understanding of the reactivity of fluorine in molecules. The notion is in sharp contrast with many recent reports (for example [10,11,30,31,32,33,34,35,36]), including some from the originators of the term ‘σ-hole’ [15,37], in which F in a variety of fluorinated hydrocarbons does indeed display a σ-hole. We have recently discussed the positive and negative nature of the σ-hole on fluorine in several molecules, and their propensity to form non-covalent interactions of diverse strength, although most fall into the weak bonding regime (<4 kcal mol−1) [16,38].
In a similar manner to Kawai et al. [19] and Khavasi et al. [22] have claimed that fluorine atoms in fluorinated metal complexes can be involved in different and non-predictable contacts as a result of its high electronegativity and low polarizability, thereby the fluorine atom usually has no σ-hole. Thus, it is expected that fluorine, as the most electron rich and least polarizable halogen, will behave as a nucleophile and act as an XB acceptor. They have stated that the nature of interactions involving the fluorine atom is still being debated within the scientific community and remains obscure. In a similar vein, Ibrahim asserted that “A fair amount is known about the halogen bond. Its bond strength is similar to that of the hydrogen bond, in the range 1–40 kcal mol−1, even larger. Its strength increases in the order chlorine < bromine < iodine. Fluorine does not form this type of bond, because it lacks a σ-hole” [39]. Wilcken and coworkers [33] computed the electrostatic potential on the simplest halobenzenes using MP2/TZVPP. From their analysis, they observed that the nature of fluorine in fluorobenzene does not follow the same trend as the halogen derivatives in other halobenzenes. It was then attributed to the considerable electronegativity of fluorine, which caused no positively charged area on it and therefore no interaction potential of it with nucleophiles. In the other halobenzenes, on the other hand, the size of the σ-hole increased with halogen size from chlorine to iodine, in agreement with the observations of many others.
We note further that interest in the understanding of hydrogen-bonding and other intermolecular interactions of C6F6 with different species has been the subject of many previous studies. Danten and coworkers studied non-covalent bonding interaction of C6F6 with H2O [40]. They reported a binding energy of about −2 kcal mol−1 and a geometry such that O of H2O was above the C6F6 molecule, with both H atoms pointing away from the ring, and with the water C2 axis collinear with the main symmetry axis of the aromatic compound. Similarly, Suzuki et al. [41] examined several complexes of C6F6 and C6H6 in which a slipped-parallel complex (Cs point group) has the most negative interaction energy (−5.38 kcal mol−1); this contrasts with a sandwich compound (C6v point group, interaction energy = −5.07 kcal mol−1) and two T-shaped (C2v) complexes (interaction energy = −1.74 and −0.88 kcal mol−1). Gung and Amicangelo [42] explored parallel displaced and sandwich dimer configurations of C6F6 with substituted-C6H6 (F in C6F6 as hydrogen bond acceptor and a π-hole donor) using ab initio molecular orbital methods to reveal how substituents in C6H6 influence the stability of various interactions examined. Two minimum energy configurations were detected, one with the substituent group away from and the other with the substituent group on top of the π-face of C6F6. Higher binding energies were predicted for dimers with the substituent on the π-face. All sandwich dimers were found to be saddle points on the potential energy surfaces. A parallel displaced minimum energy configuration was also predicted for the parent complex, C6F6-C6H6. A theoretical study of the possible interaction of the π-cloud of C6F6 with several small electron donor molecules (HF, HLi, CH2, NCH, and CNH), as well as many others, has been reported [43]. Similar studies, including anionic complexes of C6F6, have also appeared elsewhere [44,45,46,47,48], with the MP2 level binding energy for the C6F6···X− (X = F, Cl, Br) anionic complexes varying between −12.19 and −18.63 kcal mol−1 [49].
In two of our recent studies we have shown that the fluorine in perfluorobenzene (C6F6) should not be used as an exemplar of a fluorohydrocarbon in which the F carries no σ-hole. As will be discussed in the Results and Discussion section below, it does indeed have a σ-hole on the C–F bond extensions, quantified by the sign and magnitude of Vs,max. Its invisibility on the 0.0010 a.u. isodensity mapped electrostatic surface is because the lone-pairs that surround the equilateral portions dominate. We have also demonstrated the ability of the negative σ-hole on F in C6F6 to sustain favorable non-covalent interactions with negative sites, such as the F atom in another same molecule of C6F6; with the O atom in H2O and H2CO; with the F atom in HF and H3CF; with the N atom in NH3 and in fully fluorinated pyridine (C5F5N), and in fully fluoridated pyrazine, pyrimidine and pyridazine (C4F4N2). The uncorrected binding energies (varying between −0.45 and −2.56 kJ mol−1 with CCSD(T)/6-311G**//M06-2X/6-311++G(d,p)) and intermolecular contact distances (varying between 2.988 and 3.559 Å with M06-2X/6-311++G(d,p)) calculated for these dimers were close to what might be expected for weakly bound dimers (for example, dimers of alkanes and polyhedranes that involve C–H···H–C dihydrogen bond contacts have dissociation energies in the 0.52–12.38 kJ mol−1 range) [50].
Given the widespread importance of fluorine in diverse areas of chemistry, biology, materials science and crystal engineering, as well as its emerging importance in reactivity chemistry suggested by various studies referred to above, we have considered herein a series of six fluorinated benzene derivatives, H5C6F, H4C6F2, H3C6F3, H2C6F4, HC6F5, and C6F6, which are the six lightest and simplest 12-membered halogen-substituted aromatic compounds with a six-membered carbon ring. The principal aim of this study was to investigate systematically the extent to which the local negative potential on the axial and equilateral sites of F, respectively, along and around the C–F bond extensions increases or decreases as the number of F atoms on the peripheral aromatic core increases. From chemical intuition, one might anticipate that as the number of the F atoms around the peripheral sites of fluorine-substituted aromatics in increases, the axial portion on F in C–F in the resulting species becomes increasingly more positive (or less negative). Our fundamental interest towards this end was to see whether this intuitive guess is correct to some extent, and if this is so, then how effectively F could form an attractive interaction with the negative site near it. Given that the dimer systems examined comprise several halogen atoms, it is not possible for us to perform reasonably high-level calculations. We thus have employed the standard ab initio second-order Møller-Plesset perturbation theory (MP2) in combination with the molecular electrostatic surface potential (MESP) approach [51] to address these questions above.
Despite the negative potentials on F in these fluorine-substituted aromatic compounds, and in contrast to many previous thought-provoking suggestions, we show that both the axial and equatorial sites on F in the latter five fluoro-substituted benzene derivatives mentioned above can attract the entirely negative F atom(s) in another molecule of the same species, forming a variety of binary complexes. We then assess the binding strength of the intermolecular interactions formed between the entirely negative fluorine atoms in the molecules to demonstrate the extent of gas phase stabilities. We contemplate whether such interactions could be ascribed as the effect of crystal packing, and analogous to those found in the study of Kawai et al. [19], should be termed “halogen bonding”, or should these be given a different name, for ease of identification? It may be appreciated that other modes of intermolecular interaction between the monomers examined in this study are possible, but we have not considered them as they have been thoroughly studied by others; the strengths of such interactions (viz. π···π slipped-parallel interaction) are expected to be significantly larger than those considered here. Although the dependence between the various energy terms responsible for an intermolecular interaction is not exactly separable, Tognetti and coworkers have demonstrated that the concomitant use of various decomposition schemes affords a real understanding of the chemistry [52]. We have thereby performed an energy decomposing analysis using Symmetry Adapted Perturbation Theory (SAPT) [53] to shed light on the origin of attraction between the negative sites, as well as that on the directional nature of the F···F interactions investigated. The preliminary QTAIM and RDG (Reduced Density Gradient) non-covalent interaction (NCI) [54]) signatures are examined further to demonstrate whether these can be useful to discuss or speculate upon chemical bonding in the dimers studied, since some have doubted the usefulness of the signatures of the former approach. Finally, we presented the occurrences of relevant interactions in some experimentally reported crystals documented in the literature.
2. Computational Details
Because dispersion is an important aspect of intermolecular interactions, especially for weakly bound systems [55,56,57,58,59], the binary complexes of C6H4F2, C6H3F3, C6H2F4, C6HF5 and C6F6 and some of their mixed analogues were geometry optimized with second-order Møller-Plesset perturbation theory (MP2), all in conjunction with Dunning’s type correlation-consistent cc-pVTZ basis set. The stabilization energy for each complex was estimated using a supermolecular procedure. This is given by Equation (1), where E refers to the total electronic energy of the individual species involved.
ΔE (complex) = E(complex) − E(monomer1) − E(monomer2)
The Basis Set Superposition Error (BSSE) energy was determined using the counterpoise procedure of Boys and Bernardi [60] using Equation (2), where E(BSSE) is the BSSE corrected energy. All these calculations were carried out using Gaussian 09 [61].
ΔE(BSSE) = ΔE(Complex) + E(BSSE)
The interaction energy for each complex was decomposed using SAPT [62,63,64], as implemented in the PSI4 suite of programs [65]. QTAIM molecular graphs and the topological properties of the charge density (vide infra) and RDG-NCI 2D and 3D plots were evaluated with MP2 energy-minimized geometries using AIMAll [66] and Multiwfn software [67], respectively.
Without any specific bias, the geometries of H5C6F, H4C6F2, H3C6F3, H2C6F4, HC6F5, and C6F6 monomers were also energy-minimized with the Perdew–Burke–Ernzerhof (PBE) [68] density functional, PBE/6-311++G(2d,2p). For reasons discussed in earlier studies [69,70,71], a more economical Gaussian basis set of triple-ς quality was chosen for the exploration of MESPs. Since the nature of the MESP is not severely dependent on electron-electron correlation, and PBE adequately accounts for the electrostatics, this functional and the chosen basis set are presumably sufficient to describe the MESP of any molecular species examined.
The 0.0010 a.u. isodensity envelope mapped potential on the electrostatic surfaces of molecules is generally labeled as VS(r). This envelope has often been suggested to be appropriate for encompassing 96% of molecular electronic densities [12,13,14,15,37,72,73,74,75], although Bader et al. [76] have suggested the use of either 0.0010 or 0.0020 a.u. isodensity envelopes since the choice of the isodensity envelope is dependent on the nature of the atomic domains constituting the molecule. Moreover, while some have shown that the 6-31G* and 6-31G** minimal basis sets give reliable predictions of electrostatic potentials [12,13,72,73,74], others have argued that both the magnitude and sign of electrostatic potential are basis set dependent [35,77]. Thus, an appropriate basis set must be used to avoid an incorrect interpretation of the nature of surface reactivity inferred from the sign of the maxima and minima (Vs,min and Vs,max, respectively) of electrostatic potential, especially when its magnitude is close to zero. This was one of the reasons why we opted for a reasonably moderate basis set of triple-ς Gaussian quality, 6-311++G(2d,2p), for the evaluation of the extrema of MESP.
3. Results and Discussion
The 0.0010 a.u. mapped electrostatic potentials on the surfaces of the five fluoro-substituted monomers considered in this study are shown in Figure 1. In Figure 1a, the σ-hole on F along the C–F bond extension in C6H5F is very negative, with Vs,max = −15.4 kcal mol−1. The equilateral sites around F, which are dominated by electron lone-pairs, are yet more negative, with Vs,min = −17.1 kcal mol−1. This difference of electrostatic potential between the axial and equatorial sites leads to an anisotropy in distribution of the fluorine’s charge density profile.
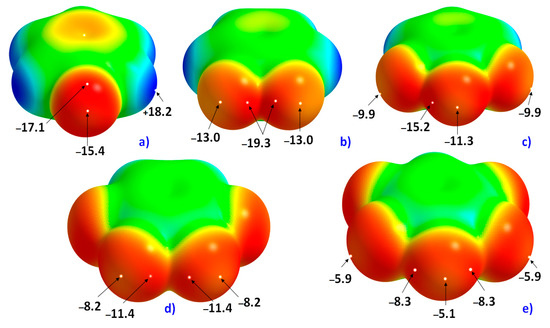
Figure 1.
PBE/6-311++G(2d,2p) level 0.001 a.u. isodensity mapped molecular electrostatic surface potential (MESP) of some partially and fully fluorinated aromatic compounds: (a) C6H5F, (b) H4C6F2, (c) H3C6F3, (d) H2C6F4 and (e) HC6F5. The maximum and minimum (Vs,max and Vs,min (in kcal mol−1), respectively) of MESP are shown on selected fluorine atoms, demonstrating anisotropy in the charge density. For clarity, yellow dots, representing Vs,max, are shown only for a few cases.
As the number of F atoms in C6H6 increases (through H atom replacement), the strength of the σ-hole becomes increasingly less negative (or more positive). For instance, the Vs,max associated with the fluorine’s σ-hole (Figure 1) in H4C6F2, H3C6F3, H2C6F4 and HC6F5 are −13.0, −11.3, −8.2 and −5.1 kcal mol−1, respectively. The least negative of σ-holes on F among all the fluoro-substituted monomers examined is found for C6F6, with Vs,min = −5.8 kcal mol−1 and Vs,max = −3.0 kcal mol−1 (not shown).
As noted above, and in all cases, the fluorine’s electrostatic potential, both along the axial site and around the equatorial sites, is negative, although the lateral sites compared to the corresponding axial ones are more negative. These show that the F atom in all six fluorine-substituted monomers is entirely negative. This result is consistent with the computed QTAIM atomic charges (an average property) conferred on each F atom in these fluorinated molecules that are all negative. This can be inferred from Figure 2, in which each fluorine carries a negative charge varying between −0.63 and −0.66 e. As found with the magnitude of the electrostatic potential, the magnitude of the atomic charge on the fluorine also decreases as one passes from H4C6F2 to H3C6F3 to H2C6F4 to HC6F5 to C6F6, meaning the fluorine atoms becomes increasingly more positive along the same direction. In this sense, there is virtually no qualitative difference between the nature of overall electrostatic potential and atomic charge when either of them is used to infer the nature of reactivity of the F atom in the monomers examined. This result is counter to what has sometimes been referred to as the “fallacy of atomic charges” [12,13,14,15,18]. While the use of MESP approach has been persistently demonstrated as robust, its ambiguity has also been shown in several different occasions, as in [78].
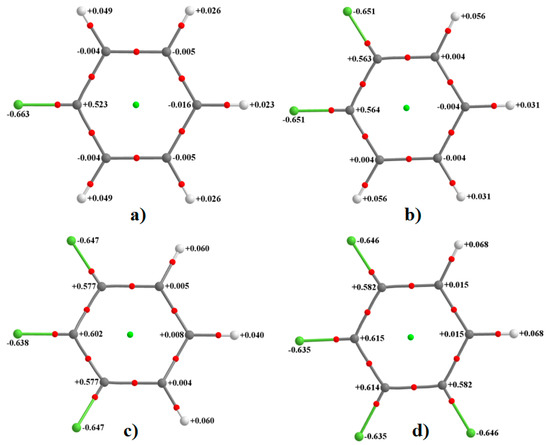
Figure 2.
MP2/cc-pVTZ QTAIM integrated charges (in e) on atoms in (a) H5C6F, (b) H4C6F2, (c) H3C6F3 and (d) H2C6F4.
In the monomer series shown in Figure 1, and including C6F6, the fluorine is found to be most negative in C6H5F. This signifies, in accord with the conceptual framework of σ-hole theory, which relies on the attraction between two sites of opposite electrostatic potential, that the negative sites on the fluorine in each of these fluoro-substituted monomers will not attract the negative site on another similar or different molecule(s). If they were to do so, they would form binary complexes, which would probably be in violation of Coulomb’s law of electrostatics. Interestingly, this was the case for (C6H5F)2. When this dimer was energy-minimized at an initial unconstrained C–F···F–C distance of approximately 3.0 Å, its geometry did not converge, and the two monomers moved significantly away from each other leading to an unbound system.
However, as the number of fluorine atoms on the peripheral aromatic core increased, the stable dimers (H4C6F2)2, (H3C6F3)2, (H2C6F4)2, (HC6F5)2, and (C6F6)2 were formed (Figure 3). The monomers in these were found to be linked with two types of C–F···F–C bonding interactions. The primary interaction is highly directional, with ∠F···F–C ≈ 175°. Its bonding topology is similar to that expected when a positive site on a covalently bound halogen attracts a negative site, as in H3N···Br–Br and H3N···FCF3, for example. The secondary interaction is non-directional, ∠F···F–C ≈ 121–124°; it is probably a consequence of the primary interaction and could be regarded as a forced interaction.
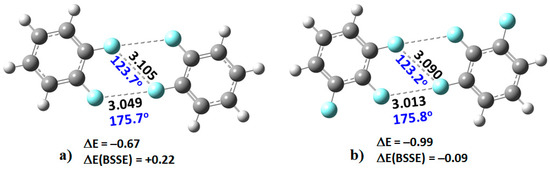
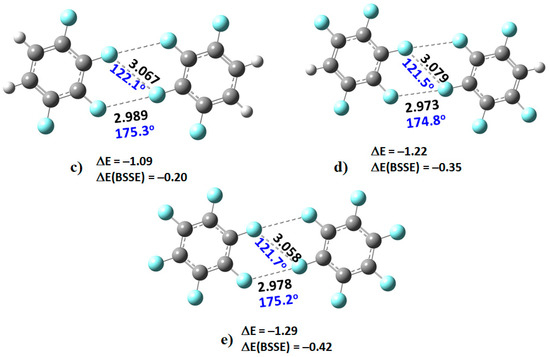
Figure 3.
MP2/cc-PVTZ level optimized geometries of the dimers of (a) C6H4F2; (b) C6H3F3; (c) C6H2F4; (d) C6HF5 and (e) C6F6. Bond lengths (Å), bond angles (deg), and uncorrected and basis set superposition corrected binding energies (ΔE and ΔE(BSSE) in kcal mol−1) are shown.
We re-emphasize that halogen bonding can broadly be viewed as the attraction between a positive site on the halogen atom in a molecule and a negative site on another species. This results in what has been referred to as type-II halogen bonding, especially when the angle of approach lies in the range 150–180°. Type-I halogen bonding occurs when the electron densities on two halogen atoms overlap within the same molecule, or between them on different molecules (not necessarily be of the same type) and where the angle of approach is between 120° and 150°. This latter interaction type is also sometimes called halogen···halogen bonding [79], and in this case, there is no such involvement between negative and positive regions localized on the interacting atoms. Nevertheless, since the angle for the formation of the directional C–F···F–C interactions in the fluoro-substituted complexes in Figure 3 is within the former range (i.e., 150–180°), they can be characterized as type-II fluorine-centered F···F bonding interactions. Similarly, since the F···F forced interactions in Figure 3 are homologous with X···X (X = Cl, Br, I) type-I halogen bonding observed in many crystals, as well as in many complexes reported theoretically using first-principles calculations, these dispersion-dominant interactions can be classed as type-I fluorine-centered F···F bonding interactions.
Illustrated in Figure 4 are four heteromolecular complexes. In all these, the number of F atoms in one molecule is less than that in the other. Such complexes offer the possibility of C–F···F–C interactions formed between entirely negative sites of unequal electrostatic potential. Both the type-I and type-II topologies of bonding interactions, and the intermolecular distances, found between F atoms in the complexes of Figure 4 are very similar to those of the complexes of Figure 3, showing similar intermolecular distance topologies in crystals are not artefacts of packing effects.
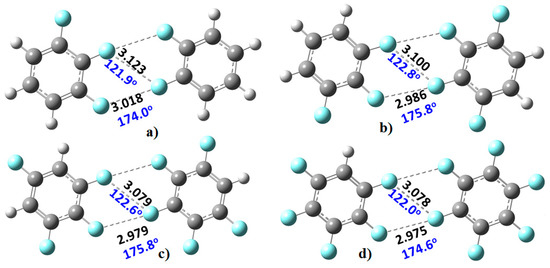
Figure 4.
MP2/cc-PVTZ level optimized geometries of (a) CH3F3···CH4F2; (b) CH3F3···CH2F4; (c) CH2F4···CHF5; (d) CHF5···CF6. Selected bond lengths (Å) and bond angles (deg) are displayed.
Are the monomers in the binary complexes illustrated in Figure 3 and Figure 4 bonded? In the solid state a “non-bonded bond” is often referred to as a “close contact” that indicates an attractive non-covalent interaction. A geometry-based criterion widely used to identify a non-covalent bond is that the distance between the interacting atoms should be less than (or approximately equal to) the sum of their van der Waals radii [73]. As such, the distance between the F atoms in the F···F directional interaction in (C6H4F2)2, at 3.049 Å, is shorter than the non-directional F···F interaction, 3.105 Å. A similar trend is observed in the remaining complexes shown in Figure 3. The shortest intermolecular distances were found in the (C6F6)2 dimer, with values of 2.978 and 3.058 Å. These distances are comparable with those found in the C6F6 crystal (CSD ref. code: HFBENZ11), where the F atoms in the C6F6 monomers are bonded to each other through type-I and/or type-II intermolecular topologies. Bauzá and Frontera [80], who have searched the CSD for C–F···F–C interaction in systems involving aromatic rings, found 497 hits that exhibit C–F···F–C contact distances that are less than the sum of their van der Waals radii of the two fluorine atoms, with the F···F–C angle varying between 170° and 180°; PXRD structures, disordered structures, ionic structures and structures with errors were excluded in the search. Generally, this specific intermolecular attribute results when one of the F atoms forming the F···F contact has a positive σ-hole.
In any case, in all the dimers examined the F···F distances are longer than twice the van der Waals radius of the fluorine atom (2.92 Å). While the International Union of Pure and Applied Chemistry (IUPAC) has suggested that the “intermolecular distance must be less than the sum of the van der Waals radii” as a valid characteristic to identify halogen bonding, this does not apply to the complexes studied in this work. A failure of this feature has been noted previously. Dance [75], Alvarez [81], and others [38,73] have pointed out that using the sum of van der Waals radii as a criterion is likely to overlook many non-covalent interactions, which may be several tenths of an Å greater than that sum. There are several other examples documented in the literature that recognize the van der Waals radii feature as a poorly defined criterion for assigning weak interactions, as in [82].
While the two equivalent F···F fluorine-centered bonding interactions in each complex in Figure 3 conform to a type-II halogen bond pattern, these cannot be designated as “halogen bonding”. It should be kept in mind that a halogen bonded pattern does not guarantee the halogen bond itself. Although this same bonding pattern, as we found in the binary complexes studied, was observed in the study of Kawai et al. [19], and to which they referred to as “halogen bonding”, these, in fact, cannot be regarded as examples of halogen bonding as it would violate the underlying definition recommended for use of the term.
Should the angular deviation from 180° associated with the two equivalent F···F fluorine-centered bonding interactions still allow one to categorize them as σ-hole centered non-covalent interactions? Some would answer yes [18,36,38]; others would say no [83,84]. As indicated in the Introduction, a σ-hole can be of s- or p-type, depending on the origin of orbitals involved. For instance, the σ-hole on an electropositive H atom (as in CH4), is an s-type, and is dispersed over the H atom. Since the H atom is entirely positive, it does form σ-hole centered non-covalent interactions with a negative site, and the angle of the interaction may or may not be precisely 180°. When the σ-hole is of p-type character (as in H3C–X (X = Cl, Br, I)), it generally, but not always, appears as a tiny region along the outer extension of the R–X bond axis, surrounded perpendicularly by a belt of negative potential. In many cases, a p-type σ-hole on atom X forms directional interactions with a negative site. However, there are numerous examples in which the p-type σ-hole on atom X deviates from the R–X bond axis. This is because the properties of the neighboring atoms (their electronegativity, polarizability, electron-withdrawing ability, etc.) tunes the precise location and strength of the σ-hole on X. Thus, the σ-hole may not be precisely along the R–X axis, which, when it interacts with a negative site, causes the development of a non-linear σ-hole centered non-covalent interaction between them, although in such a case the involvement of electron density accepting π orbitals cannot be completely ignored. While this has been pointed out several times in recent studies [18,36], claims still appear that the deviation from linearity is a failure of the σ-hole concept; this usually leads to a proposal of a new type of bonding scenario with some properties that are similar, but others that are different, to those expected of σ-hole interactions. For example, according to Wang et al. [85], the halogen geometries in CH3OCZCl+···X complexes (Z = H, F, Cl; X = F−, Cl−, Br−) cannot be explained by the σ-hole concept. They base their argument on the observation that the C–Cl+···X bond angles deviated from 180°.
Brinck and coworkers [86] have provided a similar view on the directionality of σ-hole interactions. However, according to them, surface maxima in the molecular electrostatic potential Vs,max along the lateral extensions of intramolecular bonds are known as σ-holes. They introduced a classification of σ-holes based on the electronic origin of the Vs,max. As such, if the Vs,max arises primarily because of electron deficiency in the valence s-orbitals of the compound, it is a σs-hole. Similarly, when the Vs,max originates from deficiencies in the p- or d-orbitals, these are σp- or σd-holes, respectively, arising from the diffuse (non-directional) or localized (directional) nature of the σ-hole. It was demonstrated further that the Vs,max of the hydrogen atom in HF arises upon the formation of the H–F covalent bond. The large difference in electronegativity between H and F leads to a strong polarization towards F in the bonding σ-orbital. On the other hand, the σ*-orbital is highly polarized towards the H atom. Because it is an unoccupied orbital, it will not compensate for the polarization of the σ-orbital. Consequently, the occupation of the σ-orbitals effectively results in a substantial electron deficiency on H. This is manifested by a large positive electrostatic potential at the H atom, which they refer to as a σs-hole since it originates from the hydrogen s-orbital occupation. Simultaneously a negative electrostatic potential is built up on F. Due to the spherical symmetry of the H 1s orbital, the corresponding σs-hole is diffused over the entire H end of the molecule. This explains the weak directionality of hydrogen bonded interactions, as well as the reason these can be categorized as a subclass of σ-hole interactions.
Nevertheless, it is quite evident from the results associated with the formation of the F···F interactions discussed above that the MESP model, which has often been used for the understanding of intermolecular interactions in diverse complex systems, is not appropriate to describe the intermolecular interactions in the fluorine-substituted complexes of Figure 3 and Figure 4. This is apparently due to the emergence of F···F directional bonding, which are developed due to the attraction between the fluorine atoms in two interacting monomers in these complexes, which is not due to the involvement of a site of positive potential in a fluorine atom in one monomer with the negative site on the fluorine in the other (as often observed for type-II halogen bonding). The observed interactions are entirely the consequence of attraction between sites of negative electrostatic potential. Since halogen bonding can also be viewed as an interaction between a region of charge depletion (a hole) on the halogen atom and a region of charge concentration (a lump) on the halogen in another molecule, the F···F directional bonding in the complexes of Figure 3 and Figure 4 might also be regarded as an example of a lump-hole interaction [87]. This is a valid argument because the concentration of charge density of the σ-hole region (a hole) associated with the surface of a fluorine atom in one monomer is smaller than that of the lateral interacting portion of the fluorine atom (a lump) in the partner molecule, causing the directionality of the interaction to be somewhat non-linear. The attribute can be appreciated by inspecting the sign and magnitude of the Vs,max and Vs,min values associated with the F atoms of the interacting monomers forming complexes. This result shows that the directional nature of the F···F interactions in Figure 3 and Figure 4 is not entirely due to electrostatics alone, as previously debated for halogen bonding [12,88,89,90]; it is rather a delicate balance between a variety of forces arising from electrostatics, exchange, polarization, charge transfer and dispersion (see below for further discussion).
In support of this argument, Duarte and coworkers [91] have discussed the nature of halogen···halogen contacts in R–X···X′–R complexes, where R = −H, −Cl, −F and X, X′ = Cl, Br, I; QTAIM, NBO (Nature Bond Orbital), and MESP tools were applied to characterize the X···X′ interactions. It was shown that the geometry and stability of these complexes is dominated by electrostatics, emanating from interactions involving the lump on X with the hole on X′ and vice-versa. This is reasonable because the Vs,min and Vs,max associated with the equatorial and axial portions of halogen atoms in the interacting monomers, for example in F–Br, were negative and positive, respectively, relative to each other. Since these interactions could be described as charge transfer hyperconjugations from the lone-pair electron density regions in X to the anti-bonding σ* orbital of the R–X′ and vice-versa, it was suggested that the electrostatic interactions and charge transfer play a substantial role in determining the optimal geometry of these complexes. Although this is analogous to what is observed for conventional halogen bonds, the dispersion term turns out to be the most important attractive term in the overall stabilization of the R–X···X′–R complexes.
The MESP model chemistry does not support the view that even regions of negative electrostatic potential on the F atoms of the monomers can attract to form complexes. Such negative potentials evaluated only on the atomic surfaces of the isolated monomers are alone insufficient to infer what is really happening between them when they are in an equilibrium dimeric configuration. This is evidently because the model is monomer biased, and it does not provide insight into the electron density profile existing in the intermolecular bonding region between them. Moreover, the model does not quantitatively provide any rigorous insight into which interacting monomer would polarize the other especially when both are identical. Also, because the F atoms attracting each other in the complexes shown in Figure 3 are equipotential, it is also difficult to quantitatively infer which F atom polarizes the other leading to the F···F interaction. To prove that the negative/positive σ–hole exists on the F atoms along the C–F bond extensions on the monomers in the complexes (at least in one of them), one might attempt to display the mapped potentials of the individual monomers in the complexes that form the complexes; but this is not possible because their surfaces have already overlapped upon complex formation (Figure 5). There appears to be no straightforward way that can be used to calculate the electrostatic potential on the surfaces of the fluorine atoms of the monomers in the complexes. Clearly, this as a limitation (or failure?) of the MESP model.
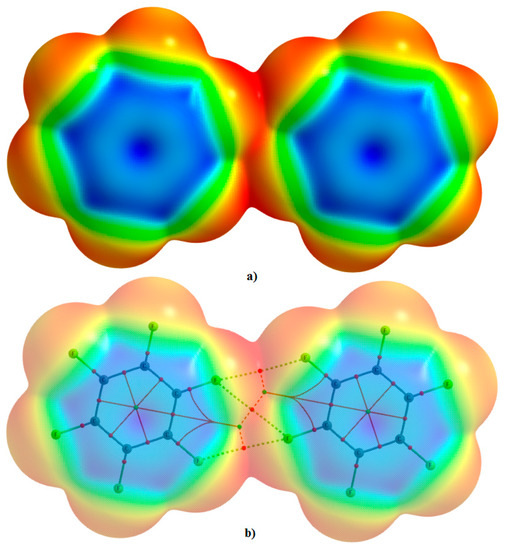
Figure 5.
MP2/cc-pVTZ level 0.0010 a.u. isodensity mapped electrostatic potential of (C6F6)2: (a) solid fill; (b) stippled fill overlaying the QTAIM molecular graph. Rcp-to-bcp connectivity is shown in (b), where Rcp refers ring critical point.
To provide further insight in support of the arguments above, Lekner considered the case of the interaction between two (positive) conducting spheres that have the same charge and size [92]. A positive electrostatic energy was evaluated for their interaction, leading to the conclusion that it is not clear which sphere will polarize the other, since, in practice, they continue to repel each other. This, however, was not the case when spheres of different sizes but carrying the same charge were examined; in this case, the larger sphere caused the development of negative surface charge on the smaller one, which then had the ability to polarize the larger sphere and attract the ensuing (relatively) positive site. The commentary of Ball provides some perspective on this [93].
A question now arises: is the interaction between similarly charged species fully explicable by Coulomb’s law of electrostatics? The answer is probably “no” since this law is based on point charges and it does not explicitly account for the significance of all-electron correlation effects. As we show below, the interaction between atomic sites of similar electrostatic potential centered on two negatively charged, or two positively charged, polarizable molecules cannot be precisely described by Coulomb’s law only because the interaction energy between them stems from several contributions, including charge-charge, charge-induced dipole, charge-quadrupole, induced dipole-induced dipole, quadrupole-quadrupole and other higher-order effects that account for the importance of dispersion. Several previous studies have shown that dispersion is the main component of the interaction energy that holds the monomers together in diverse binary complexes. In particular, it was shown that where the dispersion interactions can be strong enough, they are able to stabilize binary complexes despite the small (Coulombic) repulsion between the weakly positive (or weakly negative) sites [10,11,16,35].
Insight into the energetic origin of the C–F···F–C interactions in the complexes shown in Figure 3 can be provided by using an energy decomposition analysis (EDA) procedure. There are tens of such procedures available in literature [94], each with its own level of partitioning scheme and limitation. Opponents of the EDA approach have argued that the components are inseparable and that there is no appropriate and well-defined way to separate the interaction energy. They then argue that Coulomb type interaction is indifferent from polarization and that the intermolecular interaction between interacting species is happening largely due to polarization, and that dispersion is an integral part of Coulomb type electrostatic interaction. While this may be the case, we have employed the SAPT [62,63,64] approach to evaluate the decomposed interaction energies for all the binary complexes. In this procedure, the interaction energy is determined without computing the total energy of the monomers or dimer. The Hamiltonian (H) of a dimer is partitioned into energetic contributions from each monomer and the interaction is given by Equation (3), where FA and FB are the usual Fock operators of monomers A and B; WA and WB are their fluctuation potentials; and V is the interaction potential.
H = FA + WA + FB + WB + V
The Fock operators, FA and FB, are treated as the zeroth-order Hamiltonian and the interaction energy is evaluated through a perturbative expansion of V, WA and WB. Though first-order in V, electrostatic and exchange interactions are included; induction and dispersion first appear at second-order in V. Thus, SAPT decomposes the interaction energy into four physically meaningful components: electrostatic, exchange, induction, and dispersion terms. These can be evaluated using various levels of truncation that are available in the SAPT module of PSI4, viz. SAPT0, DFT-SAPT, SAPT2, SAPT2+, SAPT2+(3), and SAPT2+3; with and without CCD dispersion for the last three [53]. Basis sets of various size [Dunning cc-pVDZ through aug-cc-pV5Z wherever computationally tractable, including truncations of diffuse basis functions] can be used depending on the size of the chemical systems. Given that the size of the currently studied complexes is not small, the simplest (zeroth-order) truncation of SAPT, denoted by SAPT0, was invoked in this study. It is defined in Equation (4); a complete description of each of the SAPT energy terms can be found elsewhere [64]. The subscripts, elst, exch, ind, and disp denote electrostatic, exchange, induction, and dispersion, respectively, while the terms with subscript resp and subscript HF account for the orbital relaxation and higher-order induction effects, respectively.
EintSAPT0 = E(10)elst + E(10)exch + E(20)ind,resp + E(20)exch−ind,resp + E(20)disp + E(20)exch−disp + δ(2)HF
Since SAPT does not use spatial symmetry, all calculations were carried out in the C1 space group. The geometry of each dimer obtained with MP2/cc-pVTZ was kept fixed throughout the SAPT analysis calculations. The aug-cc-pVDZ basis set recommended for SAPT0 calculations was used.
The SAPT0 results are summarized in Table 1. The electrostatic term Eelst is calculated to be +1.129, +0.561, +0.406, and +0.135 kcal mol−1 for each set of F···F interactions in H4C6F2···F2C6H4, H3C6F3···F3C6H3, H2C6F4···F2C6H4, and HC6F5···F2C6H5, respectively. The electrostatic component, as well as the exchange repulsion component, is not only positive (i.e., repulsive) for these dimers, but also for the set of other dimers in Figure 4 that are heteromolecular in origin. The positive sign of the electrostatic component is in contrast with non-covalent complexes that are widely scattered in literature, in which the electrostatic component (generally negative) plays the role of attraction in complex formation. Positive Eelst values in the present case are unsurprising given that the interacting F atoms are very negative, which were gleaned from an analysis of their atomic charge and electrostatic potential (vide supra).

Table 1.
DFT-SAPT0 level energy decomposition analysis results of various energy components, obtained on the MP2/cc-pVTZ energy-minimized geometries of the fluoro-substituted benzene complexes. a
For the C6F6···F6C6 homomolecular dimer, however, the Eelst is found to be very weakly negative (Eelst = −0.019 kcal mol−1). Previously, this was reported to be repulsive since the electrostatic energy component was calculated to be weakly positive [10,19]. The difference between the previous and current results might be attributable to the levels of calculation and choice of basis set; the EDA analysis in this study is carried out using the MP2 optimized geometry of the dimer, whereas in previous studies this was undertaken on the DFT optimized geometries.
The induction (also called polarization) part of the SAPT0 interaction energy, Eind, however, is negative (attractive) for all complexes (Table 1), which is always the case regardless of the nature of the interacting partners. It is largest for the H4C6F2···F2C6H4 dimer that has strongly negative F atoms in the monomers, with Eind = −0.156 kcal mol−1. The negative sign of Eind is readily understood as a consequence of the monomers polarizing each other (at least partially) as they come close together. From the magnitudes of the sum of Eelst and Eind, it is quite apparent that electrostatics alone does not, and cannot, adequately describe what causes the negative sites on the F atoms in the monomers to attract each other to form complexes. This answers the question posed in the title of this paper, that is, whether the intermolecular interactions formed by similarly charged species can be fully appreciated by Coulomb’s law of electrostatics. This result also suggests that the alternative “minimal bonding analysis” emphasized by Politzer and coworkers [18], and Clark and coworkers [95] using the MESP model cannot explain the underlying chemical bonding attributes in the complexes examined in this work.
The variation in the exchange part of the interaction energy, Eexch, with values in the range 0.727–0.882 kcal mol−1, nearly parallels the variation in Eelst. The sum, Eelst + Eexch + Eind, is positive for all complexes. Hence the stability (and interaction energy) of none of the complexes can be explained at the Hartree-Fock level of theory, which does not account for dispersion. This shows that the common assumption that non-covalent interactions are always electrostatic in nature is clearly fallacious. Although some include the effects of polarization in the Coulombic term, others separate out polarization from charge transfer to provide a better understanding of the nature of halogen-centered non-covalent interactions. Should this mean that electrostatic and inductive effects are enough to describe non-covalent interactions? Certainly, the answer is no. Other contributions arising from exchange repulsion and dispersion play important roles in determining the equilibrium geometry of a chemical system. The same point has been made previously, especially in the context of halogen bonding [36,38,96,97,98,99,100].
The ubiquitous London dispersion part of the C–F···F–C interaction, which has an r−6 distance dependence, is quite appreciable, with values ranging from −1.408 to −1.560 kcal mol−1 (Table 1). The results show a stepwise increase in Edisp as the number of F atoms in the fluoro-substituted monomers increases. Interestingly, this increase seemingly correlates with the average decrease in the F···F intermolecular distances of separation in the dimer series on passing from (H4C6F2)2 to (C6F6)2. The result provides further evidence that even fully fluorinated systems can be considerably dispersive.
It should be noted that in earlier studies dispersion in fluorine-containing molecules was often underappreciated, probably because of the notion that F is very small; very electronegative; not polarizable; and is merely involved in halogen bonding. It was also shown to be non-dispersive. Underestimating the importance of dispersion probably arose from a lack of understanding of the chemical reactivity of fluorine in molecules since it does not always behave similarly as other halogen atoms and as fluorine-centered interactions are often viewed as non-predictable. The present results demonstrate that this view is not always correct since the F atom in molecules can be highly dispersive; this is predominantly determined by the nature of the substituents on the skeletal framework of the molecule.
Dispersion can feature as the principal component in determining the stability of the C–F···F–C interaction. The F atom can be as dispersive as observed in halogen bonding formed by other halogens in molecules. The present results clearly show that the dispersive nature of the F atom varies from molecule to molecule and should not be dismissed without consideration. As demonstrated above, the destabilization of the geometries of the complexes in Figure 3 arises mainly from the electrostatic and exchange components of the interaction energies; their stability is predominantly driven by dispersion, but the effect of polarization cannot be neglected even though it contributes to stability only marginally.
Our result is also counter to a previous study that has suggested that the electrostatic component for attractive intermolecular interactions formed between aromatic fluorine atoms in perfluoro-benzene and other electron donor moieties may not always be attractive [11]. The non-attractive nature was attributed to the absence of a σ-hole on the surface of the fluorine atom [9]. This is actually incorrect since, as already discussed above, and elsewhere [10,11,16,35], the σ-hole on the fluorine in substituted aromatic compounds is not always absent. It is present but can have a negative electrostatic potential; it should be remembered that a σ-hole cannot always be positive; it can be negative depending on how the sign of Vs,max along the C–X bond extensions is determined. When the σ-hole region on the F atom with a negative potential is in close proximity with an electron rich site on another molecular species, it generally (but not always, as discussed above) causes repulsion—as is evidenced by the repulsive nature of the electrostatic component (see Table 1 for values for most of the complexes of Figure 3 and Figure 4). The electrostatic repulsion energy does not lead, however, to any such assurance that σ-holes on F in aromatic molecules are absent.
It is also interesting to note further that in the study [9], the authors calculated a negative electrostatic potential for the fluorine atom along the extension of the C–F bond in six fluorine-substituted molecules, with values of Vs,max between −5 and −10 kcal mol−1. They suggested that this is the root cause of the inability of the F atom to make an attractive interaction with electron rich entities. However, the Vs,max on the F atom in these monomers in a set of hydrogen bonded complex geometries varied between −2 and −4 kcal mol−1. These were less negative than those found on the same atom on the six isolated monomers above, thus a relatively more attractive (or less repulsive) interaction with electron rich molecules was inferred. Clearly, the former observation cannot be generalized to all fluorine-substituted systems since this is counter to the results of the fluorine-substituted monomer systems examined in this study.
The SAPT interaction energies, EintSAPT0, although calculated with DFT, are in reasonable agreement with those estimated with the supermolecular procedure using MP2/cc-pVTZ. For instance, the uncorrected MP2/cc-pVTZ stabilization energies are calculated to be smallest (−0.67 kcal mol−1) for (C6H4F2)2, and the largest (−1.29 kcal mol−1) for (C6F6)2, similarly as found with SAPT0.
The trend both in ΔE and EintSAPT0 in the homomolecular dimer series follows the order (C6H4F2)2 < (C6H3F3)2 < C6H2F4)2 < (C6HF5)2 < (C6F6)2. These binary complexes are thus stable in the gas phase. Because the magnitude of the MP2 binding energies is all <1.5 kcal mol−1, the F···F intermolecular interactions in these complexes can be categorized as weak van der Waals type.
MP2 predicts the sign of the BSSE corrected stabilization energies ΔE(BSSE) for the first two complexes of Figure 3 to be positive, but weakly negative for the others. This shows that BSSE has a substantial effect on the uncorrected binding energy (even with an economical basis set). While the nature of the sign of the interaction energy predicted for H4C6F2···F2C6H4 with SAPT is comparable with that of MP2(BSSE), this is not so for the other dimer, H3FC6F2···F2C6FH3, probably because the BSSE appears to be spuriously large for the latter complex. Another possible reason could be that the SAPT procedure does not very accurately account for the dispersion part of the interaction energy, given there is a difference between the ΔE(BSSE) and EintSAPT0 values for each complex. There are also demonstrations that MP2 overestimates dispersion [101] since the interaction energy evaluated with this method makes use of the uncoupled Hartree-Fock dispersion energy that lacks the repulsive intramolecular correlation correction [102,103].
An anonymous reviewer suggested that it would be interesting to see whether a relatively larger basis set, aug-cc-pVTZ, that has an augmented d polarization function has any impact on the binding energy. This argument was based on the fact that the chemical systems examined are weakly bound and contain several halogen species, in which case, dispersion could be important. We continued performing similar calculations but only for some systems since combined energy-minimization and Hessian calculation for a given dimer system is very expensive. For instance, and depending on the number of the F atoms in the dimer, such calculations for a single system could take over 15–20 days’ computational time in a node of a PC cluster workstation (Xenon Intel) that comprises 32 cores, 256 GB RAM and unlimited storage. As expected, changing the basis size has affected the intermolecular geometries and interaction energies. However, this change is marginal against the results obtained with cc-pVTZ, and the various conclusions drawn with this latter basis set have only marginally affected. For instance, Table 2 summarizes the intermolecular distances, angles, and interaction energies for H4C6F2···F3C6FH3, H3C6F3···F4C6H2, H2C6F4···F5C6H and C6F6···F6C6 complexes. As can be seen from the data, the enhancement of the basis set size from cc-pVTZ to aug-cc-pVTZ has slightly decreased the F···F type-I (and sometimes type-II) distances and the F···F–C bond angles. These changes have caused negligible effect on the uncorrected interaction energies of the light weight dimers, although such energies for the heavier dimers that have five or six F atoms in the monomers are marginally affected, with ΔE increased by a value <0.2 kcal mol−1. In all cases, however, the effect of BSSE on ΔE is small, for which, the ΔE(BSSE) for the dimers are increased compared to those estimated with cc-pVTZ.

Table 2.
MP2/aug-cc-pVTZ geometrical and energetic properties of some fluoro-substituted benzene complexes. a
4. QTAIM and RDG Descriptions of Chemical Bonding
QTAIM is robust in its own way in describing chemical bonding in molecular complexes, as well as in crystals. It hinges on the zero-flux boundary condition (Equation (5), where n(rs) is the unit vector normal to the surface at rs for every point rs on the surface S(rs)).
▽ρ(rs)·n(rs) = 0,
According to Bader [104], an atom, as a constituent of some larger system, is itself an open system subject to fluxes in charge and momentum through its bounding surface. Several signatures that emanate from the theory have been suggested for the identification and subsequent characterization of chemical bonding. While there are many, two of its fundamental (minimal) signatures are (i) the presence of (3,−1) bond critical point (bcp), and (ii) the presence of bond path between bonded atomic basins; they are collectively useful in inferring the presence of bonding in chemical systems. In addition, the sign and magnitude of the Laplacian of the charge density (▽2ρb), and the total energy density (Hb), where Hb is the sum of the potential energy density (Vb) and the gradient kinetic energy density (Gb) at the bcp, provide additional information about the ionic and covalent (closed- and open-shell) nature of the interaction involved [105]. The localization and delocalization indices provide information about the extent of electronic density localization and covalent bond order, respectively. We focus here only on the first three attributes to infer, characterize and quantify each intermolecular interaction in the complexes of Figure 3 and Figure 4, and provide reasons to show why one should examine QTAIM’s fundamental signatures to infer chemical bonding.
The QTAIM molecular graphs of the homomolecular dimers of H4C6F2, H3C6F3, H2C6F4, and HC6F5 are illustrated in Figure 6, and that of C6F6 in Figure 7. Those for the heteromolecular dimers are illustrated in Figure 8. As can be seen from these, each F···F contact is accompanied by a single intermolecular bond path and a (3,−1) bcp between the fluorine atoms of the interacting monomers in each dimer configuration. There are three such bond paths in each complex; two of them are equivalent and lie along the outer extension of the C–F bond axes, confirming their directional nature. The remaining one appears between the lateral sides of these F atoms and is what we have referred to as the forced interaction, since it is the consequence of the two former interactions. The F···F bond path topologies revealed by QTAIM are fully consistent with what was inferred from the magnitudes of the equilibrium bond distances shown in Figure 3 and Figure 4. These, together with the rcp-to-bcp connectivity appearing in the intermolecular regions are consistent with that described by the overlapping MESP model for (C6F6)2, Figure 5, showing a further advantage in using QTAIM’s bond path topology.
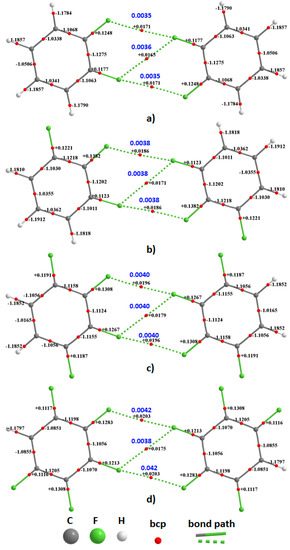
Figure 6.
MP2/cc-pVTZ QTAIM molecular graphs of (a) H4C6F2···F2C6H4; (b) H3C6F3···F3C6H3; (c) H2C6F4···F4C6H2; and (d) HC6F5···F5C6H. The charge density (ρb/a.u., blue) at selected F···F bcps and the Laplacian of the charge density (▽2ρb/a.u., black) at all bcps are shown. Ring critical points are not shown. Bcps: tiny red spheres; bond paths: solid and dotted lines in atom color.
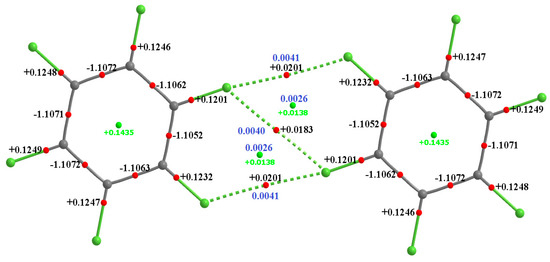
Figure 7.
MP2/cc-pVTZ level QTAIM molecular graph of the (C6F6)2 homomolecular dimer. The charge density (ρb/a.u., blue) at selected F···F bcps and rcps, and the Laplacian of the charge density (▽2ρb/a.u., black) at all bcps and rcps are shown. Bcps: tiny red spheres; rcps: tiny green spheres; bond paths: solid and dotted lines in atom color; solid and dotted lines represent the open- and closed-shell interactions, respectively.
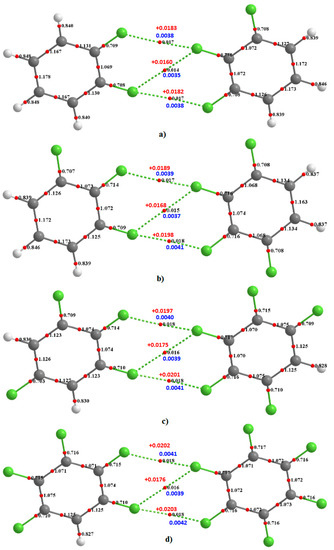
Figure 8.
MP2/cc-pVTZ level QTAIM molecular graph of some heteromolecular dimers: (a) H4C6F2···F3C6H3 (b) H3C6F3···F4C6H2 (c) H2C6F4···F5C6H and (d) HC6F5···F6C6. The charge density (ρb/a.u., blue), the Laplacian of the charge density (▽2ρb/a.u., red) at F···F bcps and the delocalization indices for each atom-atom pair (black) are shown. Bcps: tiny red spheres; bond paths: solid and dotted lines in atom color; solid and dotted lines represent the open- and closed-shell interactions, respectively. For simplicity, rcps are not shown.
There is no straightforward and convenient way that can assist to quantify the stabilization energy of each of the three individual F···F interactions in each dimer, although this could be done computationally using the so-called Interacting Quantum Atom (IQA) model of Pendás and coworkers[106,107] and employed by Tognetti et al. [52,108,109] to study halogen bonding; however, this is computationally very expensive for larger systems.
QTAIM does provide another means of quantifying individual F···F interactions through the magnitude of ρb at a bcp, a property which has been shown to correlate with the binding energy [110,111]. In any case, the ρb for each of the three F···F interactions are nearly equivalent (values for the forced interaction being marginally smaller), indicating that all the three are nearly competitive interactions. What has been summarized in Table 1 is the net binding energy for each dimer; this is collectively due to these three F···F interactions that can be individually characterized and quantified, demonstrating another advantage of QTAIM over the MESP model.
The mean F···F bond distance in the dimer decreases as the number of fluorine atoms on the monomeric aromatic core increases; this is primarily the result of attraction caused by an enhanced dispersion (but not polarization) effect between the interacting F atoms. While the magnitude of exchange repulsion increases in the dimer series with increasing number of F atoms (Table 1), the energy due to Coulombic interaction increasingly becomes more negative. Consistent with this, the mean of the predicted charge density, ρb, at the corresponding F···F bcps increases monotonically in the series (Figure 6, Figure 7 and Figure 8). This is broadly (but not exactly) consistent with the ordering noted for ΔE, ΔE(BSSE) and Eint given in Table 1. This result shows that the fundamental QTAIM signatures are useful in arriving at an understanding of intermolecular interactions.
The magnitude and sign of ▽2ρb provides information about the nature of bonding interactions [29,112]. In general, ▽2ρb > 0 is indicative of an ionic (electrostatic or closed-shell) interaction because it deals with the region in real space where there is significant depletion of charge density. On the other hand, ▽2ρb < 0 is indicative of a shared (open-shell) type of interaction and refers to the region in real space between atomic basins that features a concentration of charge density. The former and latter are generally found for non-covalent and covalent bonding interactions, respectively [29,112]. There are examples of covalent bonds with ▽2ρb > 0, but this occurs when the bond is sufficiently polar [113], such as the C–F bonds in C6F6.
From the sign and magnitude of ▽2ρb shown in Figure 6 and Figure 7, three distinct bonding features are evident in each of the molecular graphs. First, ▽2ρb is large and negative for all C–C and C–H bcps, as expected for these open-shell interactions. Second, ▽2ρb is small and positive at the C–F bcps, which signifies significant polarity in these covalent bonds; similar results have been discussed previously for highly polar covalent bonds in diverse molecules [38,113]. Third, ▽2ρb is very small and positive for F···F bcps, indicative of probable non-covalent interactions. Figure 9, for example, shows the 2D contour plot of the ▽2ρb for the pentafluorobenzene dimer. It shows various regions of charge density depletion (▽2ρb > 0) and concentration (▽2ρb < 0).
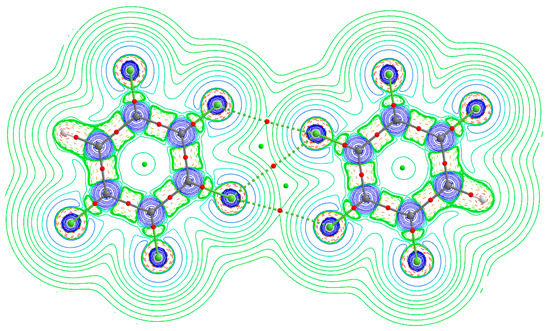
Figure 9.
MP2/cc-pVTZ level QTAIM molecular graph and the Laplacian of the charge density plot in 2D for the pentafluorobenzene dimer, HF3C6F2···F2C6F3H2; the latter is obtained in the plane defined by the three top F atoms involved in F···F bonded interactions. The green solid lines (green) and red negative lines (red) represent regions of charge depletion and concentrations, respectively. The bond and ring critical points (tiny spheres in red and green, respectively) are illustrated.
In addition to chemical bonds, each dimer features two types of ring. The six-membered rings, as expected, arise from the six carbon atoms of each planar aromatic system. Five-membered rings are a consequence of the F···F bcps and bond paths that are formed upon attraction between monomers. This attribute is illustrated in Figure 7 for (C6F6)2 and is present in all other dimers shown in Figure 6 and Figure 8. Each of these rings is characterized by a ring critical point (rcp), appearing close to the center of the ring. The magnitude of charge density, ρr, at rcps is smaller than the ρb of the F···F bcps for of each dimer. The ▽2ρr > 0 indicates significant depletion of charge density at the center of each ring, as expected; a similar pattern is found in each six-membered aromatic ring. It is known that the proximity of a rcp to a bcp is indicative of a weak ring structure. When both these critical points are in close vicinity, the ring structure may annihilate due to zero-point vibrational motion leading to the destabilization of the overall geometry of the system [114].
The appreciable separation between the rcp and the bcp in the five-membered rings of the dimers is evidence of reasonable stability of the intermolecular interactions in the structure. The delocalization indices evaluated within the framework of QTAIM, shown in Figure 8, for the heterodimeric complexes support the topological (QTAIM) rationalizations of F···F bonding interactions.
Shahbazian [115] has argued that equating (3,−1) critical points, derived from the topological analysis of the electron densities, to chemical bonds has triggered a great deal of confusion in recent years. According to him, part of this confusion stems from referring to the (3,−1) critical points as “bond” critical points. Computational studies conducted on molecular electron densities cast serious doubt on the supposed universal equivalence between chemical bonds and the (3,−1) critical points. It was instead suggested that the (3,−1) critical points should be referred to as “line” critical points to prevent further misinterpretation of the data emerging from QTAIM. There therefore may be circumstances where the disappearance of a critical point in the bonding region, which generally connects two bonded atomic basins through gradient paths, might not indicate the presence of a bonding interaction. The gradient paths terminate and appear at the (3,−1) bcp, thereby connecting the atomic basins together, and the gradient vector field could be described by lines following the steepest decent. When one refers to a (3,−1) critical point between two atomic basins, it actually refers to the critical point of charge density at which the charge density decreases in two perpendicular directions in space and increases in the third direction. This is thus a saddle point of charge density, which is a maximum in two directions in space and a minimum in the third.
In our view it is misleading to refer to a (3,−1) bond critical point as just a “line critical point”; this seems meaningless since one can draw lines between atoms arbitrarily to represent bonds between them and indicate a point on the line where the van der Waals radii of each atomic domains supposedly meet. This purely arbitrary line has no obvious connection with the underlying critical points of QTAIM, and that this, with no doubt, will create further misunderstanding of the underlying framework of the theory of atoms in molecules. Moreover, it is worth stressing that QTAIM does not provide any assurance that a (3,−1) critical point is equivalent to a chemical bond, nor a bond path. As Bader himself stressed [104], “This account takes to task papers that criticize the definition of a bond path as a criterion for the bonding between the atoms it links by mistakenly identifying it with a chemical bond”. As discussed above, in addition to the (3,−1) bcp, one should also examine the presence of a bond path between the electron exchange channels to consider the possible presence of a bonding interaction between the atomic basins, as this assists to infer the nature of bonding between the interacting atoms (such as straight, strained or curved or banana-shaped interactions). Analogous insight might be inferred from the results of the MESP model (but not always!), since this model does not provide any physically measurable quantity that can be used to quantify an intermolecular interaction between bonded atoms (as it relies only on the reactivity of isolated monomers, and researchers use this to extrapolate and provide their unified arguments about the presence or absence of such an attraction between these atoms that are bonded with each other).
As said, QTAIM does not encourage one to call either a (3,−1) bcp or a bond path a chemical bond; it only suggests that the presence of these two attributes collectively might be a useful indicator to hypothesize the presence of a bonding interaction between atomic basins [104]. Tognettii and coworkers have already provided several instances of the circumstances under which bond paths appear and have shown how the competition between primary and secondary exchange channels assists in the appearance and disappearance of both a (3,−1) bcp and bond path between atomic basins that constitute the entire molecular graph of a chemical system. Any property of a chemical system (e.g., dipole moment) is determined by the nature of its atomic constituents, and the way they are bonded with each other, which determines the geometry of the system at equilibrium. The evaluation of the property is based not only of geometry but also on symmetry. It is not unexpected that the bcp and associated bond paths would be structure dependent, and it is misleading to make conclusions on the usefulness or otherwise of the signatures of QTAIM to garner information on chemical bonding in molecular, supramolecular and solid-state systems after examining only some examples [95].
It must be appreciated that there is no unified theory at the moment that can successfully and completely explain the detailed nature of chemical bonding between interacting atoms and the nature of interacting sites. All available theories have their limitations and instances are likely to be found where they fail. Hence “polarization” should not be regarded as the only term needed to understand the chemistry of non-covalent interactions. It is just an aid in providing partial insight into what is likely to be happening in an intermolecular interaction. What has not been fully understood previously has sometimes just been misleadingly attributed to polarization. One such example is the nature of the σ-hole on the Cl atom along the C–Cl bond extension in CH3Cl. Some have suggested this has no σ-hole [15], others say it is negative [13], yet others that is positive [77,116]. The concept of polarization has been introduced to demonstrate that if a test charge is placed at a certain distance from the Cl atom, this would induce a positive σ-hole on it [117]; it will then have the ability to attract a negative site to form complexes. While a positive test charge might polarize the Cl atom, it certainly does not convert the near neutral/negative σ-hole into a positive one; moreover, the presence of the test charge cannot be removed when evaluating the nature of the electrostatic potential. Nonetheless, the positive nature of the σ-hole on the Cl atom along the C–Cl bond extension is inherent, which will be revealed if and only if an appropriate theoretical method, together with an appropriate isodensity surface for mapping of potential, is invoked [77]. This demonstrates that both the sign and magnitude of electrostatic potential are basis set dependent, which can be minimal or significant depending on the chemical system under investigation (i.e., system-by-system basis) [35,77].
As an example on the failure of the aforementioned QTAIM signatures, we cite the study of Lane et al. [118]. These authors have shown that there is no clear distinction between the nature of the intramolecular hydrogen bonding interactions in 1,2-ethanediol (ED), 1,3-propanediol (PD), and 1,4-butanediol (BD), despite the absence of a bcp in ED. This conclusion was arrived at based on the fact that there were no qualitative differences between the density characteristics of the O···H bonding region in ED compared to those in PD and BD. The geometry of ED was favorable for O···H intramolecular hydrogen-bonding because the observed vibrational spectra [119,120] were consistent with this. The absence of a bcp in ED should thus not be viewed as evidence against hydrogen-bonding but rather more simply as the absence of a piece of QTAIM characteristic useful for its identification. The absence of the QTAIM’s intermolecular bonding topologies in ED could be rationalized as due to the annihilation of the (3,−1) bcp with the (3,+1) rcp, causing the disappearance of the intramolecular interaction between H and O atomic basin in ED. While these specific QTAIM criteria for hydrogen-bonding might be stringent, it was suggested that the RDG-based NCI index analysis tool can present a more global description of bonding than analysis of QTAIM critical points alone, broadening the scope of characterization of non-covalent interactions. The RDG identification of O···H bonding in ED was not very surprising since this approach accounts for the exploration of the gradient of charge density around the vicinity of the bond critical point where ▽ρ(rs)·n(rs) = 0.
We have also used the RDG-NCI index approach to examine whether the C–F···F–C bonding information signaled by QTAIM for the various fluorinated complexes examined are real. The results are shown in Figure 10 for H3C6F3···F4C6H2. As can be seen, one does indeed observe various RDG domains between the bonded F atom basins that were indicated by QTAIM signatures. Each of the two equivalent C–F···F–C type-II interactions is characterized by a dumbbell-shaped RDG isosurface in 3D, whereas the C–F···F–C type-I intermolecular topology is described by an irregular isosurface between them (see Figure 10 (right)). These two isosurfaces correspond to the narrow (green) spike in the sign(λ2) < 0 region of the ρ × sign(λ2) vs. RDG plot in 2D (see Figure 10 (left)), where λ2 is the second eigenvalue of the Hessian of the charge density matrix. The weak spike (greenish light brown) appearing in the sign(λ2) > 0 region refers to the presence of a van der Waals domain between the monomers, which is a characteristic of the light brownish isosurface and the 5-membered rings. The broad spike (red) in the sign(λ2) > 0 region corresponds to an RDG domain that is appearing at the center of the six-membered C6F6 rings and is corresponding to the red isosurface stands out at the center of the C6 rings, indicative of (steric) repulsion. Very similar results were obtained for the all other complexes examined. Figure 11, for instance, illustrates RDG-NCI index plots in 3D for some of these complexes.
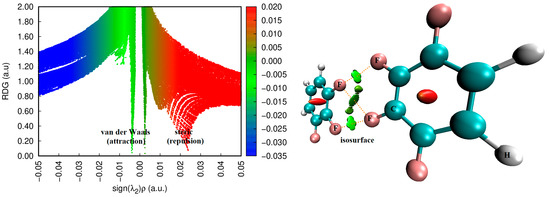
Figure 10.
MP2/cc-pVTZ level ρ × sign(λ2) vs. RDG plot (left) and RDG-NCI index isosurface plot (0.50 a.u.) (right) for H3C6F3···F4C6H2. Isosurface 3D plot is generated using VMD [121] software.
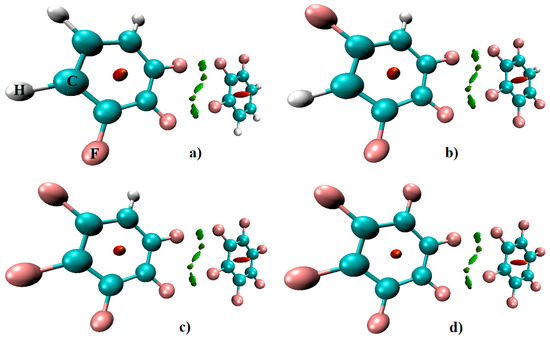
Figure 11.
MP2/cc-pVTZ level RDG-NCI index isosurface plot (0.50 a.u.) for (a) H3C6F3···F3C6H3; (b) H2C6F4···F5C6H; (c) HC6F5···F6C6 and (d) C6F6···F6C6. Atom labeling is shown in (a).
5. Evidence of F···F Interactions in Molecules and Crystals
Matta and coworkers [122] have previously examined closed-shell F···F bonding interactions in several fluoro-substituted aromatic compounds on the basis of electron density. This is analogous to the topology of F···F type-I intermolecular interactions discussed in this study, but the angle of interaction is <120° since the interacting F atoms were confined in a monomer. A bond path linking two saturated F atoms was shown to be ubiquitous in crowded difluorinated aromatic compounds, with the internuclear distances in the range 2.3–2.8 Å. They further demonstrated that the observed F···F bonding displays the hallmarks of a closed-shell weak interaction. The presence of a bond path between the two F atoms imparted as much as 14 kcal mol−1 of local stabilization to the molecule in which it exists. This is a stabilization that can be offset, or indeed completely overwhelmed, by destabilization in other regions in the molecule.
There are several other recent studies that advocate the importance of F···F bonding in the stability of the equilibrium geometries of a variety of complexes [28]. For instance, Sanna et al. [123] have reported the X-ray diffraction characterization of a pair of CCl3F (CFC-11) molecules trapped in a molecular sponge. The encapsulated molecules were found arranged in two crystallographically independent relative orientations inside the channels. An uncommon type of C(sp3)–F···F–C(sp3) interaction between the CCl3F molecules was observed, together with halogen (X)···π interactions, to show these interactions are indeed real.
Given that fluorine substitution in π-conjugated systems has been a feature of many recent reports, primarily aimed towards the development of materials with enhanced optical and optoelectronic behavior, Calvo-Castro and colleagues [124] have examined the effect of fluorine substitution on the intermolecular interactions, energetics, and packing behavior of a series of π-conjugated N-benzyl substituted diketopyrrolopyrroles. Using the M06-2X density functional at the 6-311G(d) level, they have shown that that substitution of hydrogen by fluorine can also lead to dramatic changes in solid-state packing behavior because of this kind of weak interaction as above, leading to the emergence of significant fluorine-induced stabilization. Such fluorine-based intermolecular interactions were extracted from the single crystal nearest neighbor dimer pairs.
Khavasi and Rahimi [125] have also demonstrated the importance of F···F interactions in crystals. They noted that in coordination compounds fluorinated ligands exercise influence not only on the first coordination sphere but also on the supramolecular architecture and overall construction of the compounds [126]. It was shown that the two-dimensional polymeric complexes of N-(fluorinatedphenyl)-2-pyrazinecarboxamides ligands, carrying three and four fluorine atoms on phenyl rings, were stabilized by F···F type-II synthons between adjacent rings, in addition to participating in F···π interactions. Their Hirshfeld surface analysis has confirmed the importance of these interactions in crystal stability.
Li et al. [127] have examined a series of N-arylimide molecular systems that were stabilized by fluorine–aromatic (F···π) interactions. Similarly, Baker and coworkers [28], as well as others [128,129,130], have provided evidence of the importance of fluorine substituents that gave rise to increasingly more stabilizing interactions with more electron-deficient aromatic surfaces. They concluded that the attractive F···π interaction is electrostatically driven and is stronger than other halogen–π interactions.
There are thousands of structures of fluorine-substituted compounds deposited in the CSD. Figure 12 shows an example of the unit-cell of a fluorine reinforced system required for the development of the 4,4′-bis(nonafluorobutyl)-2,2′-bipyridine crystal [131], wherein F···F intermolecular distances vary between 2.9 and 3.4 Å. Figure 13 depicts the unit-cells of the solid-state structures of 8-(nonafluorobutyl)-3-(pyrimidin-2-yl)-3,4-dihydro-2H,6H-pyrimido[2,1-b][1,3,5]thiadiazin-6-one (left) and trans-4,4′-azobipyridine 1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8-hexadecafluoro-1,8-diiodooctane (right) crystals. The latter molecule and its derivatives have been identified as a halogen bond donor in many co-crystals. While the main driving force in such crystals were N···I type-II halogen bonding, the F···F intermolecular distances between the 1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8-hexadecafluoro-1,8-diiodooctane molecules varied between 2.9 and 3.4 Å. This means that they contribute to the overall stability and layered structure of the system. A similar argument can be applicable to the large-scale crystal structure of 8-(nonafluorobutyl)-3-(pyrimidin-2-yl)-3,4-dihydro-2H,6H-pyrimido[2,1-b][1,3,5]thiadiazin-6-one.
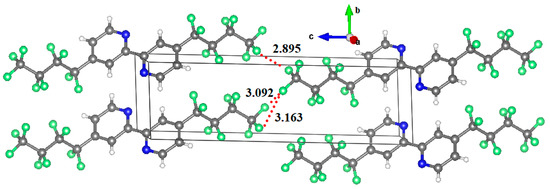
Figure 12.
An example of the solid-state structure of a fluorine-containing compound, 4,4′-bis(nonafluorobutyl)-2,2′-bipyridine, obtained from Cambridge Structure Database (CSD), refcode PEJZOV. A few F···F intermolecular distances are shown; actual values varying between 2.9 and 3.4 Å.
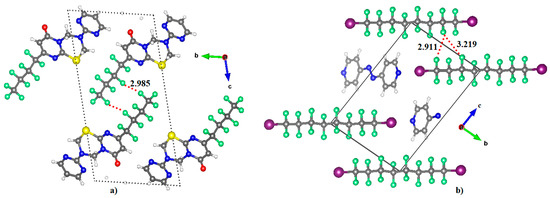
Figure 13.
Examples of experimentally reported fluorine-substituted crystals: (a) 8-(Nonafluorobutyl)-3-(pyrimidin-2-yl)-3,4-dihydro-2H,6H-pyrimido[2,1-b][1,3,5]thiadiazin-6-one and (b) trans-4,4′-azobipyridine 1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8-hexadecafluoro-1,8-diiodooctane (CSD ref. code KIQSUA and COKNUM, respectively), obtained from CSD. A few F···F intermolecular distances in these compounds are shown.
Figure 14 and Figure 15 show the crystal structures of perfluorohexane and dichloro-bis(perfluoro-n-propyl)-tellurium(IV). The main driving force in the formation of the crystal in the former is presumably the F···F interactions since the intermolecular distances between the F atoms in this crystal lie between 2.9 and 3.4 Å. The same can be said of the latter, although in this case Te···Te interactions play a structure-determining role and fluorination promotes such an interaction.
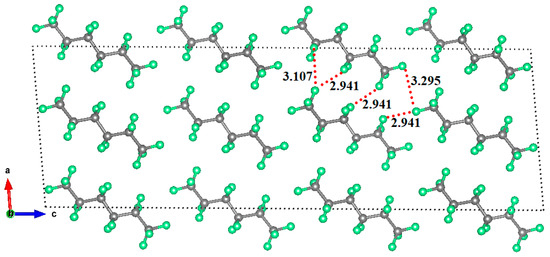
Figure 14.
The crystal structure of perfluorohexane (CSD refcode OLAWUT) [133]. The F···F intermolecular distances in the crystal vary between 2.9 and 3.4 Å; a few of them are marked.
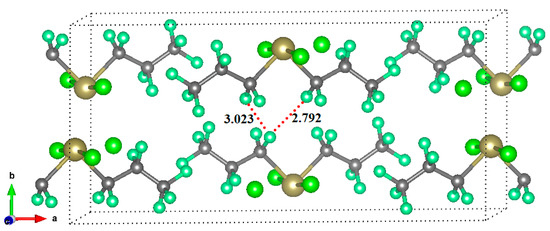
Figure 15.
The crystal structure of dichloro-bis(perfluoro-n-propyl)-tellurium(IV), CSD refcode MIHFEO [134]. A few F···F intermolecular distances are shown; they vary between 2.79 and 3.20 Å.
The long-range nature of the F···F interactions in all the crystals illustrated as examples provide further evidence that “less than the sum of the van der Waals criterion” often invoked to identify and characterize attractive non-covalent interactions in crystal lattices, which ignores the importance of weakly bound interactions, is misleading. Moreover, it should also be kept in mind that the forces that govern the lattice structures of molecular crystals of the types given above as examples are not always purely Coulombic interactions between regions of positive and negative charge as emphasized on several occasions [18,132].
These selected studies show the structural and interaction diversity of fluorine-centered interactions in the rational design and functionalization of materials. Most of these suggest that the theoretical exploration of fluorine-based contacts is largely lacking compared with those featuring halogen- and hydrogen-bonding with other halogen derivatives. Clearly, a concerted effort is required to enhance our current knowledge concerning the physical chemistry and chemical physics of fluorine in fluorine-based materials.
6. Summary
We have examined the non-covalent interaction ability of F in six fluorine-substituted benzene derivatives using the MESP model and ab initio MP2 calculations. From the nature of the MESP, we have shown that the fluorine in these molecules is entirely negative, both along its axial and equatorial regions; a similar conclusion on the negativity of the F atom was arrived at using the computed QTAIM integrated charges. As the number of the F atoms replacing H atoms in C6H6 increased from one to six, its negative nature concomitantly decreased. This is reasonable since the competition between them within the same molecule increases due to the very high electronegative and electron-withdrawing natures of the F atom. This specific feature did not prevent it from forming fluorine-centered non-covalent interactions, which resulted in dimeric complexes when one of the fluoro-substituted aromatic molecules was in proximity to a structurally identical or similar fluorinated compound. The MESP model approach, which was shown to be useful for inferring inter- and intramolecular interactions between sites of opposite polarity, is found to be incapable of explaining these unusual F···F non-covalent interactions both qualitatively and quantitatively; this is simply because this model does not account for the possibility of Coulombic attraction between sites of similar polarities. The attractive interactions between negative sites in the complexes examined were, however, successfully described by both QTAIM and RDG-NCI-based bonding descriptors, presenting, in general, yet another example of the usefulness and richness of the bond critical point and bond path concept and the theory of atoms in molecules; therefore, it is always recommended to examine these specific properties regardless of the chemical system being studied. Finally, we showed that of the four interaction energy contribution terms analyzed the stabilization energies arising from combined electrostatic and polarization effects alone cannot explain the structural stability of the fluoro-substituted dimers that we examined. Often underappreciated, dispersion energy turns out to be the main driving force behind dimer formation and its stabilization, overcoming all other repulsive effects, and was present in all the dimers examined. It is a common belief that this term dominates when interacting molecules are non-polar or slightly polar. This study showed it is not always true since it is found dominant even when the interacting species is either appreciably polar, weakly polar or even non-polar. While others have shown dispersion to be non-directional on several occasions, this study shows that dispersion, together with other attractive and repulsive interactions, do assist in enforcing an F···F intermolecular interaction to become directional. It is expected that this study will assist in the fundamental understanding of future studies involving the noncovalent chemistry of fluorine-centered interactions, as well as in the way they drive the design of novel supramolecular materials.
Author Contributions
Conceptualization and project design, P.R.V.; Investigation, P.R.V. and A.V.; Software, P.R.V. and K.Y.; Supervision, P.R.V. and K.Y.; Writing—original draft, P.R.V.; Writing—review & editing, P.R.V., A.V., H.M.M. and K.Y.
Funding
P.R.V., A.V. and K.Y. thank computer center of Institute of Molecular Science, Okazaki, Japan, for providing superconducting facilities and the University of Tokyo for partial funding. HMM thanks the National Research Foundation, Pretoria, South Africa, and the University of the Witwatersrand, for funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Puy, D.; Dubrovich, V.; Lipovka, A.; Talb, D.; Vonlanthen, P. Molecular fluorine chemistry in the early universe. Astron. Astrophys. 2007, 476, 685–689. [Google Scholar] [CrossRef]
- Dichiarante, V.; Milani, R.; Metrangolo, P. Natural surfactants towards a more sustainable fluorine chemistry. Green Chem. 2018, 20, 13–27. [Google Scholar] [CrossRef]
- Wang, B.-C.; Wang, L.-J.; Jiang, B.; Wang, S.-Y.; Wu, N.; Li, X.-Q.; Shi, D.-Y. Application of fluorine in drug design during 2010–2015 years: A mini-review. Mini Rev. Med. Chem. 2017, 17, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Gillis, E.P.; Eastman, K.J.; Hill, M.D.; Donnelly, D.J.; Meanwell, N.A. Applications of fluorine in medicinal chemistry. J. Med. Chem. 2015, 58, 8315–8359. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Koh, C.Y.; Ranade, R.M.; Shibata, S.; Gillespie, J.R.; Hulverson, M.A.; Huang, W.; Nguyen, J.; Pendem, N.; Gelb, M.H.; et al. 5-fluoroimidazo[4,5-b]pyridine is a privileged fragment that conveys bioavailability to potent trypanosomal methionyl-tRNA synthetase inhibitors. ACS Infect. Dis. 2016, 2, 399–404. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Pi, X.; Yang, D. Fluorine-passivated silicon nanocrystals: Surface chemistry versus quantum confinement. J. Phys. Chem. C 2012, 116, 5401–5406. [Google Scholar] [CrossRef]
- Lowe, D. One Does Not Simply Walk into Fluorine Chemistry. Available online: http://blogs.sciencemag.org/pipeline/archives/2012/02/28/one_does_not_simply_walk_into_fluorine_chemistry (accessed on 31 July 2018).
- Menaa, F.; Menaa, B.; Sharts, O.N. Importance of fluorine and fluorocarbons in medicinal chemistry and oncology. J. Mol. Pharm. Org. Process. Res. 2013, 1, 1000104. [Google Scholar]
- Bauzá, A.; Frontera, A. Electrostatically enhanced F⋯F interactions through hydrogen bonding, halogen bonding and metal coordination: An ab initio study. Phys. Chem. Chem. Phys. 2016, 18, 20381–20388. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Unusual bonding modes of perfluorobenzene in its polymeric (dimeric, trimeric and tetrameric) forms: Entirely negative fluorine interacting cooperatively with entirely negative fluorine. Phys. Chem. Chem. Phys. 2015, 17, 31624–31645. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Jin, B.-Y. Can an entirely negative fluorine in a molecule, viz. Perfluorobenzene, interact attractively with the entirely negative site(s) on another molecule(s)? Like liking like! RSC Adv. 2016, 6, 19098–19110. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Politzer, P. Expansion of the σ-hole concept. J. Mol. Model. 2009, 15, 723–729. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. Comment on “Extended Halogen Bonding between Fully Fluorinated Aromatic Molecules: Kawai et al., ACS Nano, 2015, 9, 2574. arXiv, 2018; arXiv:1802.09995.Condmat Public Archive. Available online: https://arxiv.org/ftp/arxiv/papers/1802/1802.09995.pdf (accessed on 31 July 2018).
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The s-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef] [PubMed]
- Kawai, S.; Sadeghi, A.; Xu, F.; Peng, L.; Orita, A.; Otera, J.; Goedecker, S.; Meyer, E. Extended halogen bonding between fully fluorinated aromatic molecules. ACS Nano 2015, 9, 2574–2583. [Google Scholar] [CrossRef] [PubMed]
- Reddy, C.M.; Kirchner, M.T.; Gundakaram, R.C.; Padmanabhan, K.A.; Desiraju, G.R. Isostructurality, polymorphism and mechanical properties of some hexahalogenated benzenes: The nature of halogen⋯halogen interactions. Chem. Eur. J. 2006, 12, 2222–2234. [Google Scholar] [CrossRef] [PubMed]
- Walch, H.; Gutzler, R.; Sirtl, T.; Eder, G.; Lackinger, M. Material- and orientation-dependent reactivity for heterogeneously catalyzed carbon−bromine bond homolysis. J. Phys. Chem. C 2010, 114, 12604–12609. [Google Scholar] [CrossRef]
- Khavasi, H.R.; Rahimi, N. Are fluorine-based contacts predictable? A case study in three similar coordination compounds. CrystEngComm 2017, 19, 1361–1365. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J. Fluorine–fluorine interactions: NMR and AIM analysis. J. Struct. Chem. 2004, 15, 117–120. [Google Scholar] [CrossRef]
- Halper, S.R.; Cohen, S.M. Self-assembly of heteroleptic [Cu(dipyrrinato)(hfacac)] complexes directed by fluorine−fluorine interactions. Inorg. Chem. 2005, 44, 4139–4141. [Google Scholar] [CrossRef] [PubMed]
- Barcelo-Oliver, M.; Estarellas, C.; Garcia-Raso, A.; Terron, A.; Frontera, A.; Quinonero, D.; Mata, I.; Molins, E.; Deya, P.M. Experimental and theoretical study of uracil derivatives: The crucial role of weak fluorine-fluorine noncovalent interactions. CrystEngComm 2010, 12, 3758–3767. [Google Scholar] [CrossRef]
- Karnoukhova, V.A.; Fedyanin, I.V.; Lyssenko, K.A. Directionality of intermolecular C–F···F–C interactions in crystals: Experimental and theoretical charge density study. Struct. Chem. 2016, 27, 17–24. [Google Scholar] [CrossRef]
- Brea, O.; Mó, O.; Yáñez, M.; Alkorta, I.; Elguero, J. Creating σ-holes through the formation of beryllium bonds. Chem. Eur. J. 2015, 21, 12676–12682. [Google Scholar] [CrossRef] [PubMed]
- Baker, R.J.; Colavita, P.E.; Murphy, D.M.; Platts, J.A.; Wallis, J.D. Fluorine–fluorine interactions in the solid state: An experimental and theoretical study. J. Phys. Chem. A 2012, 116, 1435–1444. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Chopra, D.; Row, T.N.G. Role of organic fluorine in crystal engineering. CrystEngComm 2011, 13, 2175–2186. [Google Scholar] [CrossRef]
- Sirohiwal, A.; Hathwar, V.R.; Dey, D.; Regunathan, R.; Chopra, D. Characterization of fluorine-centred ‘F···O’ σ-hole interactions in the solid state. Acta Crystallogr. Sec. B 2017, 73, 140–152. [Google Scholar] [CrossRef] [PubMed]
- Pavan, M.S.; Prasad, K.D.; Guru Row, T.N. Halogen bonding in fluorine: Experimental charge density study on intermolecular F⋯F and F⋯S donor-acceptor contacts. Chem. Commun. 2013, 49, 7558–7560. [Google Scholar] [CrossRef] [PubMed]
- Wilcken, R.; Zimmermann, M.O.; Lange, A.; Joerger, A.C.; Boeckler, F.M. Principles and applications of halogen bonding in medicinal chemistry and chemical biology. J. Med. Chem. 2013, 56, 1363–1388. [Google Scholar] [CrossRef] [PubMed]
- Sirimulla, S.; Bailey, J.B.; Vegesna, R.; Narayan, M. Halogen interactions in protein–ligand complexes: Implications of halogen bonding for rational drug design. J. Chem. Inf. Model. 2013, 53, 2781–2791. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Jin, B.-Y. Fluorines in tetrafluoromethane as halogen bond donors: Revisiting address the nature of the fluorine’s σ-hole. Int. J. Quantum Chem. 2015, 115, 453–470. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Do surfaces of positive electrostatic potential on different halogen derivatives in molecules attract? Like attracting like! J. Comput. Chem. 2018, 39, 343–350. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Clark, T.; Politzer, P. Σ-hole bonding: Molecules containing group VI atoms. J. Mol. Model. 2007, 13, 1033–1038. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. Revealing factors influencing the fluorine-centered non-covalent interactions in some fluorine-substituted molecular complexes: Insights from first-principles studies. ChemPhysChem 2018. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.A.A. Molecular mechanical study of halogen bonding in drug discovery. J. Comput. Chem. 2011, 32, 2564–2574. [Google Scholar] [CrossRef] [PubMed]
- Danten, Y.; Tassaing, T.; Besnard, M. On the nature of the water−hexafluorobenzene interaction. J. Phys. Chem. A 1999, 103, 3530–3534. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Uchimaru, T.; Mikami, M. Intermolecular interaction between hexafluorobenzene and benzene: Ab initio calculations including CCSD(T) level electron correlation correction. J. Phys. Chem. A 2006, 110, 2027–2033. [Google Scholar] [CrossRef] [PubMed]
- Gung, B.W.; Amicangelo, J.C. Substituent effects in C6F6C6H5X stacking interactions. J. Org. Chem. 2006, 71, 9261–9270. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Rozas, I.; Jimeno, M.L.; Elguero, J. A theoretical and experimental study of the interaction of c6f6 with electron donors. Struct. Chem. 2001, 12, 459–464. [Google Scholar] [CrossRef]
- Quiñonero, D.; Frontera, A.; Garau, C.; Ballester, P.; Costa, A.; Deyà, P.M. Interplay between cation–π, anion–π and π–π interactions. ChemPhysChem 2006, 7, 2487–2491. [Google Scholar] [CrossRef] [PubMed]
- Hiraoka, K.; Mizuse, S. A determination of the stabilities and structures of F−(C6H6) and F− (C6F6) clusters. J. Chem. Phys. 1987, 86, 4102. [Google Scholar] [CrossRef]
- Papp, D.; Rovó, P.; Jákli, I.; Császár, A.G.; Perczel, A. Four faces of the interaction between ions and aromatic rings. J. Comput. Chem. 2017, 38, 1762–1773. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Deyà, P.; Frontera, A. Anion-π interactions in supramolecular chemistry and catalysis. In Noncovalent Forces. Challenges and Advances in Computational Chemistry and Physics; Scheiner, S., Ed.; Springer: Cham, Switzerland, 2015; Volume 19. [Google Scholar]
- Marín-Luna, M.; Alkorta, I.; Elguero, J.; Mó, O.; Yáñez, M. Interplay between beryllium bonds and anion-π interactions in BeR2:C6X6:Y− complexes (R = H, F and Cl, X = H and F, and Y = Cl and Br). Molecules 2015, 20, 9961–9976. [Google Scholar] [CrossRef] [PubMed]
- Ballester, P. Anions and p-aromatic systems. Do they interact attractively? In Recognition of Anions. Structure and Bonding; Vilar, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 129, pp. 127–174. [Google Scholar]
- Echeverría, J.; Aullón, G.; Danovich, D.; Shaik, S.; Alvarez, S. Dihydrogen contacts in alkanes are subtle but not faint. Nat. Chem. 2011, 3, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Laurence, P.R.; Jayasuriya, K. Molecular electrostatic potentials: An effective tool for the elucidation of biochemical phenomena. Environ. Health Perspect. 1985, 61, 191–202. [Google Scholar] [CrossRef] [PubMed]
- Tognetti, V.; Joubert, L. On atoms-in-molecules energies from kohn-sham calculations. ChemPhysChem 2017, 18, 2675–2687. [Google Scholar] [CrossRef] [PubMed]
- Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies. J. Chem. Phys. 2014, 140, 094106. [Google Scholar] [CrossRef] [PubMed]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Guttmann, R.; Sax, A.F. Dispersion interactions and the stability of amine dimers. ChemistryOpen 2017, 6, 571–584. [Google Scholar] [CrossRef] [PubMed]
- Qing, L.; Frank, N.; Giovanni, B. Formation of agostic structures driven by London dispersion. Angew. Chem. Int. Ed. 2018, 57, 4760–4764. [Google Scholar]
- Holzer, C.; Klopper, W. Quasi-relativistic two-component computations of intermolecular dispersion energies. Mol. Phys. 2017, 115, 2775–2781. [Google Scholar] [CrossRef]
- Holzer, C.; Klopper, W. Symmetry-adapted perturbation theory with intermolecular induction and dispersion energies from the bethe-salpeter equation. J. Chem. Phys. 2017, 147, 181101. [Google Scholar] [CrossRef] [PubMed]
- Otlyotov, A.A.; Lamm, J.-H.; Blomeyer, S.; Mitzel, N.W.; Rybkin, V.V.; Zhabanov, Y.A.; Tverdova, N.V.; Giricheva, N.I.; Girichev, G.V. Gas-phase structure of 1,8-bis[(trimethylsilyl)ethynyl]anthracene: Cog-wheel-type vs. Independent internal rotation and influence of dispersion interactions. Phys. Chem. Chem. Phys. 2017, 19, 13093–13100. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision A 02; Gaussian, Inc.: Wallinford, CT, USA, 2009. [Google Scholar]
- SAPT: Symmetry Adapted Perturbation Theory. Available online: http://www.psicode.org/psi4manual/master/sapt.html (accessed on 16 November 2017).
- Krzysztof, S. Symmetry-adapted perturbation theory of intermolecular forces. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 254–272. [Google Scholar]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation theory approach to intermolecular potential energy surfaces of van der Waals complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Parrish, R.M.; Burns, L.A.; Smith, D.G.A.; Simmonett, A.C.; DePrince, A.E.; Hohenstein, E.G.; Bozkaya, U.; Sokolov, A.Y.; Di Remigio, R.; Richard, R.M.; et al. Psi4 1.1: An open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J. Chem. Theory Comp. 2017, 13, 3185–3197. [Google Scholar] [CrossRef] [PubMed]
- Keith, T.A. Aimall, version 17.01.25; TK Gristmill Software; AIMALL: Overland Park, KS, USA, 2016.
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comp. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Arghya, C.; Lin, L.; Emil, A. Electrostatic component of binding energy: Interpreting predictions from poisson–boltzmann equation and modeling protocols. J. Comp. Chem. 2016, 37, 2495–2507. [Google Scholar]
- Lever, G.; Cole, D.J.; Hine, N.D.M.; Haynes, P.D.; Payne, M.C. Electrostatic considerations affecting the calculated homo–lumo gap in protein molecules. J. Phys. Condens. Matter 2013, 25, 152101. [Google Scholar] [CrossRef] [PubMed]
- Boschitsch, A.H.; Fenley, M.O. A fast and robust poisson–boltzmann solver based on adaptive cartesian grids. J. Chem. Theory Comp. 2011, 7, 1524–1540. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Tran, K.-A.; Lane, P.; Murray, J.S.; Politzer, P. Comparative analysis of electrostatic potential maxima and minima on molecular surfaces, as determined by three methods and a variety of basis sets. J. Comp. Sci. 2016, 17, 273–284. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Σ-hole interactions: Perspectives and misconceptions. Crystals 2017, 7, 212. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Dance, I. Distance criteria for crystal packing analysis of supramolecular motifs. New J. Chem. 2003, 27, 22–27. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Halogen bonding interaction of chloromethane withseveral nitrogen donating molecules: Addressing thenature of the chlorine surface σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 19573–19589. [Google Scholar] [CrossRef] [PubMed]
- Bultinck, P.; Cardenas, C.; Fuentealba, P.; Johnson, P.A.; Ayers, P.W. Atomic charges and the electrostatic potential are ill-defined in degenerate ground states. J. Chem. Theory Comput. 2013, 9, 4779–4788. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.P.; Swart, M. Intramolecular halogen–halogen bonds? Phys. Chem. Chem. Phys. 2013, 15, 11543–11553. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. Theoretical study on σ- and π-hole carbon···carbon bonding interactions: Implications in CFC chemistry. Phys. Chem. Chem. Phys. 2016, 18, 32155–32159. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S. A cartography of the van der waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [PubMed]
- Aakeröy, C.B.A.; Evans, T.R.; Seddon, K.; Pálinkó, I. The C–H···Cl hydrogen bond: Does it exist? New J. Chem. 1999, 23, 145–152. [Google Scholar] [CrossRef]
- Angarov, V.; Kozuch, S. On the σ, π and δ hole interactions: A molecular orbital overview. New J. Chem. 2018, 42, 1413–1422. [Google Scholar] [CrossRef]
- Koohi, A.M.; Mahdavifar, Z.; Noorizadeh, S. Can fluorine form halogen bond? Investigation of halogen bonds through steric charge. ChemistrySelect 2017, 2, 2713–2717. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, N.; Wang, W. A new class of halogen bonds that avoids the σ-hole. Chem. Phys. Lett. 2012, 532, 27–30. [Google Scholar] [CrossRef]
- Stenlid, J.H.; Johansson, A.J.; Brinck, T. Σ-holes on transition metal nanoclusters and their influence on the local lewis acidity. Crystals 2017, 7, 222. [Google Scholar] [CrossRef]
- Eskandari, K.; Zariny, H. Halogen bonding: A lump-hole interaction. Chem. Phys. Lett. 2010, 492, 9–13. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Huber, S.M.; Scanlon, J.D.; Jimenez-Izal, E.; Ugalde, J.M.; Infante, I. On the directionality of halogen bonding. Phys. Chem. Chem. Phys. 2013, 15, 10350–10357. [Google Scholar] [CrossRef] [PubMed]
- Tsuzuki, S. Origin of attraction and directionality of hydrogen bond and halogen bond: Analysis by ab initio MO calculations. AIP Conf. Proc. 2015, 1702, 090044. [Google Scholar]
- Duarte, D.J.R.; Peruchena, N.M.; Alkorta, I. Double hole-lump interaction between halogen atoms. J. Phys. Chem. A 2015, 119, 3746–3752. [Google Scholar] [CrossRef] [PubMed]
- Lekner, J. Electrostatics of two charged conducting spheres. Proc. Roy. Soc. A 2012, 468, 2829–2848. [Google Scholar] [CrossRef]
- Ball, P. Like attracts like? Everything you thought you knew about electrostatics is probably wrong. Nature 2012. [Google Scholar] [CrossRef]
- Phipps, M.J.S.; Fox, T.; Tautermann, C.S.; Skylaris, C.-K. Energy decomposition analysis approaches and their evaluation on prototypical protein-drug interaction patterns. Chem. Soc. Rev. 2015, 44, 3177–3211. [Google Scholar] [CrossRef] [PubMed]
- Wick, C.R.; Clark, T. On bond-critical points in qtaim and weak interactions. J. Mol. Model. 2018, 24, 142. [Google Scholar] [CrossRef] [PubMed]
- Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The many faces of halogen bonding: A review of theoretical models and methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
- Gropp, C.; Husch, T.; Trapp, N.; Reiher, M.; Diederich, F. Dispersion and halogen-bonding interactions: Binding of the axial conformers of monohalo- and (±)-trans-1,2-dihalocyclohexanes in enantiopure alleno-acetylenic cages. J. Am. Chem. Soc 2017, 139, 12190–12200. [Google Scholar] [CrossRef] [PubMed]
- Matczak, P. Description of weak halogen bonding using various levels of symmetry-adapted perturbation theory combined with effective core potentials. J. Chem. 2017, 2017, 9031494. [Google Scholar] [CrossRef]
- Řezáč, J.; de la Lande, A. On the role of charge transfer in halogen bonding. Phys. Chem. Chem. Phys. 2017, 19, 791–803. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Halogen bonds formed between substituted imidazoliums and n bases of varying n-hybridization. Molecules 2017, 22, 1634. [Google Scholar] [CrossRef] [PubMed]
- Tkatchenko, A.; DiStasio, R.A.; Head-Gordon, M.; Scheffler, M. Dispersion-corrected møller–plesset second-order perturbation theory. J. Chem. Phys. 2009, 131, 094106. [Google Scholar] [CrossRef] [PubMed]
- Cybulski, S.M.; Chałasiński, G.; Moszyński, R. On decomposition of second-order møller-plesset supermolecular interaction energy and basis set effects. J. Chem. Phys. 1990, 92, 4357–4363. [Google Scholar] [CrossRef]
- Cybulski, S.M.; Lytle, M.L. The origin of deficiency of the supermolecule second-order moller-plesset approach for evaluating interaction energies. J. Chem. Phys. 2007, 127, 141102. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.W.F. Bond paths are not chemical bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef] [PubMed]
- Buralli, G.J.; Petelski, A.N.; Peruchena, N.M.; Sosa, G.L.; Duarte, D.R.J. Multicenter (FX)n/NH3 halogen bonds (X = Cl, Br and n = 1–5). Qtaim descriptors of the strength of the X∙∙∙N interaction. Molecules 2017, 22, 2034. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, P.; Pendás, A.M.; Popelier, P.L.A. Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory (DFT). Phys. Chem. Chem. Phys. 2016, 18, 20986–21000. [Google Scholar] [CrossRef] [PubMed]
- Pendás, A.M.; Francisco, E.; Blanco, M.A. Two-electron integrations in the quantum theory of atoms in molecules with correlated wave functions. J. Comp. Chem. 2005, 26, 344–351. [Google Scholar] [CrossRef] [PubMed]
- Syzgantseva, O.A.; Tognetti, V.; Joubert, L. On the physical nature of halogen bonds: A QTAIM study. J. Phys. Chem. A 2013, 117, 8969–8980. [Google Scholar] [CrossRef] [PubMed]
- Thacker, J.C.R.; Popelier, P.L.A. Fluorine gauche effect explained by electrostatic polarization instead of hyperconjugation: An interacting quantum atoms (IQA) and relative energy gradient (REG) study. J. Phys. Chem. A 2018, 122, 1439–1450. [Google Scholar] [CrossRef] [PubMed]
- Rincón, L.; Almeida, R.; García-Aldea, D.; Riega, H.D.Y. Hydrogen bond cooperativity and electron delocalization in hydrogen fluoride clusters. J. Chem. Phys. 2001, 114, 5552–5561. [Google Scholar] [CrossRef]
- Bankiewicz, B.; Matczak, P.; Palusiak, M. Electron density characteristics in bond critical point (QTAIM) versus interaction energy components (SAPT): The case of charge-assisted hydrogen bonding. J. Phys. Chem. A 2012, 116, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Matta, C.F.; Boyd, R.J.T. The Quantum Theory of Atoms in Molecules; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Love, I. Polar covalent bonds: An aim analysis of S,O bonds. J. Phys. Chem. A 2009, 113, 2640–2646. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules. Available online: http://www.wiley.com/legacy/wileychi/ecc/samples/sample02.pdf (accessed on 31 July 2018).
- Shahbazian, S. Why bond critical points are not “bond” critical points. Chem. Eur. J. 2018, 24, 5401–5405. [Google Scholar] [CrossRef] [PubMed]
- Kolář, M.H.; Hobza, P. Computer modeling of halogen bonds and other σ-hole interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Murray, J.S.; Politzer, P. Role of polarization in halogen bonds. Aust. J. Chem. 2014, 67, 451–456. [Google Scholar] [CrossRef]
- Lane, J.R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B.J.; Kjaergaard, H.G. Are bond critical points really critical for hydrogen bonding? J. Chem. Theory Comput. 2013, 9, 3263–3266. [Google Scholar] [CrossRef] [PubMed]
- Howard, D.L.; Jørgensen, P.; Kjaergaard, H.G. Weak intramolecular interactions in ethylene glycol identified by vapor phase OH−stretching overtone spectroscopy. J. Am. Chem. Soc. 2005, 127, 17096–17103. [Google Scholar] [CrossRef] [PubMed]
- Howard, D.L.; Kjaergaard, H.G. Influence of intramolecular hydrogen bond strength on OH-stretching overtones. J. Phys. Chem. A 2006, 110, 10245–10250. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Matta, C.F.; Castillo, N.; Boyd, R.J. Characterization of a closed-shell fluorine−fluorine bonding interaction in aromatic compounds on the basis of the electron density. J. Phys. Chem. A 2005, 109, 3669–3681. [Google Scholar] [CrossRef] [PubMed]
- Sanna, E.; Bauzá, A.; Escudero-Adán, E.C.; Rotger, C.; Frontera, A.; Costa, A. The mouse in a trap: Observation of a C(sp3)–F···F–C(sp3) interaction in a discrete CFC pair by the crystal sponge method. Cryst. Growth Des. 2017, 17, 3611–3615. [Google Scholar] [CrossRef]
- Calvo-Castro, J.; Morris, G.; Kennedy, A.R.; McHugh, C.J. Effects of fluorine substitution on the intermolecular interactions, energetics, and packing behavior of N-benzyl substituted diketopyrrolopyrroles. Cryst. Growth Des. 2016, 16, 2371–2384. [Google Scholar] [CrossRef]
- Khavasi, H.R.; Rahimi, N. Coordination polymers with intramolecular fluorine-involved contacts in two-dimensional sheet windows. Cryst. Growth Des. 2017, 17, 834–845. [Google Scholar] [CrossRef]
- Khavasi, H.R.; Rahimi, N. Fluorine-substituted ligands induce structural diversity of coordination compounds. ChemistrySelect 2017, 2, 11314–11321. [Google Scholar] [CrossRef]
- Li, P.; Maier, J.M.; Vik, E.C.; Yehl, C.J.; Dial, B.E.; Rickher, A.E.; Smith, M.D.; Pellechia, P.J.; Shimizu, K.D. Stabilizing fluorine–π interactions. Angew. Chem. Int. Ed. 2017, 56, 7209–7212. [Google Scholar] [CrossRef] [PubMed]
- Rybalova, T.V.; Bagryanskaya, I.Y. C-F···π, F···H, and F···F intermolecular interactions and F-aggregation: Role in crystal engineering of fluoroorganic compounds. J. Struct. Chem. 2009, 50, 741–753. [Google Scholar] [CrossRef]
- Esterhuysen, C.; Heßelmann, A.; Clark, T. Trifluoromethyl: An amphiphilic noncovalent bonding partner. ChemPhysChem 2017, 18, 772–784. [Google Scholar] [CrossRef] [PubMed]
- Cormanich, R.A.; Rittner, R.; O’Hagan, D.; Bühl, M. Analysis of CF···FC interactions on cyclohexane and naphthalene frameworks. J. Phys. Chem. A 2014, 118, 7901–7910. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Tottempudi, U.K.; Mottishaw, J.D.; Basa, P.N.; Putta, A.; Sykes, A.G. CCDC 889164: Experimental Crystal Structure Determination. Available online: https://www.ccdc.cam.ac.uk/structures/search?id=doi:10.5517/ccyv7qq&sid=DataCite (accessed on 31 July 2018).
- Murray, J.S.; Resnati, G.; Politzer, P. Close contacts and noncovalent interactions in crystals. Faraday Discuss. 2017, 203, 113–130. [Google Scholar] [CrossRef] [PubMed]
- Kuduva, S.S.; Boese, R. CCDC 220154: Experimental Crystal Structure Determination. Available online: https://www.ccdc.cam.ac.uk/structures/search?id=doi:10.5517/cc7d2rf&sid=DataCite (accessed on 31 July 2018).
- Gockel, S.; Haas, A.; Probst, V.; Boese, R.; Muller, I. Contributions to bis(perfluoroalkyl) chalkogenide chemistry: Preparation of (Rf)2SeO [Rf = C2F5, (CF3)2CF, n-C4F9], (Rf′)2TeX2 [X = F, Cl: Rf′ = n-C3F7, (CF3)2CF, n-C4F9; X = Br: Rf′ = n-C3F7, n-C4F9], (CF3)2Te(NSO)2 and (C2F5)2Te(OH)NO3. J. Fluor. Chem. 2000, 102, 301–311. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).