1. Introduction
Atmospheric aerosols are important drivers of air quality, atmospheric heat radiative balance, human health and climate, etc. Generally, there are three vitally important properties of aerosols, i.e., aerosol size distributions (ASDs), aerosol optical depths (AODs) and Ångström exponents [
1,
2]. The knowledge of ASDs is essential to a better understanding of their potential contributions to climate change, source identification and environmental quality, necessary to control pollution and preserve citizen health. Therefore, in situ measuring the ASDs presented in the atmosphere is of great necessity [
3,
4]. Nowadays, although there are several global ground-based aerosol observation networks and satellite instrument networks that have been established to study the properties of the atmospheric aerosols, e.g., AERONET, MODIS [
5,
6,
7,
8], determining the ASDs accurately is still regarded as an unsolved problem and needs further research.
During the past several years, various types of methods have been proposed to study the ASDs, e.g., the aerodynamic method, the optical measurement method, electrical mobility and condensation method, electrical sensing zone method and the electron microscopy method [
9]. Owing to offering a useful and effective approach, reliable measurement results and broad size ranges, the optical measurement method coupled with inverse methods has drawn much attention in the field of determining the ASDs [
10]. Usually the optical measurement method could be divided into several categories, such as spectral extinction method (SEM), angular light-scattering method (ALSM) and optical depth measurement method, etc. During our previous work, the ASDs were reconstructed effectively by using SEM, and the retrieval accuracy was improved by increasing the number of measurement wavelengths [
11]. However, all the satisfactory results obtained by using SEM were based on having sufficient spectral measurement information about the aerosol dispersion system beforehand, e.g., the multi-spectral transmittance signals. To obtain these information measurements, the multi-spectral light source and detector should be needed, and the multi-spectral optical constants of aerosol should be known, which may increase the difficulty and the cost of experiment. Unlike the SEM, only single spectral information of aerosol is required by using ALSM, and the ASDs can be recovered by measuring multi-angle light-scattering signals [
12,
13].
In the present study, the comparison of ALSM and SEM in retrieval of ASDs are studied. The inverse problem is solved by using a SPSO-DE hybrid algorithm, which is based on the stochastic particle swarm optimization (SPSO) algorithm and differential evolution (DE) algorithm. The research is organized as follows. First, the principles of ALSM and SPSO-DE hybrid algorithm are introduced, and that of SEM, available in Reference [
14], is not repeated here. Then, the sensitivity analysis of optical measurement signals to characteristic parameters in ASDs is studied, and the corresponding optimal measurement angle selection region for ALSM and optimal measurement wavelength selection region for SEM are proposed. Finally, common monomodal and bimodal ASDs are retrieved by SEM and ALSM, respectively, and the main conclusions and perspectives are provided.
3. The Aerosol Size Distribution and Optical Constants
The mathematical representations of particle size distribution functions studied here are shown below [
11]:
where the superscript ‘mono’ and ‘bi’ denote the monomodal and bimodal distributions; the superscript ‘L-N’ and ‘Gamma’ denote the Logarithmic Normal distribution and the Gamma distribution. The detailed description of these functions is available in our previous work [
11]. To meet the need of optical measurement methods, the particle size range is set within [0.001, 10.0] μm [
24].
Table 1 lists the true values of the ASDs mentioned above.
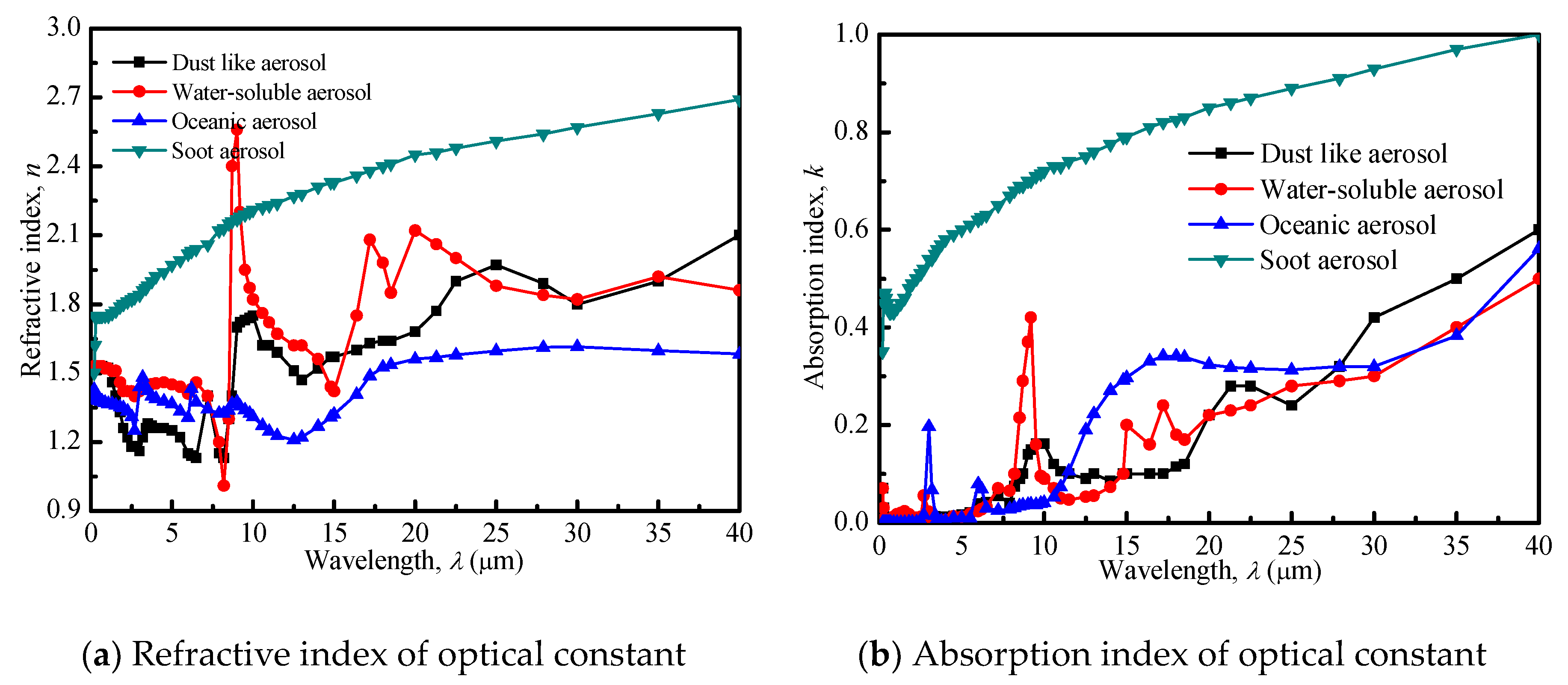
According to the standard radiation atmospheric model (SRA) of atmospheric aerosols, which was recommended by the radiation committee of the International Association of Meteorology and Atmospheric Physics (IAMAP) in 1983, the atmospheric aerosols with different composition were divided into six categories, i.e., dust-like aerosol, water-soluble aerosol, oceanic aerosol, soot aerosol, volcanic ash aerosol and sulfuric acid aerosol [
25]. Later, D’Almeida and coworkers [
26] proposed a new kind of global aerosol model and added the mineral aerosol into the model, which represents the aerosol of one-third of global terrestrial deserts and grassland (arid or semi-arid) areas.
Figure 1 depicts the spectral optical constants of four kinds of common aerosols, i.e., dust-like aerosol, water-soluble aerosol, oceanic aerosol and soot aerosol, which are available in Reference [
25,
26]. In the present work, the spectral optical constants are selected according to soot aerosol.
4. Sensitivity Analysis of Optical Measurement Signals to Characteristic Parameters in ASDs
Because the inverse accuracy of ASDs is relevant to the information obtained from the optical measurement signals, i.e., spectral transmittance signals or angular light-scattering signals, it is necessary to optimize the measurement signals.
Generally, to improve retrieval accuracy, the optical measurement signals are usually selected irrelevant to each other and sensitive to changes of inverse parameters. With this idea, the sensitivity analysis of optical measurement signals to unsolved characteristic parameters in ASDs at a different measurement wavelength or angle is employed to find the optimal measurement wavelength selection region for SEM and optimal measurement angle selection region for ALSM. The sensitivity coefficient is one of the most important characteristic parameters in the sensitivity analysis, which is the first derivative of the optical measurement signals, i.e.,
or
, to a certain inverse characteristic parameter. The sensitivity coefficient at every wavelength or angle
is defined as [
27]:
where a denotes the inverse characteristic parameters in ASDs;
represents a tiny change and is set at 0.5% in this study,
;
is the angular light-scattering measurement signals;
is the spectral transmittance obtained in the SEM. It is obvious that to improve the retrieval accuracy, the optical measurement signals with larger absolute values of sensitivity coefficient should better be selected.
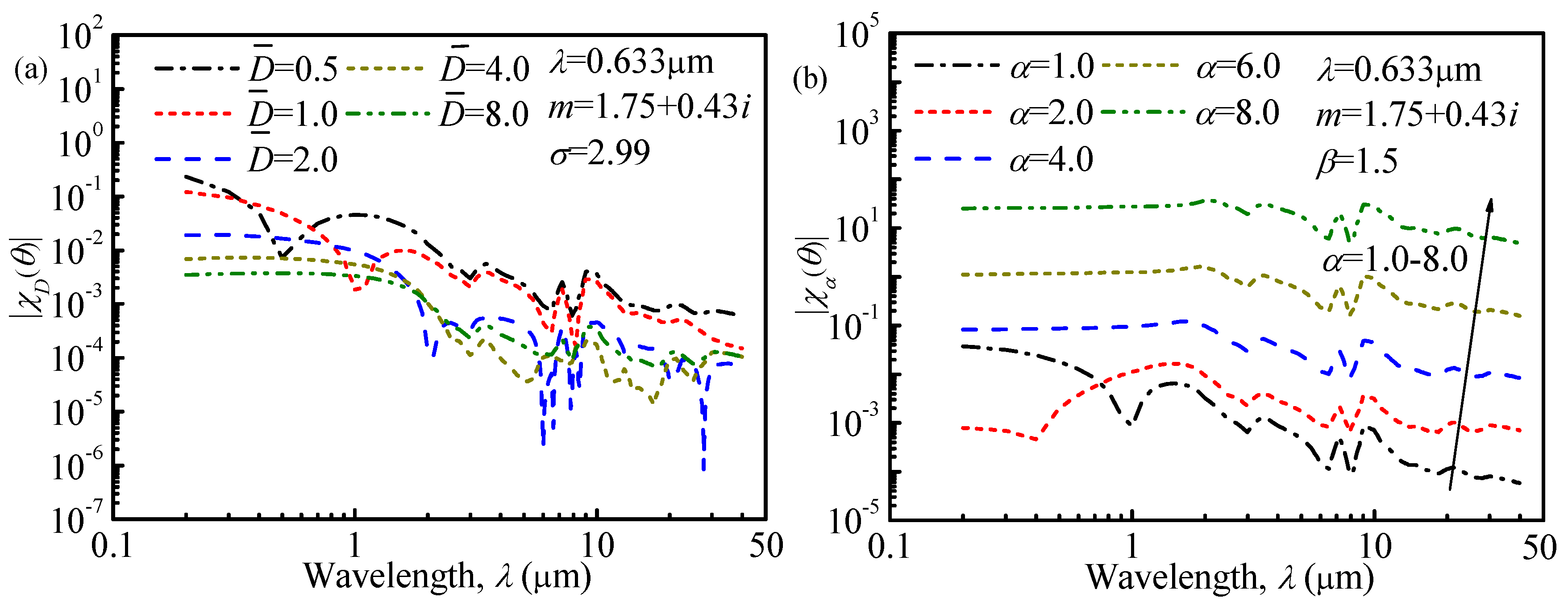
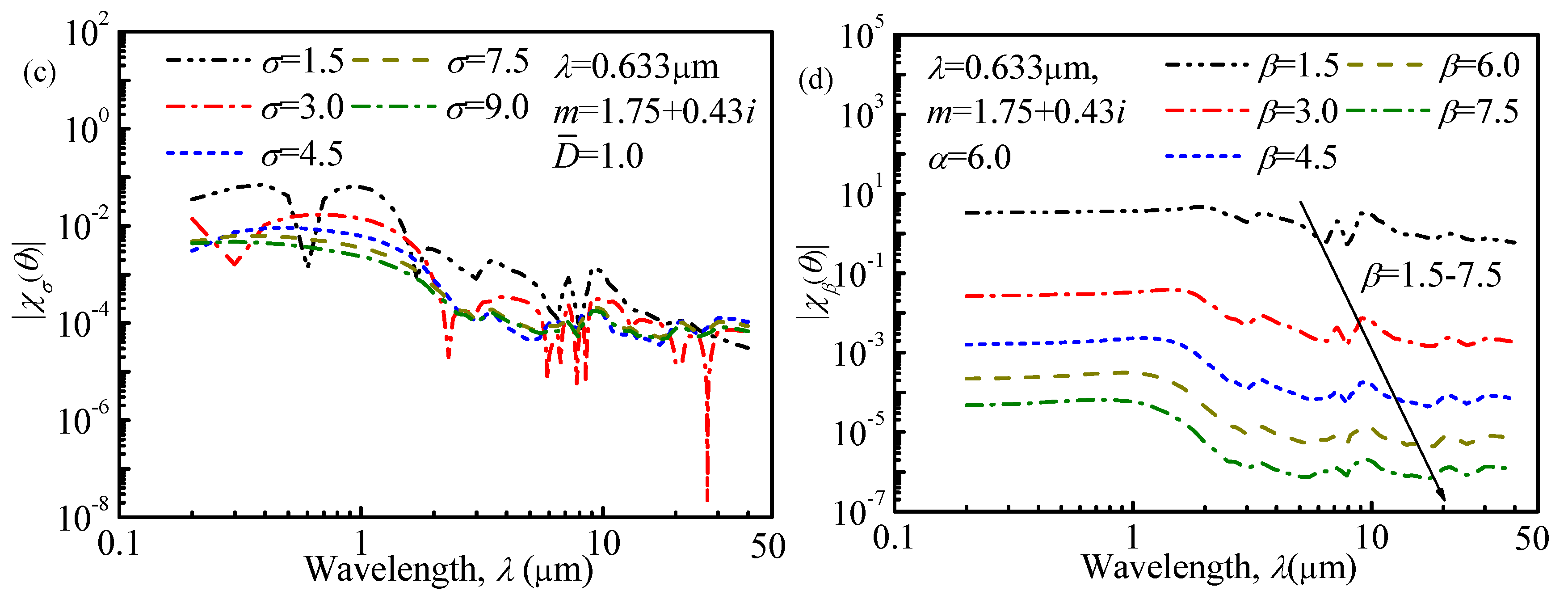
Figure 2 and
Figure 3 depict the sensitivity coefficient for different monomodal ASDs with respect to spectral transmittance signals and angular light-scattering signals, respectively. From
Figure 2, it can be found that increasing the measurement wavelength will reduce the sensitivity coefficient in general, so to ensure the retrieval accuracy, the measurement wavelengths in this study are selected from
. From
Figure 3, it is obvious that the value of the sensitivity coefficient will decline with an increase in the measurement angles. According to References [
28,
29], for a small angle, the scattered intensities are weakly dependent upon the particle’s composition but strongly dependent upon the particle’s roughness and size, so the measurement angles in this study are selected from
to obtain more accurate retrieval results. Similar conclusions can be obtained in studying bimodal ASDs, and the measurement wavelengths and angles are also selected from
and
, respectively. The details in studying the bimodal ASDs are not shown here and interested readers can contact us.
5. Numerical Simulation
The true values of characteristic parameters of monomodal and bimodal ASDs in this study are listed in
Table 1. According to our former studies [
11], the number of measurement wavelengths and angles are set as 4 for monomodal ASDs and 7 for bimodal ASDs to make sure the retrieval accuracy, and the corresponding measurement wavelengths and angles are listed in
Table 2.
The retrieval of the ASDs is solved by minimizing the objective function value, which is the sum of the square residuals between the estimated and measured transmittance:
where
and
denote the estimated and measured optical measurement signals, respectively. For the algorithm is a stochastic optimization method and all optimizations have certain randomness, all the calculations are repeated 30 times. Moreover, the relative deviation of ASDs δ is used to evaluate the quality of estimated results:
where
denotes the number of subintervals which the particle size range [
,
] is divided into;
is the midpoint of the
ith subinterval [
,
];
is the true volume frequency distribution in the
ith subinterval; and
is the estimated volume frequency distribution in the
ith subinterval.
5.1. Comparison of SPSO and Hybrid SPSO-DE Algorithms
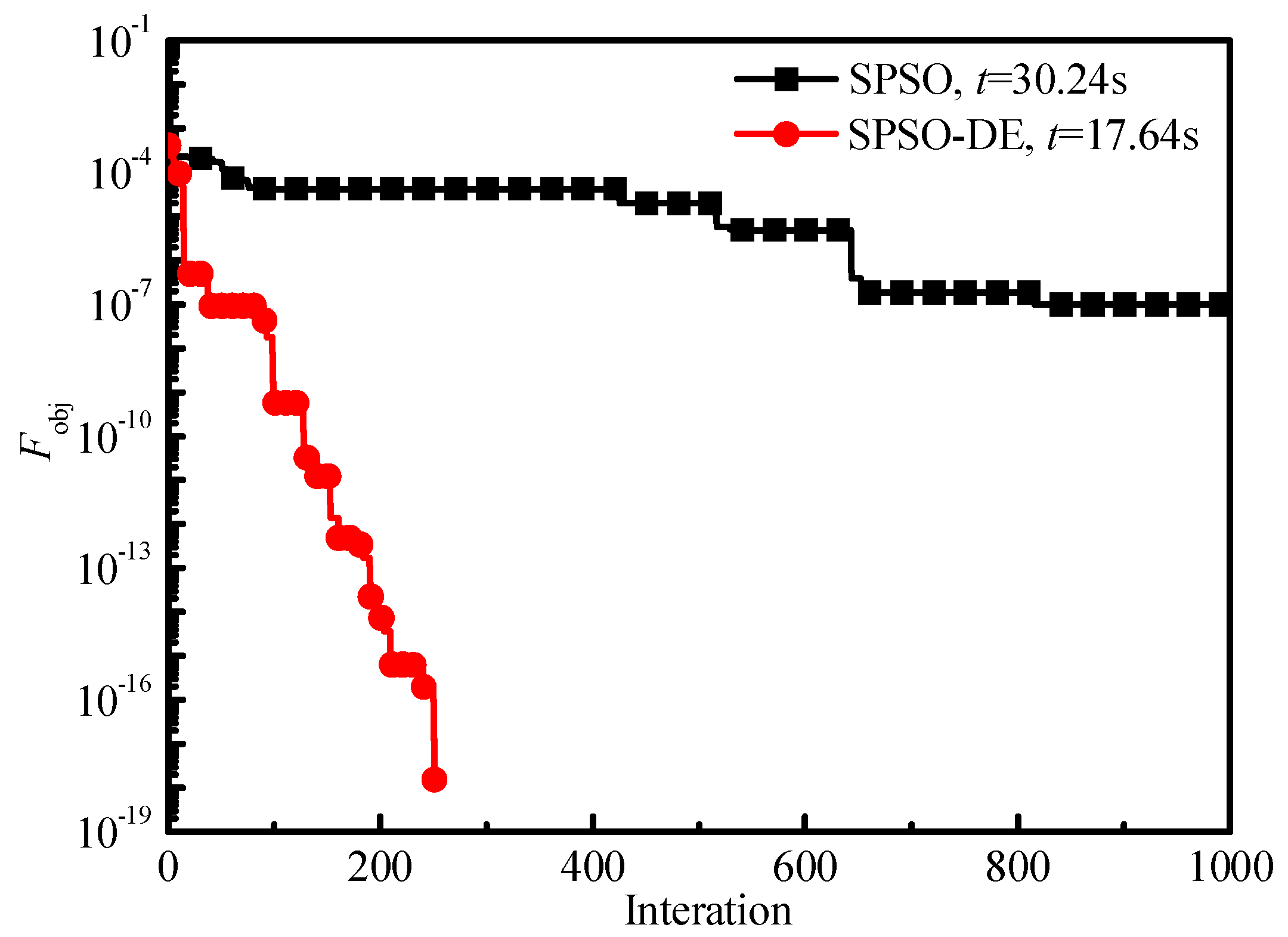
At first, the performance of the hybrid SPSO-DE algorithm is investigated through comparison with the SPSO algorithm in retrieving the monomodal Gamma distribution by using an angular light-scattering method (See
Figure 4).
Table 3 lists the system control parameters. When the objective function value is less than 10
−16 or the iteration number is larger than 1000, finish the calculation and output the results. The investigation shows that the convergence speed and the value of the objective function of the SPSO-DE hybrid algorithm are superior to the SPSO algorithm, which means the local optima and low convergence accuracy exiting in the SPSO can be avoided in the hybrid SPSO-DE algorithm.
5.2. Retrieval of the Aerosol Size Distribution
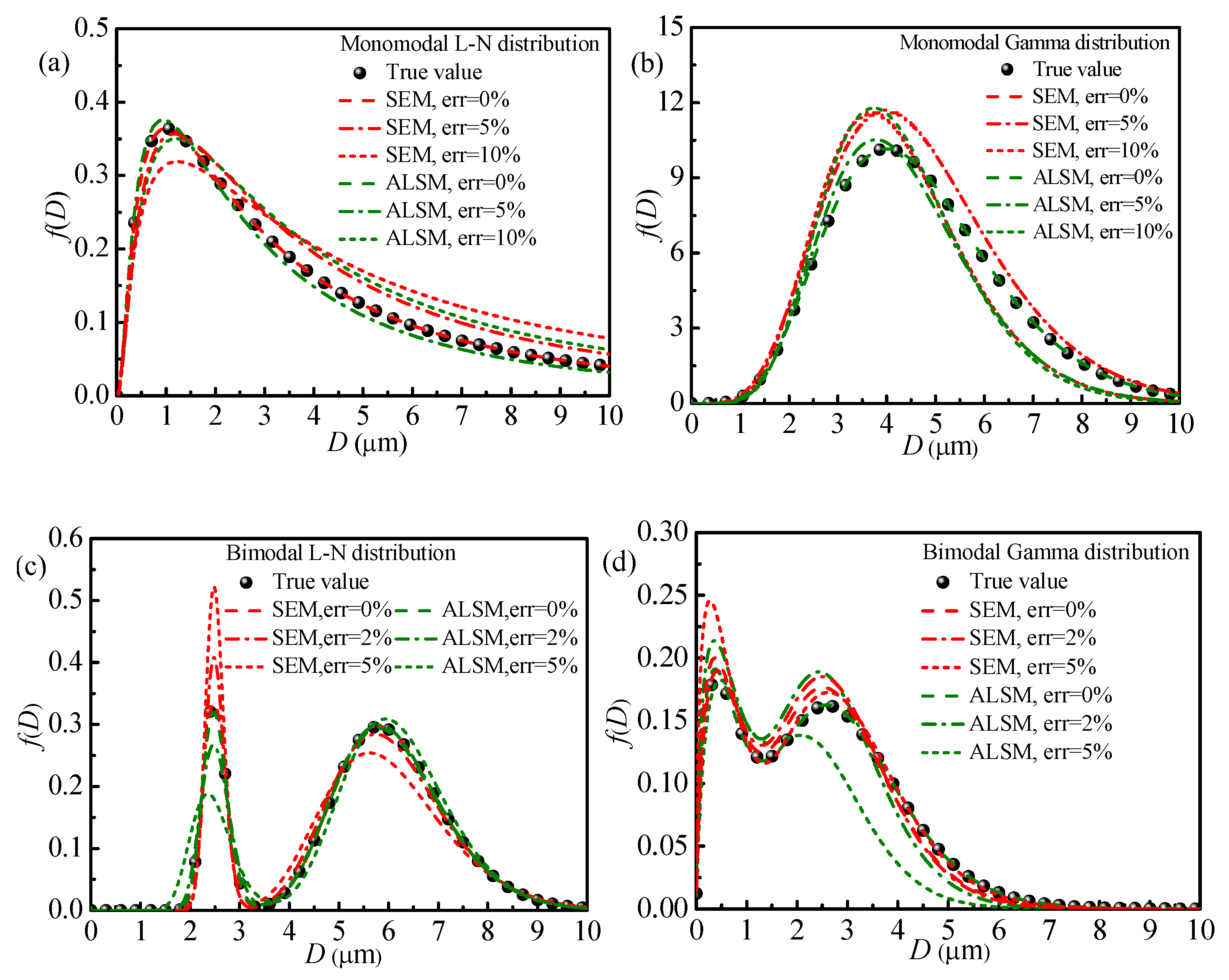
With the help of hybrid SPSO-DE algorithm, the ASDs mentioned above are reconstructed under different random measurement errors by using the SEM and ALSM, respectively, which are showed in
Table 4 and
Figure 5. Satisfactory retrieval accuracy can be obtained by both SEM and ASLM without measurement errors. The retrieval accuracy deteriorates with more random measurement errors, but are still reasonable even with 10% errors. Comparing the convergence accuracy of retrieval results by using the SEM with that by using the ALSM, it can be found that the robustness of retrieval results by using the ASLM is better than those by using the SEM. Moreover, in studying the bimodal ASDs, there is more satisfactory agreement between the estimated results and the true values of the major peak than those of the other peak.
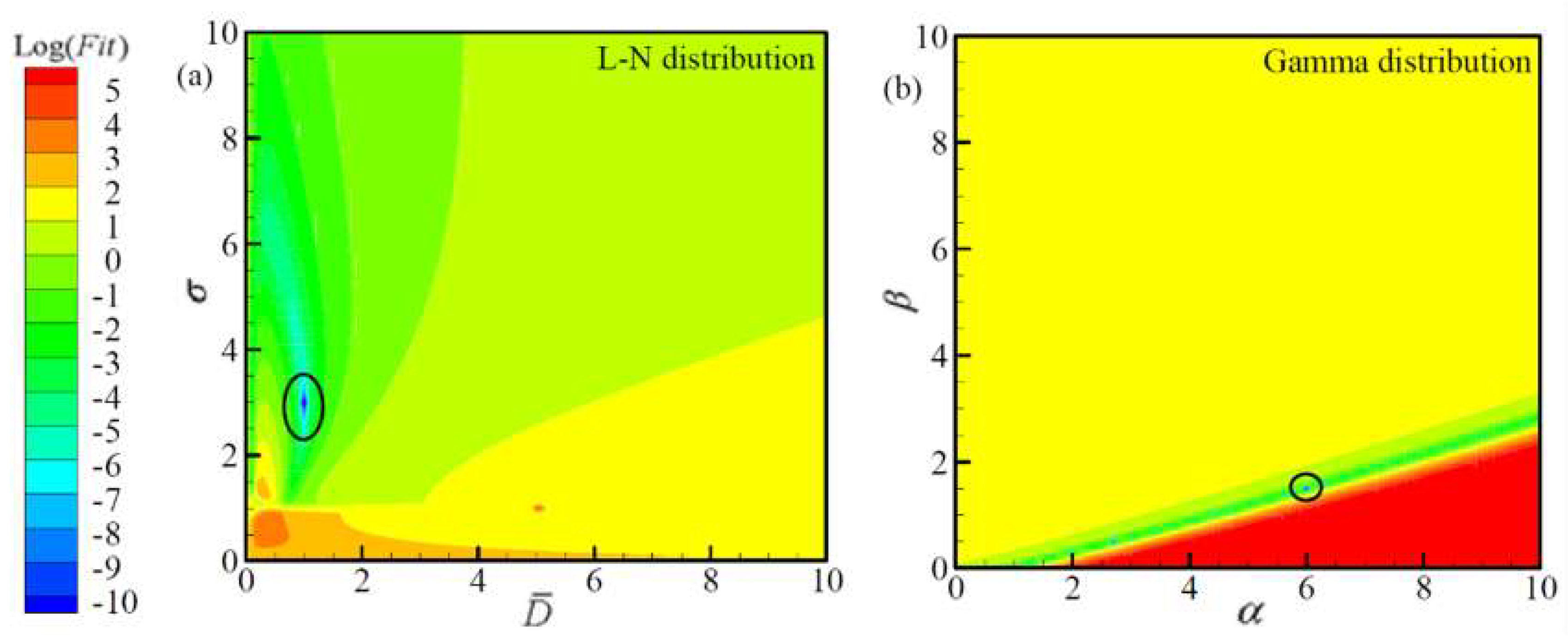
Figure 6 and
Figure 7 depict the distributions of the objective function values for monomodal ASDs by using two different type of optical measurement methods.
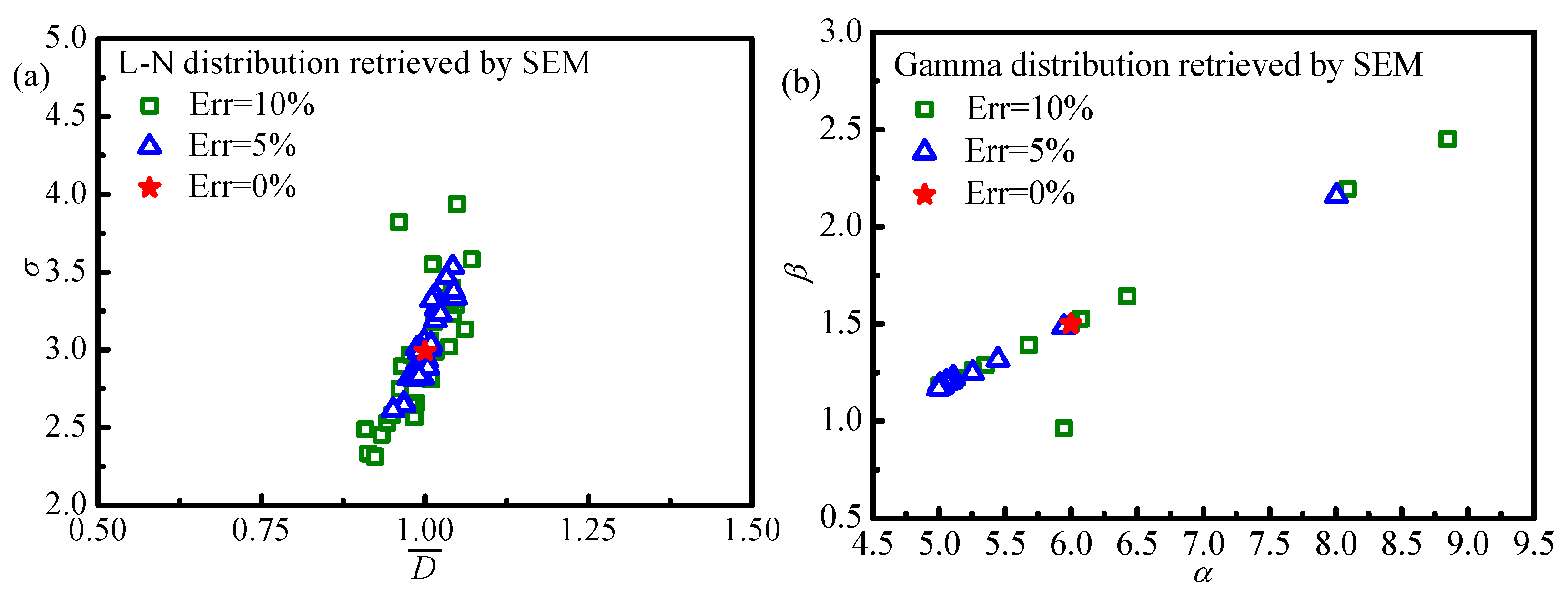
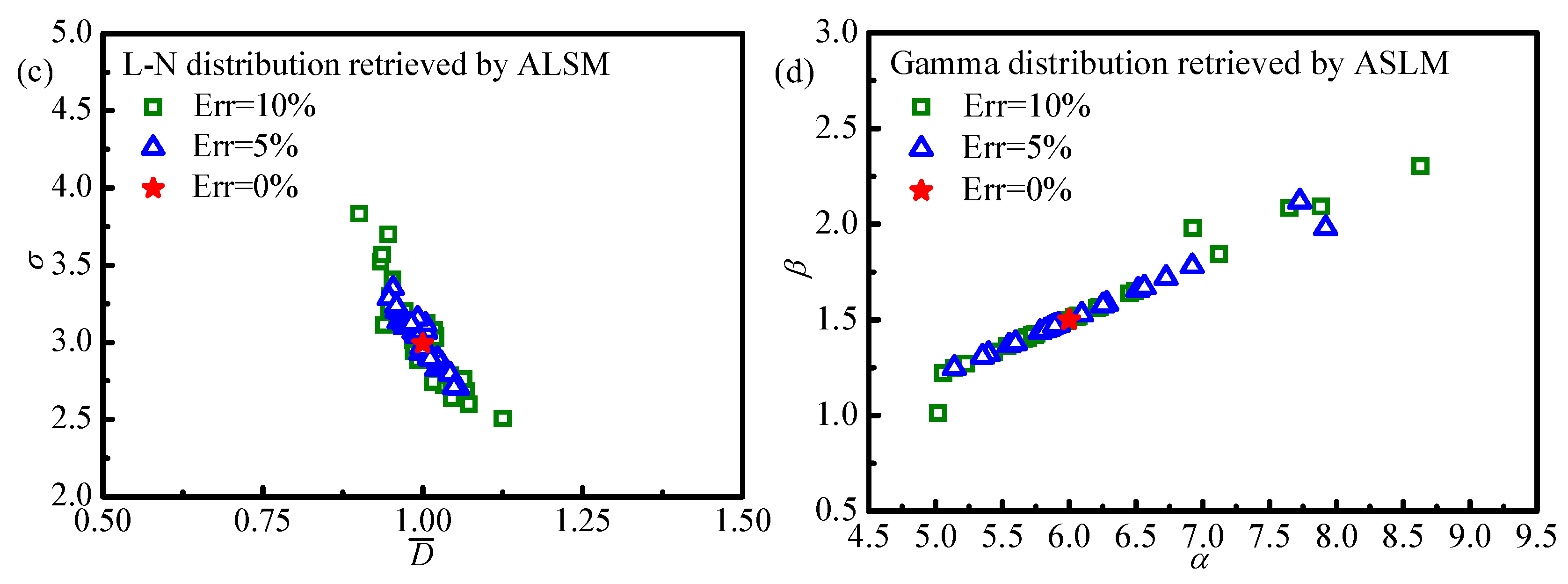
Figure 8 shows the corresponding distributions of estimated results. From
Figure 6 and
Figure 7, it is obvious that the minimum value region of the objective function is a point, which means the optimal retrieval result is unique, especially for the monomodal Gamma distribution. Moreover, comparing the distributions of objective function by using the SEM and that by using the ALSM, it is obvious that the objective function value by using the SEM is smaller than that by using the ALSM. So, to obtain more accurate retrieval results by using the SEM, the lower objective function value should be obtained during inverse calculation, which will increase the convergence difficulty and time. This phenomenon can explain the reason for the better retrieval accuracies by using the ALSM than those by using the SEM. From
Figure 8, it can be found that the distributions of the results retrieved by using the SEM show more dispersion than those retrieved by using ALSM, which also confirms the results obtained above.