Abstract
The widespread use of nanofiltration and electrodialysis membrane processes is slowed down by the difficulties in predicting the membrane performances for treating streams of variable ionic compositions. Correlations between ion hydration properties and solute transfer can help to overcome this drawback. This research aims to investigate the correlation between theoretically evaluated hydration properties of major ions in solution and experimental values of neutral organic solute fluxes. In particular, ion hydration energies, coordination and hydration number and the average ion-water distance of Na+, Ca2+, Mg2+, Cl− and SO42− were calculated at a high quantum mechanics level and compared with experimental sugar fluxes previously reported. The properties computed by simple and not computationally expensive models were validated with information from the literature. This work discusses the correlation between the hydration energies of ions and fluxes of three saccharides, measured through nanofiltration and ionic-exchange membranes. In nanofiltration, the sugar flux increases with the presence of ions of increasing hydration energy. Instead, inverse linear correlations were found between the hydration energy and the sugar fluxes through ion exchange membranes. Finally, an empirical model is proposed for a rough evaluation of the variation in sugar fluxes as function of hydration energy for the ion exchange membranes in diffusion experiments.
1. Introduction
Membrane technology is used in a number of civil and industrial applications such as the food industry, biological and chemical fields, pharmaceutical productions, water treatment, complex fluid treatment, gas separation and more [1,2,3]. Its increasing widespread use is due to its ability to meet the process intensification requirements: low energy demand, selective transport of specific compounds, potential to boost reaction processes and reduced soil consumption. The treatment of complex fluids is an active field in industrial applications for both economic reasons and sustainability.
In this frame, nanofiltration (NF) plays a fundamental role, while electrodialysis (ED) has found a second life [4]. Salty environments are very common in applications where nanofiltration and electrodialysis are used and previous studies have shown that the nature and concentration of ions affects the transfer of neutral organic solutes through these kinds of membranes [5,6,7,8]. The impact of the electrolytes on the organic solute fluxes was investigated experimentally. It was found that in nanofiltration [5], ions with a larger hydration shell cause an increase in the sugar fluxes, whereas Galier et al. [6,9] highlighted that the sugar fluxes decrease when an ionic exchange membrane (IEM) is equilibrated with counter-ions with a larger hydration number.
The transfer of neutral organic matter through a membrane is governed by two key factors: the free volume/pore size of the membrane and the solute dimension. In particular, the neutral organic matter transfer could increase if there is an increase in the free volume/pore size of the membrane or if there is a decrease in the solute dimension, or a combination of both. Thus, if the transport rate changes, the membrane properties or the solute properties should change. In the literature, several works assume that the influence of ions on the transfer of neutral organic solutes through a NF membrane is related to the change in solute dimension [5,10,11]. However, other works explain the influence of the ions by a modification in the free volume/pore size of the membrane [7,8]. Fuoco et al. [12,13] performed quantum and molecular mechanics calculations to evaluate the noncovalent interactions between sugars and a cation exchange polymer (equilibrated with the investigated counter-ions) as well as among the polymer chains. It was stated that the influence of the counter-ions on the sugar fluxes is correlated with a change in the membrane properties, in agreement with the empirical interpretation given by Galier et al. [6]. The conclusion, reported in reference [13], claims that the ion effect on the IEM is mainly due to the modification of free volume, but in a dynamic way that has a different cohesion energy between the polymer chains. In order to clarify that membrane change is the driving force behind these correlations, Fuoco et al. calculated some key properties of the counter-ions interacting with the negative fixed charges along the polymer chains, i.e., the properties of the counter-ions in the bulk of the soaked membranes. Compared to previous work, herein we have theoretically verified the correlations between saccharide permeability and the hydration properties of the counter-ions in solutions. The computed hydration properties, independent from particular experimental conditions, are more suitable for the development of a subsequent predictive model. Moreover, even if water is used as solvent in these calculations, the same procedure can be proposed for the calculation of the hydration properties of the ions in non-aqueous solutions. When determined experimentally, hydration numbers, as well as the hydration energies of ions, depend on the experimental methods used [14]. For example, during the evaluation of the coordination number, it is very common to obtain data from the salts, and not for the single dissolved cation or anion in dilute solutions; thus, the criteria used to split the contributions can confer some differences. With the development of computing approaches, such as the one presented here, the properties of ions in solution can be evaluated independently from particular experimental conditions and methodologies [15].
In particular, we present an ab-initio computational method to investigate the hydration properties of ions correlated with organic solute transfer, both in nanofiltration and IEM. The main hydration properties of some cations and anions were experimentally recognized to affect the transfer of neutral organic solutes, such as coordination and hydration number (CN, NH), average ion-water distance (d) and hydration energy. Hydrated ion clusters were modeled considering the various number of water molecules, and then the ion-water interaction energies were calculated as a function of the increasing number of H2O molecules. The computed CN, NH and average ion-water distance are correlated with the experimental data obtained in previous works concerning sugar transfer through nanofiltration [5] and IE membranes [6]. Moreover, an empirical model is proposed for a rough evaluation of the variation of sugar fluxes as a function of hydration energy for the ion exchange membranes in diffusion experiments.
2. Materials and Methods
2.1. Computational Details
The quantum calculations were carried out in the framework of density functional theory (DFT) using the X3LYP potential and energy functional [16,17]. This functional is well known for its reliability in describing H-bonds in clusters involving ions. Generally, similar systems have shown an error of less than 1.5 kcal mol−1 for each H-bond [18]. All the water-ion clusters were fully optimized using analytical energy gradients and the quasi-Newton optimization with approximate energy Hessian updates [19]. The convergence thresholds were 4.5 × 10−4 and 3.0 × 10−4 a.u. for the maximum and root-mean-square gradient, respectively, and (1.8 and 1.2) 10−3 a.u. for the maximum and root-mean-square of the Cartesian displacements, respectively. The energy convergence threshold for the self-consistent field procedure was set to 10-6 a.u., and the root-mean-square of the electron density was set to 10−5 a.u. The reliability of these thresholds was proven in previous studies [12,13,20]. The “6-31+G*” atomic orbital basis sets were used for H, O, Na, Mg, Ca and S while “6-311++G**” were used for the optimization in which Cl− was involved. Polarization orbitals were used since they give appreciable contributions for the hydrogen bonding modeling [21], while the diffuse function is required for a better description of cations and oxygen-containing systems [22,23].
The ion-water interaction energy, ΔEiw (kcal mol−1), is calculated as the difference between the energy of the complex, EComplex, and those of the two single fragments, i.e., the single ion, Eion, and the optimized water cluster around it, EHyd.shell.
ΔEiw = EComplex − Eion − E Hyd.shell
Basis set superposition error (BSSE) correction [23] was applied to increase the accuracy of the calculated interaction energy [24,25].
The starting geometries of each cluster, containing an increasing number of water molecules around the target ions (from 1–16), were built each time ex-novo. Examples of the initial highly symmetrical structures are shown in Figure 1. In the starting geometries, the distances between cations and oxygen atoms of the first water molecules were set at 2.3 Å, while it was set at 2.1 Å for the closest hydrogen atoms and the Cl− anion. For the SO42−, the distance between the sulfur atom and the hydrogen of the water molecules was set at 3.6 Å. These distances were chosen to avoid dummy H-bonds in the starting geometry.
Figure 1.
Initial structure with 16 H2O for the Mg2+ cation on the left, and the SO42− anion on the right.
To avoid confusion, with the term coordination number, CN, we have indicated the total number of water molecules directly interacting with the target ions. A molecule of water is considered directly interacting with the central ion if the ion-water distance is less than 2.8 Å for monoatomic ions [25] while, for the SO42− anion, a hydrogen bond has to be formed between the H2O molecule and one oxygen of the sulfonated molecule. The geometrical thresholds, used to establish the H-bond formation, were a donor-acceptor distance of 2.1 Å and a cutoff angle of 120° [26]. Instead, the hydration number, NH, is defined as the number of water molecules required for achieving the asymptotic convergence of the interaction energy. It corresponds to the first points of the plateau in the curves displaying the variation of the interaction energy versus the number of interacting water molecules, as shown in Figure 2. Thus, the coordination number plus any successive shells forms the total hydration shell of the considered ions.
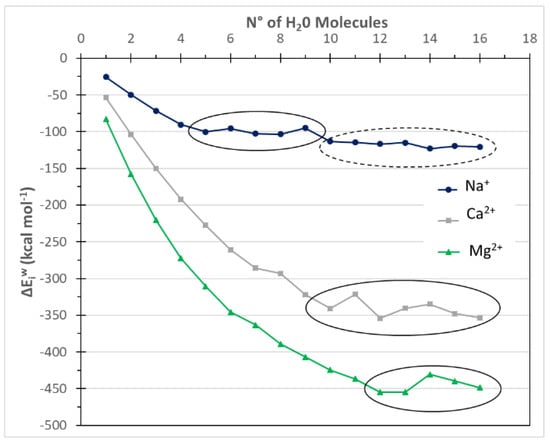
Figure 2.
ΔEiw for the target cation as function of the hydration level, i.e., N° is the number of water molecules. Solid circles indicate the ΔEiw plateaus referred to the first hydration shell, while the dashed circle indicates the formation of the second hydration shell.
2.2. Experimental Conditions
In this work, we used some experimental fluxes from the literature that were carried out under diffusion conditions on NF or IE membranes as a reference, i.e., the sugar transfer is governed by the difference of concentration across the membrane, without other driving forces. In particular, the works of Boy et al. [5] and Galier et al. [6] were chosen as references for the NF and IE membranes respectively. This decision was made since the experiments were carried out under the same conditions: the temperature was set at 25 °C and the initial saccharide and electrolyte concentrations were fixed at 1 mol L−1 and 1 equiv. L−1, respectively. Moreover, the experiments were carried out with the same saccharides of increasing weights, i.e., xylose (150.13 g mol−1), glucose (180.16 g mol−1) and sucrose (342.29 g mol−1).
The nanofiltration experiments were carried out with a Dow Filmtec NF-45 membrane, which has an average molecular weight cut-off of 150–200 g mol−1 [5], while an electrodialysis stack (EUR-2B-10, Eurodia Industries, France) equipped with cation exchange (CMX) or anion exchange (AMX) membranes was used for the experiments on ion exchange membranes [6].
3. Results and Discussion
3.1. Ion Hydration Properties
The interaction energies between the target cations and the water molecules as a function of the number of H2O molecules, i.e., for different hydration levels, were modelled by using the approach illustrated in the previous section and reported in Figure 2 and Figure 3. Two different regions can be observed for each curve. In the initial stage, the interaction energy drastically decreases as the number of water molecules increases. The energy difference between two consecutive points is the contribution of the last added water molecule to the more stable water-ion cluster. The second region is when the interaction energy, ΔEiw, does not significantly change by the addition of other water molecules. At this stage, an energy plateau is reached and the ion hydration shell is considered completed. This means that the addition of further water molecules does not change the hydration cluster surrounding the ion. The structures at the beginning of the plateau are used for model validation and further comparison with experimental fluxes.
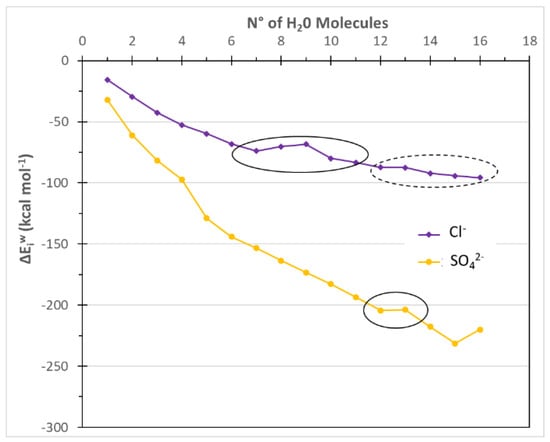
Figure 3.
ΔEiw for the anions as function of the hydration level. Solid circles indicate the ΔEiw plateaus referred to the first hydration shell, while the dashed circle indicates the formation of the second hydration shell.
The computed results were summarized in Table 1 and compared with experimental data taken from the literature in order to assess the reliability of the computational approach. In general, the computational values and experimental data show a good agreement, highlighting the reliability of the computational method used. The hydration number is the number of water molecules at the starting point of the first plateau in Figure 2 and Figure 3. For Na+ and Mg2+, CN values of 5 and 6 were obtained in agreement with the literature values; moreover, the coordination number of Cl− and SO42− were also well reproduced (Table 1). It is worth noting that for some ions such as Na+ and Cl−, the CN and NH values are equal or quite similar. On the contrary, the CN and NH are different for the other ions.

Table 1.
Comparison between computed (grey rows) and experimental (from literature, white rows) solvation properties: coordination number (CN), ion-water minimum distance (d), hydration number (NH), hydration energy and hydration enthalpy (ΔH).
For Na+ and Cl−, two plateaus are found in Figure 2 and Figure 3, which means that the second hydration shell is formed for the two small ions with 10 or 12 water molecules respectively. In this paper, the interaction energies of the first hydration shells were correlated with the sugar fluxes through NF and IE membranes. Thus, for Na+ and Cl− ions, the interaction energies of the clusters with a higher hydration level are not used.
The minimum distances between water molecules and ions were also well reproduced. Although the clusters containing Mg2+ and Na+ show equal coordination numbers, the shorter Mg2+-H2O distance, i.e., 2.09 Å, with respect to the Na+-H2O length (2.40 Å) is well reproduced, in agreement with the literature data. A deeper discussion on the structural properties of these hydrated ions, investigated by this computational methodology, including the analysis of the coordination structure, is reported elsewhere [20].
In general, the interaction energy is related to thermodynamic properties, such as the Gibbs free hydration energy and/or the hydration enthalpy of the solvated ions. The comparison between the computed ΔEiw and the experimental hydration enthalpy, ΔH, presented in Table 1, shows that the computational method used for characterizing the properties of the target ions interacting with the water molecules is sufficiently accurate.
3.2. Hydration Energy vs. Experimental Sugars Fluxes through NF or IE Membranes
The computed hydration numbers follow the trend NHNa+ < NHCa2+ < NHMg2+ for cations and NHCl− < NHSO42− for anions (Table 1). A higher ion hydration number gives an increase in the sugar flux with the NF membrane (JNa+ < JCa2+ < JMg2+ in reference [5]). Remarkably, an increase of the ion hydration number leads to a decrease of sugar flux with the IEM (JNa+ < JCa2+ < JMg2+ in reference [6]). In general, higher NH corresponds to higher impact of the ion on the sugar flux for the two membrane systems. One can also remark that no correlation between the experimental sugar fluxes and ion coordination number was found (CNNa+ ≈ CNMg2+ < CNCa2+). Even if these two quantities are strictly related, CN takes into account only very local interactions that do not influence macroscopic properties. On the other hand, NH can be correlated with the macroscopic fluxes since it is also related to long range interactions.
Figure 4 shows the experimental fluxes obtained by Boy et al. [5] with a NF membrane for xylose, glucose and sucrose versus the hydration energies computed in this study. Firstly, the experimental flux for each investigated sugar increases with increasing hydration energy of the ions in solution. Thus, the computed hydration energies between ions and water molecules correlate with the experimental fluxes of the sugars. Boy et al. [5] already reported a correlation between the sugar flux and a volumetric property of the sugar/electrolyte solution, the partial molar volume, which characterizes the hydration of the sugar.
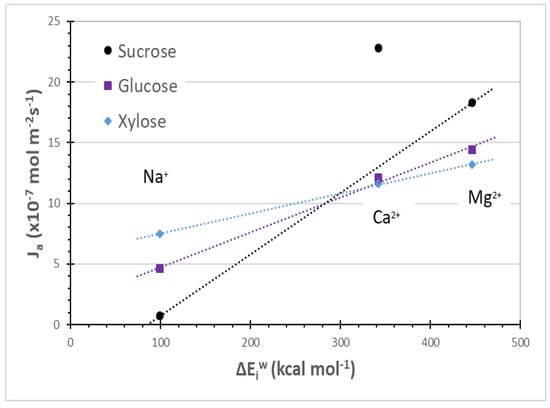
Figure 4.
Sugars fluxes through a NF membrane versus cation hydration energies (Cl− is used as common anion). Sugar fluxes (Ja) measured in diffusion regime [Sugar] = 1 mol L−1 [electrolyte] = 1equiv. L−1 [5].
At the molecular level, the hydration shell of the sugar is composed of two kinds of water molecules: strongly interacting ones forming hydrogen bonds with the sugar OH groups and weakly interacting ones forming only weak interactions with the hydrated sugar structure. These two kinds of water molecules behave in very different ways. The weak interacting water molecules can be easily lost by the sugar during the transfer through the membrane, because their removal from the hydration shell does not require much energy. On the contrary, the strongly interacting water molecules cannot be easily lost even in confined spaces, i.e., during the transfer through the membrane, due to the energy needed to break the hydrogen bonds. The strength of these hydrogen bonds, and thus the energy needed to dehydrate the sugar, can be influenced by electrostatic interactions with ions in solution. When ions and sugar are at an interaction distance such as that which exists at the solution-membrane interface, the ions influence the electron density of the system, modifying the energy of noncovalent interactions between the strongly bound water molecules and the sugars. A cation with a stronger interaction energy reduces the strength of the sugar-water interactions. As a consequence, the sugar can lose one or more water molecules during its transfer through the membrane, resulting in a smaller hydration shell and thus a smaller effective diameter. The correlations found here support the above described molecular mechanism (i.e., the ion showing greater interaction with the water molecules can also affect the water molecules coordinating the neutral organic solute, and then influence the sugars fluxes in NF processes), although further molecular modeling is necessary for a deeper investigation.
Secondly, the slope of the curves in Figure 4 is correlated with the sugar size. The slope is higher for increasing sugar size, as can be observed by comparing the results obtained with the three different sugars. Although xylose and glucose have similar chemical structures, glucose (C6H12O6) is bigger than xylose (C5H10O5), and has more OH groups in the structure. The additional OH groups make the glucose hydration shell larger than the xylose, since the OH groups form more hydrogen bonds with the water molecules. As pointed out, ions at interaction bonding distance change the strength of these H-bonds, modifying the effective hydration shell of the sugars. The effective size of a sugar is strongly dependent on its hydration shell, as well as on its geometrical structure. Electrolytes in solution affect the sugar hydration shell, where one sugar with a bigger effective size in pure water can show smaller effective dimensions in the presence of electrolytes in solution. It can be dependent on the degree of interaction between electrolytes and water molecules; thus, it may be related to ion hydration energy.
Particular is the behavior of the sucrose in presence of Ca2+ due to its specific interactions with the sucrose. In fact, specific interactions among electrolytes and sugars were already observed, especially between fructose and Ca2+ [36,37]. Because the sucrose is composed of two subunits, glucose and fructose, it is reasonable to extend the explanation of the specific interactions among divalent cations and fructose to the sucrose. However, these conclusions should be confirmed by deep molecular modeling since accurate experimental measurements of these interactions are very difficult.
Ion exchange membranes were also found to be sensitive to the composition of the electrolyte solutions. In fact, in diffusion conditions, it has been experimentally observed that the ions act prevalently on the membrane transport properties [6,27]. The electrolytes present in solution show an opposite effect to that observed with the NF membrane. For both CMX and AMX membranes, electrolytes with ions of higher hydration energies induce a decrease in the sugar fluxes.
In Figure 5, the fluxes of the three investigated sugars, as obtained through ion exchange membranes in the diffusion regime by Galier et al. [6], are reported as a function of the hydration energies of the ions used to equilibrate the fixed charge of the membranes. In these cases, all fluxes linearly decrease with respect to the ion hydration energies. A correlation between the computed ion hydration energies and the experimental sugar fluxes is found according to the following relationship:
where Ja is the sugar flux measured through an ionic exchange membrane equilibrated with a given counter-ion. It is essential to pay close attention to the above correlation since the two quantities refer to different chemical environments. Indeed, Ja is the sugar flux through the IE membrane while the ion hydration energy refers to the interaction between the ion and water molecules in solution as obtained in the plateau limit. As a result, a distinction between the ion-water interaction in the polymer matrix and the ion-water interaction in the bulk solution should be made. In a previous study [13], we have investigated the correlation between the ion-water interaction in a CMX membrane and sugar fluxes. It was concluded that cations affect the membrane properties prevalently.
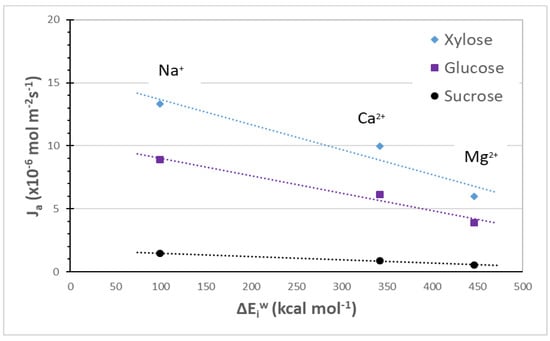
Figure 5.
Sugars fluxes through cation exchange membranes (CMX) versus cation hydration energies (Cl− is used as common anion). Sugar fluxes measured in diffusion regime [Sugar] = 1 mol L−1 [electrolyte] = 1equiv. L−1 [6].
Considering the inverse proportionality between experimental fluxes and computed hydration energies, an empirical correlation was defined:
where Ja and Jb are the sugar fluxes through the membranes equilibrated with a and b counter-ions, respectively, while the hydration energies are normalized with respect to the valence of the considered ions, za, and zb. The valence of the ions is used since a divalent ion can equilibrate two functional groups of the membrane. In Table 2, the ratios between the experimental fluxes of the investigated sugars through CMX membranes equilibrated with Ca2+ and Mg2+ were compared with the ratios of the hydration energies of the same ions normalized with respect to the sodium hydration energy. Also in Table 2, the same quantities referring to the sugar fluxes through AMX membranes equilibrated with Cl− and SO42− were compared. For both membranes, the hydration energies, normalized with respect to the valence ratios outlined in Equation (3), give a satisfactory evaluation of the ratios between sugar fluxes through IEMs equilibrated with the considered ions. For example, the computed value of (hydration energyMg2+/zMg2+)/(hydration energyNa+/zNa+) is 2.25, while the experimental values of the associated fluxes ratios are 2.22, 2.28 and 2.5. In the case of Ca2+, the ratio between normalized hydration energies is 1.51, which is comparable with the ratios between the sugar fluxes of sucrose. Even if this comparison cannot fully describe the system, since other parameters such as molecular size should also be considered, there is a clear trend of the effect on the cation or anion in solution and the performance of the membrane. This empirical model should be used to get an idea of the order of magnitude of the impact of ion properties on the neutral mass transfer through these membranes, and not as a fully quantitative model for the entire application.

Table 2.
Summary of the normalized ions properties and sugar fluxes measured with CMX or anion exchange (AMX) membranes.
4. Conclusions
In this work, CN, NH, ion-water average distance and the hydration energies of Na+, Ca2+, Mg2+, Cl− and SO42− were evaluated by an accurate quantum mechanics computational approach. The calculation of these properties was validated by comparing their values with experimental data from the literature. The agreement between theoretical and experimental values was good, showing that the proposed computational procedure is reliable. Once the reliability of the computational approach was established, the experimental fluxes of three sugars through nanofiltration and ion exchange membranes, as obtained in a previous investigation, were plotted as a function of the computed hydration energies.
In nanofiltration, the sugar flux increases with the presence of ions of increasing hydration energy in the bulk solution, i.e., ions having a stronger interaction with the water clusters constituting their hydration shell. On the contrary, the sugar flux through an ion exchange membrane, equilibrated with the same electrolyte that is present in the solution, decreases as the hydration energy of the investigated ions increases. Moreover, for the IEM case, a quantitative correlation between the theoretical hydration energy of the ions and the sugar fluxes was pointed out. Specifically, this relationship correlates the fluxes of the considered sugars through ion exchange membranes, where the counter-ions in solution balance the negative or positive charges of the polymer chains with the hydration energy of these counter-ions. A good agreement is obtained by comparing the ratios between the hydration energies of a pair of ions with those between the related experimental sugar fluxes. The influence of ions on the mass transfer through nanofiltration or ion exchange membranes is a challenging field. The correlations found in this work between computed hydration energies and experimental sugar fluxes can help to face this challenge. Considering the simplicity of the model used in this work, the same computational procedure can be used for the investigation of the ion properties in non-aqueous solutions, paving the way for the first approximation of membrane performance when complex fluids are treated. This research encourages further work that should be carried out to better understand the involved mechanisms at the molecular scale, such as the study of sugar hydration shells in constricted space, i.e., pores of nanofiltration membranes or microstructures of the polymer network of ion exchange ones, or in the presence of non-aqueous solvents.
Author Contributions
Conceptualization, A.F., S.G., H.R.-d.B. and G.D.L.; Data curation, A.F.; Formal analysis, A.F.; Funding acquisition, H.R.-d.B. and G.D.L.; Supervision, S.G., H.R.-d.B. and G.D.L.; Validation, A.F.; Writing—review & editing, A.F., S.G., H.R.-d.B. and G.D.L.
Funding
The authors would like to thank the Education, Audiovisual and Culture Executive Agency (EACEA) under the Program “Erasmus Mundus Doctorate in Membrane Engineering”—EUDIME (FPA 2011-0014, http://www.eudime.unical.it) for funding this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van der Bruggen, B. Membrane Technology; Major Reference Works; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; ISBN 9780471238966. [Google Scholar]
- Noble, R.D.; Stern, A.S. Membrane Separations Technology Principles and Applications; Elsevier: Amsterdam, The Netherlands, 1995; Volume 2, ISBN 0927-5193. [Google Scholar]
- Nunes, S.P.; Peinemann, K. Membrane Technology: In the Chemical Industry; Nunes, S.P., Peinemann, K.-V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; ISBN 3527284850. [Google Scholar]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Boy, V.; Roux-de Balmann, H.; Galier, S. Relationship between volumetric properties and mass transfer through NF membrane for saccharide/electrolyte systems. J. Membr. Sci. 2012, 390, 254–262. [Google Scholar] [CrossRef]
- Galier, S.; Savignac, J.; Roux-de Balmann, H. Influence of the ionic composition on the diffusion mass transfer of saccharides through a cation-exchange membrane. Sep. Purif. Technol. 2013, 109, 1–8. [Google Scholar] [CrossRef]
- Bargeman, G.; Vollenbroek, J.M.; Straatsma, J.; Schroën, C.G.P.H.; Boom, R.M. Nanofiltration of multi-component feeds. Interactions between neutral and charged components and their effect on retention. J. Memb. Sci. 2005, 247, 11–20. [Google Scholar] [CrossRef]
- Wang, X.-L.; Zhang, C.; Ouyang, P. The possibility of separating saccharides from a NaCl solution by using nanofiltration in diafiltration mode. J. Membr. Sci. 2002, 204, 271–281. [Google Scholar] [CrossRef]
- Han, L.; Galier, S.; Roux-de Balmann, H. Transfer of neutral organic solutes during desalination by electrodialysis: Influence of the salt composition. J. Membr. Sci. 2016, 511, 207–218. [Google Scholar] [CrossRef]
- Bouranene, S.; Szymczyk, A.; Fievet, P.; Vidonne, A. Influence of inorganic electrolytes on the retention of polyethyleneglycol by a nanofiltration ceramic membrane. J. Membr. Sci. 2007, 290, 216–221. [Google Scholar] [CrossRef]
- Bouchoux, A.; Balmann, H.; Lutin, F. Nanofiltration of glucose and sodium lactate solutionsVariations of retention between single- and mixed-solute solutions. J. Membr. Sci. 2005, 258, 123–132. [Google Scholar] [CrossRef]
- Fuoco, A.; Zwijnenberg, H.; Galier, S.; Balmann, H.R.; De Luca, G. Structural properties of cation exchange membranes: Characterization, electrolyte effect and solute transfer. J. Membr. Sci. 2016, 520, 45–53. [Google Scholar] [CrossRef]
- Fuoco, A.; Galier, S.; Roux-de Balmann, H.; De Luca, G. Correlation between macroscopic sugar transfer and nanoscale interactions in cation exchange membranes. J. Membr. Sci. 2015, 493, 311–320. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, X.; Wang, Y.; Shi, J. Molecular dynamics study on ionic hydration. Fluid Phase Equilib. 2002, 194–197, 257–270. [Google Scholar] [CrossRef]
- Tongraar, A.; Michael Rode, B. The hydration structures of F− and Cl− investigated by ab initio QM/MM molecular dynamics simulations. Phys. Chem. Chem. Phys. 2003, 5, 357–362. [Google Scholar] [CrossRef]
- Bryantsev, V.S.; Diallo, M.S.; van Duin, A.C.T.; Goddard, W.A. Evaluation of B3LYP, X3LYP, and M06-Class Density Functionals for Predicting the Binding Energies of Neutral, Protonated, and Deprotonated Water Clusters. J. Chem. Theory Comput. 2009, 5, 1016–1026. [Google Scholar] [CrossRef] [PubMed]
- De Luca, G.; Gugliuzza, A.; Drioli, E. Competitive hydrogen-bonding interactions in modified polymer membranes: A density functional theory investigation. J. Phys. Chem. B 2009, 113, 5473–5477. [Google Scholar] [CrossRef] [PubMed]
- Ireta, J.; Neugebauer, J.; Scheffler, M. On the Accuracy of DFT for Describing Hydrogen Bonds: Dependence on the Bond Directionality. J. Phys. Chem. A 2004, 108, 5692–5698. [Google Scholar] [CrossRef]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Dam, H.J.J. Van; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. De NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Fuoco, A. Computational and Experimental Studies on Membrane-Solute Interactions in Desalination Systems Using Ion-Exchange Membranes; Université Paul Sabatier: Toulouse, France, 2015. [Google Scholar]
- Barkaline, V.V.; Douhaya, Y.V.; Tsakalof, A. Computer simulation based selection of optimal monomer for imprinting of tri-O-acetiladenosine in polymer matrix: Vacuum calculations. J. Mol. Model. 2013, 19, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, M.; Siegbahn, P.E.M.; Sandstrom, M. Hydration of Beryllium, Magnesium, Calcium, and Zinc Ions Using Density Functional Theory. J. Phys. Chem. A 1998, 102, 219–228. [Google Scholar] [CrossRef]
- Davidson, E.R.; Chakravorty, S.J. A possible definition of basis set superposition error. Chem. Phys. Lett. 1994, 217, 48–54. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry Introduction to Advanced Electronic Structure Theory; McGraw-Hill: New York, NY, USA, 1989; reprinted by Dover publications: Mineola, NY, USA, 1996. [Google Scholar]
- Cappa, C.D.; Smith, J.D.; Wilson, K.R.; Messer, B.M.; Gilles, M.K.; Cohen, R.C.; Saykally, R.J. Effects of Alkali Metal Halide Salts on the Hydrogen Bond Network of Liquid Water. J. Phys. Chem. B 2005, 109, 7046–7052. [Google Scholar] [CrossRef] [PubMed]
- Gugliuzza, A.; Luca, G. De; Tocci, E.; Lorenzo, L. De; Drioli, E. Intermolecular interactions as controlling factor for water sorption into polymer membranes. J. Phys. Chem. B 2007, 111, 8868–8878. [Google Scholar] [CrossRef] [PubMed]
- Persson, I. Hydrated metal ions in aqueous solution: How regular are their structures? Pure Appl. Chem. 2010, 82, 1901–1917. [Google Scholar] [CrossRef]
- Karlstrom, G.O. Anders A Combined Quantum Chemical Statistical Mechanical Simulation of the Hydration of Li+, Na+, F−, and Cl−. J. Phys. Chem. B 2004, 108, 8452–8459. [Google Scholar]
- Ikeda, T.; Boero, M.; Terakura, K. Hydration properties of magnesium and calcium ions from constrained first principles molecular dynamics. J. Chem. Phys. 2007, 127, 074503. [Google Scholar] [CrossRef] [PubMed]
- Musinu, A.; Paschina, G.; Piccaluga, G. On the structure of the NH+4 ion in aqueous solution. Chem. Phys. Lett. 1981, 80, 163–167. [Google Scholar] [CrossRef]
- Marcus, Y. Ion Properties; CRC Press: New York, NY, USA, 1997. [Google Scholar]
- Mezei, M.; Beveridge, D.L. Monte Carlo studies of the structure of dilute aqueous sclutions of Li+, Na+, K+, F−, and Cl−. J. Chem. Phys. 1981, 74, 6902. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Sokalski, W.A.; Dyguda, E.; Leszczyn, J. Quantitative Classification of Covalent and Noncovalent H-Bonds. J. Phys. Chem. B 2006, 110, 6444–6446. [Google Scholar] [CrossRef] [PubMed]
- Burda, J.V.; Pavelka, M.; Šimánek, M. Theoretical model of copper Cu(I)/Cu(II) hydration. DFT and ab initio quantum chemical study. J. Mol. Struct. THEOCHEM 2004, 683, 183–193. [Google Scholar] [CrossRef]
- Marcus, Y. The Thermodynamics of Solvation of Ions. Part 2. The Enthalpy of Hydration at 298.15 K. J. Chem. Soc. Faraday Trans. 1987, 83, 339–349. [Google Scholar] [CrossRef]
- Pedruzzi, I.; Borges da Silva, E.A.; Rodrigues, E.A. Selection of resins, equilibrium and sorption kinetics of lactobionic acid, fructose, lactose and sorbitol. Sep. Purif. Technol. 2008, 63, 600–611. [Google Scholar] [CrossRef]
- Nobre, C.; Santos, M.J.; Dominguez, A.; Torres, D.; Rocha, O.; Peres, A.M.; Rocha, I.; Ferreira, E.C.; Teixeira, J.A.; Rodrigues, L.R. Comparison of adsorption equilibrium of fructose, glucose and sucrose on potassium gel-type and macroporous sodium ion-exchange resins. Anal. Chim. Acta 2009, 654, 71–76. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).