Aerodynamic Optimization of Airfoil Profiles for Small Horizontal Axis Wind Turbines
Abstract
:1. Introduction
2. Model Description
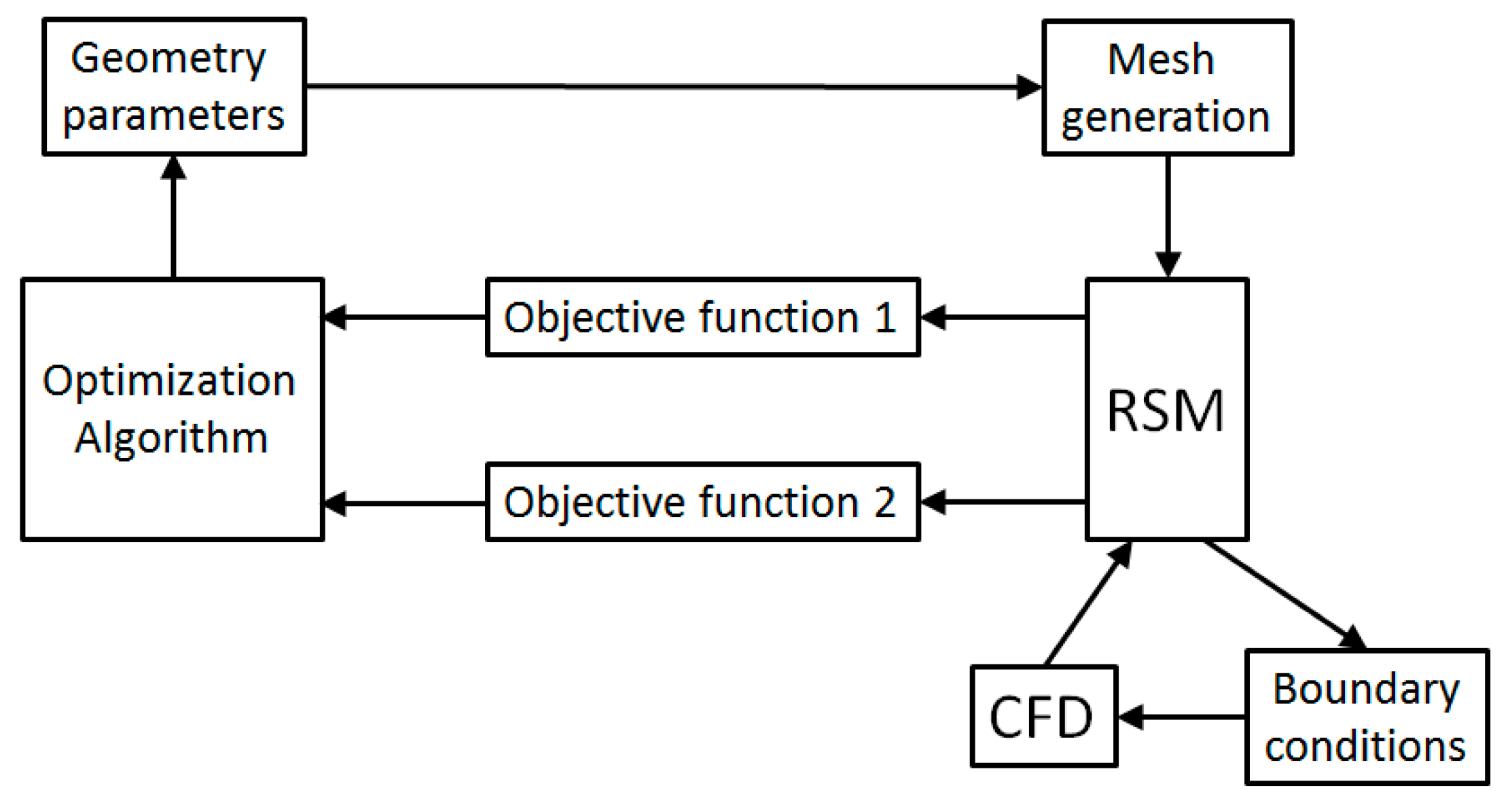
2.1. Overview of the Optimization Procedure
2.2. Mathematical and Numerical Modelling of the Aerodynamics
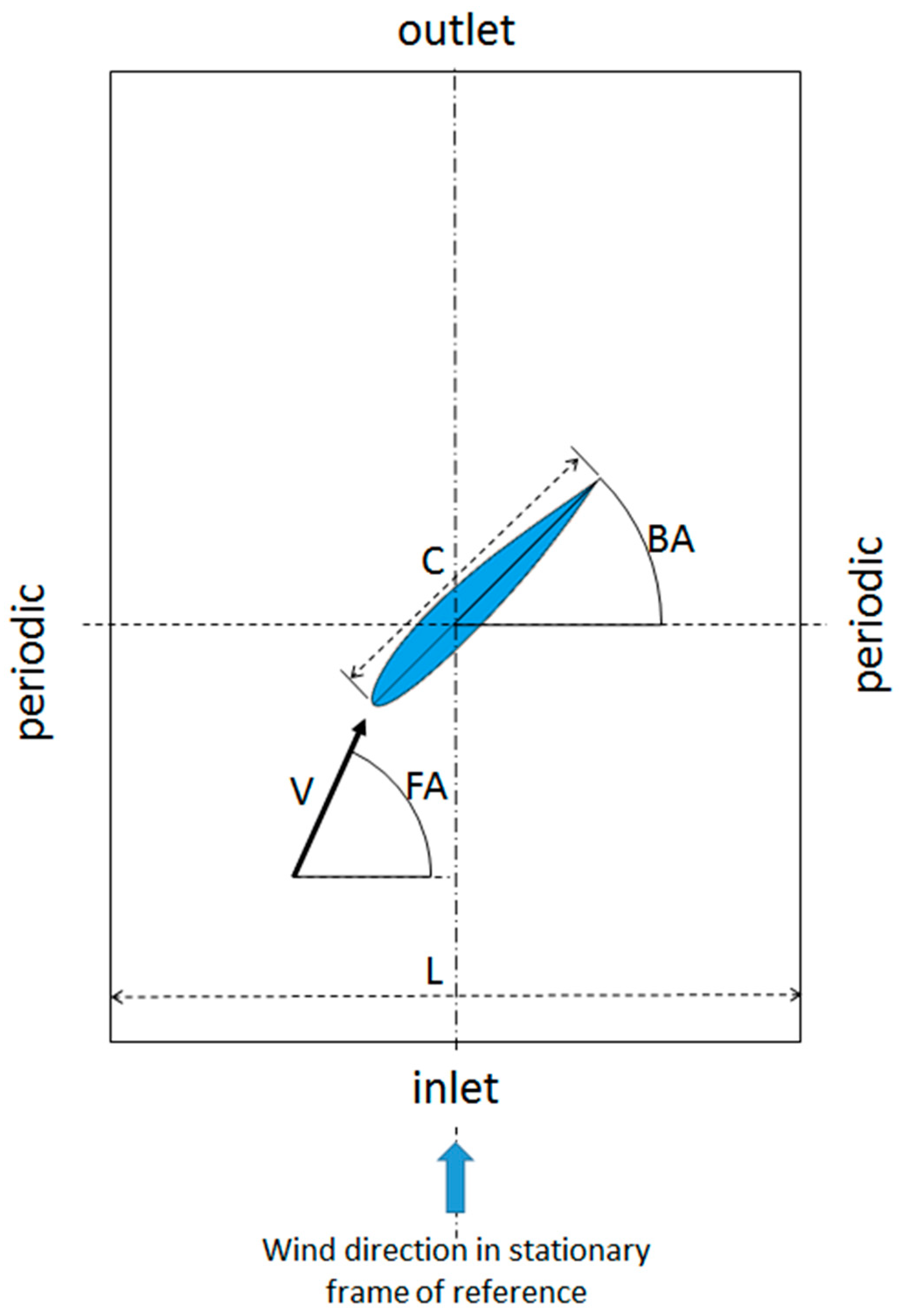
2.3. Flow Solution Domain and Boundary Conditions
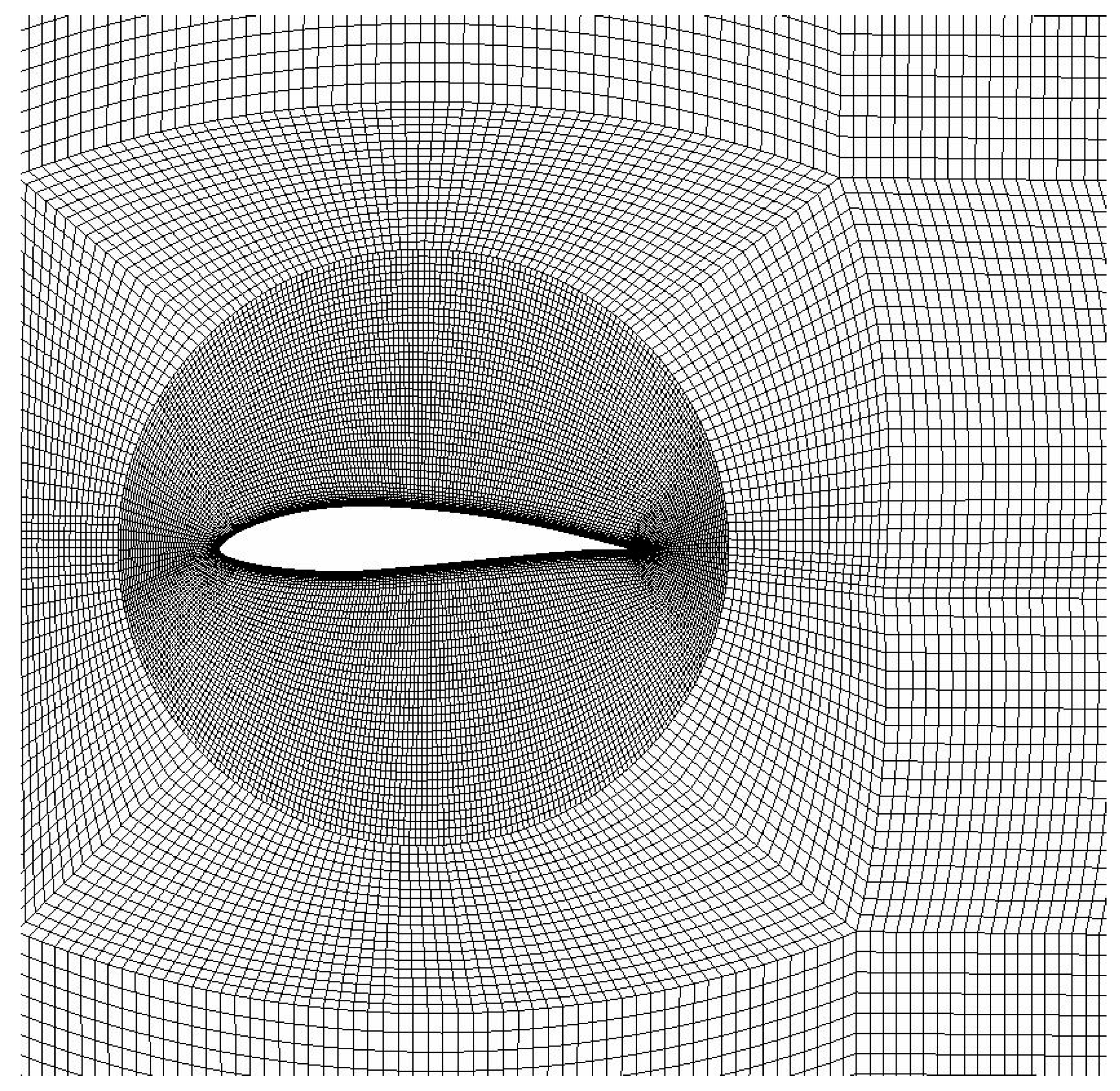
2.4. Generation of Computational Grid for Flow Simulation
2.5. Parametrization of the Airfoil Shape
2.6. Response Surface Methodology and the Optimization Algorithm
3. Results
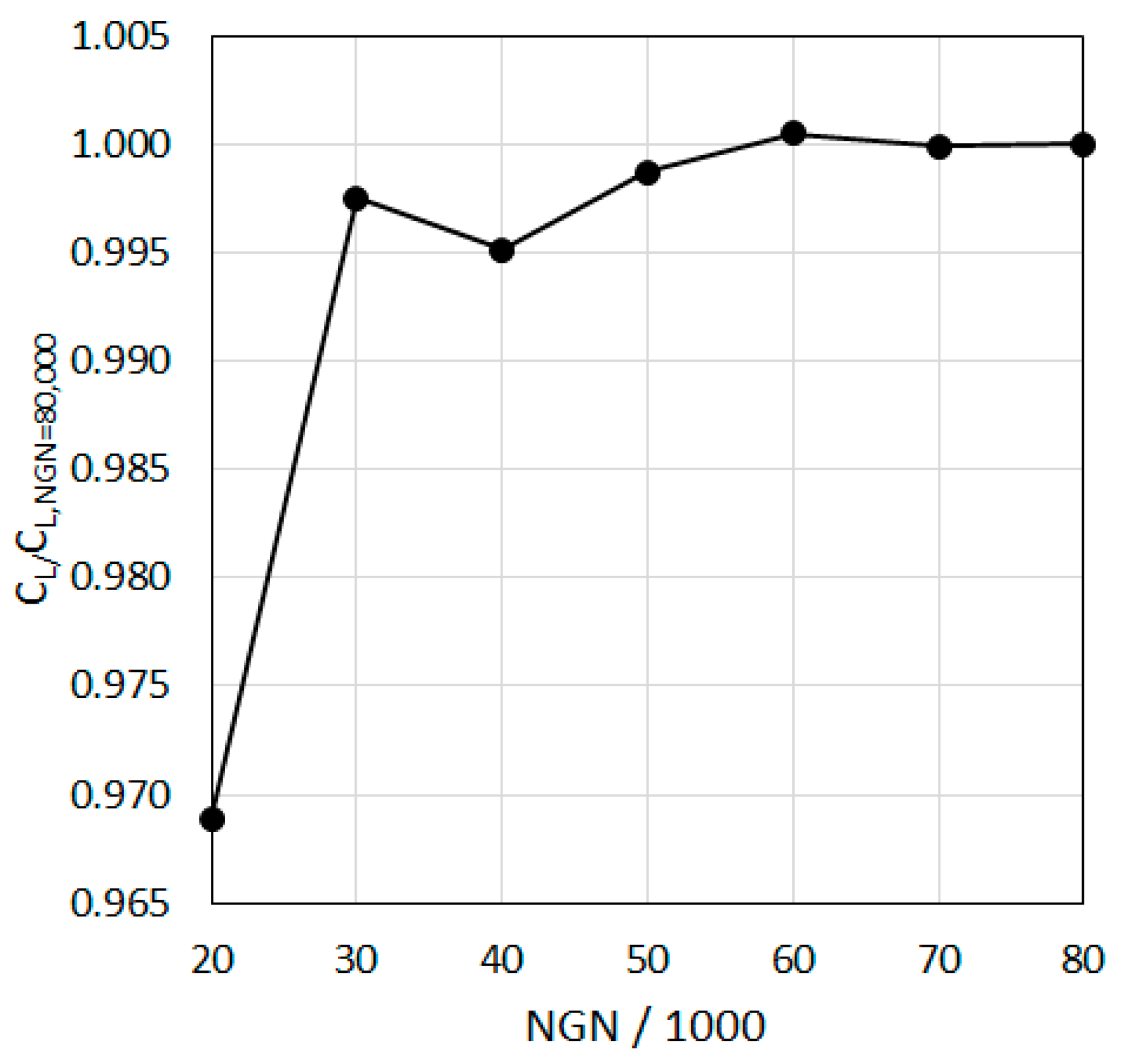
3.1. Grid Independence
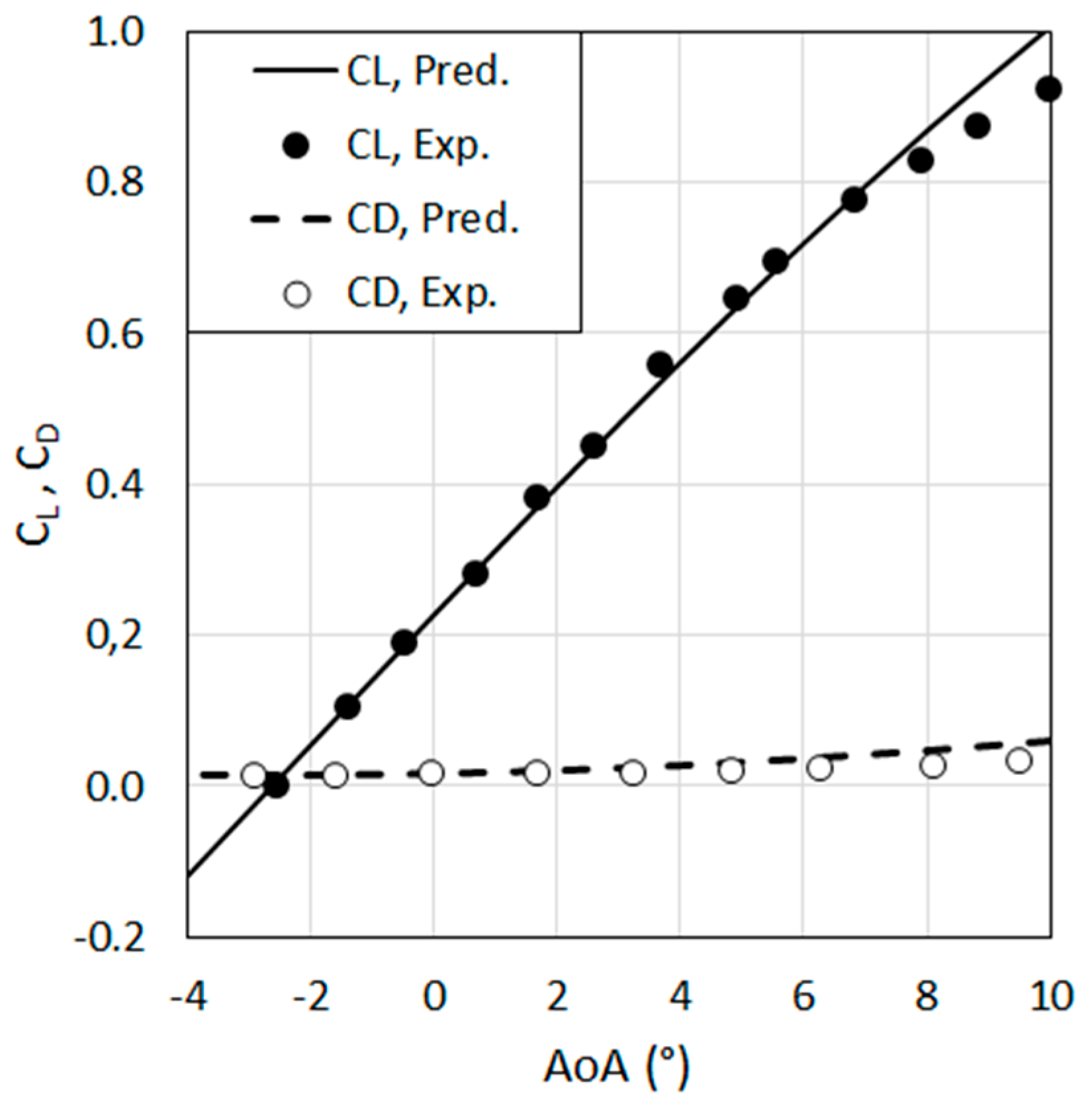
3.2. Validation
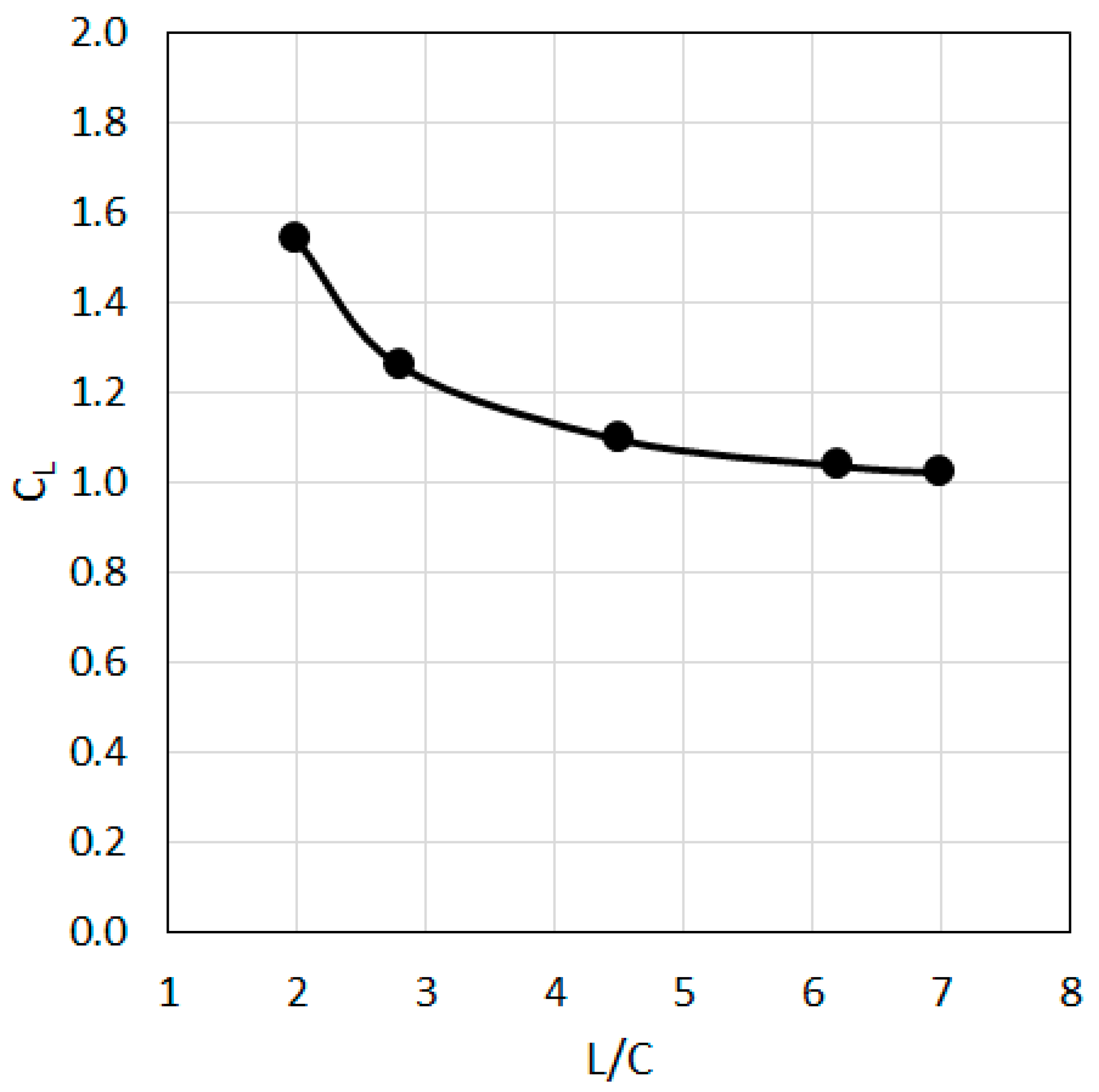
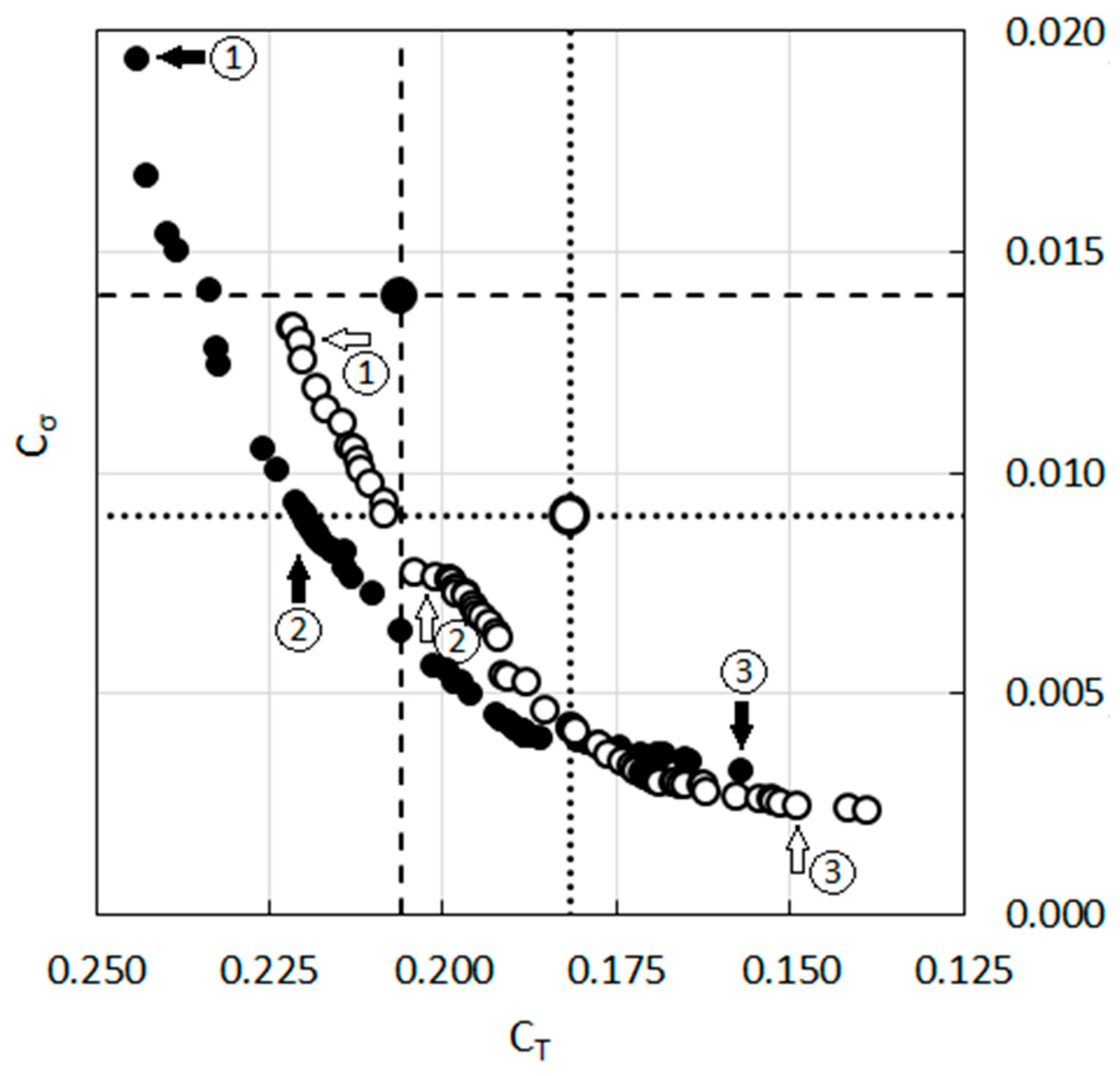
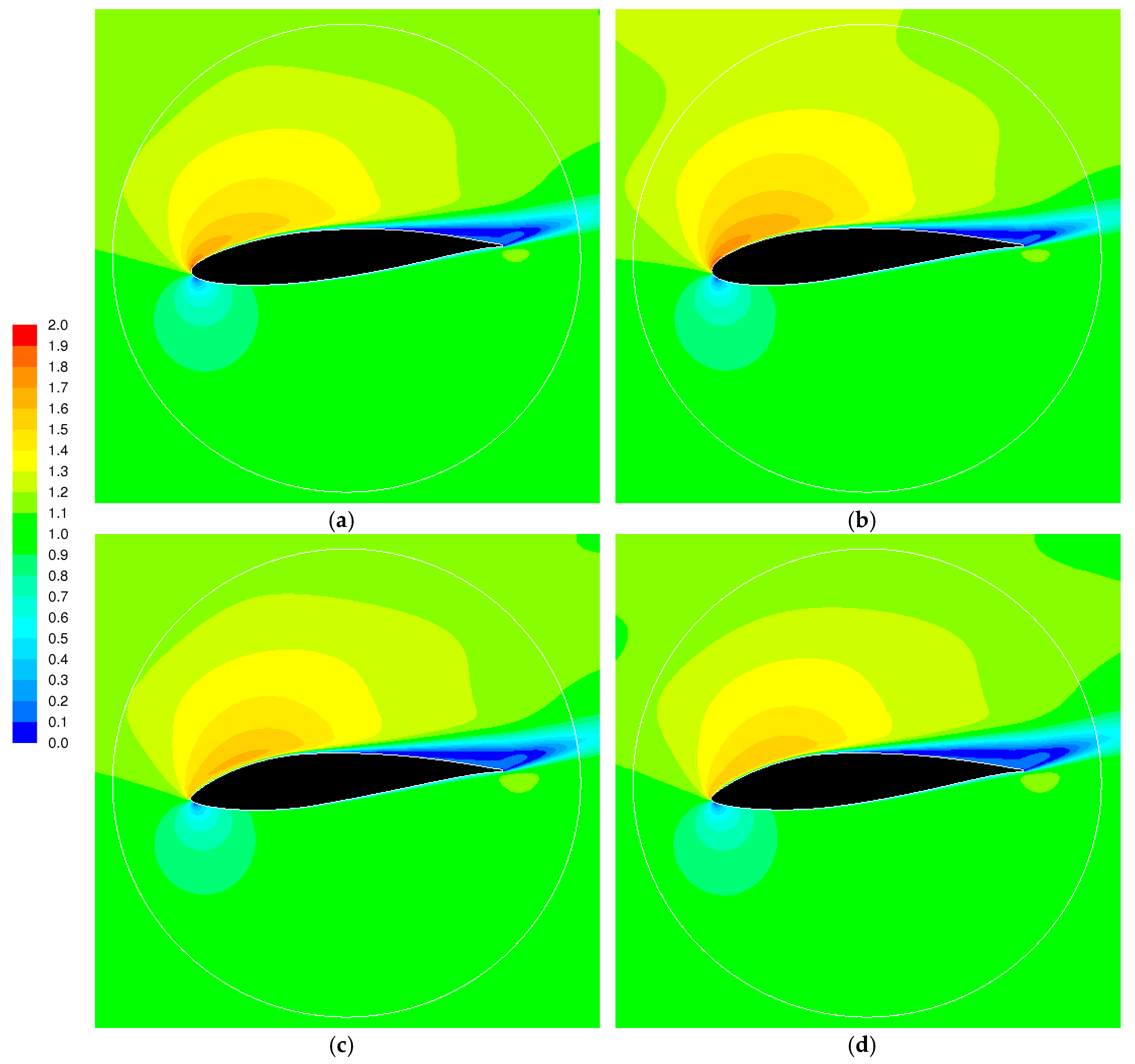
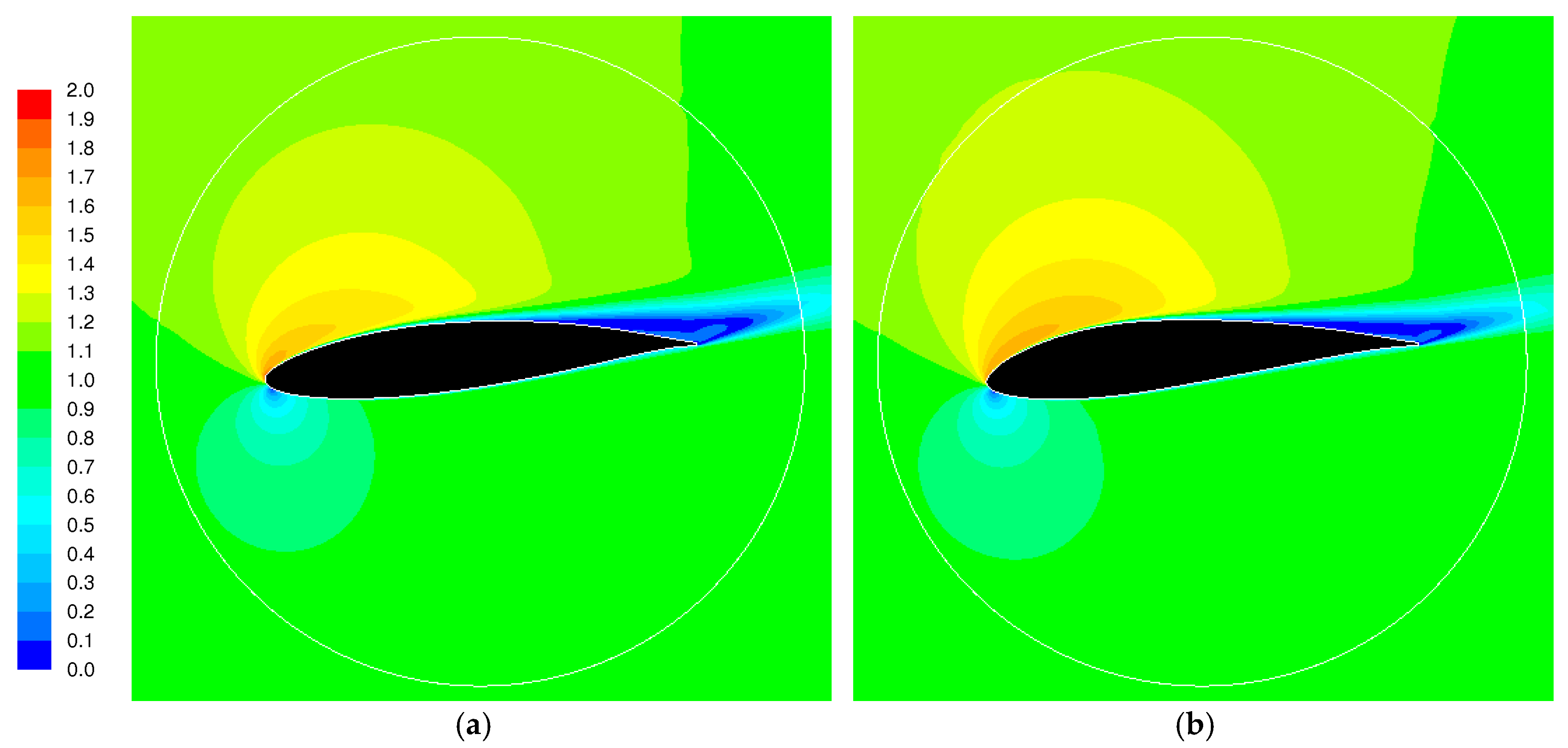
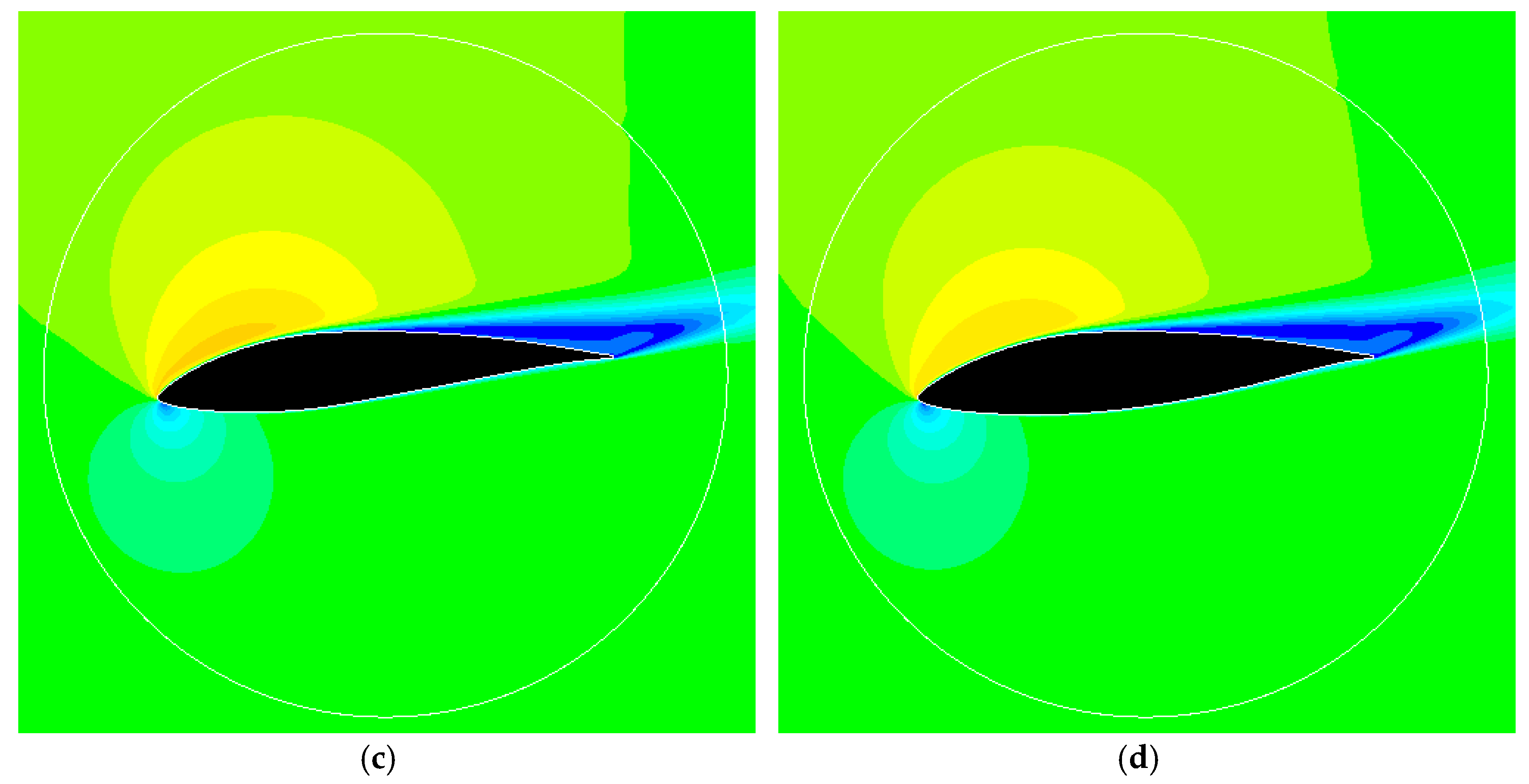
3.3. Influence of the Domain Size, Blade to Blade Interaction
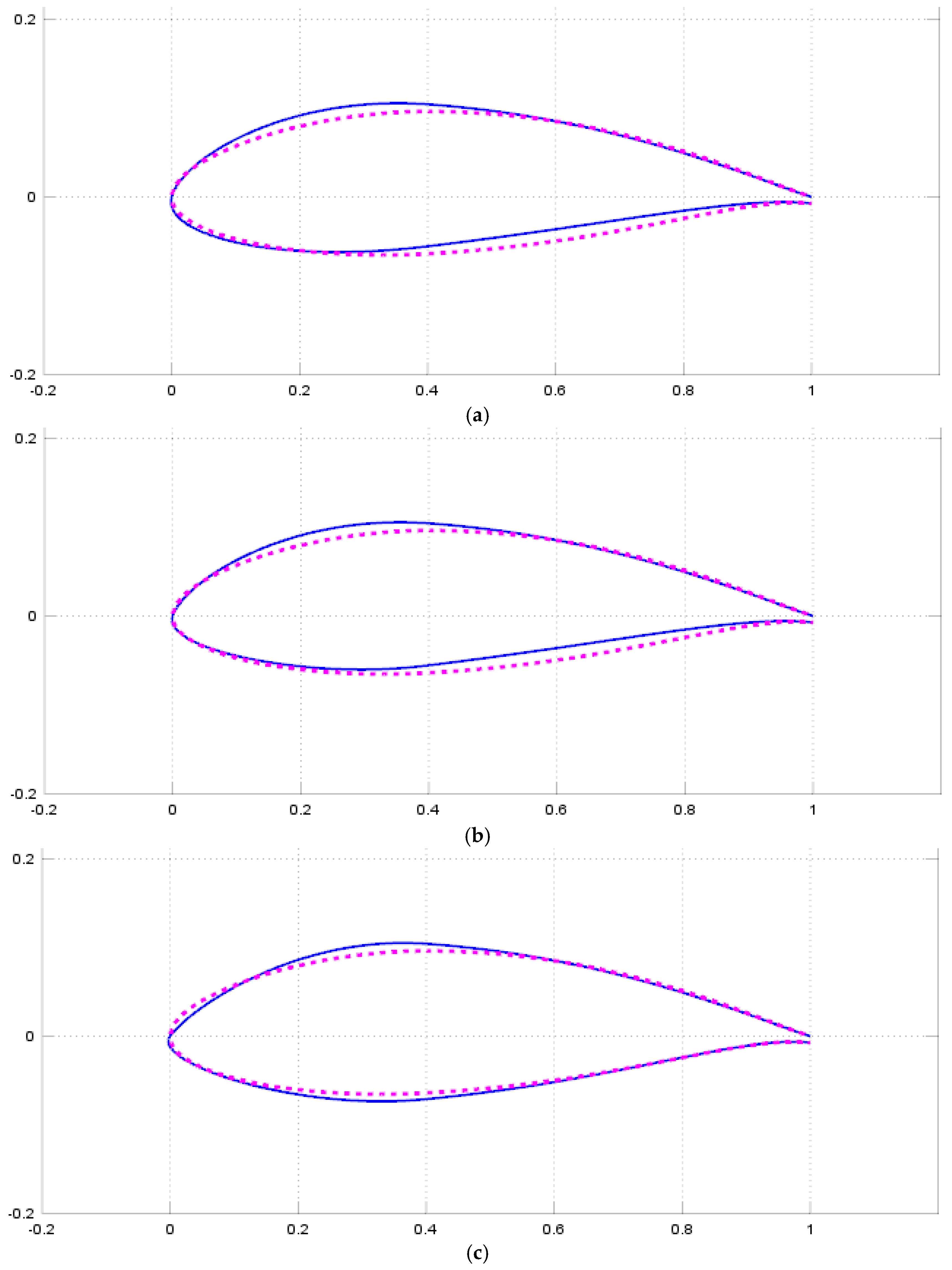
3.4. Optimization
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| C | chord length |
| CD | drag coefficient |
| CL | lift coefficient |
| CT | average thrust coefficient |
| Cσ | coefficient of thrust standard deviation |
| L | circumferential domain size (distance between periodic boundaries) |
| Re | Reynolds number |
| T | thrust |
| V | magnitude of approach velocity at Re = 100,000 |
| y+ | distance to wall non-dimensionalized by wall shear stress, viscosity and density |
| ρ | density |
| σ | standard deviation of thrust |
| AoA | Angle of Attack |
| BA | Blade Angle |
| BiMADS | Biobjective Mesh Adaptive Direct Search |
| BEM | Blade Element Momentum |
| CFD | Computational Fluid Dynamics |
| FA | Flow Angle |
| FVM | Finite Volume Method |
| GA | Genetic Algorithms |
| HAWT | Horizontal Axis Wind Turbines |
| LES | Large Eddy Simulations |
| NGN | Number of Grid Nodes |
| OCCD | Orthogonal Central Composite Design |
| RANS | Reynolds Averaged Numerical Simulations |
| RSM | Response Surface Methodology |
| SST | Shear Stress Transport |
References
- Hau, E. Wind Turbines; Springer: Berlin, Germany, 2013. [Google Scholar]
- Oyama, A.; Liou, M.-S.; Obayashi, S. Transonic axial-flow blade shape optimization using evolutionary algorithm and three-dimensional Navier-Stokes solver. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization (AIAA 2002-5642), Atlanta, GA, USA, 4–6 September 2002. [Google Scholar]
- Semenova, A.; Chrikov, D.; Lyutiv, A.; Cherny, S.; Skorospelov, V.; Pylev, I. Multi-objective shape optimization of runner blade for Kaplan turbine. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 012025. [Google Scholar] [CrossRef]
- Thumthae, C.; Chitsomboon, T. Optimal angle of attack for untwisted blade wind turbine. Renew. Energy 2009, 34, 1279–1284. [Google Scholar] [CrossRef]
- Jureczko, M.; Pawlak, M.; Mezyk, A. Optimisation of wind turbine blades. J. Mater. Process. Technol. 2005, 167, 463–471. [Google Scholar] [CrossRef]
- Mendez, J.; Greiner, D. Wind blade chord and twist angle optimization by using genetic algorithms. In Proceedings of the 5th Conference on Engineering Computational Technology, Las Palmas de Gran Canaria, Spain, 12–15 September 2006. [Google Scholar]
- Burger, C.; Hartfield, R. Wind turbine airfoil performance optimization using the vortex lattice method and a genetic algorithm. In Proceedings of the 4th AIAA Energy Conversion Conference, San Diego, CA, USA, 26–29 June 2006. [Google Scholar]
- Clifton-Smith, M.; Wood, D. Further dual purpose evolutionary optimization of small wind turbine blades. J. Phys. Conf. Ser. 2007, 75, 012017. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Ye, Z. Optimization model for rotor blades of horizontal axis wind turbines. Front. Mech. Eng. China 2007, 2, 483–488. [Google Scholar] [CrossRef]
- XFOIL Subsonic Airfoil Development System. Available online: http://web.mit.edu/drela/Public/web/xfoil/ (accessed on 12 April 2018).
- Kenway, G.; Martins, J.R.R.A. Aerostructural shape optimization of wind turbine blades considering site-specific winds. In Proceedings of the AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar]
- Xudong, W.; Shen, W.Z.; Zhu, W.J.; Sorensen, J.N.; Jin, C. Shape optimization of wind turbine blades. Wind Energy 2009, 12, 781–803. [Google Scholar] [CrossRef]
- Ceyhan, O.; Sezer-Uzol, N.; Tuncer, I. Optimization of horizontal axis wind turbines by using BEM theory and genetic algorithm. In Proceedings of the 5th Ankara International Aerospace Conference, METU, Ankara, Turkey, 17–19 August 2009; pp. 17–19. [Google Scholar]
- Li, J.Y.; Li, R.; Gao, Y.; Huang, J. Aerodynamic optimization of wind turbine airfoils using response surface techniques. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 827–838. [Google Scholar] [CrossRef]
- Grujicic, M.; Arakere, G.; Pandurangan, B.; Sellappan, V.; Vallejo, A.; Ozen, M. Multidisciplinary design optimization for glass-fibre epoxy-matrix composite 5 MW horizontal-axis wind-turbine blades. J. Mater. Eng. Perform. 2010, 19, 1116–1127. [Google Scholar] [CrossRef]
- Bottasso, C.; Campagnolo, F.; Croce, A. Computational Procedures for the Multidisciplinary Constrained Optimization of Wind Turbines; Scientific Report DIA-SR; Dipartimento di Ingegneria Aerospaziale, Politecnico di Milano: Milano, Italy, 2010. [Google Scholar]
- Kusiak, A.; Zheng, H.Y. Optimization of wind turbine energy and power factor with an evolutionary computation algorithm. Energy 2010, 35, 1324–1332. [Google Scholar] [CrossRef]
- Song, F.F.; Ni, Y.H.; Tan, Z.Q. Optimization design, modeling and dynamic analysis for composite wind turbine blade. Procedia Eng. 2011, 16, 369–375. [Google Scholar] [CrossRef]
- Wang, L.; Wang, T.G.; Luo, Y. Improved non-dominated sorting genetic algorithm (NSGA)-II in multi-objective optimization studies of wind turbine blades. Appl. Math. Mech. Engl. Ed. 2011, 32, 739–748. [Google Scholar] [CrossRef]
- Grasso, F. Hybrid optimization for wind turbine thick airfoils. In Proceedings of the 53rd AIAAJASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. AIAA Paper AIAA-2012. [Google Scholar]
- Chen, X.M.; Agarwal, R. Optimization of flatback airfoils for wind-turbine blades using a genetic algorithm. J. Aircr. 2012, 49, 622–629. [Google Scholar] [CrossRef]
- Ribeiro, A.F.P.; Awruch, A.M.; Gomes, H.M. An airfoil optimization technique for wind turbines. Appl. Math. Model. 2012, 36, 4898–4907. [Google Scholar] [CrossRef]
- Jeong, J.; Park, K.; Jun, S.; Song, K.; Lee, D.H. Design optimization of a wind turbine blade to reduce the fluctuating unsteady aerodynamic load in turbulent wind. J. Mech. Sci. Technol. 2012, 26, 827–838. [Google Scholar] [CrossRef]
- Ju, Y.P.; Zhang, C.H. Multi-point robust design optimization of wind turbine airfoil under geometric uncertainty. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 245–261. [Google Scholar] [CrossRef]
- Liao, C.C.; Zhao, X.L.; Xu, J.Z. Blade layers optimization of wind turbines using FAST and improved PSO algorithm. Renew. Energy 2012, 42, 227–233. [Google Scholar] [CrossRef]
- Polat, O.; Tuncer, I.H. Aerodynamic shape optimization of wind turbine blades using a parallel genetic algorithm. Procedia Eng. 2013, 61, 28–31. [Google Scholar] [CrossRef]
- Sessarego, M.; Dixon, K.R.; Rival, D.E.; Wood, D.H. A hybrid multi-objective evolutionary algorithm for wind-turbine blade optimization. Eng. Optim. 2015, 47, 1043–1062. [Google Scholar] [CrossRef]
- Shen, X.; Chen, J.E.; Zhu, X.C.; Liu, P.Y.; Du, Z.H. Multi-objective optimization of wind turbine blades using lifting surface method. Energy 2015, 90, 1111–1121. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Hassanabad, A.H.; Dadvand, A. Aerodynamic shape optimization and analysis of small wind turbine blades employing the Viterna approach for post-stall region. Alex. Eng. J. 2016, 55, 2035–2043. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Afshar, P.A.N.; Ahmadizadeh, M.; Wood, D. Aero-structural design optimization of a small wind turbine blade. Renew. Energy 2016, 87, 837–848. [Google Scholar] [CrossRef]
- Dal Monte, A.; De Betta, S.; Castelli, M.R.; Benini, E. Proposal for a coupled aerodynamic-structural wind turbine blade optimization. Compos. Struct. 2017, 159, 144–156. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Ilinca, A.; Perron, J. Review of performance optimization applied to wind turbines. Appl. Energy 2015, 142, 361–388. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Benim, A.C.; Brillert, D.; Cagan, M. Investigation into the computational analysis of direct-transfer pre-swirl systems for gas turbine cooling. In Proceedings of the ASME Turbo Expo 2004, Vienna, Austria, 14–17 June 2004; Volume 4, pp. 453–460, Paper No. GT2004-54151. [Google Scholar] [CrossRef]
- Benim, A.C.; Geiger, M.; Doehler, S.; Schoenenberger, M.; Roemer, H. Modelling the Flow in the Exhaust Hood of Steam Turbines under Consideration of Turbine-Exhaust Hood Interaction. In Proceedings of the 1st European Conference on Turbomachinery—Fluid Dynamic and Thermodynamic Aspects: Computational Methods, Erlangen, Germany, 1–3 March 1995; Book Series: VDI Berichte; VDI Verlag: Duesseldorf, Germany, 1995; Volume 1185, pp. 343–357. [Google Scholar]
- Engineering Simulations and 3-D Design Software. Available online: www.ansys.com (accessed on 17 October 2018).
- Durbin, P.A.; Pettersson Reif, B.A. Statistical Theory and Modeling for Turbulent Flows, 2nd ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- Benim, A.C.; Nahavandi, A.; Syed, K. URANS and LES analysis of turbulent swirling flows. Prog. Comput. Fluid Dyn. An Int. J. 2005, 5, 444–454. [Google Scholar] [CrossRef]
- Benim, A.C.; Chattopadhyay, H.; Nahavandi, A. Computational analysis of turbulent forced convection in a channel with a triangular prism. Int. J. Therm. Sci. 2011, 50, 1973–1983. [Google Scholar] [CrossRef]
- Menter, F.; Esch, T.; Kubacki, S. Transition modelling based on local variables. In Proceedings of the Fifth International Symposium on Engineering Turbulence Modelling and Measurements, Mallorca, Spain, 16–18 September 2002; Engineering Turbulence Modelling and Experiments 5. Rodi, W., Fueye, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; pp. 555–564. [Google Scholar]
- Benim, A.C.; Cagan, M.; Gunes, D. Computational analysis of transient heat transfer in turbulent pipe flow. Int. J. Therm. Sci. 2004, 43, 725–732. [Google Scholar] [CrossRef]
- Benim, A.C.; Ozkan, K.; Cagan, M.; Gunes, D. Computational investigation of turbulent jet impinging onto rotating disk. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 284–301. [Google Scholar] [CrossRef]
- Assmann, A.; Benim, A.C.; Gül, F.; Lux, P.; Akhyari, P.; Boeken, U.; Joos, F.; Feindt, P.; Lichtenberg, A. Pulsatile extracorporeal circulation during on-pump cardiac surgery enhances aortic wall shear stress. J. Biomech. 2012, 45, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.B.; Ferry, M.; Piquet, J.; Queutey, P.; Visonneau, M. New fully coupled solutions of the Navier-Stokes equations. In Notes on Numerical Fluid Mechanics (NNFM), Proceedings of the 9th GAMM Conference on Numerical Methods in Fluid Mechanics, Lausanne, Switzerland, 25–27 September 1991; Vos, J.B., Ed.; Springer: Wiesbaden, Germany, 1992; Volume 35, pp. 191–200. [Google Scholar]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Barth, T.J.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the AIAA 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. Technical Report AIAA-89-0366. [Google Scholar]
- Benim, A.C.; Pasqualotto, E.; Suh, S.H. Modeling turbulent flow past a circular cylinder by RANS, URANS, LES and DES. Prog. Computat. Fluid Dyn. An Int. J. 2008, 8, 299–307. [Google Scholar] [CrossRef]
- GNU Octave. Available online: https://www.gnu.org/software/octave/ (accessed on 17 April 2018).
- Conn, A.R.; Scheinberg, K.; Vincente, L.N. Introduction to Derivative-Free Optimization; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Le Digabel, S. Algorithm 909: NOMAD: Nonlinear Optimization with the MADS Algorithm. ACM Trans. Math. Softw. 2011, 37, 44. [Google Scholar] [CrossRef]
- Selig, M.S.; Lyon, C.A.; Giguère, P.; Ninham, C.P.; Guglielmo, J.J. Summary of Low-Speed Airfoil Data; Soar Tech Publications: Virginia Beach, VA, USA, 1996; Volume 2. [Google Scholar]
- Branke, J.; Deb, K.; Miettinen, K.; Slowinski, R. (Eds.) Multiobjective Optimization; Springer: Berlin, Germany, 2008. [Google Scholar]



| Normalized Scale Parameters | |||||
|---|---|---|---|---|---|
| Variable | −1.414 | −1 | 0 | 1 | 1.414 |
| Re/103 | 90 | 92.93 | 100 | 107.07 | 110 |
| FA (°) | 10 | 11.46 | 15 | 18.54 | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benim, A.C.; Diederich, M.; Pfeiffelmann, B. Aerodynamic Optimization of Airfoil Profiles for Small Horizontal Axis Wind Turbines. Computation 2018, 6, 34. https://doi.org/10.3390/computation6020034
Benim AC, Diederich M, Pfeiffelmann B. Aerodynamic Optimization of Airfoil Profiles for Small Horizontal Axis Wind Turbines. Computation. 2018; 6(2):34. https://doi.org/10.3390/computation6020034
Chicago/Turabian StyleBenim, Ali Cemal, Michael Diederich, and Björn Pfeiffelmann. 2018. "Aerodynamic Optimization of Airfoil Profiles for Small Horizontal Axis Wind Turbines" Computation 6, no. 2: 34. https://doi.org/10.3390/computation6020034
APA StyleBenim, A. C., Diederich, M., & Pfeiffelmann, B. (2018). Aerodynamic Optimization of Airfoil Profiles for Small Horizontal Axis Wind Turbines. Computation, 6(2), 34. https://doi.org/10.3390/computation6020034






