Kohn Anomaly and Phase Stability in Group VB Transition Metals
Abstract
1. Introduction
2. FS Nesting and Kohn Anomaly in V, Nb, and Ta
2.1. Early Search for Phase Transformations in V, Nb, and Ta
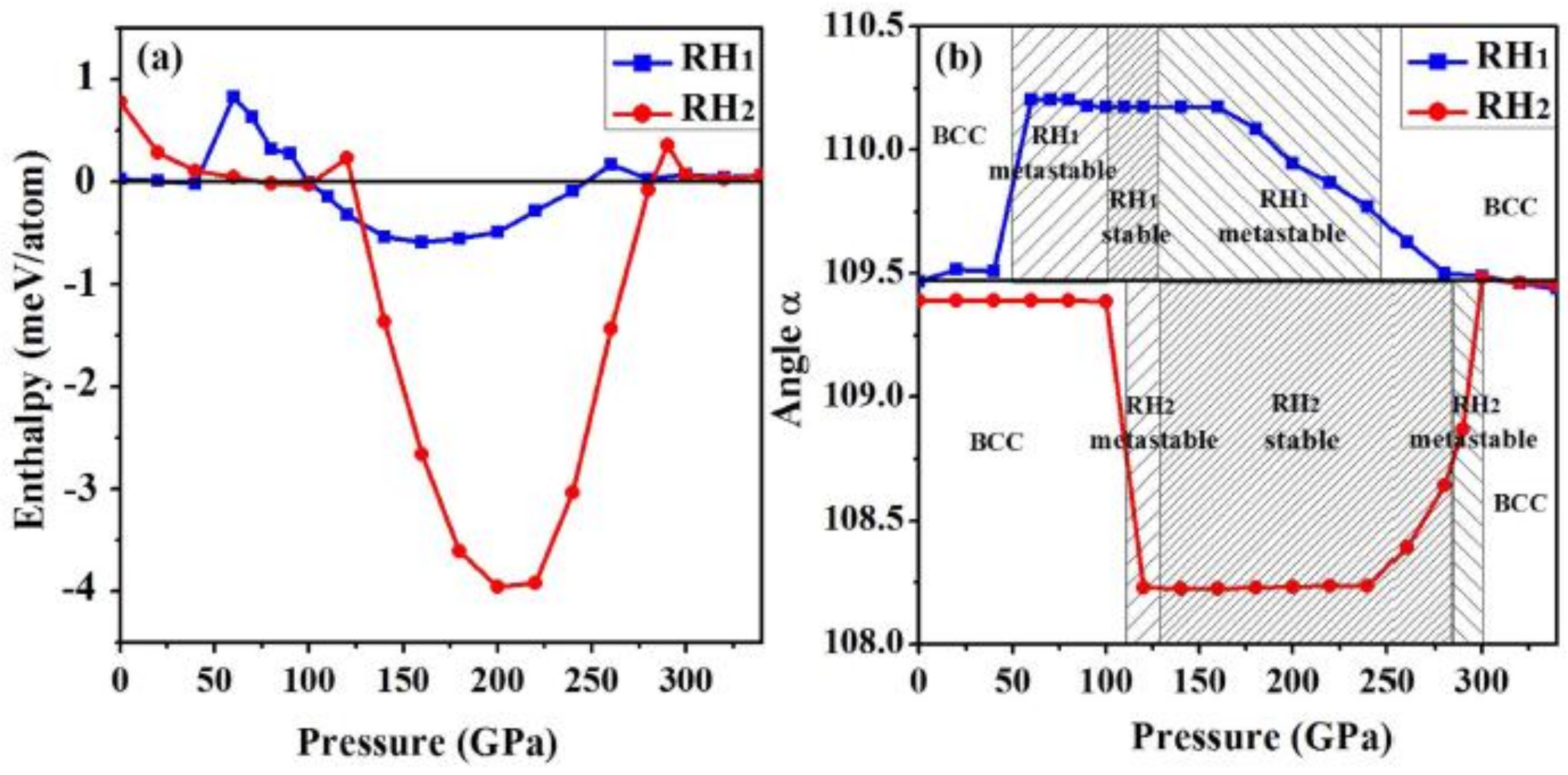
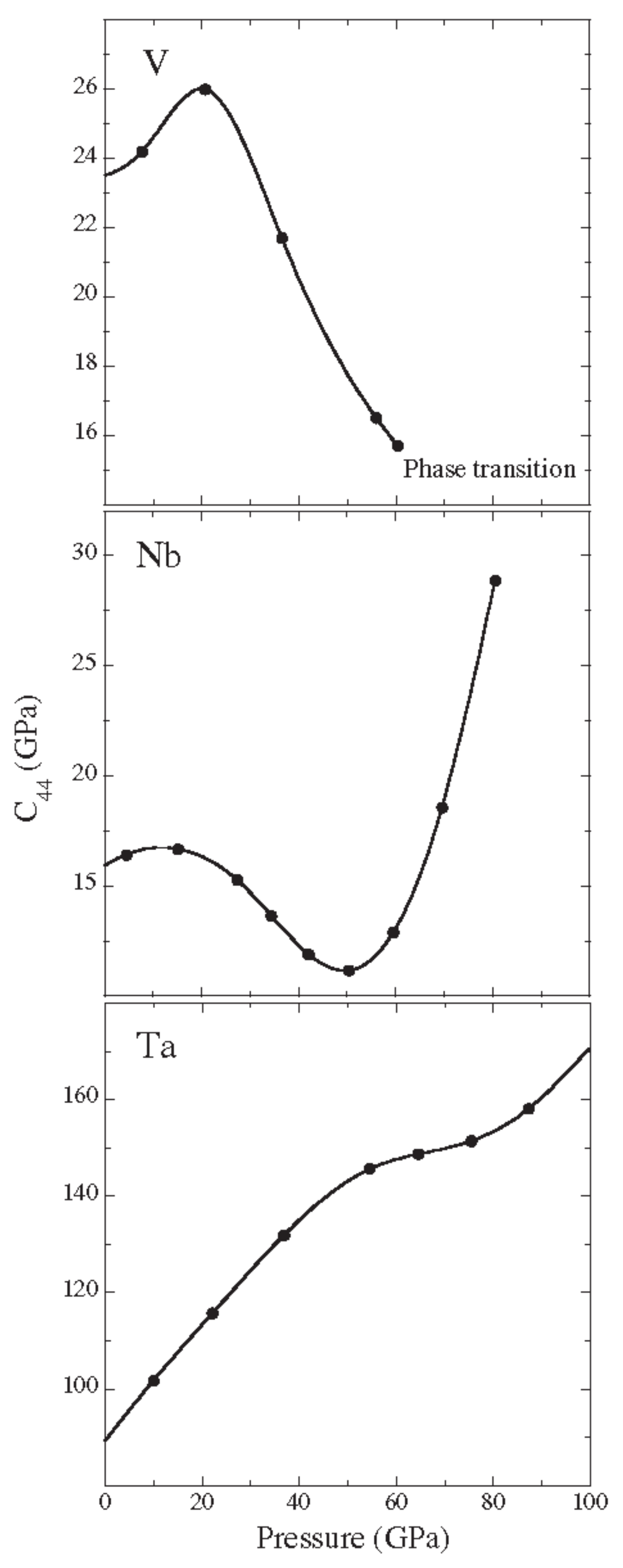
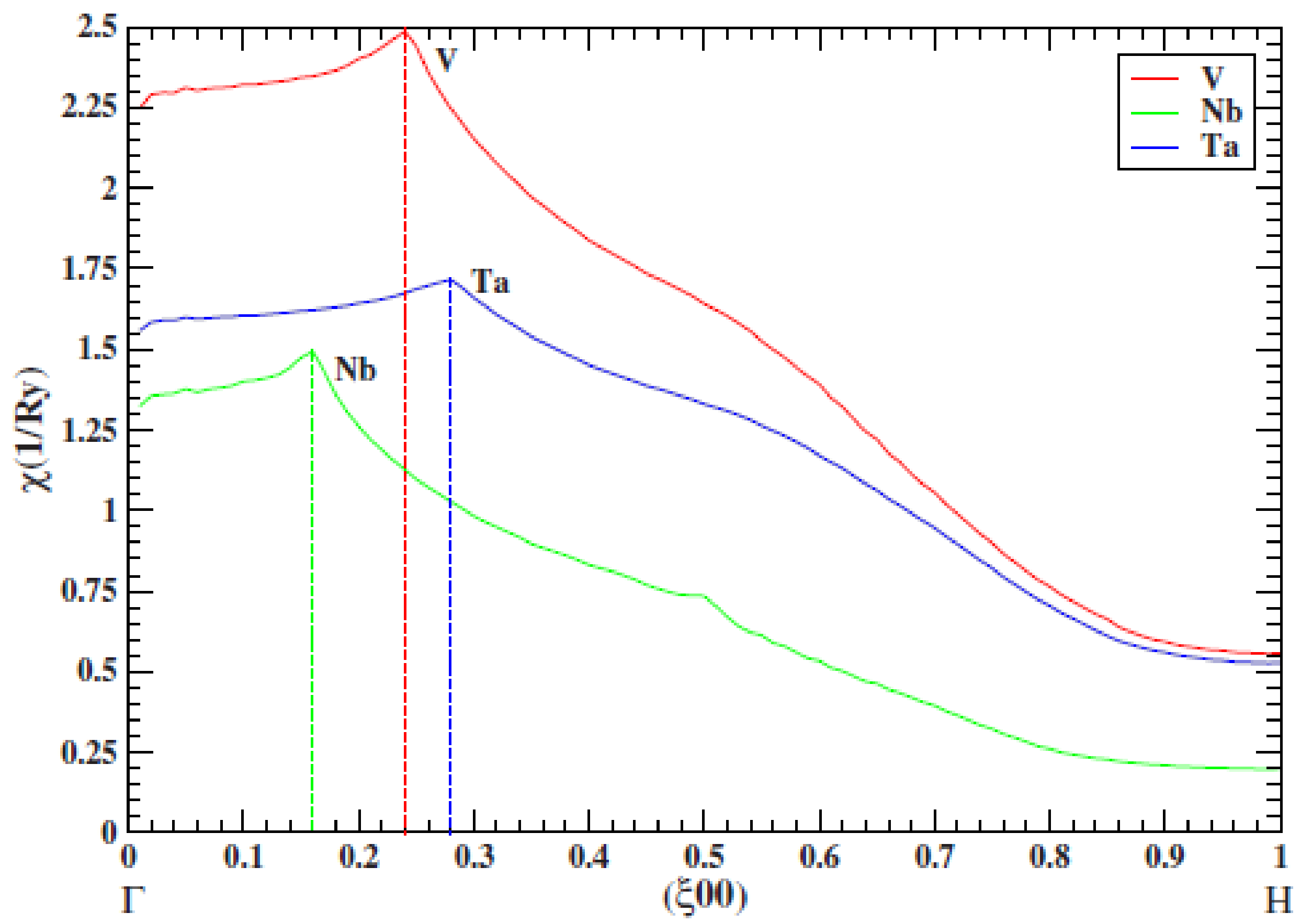
2.2. Fermi Surface Nesting and Pre-Martensitic Softening in V, Nb, and Ta at High Pressures
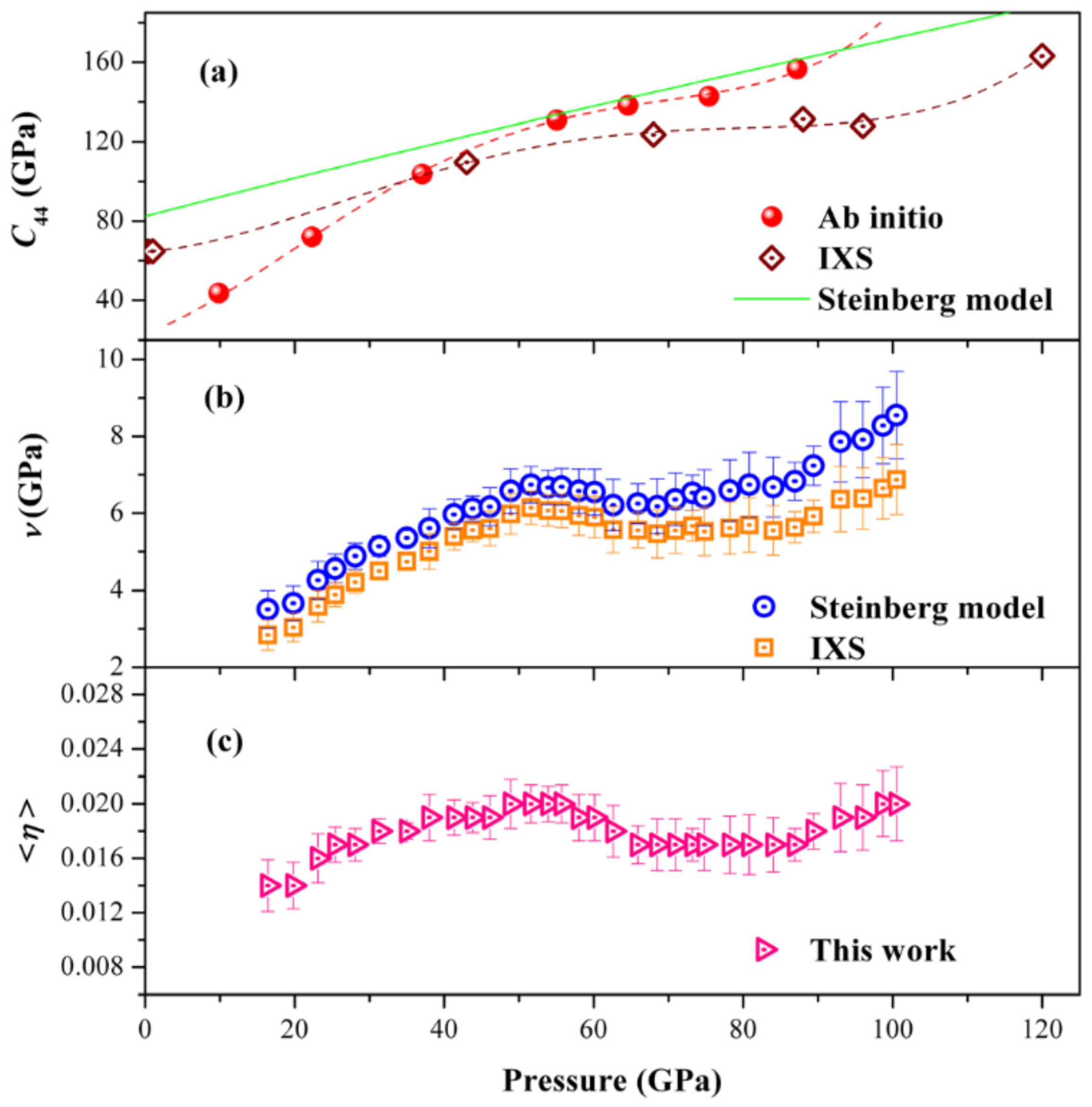
2.3. Strength and Elasticity of Nb and Ta
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kohn, W. Image of the Fermi surface in the vibration spectrum of a metal. Phys. Rev. Lett. 1959, 2, 393–394. [Google Scholar] [CrossRef]
- Woll, E.J.; Kohn, W. Images of the Fermi Surface in phonon spectra in metals. Phys. Rev. 1962, 126, 1693–1697. [Google Scholar] [CrossRef]
- Peierls, R.E. Quantum Theory of Solids; Oxford University: New York, NY, USA, 1955. [Google Scholar]
- Bulaevskii, L.N. Structural and superconducting properties of system with one-dimensional anisotropy. In High-Temperature Superconductivity; Ginzburg, V.L., Kirzhnits, D.A., Eds.; Consultants Bureau: New York, NY, USA; London, UK, 1982; pp. 241–281. [Google Scholar]
- Zhu, X.; Guo, J.; Zhang, J.; Plummer, E.W. Misconceptions associated with the origin of charge density waves. Adv. Phys. X 2017, 2, 622–640. [Google Scholar] [CrossRef]
- Taylor, P.L. Theory of Kohn anomalies in the phonon spectra of metals. Phys. Rev. 1963, 131, 1995–1999. [Google Scholar] [CrossRef]
- Afanas’ev, A.M.; Kagan, Y. Singularities caused by electron-phonon interaction in the phonon dispersion law. Sov. J. Exp. Theor. Phys. 1963, 16, 1030–1034. [Google Scholar]
- Katsnelson, M.I.; Naumov, I.I.; Trefilov, A.V. Singularities of the electronic anomalies of lattice properties in structure and pre-martensitic β-phases of metals and alloys. Phase Trans. 1994, 49, 143–191. [Google Scholar] [CrossRef]
- Kopaev, Y.V. Possibility of an increase in the critical temperature as a result of a structural-transition-induced change in the electron spectrum. In High-Temperature Superconductivity; Ginzburg, V.L., Kirzhnits, D.A., Eds.; Consultants Bureau: New York, NY, USA; London, UK, 1982; pp. 179–211. [Google Scholar]
- Johannes, M.D.; Mazin, I.I.; Howells, C.A. Fermi-surface nesting and the origin of the charge-density wave in NbSe2. Phys. Rev. B 2006, 73, 205102. [Google Scholar] [CrossRef]
- Johannes, M.D.; Mazin, I.I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 2008, 77, 165135. [Google Scholar] [CrossRef]
- Keldysh, L.V.; Kopaev, Y. Possible instability of semimetallic state toward Coulomb interaction. Sov. Phys. Solid State 1965, 6, 2219–2224. [Google Scholar]
- Halperin, B.I.; Rice, T.M. Possible anomalies at a semimetal-semiconductor transition. Rev. Mod. Phys. 1968, 40, 755–766. [Google Scholar] [CrossRef]
- Barzykin, V.V.; Gor’kov, L.P. Ferromagnetism and superstructure in Ca1−xLaxB6. Phys. Rev. Lett. 2000, 84, 2207–2210. [Google Scholar] [CrossRef] [PubMed]
- Faraggi, M.N.; Zubizarreta, X.; Arnau, A.; Silkin, V.M. On the stability of the electronic system in transition metal dichalcogenides. J. Phys. Condens. Matter 2016, 28, 184004. [Google Scholar] [CrossRef] [PubMed]
- Gor’kov, L.P. Strong electron-lattice coupling as the mechanism behind charge density wave transformations in transition-metal dichalcogenides. Phys. Rev. B 2012, 85, 165142. [Google Scholar] [CrossRef]
- Lander, G.H.; Fisher, E.S.; Bader, S.D. The solid-state properties of uranium a historical perspective and review. Adv. Phys. 1994, 43, 1–111. [Google Scholar] [CrossRef]
- Marmeggi, J.C.; Currat, R.; Bouvet, A.; Lander, G.H. Phonon softening in alpha-uranium associated with the CDW transition. Phys. B Condens. Matter 1999, 263–264, 624–626. [Google Scholar] [CrossRef]
- Fast, L.; Eriksson, O.; Johansson, B.; Wills, J.M.; Straub, G.; Roeder, H.; Nordström, L. Theoretical aspects of the charge density waves in uranium. Phys. Rev. Lett. 1998, 81, 2978–2981. [Google Scholar] [CrossRef]
- Chan, S.-K.; Heine, V. Spin density wave and soft phonon mode from nesting Fermi surfaces. J. Phys. F Met. Phys. 1973, 3, 795–809. [Google Scholar] [CrossRef]
- Zhao, G.-L.; Leung, T.C.; Harmon, B.N.; Keil, M.; Müllner, M.; Weber, W. Electronic origin of the intermediate phase of NiTi. Phys. Rev. B 1989, 40, 7999–8001. [Google Scholar] [CrossRef]
- Naumov, I.I.; Velikokhatnyi, O.I.; Bashirov, V.Z. Charge density waves in B2 titanium compounds. JETP Lett. 1991, 54, 573–577. [Google Scholar]
- Velikokhatnyi, O.I.; Naumov, I.I. Electronic structure and instability of Ni2MnGa. Phys. Solid State 1999, 41, 617–623. [Google Scholar] [CrossRef]
- Lee, Y.; Rhee, J.Y.; Harmon, B.N. Generalized susceptibility of the magnetic shape-memory alloy Ni2MnGa. Phys. Rev. B 2002, 66, 54424. [Google Scholar] [CrossRef]
- Bungaro, C.; Rabe, K.M.; Dal Gorso, A. First-principles study of lattice instabilities in ferromagnetic Ni2MnGa. Phys. Rev. B 2003, 68, 134104. [Google Scholar] [CrossRef]
- Zayak, A.T.; Entel, P.A. Critical discussion of calculated modulated structures, Fermi surface nesting and phonon softening in magnetic shape memory alloys Ni2Mn(Ga, Ge, Al) and Co2Mn(Ga, Ge). J. Magn. Magn. Mater. 2005, 290–291, 874–877. [Google Scholar] [CrossRef]
- Haynes, T.D.; Watts, R.J.; Laverock, J.; Major, Z.; Alam, M.A.; Taylor, J.W.; Duffy, J.A.; Dugdale, S.B. Positron annihilation study of the Fermi surface of Ni2MnGa. New J. Phys. 2012, 14, 035020. [Google Scholar] [CrossRef]
- Zhao, G.L.; Harmon, B.N. Phonon anomalies in β-phase NixAl1−x alloys. Phys. Rev. B 1992, 45, 2818. [Google Scholar] [CrossRef]
- Naumov, I.I.; Velikokhatnyi, O.I. Simultaneous manifestations of the 2D van Hove singularity and the Fermi surface nesting in the acoustic soft mode of β-NiAl alloys. J. Phys. Condens. Matter 1997, 9, 10339–10351. [Google Scholar] [CrossRef]
- Huang, X.; Naumov, I.I.; Rabe, K.M. Phonon anomalies and elastic constants of cubic NiAl from first principles. Phys. Rev. B 2004, 70, 064301. [Google Scholar] [CrossRef]
- Kakeshita, T.; Fukuda, T.; Saburi, T. Time-dependent nature and origin of displacive transformation. Sci. Technol. Adv. Mater. 2000, 1, 63–72. [Google Scholar] [CrossRef]
- Velikokhatnyi, O.I.; Naumov, I.I.; Bashirov, V.Z. Geometric features of the Fermi surface and the premartensitic anomalies in the Hume-Rothery β-Phases. Phys. Met. Metallogr. 1992, 74, 557–564. [Google Scholar]
- Velikokhatnyi, O.I.; Eremeev, S.V.; Naumov, I.I.; Potekaev, A.I. Long-period incommensurate superstructures in Cu–Au alloys: Relation with short-period ordering. J. Exp. Theor. Phys. 2000, 90, 479–487. [Google Scholar] [CrossRef]
- Velikokhatnyi, O.I.; Naumov, I.I.; Eremeev, S.V.; Potekaev, A.I. Two-dimensional incommensurate superlattices in precious-metals alloys: Nature of formation. JETP Lett. 1999, 69, 589–595. [Google Scholar] [CrossRef]
- Velikokhatnyi, O.I.; Eremeev, S.V.; Naumov, I.I.; Potekaev, A.I. Electronic structure and long period states in Ag3Mg: Comparison with Cu–Au alloys. J. Phys. Condens. Matter 2000, 12, 8825–8830. [Google Scholar] [CrossRef]
- Velikokhatnyi, O.I.; Eremeev, S.V.; Naumov, I.I.; Potekaev, A.I. Al3Ti alloy: Long-period states and electronic structure. J. Phys. Condens. Matter 2002, 14, 8763–8769. [Google Scholar] [CrossRef]
- Naumov, I.I.; Cohen, R.E.; Hemley, R.J. Graphene physics and insulator-metal transition in compressed hydrogen. Phys. Rev. B 2013, 88, 045125. [Google Scholar] [CrossRef]
- Politano, A.; Marino, A.R.; Formoso, V.; Chiarello, G. Evidence of Kohn anomalies in quasi-freestanding graphene on Pt(111). Carbon 2012, 50, 734–736. [Google Scholar] [CrossRef]
- Politano, A.; de Juan, F.; Chiarello, G.; Fertig, H.A. Emergence of an out-of-plane optical phonon (ZO) Kohn anomaly in quasifreestanding epitaxial graphene. Phys. Rev. Lett. 2015, 115, 075504. [Google Scholar] [CrossRef] [PubMed]
- Struzhkin, V.V.; Timofeev, Y.A.; Hemley, R.J.; Mao, H.-K. Superconducting Tc and electron-phonon coupling in Nb to 132 GPa: Magnetic susceptibility at megabar pressures. Phys. Rev. Lett. 1997, 79, 4262–4965. [Google Scholar] [CrossRef]
- Söderlind, P.; Moriarty, J.A. First-principles theory of Ta up to 10 Mbar pressure: Structural and mechanical properties. Phys. Rev. B 1998, 57, 10340. [Google Scholar] [CrossRef]
- Weir, S.T.; Akella, J.; Ruddle, C.; Goodwin, T.; Hsiung, L. Static strengths of Ta and U under ultrahigh pressures. Phys. Rev. B 1998, 58, 11258. [Google Scholar] [CrossRef]
- Cynn, H.; Yoo, C.-S. Equation of state of tantalum to 174 GPa. Phys. Rev. B 1999, 59, 8526. [Google Scholar] [CrossRef]
- Takemura, K. Equation of state of V and Nb under truly hydrostatic conditions. In Proceedings of the International Conference on High Pressure Science and Technology (AIRAPT-17), Honolulu, HI, USA, 25–30 July 1999; Manghnani, M.H., Nellis, W.J., Nicol, M.F., Eds.; Universities Press: Hyderabad, India, 2000; pp. 443–444. [Google Scholar]
- Ostanin, S.A.; Trubitsin, V.Y.; Savrasov, S.Y.; Alouani, M.; Dreyssé, H. Calculated Nb superconducting transition temperature under hydrostatic pressure. Comput. Mater. Sci. 2000, 17, 202–205. [Google Scholar] [CrossRef]
- Ishizuka, M.; Iketani, M.; Endo, S. Pressure effect on superconductivity of vanadium at megabar pressures. Phys. Rev. B 2000, 61, R3823. [Google Scholar] [CrossRef]
- Yang, L.H.; Söderlind, P.; Moriarty, J.A. Atomistic simulation of pressure-dependent screw dislocation properties in bcc tantalum. Mater. Sci. Eng. A 2001, 309–310, 102–107. [Google Scholar] [CrossRef]
- Singh, A.K.; Takemura, K. Measurement and analysis of nonhydrostatic lattice strain component in niobium to 145 GPa under various fluid pressure-transmitting media. J. Appl. Phys. 2001, 90, 3269–3275. [Google Scholar] [CrossRef]
- Suzuki, N.; Otani, M. Theoretical study on the lattice dynamics and electron-phonon interaction of vanadium under high pressures. J. Phys. Condens. Matter 2002, 14, 10869–10872. [Google Scholar] [CrossRef]
- Gülseren, O.; Cohen, R.E. High-pressure thermoelasticity of body-centered-cubic tantalum. Phys. Rev. B 2002, 65, 064103. [Google Scholar] [CrossRef]
- Louis, C.N.; Iyakutti, K. Electron phase transition and superconductivity of vanadium under high pressures. Phys. Rev. B 2003, 67, 094509. [Google Scholar] [CrossRef]
- Nnolim, N.O.; Tyson, T.A.; Axe, L. Theory of the structural phases of group 5B–6B metals and their transport properties. J. Appl. Phys. 2003, 93, 4543–4560. [Google Scholar] [CrossRef]
- Tse, J.S.; Li, Z.; Uehara, K.; Ma, Y. Electron phonon coupling in high-pressure Nb. Phys. Rev. B 2004, 69, 132101. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Mezouar, M. Refinement of the equation of state of tantalum. Phys. Rev. B 2004, 69, 092106. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P. Mechanical properties of tantalum under high pressure. Phys. Rev. B 2005, 72, 134106. [Google Scholar] [CrossRef]
- Klepeis, J.E.; Landa, A.; Söderlind, P. Electronic Topological Transitions in High-Pressure BCC Metals. In Proceedings of the 2005 APS March Meeting, Los Angeles, CA, USA, 21–25 March 2005; American Institute of Physics: College Park, MD, USA, 2005; Volume 50, p. 600. [Google Scholar]
- Takemura, K.; Singh, A.K. High-pressure equation of state for Nb with helium-pressure medium: Powder X-ray diffraction experiments. Phys. Rev. B 2006, 73, 224119. [Google Scholar] [CrossRef]
- Orlikowski, D.; Söderlind, P.; Moriarty, J.A. First-principles thermoelasticity of transition metals at high pressure: Tantalum prototype in the quasiharmonic limit. Phys. Rev. B 2006, 74, 054109. [Google Scholar] [CrossRef]
- Landa, A.; Klepeis, J.; Söderlind, P.; Naumov, I.; Velikokhatnyi, O.; Vitos, L.; Ruban, A. Fermi surface nesting and pre-martensitic softening in V and Nb at high pressures. J. Phys. Condens. Matter 2006, 18, 5079–5085. [Google Scholar] [CrossRef]
- Landa, A.; Klepeis, J.; Söderlind, P.; Naumov, I.; Velikokhatnyi, O.; Vitos, L.; Ruban, A. Ab initio calculations of elastic constants of the bcc V–Nb system at high pressures. J. Phys. Chem. Solids 2006, 67, 2056–2064. [Google Scholar] [CrossRef]
- Suzuki, N.; Otani, M. The role of the phonon anomaly in the superconductivity of vanadium and selenium under high pressures. J. Phys. Condens. Matter 2007, 19, 125206. [Google Scholar] [CrossRef]
- Ding, Y.; Ahuja, R.; Shu, J.; Chow, P.; Luo, W.; Mao, H.K. Structural phase transition of vanadium at 69 GPa. Phys. Rev. Lett. 2007, 98, 085502. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Ahuja, R.; Ding, Y.; Mao, H.K. Unusual lattice dynamics of vanadium under high pressure. Proc. Natl. Acad. Sci. USA 2007, 104, 16428–16431. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Rudd, R.E.; Klepeis, J.E.; Söderlind, P.; Landa, A. Theoretical confirmation of a high-pressure rhombohedral phase in vanadium metal. Phys. Rev. B 2007, 75, 180101. [Google Scholar] [CrossRef]
- Lee, B.; Rudd, R.E.; Klepeis, J.E.; Becker, R. Elastic constants and volume changes associated with two high-pressure rhombohedral phase transformations in vanadium. Phys. Rev. B 2008, 77, 134105. [Google Scholar] [CrossRef]
- Rudd, R.E.; Klepeis, J.E. Multiphase improved Steinberg-Guinan model for vanadium. J. Appl. Phys. 2008, 104, 093528. [Google Scholar] [CrossRef]
- Verma, A.K.; Modak, P. Structural phase transitions in vanadium under high pressure. Europhys. Lett. 2008, 81, 37003. [Google Scholar] [CrossRef]
- Qiu, S.L.; Marcus, P.M. Phases of vanadium under pressure investigated from first principles. J. Phys. Condens. Matter 2008, 20, 275218. [Google Scholar] [CrossRef] [PubMed]
- Koči, L.; Ma, Y.; Oganov, A.R.; Souvatzis, P.; Ahuja, R. Elasticity of the superconducting metals V, Nb, Ta, Mo, and W at high pressure. Phys. Rev. B 2008, 77, 214101. [Google Scholar] [CrossRef]
- Bosak, A.; Hoesch, M.; Antonangeli, D.; Farber, D.L.; Fischer, I.; Krisch, M. Lattice dynamics of vanadium: Inelastic X-ray scattering measurements. Phys. Rev. B 2008, 78, 020301. [Google Scholar] [CrossRef]
- Landa, A.; Söderlind, P.; Ruban, A.V.; Peil, A.V.; Vitos, L. Stability in BCC transition metals: Madelung and band-energy effects due to alloying. Phys. Rev. Lett. 2009, 103, 235501. [Google Scholar] [CrossRef] [PubMed]
- Vekilov, Y.K.; Krasil’nikov, O.M. Structural transformations in metals at high compression ratios. Phys. Usp. 2009, 52, 831–834. [Google Scholar] [CrossRef]
- Antonangeli, D.; Farber, D.L.; Said, A.H.; Benedetti, L.R.; Aracne, C.M.; Landa, A.; Söderlind, P.; Klepeis, J.E. Shear softening of tantalum at megabar pressures. Phys. Rev. B 2010, 82, 132101. [Google Scholar] [CrossRef]
- Bondarenko, N.G.; Vekilov, Y.K.; Isaev, E.I.; Krasil’nikov, O.M. Deformation Phase Transition in Vanadium under High Pressure. JETP Lett. 2010, 91, 611–613. [Google Scholar] [CrossRef]
- Klepeis, J.-H.P.; Cynn, H.; Evans, W.J.; Rudd, R.E.; Yang, L.H.; Liermann, H.P.; Yang, W. Diamond anvil cell measurement of high-pressure yield strength of vanadium using in situ thickness determination. Phys. Rev. B 2010, 81, 134107. [Google Scholar] [CrossRef]
- Landa, A.; Söderlind, P.; Velikokhatnyi, O.I.; Naumov, I.I.; Ruban, A.V.; Peil, O.E.; Vitos, L. Alloying-driven phase stability in group-VB transition metals under compression. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
- Jenei, Z.; Liermann, H.P.; Cynn, H.; Klepeis, J.-H.P.; Baer, B.J.; Evans, W.J. Structural phase transition in vanadium at high pressure and high temperature: Influence of nonhydrostatic conditions. Phys. Rev. B 2011, 83, 054101. [Google Scholar] [CrossRef]
- Krasil’nikov, O.M.; Vekilov, Y.K.; Isaev, E.I.; Bondarenko, N.G. Theory of elastic phase transitions in metals at high pressures. Application to vanadium. J. Exp. Theor. Phys. 2011, 112, 240–245. [Google Scholar] [CrossRef]
- Liu, Z.; Shang, J. First principles calculations of electronic properties and mechanical properties of bcc molybdenum and niobium. Rare Met. 2011, 30, 354–358. [Google Scholar] [CrossRef]
- Singh, A.K.; Liermann, H.-P. Strength and elasticity of niobium under high pressure. J. Appl. Phys. 2011, 109, 113539. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Shang, J.-X. Elastic properties of Nb-based alloys by using the density functional theory. Chin. Phys. B 2012, 21, 016202. [Google Scholar] [CrossRef]
- Krasil’nikov, O.M.; Vekilov, Y.K.; Mosyagin, I.Y.; Isaev, E.I.; Bondarenko, N.G. Elastic phase transitions in metals at high pressures. J. Phys. Condens. Matter 2012, 24, 195402. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Dai, C.; Yu, Y.; Liu, Z.; Tan, Y.; Zhou, X.; Tan, H.; Cai, L.; Wu, Q. Sound velocity measurements of tantalum under shock compression in the 10–110 GPa range. J. Appl. Phys. 2012, 111, 033511. [Google Scholar] [CrossRef]
- Guerrero, O.; Marucho, M. Elastic-Plastic transition under uniaxial stress BCC tantalum. J. Mater. Sci. Eng. B 2013, 3, 153–160. [Google Scholar]
- Yu, Y.; Tan, Y.; Dai, C.; Li, X.; Li, Y.; Wu, Q.; Tan, H. Phase transition and strength of vanadium under shock compression up to 88 GPa. Appl. Phys. Lett. 2014, 105, 201910. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Cheng, Y.; Niu, Z.W. Elastic properties and phonon dispersion of bcc vanadium under pressure from first principles. J. At. Mol. Sci. 2014, 5, 81–94. [Google Scholar] [CrossRef]
- Krasil’nikov, O.M.; Vekilov, Y.K.; Lugovskoy, A.V.; Mosyagin, I.Y.; Belov, M.P.; Bondarenko, N.G. Structural transformations at high pressure in the refractory metals (Ta, Mo, V). J. Alloy. Compd. 2014, 586, S242–S245. [Google Scholar]
- Jing, Q.; Wu, Q.; Xu, J.-A.; Bi, Y.; Liu, L.; Liu, S.; Zhang, Y.; Geng, H. Anomalous softening of yield strength in tantalum at high pressures. J. Appl. Phys. 2015, 117, 055903. [Google Scholar] [CrossRef]
- Hamlin, J.J. Superconductivity in the metallic elements at high pressures. Phys. C 2015, 514, 59–76. [Google Scholar] [CrossRef]
- Wang, Y.X.; Wu, Q.; Xiang, R.; Chen, X.R.; Geng, H.Y. Stability of rhombohedral phases in vanadium at high-pressure and high-temperature: First-principles investigations. Sci. Rep. 2016, 6, 32419. [Google Scholar] [CrossRef] [PubMed]
- Antonangeli, D.; Farber, D.L.; Bosak, A.; Aracne, C.M.; Ruddle, D.G.; Krisch, M. Phonon triggered rhombohedral lattice distortion in vanadium at high pressure. Sci. Rep. 2016, 6, 31887. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Geng, H.Y.; Wu, Q.; Chen, X.R.; Sun, Y. First-principles investigation of elastic anomalies in niobium at high pressure and temperature. J. Appl. Phys. 2017, 122, 235903. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Pergamon Press: Oxford, UK, 1980; Volume 1. [Google Scholar]
- Nakagawa, Y.; Woods, A.D.B. Lattice Dynamics of Nb. Phys. Rev. Lett. 1963, 11, 271–274. [Google Scholar] [CrossRef]
- Woods, A.D.B. Lattice dynamics of tantalum. Phys. Rev. 1964, 136, A781–A783. [Google Scholar] [CrossRef]
- Bosak, A. (European Synchrotron Radiation Facility, Grenoble, France). Personal communication, 2010.
- Powell, B.M.; Martel, R.; Woods, A.D.B. Lattice Dynamics of Niobium-Molybdenum Alloys. Phys. Rev. 1968, 171, 727–736. [Google Scholar] [CrossRef]
- Powell, B.M.; Martel, R.; Woods, A.D.B. Phonon properties of niobium, molybdenum, and their alloys. Can. J. Phys. 1977, 55, 1601–1612. [Google Scholar] [CrossRef]
- Ahuja, R.; Söderlind, P.; Trygg, J.; Melsen, J.; Wills, J.M.; Johansson, B.; Eriksson, O. Influence of pseudocore valence-band hybridization on the crystal-structure phase stabilities of transition metals under extreme compressions. Phys. Rev. B 1994, 50, 14690. [Google Scholar] [CrossRef]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef]
- Fridel, J. Electronic structure of primary solid solutions in metals. Adv. Phys. 1954, 3, 446–507. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theory of the crystal structures of transition metals. J. Phys. C 1970, 3, 367–377. [Google Scholar] [CrossRef]
- Skriver, H.L. Crystal structure from one-electron theory. Phys. Rev. B 1985, 31, 1909–1923. [Google Scholar] [CrossRef]
- Söderlind, P.; Ahuja, R.; Erikson, O.; Wills, J.M.; Johansson, B. Crystal structure and elastic-constant anomalies in the magnetic 3d transition metals. Phys. Rev. B 1994, 50, 5918. [Google Scholar] [CrossRef]
- Clatterbuck, D.; Krenn, C.; Cohen, M.; Morris, J. Phonon instabilities and the ideal strength of aluminum. Phys. Rev. Lett. 2003, 91, 135501. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhu, T.; Yip, S.; Van Vliet, K.J.; Suresh, S. Elastic criterion for dislocation nucleation. Mater. Sci. Eng. A 2004, 365, 25–30. [Google Scholar] [CrossRef][Green Version]
- Landa, A.; Söderlind, P.; Yang, L.H. Ab initio phase stability at high temperatures and pressures in the V–Cr system. Phys. Rev. B 2014, 89, 020101. [Google Scholar] [CrossRef]
- Dai, C.; Jin, X.; Zhou, X.; Liu, J.; Hu, J. Sound velocity variations and melting of vanadium under shock compression. J. Phys. Appl. Phys. 2001, 34, 3064–3070. [Google Scholar] [CrossRef]
- Errandonea, D.; Schwager, B.; Ditz, R.; Gessmann, C.; Boehler, R.; Ross, M. Systematics of transition-metal melting. Phys. Rev. B 2001, 63, 132104. [Google Scholar] [CrossRef]
- Okamoto, H. N-V (Nitrogen-Vanadium). J. Phase Equilibria 2001, 22, 362–364. [Google Scholar] [CrossRef]
- Kubel, F.; Lengauer, W.; Yvon, K.; Knorr, K.; Junod, A. Structural phase transition at 205 K in stoichiometric vanadium nitride. Phys. Rev. B 1988, 38, 12908–12912. [Google Scholar] [CrossRef]
- Wolf, W.; Podloucky, R.; Antretter, T.; Fisher, F.D. First-principles study of elastic and thermal properties of refractory carbides and nitrides. Philos. Mag. B 1999, 79, 839–858. [Google Scholar] [CrossRef]
- Isaev, E.I.; Simak, S.I.; Abrikosov, I.A.; Ahuja, R.; Vekilov, Y.K.; Katsnelson, M.I.; Lichtenstein, A.I.; Johansson, B. Phonon related properties of transition metals, their carbides, and nitrides: A first-principles study. J. Appl. Phys. 2007, 101, 123519. [Google Scholar] [CrossRef]
- Ivashchenko, V.I.; Turchi, P.E.A. Phonon softening and the phase transition in VN. Phys. Rev. B 2008, 78, 224113. [Google Scholar] [CrossRef]
- Řehák, P.; Černý, M.; Holec, D. Interface-induced electronic structure toughening of nitride superlattices. Surf. Coat. Technol. 2017, 325, 410–416. [Google Scholar] [CrossRef]
- Mei, A.B.; Hellman, O.; Wireklint, N.; Schlepütz, C.M.; Sangiovanni, D.G.; Alling, B.; Rockett, A.; Hultman, L.; Petrov, I.; Greene, J.E. Dynamic and structural stability of cubic vanadium nitride. Phys. Rev. B 2015, 91, 054101. [Google Scholar] [CrossRef]
- Kubel, F.; Flack, H.D.; Yvon, K. Electron densities in VN. I. High-precission X-ray diffraction determination of the valence-electron density distribution and atomic displacement parameters. Phys. Rev. B 1987, 36, 1415. [Google Scholar] [CrossRef]
- Zheng, Q.; Mei, A.B.; Tuteja, M.; Sangiovanni, D.G.; Hultman, L.; Petrov, I.; Greene, J.E.; Cahill, D.G. Phonon and electron contributions to the thermal conductivity of VNx epitaxial layers. Phys. Rev. Mater. 2017, 1, 065002. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landa, A.; Söderlind, P.; Naumov, I.I.; Klepeis, J.E.; Vitos, L. Kohn Anomaly and Phase Stability in Group VB Transition Metals. Computation 2018, 6, 29. https://doi.org/10.3390/computation6020029
Landa A, Söderlind P, Naumov II, Klepeis JE, Vitos L. Kohn Anomaly and Phase Stability in Group VB Transition Metals. Computation. 2018; 6(2):29. https://doi.org/10.3390/computation6020029
Chicago/Turabian StyleLanda, Alexander, Per Söderlind, Ivan I. Naumov, John E. Klepeis, and Levente Vitos. 2018. "Kohn Anomaly and Phase Stability in Group VB Transition Metals" Computation 6, no. 2: 29. https://doi.org/10.3390/computation6020029
APA StyleLanda, A., Söderlind, P., Naumov, I. I., Klepeis, J. E., & Vitos, L. (2018). Kohn Anomaly and Phase Stability in Group VB Transition Metals. Computation, 6(2), 29. https://doi.org/10.3390/computation6020029





