Recent Progress in First-Principles Methods for Computing the Electronic Structure of Correlated Materials
Abstract
1. Introduction
2. Theoretical Background and Historical Development
2.1. LDA+U
2.2. The Method
2.3. Dynamical Mean-Field Theory
2.4. LDA+DMFT
3. Recent Theoretical Progress
3.1. +EDMFT
3.1.1. Functional Approach
3.2. Multitier Self-Consistent +EDMFT
- Subspace 1: The correlated subspace in which self-consistent GW + EDMFT is applied.
- Subspace 2: The intermediate subspace in which self-consistent GW is active.
- Subspace 3: The remaining subspace in which a one-shot GW is active.
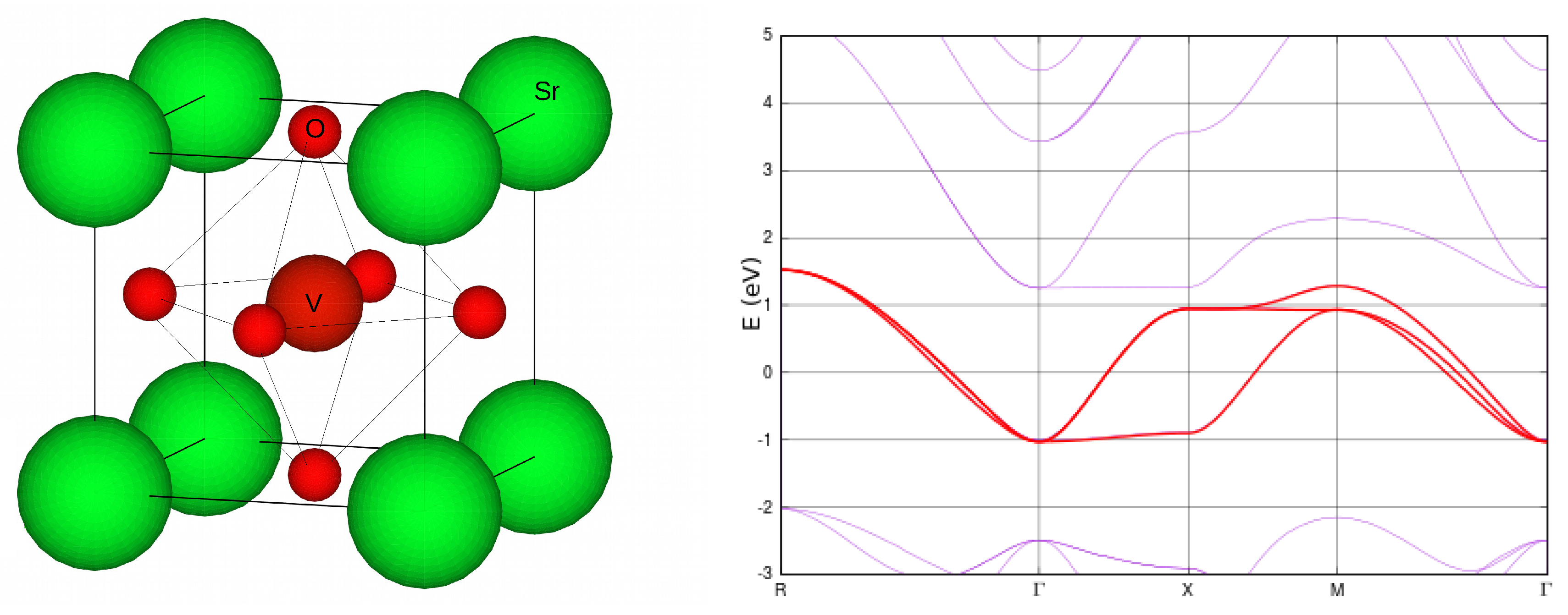
3.3. Illustrative Example: SrVO
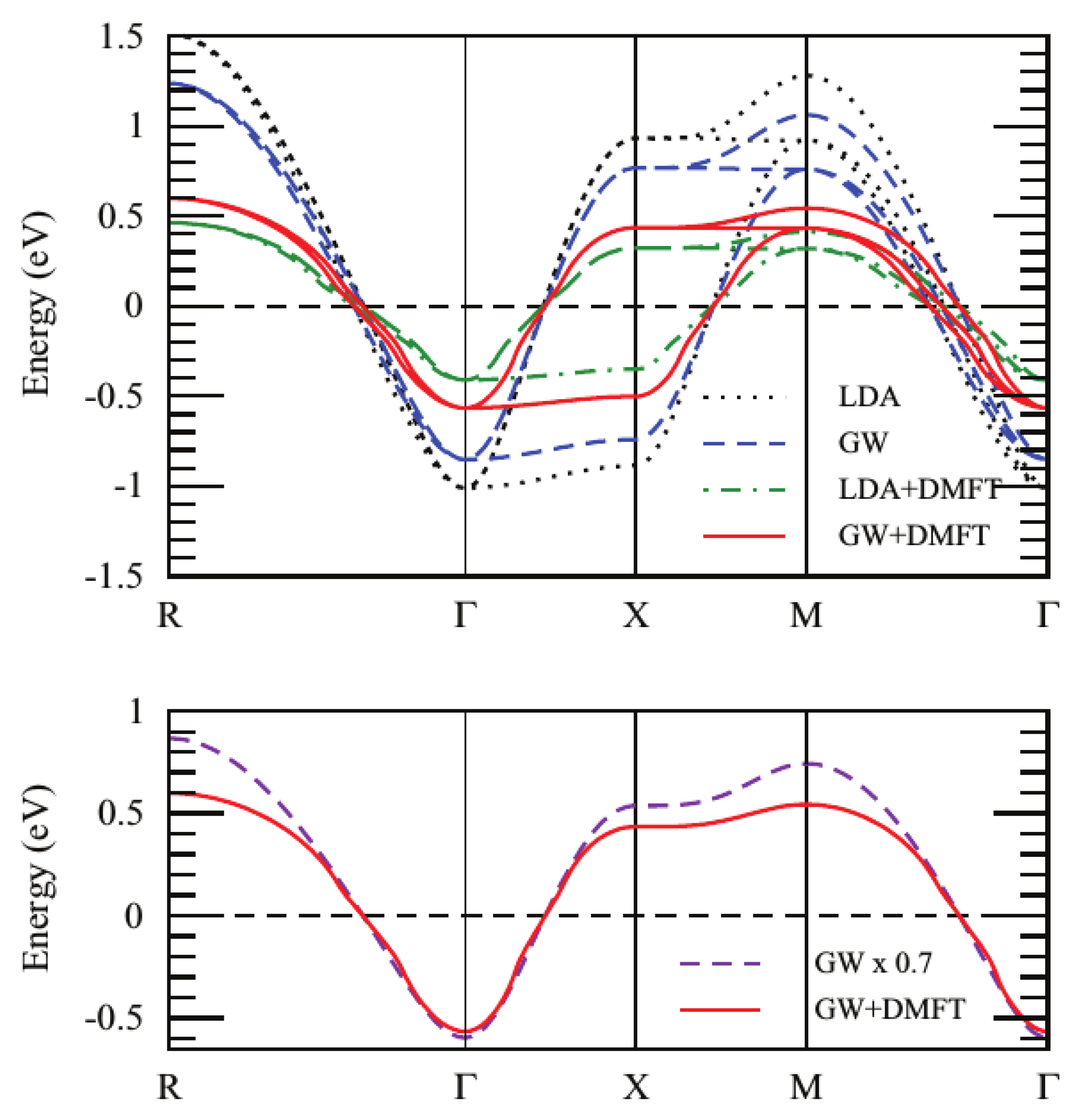
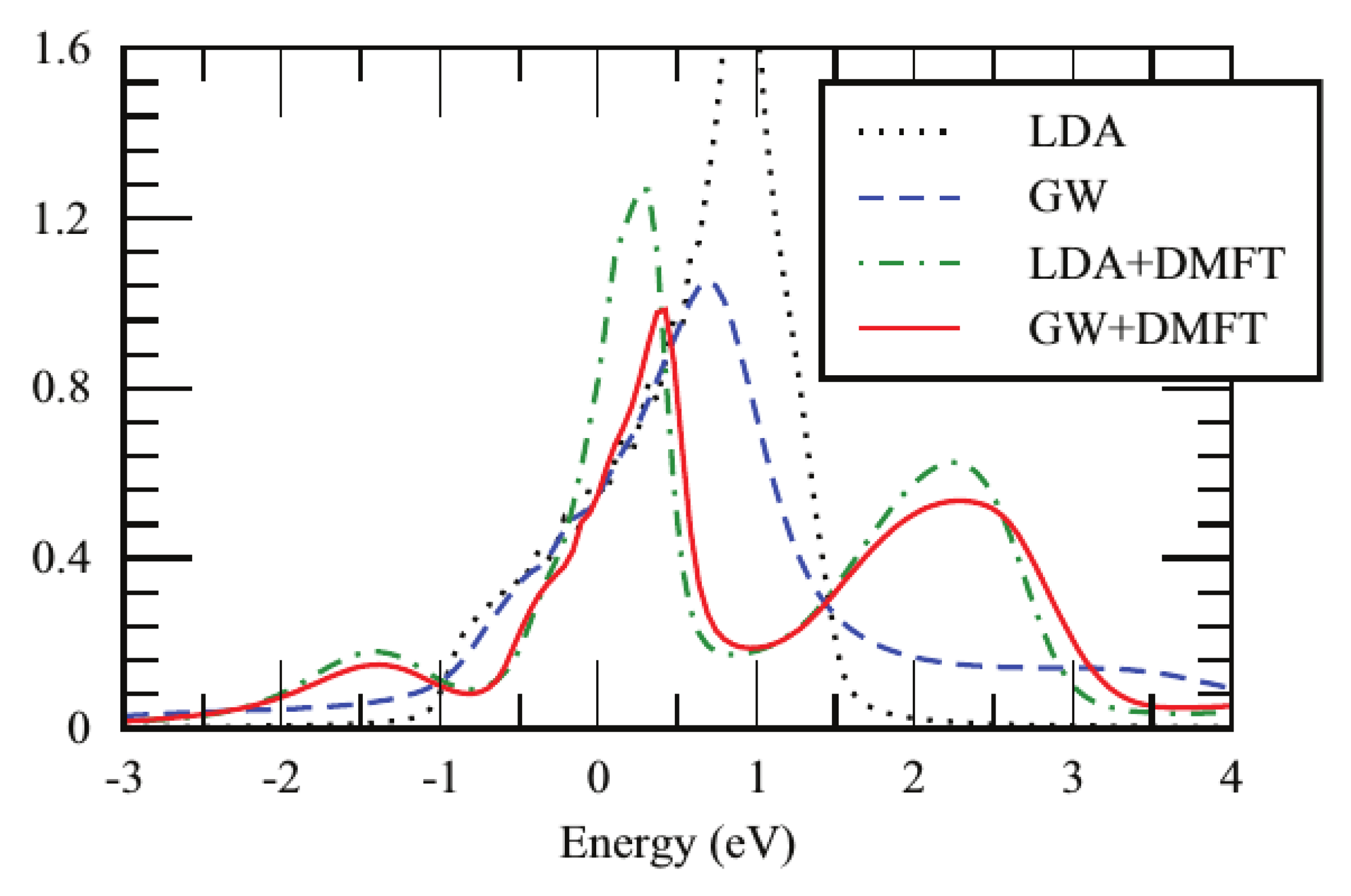
3.3.1. One-Shot GW+DMFT
3.4. Effect of Self-Consistency: Multitier +EDMFT
- Are the local vertex corrections from DMFT sufficient to counteract the detrimental effects of self-consistent ?
- What is the role of the long-range screening?
- What is the nature of the satellites in SrVO? Are they plasmons as indicated by the calculations and the cumulant expansion or are they Hubbard bands as DMFT-based calculations suggest?
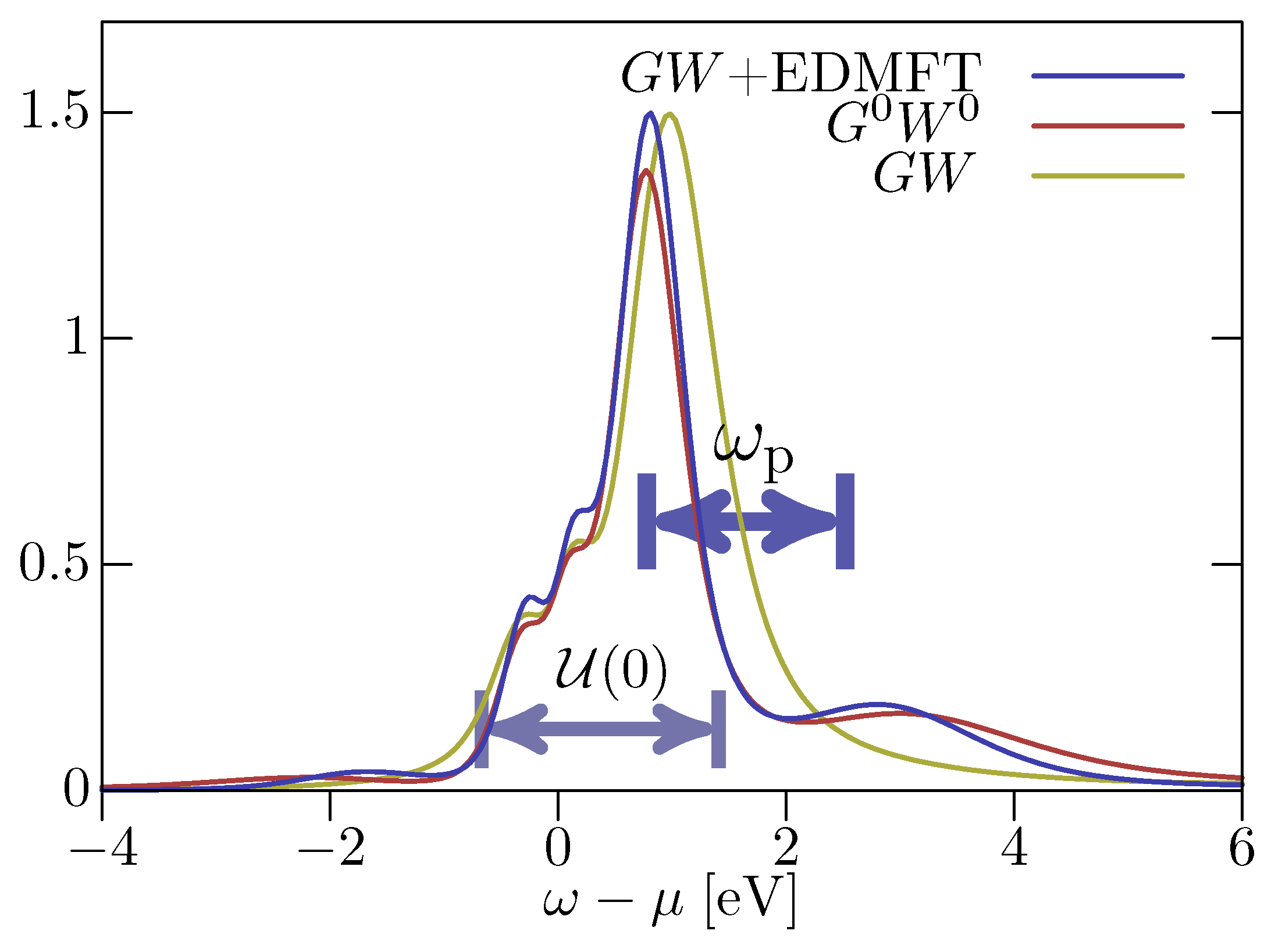
3.5. Different Levels of Self-Consistency
4. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Construction of a Low-Energy Model
Appendix A.1. Constrained RPA
Appendix A.2. Downfolding the Self-Energy
References
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Jones, R.O. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 2015, 87, 897–923. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Lichtenstein, A.I. LDA+U Method: Screened Coulomb Interaction in the Mean-Field Approximation. In Strong Coulomb Correlations in Electronic Structure Calculations. Beyond the Local Density Approximation; Anisimov, V.I., Ed.; Gordon and Breach: New York, NY, USA, 2001; Volume 1, pp. 97–165. [Google Scholar]
- Shen, Z.X.; Dessau, D. Electronic structure and photoemission studies of late transition-metal oxides—Mott insulators and high-temperature superconductors. Phys. Rep. 1995, 253, 1–162. [Google Scholar] [CrossRef]
- Lee, P.A.; Nagaosa, N.; Wen, X.G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible highTc superconductivity in the Ba-La-Cu-O system. Z. Für Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Ramirez, A.P. Colossal magnetoresistance. J. Phys. Condens. Matter 1997, 9, 8171. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Lichtenstein, A.I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA+U method. J. Phys. Condens. Matter 1997, 9, 767. [Google Scholar] [CrossRef]
- Metzner, W.; Vollhardt, D. Correlated Lattice Fermions in d = ∞ Dimensions. Phys. Rev. Lett. 1989, 62, 324–327. [Google Scholar] [CrossRef] [PubMed]
- Georges, A.; Kotliar, G. Hubbard model in infinite dimensions. Phys. Rev. B 1992, 45, 6479–6483. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Poteryaev, A.I.; Korotin, M.A.; Anokhin, A.O.; Kotliar, G. First-principles calculations of the electronic structure and spectra of strongly correlated systems: dynamical mean-field theory. J. Phys. Condens. Matter 1997, 9, 7359. [Google Scholar] [CrossRef]
- Lichtenstein, A.I.; Katsnelson, M.I. Ab initio calculations of quasiparticle band structure in correlated systems: LDA++ approach. Phys. Rev. B 1998, 57, 6884–6895. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865–951. [Google Scholar] [CrossRef]
- Held, K. Electronic structure calculations using dynamical mean field theory. Adv. Phys. 2007, 56, 829–926. [Google Scholar] [CrossRef]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Hedin, L. On correlation effects in electron spectroscopies and the GW approximation. J. Phys. Condens. Matter 1999, 11, R489. [Google Scholar] [CrossRef]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef]
- Biermann, S.; Aryasetiawan, F.; Georges, A. First-principles approach to the electronic structure of strongly correlated systems: Combining the GW approximation and dynamical mean-field theory. Phys. Rev. Lett. 2003, 90, 086402. [Google Scholar] [CrossRef] [PubMed]
- Taranto, C.; Kaltak, M.; Parragh, N.; Sangiovanni, G.; Kresse, G.; Toschi, A.; Held, K. Comparing quasiparticle GW+DMFT and LDA+DMFT for the test bed material SrVO3. Phys. Rev. B 2013, 88, 165119. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Casula, M.; Miyake, T.; Aryasetiawan, F.; Biermann, S. Combined GW and dynamical mean-field theory: Dynamical screening effects in transition metal oxides. EPL (Europhys. Lett.) 2012, 100, 67001. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Casula, M.; Miyake, T.; Biermann, S. Asymmetry in band widening and quasiparticle lifetimes in SrVO3: Competition between screened exchange and local correlations from combined GW and dynamical mean-field theory GW+DMFT. Phys. Rev. B 2014, 90, 165138. [Google Scholar] [CrossRef]
- Van Roekeghem, A.; Biermann, S. Screened exchange dynamical mean-field theory and its relation to density functional theory: SrVO3 and SrTiO3. EPL (Europhys. Lett.) 2014, 108, 57003. [Google Scholar] [CrossRef]
- Choi, S.; Kutepov, A.; Haule, K.; van Schilfgaarde, M.; Kotliar, G. First-principles treatment of Mott insulators: Linearized QSGW+DMFT approach. Npj Quantum Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Karlsson, K. Self-consistent GW combined with single-site dynamical mean field theory for a Hubbard model. J. Phys. Condens. Matter 2005, 17, 7573. [Google Scholar] [CrossRef]
- Ayral, T.; Werner, P.; Biermann, S. Spectral Properties of Correlated Materials: Local Vertex and Nonlocal Two-Particle Correlations from Combined GW and Dynamical Mean Field Theory. Phys. Rev. Lett. 2012, 109, 226401. [Google Scholar] [CrossRef] [PubMed]
- Ayral, T.; Biermann, S.; Werner, P. Screening and nonlocal correlations in the extended Hubbard model from self-consistent combined GW and dynamical mean field theory. Phys. Rev. B 2013, 87, 125149. [Google Scholar] [CrossRef]
- Hansmann, P.; Ayral, T.; Vaugier, L.; Werner, P.; Biermann, S. Long-Range Coulomb Interactions in Surface Systems: A First-Principles Description within Self-Consistently Combined GW and Dynamical Mean-Field Theory. Phys. Rev. Lett. 2013, 110, 166401. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Ayral, T.; Biermann, S.; Werner, P. Extended dynamical mean-field study of the Hubbard model with long-range interactions. Phys. Rev. B 2014, 90, 195114. [Google Scholar] [CrossRef]
- Van Loon, E.G.C.P.; Krien, F.; Hafermann, H.; Stepanov, E.A.; Lichtenstein, A.I.; Katsnelson, M.I. Double occupancy in dynamical mean-field theory and the dual boson approach. Phys. Rev. B 2016, 93, 155162. [Google Scholar] [CrossRef]
- Stepanov, E.A.; van Loon, E.G.C.P.; Katanin, A.A.; Lichtenstein, A.I.; Katsnelson, M.I.; Rubtsov, A.N. Self-consistent dual boson approach to single-particle and collective excitations in correlated systems. Phys. Rev. B 2016, 93, 045107. [Google Scholar] [CrossRef]
- Ayral, T.; Biermann, S.; Werner, P.; Boehnke, L. Influence of Fock exchange in combined many-body perturbation and dynamical mean field theory. Phys. Rev. B 2017, 95, 245130. [Google Scholar] [CrossRef]
- Boehnke, L.; Nilsson, F.; Aryasetiawan, F.; Werner, P. When strong correlations become weak: Consistent merging of GW and DMFT. Phys. Rev. B 2016, 94, 201106. [Google Scholar] [CrossRef]
- Nilsson, F.; Boehnke, L.; Werner, P.; Aryasetiawan, F. Multitier self-consistent GW+EDMFT. Phys. Rev. Mater. 2017, 1, 043803. [Google Scholar] [CrossRef]
- Slater, J.C. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385–390. [Google Scholar] [CrossRef]
- Slater, J.C. The History of the Xα Method. In The World of Quantum Chemistry; Daudel, R., Pullman, B., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1974; pp. 3–15. [Google Scholar]
- Gunnarsson, O.; Andersen, O.K.; Jepsen, O.; Zaanen, J. Density-functional calculation of the parameters in the Anderson model: Application to Mn in CdTe. Phys. Rev. B 1989, 39, 1708–1722. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Allen, J.W. Resonant Photoemission of Solids with Strongly Correlated Electrons. In Synchroton Radiation Research, Advances in Surface Interface Science, 1st ed.; Bachrach, R.Z., Ed.; Springer Science+Business Media: New York, NY, USA, 1992; pp. 253–315. [Google Scholar]
- Karlsson, K.; Aryasetiawan, F.; Jepsen, O. Method for calculating the electronic structure of correlated materials from a truly first-principles LDA+U scheme. Phys. Rev. B 2010, 81, 245113. [Google Scholar] [CrossRef]
- The FLEUR Group. The FLEUR Project. Available online: http://www.flapw.de (accessed on 10 March 2012).
- Fetter, A.; Walecka, J. Quantum Theory of Many-Particle Systems; Dover: Mineola/New York, NY, USA, 2003. [Google Scholar]
- Aulbur, W.G.; Jönsson, L.; Wilkins, J.W. Quasiparticle Calculations in Solids; Academic Press: Cambridge, MA, USA, 2000; Volume 54, pp. 1–218. [Google Scholar]
- Pines, D. Elementary Excitations in Solids; Benjamin: New York, NY, USA, 1963. [Google Scholar]
- Zhu, X.; Louie, S.G. Quasiparticle band structure of thirteen semiconductors and insulators. Phys. Rev. B 1991, 43, 14142–14156. [Google Scholar] [CrossRef]
- Rohlfing, M.; Krüger, P.; Pollmann, J. Quasiparticle band-structure calculations for C, Si, Ge, GaAs, and SiC using Gaussian-orbital basis sets. Phys. Rev. B 1993, 48, 17791–17805. [Google Scholar] [CrossRef]
- Zakharov, O.; Rubio, A.; Blase, X.; Cohen, M.L.; Louie, S.G. Quasiparticle band structures of six II–VI compounds: ZnS, ZnSe, ZnTe, CdS, CdSe, and CdTe. Phys. Rev. B 1994, 50, 10780–10787. [Google Scholar] [CrossRef]
- Godby, R.W.; Schlüter, M.; Sham, L.J. Self-energy operators and exchange-correlation potentials in semiconductors. Phys. Rev. B 1988, 37, 10159–10175. [Google Scholar] [CrossRef]
- Rubio, A.; Corkill, J.L.; Cohen, M.L.; Shirley, E.L.; Louie, S.G. Quasiparticle band structure of AlN and GaN. Phys. Rev. B 1993, 48, 11810–11816. [Google Scholar] [CrossRef]
- Schönberger, U.; Aryasetiawan, F. Bulk and surface electronic structures of MgO. Phys. Rev. B 1995, 52, 8788–8793. [Google Scholar] [CrossRef]
- Hellwege, K.H.; Madelung, O. (Eds.) Numerical Data and Functional Relationships in Science and Technology; Landolt-Börnstein, New Series, Group III, Vols. 17a and 22a; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Baldini, G.; Bosacchi, B. Optical Properties of Na and Li Halide Crystals at 55 °K. Phys. Status Solidif. 1970, 38, 325–334. [Google Scholar] [CrossRef]
- Whited, R.; Flaten, C.J.; Walker, W. Exciton thermoreflectance of MgO and CaO. Solid State Commun. 1973, 13, 1903–1905. [Google Scholar] [CrossRef]
- Holm, B.; von Barth, U. Fully self-consistent GW self-energy of the electron gas. Phys. Rev. B 1998, 57, 2108–2117. [Google Scholar] [CrossRef]
- Kotani, T.; van Schilfgaarde, M.; Faleev, S.V. Quasiparticle self-consistent GW method: A basis for the independent-particle approximation. Phys. Rev. B 2007, 76, 165106. [Google Scholar] [CrossRef]
- Sakuma, R.; Miyake, T.; Aryasetiawan, F. Self-energy and spectral function of Ce within the GW approximation. Phys. Rev. B 2012, 86, 245126. [Google Scholar] [CrossRef]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge Studies in Magnetism; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Aryasetiawan, F.; Imada, M.; Georges, A.; Kotliar, G.; Biermann, S.; Lichtenstein, A.I. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 2004, 70, 195104. [Google Scholar] [CrossRef]
- Amadon, B.; Biermann, S.; Georges, A.; Aryasetiawan, F. The α-γ Transition of Cerium Is Entropy Driven. Phys. Rev. Lett. 2006, 96, 066402. [Google Scholar] [CrossRef] [PubMed]
- Werner, P.; Comanac, A.; de’ Medici, L.; Troyer, M.; Millis, A.J. Continuous-Time Solver for Quantum Impurity Models. Phys. Rev. Lett. 2006, 97, 076405. [Google Scholar] [CrossRef] [PubMed]
- Werner, P.; Millis, A.J. Hybridization expansion impurity solver: General formulation and application to Kondo lattice and two-orbital models. Phys. Rev. B 2006, 74, 155107. [Google Scholar] [CrossRef]
- Werner, P.; Millis, A.J. Efficient Dynamical Mean Field Simulation of the Holstein-Hubbard Model. Phys. Rev. Lett. 2007, 99, 146404. [Google Scholar] [CrossRef] [PubMed]
- Werner, P.; Millis, A.J. Dynamical Screening in Correlated Electron Materials. Phys. Rev. Lett. 2010, 104, 146401. [Google Scholar] [CrossRef] [PubMed]
- Werner, P.; Casula, M. Dynamical screening in correlated electron systems—From lattice models to realistic materials. J. Phys. Condens. Matter 2016, 28, 383001. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Miyake, T.; Martins, C.; Sakuma, R.; Aryasetiawan, F. Effects of momentum-dependent self-energy in the electronic structure of correlated materials. Phys. Rev. B 2013, 87, 115110. [Google Scholar] [CrossRef]
- Si, Q.; Smith, J.L. Kosterlitz-Thouless Transition and Short Range Spatial Correlations in an Extended Hubbard Model. Phys. Rev. Lett. 1996, 77, 3391–3394. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.L.; Si, Q. Spatial correlations in dynamical mean-field theory. Phys. Rev. B 2000, 61, 5184–5193. [Google Scholar] [CrossRef]
- Chitra, R.; Kotliar, G. Effective-action approach to strongly correlated fermion systems. Phys. Rev. B 2001, 63, 115110. [Google Scholar] [CrossRef]
- Sun, P.; Kotliar, G. Extended dynamical mean-field theory and GW method. Phys. Rev. B 2002, 66, 085120. [Google Scholar] [CrossRef]
- Ayral, T.; Parcollet, O. Mott physics and spin fluctuations: A unified framework. Phys. Rev. B 2015, 92, 115109. [Google Scholar] [CrossRef]
- Ayral, T.; Parcollet, O. Mott physics and spin fluctuations: A functional viewpoint. Phys. Rev. B 2016, 93, 235124. [Google Scholar] [CrossRef]
- Almbladh, C.O.; Barth, U.V.; Leeuwen, R.V. Variational total energies from Φ- and Ψ-derivable theories. Int. J. Mod. Phys. B 1999, 13, 535–541. [Google Scholar] [CrossRef]
- Luttinger, J.M.; Ward, J.C. Ground-State Energy of a Many-Fermion System. II. Phys. Rev. 1960, 118, 1417–1427. [Google Scholar] [CrossRef]
- Morikawa, K.; Mizokawa, T.; Kobayashi, K.; Fujimori, A.; Eisaki, H.; Uchida, S.; Iga, F.; Nishihara, Y. Spectral weight transfer and mass renormalization in Mott-Hubbard systems SrVO3 and CaVO3: Influence of long-range Coulomb interaction. Phys. Rev. B 1995, 52, 13711–13714. [Google Scholar] [CrossRef]
- Sekiyama, A.; Fujiwara, H.; Imada, S.; Suga, S.; Eisaki, H.; Uchida, S.I.; Takegahara, K.; Harima, H.; Saitoh, Y.; Nekrasov, I.A.; et al. Mutual Experimental and Theoretical Validation of Bulk Photoemission Spectra of Sr1−xCaxVO3. Phys. Rev. Lett. 2004, 93, 156402. [Google Scholar] [CrossRef] [PubMed]
- Takizawa, M.; Minohara, M.; Kumigashira, H.; Toyota, D.; Oshima, M.; Wadati, H.; Yoshida, T.; Fujimori, A.; Lippmaa, M.; Kawasaki, M.; et al. Coherent and incoherent d band dispersions in SrVO3. Phys. Rev. B 2009, 80, 235104. [Google Scholar] [CrossRef]
- Aizaki, S.; Yoshida, T.; Yoshimatsu, K.; Takizawa, M.; Minohara, M.; Ideta, S.; Fujimori, A.; Gupta, K.; Mahadevan, P.; Horiba, K.; et al. Self-Energy on the Low- to High-Energy Electronic Structure of Correlated Metal SrVO3. Phys. Rev. Lett. 2012, 109, 056401. [Google Scholar] [CrossRef] [PubMed]
- Backes, S.; Rödel, T.C.; Fortuna, F.; Frantzeskakis, E.; Le Fèvre, P.; Bertran, F.; Kobayashi, M.; Yukawa, R.; Mitsuhashi, T.; Kitamura, M.; et al. Hubbard band versus oxygen vacancy states in the correlated electron metal SrVO3. Phys. Rev. B 2016, 94, 241110. [Google Scholar] [CrossRef]
- Yoshida, T.; Hashimoto, M.; Takizawa, T.; Fujimori, A.; Kubota, M.; Ono, K.; Eisaki, H. Mass renormalization in the bandwidth-controlled Mott-Hubbard systems SrVO3 and CaVO3 studied by angle-resolved photoemission spectroscopy. Phys. Rev. B 2010, 82, 085119. [Google Scholar] [CrossRef]
- Inoue, I.H.; Goto, O.; Makino, H.; Hussey, N.E.; Ishikawa, M. Bandwidth control in a perovskite-type 3d1-correlated metal Ca1−xSrxVO3. I. Evolution of the electronic properties and effective mass. Phys. Rev. B 1998, 58, 4372–4383. [Google Scholar] [CrossRef]
- Sakuma, R.; Werner, P.; Aryasetiawan, F. Electronic structure of SrVO3 within GW+DMFT. Phys. Rev. B 2013, 88, 235110. [Google Scholar] [CrossRef]
- Gatti, M.; Guzzo, M. Dynamical screening in correlated metals: Spectral properties of SrVO3 in the GW approximation and beyond. Phys. Rev. B 2013, 87, 155147. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Hedin, L.; Karlsson, K. Multiple Plasmon Satellites in Na and Al Spectral Functions from Ab Initio Cumulant Expansion. Phys. Rev. Lett. 1996, 77, 2268–2271. [Google Scholar] [CrossRef] [PubMed]
- Guzzo, M.; Lani, G.; Sottile, F.; Romaniello, P.; Gatti, M.; Kas, J.J.; Rehr, J.J.; Silly, M.G.; Sirotti, F.; Reining, L. Valence Electron Photoemission Spectrum of Semiconductors: Ab Initio Description of Multiple Satellites. Phys. Rev. Lett. 2011, 107, 166401. [Google Scholar] [CrossRef] [PubMed]
- Pavarini, E.; Biermann, S.; Poteryaev, A.; Lichtenstein, A.I.; Georges, A.; Andersen, O.K. Mott Transition and Suppression of Orbital Fluctuations in Orthorhombic 3d1 Perovskites. Phys. Rev. Lett. 2004, 92, 176403. [Google Scholar] [CrossRef] [PubMed]
- Nekrasov, I.A.; Held, K.; Keller, G.; Kondakov, D.E.; Pruschke, T.; Kollar, M.; Andersen, O.K.; Anisimov, V.I.; Vollhardt, D. Momentum-resolved spectral functions of SrVO3 calculated by LDA+DMFT. Phys. Rev. B 2006, 73, 155112. [Google Scholar] [CrossRef]
- Lechermann, F.; Georges, A.; Poteryaev, A.; Biermann, S.; Posternak, M.; Yamasaki, A.; Andersen, O.K. Dynamical mean-field theory using Wannier functions: A flexible route to electronic structure calculations of strongly correlated materials. Phys. Rev. B 2006, 74, 125120. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847–12865. [Google Scholar] [CrossRef]
- Souza, I.; Marzari, N.; Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 2001, 65, 035109. [Google Scholar] [CrossRef]
- Sakuma, R. Symmetry-adapted Wannier functions in the maximal localization procedure. Phys. Rev. B 2013, 87, 235109. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Lee, Y.S.; Souza, I.; Vanderbilt, D.; Marzari, N. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2008, 178, 685–699. [Google Scholar] [CrossRef]
- Wadati, H.; Mravlje, J.; Yoshimatsu, K.; Kumigashira, H.; Oshima, M.; Sugiyama, T.; Ikenaga, E.; Fujimori, A.; Georges, A.; Radetinac, A.; et al. Photoemission and DMFT study of electronic correlations in SrMoO3: Effects of Hund’s rule coupling and possible plasmonic sideband. Phys. Rev. B 2014, 90, 205131. [Google Scholar] [CrossRef]
- Lee, J.; Haule, K. Diatomic molecule as a testbed for combining DMFT with electronic structure methods such as GW and DFT. Phys. Rev. B 2017, 95, 155104. [Google Scholar] [CrossRef]
- Baym, G.; Kadanoff, L.P. Conservation Laws and Correlation Functions. Phys. Rev. 1961, 124, 287–299. [Google Scholar] [CrossRef]
- Baym, G. Self-Consistent Approximations in Many-Body Systems. Phys. Rev. 1962, 127, 1391–1401. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Tomczak, J.M.; Miyake, T.; Sakuma, R. Downfolded Self-Energy of Many-Electron Systems. Phys. Rev. Lett. 2009, 102, 176402. [Google Scholar] [CrossRef] [PubMed]
- Hirayama, M.; Miyake, T.; Imada, M.; Biermann, S. Low-energy effective Hamiltonians for correlated electron systems beyond density functional theory. Phys. Rev. B 2017, 96, 075102. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nilsson, F.; Aryasetiawan, F. Recent Progress in First-Principles Methods for Computing the Electronic Structure of Correlated Materials. Computation 2018, 6, 26. https://doi.org/10.3390/computation6010026
Nilsson F, Aryasetiawan F. Recent Progress in First-Principles Methods for Computing the Electronic Structure of Correlated Materials. Computation. 2018; 6(1):26. https://doi.org/10.3390/computation6010026
Chicago/Turabian StyleNilsson, Fredrik, and Ferdi Aryasetiawan. 2018. "Recent Progress in First-Principles Methods for Computing the Electronic Structure of Correlated Materials" Computation 6, no. 1: 26. https://doi.org/10.3390/computation6010026
APA StyleNilsson, F., & Aryasetiawan, F. (2018). Recent Progress in First-Principles Methods for Computing the Electronic Structure of Correlated Materials. Computation, 6(1), 26. https://doi.org/10.3390/computation6010026



