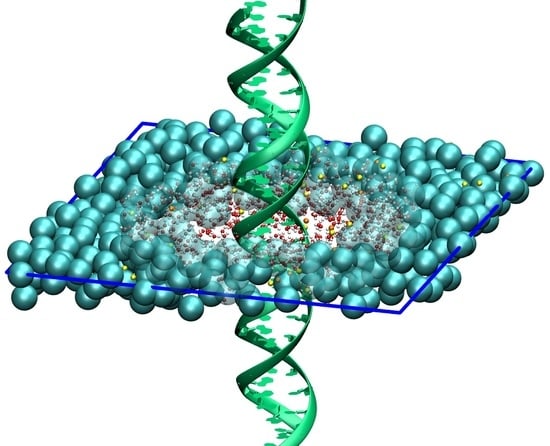
Molecular Dynamics Simulation of High Density DNA Arrays
Abstract
1. Introduction
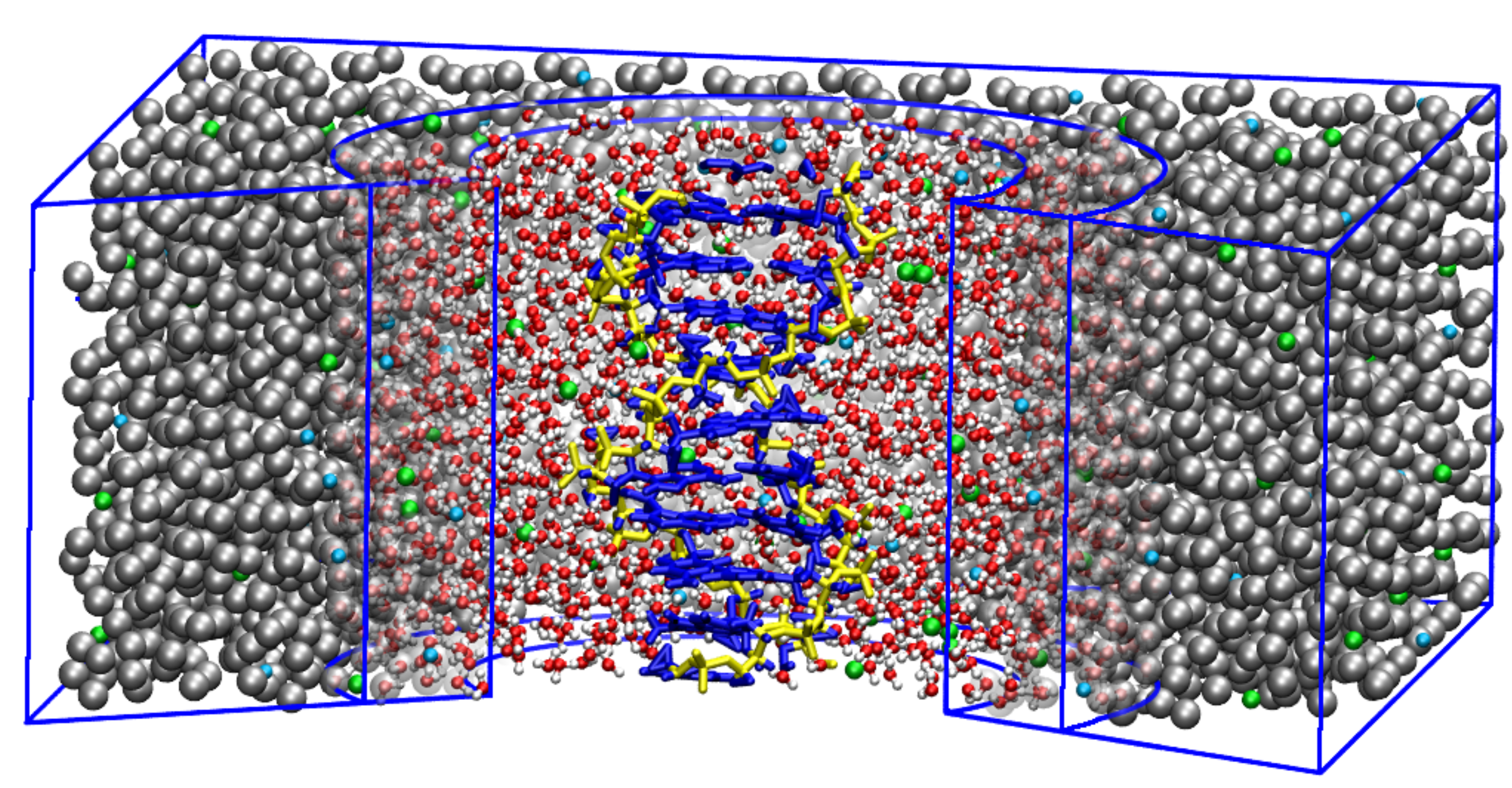
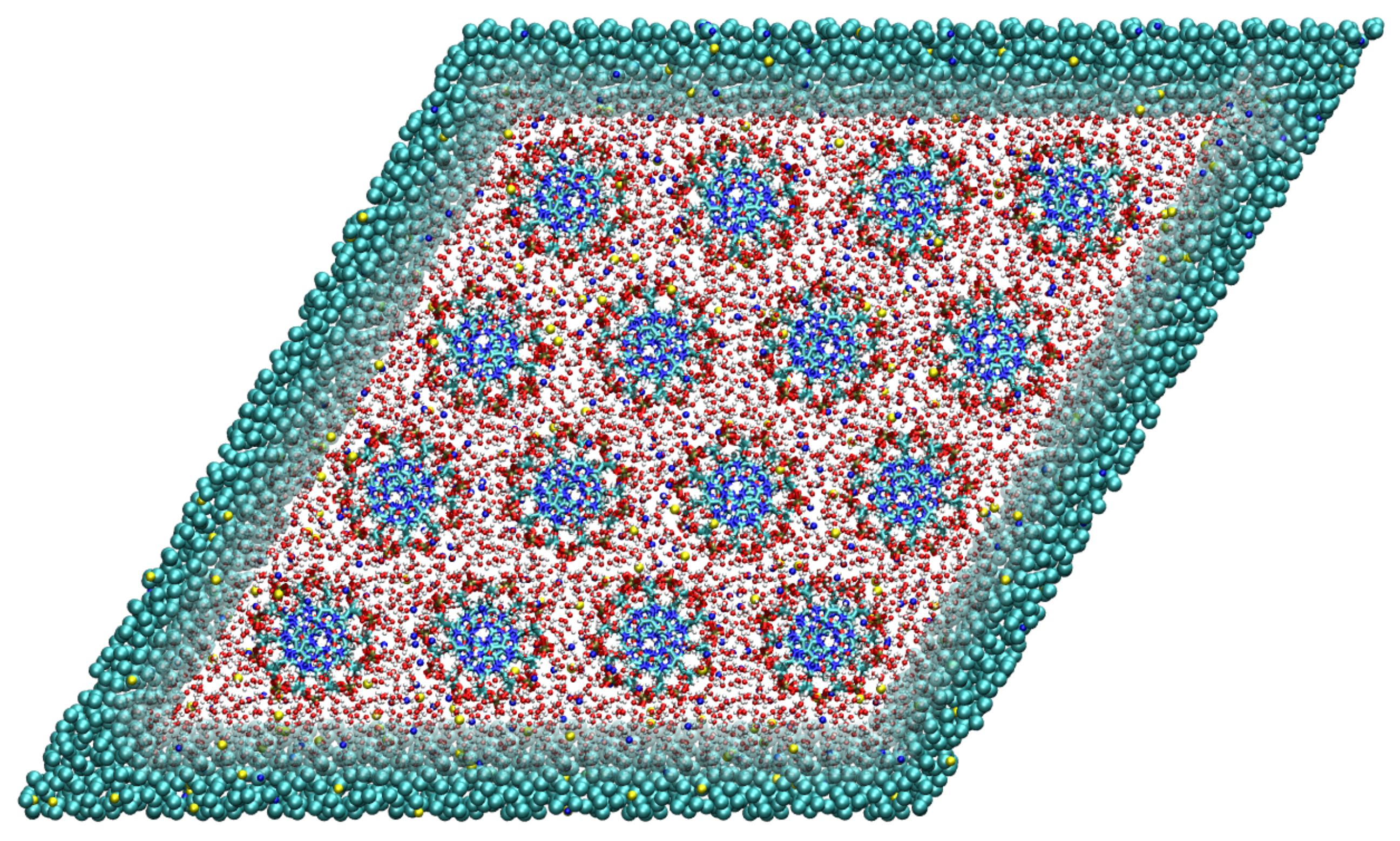
2. Simulating DNA Arrays
2.1. Modeling the Solvent Grand Canonical (Osmotic Isobaric) Ensemble
2.2. Bathing Solution
2.3. Model Interaction Potential Parametrization in DNA Arrays
2.4. Structural Characterization of the High Density DNA Subphase
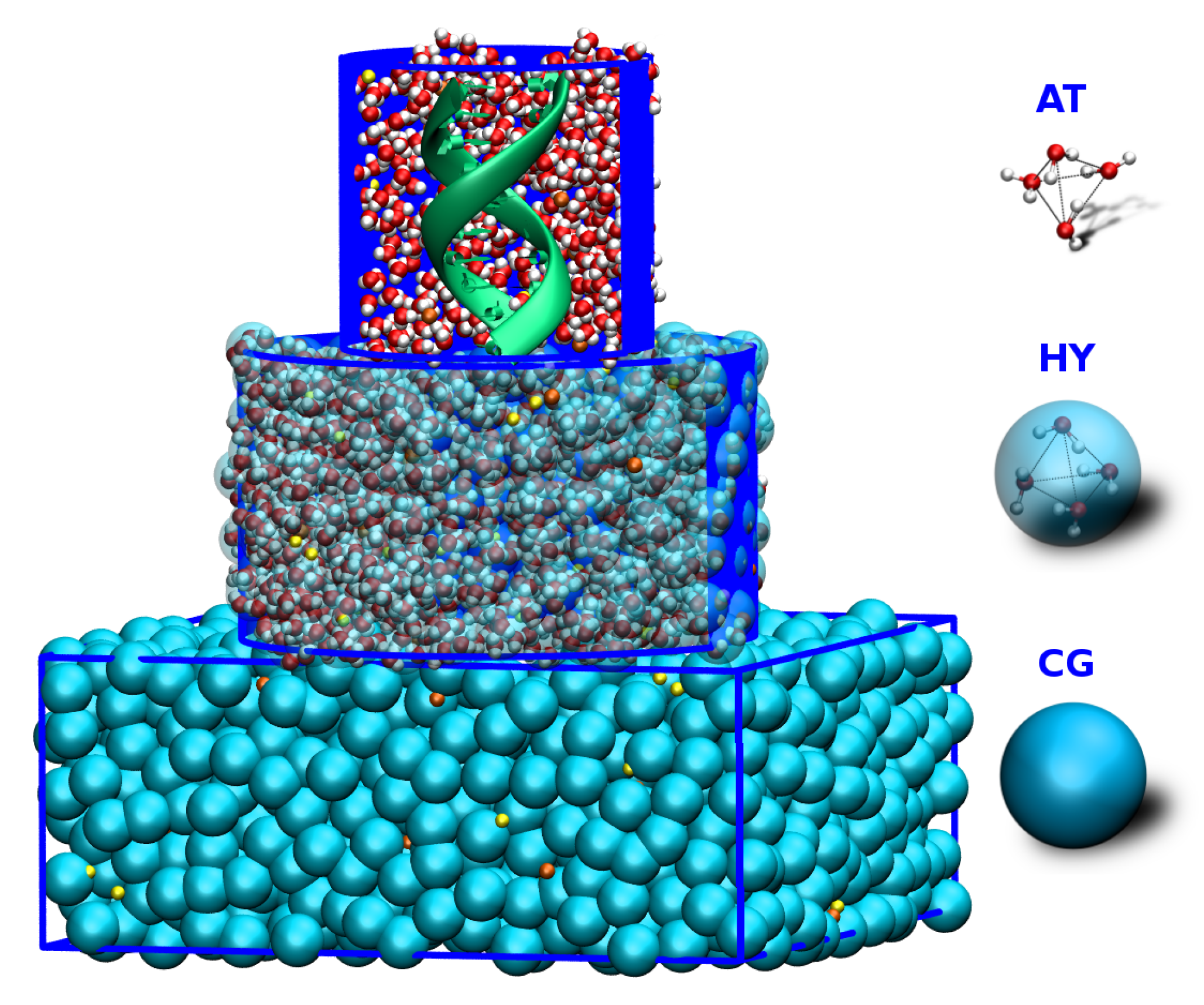
3. Adaptive Resolution Simulations of a DNA Molecule Solvated in Salt Solution
3.1. AdResS—Single DNA
3.2. Dielectric Properties
4. Simulating Osmotic Isobaric Ensemble: Densely Packed DNA Arrays
4.1. Computation of Osmotic Pressure
4.2. Hexagonal Columnar (H) → Orthorhombic (OR) Phase Transition
4.3. Orientational Order Parameters
5. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
References
- Livolant, F.; Leforestier, A. Condensed Phases of DNA: Structures and Phase Transitions. Prog. Polym. Sci. 1996, 21, 1115–1164. [Google Scholar] [CrossRef]
- Bellini, T.; Cerbino, R.; Zanchetta, G. DNA-Based Soft Phases. Top. Curr. Chem. 2011, 318, 225–279. [Google Scholar]
- Podgornik, R.; Strey, H.H.; Gawrisch, K.; Rau, D.C.; Rupprecht, A.; Parsegian, V.A. Bond orientational order, molecular motion, and free energy of high-density DNA mesophases. Proc. Natl. Acad. Sci. USA 1996, 93, 4261–4266. [Google Scholar] [CrossRef] [PubMed]
- Rau, D.C.; Lee, B.; Parsegian, V.A. Measurement of the repulsive force between polyelectrolyte molecules in ionic solution: Hydration forces between parallel DNA double helices. Proc. Natl. Acad. Sci. USA 1984, 81, 2621–2625. [Google Scholar] [CrossRef] [PubMed]
- Parsegian, V.; Rand, R.; Fuller, N.; Rau, D. Osmotic Stress for the Direct Measurement of Intermolecular Forces. Meth. Enzym. 1986, 127, 400–416. [Google Scholar] [PubMed]
- Strey, H.H.; Podgornik, R.; Rau, D.C.; Parsegian, V.A. DNA-DNA interactions. Curr. Opin. Struct. Biol. 1998, 8, 309–313. [Google Scholar] [CrossRef]
- Podgornik, R.; Rau, D.C.; Parsegian, V.A. The action of interhelical forces on the organization of DNA double helixes: Fluctuation-enhanced decay of electrostatic double-layer and hydration forces. Macromolecules 1989, 22, 1780–1786. [Google Scholar] [CrossRef]
- Strey, H.H.; Parsegian, V.A.; Podgornik, R. Equation of state for polymer liquid crystals: Theory and experiment. Phys. Rev. E 1999, 59, 999–1008. [Google Scholar] [CrossRef]
- Yasar, S.; Podgornik, R.; Parsegian, V. Continuity of states in cholesteric—Line hexatic transition in univalent and polyvalent salt DNA solutions. MRS Proc. 2013, 1619. [Google Scholar] [CrossRef]
- Yasar, S.; Podgornik, R.; Valle-Orero, J.; Johnson, M.; Parsegian, V.A. Continuity of states between the cholesteric → line hexatic transition and the condensation transition in DNA solutions. Sci. Rep. 2014, 4, 6877. [Google Scholar] [CrossRef] [PubMed]
- Durand, D.; Doucet, J.; Livolant, F. A study of the structure of highly concentrated phases of DNA by X-ray diffraction. J. Phys. II Fr. 1992, 2, 1769–1783. [Google Scholar] [CrossRef]
- Nakata, M.; Zanchetta, G.; Chapman, B.D.; Jones, C.D.; Cross, J.O.; Pindak, R.; Bellini, T.; Clark, N.A. End-to-End Stacking and Liquid Crystal Condensation of 6-to-20-Base Pair DNA Duplexes. Science 2007, 318, 1276–1279. [Google Scholar] [CrossRef] [PubMed]
- Lorman, V.; Podgornik, R.; Žekš, B. Positional, reorientational, and bond orientational order in DNA mesophases. Phys. Rev. Lett. 2001, 87, 218101. [Google Scholar] [CrossRef] [PubMed]
- Grason, G.M. Structural transitions and soft modes in frustrated DNA crystals. EPL Europhys. Lett. 2008, 83, 58003. [Google Scholar] [CrossRef]
- Strzelecka, T.E.; Davidson, M.W.; Rill, R.L. Multiple liquid crystal phases of DNA at high concentrations. Nature 1988, 331, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Kornyshev, A.A.; Leikin, S. Electrostatic interaction between helical macromolecules in dense aggregates: An impetus for DNA poly- and meso-morphism. Proc. Natl. Acad. Sci. USA 1998, 95, 13579–13584. [Google Scholar] [CrossRef] [PubMed]
- Harreis, H.; Kornyshev, A.; Likos, C.; Löwen, H.; Sutmann, G. Phase behavior of columnar DNA assemblies. Phys. Rev. Lett. 2002, 89, 018303. [Google Scholar] [CrossRef] [PubMed]
- Mangenot, S.; Leforestier, A.; Durand, D.; Livolant, F. X-Ray Diffraction Characterization of the Dense Phases Formed by Nucleosome Core Particles. Biophys. J. 2003, 84, 2570–2584. [Google Scholar] [CrossRef]
- Zanchetta, G.; Bellini, T.; Nakata, M.; Clark, N. Physical Polymerization and Liquid Crystallization of RNA Oligomers. J. Am. Chem. Soc. 2008, 130, 12864. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Rau, D. Incomplete Ion Dissociation Underlies the Weakened Attraction between DNA Helices at High Spermidine Concentrations. Biophys. J. 2005, 89, 1932–1940. [Google Scholar] [CrossRef] [PubMed]
- Rau, D.; Parsegian, V. Direct measurement of the intermolecular forces between counterion-condensed DNA double helices. Evidence for long range attractive hydration forces. Biophys. J. 1992, 61, 246–259. [Google Scholar] [CrossRef]
- Rau, D.C.; Parsegian, V.A. Direct measurment of temperature-dependent solvent forces between DNA double helices. Biophys. J. 1992, 61, 260–271. [Google Scholar] [CrossRef]
- Todd, B.A.; Parsegian, V.A.; Shirahata, A.; Thomas, T.J.; Rau, D.C. Attractive forces between cation condensed DNA double helices. Biophys. J. 2008, 94, 4775–4782. [Google Scholar] [CrossRef] [PubMed]
- Bloomfield, V. DNA condensation by multivalent cations. Biopolymers 1997, 44, 269–282. [Google Scholar] [CrossRef]
- Kornyshev, A.A.; Lee, D.J.; Leikin, S.; Wynveen, A. Structure and Interactions of Biological Helices. Rev. Mod. Phys. 2007, 79, 943–996. [Google Scholar] [CrossRef]
- Podgornik, R.; Rau, D.; Parsegian, V. Parametrization of direct and soft-undulatory forces between DNA double helical polyelectrolytes in solutions of several different anions and cations. Biophys. J. 1994, 66, 962–971. [Google Scholar] [CrossRef]
- Bloomfield, V. DNA condensation. Curr. Opin. Struct. Biol. 1996, 6, 334–341. [Google Scholar] [CrossRef]
- Gelbart, W.M.; Bruinsma, R.F.; Pincus, P.A.; Parsegian, V.A. DNA-inspired electrostatics. Phys. Today 2000, 53, 38–44. [Google Scholar] [CrossRef]
- Qiu, X.; Rau, D.C.; Parsegian, V.; Fang, L.T.; Knobler, C.M.; Gelbart, W.M. Salt-dependent DNA-DNA spacings in intact bacteriophage λ eflect relative importance of DNA self-repulsion and bending energies. Phys. Rev. Lett. 2011, 106, 028102. [Google Scholar] [CrossRef] [PubMed]
- Kornyshev, A.A. Physics of DNA: Unravelling hidden abilities encoded in the structure of ’the most important molecule’. Phys. Chem. Chem. Phys. 2010, 12, 12352–12378. [Google Scholar] [CrossRef] [PubMed]
- Yasar, S.; Schimelman, J.; Aksoyoglu, M.A.; Steinmetz, N.; French, R.; Parsegian, V.; Podgornik, R. X-ray characterization of mesophases of human telomeric G-quadruplexes and other DNA analogues. Sci. Rep. 2016, 6, 27079. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Rau, D.C.; Parsegian, V. Divalent counterion-induced condensation of triple-strand DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 21482–21486. [Google Scholar] [CrossRef] [PubMed]
- Markovich, T.; Andelman, D.; Podgornik, R. Handbook of Lipid Membranes; Safynia, C., Raedler, J., Eds.; Taylor and Francis: Sausalito, CA, USA, 2018; Chapter 9. [Google Scholar]
- Rouzina, I.; Bloomfield, V.A. Macroion Attraction Due to Electrostatic Correlation between Screening Counterions. 1. Mobile Surface-Adsorbed Ions and Diffuse Ion Cloud. J. Phys. Chem. 1996, 100, 9977–9989. [Google Scholar] [CrossRef]
- Grosberg, A.; Nguyen, T.; Shklovskii, B. Colloquium: The physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002, 74, 329–345. [Google Scholar] [CrossRef]
- Naji, A.; Kanduč, M.; Forsman, J.; Podgornik, R. Perspective: Coulomb fluids—Weak coupling, strong coupling, in between and beyond. J. Chem. Phys. 2013, 139, 150901. [Google Scholar] [CrossRef] [PubMed]
- Angelini, T.; Golestanian, R.; Coridan, R.; Butler, J.; Beraud, A.; Krisch, M.; Sinn, H.; Schweizer, K.; Wong, G. Counterions between charged polymers exhibit liquid-like organization and dynamics. Proc. Natl. Acad. Sci. USA 2006, 103, 7962–7967. [Google Scholar] [CrossRef] [PubMed]
- Raspaud, A.; Olvera de la Cruz, M.; Sikorav, J.L.; Livolant, F. Precipitation of DNA by Polyamines: A Polyelectrolyte Behavior. Biophys. J. 1998, 74, 381–393. [Google Scholar] [CrossRef]
- Kanduč, M.; Dobnikar, J.; Podgornik, R. Counterion-mediated electrostatic interactions between helical molecules. Soft Matter 2009, 5, 868–877. [Google Scholar] [CrossRef]
- Podgornik, R.; Strey, H.H.; Parsegian, V.A. Equation of State for DNA Liquid Crystals: Fluctuation Enhanced Repulsion. Phys. Rev. E 1997, 78, 895–898. [Google Scholar]
- Lyubartsev, A.P.; Nordenskiöld, L. Monte Carlo simulation study of ion distribution and osmotic pressure in hexagonally oriented DNA. J. Phys. Chem. 1995, 99, 10373–10382. [Google Scholar] [CrossRef]
- Allahyarov, E.; Gompper, G.; Löwen, H. DNA condensation and redissolution: Interaction between overcharged DNA molecules. J. Phys. Condens. Matter 2005, 17, 1827–1840. [Google Scholar] [CrossRef]
- Nguyen, T.; Grosberg, A.; Shklovskii, B. Macroions in salty water with multivalent ions: Giant inversion of charge. Phys. Rev. Lett. 2000, 14, 1568–1571. [Google Scholar] [CrossRef] [PubMed]
- Cherstvy, A. Electrostatic interactions in biological DNA-related systems. Phys. Chem. Chem. Phys. 2011, 13, 9942–9968. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T. Grand-canonical simulation of DNA condensation with two salts, effect of divalent counterion size. J. Chem. Phys. 2016, 144, 065102. [Google Scholar] [CrossRef] [PubMed]
- Maffeo, C.; Yoo, J.; Comer, J.; Wells, D.B.; Luan, B.; Aksimentiev, A. Close encounters with DNA. J. Phys. Condens. Matter 2014, 26, 413101. [Google Scholar] [CrossRef] [PubMed]
- Guldbrand, L.; Nilsson, L.; Nordenskiold, L. A Monte Carlo simulation study of electrostatic forces between hexagonally packed DNA double helicess. J. Chem. Phys. 1986, 85, 6686–6698. [Google Scholar] [CrossRef]
- Korolev, N.; Lyubartsev, A.P.; Laaksonen, A.; Nordenskiöld, L. A molecular dynamics simulation study of oriented DNA with polyamine and sodium counterions: Diffusion and averaged binding of water and cations. Nucleic Acids Res. 2006, 31, 5971–5981. [Google Scholar] [CrossRef]
- Dai, L.; Mu, Y.; Nordenskiöld, L.; van der Maarel, J.R.C. Molecular dynamics simulation of multivalent-ion mediated attraction between DNA molecules. Phys. Rev. Lett. 2008, 100, 118301. [Google Scholar] [CrossRef] [PubMed]
- Potoyan, D.A.; Savelyev, A.; Papoian, G.A. Recent successes in coarse-grained modeling of DNA. WIREs Comput. Mol. Sci. 2013, 3, 69–83. [Google Scholar] [CrossRef]
- Yoo, J.; Aksimentiev, A. The structure and intermolecular forces of DNA condensates. Nucleic Acids Res. 2016, 44, 2036–2046. [Google Scholar] [CrossRef] [PubMed]
- Laughton, C.A.; Harris, S.A. The atomistic simulation of DNA. WIREs Comput. Mol. Sci. 2011, 1, 590–600. [Google Scholar] [CrossRef]
- Yoo, J.; Aksimentiev, A. Improved parametrization of Li+, Na+, K+ and Mg2+ ions for all-atom molecular dynamics simulations of nucleic acid systems. J. Phys. Chem. Lett. 2011, 3, 45–50. [Google Scholar] [CrossRef]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive resolution molecular-dynamics simulation: Changing the degrees of freedom on the fly. J. Chem. Phys. 2005, 123, 224106. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Multiscale simulation of soft matter: From scale bridging to adaptive resolution. Annu. Rev. Phys. Chem. 2008, 59, 545–571. [Google Scholar] [CrossRef] [PubMed]
- Fritsch, S.; Poblete, S.; Junghans, C.; Ciccotti, G.; Delle Site, L.; Kremer, K. Adaptive resolution molecular dynamics simulation through coupling to an internal particle reservoir. Phys. Rev. Lett. 2012, 108, 170602. [Google Scholar] [CrossRef] [PubMed]
- Delle Site, L.; Praprotnik, M. Molecular systems with open boundaries: Theory and Simulation. Phys. Rep. 2017, 693, 1–56. [Google Scholar] [CrossRef]
- Wang, H.; Hartmann, C.; Schütte, C.; Delle Site, L. Grand-canonical-like molecular-dynamics simulations by using an adaptive-resolution technique. Phys. Rev. X 2013, 3, 011018. [Google Scholar] [CrossRef]
- Agarwal, A.; Delle Site, L. Path integral molecular dynamics within the grand canonical-like adaptive resolution technique: Simulation of liquid water. J. Chem. Phys. 2015, 143, 094102. [Google Scholar] [CrossRef] [PubMed]
- Delle Site, L. Formulation of Liouville’s theorem for grand ensemble molecular simulations. Phys. Rev. E 2016, 93, 022130. [Google Scholar] [CrossRef] [PubMed]
- Delle Site, L. Grand Canonical Adaptive Resolution Simulation for Molecules with Electrons: A Theoretical Framework based on Physical Consistency. Comput. Phys. Commun. 2017. [Google Scholar] [CrossRef]
- Potestio, R.; Fritsch, S.; Español, P.; Delgado-Buscalioni, R.; Kremer, K.; Everaers, R.; Donadio, D. Hamiltonian adaptive resolution simulation for molecular liquids. Phys. Rev. Lett. 2013, 110, 108301. [Google Scholar] [CrossRef] [PubMed]
- Potestio, R.; Español, P.; Delgado-Buscalioni, R.; Everaers, R.; Kremer, K.; Donadio, D. Monte Carlo adaptive resolution simulation of multicomponent molecular liquids. Phys. Rev. Lett. 2013, 111, 060601. [Google Scholar] [CrossRef] [PubMed]
- Español, P.; Delgado-Buscalioni, R.; Everaers, R.; Potestio, R.; Donadio, D.; Kremer, K. Statistical mechanics of hamiltonian adaptive resolution simulations. J. Chem. Phys. 2015, 142, 064115. [Google Scholar] [CrossRef] [PubMed]
- Tarenzi, T.; Calandrini, V.; Potestio, R.; Giorgetti, A.; Carloni, P. Open Boundary Simulations of Proteins and Their Hydration Shells by Hamiltonian Adaptive Resolution Scheme. J. Chem. Theory Comput. 2017. [Google Scholar] [CrossRef] [PubMed]
- Everaers, R. Thermodynamic translational invariance in concurrent multiscale simulations of liquids. Eur. Phys. J. Spec. Top. 2016, 225, 1483–1503. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R. Thermodynamics of adaptive molecular resolution. Philos. Trans. R. Soc. A 2016, 374, 20160152. [Google Scholar] [CrossRef] [PubMed]
- Bevc, S.; Junghans, C.; Kremer, K.; Praprotnik, M. Adaptive resolution simulation of salt solutions. New J. Phys. 2013, 15, 105007. [Google Scholar] [CrossRef]
- Zavadlav, J.; Melo, M.N.; Marrink, S.J.; Praprotnik, M. Adaptive resolution simulation of an atomistic protein in MARTINI water. J. Chem. Phys. 2014, 140, 054114. [Google Scholar] [CrossRef] [PubMed]
- Zavadlav, J.; Podgornik, R.; Praprotnik, M. Adaptive resolution simulation of a DNA molecule in salt solution. J. Chem. Theory Comput. 2015, 11, 5035–5044. [Google Scholar] [CrossRef] [PubMed]
- Zavadlav, J.; Podgornik, R.; Melo, M.N.; Marrink, S.J.; Praprotnik, M. Adaptive resolution simulation of an atomistic DNA molecule in MARTINI salt solution. Eur. Phys. J. Spec. Top. 2016, 225, 1595–1607. [Google Scholar] [CrossRef]
- Zavadlav, J.; Marrink, S.J.; Praprotnik, M. Adaptive resolution simulation of supramolecular water: The concurrent making, breaking, and remaking of water bundles. J. Chem. Theory Comput. 2016, 12, 4138–4145. [Google Scholar] [CrossRef] [PubMed]
- Zavadlav, J.; Podgornik, R.; Praprotnik, M. Order and interactions in DNA arrays: Multiscale molecular dynamics simulation. Sci. Rep. 2017, 7, 4775–4786. [Google Scholar] [CrossRef] [PubMed]
- Zavadlav, J.; Bevc, S.; Praprotnik, M. Adaptive resolution simulations of biomolecular systems. Eur. Biophys. J. 2017, 46, 821–835. [Google Scholar] [CrossRef] [PubMed]
- Kreis, K.; Potestio, R.; Kremer, K.; Fogarty, A.C. Adaptive resolution simulations with self-adjusting high-resolution regions. J. Chem. Theory Comput. 2016, 12, 4067–4081. [Google Scholar] [CrossRef] [PubMed]
- Fogarty, A.C.; Potestio, R.; Kremer, K. A multi-resolution model to capture both global fluctuations of an enzyme and molecular recognition in the ligand-binding site. Proteins 2016, 84, 1902–1913. [Google Scholar] [CrossRef] [PubMed]
- Guzman, H.V.; Junghans, C.; Kremer, K.; Stuehn, T. Scalable and fast heterogeneous molecular simulation with predictive parallelization schemes. Phys. Rev. E 2017, 96, 053311. [Google Scholar] [CrossRef]
- Hua, L.; Zangi, R.; Berne, B.J. Hydrophobic Interactions and Dewetting between Plates with Hydrophobic and Hydrophilic Domains. J. Phys. Chem. C 2009, 113, 5244–5253. [Google Scholar] [CrossRef]
- Hayashi, T.; Pertsin, A.J.; Grunze, M. Grand canonical Monte Carlo simulation of hydration forces between nonorienting and orienting structureless walls. J. Chem. Phys. 2002, 117, 6271–6280. [Google Scholar] [CrossRef]
- Pertsin, A.; Fedyanin, I.; Grunze, M. Computer simulation of water-mediated forces between gel-phase phospholipid bilayers. J. Chem. Phys. 2009, 113, 215102. [Google Scholar] [CrossRef] [PubMed]
- Schneck, E.; Sedlmeier, F.; Netz, R.R. Hydration repulsion between biomembranes results from an interplay of dehydration and depolarization. Proc. Natl. Acad. Sci. USA 2012, 109, 14405–14409. [Google Scholar] [CrossRef] [PubMed]
- Kanduc, M.; Schlaich, A.; Schneck, E.; Netz, R. Water-Mediated Interactions between Hydrophilic and Hydrophobic Surfaces. Langmuir 2016, 32, 8767–8782. [Google Scholar] [CrossRef] [PubMed]
- Kanduc, M.; Schneck, E.; Netz, R.R. Hydration Interaction between Phospholipid Membranes: Insight into Different Measure- ment Ensembles from Atomistic Molecular Dynamics Simulations. Langmuir 2013, 29, 9126–9137. [Google Scholar] [CrossRef] [PubMed]
- Pabst, G.; Katsaras, J.; Raghunathan, V.A.; Rappolt, M. Structure and interactions in the anomalous swelling regime of phospholipid bilayers. Langmuir 2003, 19, 1716–1722. [Google Scholar] [CrossRef]
- Lu, B.S.; Gupta, S.; Belicka, M.; Podgornik, R.; Pabst, G. Modulation of elasticity and interactions in charged lipid multibilayers: Monovalent salt solutions. Langmuir 2016, 32, 13546–13555. [Google Scholar] [CrossRef] [PubMed]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.E.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM General Force Field (CGenFF): A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [PubMed]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS Force Field for Proteins. Energy Minimizations for Crystals of Cyclic Peptides and Crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef] [PubMed]
- Ricci, C.G.; de Andrade, A.S.C.; Mottin, M.; Netz, P.A. Molecular dynamics of DNA: Comparison of force fields and terminal nucleotide definitions. J. Phys. Chem. B 2010, 114, 9882–9893. [Google Scholar] [CrossRef] [PubMed]
- Snodin, B.E.K.; Randisi, F.; Mosayebi, M.; Sulc, P.; Schreck, J.S.; Romano, F.; Ouldridge, T.E.; Tsukanov, R.; Nir, E.; Louis, A.A.; et al. Introducing improved structural properties and salt dependence into a coarse-grained model of DNA. J. Chem. Phys. 2015, 142, 234901. [Google Scholar] [CrossRef] [PubMed]
- Maciejczyk, M.; Spasic, A.; Liwo, A.; Scheraga, H.A. DNA duplex formation with a coarse-grained model. J. Chem. Theory Comput. 2014, 10, 5020–5035. [Google Scholar] [CrossRef] [PubMed]
- Knotts, T.A.I.; Rathore, N.; Schwartz, D.C.; de Pablo, J.J. A coarse grain model for DNA. J. Chem. Phys. 2007, 126, 084901. [Google Scholar] [CrossRef] [PubMed]
- Voltz, K.; Trylska, J.; Tozzini, V.; Kurkal-Siebert, V.; Langowski, J.; Smith, J. Coarse-grained force field for the nucleosome from self-consistent multiscaling. J. Comput. Chem. 2008, 29, 1429–1439. [Google Scholar] [CrossRef] [PubMed]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Ayton, G.S.; Noid, W.G.; Voth, G.A. Multiscale modeling of biomolecular systems: In serial and in parallel. Curr. Opin. Struct. Biol. 2007, 17, 192–198. [Google Scholar] [CrossRef] [PubMed]
- Mullinax, J.W.; Noid, W.G. Extended ensemble approach for deriving transferable coarse-grained potentials. J. Chem. Phys. 2009, 131, 104110. [Google Scholar] [CrossRef]
- Rudzinski, J.F.; Noid, W.G. Bottom-up coarse-graining of peptide ensembles and helix–coil transitions. J. Chem. Theory Comput. 2015, 11, 1278–1291. [Google Scholar] [CrossRef] [PubMed]
- Shell, M.S. The relative entropy is fundamental to thermodynamic ensemble optimization. J. Chem. Phys. 2008, 129, 144108. [Google Scholar] [CrossRef] [PubMed]
- Carmichael, S.P.; Shell, M.S. A new multiscale algorithm and its application to coarse-grained peptide models for self-assembly. J. Phys. Chem. B 2012, 116, 8383–8393. [Google Scholar] [CrossRef] [PubMed]
- Foley, T.; Shell, M.S.; Noid, W.G. The impact of resolution upon entropy and information in coarse-grained models. J. Chem. Phys. 2015, 143, 243104. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Uusitalo, J.J.; Ingólfsson, H.I.; Akhshi, P.; Tieleman, D.P.; Marrink, S.J. Martini Coarse-Grained Force Field: Extension to DNA. J. Chem. Theory Comput. 2015, 11, 3932–3945. [Google Scholar] [CrossRef] [PubMed]
- Grönbech-Jensen, N.; Mashl, R.J.; Bruinsma, R.F.; Gelbart, W.M. Counterions-induced attraction between rigid polyelectrolytes. Phys. Rev. Lett. 1997, 78, 2477. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E.r. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
- Bevc, S.; Junghans, C.; Praprotnik, M. Stock: Structure mapper and online coarse-graining kit for molecular simulations. J. Comput. Chem. 2015, 36, 467–477. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition path sampling: Throwing Ropes over Rough Mountain Passes, in the Dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef] [PubMed]
- Grünwald, M.; Dellago, C. Transition path sampling studies of solid-solid transformations in nanocrystals under pressure. In Trends in Computational Nanomechanics: Transcending Length and Time Scales; Dumitrica, T., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 61–84. [Google Scholar]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.Q.; Lu, J.; Abrams, C.F.; Vanden-Eijnden, E. Multiscale implementation of infinite-swap replica exchange molecular dynamics. Proc. Natl. Acad. Sci. USA 2016, 113, 11744–11749. [Google Scholar] [CrossRef] [PubMed]
- Soddemann, T.; Dunweg, B.; Kremer, K. Dissipative particle dynamics: A useful thermostat for equilibrium and nonequilibrium molecular dynamics simulations. Phys. Rev. E 2003, 68, 046702. [Google Scholar] [CrossRef] [PubMed]
- Zavadlav, J.; Melo, M.N.; Cunha, A.V.; de Vries, A.H.; Marrink, S.J.; Praprotnik, M. Adaptive resolution simulation of MARTINI solvents. J. Chem. Theory Comput. 2014, 10, 2591–2598. [Google Scholar] [CrossRef] [PubMed]
- Poblete, S.; Praprotnik, M.; Kremer, K.; Delle Site, L. Coupling different levels of resolution in molecular simulations. J. Chem. Phys. 2010, 132, 114101. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Poblete, S.; Kremer, K. Statistical physics problems in adaptive resolution computer simulations of complex fluids. J. Stat. Phys. 2011, 145, 946–966. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R.; Sablić, J.; Praprotnik, M. Open boundary molecular dynamics. Eur. Phys. J. Spec. Top. 2015, 224, 2331–2349. [Google Scholar] [CrossRef]
- Junghans, C.; Praprotnik, M.; Kremer, K. Transport properties controlled by a thermostat: An extended dissipative particle dynamics thermostat. Soft Matter 2008, 4, 156–161. [Google Scholar] [CrossRef]
- Matysiak, S.; Clementi, C.; Praprotnik, M.; Kremer, K.; Delle Site, L. Modeling diffusive dynamics in adaptive resolution simulation of liquid water. J. Chem. Phys. 2008, 128, 024503. [Google Scholar] [CrossRef] [PubMed]
- Hijon, C.; Español, P.; Vanden-Eijnden, E.; Delgado-Buscalioni, R. Mori-Zwanzig formalism as a practical computational tool. Faraday Discuss. 2010, 144, 301–322. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Bian, X.; Caswell, B.; Karniadakis, G.E. Construction of dissipative particle dynamics models for complex fluids via the Mori-Zwanzig formulation. Soft Matter 2014, 10, 8659. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Bian, X.; Li, X.; Karniadakis, G.E. Incorporation of memory effects in coarse-grained modeling via the Mori-Zwanzig formalism. J. Chem. Phys. 2015, 143, 243128. [Google Scholar] [CrossRef] [PubMed]
- Yoshimoto, Y.; Li, Z.; Kinefuchi, I.; Karniadakis, G.E. Construction of non-Markovian coarse-grained models employing the Mori-Zwanzig formalism and iterative Boltzmann inversion. J. Chem. Phys. 2017, 147, 244110. [Google Scholar] [CrossRef] [PubMed]
- Jung, G.; Hanke, M.; Schmid, F. Iterative Reconstruction of Memory Kernels. J. Chem. Theory Comput. 2017. [Google Scholar] [CrossRef] [PubMed]
- Izvekov, S. Microscopic derivation of particle-based coarse-grained dynamics: Exact expression for memory function. J. Chem. Phys. 2017, 146, 124109. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Song, J.; Jeong, C.; Hsu, D.D.; Phelan, F.R.J.; Douglas, J.F.; Keten, S. Energy-Renormalization for Achieving Temperature Transferable Coarse-Graining of Polymer Dynamics. Macromolecules 2017, 50, 8787–8796. [Google Scholar] [CrossRef]
- Haddadian, E.J.; Zhang, H.; Freed, K.F.; Douglas, J.F. Comparative Study of the Collective Dynamics of Proteins and Inorganic Nanoparticles. Sci. Rep. 2017, 7, 41671. [Google Scholar] [CrossRef] [PubMed]
- Louis, A.A. Beware of density dependent pair potentials. J. Phys. Condens. Matter 2002, 14, 9187. [Google Scholar] [CrossRef]
- Young, M.A.; Jayaram, B.; Beveridge, D.L. Local dielectric environment of B-DNA in solution: Results from a 14 ns molecular dynamics trajectory. J. Phys. Chem. B 1998, 102, 7666–7669. [Google Scholar] [CrossRef]
- Jin, R.; Breslauer, K.J. Characterization of the minor groove environment in a drug-DNA complex: Bisbenzimide bound to the poly[d(AT)]poly[d(AT)]duplex. Proc. Natl. Acad. Sci. USA 1988, 85, 8939–8942. [Google Scholar] [CrossRef] [PubMed]
- Barawkar, A.; Ganesh, K.N. Fluorescent d(CGCGAATTCGCG): Characterization of major groove polarity and study of minor groove interactions through a major groove semantophore conjugate. Nucleic Acids Res. 1995, 23, 159–164. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.A.; Podgornik, R.; Hansen, P.L.; Parsegian, V.A. A Phenomenological One-Parameter Equation of State for Osmotic Pressures of PEG and Other Neutral Flexible Polymers in Good Solvents. J. Phys. Chem. B 2009, 113, 3709–3714. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.W.; Li, C.; van der Vegt, N.F.A.; Peter, C. Transferability of coarse grained potentials: Implicit solvent models for hydrated ions. J. Chem. Theory Comput. 2011, 7, 1916–1927. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Roux, B. Simulation of osmotic pressure in concentrated aqueous salt solutions. J. Phys. Chem. Lett. 2010, 1, 183–189. [Google Scholar] [CrossRef]
- Podgornik, R.; Strey, H.H.; Parsegian, V.A. Colloidal DNA. Curr. Opin. Colloid Interface Sci. 1998, 3, 534–539. [Google Scholar] [CrossRef]
- Kanduč, M.; Schlaich, A.; Schneck, E.; Netz, R.R. Hydration repulsion between membranes and polar surfaces: Simulation approaches versus continuum theories. Adv. Colloid Interface Sci. 2014, 208, 142–152. [Google Scholar] [CrossRef] [PubMed]
- Sablić, J.; Praprotnik, M.; Delgado-Buscalioni, R. Open boundary molecular dynamics of sheared star-polymer melts. Soft Matter 2016, 12, 2416–2439. [Google Scholar] [CrossRef] [PubMed]
- Sablić, J.; Praprotnik, M.; Delgado-Buscalioni, R. Deciphering the dynamics of star molecules in shear flow. Soft Matter 2017, 13, 4971–4987. [Google Scholar] [CrossRef] [PubMed]
- Sablić, J.; Delgado-Buscalioni, R.; Praprotnik, M. Application of the Eckart frame to soft matter: Rotation of star polymers under shear flow. Soft Matter 2017, 13, 6988–7000. [Google Scholar] [CrossRef] [PubMed]
- Flekkoy, E.G.; Delgado-Buscalioni, R.; Coveney, P.V. Flux boundary conditions in particle simulations. Phys. Rev. E 2005, 72, 026703. [Google Scholar] [CrossRef] [PubMed]
- Delgado-Buscalioni, R. Tools for multiscale simulation of liquids using open molecular dynamics. In Numerical Analysis of Multiscale Computations. Lecture Notes in Computational Science and Engineering; Engquist, B., Runborg, O., Tsai, Y.H., Eds.; Springer: Dordrecht, The Netherlands, 2012; Volume 82, pp. 145–166. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podgornik, R.; Zavadlav, J.; Praprotnik, M. Molecular Dynamics Simulation of High Density DNA Arrays. Computation 2018, 6, 3. https://doi.org/10.3390/computation6010003
Podgornik R, Zavadlav J, Praprotnik M. Molecular Dynamics Simulation of High Density DNA Arrays. Computation. 2018; 6(1):3. https://doi.org/10.3390/computation6010003
Chicago/Turabian StylePodgornik, Rudolf, Julija Zavadlav, and Matej Praprotnik. 2018. "Molecular Dynamics Simulation of High Density DNA Arrays" Computation 6, no. 1: 3. https://doi.org/10.3390/computation6010003
APA StylePodgornik, R., Zavadlav, J., & Praprotnik, M. (2018). Molecular Dynamics Simulation of High Density DNA Arrays. Computation, 6(1), 3. https://doi.org/10.3390/computation6010003