Ionic Liquids Treated within the Grand Canonical Adaptive Resolution Molecular Dynamics Technique
Abstract
:1. Introduction
2. Results
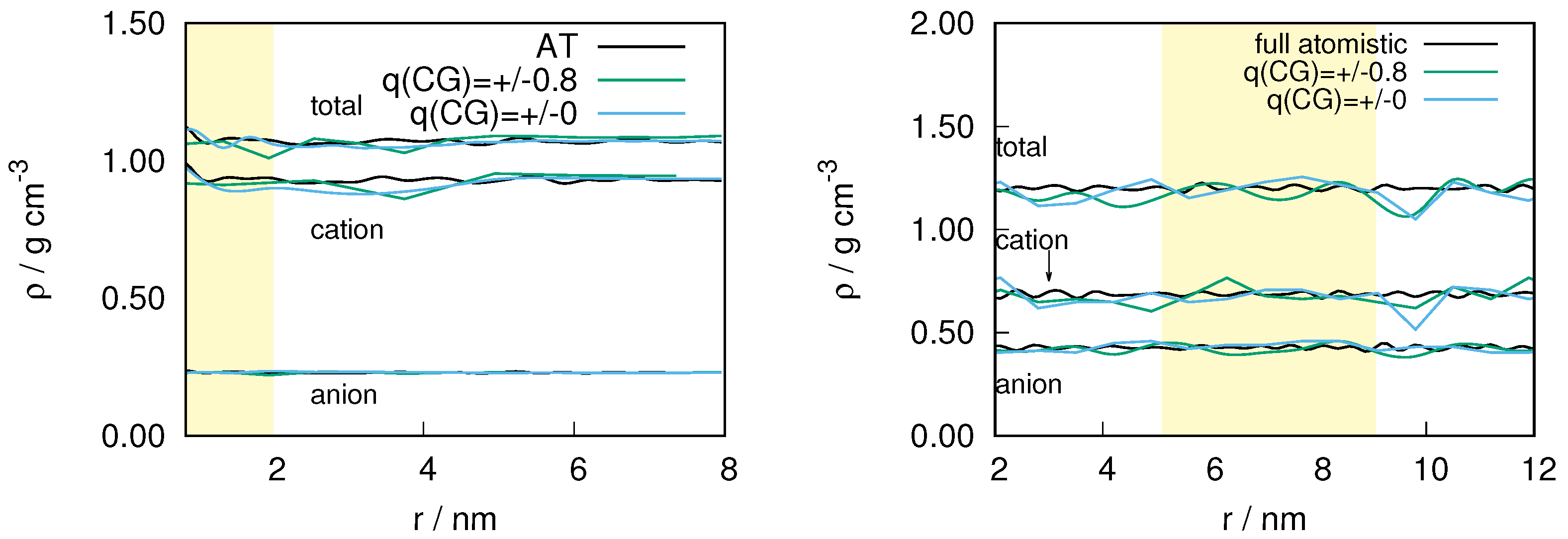
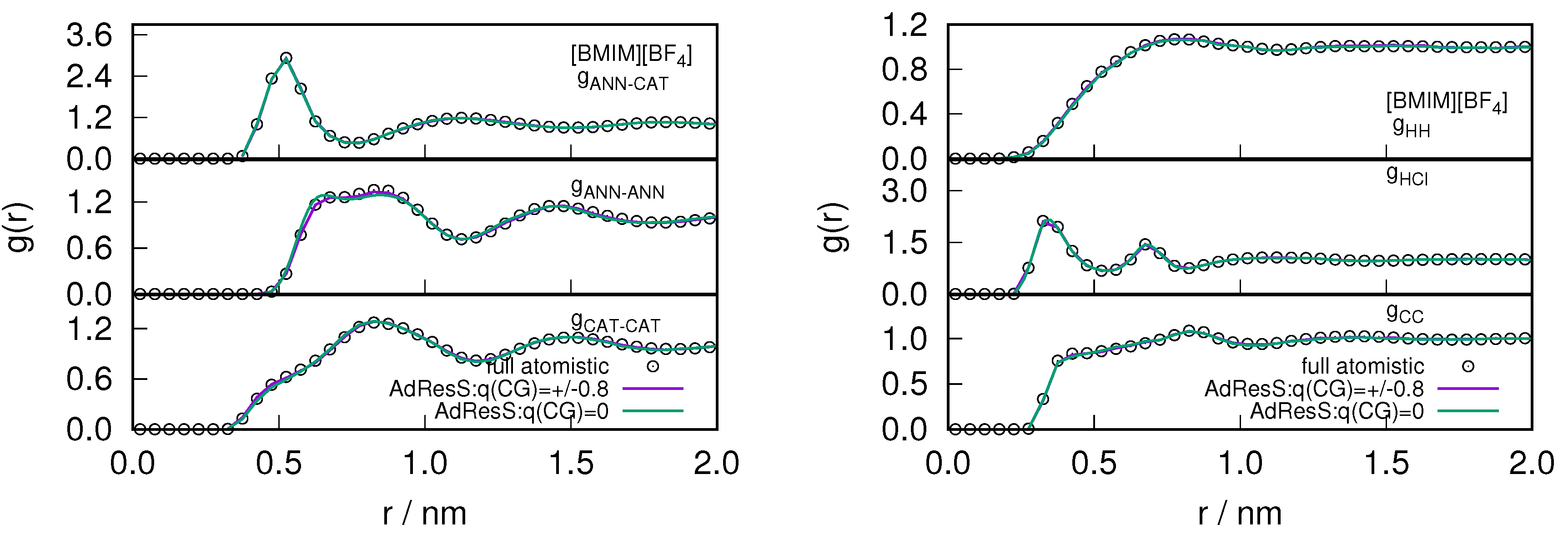
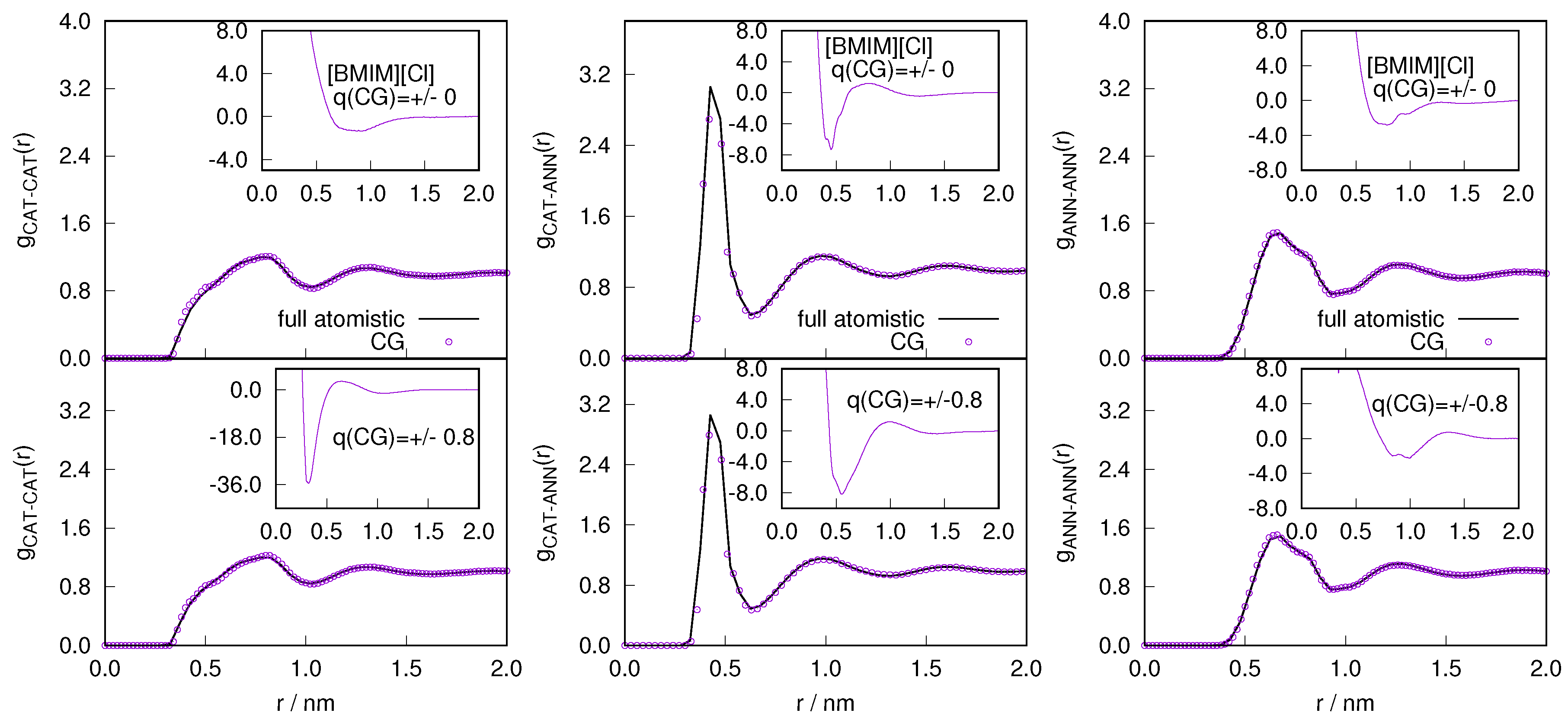
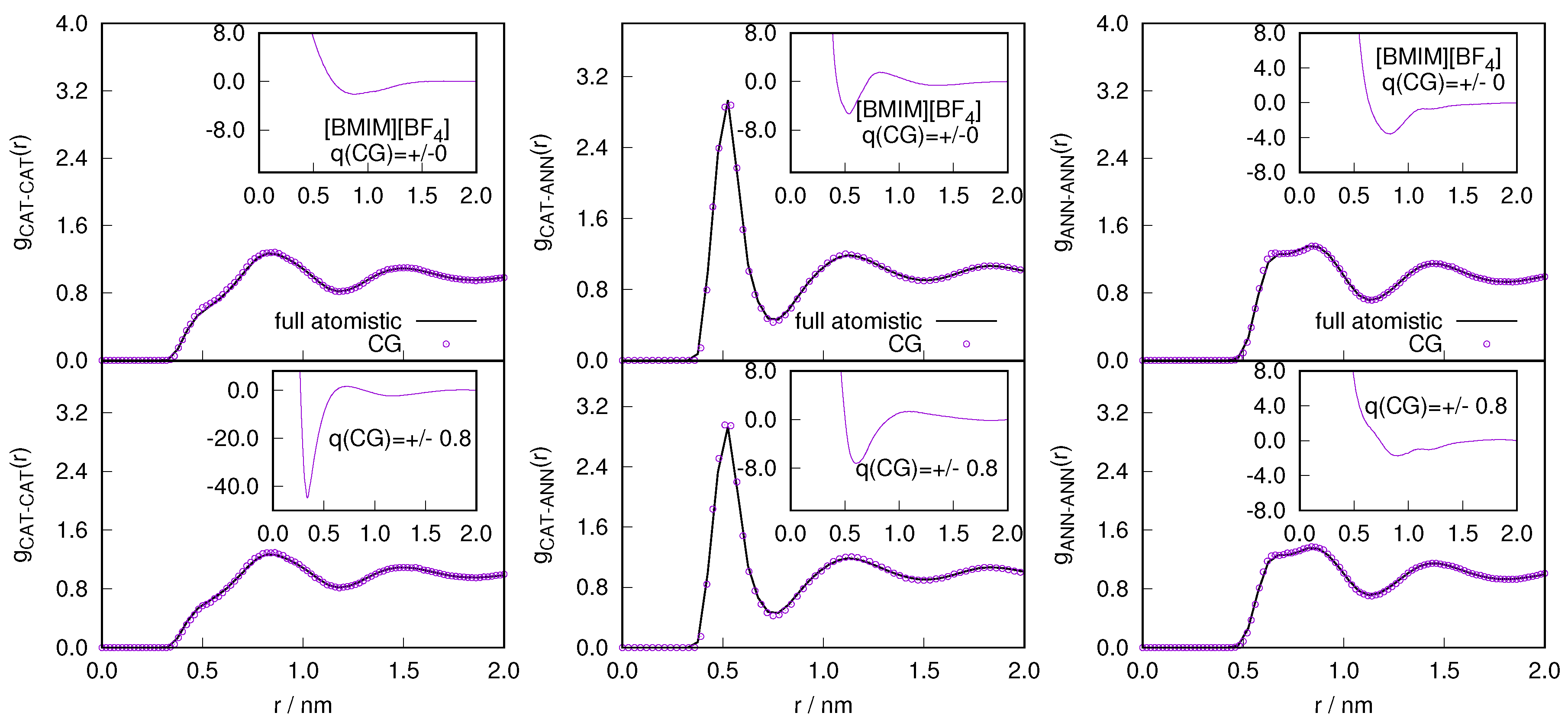
2.1. Structural Properties of ILs
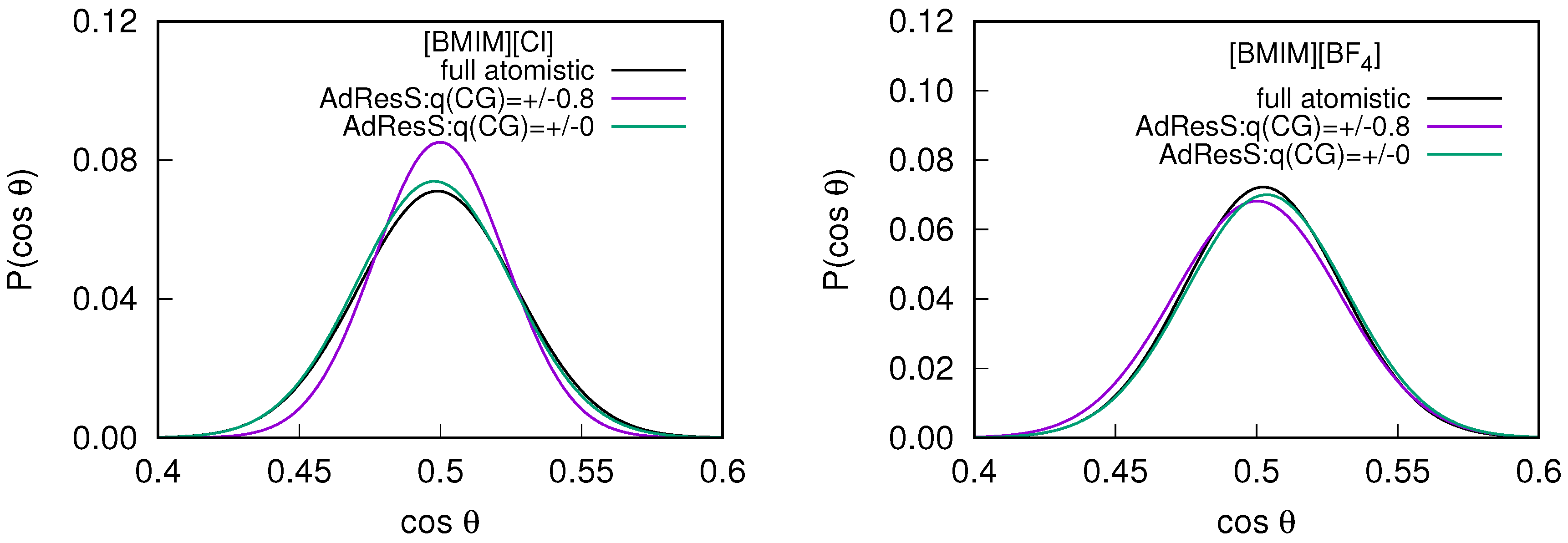
2.2. Orientational Properties of ILs
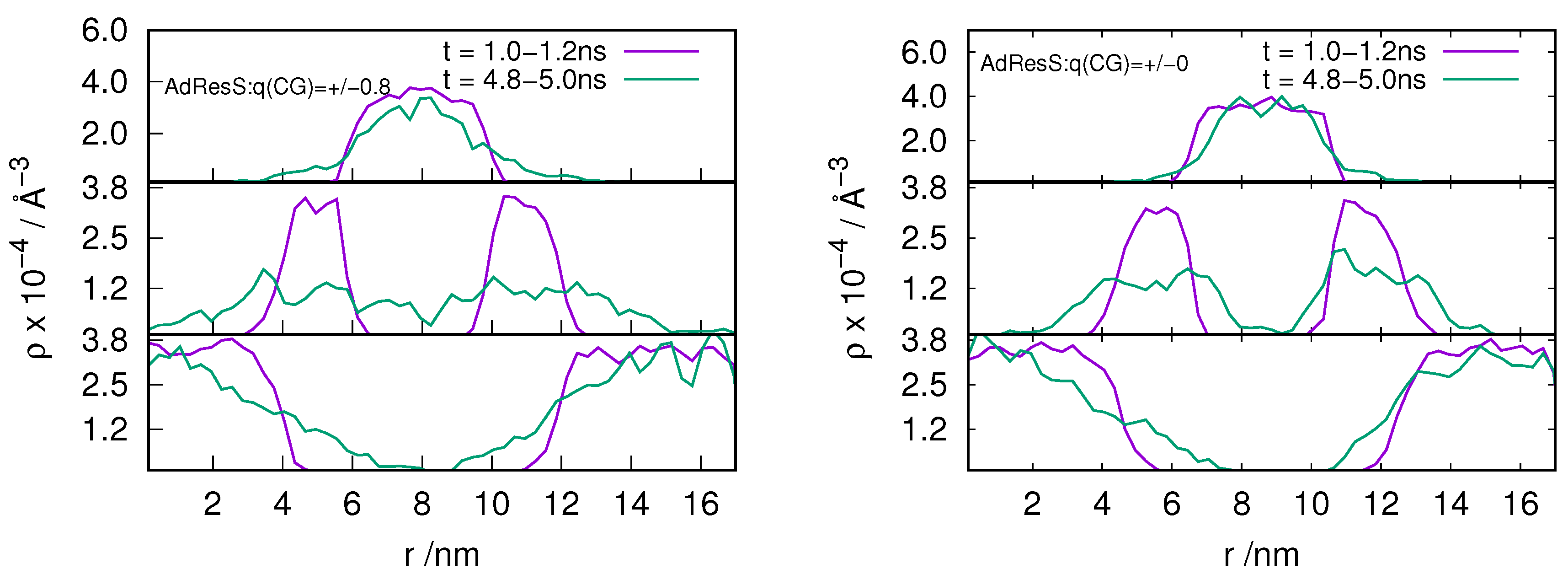
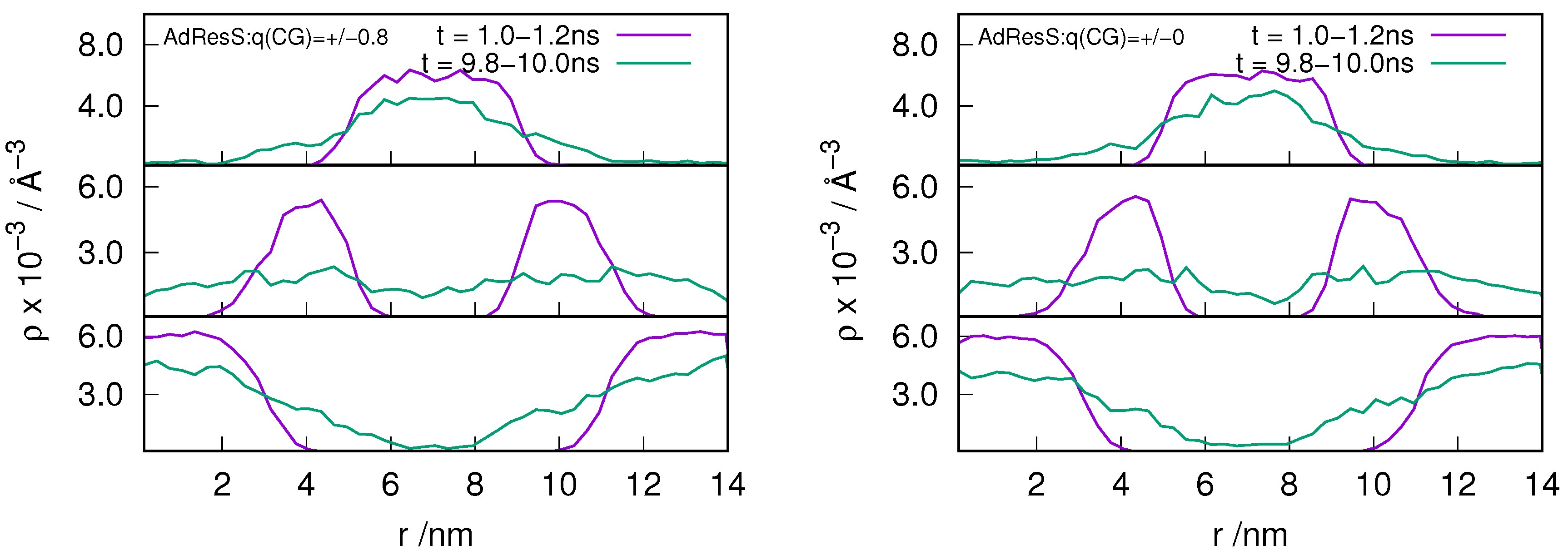
2.3. Locality of Structural Properties
3. Materials and Methods
3.1. Method
3.2. Models
3.3. Technical Details
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GC-AdResS | Grand Canonical Adaptive Resolution Scheme |
| MD | Molecular Dynamics |
| IBI | Inverse Boltzmann Iteration |
| PME | Particle Mesh Ewald |
| AT | Atomistic |
| CG | Coarse-Grained |
| HY | Hybrid |
| RDF | Radial Distribution Functions |
| PCF | Pair Correlation Function |
References
- Plechkova, N.V.; Seddon, K.R. Applications of Ionic Liquids in the Chemical Industry. Chem. Soc. Rev. 2008, 37, 123–150. [Google Scholar] [CrossRef] [PubMed]
- Hapiot, P.; Lagrost, C. Electrochemical Reactivity in Room-Temperature Ionic Liquids. Chem. Rev. 2008, 108, 2238–2264. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Wang, Y. Dual Ionic and Organic Nature of Ionic Liquids. Sci. Rep. 2016, 6, 19644. [Google Scholar] [CrossRef] [PubMed]
- Giernoth, R. Task-Specific Ionic Liquids. Angew. Chem. Int. Ed. 2010, 49, 2834–2839. [Google Scholar] [CrossRef] [PubMed]
- Sawant, A.; Raut, D.; Darvatkar, N.; Salunkhe, M. Recent Developments of Task-Specific Ionic Liquids in Organic Synthesis. Green Chem. Lett. Rev. 2011, 4, 41–54. [Google Scholar] [CrossRef]
- Sahbaz, Y.; Williams, H.D.; Nguyen, T.; Saunders, J.; Ford, L.; Charman, S.A.; Scammells, P.J.; Porter, C.J.H. Transformation of Poorly Water-Soluble Drugs into Lipophilic Ionic Liquids Enhances Oral Drug Exposure from Lipid Based Formulations. Mol. Pharm. 2015, 12, 1980–1991. [Google Scholar] [CrossRef] [PubMed]
- Hart, M.L.; Do, D.P.; Ansari, R.A.; Rizvi, S.A. Brief Overview of Various Approaches to Enhance Drug Solubility. J. Dev. Drugs 2013, 2, 1000110–1000116. [Google Scholar] [CrossRef]
- Lin, M.; Gong, M.; Lu, B.; Wu, Y.; Wang, D.; Guan, M.; Angell, M.; Chen, C.; Yang, J.; Hwang, B.; et al. An Ultrafast Rechargeable Aluminium-Ion Battery. Nature 2015, 520, 324–328. [Google Scholar] [CrossRef] [PubMed]
- Girard, G.M.A.; Hilder, M.; Zhu, H.; Nucciarone, D.; Whitbread, K.; Zavorine, S.; Moser, M.; Forsyth, M.; MacFarlane, D.R.; Howlett, P.C. Electrochemical and Physicochemical Properties of Small Phosphonium Cation Ionic Liquid Electrolytes with High Lithium Salt Content. Phys. Chem. Chem. Phys. 2015, 17, 8706–8713. [Google Scholar] [CrossRef] [PubMed]
- Piper, D.M.; Evans, T.; Leung, K.; Watkins, T.; Olson, J.; Kim, S.C.; Han, S.S.; Bhat, V.; Oh, K.H.; Buttry, D.A.; et al. Stable Silicon-Ionic Liquid Interface for Next-Generation Lithium-Ion Batteries. Nat. Commun. 2015, 6, 6230. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yamazaki, A.; Murai, J.; Park, J.; Mandai, T.; Ueno, K.; Dokko, K.; Watanabe, M. Chelate Effects in Glyme/Lithium Bis-(Trifluoromethanesulfonyl)Amide Solvate Ionic Liquids, Part 2: Importance of Solvate-Structure Stability for Electrolytes of Lithium Batteries. J. Phys. Chem. C 2014, 118, 17362–17373. [Google Scholar] [CrossRef]
- Taha, M.; Almeida, M.R.; Silva, F.A.; Domingues, P.; Ventura, S.P.M.; Coutinho, J.A.P.; Freire, M.G. Novel Biocompatible and Self-Buffering Ionic Liquids for Biopharmaceutical Applications. Chem. Eur. J. 2015, 21, 4781–4788. [Google Scholar] [CrossRef] [PubMed]
- Gorke, J.; Srienc, F.; Kazlauskas, R. Toward Advanced Ionic Liquids. Polar, Enzyme-Friendly Solvents for Biocatalysis. Biotechnol. Bioprocess Eng. 2010, 15, 40–53. [Google Scholar] [CrossRef]
- Socha, A.M.; Parthasarathi, R.; Shi, J.; Pattathil, S.; Whyte, D.; Bergeron, M.; George, A.; Tran, K.; Stavila, V.; Venkatachalam, S.; et al. Efficient Biomass Pretreatment Using Ionic Liquids Derived from Lignin and Hemicellulose. Proc. Natl. Acad. Sci. USA 2014, 111, E3587–E3595. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Gurau, G.; Rogers, R.D. Ionic Liquid Processing of Cellulose. Chem. Soc. Rev. 2012, 41, 1519–1537. [Google Scholar] [CrossRef] [PubMed]
- Armand, M.; Endres, F.; MacFarlane, D.R.; Ohno, H.; Scrosati, B. Ionic-Liquid Materials for the Electrochemical Challenges of the Future. Nat. Mater. 2009, 8, 621. [Google Scholar] [CrossRef] [PubMed]
- Russina, O.; Triolo, A.; Gontrani, L.; Caminiti, R. Mesoscopic Structural Heterogeneities in Room-Temperature Ionic Liquids. J. Phys. Chem. Lett. 2012, 3, 27–33. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Santos, C.S.; Annapureddy, H.V.R.; Murthy, N.S.; Margulis, C.J.; Castner, E.W., Jr. Temperature-Dependent Structure of Ionic Liquids: X-ray Scattering and Simulations. Faraday Discuss. 2012, 154, 133–143. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, H.K.; Santos, C.S.; Murthy, N.S.; Hettige, J.J.; Kerr, K.; Ramati, S.; Gwon, J.; Gohdo, M.; Lall-Ramnarine, S.I.; Wishart, J.F.; et al. Structure of 1-Alkyl-1-methylpyrrolidinium Bis(trifluoromethylsulfonyl)amide Ionic Liquids with Linear, Branched, and Cyclic Alkyl Groups. J. Phys. Chem. B 2013, 117, 15328–15337. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.; McDonald, I.R. Theory of Simple Liquids: With Applications to Soft Matters; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Dhabal, D.; Gupta, A.; Kashyap, H.K. Structural Investigation of Room-Temperature Ionic Liquids and High-Temperature Ionic Melts Using Triplet Correlation Functions. J. Chem. Phys. 2017, 146, 094503. [Google Scholar] [CrossRef]
- Krekeler, C.; Dommert, F.; Schmidt, J.; Zhao, Y.Y.; Holm, C.; Berger, R.; Delle Site, L. Electrostatic Properties of Liquid 1,3-Dimethylimidazolium Chloride: Role of Local Polarization and Effect of the Bulk. Phys. Chem. Chem. Phys. 2010, 12, 1817–1821. [Google Scholar] [CrossRef] [PubMed]
- Wendler, K.; Zahn, S.; Dommert, F.; Berger, R.; Holm, C.; Kirchner, B.; Delle Site, L. Locality and Fluctuations: Trends in Imidazolium-Based Ionic Liquids and Beyond. J. Chem. Theory Comput. 2011, 7, 3040. [Google Scholar] [CrossRef] [PubMed]
- Wendler, K.; Dommert, F.; Zhao, Y.Y.; Berger, R.; Holm, C.; Delle Site, L. Ionic Liquids Studied Across Different Scales: A Computational Perspective. Faraday Discuss. 2012, 154, 111–132. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive Resolution Molecular-Dynamics Simulation: Changing the Degrees of Freedom on the Fly. J. Chem. Phys. 2005, 123, 224106. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Multiscale Simulation of Soft Matter: From Scale Bridging to Adaptive Resolution. Annu. Rev. Phys. Chem. 2008, 59, 545. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Schütte, C.; Delle Site, L. Adaptive Resolution Simulation (AdResS): A Smooth Thermodynamic and Structural Transition from Atomistic to Coarse Grained Resolution and Vice Versa in a Grand Canonical Fashion. J. Chem. Theory Comput. 2012, 8, 2878–2887. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hartmann, C.; Schütte, C.; Delle Site, L. Grand-Canonical-Like Molecular-Dynamics Simulations by Using an Adaptive-Resolution Technique. Phys. Rev. X 2013, 3, 011018. [Google Scholar] [CrossRef]
- Agarwal, A.; Zhu, J.; Hartmann, C.; Wang, H.; Delle Site, L. Molecular Dynamics in a Grand Ensemble: Bergmann-Lebowitz Model and Adaptive Resolution Simulation. New J. Phys. 2015, 17, 083042. [Google Scholar] [CrossRef]
- Delle Site, L. Formulation of Liouville’s Theorem for Grand Ensemble Molecular Simulations. Phys. Rev. E 2016, 93, 022130. [Google Scholar] [CrossRef] [PubMed]
- Krekeler, C.; Delle Site, L. Towards Open Boundary Molecular Dynamics Simulation of Ionic Liquids. Phys. Chem. Chem. Phys. 2017, 19, 4701–4709. [Google Scholar] [CrossRef] [PubMed]
- Jabes, B.S.; Krekeler, C.; Klein, R.; Delle Site, L. Probing Spatial Locality in Ionic Liquids with the Grand Canonical Adaptive Resolution Molecular Dynamics Technique. J. Chem. Phys. 2018, 148, 193804. [Google Scholar]
- Agarwal, A.; Delle Site, L. Grand-Canonical Adaptive Resolution Centroid Molecular Dynamics: Implementation and Application. Comput. Phys. Commun. 2016, 206, 26–34. [Google Scholar] [CrossRef]
- Lambeth, B.P.; Junghans, C.; Kremer, K.; Clementi, C.; Delle Site, L. Communication: On the Locality of Hydrogen Bond Networks at Hydrophobic Interfaces. J. Chem. Phys. 2010, 133, 221101. [Google Scholar] [CrossRef] [PubMed]
- Bingham, R.J.; Ballone, P. Computational Study of Room-Temperature Ionic Liquids Interacting with a POPC Phospholipid Bilayer. J. Phys. Chem. B 2012, 116, 11205–11216. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, G.; Giri, R.P.; Saxena, H.; Agrawal, V.V.; Gupta, A.; Mukhopadhyay, M.K.; Ghosh, S.K. X-ray Reflectivity Study of the Interaction of an Imidazolium-Based Ionic Liquid With a Soft Supported Lipid Membrane. Langmuir 2017, 33, 1295–1304. [Google Scholar] [CrossRef] [PubMed]
- Kavitha, T.; Vasantha, T.; Venkatesu, P.; Devi, R.S.R.; Hofman, T. Thermophysical Properties for the Mixed Solvents of N-methyl-2-pyrrolidone with Some of the Imidazolium-Based Ionic Liquids. J. Mol. Liq. 2014, 198, 11–20. [Google Scholar] [CrossRef]
- Delle Site, L.; Praprotnik, M. Molecular Systems with Open Boundaries: Theory and Simulation. Phys. Rep. 2017, 693, 1–56. [Google Scholar] [CrossRef]
- Praprotnik, M.; Matysiak, S.; Delle Site, L.; Kremer, K.; Clementi, C. Adaptive Resolution Simulation of Liquid Water. J. Phys. Condens. Matter 2007, 19, 292201. [Google Scholar] [CrossRef]
- Poblete, S.; Praprotnik, M.; Kremer, K.; Delle Site, L. Coupling Different Levels of Resolution in Molecular Simulations. J. Chem. Phys. 2010, 132, 114101. [Google Scholar] [CrossRef] [PubMed]
- Fritsch, S.; Poblete, S.; Junghans, C.; Ciccotti, G.; Delle Site, L.; Kremer, K. Adaptive Resolution Molecular Dynamics Simulation Through Coupling to an Internal Particle Reservoir. Phys. Rev. Lett. 2012, 108, 170602. [Google Scholar] [CrossRef] [PubMed]
- Dommert, F.; Wendler, K.; Bergerm, R.; Delle Site, L.; Holm, C. Force Fields for Studying the Structure and Dynamics of Ionic Liquids: A Critical Review of Recent Developments. ChemPhysChem 2012, 13, 1625. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, S.B.C.; Roatsch, M.; Schoppke, M.; Kirchner, B. On the Physical Origin of the Cation-Anion Intermediate Bond in Ionic Liquids Part I. Placing a (Weak) Hydrogen Bond Between Two Charges. Phys. Chem. Chem. Phys. 2010, 12, 7473–7486. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182. [Google Scholar] [CrossRef]
- Reith, D.; Putz, M.; Muller-Plathe, F. Deriving Effective Mesoscale Potentials from Atomistic Simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Fritsch, S.; Junghans, C.; Kremer, K. Structure Formation of Toluene Around C60: Implementation of the Adaptive Resolution Scheme (AdResS) into GROMACS. J. Chem. Theory Comput. 2012, 8, 398–403. [Google Scholar] [CrossRef] [PubMed]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shadrack Jabes, B.; Krekeler, C. Ionic Liquids Treated within the Grand Canonical Adaptive Resolution Molecular Dynamics Technique. Computation 2018, 6, 23. https://doi.org/10.3390/computation6010023
Shadrack Jabes B, Krekeler C. Ionic Liquids Treated within the Grand Canonical Adaptive Resolution Molecular Dynamics Technique. Computation. 2018; 6(1):23. https://doi.org/10.3390/computation6010023
Chicago/Turabian StyleShadrack Jabes, B., and Christian Krekeler. 2018. "Ionic Liquids Treated within the Grand Canonical Adaptive Resolution Molecular Dynamics Technique" Computation 6, no. 1: 23. https://doi.org/10.3390/computation6010023
APA StyleShadrack Jabes, B., & Krekeler, C. (2018). Ionic Liquids Treated within the Grand Canonical Adaptive Resolution Molecular Dynamics Technique. Computation, 6(1), 23. https://doi.org/10.3390/computation6010023



