Abstract
We use the Grand Canonical Adaptive Resolution Molecular Dynamics Technique (GC-AdResS) to examine the essential degrees of freedom necessary for reproducing the structural properties of the imidazolium class of ionic liquids. In this technique, the atomistic details are treated as an open sub-region of the system while the surrounding environment is modelled as a generic coarse-grained model. We systematically characterize the spatial quantities such as intramolecular, intermolecular radial distribution functions, other structural and orientational properties of ILs. The spatial quantities computed in an open sub-region of the system are in excellent agreement with the equivalent quantities calculated in a full atomistic simulation, suggesting that the atomistic degrees of freedom outside the sub-region are negligible. The size of the sub-region considered in this study is 2 nm, which is essentially the size of a few ions. Insight from the study suggests that a higher degree of spatial locality seems to play a crucial role in characterizing the properties of imidazolium based ionic liquids.
1. Introduction
Ionic liquids are a new class of chemical compounds that are highly tunable in nature with unusual properties such as high electrical conductivities, improved electrical and thermal stabilities, good solvation ability, negligible vapor pressures, non-flammability, to mention a few [1,2,3]. By chemical modification of the polar or apolar components or charge of the ions, numerous ILs with a range of physicochemical properties such as viscosity, catalytic activity, or solvation can be generated. We now have task specific ionic liquids that can be applied for a range of designated applications [4,5]: ionic liquids as drugs [6,7], as batteries and super-capacitors for solving energy demands of the environment [8,9,10,11], to capture greenhouse gases, to dissolve proteins [12,13] and cellulose [14,15].
The physicochemical properties of ionic liquids can be understood by studying the morphological structure of these novel materials. Therefore, a plethora of experiments and simulations have been performed to probe the structural morphology of ionic liquids with an emphasis on pair correlation functions (PCFs) [16,17,18,19]. The conventional approach to probe the structure of ionic liquids using scattering experiments involves determination of structure factor that can be Fourier transformed to obtain pair correlation functions (PCFs) or radial distribution functions (RDFs) [20]. Atomic-level organization of ILs can be obtained by properly analyzing the structure factor and corresponding pair correlation functions including large scale correlation functions [21] of various components of ionic liquids. However, in our previous studies on ILs, we have shown that a large class of ILs can be characterized by a local scale where important properties that may be expected to be dominated by large scale pair correlations, are instead highly localized and depend only on the immediate neighboring molecules [22,23,24]. Motivated by these results, the adaptive resolution scheme (AdResS) [25,26] has been extended to grand canonical-like version [27,28,29,30] for the study of ILs.
In fact, AdResS simulation allows one to obtain full atomistic details of a region of interest and couple it with a coarse-grained region modeled without any atomistic details. The generic coarse-grained region acts as a reservoir of particles and energy, which suggests that GC-AdResS can be used as a tool to identify the essential atomistic degrees of freedom required to have a certain property. This idea already been used in previous AdResS studies to infer the locality of ionic liquids [31,32], IR spectrum in water [33] and solvation properties for hydrophobic molecules in water [34]. In this perspective, the aim of this work is to show the technical feasibility of an AdResS study of ILs consisting of cations with longer alkyl chains and relatively larger anions compared to our earlier study [31,32]. In this work, we have chosen and as the test systems for our simulation not only for its inherent complexity but because these ILs have been shown to be useful in the development of breakthrough application in bio-nanotechnology [35,36].
2. Results
The analysis of GC-AdResS simulation firstly involves whether the necessary thermodynamic conditions for physical consistency such as the structural and orientational properties of the ILs are fulfilled.
2.1. Structural Properties of ILs
In Figure 1 we show the density of ion pairs for the and system as a function of the distance from the center of the atomistic region. As expected, the largest deviation in density occurs in the hybrid region with an upper bound of about 10% and 7% for and respectively. However, within the atomistic region, which is the region of interest in our study, the largest deviation observed is ≤5 for both the systems. Given the critical technical conditions, in addition to the inherent complexity of the ILs (for example: viscosity, of and at 298 K are 101 cP and 29 cP respectively [37]) we consider the density difference to be satisfactory for studying the structural properties of ILs. The fluctuations in the density can be further reduced by improving the convergence of the thermodynamic force.
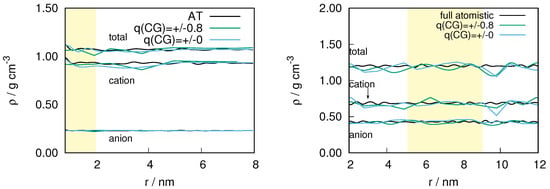
Figure 1.
The density of ion pairs as a function of the distance from the center of the atomistic region for (left) and (right). For the , the simulation box was split in x-direction, so the weight is a function of the x-coordinate and all distances are measured using the x-coordinate. In the case of , the AdResS simulation was performed with spherical explicit zone. The radius of the atomistic (shown in yellow) is 2 nm. The width of the hybrid region that borders the atomistic region is set to 2 nm. The remaining region corresponds to the coarse-grained region in the AdResS simulation.
In order to understand the behavior of the particle number fluctuation (ie) the exchange of matter with the large reservoir, we plot the diffusive number density profile for the ion pairs located in the AT, HY and CG regions at various time frames for the and system (see Figure 2 and Figure 3). The results show that there is diffusion of particles from each region to the other suggesting that the GC-AdResS method behaves reasonably well.
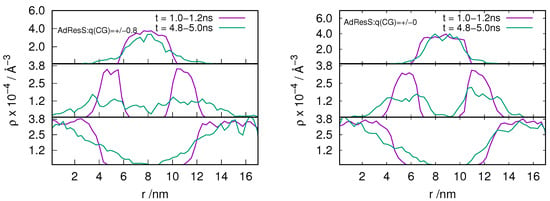
Figure 2.
Evolution in time of an instantaneous diffusive number density profile along the trajectory for the ion pairs that are at time, t = 0, located in the atomistic region (top panel), hybrid region (middle panel) and in the coarse-grained region (bottom panel). GC-AdResS simulation with the charged and uncharged coarse-grained model of the [BMIM][Cl] system is shown in left and right respectively. Exchange of ion pairs among different regions are shown.
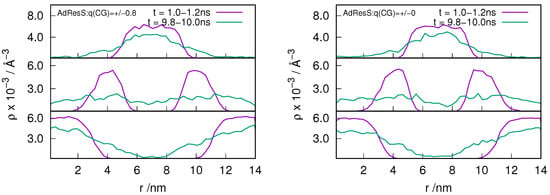
Figure 3.
Evolution in time of an instantaneous number diffusive density profile along the trajectory for the ion pairs that are at time, t = 0, located in the atomistic region (top panel), hybrid region (middle panel) and in the coarse-grained region (bottom panel). GC-AdResS simulation with the charged and uncharged coarse-grained model of the system is shown in left and right respectively. Exchange of ion pairs among different regions are shown.
2.2. Orientational Properties of ILs
In addition to the structural properties, we compute the orientational alignment of the molecules to ensure the possibility of any artificial molecular orientation due to the interface introduced by the different spacial resolution of the coarse grained models. The orientational order parameter is defined as , where is the unit vector along the principal axis of symmetry of the cation and is the unit vector defined between the cation and the center of the atomistic region [31]. For a random rotation of the molecules, the value of must be 0.5. The probability distribution of the average order parameter, measured within the sub-regions of the AdResS simulations are compared with the corresponding quantity in the equivalent sub-region of the full atomistic simulation (see Figure 4). The average value of obtained is for the AdResS simulations compared to the reference system, suggesting that the rotation of the molecules are random.
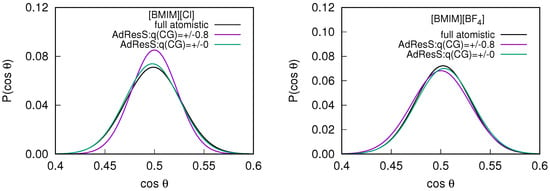
Figure 4.
The probability distribution of the averaged order parameter in the atomistic region of the 2 nm AdResS simulations compared with the corresponding quantity in the equivalent sub-region of the full atomistic simulation for the (left) and (right) system.
2.3. Locality of Structural Properties
After assuring the thermodynamic and statistical behavior of the atomistic region, we studied the essential degrees of freedom necessary for reproducing the local structural properties of ILs. The intermolecular (anion-anion, anion-cation, cation-cation) and intramolecular (H-H, H-Cl, C-C) radial distribution functions are shown in Figure 5 for and in Figure 6 for system respectively. The center of mass of the cations and anions are represented as CAT, ANN or Cl respectively. is the carbon, of the methyl group attached to the imidazolium ring and H is the hydrogen that is present in between the 1-methyl and 3-butyl chain of the cations. The intermolecular and intramolecular RDFs are calculated in the atomistic region (2 nm) and compared with the equivalent functions in the corresponding sub-region of the full atomistic system. The radial distribution functions represent a second order probability distribution function of the system, as it is reduced from a -probability distribution function to a factorized function of independent two-body terms (see also [28]). Therefore, reproducing the radial distribution functions of the atomistic region of GC-AdResS reproduce the behavior of the same quantities calculated in the sub region of a full atomistic simulation, suggesting that the two sub-regions are statistically equivalent at least up to the second order. Our results for the atom-atom radial distribution functions in the AT region of AdResS reproduce the results of the reference full atomistic simulation, which implies that the only relevant atomistic degrees of freedom are those of the AT region of 2 nm radius. Thus from these local radial distribution functions we can further infer that the ensemble average of quantities, depending on spatial coordinates, can be localized in the sub-region with an accuracy at least up to the second order in the probability distribution.
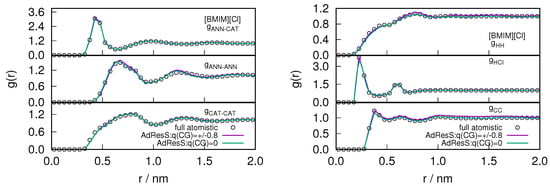
Figure 5.
The variation of intermolecular (left) and intramolecular (right) radial distribution profile calculated in the atomistic region of AdResS for (charged/neutral) coarse-grained models and compared with the corresponding quantity calculated in the equivalent region of a full atomistic simulation for the system. The center of mass of the cations and anions are represented as CAT, ANN or Cl respectively. is the carbon, of the methyl group attached to the imidazolium ring and H is the hydrogen that is present in between the 1-methyl and 3-butyl chain of the cations.
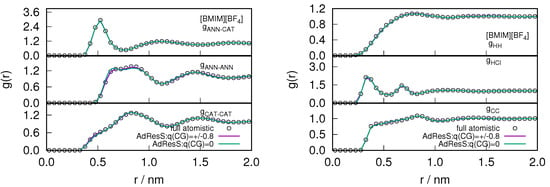
Figure 6.
The variation of intermolecular (left) and intramolecular (right) radial distribution profile calculated in the atomistic region of AdResS for (charged) coarse-grained models and compared with the corresponding quantity calculated in the equivalent region of a full atomistic simulation for the .
3. Materials and Methods
3.1. Method
In this study we employ the Grand Canonical Adaptive Resolution Simulation Scheme (GC-AdResS) for molecular dynamics [25,26,28,29,30,38]. Two regions of a simulation box having different resolution regions: 1. atomistic (AT) and 2. a coarse-grained (CG) system can be linked using this multi-resolution simulation method. Free exchange of particles between the two resolution regions are ensured through a coupling transition region (HY) where molecules have space-dependent hybrid atomistic/coarse-grained resolution. The force between two molecules and present in the hybrid region is computed via a space-dependent interpolation formula and can be written as
here, the force between the particles derived using the atomistic and CG potentials are and respectively. The interpolating switch is defined as:
In the above equation, the spatial extent of the atomistic and hybrid regions are represented as and respectively (see Figure 7). The yellow line represents the weighting function that allows the coarse grained particles to change their resolution into an atomistic molecule as it varies smoothly from 0 to 1 and vice versa. Earlier studies have shown that this simulation setup is sufficient for performing accurate simulations in both the atomistic and coarse-grained region [39].
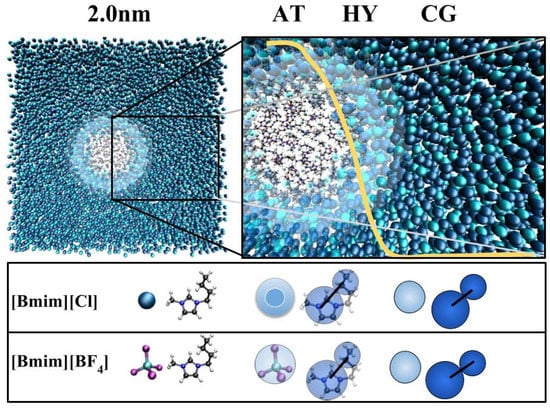
Figure 7.
GC-AdResS scheme is shown in the (top column); Simulation snapshot of the [BMIM][Cl] system with the radius of the atomistic region set to 2 nm. The CG, HY and AT represents the coarse-grained region, hybrid region and the atomistic region respectively. The forces in the AT and CG regions are derived from the respective potentials. In the HY region, a space dependent interpolation scheme with a weighting function w(x) (shown in yellow) is used for obtaining the forces between two particles. The cation is modelled as two coarse grained beads. One sphere for the imidazolium ring and the other sphere for the alkyl side chain. Similarly, the anion is modelled as one coarse grained bead (bottom column).
In order to ensure proper thermodynamic equilibrium and correct particles’ exchange between he AT and CG region [40,41], thermodynamic force is introduced in the transition region. Studies have shown that models that can reproduce macroscopic thermodynamic quantities such as density and temperature can be used as coarse-grained models, so that AdResS is re-framed within the Grand Ensemble idea of open boundary systems [29,30,38]. In this work, we use a spherical atomistic region of radius that is surrounded by a hybrid region of width . The remainder of the box is treated as the CG region that serves as a particle reservoir for the AT region. The force field parameters of the atomistic and coarse-grained model are discussed below in Section 3.2 and Section 3.3.
3.2. Models
The all atom forcefield parameters to model imidazolium ionic liquids that has long alkyl chains attached to the cation ([BMIM]) and relatively hydrophobic anions () were taken from the Dommert et al. [42] and Kirchner, B. et al. [43]. The model considers reduced/scaled charges of +0.8 e and e instead of the full formal charges +1.0 e and e. Within the CG region, ionic liquids are modelled as charged/neutral spherical atoms. We use two spherical beads to model the cation (in which the imidazolium ring and the alkyl chain are modeled using separate spherical beads) and one bead to represent the anion. We use Inverse Boltzmann Iterative procedure (IBI) to develop the coarse-grained interaction parameters. This procedure takes into account the corresponding charge in the coarse-grained model during the iterative process.
3.3. Technical Details
: We performed all the MD simulations using GROMACS package [44]. We set up two systems, a relatively smaller system consisting of 400 ion pairs and a larger system with 19,968 ion pairs. The full atomistic 400 ion pairs simulation was used to generate coarse-grained models, which was used in GC-AdResS simulations. However, the full atomistic 19,968 ion pairs simulation was used as a reference system to compare the statistical quantities computed within the sub-region of the GC-AdResS simulations with that computed in the equivalent subregion of the atomistic simulations. Both the systems were optimized using full atomistic NPT calculations. The temperature of the system was set to 400 K with a simulation time step of 2 fs. The particle mesh Ewald (PME) technique was used to calculate the electrostatic interactions between ions. Berendsen barostat [45] was used for the first 5 ns and then Parrinello-Rahman [46] barostat was used for another 5 ns. The box size is considered to be converged, when the changes in the box length were of the order of 0.0001 nm. For 400 and 19,968 ion pairs we obtained a cubic box with 4.31080 nm and 15.88645 nm respectively. The production runs are performed using NVT ensemble. The radial distribution function was obtained after 5 ns full atomistic NVT simulations at 380 K and with 2 fs timesteps. The two coarse-grained models were derived from the 400 ion pairs configuration. Inverse Boltzmann iteration (IBI) procedure [47] was used to reproduce the radial distribution functions of the full atomistic target systems (for neutral and charged model see Figure 8). We used the tabulated coarse grained potentials to set up 19,968 ion pairs GC-AdResS system. We fix the resolution of the atomistic region in the GC-AdResS simulation to 2 nm, which is sufficient to capture the structural properties of the system similar to the reference atomistic system. The width of the hybrid region that borders the atomistic region is set to 2 nm, and the remaining length corresponds to the CG region. A Langevin thermostat is used with = 5 . Generalized reaction field method with a self-consistent dielectric constant was used to compute electrostatic interactions between ions [48]. In the case of charged coarse-grained model, the reaction field method is applied in the coarse-graining region similar to the atomistic region. The thermodynamic force through the iterative procedure was considered converged after 100 iterations, sufficient to reach an accuracy of <5 particle density and for the ion-ion radial distribution functions ( compared to the full atomistic of the reference).

Figure 8.
The radial distribution function obtained from reference atomistic and coarse-grained simulation with charged (bottom) and neutral model (top) as a function of distance r for the . The CG simulation employs the IBI potential, for the charged and uncharged CG model (inset).
: We set up two systems, a relatively smaller system consisting of 313 ion pairs and a larger system with 939 ion pairs. Both the systems were optimized using full atomistic NPT calculations. The temperature of the system was set to 400 K with a simulation time step of 2 fs. The particle mesh Ewald (PME) technique was used to calculate the electrostatic interactions between ions. Berendsen barostat [45] was used for the first 1 ns and then Parrinello-Rahman [46] barostat was used for another 3 ns. The box size is considered to be converged, when the changes in the box length were of the order of 0.0001 nm. For 313 and 939 ion pairs, we obtained a cubic and orthogonal box of nm and nm × nm × nm respectively. The production runs are performed using NVT ensemble. The radial distribution function was obtained after 10 ns full atomistic NVT simulations at 400 K and with 2 fs timesteps. The two coarse-grained models were derived from the 313 ion pairs configuration. Inverse Boltzmann iteration, IBI, procedure [47] was used to reproduce the radial distribution functions of the full atomistic target systems (for charged model see Figure 9). We used the tabulated coarse grained potentials to set up 939 ion pairs GC-AdResS system. We fix the resolution of the atomistic region in the GC-AdResS simulation to 2 nm, which is sufficient to capture the structural properties of the system similar to the reference atomistic system. The width of the hybrid region that borders the atomistic region is set to 2 nm, and the remaining length corresponds to the CG region. A Langevin thermostat is used with = 5 . Generalized reaction field method with a self-consistent dielectric constant was used to compute electrostatic interactions between ions [48]. In the case of charged coarse-grained model, the reaction field method is applied in the coarse-graining region similar to the atomistic region. The thermodynamic force through the iterative procedure was considered converged after 30 iterations, sufficient to reach an accuracy of <5% particle density and for the ion-ion radial distribution functions (compared to the full atomistic of the reference).
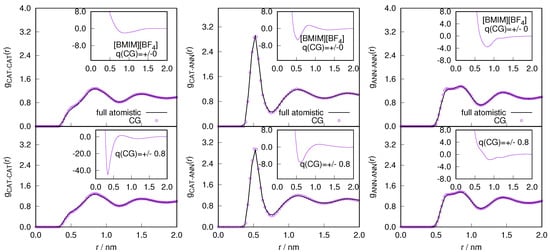
Figure 9.
The radial distribution function obtained from reference atomistic and coarse-grained simulation with charged (bottom) and neutral model (top) as a function of distance r for the . The CG simulation employs the IBI potential, for the charged and neutral CG models. (inset).
4. Conclusions
We have tested the spatial locality of complex ILs consisting of cations with long alkyl chains and hydrophobic anions using the Grand Canonical Adaptive Resolution Molecular Dynamics technique. By calculating various radial distribution functions between anions and cations within an atomistic region of radius 2 nm and comparing them with the equivalent quantities in a full atomistic simulation, we could conclude that even for a spherical region of radius 2 nm, the atomistic degrees of freedom of the bulk do not play a relevant role. Although, the spatial localization has been observed in complex liquids characterized by strong local anisotropic interactions such as: class of imidazolium based ionic liquids [31,32], water [33], the spherical region of radius 2 nm is system specific and could vary depending upon the complexity of the system of study. The insight from this study can be used for designing ILs at the molecular level in the framework of structure-function relations.
Acknowledgments
We thank Luigi Delle Site for his insight and comments that greatly improved the manuscript. This research has been funded by Deutsche Forschungsgemeinschaft (DFG) through grants CRC 1114 “Scaling Cascades in Complex Systems”, project C01. This work has also received funding from the European Union’s Horizon 2020 research and innovation program under the grant agreement No. 676531 (project E-CAM).
Author Contributions
B.S.J. and C.K. conceived and designed the simulation study; B.S.J. and C.K. performed the experiments; B.S.J. analyzed the data; B.S.J. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GC-AdResS | Grand Canonical Adaptive Resolution Scheme |
| MD | Molecular Dynamics |
| IBI | Inverse Boltzmann Iteration |
| PME | Particle Mesh Ewald |
| AT | Atomistic |
| CG | Coarse-Grained |
| HY | Hybrid |
| RDF | Radial Distribution Functions |
| PCF | Pair Correlation Function |
References
- Plechkova, N.V.; Seddon, K.R. Applications of Ionic Liquids in the Chemical Industry. Chem. Soc. Rev. 2008, 37, 123–150. [Google Scholar] [CrossRef] [PubMed]
- Hapiot, P.; Lagrost, C. Electrochemical Reactivity in Room-Temperature Ionic Liquids. Chem. Rev. 2008, 108, 2238–2264. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Wang, Y. Dual Ionic and Organic Nature of Ionic Liquids. Sci. Rep. 2016, 6, 19644. [Google Scholar] [CrossRef] [PubMed]
- Giernoth, R. Task-Specific Ionic Liquids. Angew. Chem. Int. Ed. 2010, 49, 2834–2839. [Google Scholar] [CrossRef] [PubMed]
- Sawant, A.; Raut, D.; Darvatkar, N.; Salunkhe, M. Recent Developments of Task-Specific Ionic Liquids in Organic Synthesis. Green Chem. Lett. Rev. 2011, 4, 41–54. [Google Scholar] [CrossRef]
- Sahbaz, Y.; Williams, H.D.; Nguyen, T.; Saunders, J.; Ford, L.; Charman, S.A.; Scammells, P.J.; Porter, C.J.H. Transformation of Poorly Water-Soluble Drugs into Lipophilic Ionic Liquids Enhances Oral Drug Exposure from Lipid Based Formulations. Mol. Pharm. 2015, 12, 1980–1991. [Google Scholar] [CrossRef] [PubMed]
- Hart, M.L.; Do, D.P.; Ansari, R.A.; Rizvi, S.A. Brief Overview of Various Approaches to Enhance Drug Solubility. J. Dev. Drugs 2013, 2, 1000110–1000116. [Google Scholar] [CrossRef]
- Lin, M.; Gong, M.; Lu, B.; Wu, Y.; Wang, D.; Guan, M.; Angell, M.; Chen, C.; Yang, J.; Hwang, B.; et al. An Ultrafast Rechargeable Aluminium-Ion Battery. Nature 2015, 520, 324–328. [Google Scholar] [CrossRef] [PubMed]
- Girard, G.M.A.; Hilder, M.; Zhu, H.; Nucciarone, D.; Whitbread, K.; Zavorine, S.; Moser, M.; Forsyth, M.; MacFarlane, D.R.; Howlett, P.C. Electrochemical and Physicochemical Properties of Small Phosphonium Cation Ionic Liquid Electrolytes with High Lithium Salt Content. Phys. Chem. Chem. Phys. 2015, 17, 8706–8713. [Google Scholar] [CrossRef] [PubMed]
- Piper, D.M.; Evans, T.; Leung, K.; Watkins, T.; Olson, J.; Kim, S.C.; Han, S.S.; Bhat, V.; Oh, K.H.; Buttry, D.A.; et al. Stable Silicon-Ionic Liquid Interface for Next-Generation Lithium-Ion Batteries. Nat. Commun. 2015, 6, 6230. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yamazaki, A.; Murai, J.; Park, J.; Mandai, T.; Ueno, K.; Dokko, K.; Watanabe, M. Chelate Effects in Glyme/Lithium Bis-(Trifluoromethanesulfonyl)Amide Solvate Ionic Liquids, Part 2: Importance of Solvate-Structure Stability for Electrolytes of Lithium Batteries. J. Phys. Chem. C 2014, 118, 17362–17373. [Google Scholar] [CrossRef]
- Taha, M.; Almeida, M.R.; Silva, F.A.; Domingues, P.; Ventura, S.P.M.; Coutinho, J.A.P.; Freire, M.G. Novel Biocompatible and Self-Buffering Ionic Liquids for Biopharmaceutical Applications. Chem. Eur. J. 2015, 21, 4781–4788. [Google Scholar] [CrossRef] [PubMed]
- Gorke, J.; Srienc, F.; Kazlauskas, R. Toward Advanced Ionic Liquids. Polar, Enzyme-Friendly Solvents for Biocatalysis. Biotechnol. Bioprocess Eng. 2010, 15, 40–53. [Google Scholar] [CrossRef]
- Socha, A.M.; Parthasarathi, R.; Shi, J.; Pattathil, S.; Whyte, D.; Bergeron, M.; George, A.; Tran, K.; Stavila, V.; Venkatachalam, S.; et al. Efficient Biomass Pretreatment Using Ionic Liquids Derived from Lignin and Hemicellulose. Proc. Natl. Acad. Sci. USA 2014, 111, E3587–E3595. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Gurau, G.; Rogers, R.D. Ionic Liquid Processing of Cellulose. Chem. Soc. Rev. 2012, 41, 1519–1537. [Google Scholar] [CrossRef] [PubMed]
- Armand, M.; Endres, F.; MacFarlane, D.R.; Ohno, H.; Scrosati, B. Ionic-Liquid Materials for the Electrochemical Challenges of the Future. Nat. Mater. 2009, 8, 621. [Google Scholar] [CrossRef] [PubMed]
- Russina, O.; Triolo, A.; Gontrani, L.; Caminiti, R. Mesoscopic Structural Heterogeneities in Room-Temperature Ionic Liquids. J. Phys. Chem. Lett. 2012, 3, 27–33. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Santos, C.S.; Annapureddy, H.V.R.; Murthy, N.S.; Margulis, C.J.; Castner, E.W., Jr. Temperature-Dependent Structure of Ionic Liquids: X-ray Scattering and Simulations. Faraday Discuss. 2012, 154, 133–143. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, H.K.; Santos, C.S.; Murthy, N.S.; Hettige, J.J.; Kerr, K.; Ramati, S.; Gwon, J.; Gohdo, M.; Lall-Ramnarine, S.I.; Wishart, J.F.; et al. Structure of 1-Alkyl-1-methylpyrrolidinium Bis(trifluoromethylsulfonyl)amide Ionic Liquids with Linear, Branched, and Cyclic Alkyl Groups. J. Phys. Chem. B 2013, 117, 15328–15337. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.; McDonald, I.R. Theory of Simple Liquids: With Applications to Soft Matters; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Dhabal, D.; Gupta, A.; Kashyap, H.K. Structural Investigation of Room-Temperature Ionic Liquids and High-Temperature Ionic Melts Using Triplet Correlation Functions. J. Chem. Phys. 2017, 146, 094503. [Google Scholar] [CrossRef]
- Krekeler, C.; Dommert, F.; Schmidt, J.; Zhao, Y.Y.; Holm, C.; Berger, R.; Delle Site, L. Electrostatic Properties of Liquid 1,3-Dimethylimidazolium Chloride: Role of Local Polarization and Effect of the Bulk. Phys. Chem. Chem. Phys. 2010, 12, 1817–1821. [Google Scholar] [CrossRef] [PubMed]
- Wendler, K.; Zahn, S.; Dommert, F.; Berger, R.; Holm, C.; Kirchner, B.; Delle Site, L. Locality and Fluctuations: Trends in Imidazolium-Based Ionic Liquids and Beyond. J. Chem. Theory Comput. 2011, 7, 3040. [Google Scholar] [CrossRef] [PubMed]
- Wendler, K.; Dommert, F.; Zhao, Y.Y.; Berger, R.; Holm, C.; Delle Site, L. Ionic Liquids Studied Across Different Scales: A Computational Perspective. Faraday Discuss. 2012, 154, 111–132. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive Resolution Molecular-Dynamics Simulation: Changing the Degrees of Freedom on the Fly. J. Chem. Phys. 2005, 123, 224106. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Multiscale Simulation of Soft Matter: From Scale Bridging to Adaptive Resolution. Annu. Rev. Phys. Chem. 2008, 59, 545. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Schütte, C.; Delle Site, L. Adaptive Resolution Simulation (AdResS): A Smooth Thermodynamic and Structural Transition from Atomistic to Coarse Grained Resolution and Vice Versa in a Grand Canonical Fashion. J. Chem. Theory Comput. 2012, 8, 2878–2887. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hartmann, C.; Schütte, C.; Delle Site, L. Grand-Canonical-Like Molecular-Dynamics Simulations by Using an Adaptive-Resolution Technique. Phys. Rev. X 2013, 3, 011018. [Google Scholar] [CrossRef]
- Agarwal, A.; Zhu, J.; Hartmann, C.; Wang, H.; Delle Site, L. Molecular Dynamics in a Grand Ensemble: Bergmann-Lebowitz Model and Adaptive Resolution Simulation. New J. Phys. 2015, 17, 083042. [Google Scholar] [CrossRef]
- Delle Site, L. Formulation of Liouville’s Theorem for Grand Ensemble Molecular Simulations. Phys. Rev. E 2016, 93, 022130. [Google Scholar] [CrossRef] [PubMed]
- Krekeler, C.; Delle Site, L. Towards Open Boundary Molecular Dynamics Simulation of Ionic Liquids. Phys. Chem. Chem. Phys. 2017, 19, 4701–4709. [Google Scholar] [CrossRef] [PubMed]
- Jabes, B.S.; Krekeler, C.; Klein, R.; Delle Site, L. Probing Spatial Locality in Ionic Liquids with the Grand Canonical Adaptive Resolution Molecular Dynamics Technique. J. Chem. Phys. 2018, 148, 193804. [Google Scholar]
- Agarwal, A.; Delle Site, L. Grand-Canonical Adaptive Resolution Centroid Molecular Dynamics: Implementation and Application. Comput. Phys. Commun. 2016, 206, 26–34. [Google Scholar] [CrossRef]
- Lambeth, B.P.; Junghans, C.; Kremer, K.; Clementi, C.; Delle Site, L. Communication: On the Locality of Hydrogen Bond Networks at Hydrophobic Interfaces. J. Chem. Phys. 2010, 133, 221101. [Google Scholar] [CrossRef] [PubMed]
- Bingham, R.J.; Ballone, P. Computational Study of Room-Temperature Ionic Liquids Interacting with a POPC Phospholipid Bilayer. J. Phys. Chem. B 2012, 116, 11205–11216. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, G.; Giri, R.P.; Saxena, H.; Agrawal, V.V.; Gupta, A.; Mukhopadhyay, M.K.; Ghosh, S.K. X-ray Reflectivity Study of the Interaction of an Imidazolium-Based Ionic Liquid With a Soft Supported Lipid Membrane. Langmuir 2017, 33, 1295–1304. [Google Scholar] [CrossRef] [PubMed]
- Kavitha, T.; Vasantha, T.; Venkatesu, P.; Devi, R.S.R.; Hofman, T. Thermophysical Properties for the Mixed Solvents of N-methyl-2-pyrrolidone with Some of the Imidazolium-Based Ionic Liquids. J. Mol. Liq. 2014, 198, 11–20. [Google Scholar] [CrossRef]
- Delle Site, L.; Praprotnik, M. Molecular Systems with Open Boundaries: Theory and Simulation. Phys. Rep. 2017, 693, 1–56. [Google Scholar] [CrossRef]
- Praprotnik, M.; Matysiak, S.; Delle Site, L.; Kremer, K.; Clementi, C. Adaptive Resolution Simulation of Liquid Water. J. Phys. Condens. Matter 2007, 19, 292201. [Google Scholar] [CrossRef]
- Poblete, S.; Praprotnik, M.; Kremer, K.; Delle Site, L. Coupling Different Levels of Resolution in Molecular Simulations. J. Chem. Phys. 2010, 132, 114101. [Google Scholar] [CrossRef] [PubMed]
- Fritsch, S.; Poblete, S.; Junghans, C.; Ciccotti, G.; Delle Site, L.; Kremer, K. Adaptive Resolution Molecular Dynamics Simulation Through Coupling to an Internal Particle Reservoir. Phys. Rev. Lett. 2012, 108, 170602. [Google Scholar] [CrossRef] [PubMed]
- Dommert, F.; Wendler, K.; Bergerm, R.; Delle Site, L.; Holm, C. Force Fields for Studying the Structure and Dynamics of Ionic Liquids: A Critical Review of Recent Developments. ChemPhysChem 2012, 13, 1625. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, S.B.C.; Roatsch, M.; Schoppke, M.; Kirchner, B. On the Physical Origin of the Cation-Anion Intermediate Bond in Ionic Liquids Part I. Placing a (Weak) Hydrogen Bond Between Two Charges. Phys. Chem. Chem. Phys. 2010, 12, 7473–7486. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182. [Google Scholar] [CrossRef]
- Reith, D.; Putz, M.; Muller-Plathe, F. Deriving Effective Mesoscale Potentials from Atomistic Simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Fritsch, S.; Junghans, C.; Kremer, K. Structure Formation of Toluene Around C60: Implementation of the Adaptive Resolution Scheme (AdResS) into GROMACS. J. Chem. Theory Comput. 2012, 8, 398–403. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).