Temporal Variation of the Pressure from a Steady Impinging Jet Model of Dry Microburst-Like Wind Using URANS
Abstract
:1. Introduction
2. Computational Method
2.1. Governing Equations
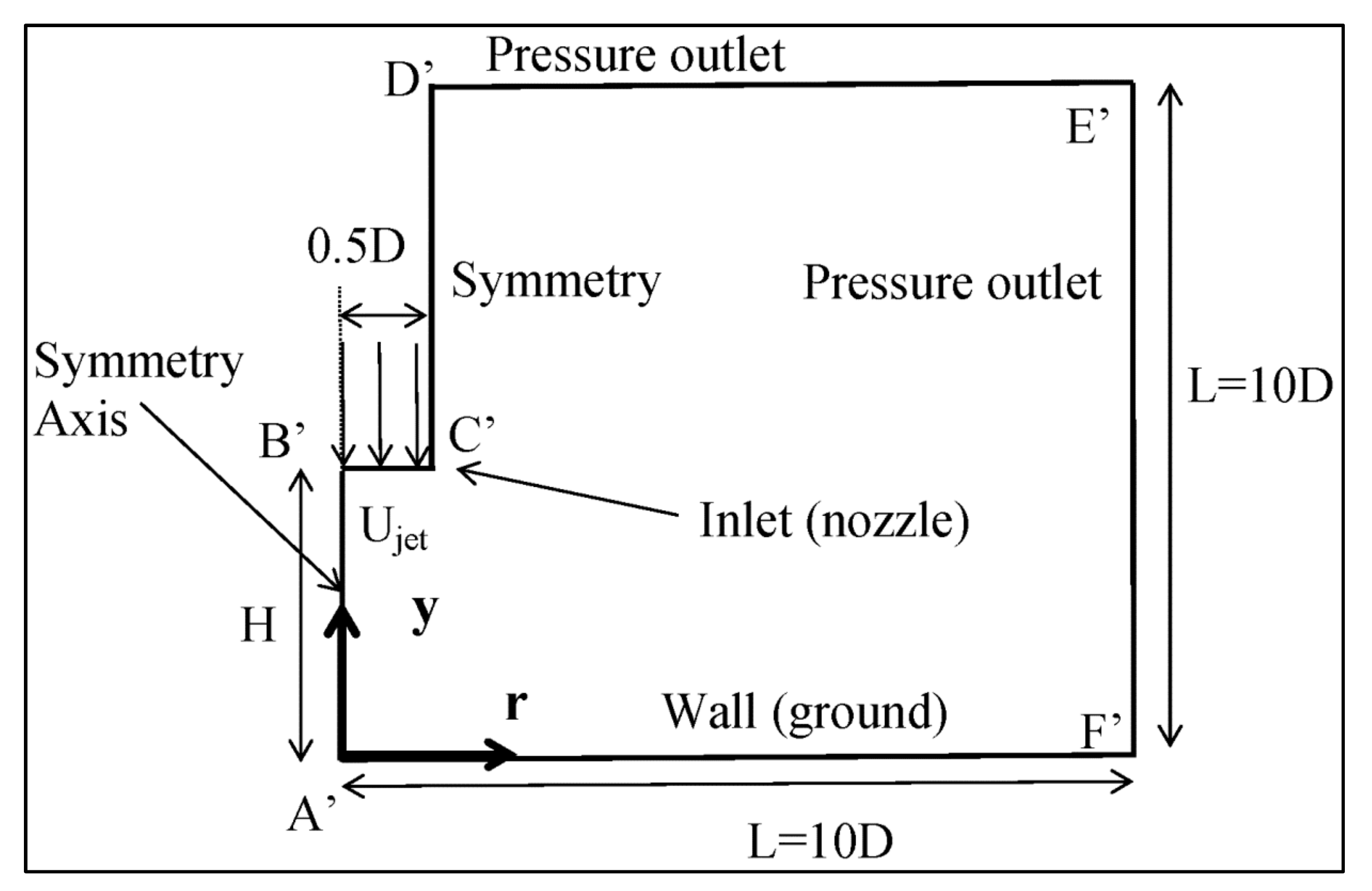
2.2. Computational Domain, Boundary Conditions and Numerical Schemes
2.3. Scaling Factors of the Impinging Jet Model
2.4. Grid Convergence
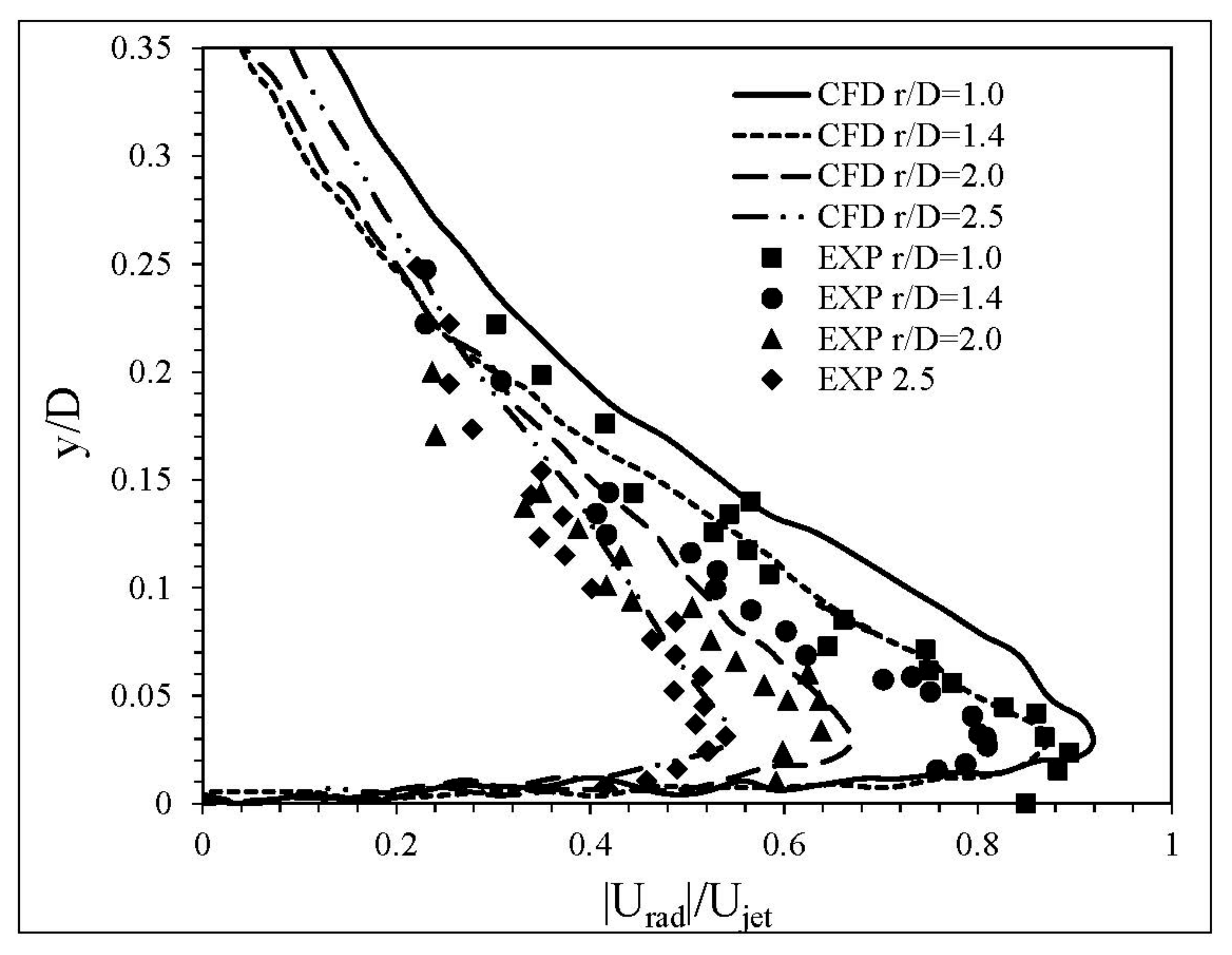
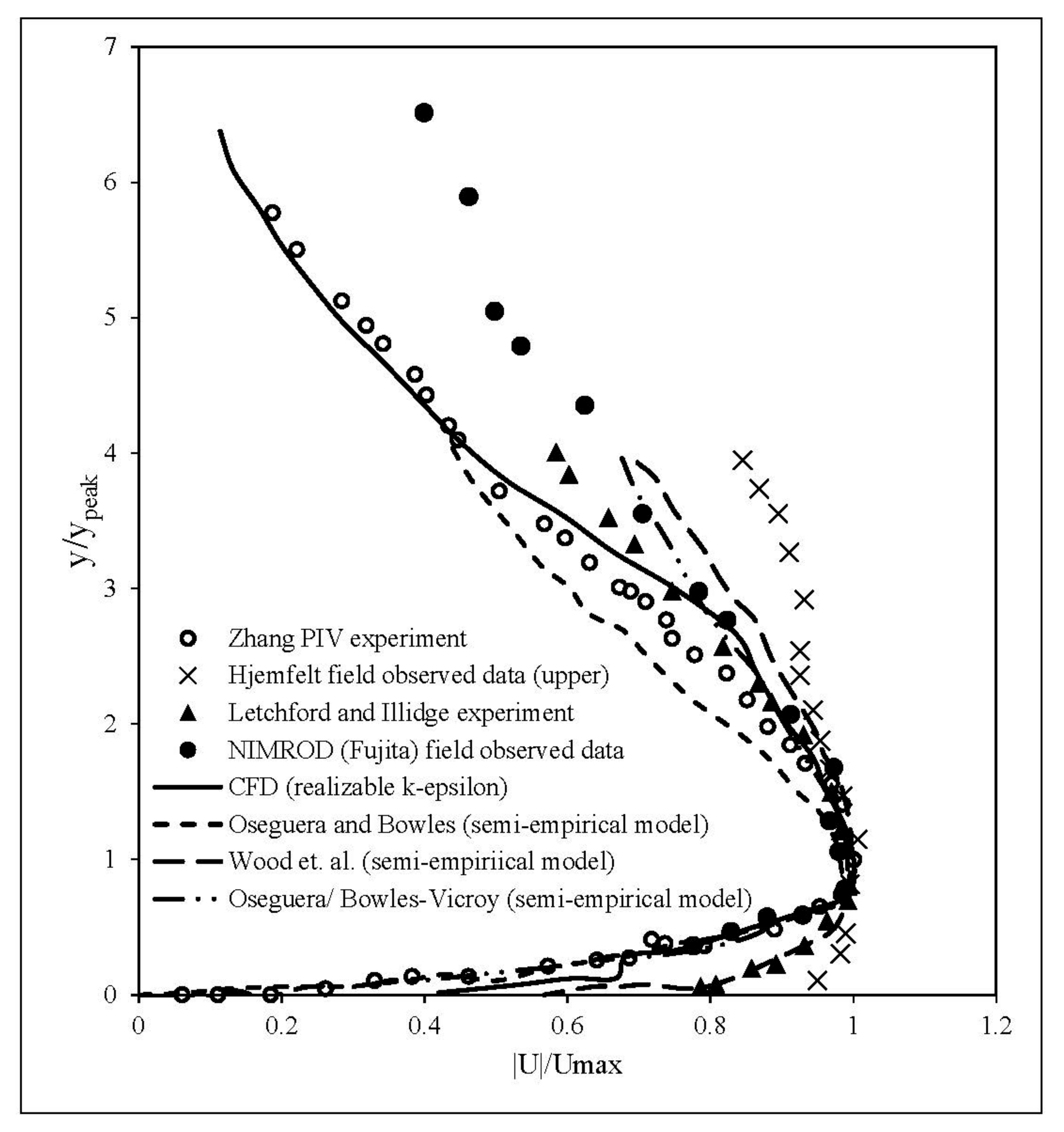
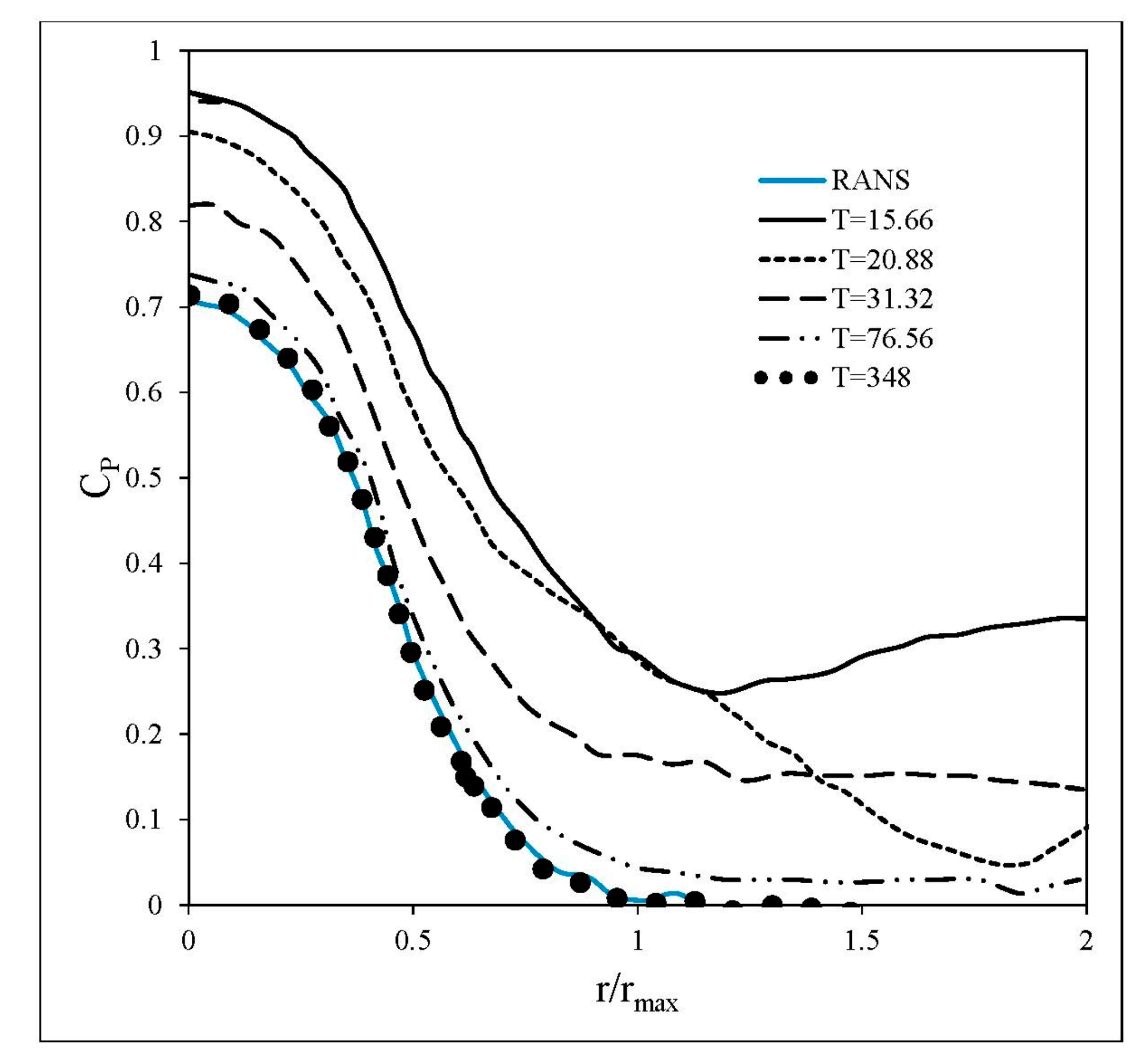
2.5. Validation of RANS Results
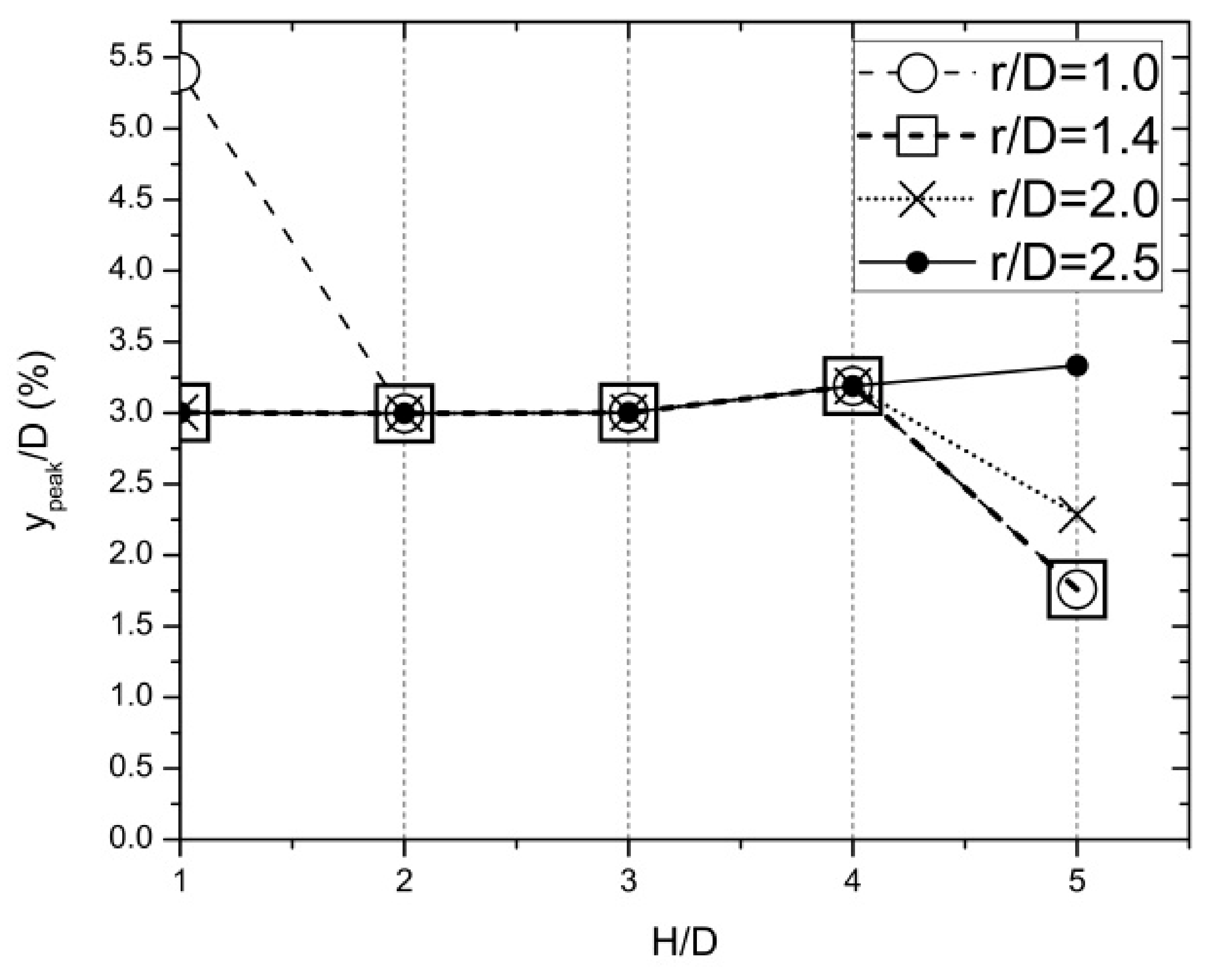
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fujita, T.T. The Downburst: Microburst and Macroburst: Report of Projects NIMROD and JAWS, Satellite and Mesometeorology Research Project; Dept. of the Geophysical Sciences, University of Chicago Press: Chicago, IL, USA, 1985. [Google Scholar]
- Atkins, N.T.; Wakimoto, R.M. Wet Microburst Activity over the Southeastern United States: Implications for Forecasting. Weather Forecast. 1991, 6, 470–482. [Google Scholar] [CrossRef]
- Hjelmfelt, M.R. Structure and Life Cycle of Microburst Outflows Observed in Colorado. J. Appl. Meteorol. 1988, 27, 900–927. [Google Scholar] [CrossRef]
- Mårtensson, G.; Skote, M.; Malmqvist, M.; Falk, M.; Asp, A.; Svanvik, N.; Johansson, A.V. Rapid PCR amplification of DNA utilizing Coriolis effects. Eur. Biophys. J. 2006, 35, 453–458. [Google Scholar] [CrossRef] [PubMed]
- Fujita, T.T. Objectives, operation, and results of Project NIMROD. In Proceedings of the 11th Conference on Severe Local Storms, Kansas City, MO, USA, 2–5 October 1979; American Meteorological Society: Boston, MA, USA, 1979; pp. 259–266. [Google Scholar]
- McCarthy, J.; Wilson, J.W.; Fujita, T.T. The Joint Airport Weather Studies Project; Bulletin of the American Meteorological Society; American Meteorological Society: Boston, MA, USA, 1982; Volume 63, p. 15. [Google Scholar]
- Wolfson, M.M.; DiStafano, J.T.; Forman, B.E. The FLOWS (FAA-Lincoln Laboratory Operational Weather Studies) Automatic Weather Station Network in Operation; Defense Technical Information Center: Fort Belvoir, VA, USA, 1987. [Google Scholar]
- Choi, E.C.C. Field measurement and experimental study of wind speed profile during thunderstorms. J. Wind Eng. Ind. Aerodyn. 2004, 92, 275–290. [Google Scholar] [CrossRef]
- Burlando, M.; Romanić, D.; Solari, G.; Hangan, H.; Zhang, S. Field data analysis and weather scenario of a downburst event in Livorno, Italy, on 1 October 2012. Mon. Weather Rev. 2017, 145, 3507–3527. [Google Scholar] [CrossRef]
- De Gaetano, P.; Repetto, M.P.; Repetto, T.; Solari, G. Separation and classification of extreme wind events from anemometric records. J. Wind Eng. Ind. Aerodyn. 2014, 126, 132–143. [Google Scholar] [CrossRef]
- Solari, G.; Repetto, M.P.; Burlando, M.; De Gaetano, P.; Pizzo, M.; Tizzi, M.; Parodi, M. The wind forecast for safety management of port areas. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 266–277. [Google Scholar] [CrossRef]
- Gunter, W.S.; Schroeder, J.L. High-resolution full-scale measurements of thunderstorm outflow winds. J. Wind Eng. Ind. Aerodyn. 2015, 138, 13–26. [Google Scholar] [CrossRef]
- Holmes, J.D.; Hangan, H.M.; Schroeder, J.L.; Letchford, C.W.; Orwig, K.D. A forensic study of the Lubbock-Reese downdraft of 2002. Wind Struct. 2008, 11, 137–152. [Google Scholar] [CrossRef]
- Holmes, J.D. Modelling of extreme thunderstorm winds for wind loading of structures and risk assessment. In Proceedings of the Tenth International Conference on Wind Engineering, Copenhagen, Denmark, 21–24 June 1999; Volume 2, pp. 1409–1416. [Google Scholar]
- Chay, M.T.; Letchford, C.W. Pressure distributions on a cube in a simulated thunderstorm downburst—Part A: Stationary downburst observations. J. Wind Eng. Ind. Aerodyn. 2002, 90, 711–732. [Google Scholar] [CrossRef]
- Letchford, C.W.; Chay, M.T. Pressure distributions on a cube in a simulated thunderstorm downburst. Part B: Moving downburst observations. J. Wind Eng. Ind. Aerodyn. 2002, 90, 733–753. [Google Scholar] [CrossRef]
- Kim, J.; Hangan, H.; Ho, T.C.E. Downburst versus boundary layer induced wind loads for tall buildings. Wind Struct. 2007, 10, 481–494. [Google Scholar] [CrossRef]
- Cui, B.; Chen, Y. CFD Simulation of Curved-roof subjected to Thunderstorm Downburst. In Key Engineering Materials; Trans Tech Publications: Zürich, Switzerland, 2017; Volume 474, pp. 1243–1248. [Google Scholar]
- Nguyen, H.H.; Manuel, L.; Veers, P.S. Wind turbine loads during simulated thunderstorm microbursts. J. Renew. Sustain. Energy 2011, 3, 053104–053119. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Manuel, L. Thunderstorm downburst risks to wind farms. J. Renew. Sustain. Energy 2013, 5, 013120. [Google Scholar] [CrossRef]
- Zhang, Y. Study of Microburst-Like Wind and Its Loading Effects on Structures Using Impinging Jet and Cooling Source Approach; Iowa State University: Ames, IA, USA, 2013. [Google Scholar]
- Zhang, Y.; Hu, H.; Sarkar, P.P. Modeling of microburst outflows using impinging jet and cooling source approaches and their comparison. Eng. Struct. 2013, 56, 779–793. [Google Scholar] [CrossRef]
- Anderson, J.R.; Orf, L.G.; Straka, J.M. A 3-D model system for simulating thunderstorm microburst outflows. Meteorl. Atmos. Phys. 1992, 49, 125–131. [Google Scholar] [CrossRef]
- Orf, L.G.; Anderson, J.R.; Straka, J.M. A Three-Dimensional Numerical Analysis of Colliding Microburst Outflow Dynamics. J. Atmos. Sci. 1996, 53, 2490–2511. [Google Scholar] [CrossRef]
- Orf, L.G.; Anderson, J.R. A Numerical Study of Traveling Microbursts. Mon. Weather Rev. 1999, 127, 1244–1258. [Google Scholar] [CrossRef]
- Orf, L.G.; Kantor, E.; Savory, E. Simulation of a downburst-producing thunderstorm using a very high-resolution three-dimensional cloud model. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 547–557. [Google Scholar] [CrossRef]
- Vermeire, B.C.; Orf, L.G.; Savory, E. A parametric study of downburst line near-surface outflows. J. Wind Eng. Ind. Aerodyn. 2011, 99, 226–238. [Google Scholar] [CrossRef]
- Kim, J.; Hangan, H. Numerical simulations of impinging jets with application to downbursts. J. Wind Eng. Ind. Aerodyn. 2007, 95, 279–298. [Google Scholar] [CrossRef]
- Xu, Z.; Hangan, H. Scale, boundary and inlet condition effects on impinging jets. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2383–2402. [Google Scholar] [CrossRef]
- Chay, M.T.; Albermani, F.; Wilson, R. Numerical and analytical simulation of downburst wind loads. Eng. Struct. 2006, 28, 240–254. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Li, Q.S.; Xiao, Y.Q.; Ou, J.P. Simulations of moving downbursts using CFD. In Proceedings of the Seventh Asia-Pacific Conference on Wind Engineering, Taiwan, 8–12 November 2009. [Google Scholar]
- Wood, G.S.; Kwok, K.C.S.; Motteram, N.A.; Fletcher, D.F. Physical and numerical modelling of thunderstorm downbursts. J. Wind Eng. Ind. Aerodyn. 2001, 89, 535–552. [Google Scholar] [CrossRef]
- Sengupta, A.; Sarkar, P.P. Experimental measurement and numerical simulation of an impinging jet with application to thunderstorm microburst winds. J. Wind Eng. Ind. Aerodyn. 2008, 96, 345–365. [Google Scholar] [CrossRef]
- Das, K.K.; Ghosh, A.K.; Sinhamahapatra, K.P. Experimental and Numerical simulation of the Translational Downburst using impinging jet model. Int. J. Eng. Sci. Technol. (IJEST) 2011, 3, 4656–4667. [Google Scholar]
- Landreth, C.C.; Adrian, R.J. Impingement of a low Reynolds number turbulent circular jet onto a flat plate at normal incidence. Exp. Fluids 1990, 9, 74–84. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, H.; Sarkar, P.P. Comparison of microburst-wind loads on low-rise structures of various geometric shapes. J. Wind Eng. Ind. Aerodyn. 2014, 133, 181–190. [Google Scholar] [CrossRef]
- Zhang, Y.; Sarkar, P.; Hu, H. An experimental study on wind loads acting on a high-rise building model induced by microburst-like winds. J. Fluids Struct. 2014, 50, 547–564. [Google Scholar] [CrossRef]
- Oseguera, R.M.; Bowles, R.L. A Simple, Analytic 3-Dimensional Downburst Model Based on Boundary Layer Stagnation Flow; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 1988. [Google Scholar]
- Vicroy, D.D. A Simple, Analytical, Axisymmetric Microburst Model for Downdraft Estimation; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 1991. [Google Scholar]
- Li, C.; Li, Q.S.; Xiao, Y.Q.; Ou, J.P. A revised empirical model and CFD simulations for 3D axisymmetric steady-state flows of downbursts and impinging jets. J. Wind Eng. Ind. Aerodyn. 2012, 102, 48–60. [Google Scholar] [CrossRef]
- ANSYS Fluent User Manual by ANSYS Inc. Available online: www.ansys.com (accessed on 5 January 2018).
- Holmes, J.D. Wind turbines-Part 1: Design Requirements. In Wind Loading of Structures; IEC 61400-1; Taylor & Francis International Electrotechnical Commission: Boca Raton, FL, USA, 2007. [Google Scholar]
- Fujita, T.T. Tornadoes and Downbursts in the Context of Generalized Planetary Scales. J. Atmos. Sci. 1981, 38, 1511–1534. [Google Scholar] [CrossRef]
- Skote, M. Scaling of the velocity profile in strongly drag reduced turbulent flows over an oscillating wall. Int. J. Heat Fluid Flow 2014, 50, 352–358. [Google Scholar] [CrossRef]
- Wolfstein, M. The Velocity and Temperature Distribution of One-Dimensional Flow with Turbulence Augmentation and Pressure Gradient. Int. J. Heat Mass Transf. 1969, 12, 301–318. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.; Shabbir, Z.Y.; Zhu, J. A New k-ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows—Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Kader, B. Temperature and Concentration Profiles in Fully Turbulent Boundary Layers. Int. J. Heat Mass Transf. 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Mangani, L.; Bianchini, C. Heat transfer applications in turbomachinery. In Proceedings of the OpenFOAM International Conference, London, UK, 26–27 November 2007. [Google Scholar]
- Mason, M.S.; Letchford, C.W.; James, D.L. Pulsed wall jet simulation of a stationary thunderstorm downburst, Part A: Physical structure and flow field characterization. J. Wind Eng. Ind. Aerodyn. 2005, 93, 557–580. [Google Scholar] [CrossRef]
- Das, K.K.; Ghosh, A.K.; Sinhamahapatra, K.P. Development of a numerical code for simulation of dry microburst using impinging jet model. Int. J. Appl. Math. Mech. 2011, 7, 56–71. [Google Scholar]
- Lim, H.C.; Castro, I.P.; Hoxey, R.P. Bluff bodies in deep turbulent boundary layers: Reynolds-number issues. J. Fluid Mech. 2007, 571, 97–118. [Google Scholar] [CrossRef]
- Claus, J.; Coceal, O.; Thomas, T.G.; Branford, S.; Belcher, S.E.; Castro, I. Wind-Direction Effects on Urban-Type Flows. Bound. Layer Meteorol. 2012, 142, 265–287. [Google Scholar] [CrossRef]
- Claus, J.; Krogstad, P.Å.; Castro, I. Some Measurements of Surface Drag in Urban-Type Boundary Layers at Various Wind Angles. Bound. Layer Meteorol. 2002, 145, 407–442. [Google Scholar] [CrossRef]
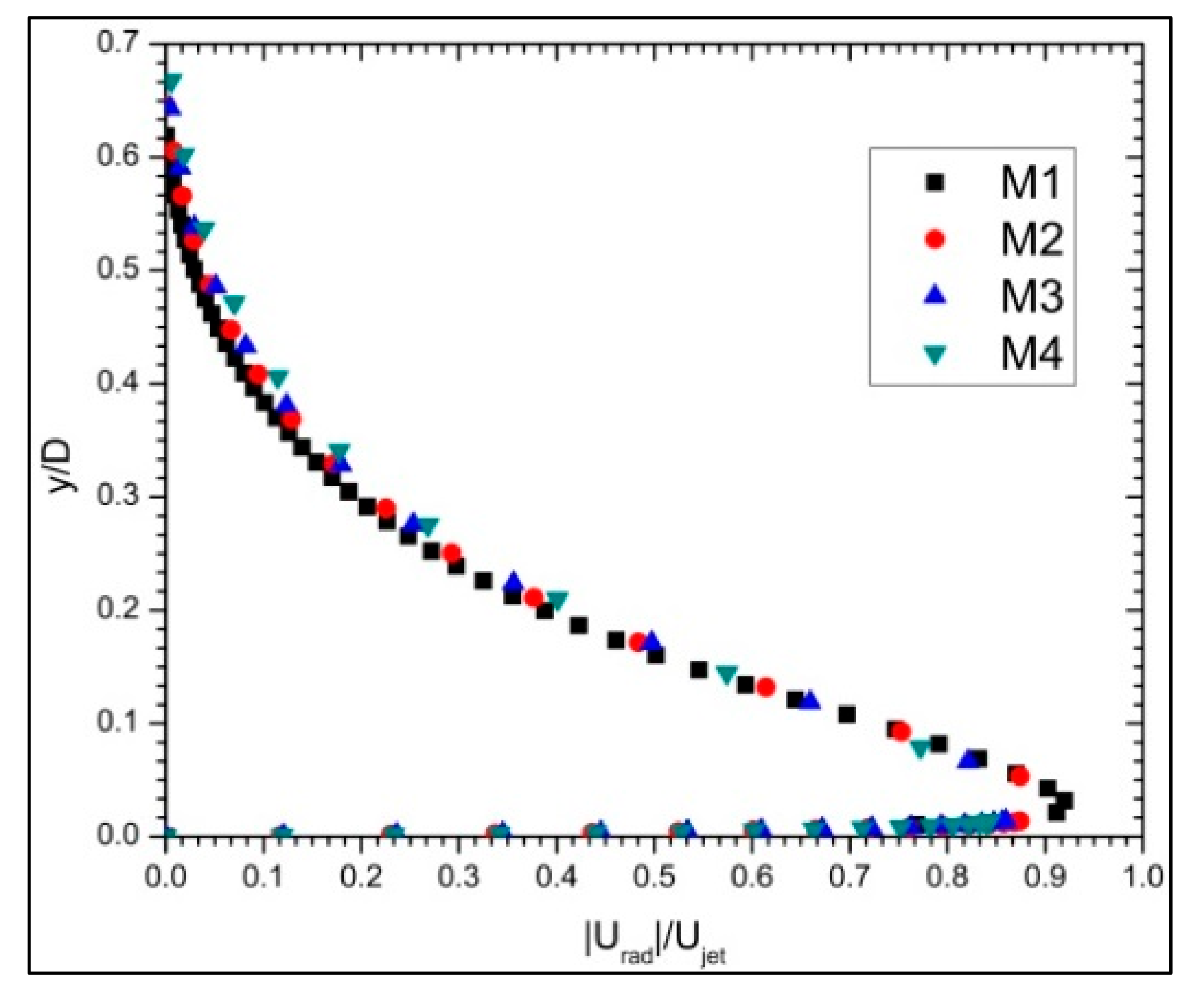
| Mesh Case Notations | M1 | M2 | M3 | M4 |
| Number of Elements | 565,566 | 66,861 | 38,412 | 25,144 |
| t (s) | 0.045 | 0.060 | 0.090 | 0.220 | 1.00 |
| 15.7 | 20.9 | 31.3 | 76.6 | 348 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skote, M.; Sim, T.S.; Srikanth, N. Temporal Variation of the Pressure from a Steady Impinging Jet Model of Dry Microburst-Like Wind Using URANS. Computation 2018, 6, 2. https://doi.org/10.3390/computation6010002
Skote M, Sim TS, Srikanth N. Temporal Variation of the Pressure from a Steady Impinging Jet Model of Dry Microburst-Like Wind Using URANS. Computation. 2018; 6(1):2. https://doi.org/10.3390/computation6010002
Chicago/Turabian StyleSkote, Martin, Tze Siang Sim, and Narasimalu Srikanth. 2018. "Temporal Variation of the Pressure from a Steady Impinging Jet Model of Dry Microburst-Like Wind Using URANS" Computation 6, no. 1: 2. https://doi.org/10.3390/computation6010002
APA StyleSkote, M., Sim, T. S., & Srikanth, N. (2018). Temporal Variation of the Pressure from a Steady Impinging Jet Model of Dry Microburst-Like Wind Using URANS. Computation, 6(1), 2. https://doi.org/10.3390/computation6010002






