1. Introduction
The lymphatic system is a body-wide network of lymphatic vessels and lymphoid organs [
1], with the lymph nodes being the most numerous secondary lymphoid organs. The lymphatic system is responsible for maintaining the fluid balance in tissues and the functioning of the immune system [
2]. The lymphatic vessels represent the channels for eventually transporting the lymph collected from interstitial space via the lymph nodes to the blood and the pathogens and immune cells to the tissue-draining lymph nodes where the host’s immune defenses take place. As the lymphatic system is central to many pathological processes (e.g., cancer, organ rejection after transplantation, lymphedema [
3]), imaging and visualization of the lymphatic system are important for understanding its anatomy and function [
4]. It has been acknowledged that the current knowledge of the lymphatic system lags behind that of the cardiovascular system [
4]. Many important aspects of the lymphatic system’s functioning (e.g., the effect of lymphangiogenesis and lymphatic pumping of the lymph flow, the control of immune cells’ migration to the draining lymph nodes under normal conditions and during inflammation) remain to be answered [
2].
The complexity of the structural and functional organization of the lymphatic system implies the necessity of using computational modeling approaches to unravel the mechanisms of its regulation in quantitative terms. Although it is a vital part of the circulatory and immune systems, the lymphatic system remains poorly investigated as a mathematical modeling object as compared to the circulatory system [
5]. One of the key issues in modeling blood circulation is the construction of the vascular graph of the circulatory system. The branching network of vessels is modeled as a graph with the edges representing the blood vessels, the nodes standing for the branching points or organs (heart, tissues) and the vessel groups (arteries or veins) being identified based on specific topological criteria (e.g., [
6,
7,
8,
9]). The construction of the blood vascular network graph depends on data availability and the modeling objectives, thus resulting in a number of available vascular system graph models of various complexity [
10,
11].
The first network graph model of the whole human body lymphatic system was proposed a long time ago [
12]. It considers a simplified version of the lymphatic anatomy, reduced to about 15 distinct organs and 29 major lymphatic vessels subdivided into 297 compartments (lymphangions). It was only recently that a more detailed lymphatic system graph was elaborated based on anatomical data and expert knowledge [
13]. Some general assumptions about the universal properties of the lymphoid tissue network organization were presented in a study on human immunodeficiency virus (HIV) modeling [
14] and can be summarized as follows:
the network can be modeled as a graph,
no long-distance edges are allowed,
multiple edges can enter a node,
the nodes’ connections are locally acyclic,
the lymphatic system network is a circular graph.
Notice that the second assumption seems to be a simplification of the real anatomy, as there exist long vessels like the thoracic duct, as well as the lymphatic vessels of the limbs. The constructed graph considered about 1000 (lymph) nodes based on the data presented in [
15].
Overall, compared to the blood circulatory system, modeling of the lymphatic vessel network remains to be put on a systematic ground in order to advance modeling-driven research of this important physiological system. The aims of our study are (1) to elucidate key general features underlying the 3D structural organization of the lymphatic system, (2) to develop a 3D computational geometry model of the human lymphatic system based on anatomical data and (3) to analyze the topological properties of the resulting network graph.
2. Anatomy of the Human Lymphatic System
2.1. General Characteristics of the Lymphatic System: Invariant Features and Variable Characteristics
The lymphatic system is present in all vascularized tissues and organs, including the central nervous system [
16]. It is a network of lymphatic vessels and nodes that transport the lymph into the venous system, and it is an integral part of the immune system [
15]. The lymph fluid originating in the interstitial space enters lymphatic capillaries. The capillaries coalesce into contractile vessels called collecting vessels [
1]. Prenodal collectors drain the capillary network to transport the lymph to the regional lymph nodes [
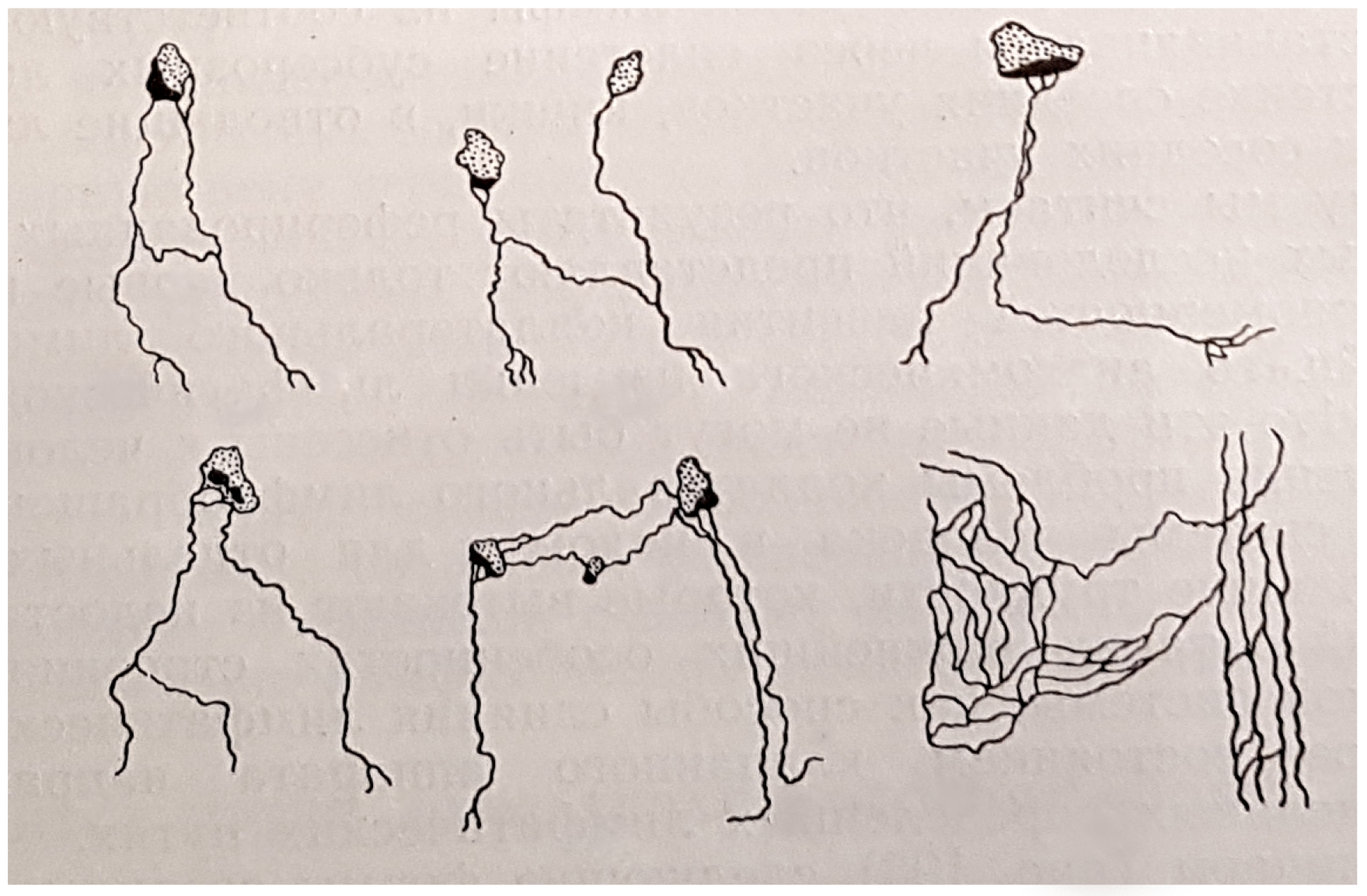
17]. Leaving the draining lymph nodes, the lymph is carried either to the next lymph nodes or directly into lymphatic ducts. On its way to the blood circulatory system, the lymph passes through one or several lymph nodes (e.g., the lymph from the stomach region passes through four to six lymph nodes). The complexity and types of connections present in the small lymphatic vessels network are shown in
Figure 1.
The lymph transport is carried via passive and active mechanisms; the first one refers to lymph propulsion due to extrinsic forces generated by rhythmic tissue compression (e.g., respiratory movement, pulsative pressure of adjacent arteries, intestinal and skeletal muscle contraction) and the second one based on the contractile function of lymphangions [
17]. An active lymph propulsion is characterized by a number of feedback control loops and is regulated in order to adjust the pumping function of the lymphatic vessel network to the intensity of lymph formation in tissues.
A comprehensive description of the lymphatic distribution in relation to other organs and tissues presents a challenge due to the enormous morphological complexity and variability in its appearance. For example, the empirical data presented in [
19] show the extent of variation in the number of lymph nodes draining various parts of the human body:
inguinal lymph nodes, 4-20,
axillary lymph nodes, 12–45,
mesenteric lymph nodes, 64–404,
lumbar lymph nodes, 1–17,
cardiac gastric lymph nodes, 1–11,
pyloric lymph nodes, 2–16,
bronchopulmonary lymph nodes, 4–25,
hepatic lymph nodes, 1–10,
parasternal lymph nodes, 2–20.
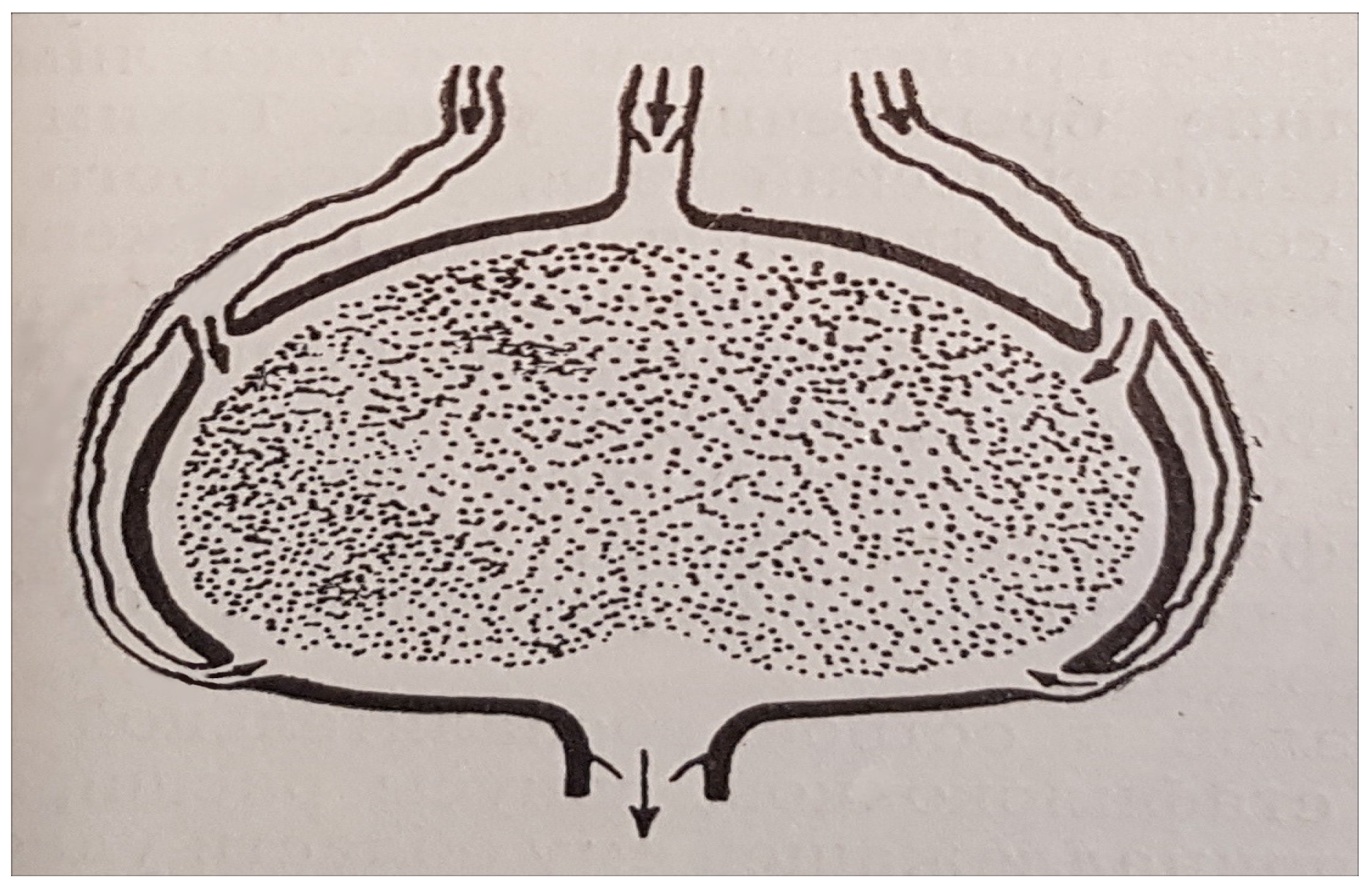
A schematic view of a lymph node with several afferent lymphatic vessels is shown in
Figure 2.
The number of afferent lymphatics is also variable and ranges between three and eleven [
18]. The number of efferent lymphatics ranges between two and three [
18]. The above variability in the number of tissue draining lymph nodes and afferent lymphatics implies an even larger variation in the number and location of lymphatic vessels. Therefore, the development of an idealized geometric model is required to provide a reference structure to be used as a basis for computational studies of the lymph flow and transport phenomena in the lymphatic system.
2.2. 3D Anatomy Model of the Human Male Lymphatic System
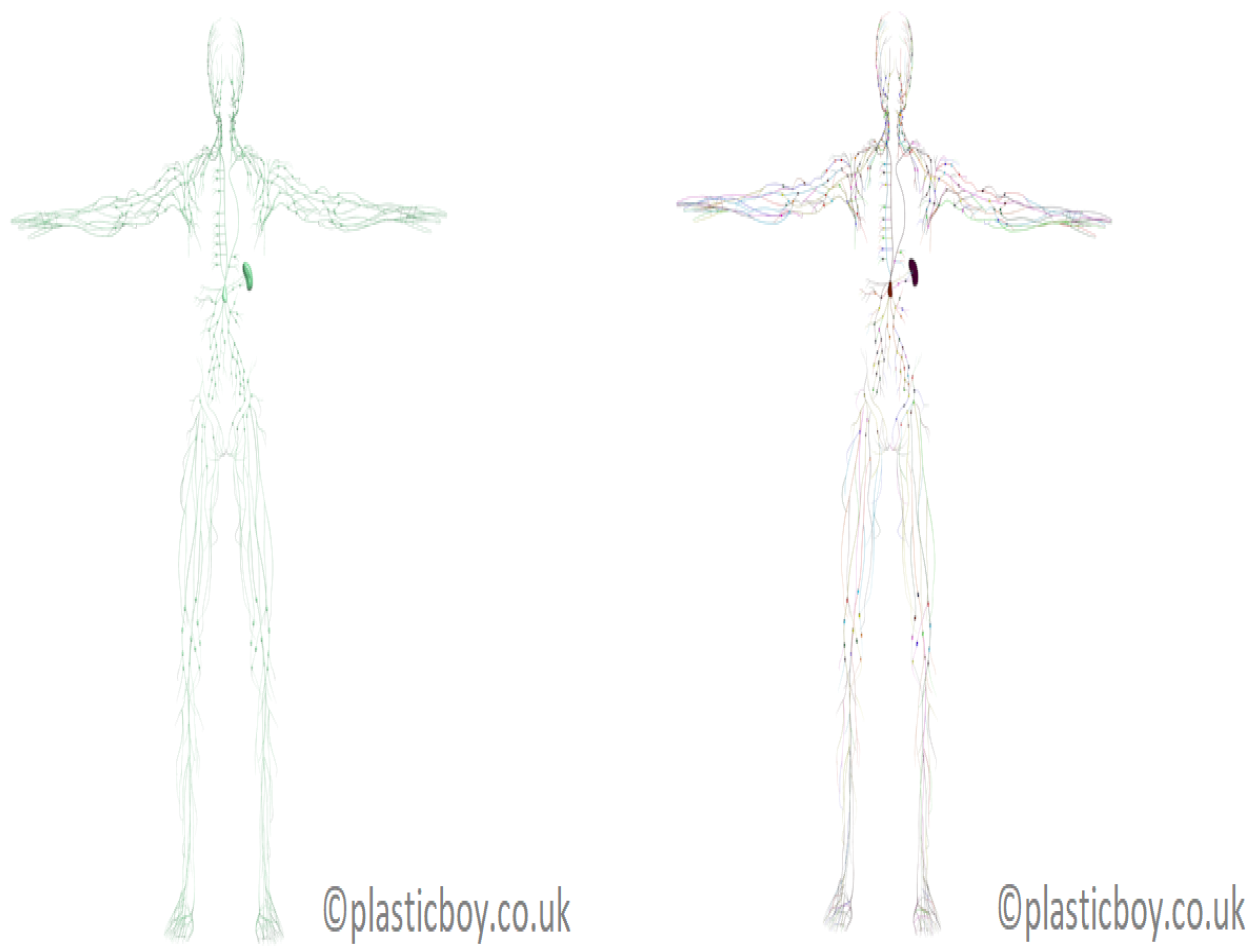
The only publicly-available realistic model of the human lymphatic system was developed as a component of the PlasticBoy project [
20] (see
Figure 3). The 3D polygonal lymphatic system model of PlasticBoy was developed based on various sources (e.g., Wikipedia; personal communication from the PlasticBoy team [
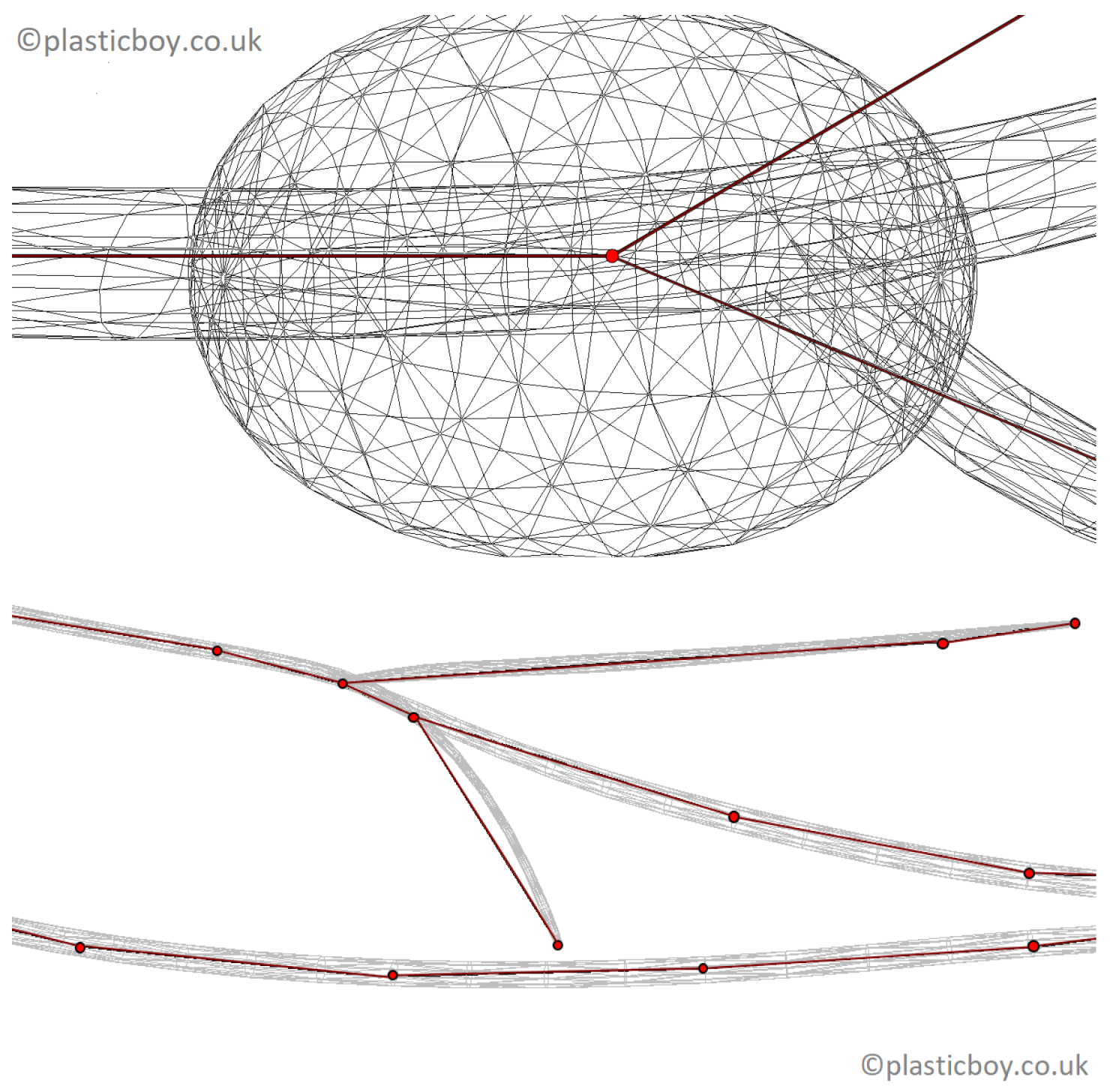
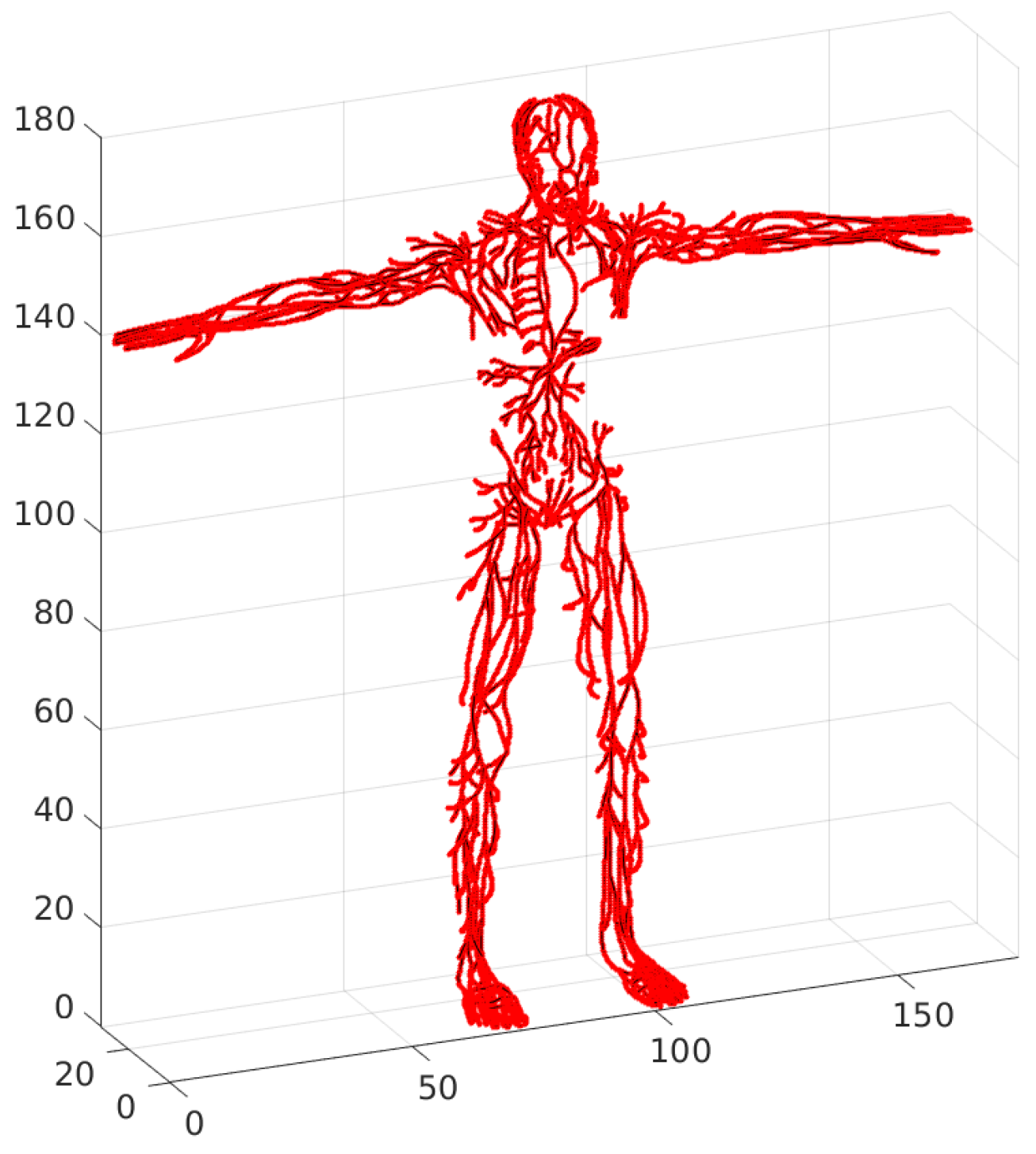
20]). The PlasticBoy model cannot be considered as a measured dataset, but as an estimate of the structure of the lymphatic system as it is not rigorously derived from measurements and an anatomical dataset. It is a surface model that describes about 270 lymph nodes and a system of lymphatic vessels by a series of rectangles. This model considers all major lymph nodes and the spleen. It includes high-resolution textures (
). The above anatomical model is used in the following to study the topological properties of the lymphatic system.
It is a highly complex model, and some pre-processing is needed to use it for topological analysis. A few elements, when looked at in high resolution (e.g., stand-alone lymph nodes or disconnected lymphatic vessels), had to be moved locally to ensure intersection with neighboring elements of the lymphatic system model (see
Figure 4).
The entire lymphatic vessels network model is described as one object. It consists of 443 independent elements. Although the model is not suitable for three-dimensional fluid flow modeling, it provides an anatomically-consistent data structure for derivation of the lymphatic vessels’ network topology as a one-dimensional graph of the lymphatic system.
The shell model required additional processing to remove some mismatches, as mentioned above. The processing was done manually in the Autodesk 3DS Max [
21] environment. The computational algorithm is described in the next section. In brief, the pendant objects were moved or connected to the main network. The lymphatic system was subdivided into vessels so that any two vessels had no common points. In addition, the vessels were systematically named according to their anatomical position. For example, the vessels in the arm were annotated with the prefixes palm, hand, arm, armpit or shoulder.
Figure 5 shows the fragments of the lymphatic system network after processing for specific anatomical regions.
Figure 3, right, displays the tuned 3D model of the lymphatic system.
3. Computational Algorithm for Generating a Graph from a 3D Polygonal Model
The original polygonal model of the lymphatic vessel network requires additional processing to obtain a connected network graph. This is because the model consists of disconnected surface elements corresponding to individual vessels and lymph nodes. To combine all these elements in a single solid object-type model, it was decided to use the transformation of the polygonal model into a voxel-based model. The voxel-based approximation makes it easy to eliminate connectivity problems in the 3D model. In addition, bringing the model to a voxel form allows one to construct the connected graph of the lymphatic network.
The transformation to a voxel model starts with a voxel approximation of the surfaces of the polygonal model. Then, a computational algorithm for filling the closed cavities inside the voxel model is applied. To this end, the voxel model was presented in the form of a graph, for which a “width” search was performed. This approach made it possible to detect and fill all cavities in the voxel-based approximation of the model.
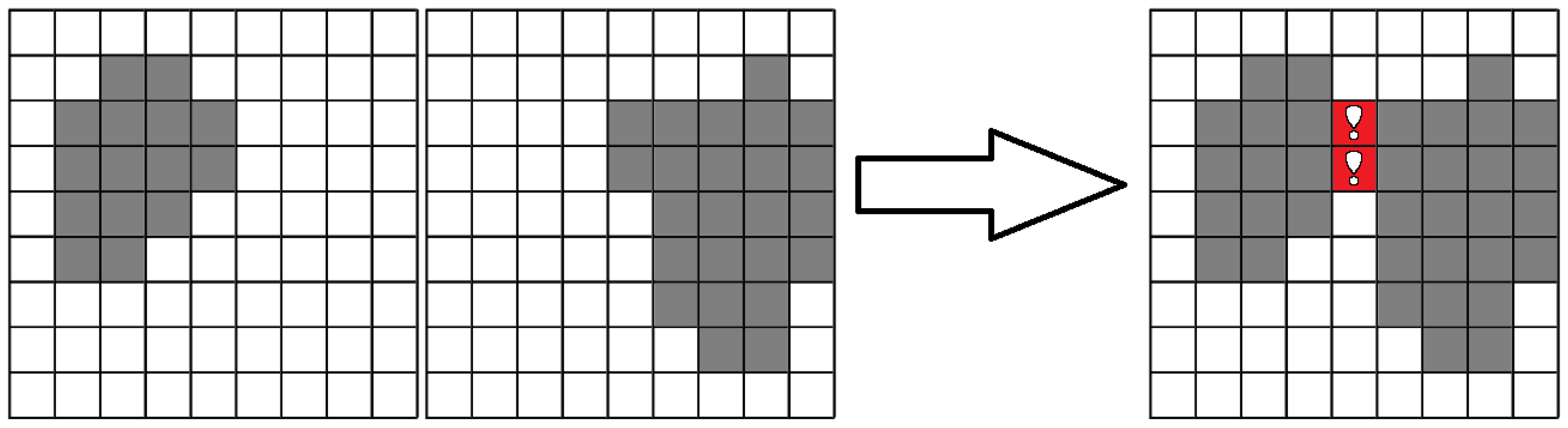
The algorithm can be easily illustrated in the two-dimensional case as shown in
Figure 6 for closed domains and in
Figure 7 for open domains.
To proceed with the construction of a network graph from the obtained voxel-based approximation of the lymphatic system network, we used the stratification algorithm, which can be described as follows. The voxel model was divided into layers, each one with a thickness of one voxel. Then, the groups of voxels interconnected in each layer were identified. After that, for each such group, the center was calculated and considered as the vertex of the graph. Next, the adjacent layers were pair-wise compared to determine the presence of groups with intersections, as shown in
Figure 8.
If an intersection was detected, the centers of the groups (nodes) were connected, thus generating an edge of the graph. This approach allows one to avoid duplication of edges in the graph, as well as a significant displacement of the graph relative to the initial polygonal model of the lymphatic network. Overall, the procedure allows one to reliably estimate the lengths of all the vessels approximated by the graph edges.
The developed computational algorithm for constructing the lymphatic system graph from the original 3D polygonal model can be represented as follows:
Construct a voxel-based approximation of the polygonal model of the vascular system. To do this, each polygon of the model to be approximated is covered by a regular grid with a quarter-size voxel step. After that, the coordinates of the grid points are converted to the coordinates of the voxel, and it is entered in the list of voxels approximating the model.
Complete the void filling in the voxel-based approximation of the model under study, as shown in
Figure 6.
Divide the model into layers, and within the layers, isolate the connected groups of voxels.
Identify the intersections of the voxel groups on adjacent layers and connect (with edges) their centers (nodes) to the branch of the emerging graph, as shown in
Figure 8.
4. Graph Representation of the Human Lymphatic System
4.1. Lymphatic System Network Graph Refinement
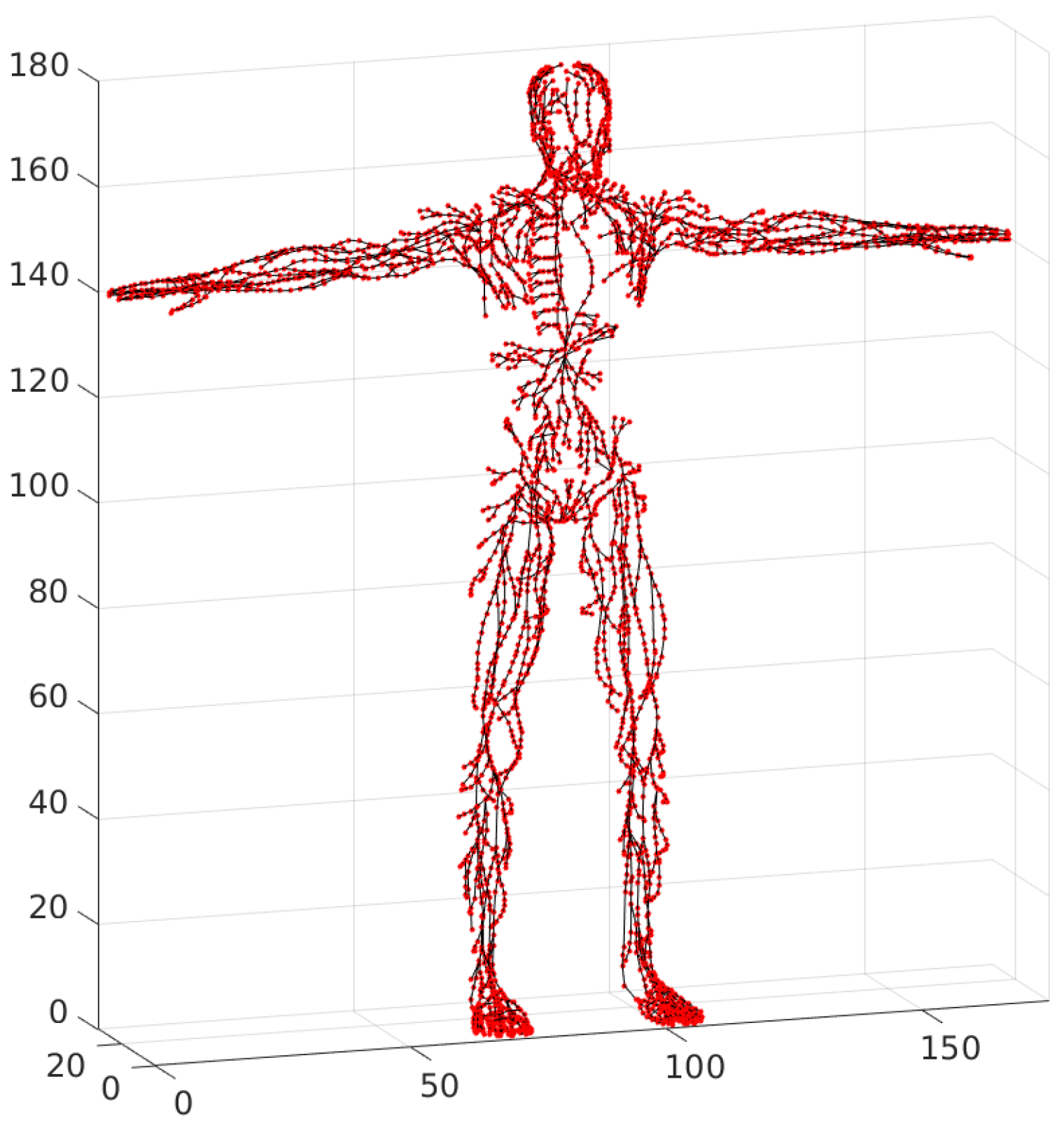
The one-dimensional graph of the lymphatic system network produced by the above-described algorithm of slice-based graph construction requires further refinement. The problem is that the algorithm creates a large number of fictitious vertices, which could not be removed automatically, since the algorithms removed fictitious vertices, as well as some correct vertices. As a result, the procedure of improving the consistency of the graph by eliminating fictitious vertices was performed manually in Autodesk 3DS Max [
21]. The resulting “consistent” graph will further be referred to as the “basis” network graph. The basis graph has the following properties: every lymph node is represented by a single node, and each lymphatic vessel is represented by a chain of vertices and edges, as shown in
Figure 9.
In the following, the chain of vertices and edges refers to a part of the graph consisting of at least two vertices, connected by an edge, or a series of edges, all with the respective vertices (which can be interpreted as representing lymphangions) having degree
. The generated basis graph is represented in
Figure 10.
We developed a data structure to store the key information of the 3D polygonal surface model of the lymphatic vessels and lymph nodes and the topology of the vascular network graph . The data structure also describes the relations between the three-dimensional and one-dimensional network graphs objects:
each edge corresponds to a certain single vessel,
each vertex belongs to one or several vessels,
each lymph node from the 3D model is represented by one vertex in the 1D model,
each lymphatic vessel is represented by at least one chain of vertices and edges.
We note that the lymphatic vessel is represented by several chains if there is a junction point (a smaller vessel draining to a larger one) or lymph node inside a vessel. The degree parameter characterizes each vertex of the 1D network model:
for inputs and outputs of the system,
for the inner point of the vessel,
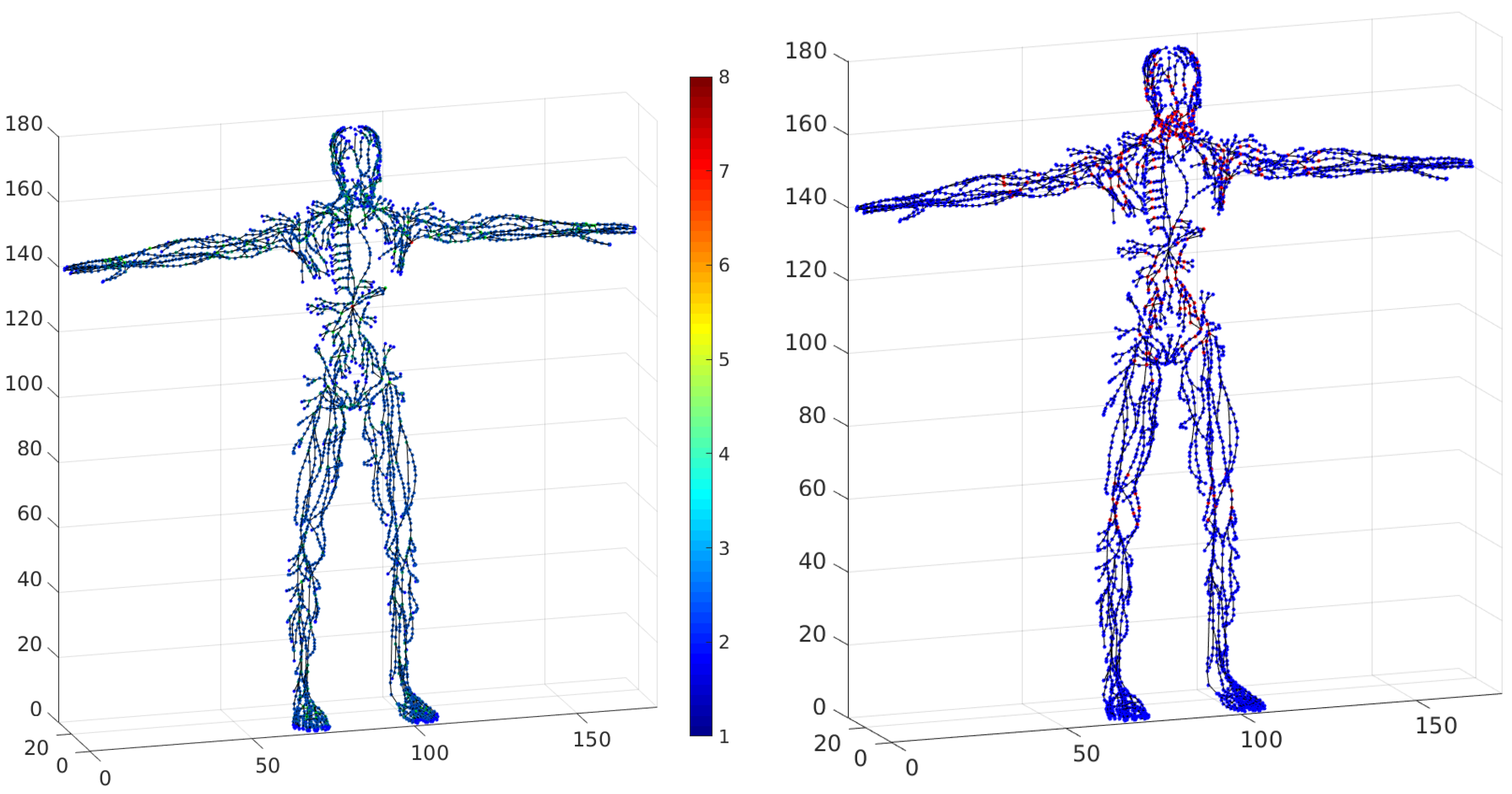
for vessel junction. The degrees of freedom for the basis graph are represented in
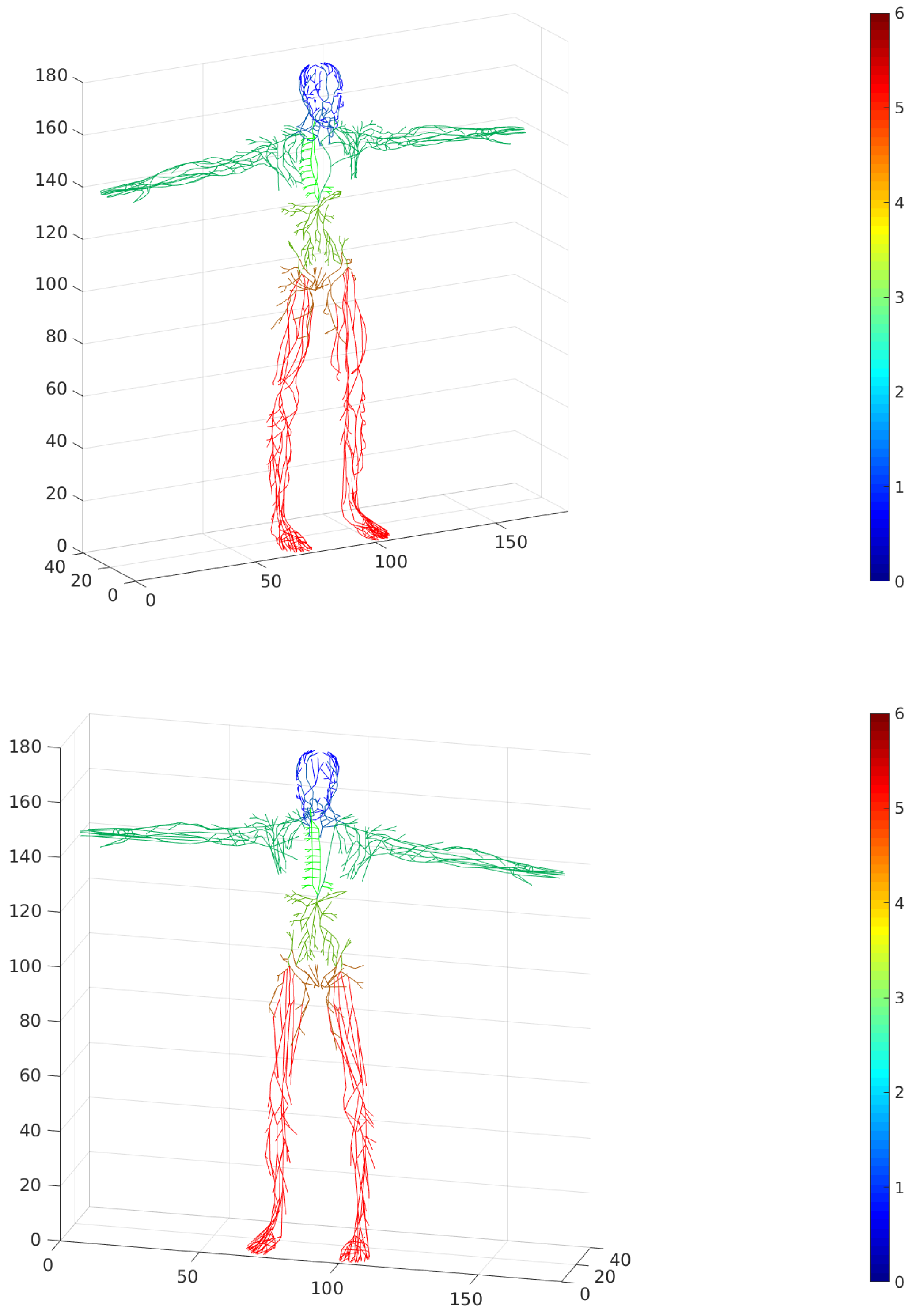
Figure 11 (left) , and all vertices corresponding to lymph nodes are marked red in
Figure 11 (right).
4.2. Topological Analysis of the Lymphatic System Network Graph
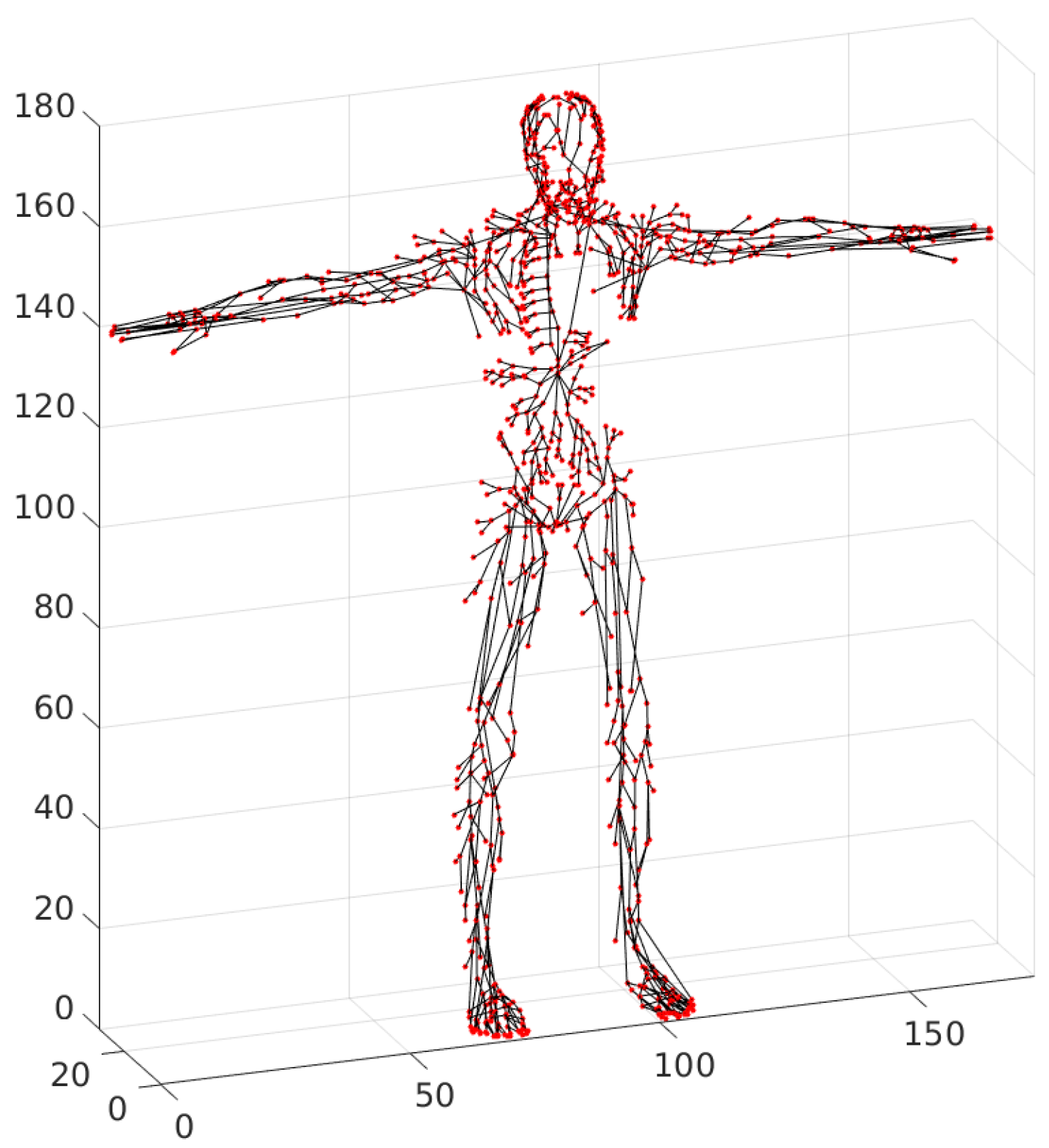
For a topological analysis of the lymphatic system network, we extracted the lymphatic network skeleton from the basis graph. To this end, we excluded all inner vertices () that were not related to the lymph nodes. Since vessel junctions can take place without engaging lymph nodes, we must take into consideration only the nodes located on the vessels. In this way, all chains of vertices and edges were replaced by a single edge (or multiple edges if there was a lymph node at the converging vessels), and each edge of the basis graph belongs to one particular edge of the skeleton.
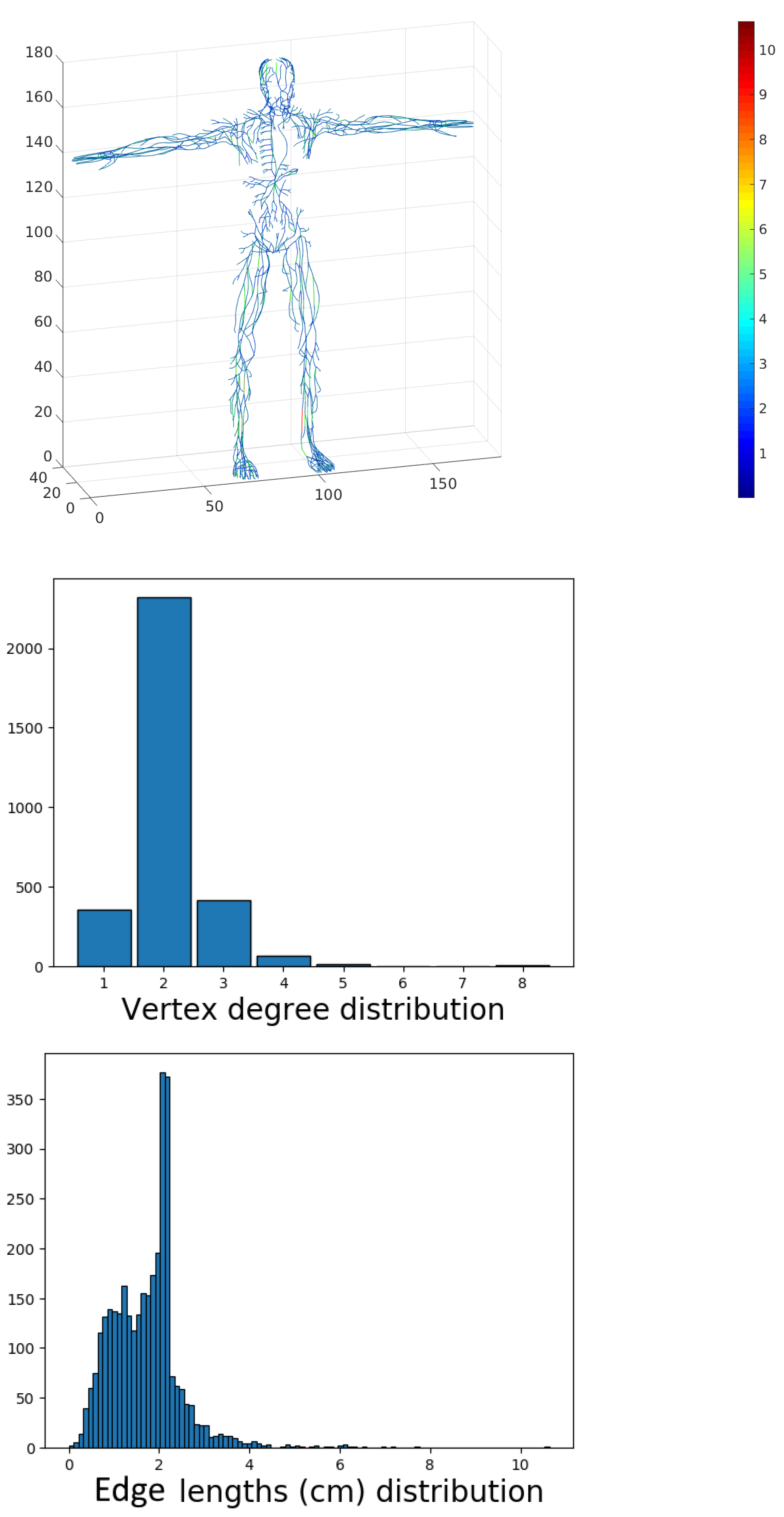
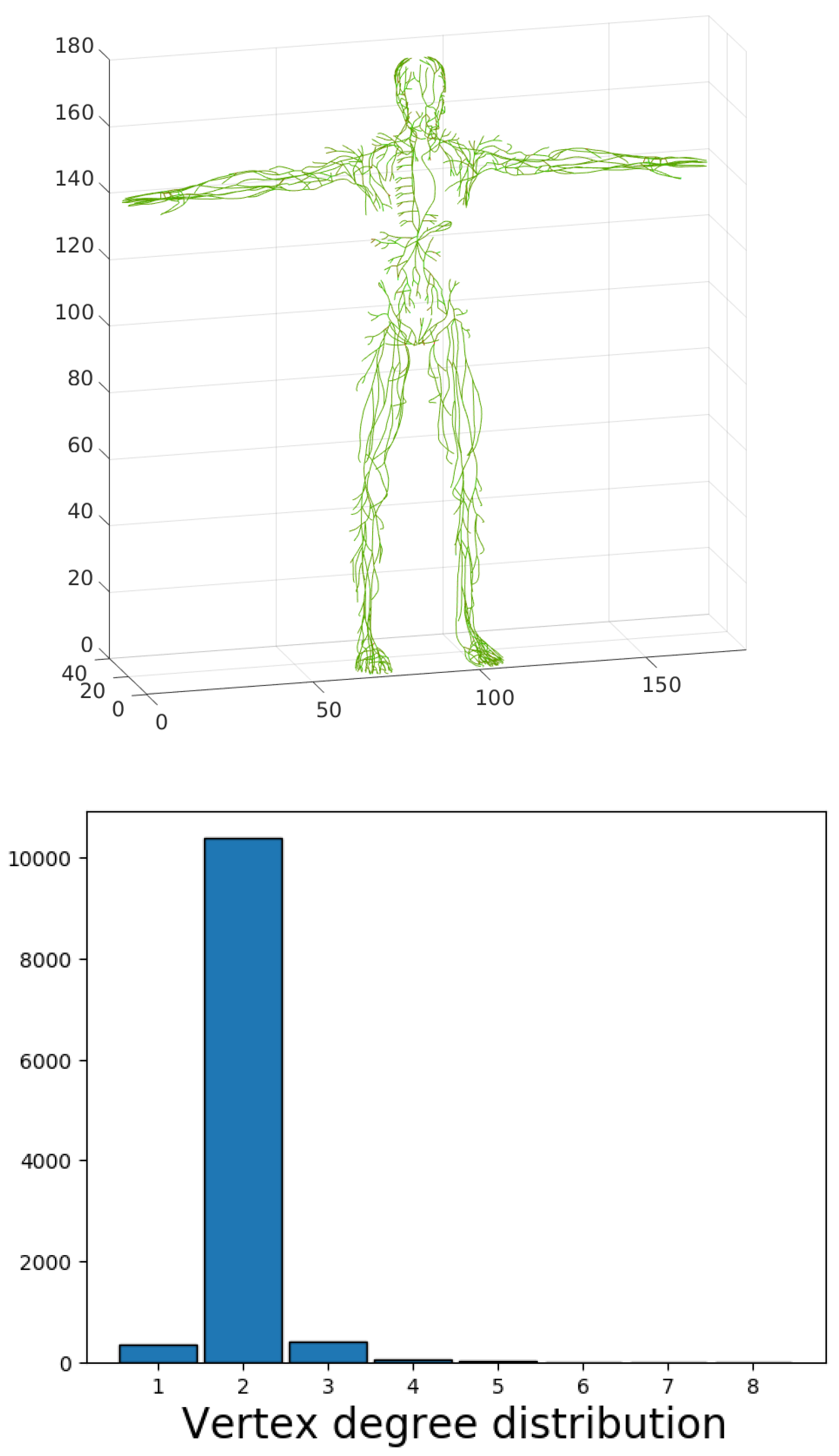
All input and output vertices, vessel junctions and lymph node-related vertices retain their positions. The number of vertices in the constructed skeleton network graph is 983, and the number of edges is 1102. Thus, one or more edge chains correspond to each vessel, as the number of edges is 1102 and the number of vessels is 443. The skeleton is depicted in
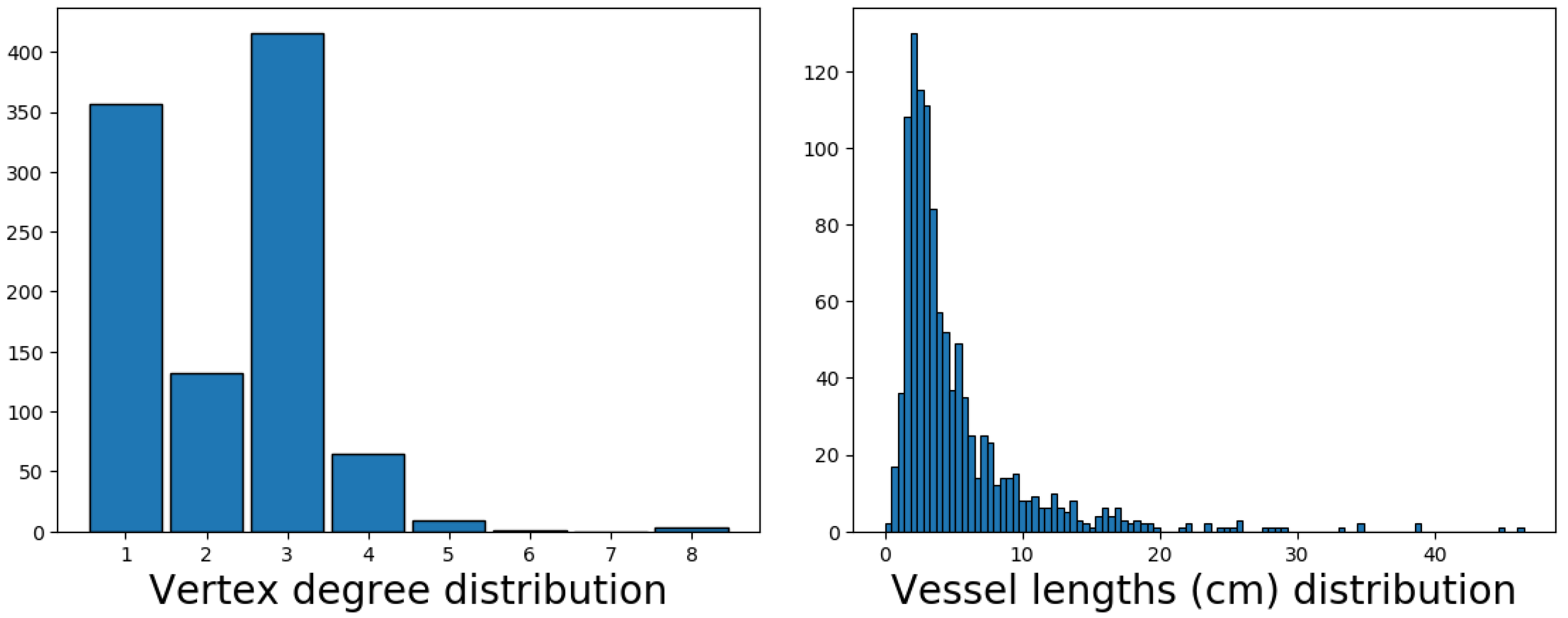
Figure 12. The constructed skeleton of the lymphatic system network graph provides a more accurate statistical characterization of the distributions of edge length and node degrees. Indeed, the appearance of the inner vertices in the network that are not the lymph nodes was produced by the above algorithm of slice-based graph generation. These points have no physiological meaning, so they should not be taken into consideration during statistical analysis. The topological characteristics are presented in
Figure 13. The model indicates the existence of nodes with degree up to eight; i.e., the sum of afferent and efferent vessels in the case of a lymph node.
5. Towards a Large-Scale 3D Modeling of the Lymphatic System
5.1. Anatomically-Distinct Parts of the Lymphatic System Model
Lymphatic vessels have certain biophysical characteristics, such as the radius and length of the lymphangions chain in a particular vessel, the wall thickness and wall tension threshold. These parameters are critical for modeling an active contraction-dependent lymph flow in the system. In general, these parameters can be regarded as common for anatomically-clustered groups of vessels (e.g., located in the head, neck, arms, chest, trunk, waist and legs). We performed an anatomy-based subdivision of vessels developed previously to unite the vessels into groups, so that fewer parameters could be used in lymph flow modeling studies.
Figure 14 demonstrates the association of the lymphatic network graph elements with anatomically-specific vessel groups for the skeleton and basis graphs.
5.2. Lymphangion-Oriented Transformations of the Lymphatics Network Graph
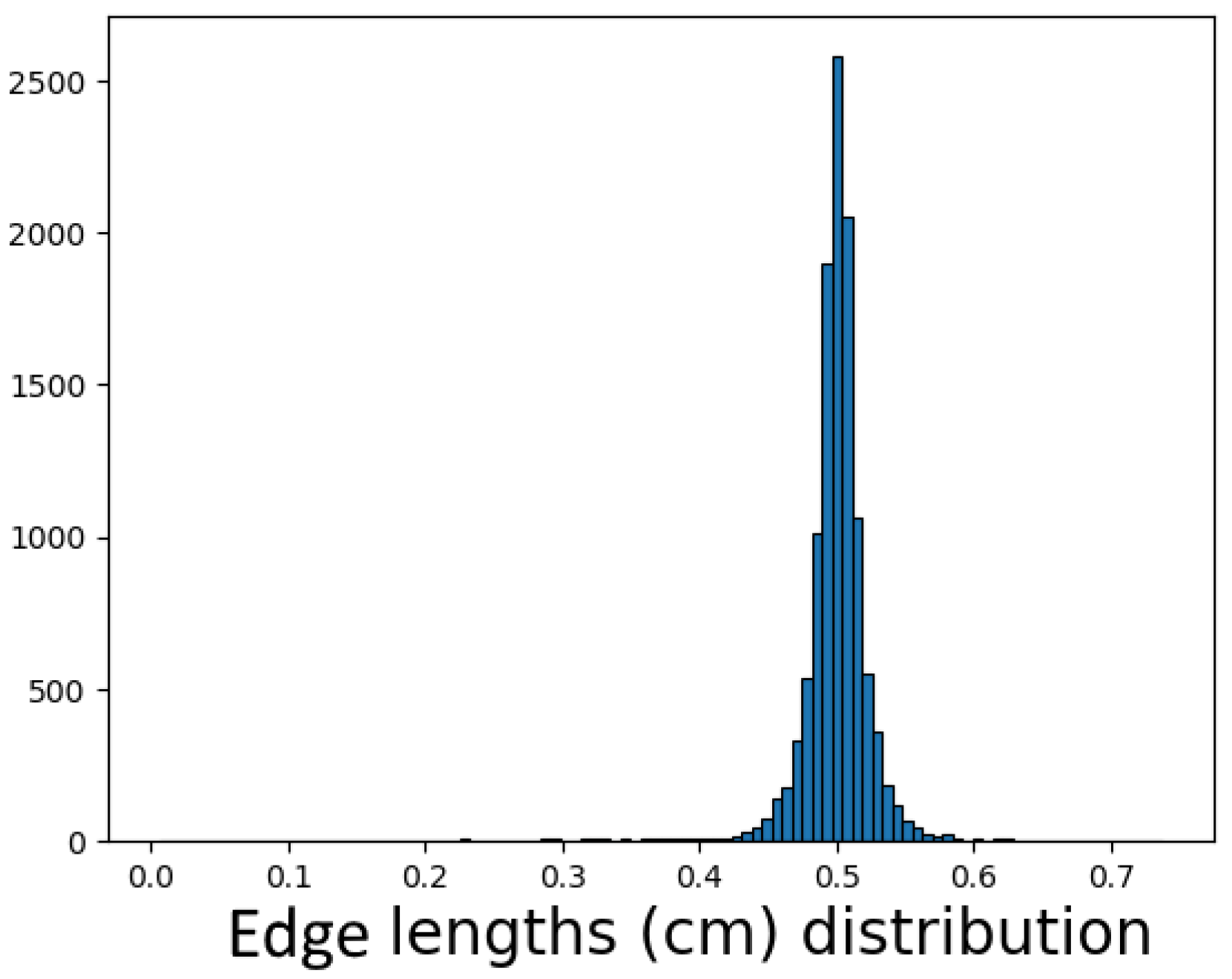
The vertices in the basis graph model appear to be unevenly distributed across the body (in space). Edge lengths are highlighted in
Figure 15, and the vertex degree and the edge lengths’ distribution are presented.
As was mentioned before, the computational algorithm determined that the placement of many vertices of is arbitrary and has no relation to anatomical ground. One can see a peak in edge (not the vessels, which consist of several edges) length distribution provided by edges of -length. It is important that all vertices are placed inside the 3D objects representing the lymphatic vessels. These vertices can be utilized as reference knots for smoothing the piecewise linear-shaped vessels via spline interpolation to be further used in the 1D network graph model. The vessel produced by smooth interpolation can be subdivided into sections by points which are separated by an equal distance from each other. This distance can be set to be the length of lymphangions. The length differs for different parts of the body and is defined ad hoc by vessel group. We will refer to the network graph constructed in such a way (i.e., with consideration of lymphangions) as the “uniform” network graph model.
The above procedure is implemented as a computational algorithm uniform graph construction as follows:
Take the skeleton of the basis network graph. Its vertices are invariant.
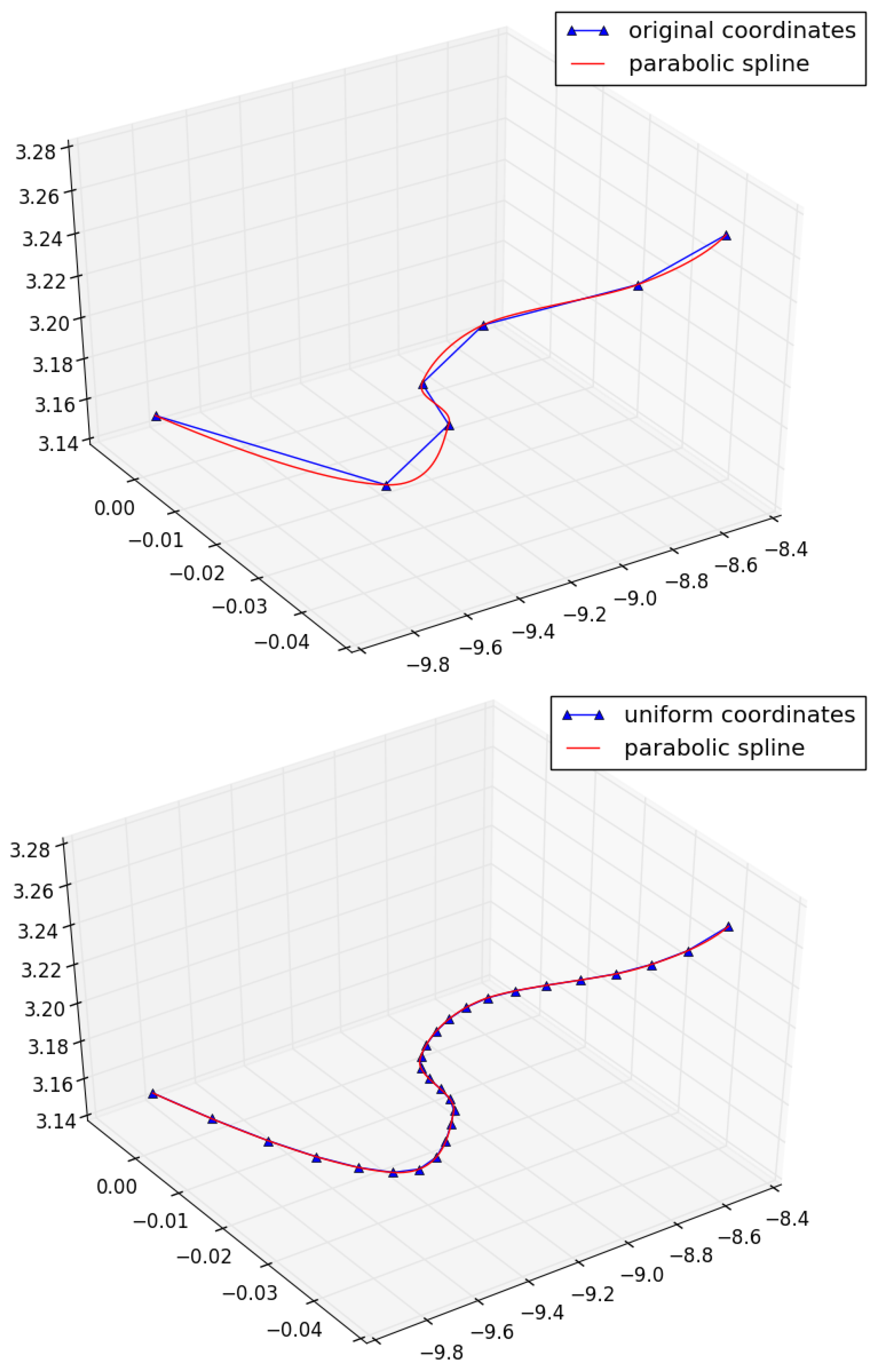
Replace each edge of the skeleton by a parabolic spline (see
Figure 16) with vertices of the basis graph specified as knots.
Place equidistant points on each spline curve (the distance is defined separately for each anatomically-specific group of vessels) and link them into a chain by consequent edges.
Replace each edge of the skeleton with a chain of equidistant vertices and edges.
As an example, we constructed a uniform network graph model of the lymphatic system; see
Figure 17 with all lengths equal to 0.5 cm.
Figure 18 shows the distribution of the vertex degree and the edge lengths for the uniform graph.
The uniform graph model of the lymphatic system provides an anatomically-consistent structure to be used in studies on lymph flow modeling.
6. Conclusions
Mathematical modeling of the functioning of the whole human body lymphatic system presents a challenge. The only available systematic modeling work goes back to the work of Reddy [
12]. In our previous studies, we addressed a number of basic issues related to computational modeling of lymph nodes [
22] and the flow processes through the conduit network of a lymph node [
23,
24]. In the present study, we make use of the available anatomical model of the human lymphatic system (from the project PlasticBoy project [
20]), which can be obtained through
http://www.plasticboy.co.uk/store/Human_Lymphatic_System_no_textures.html.
One should be aware of the non-measurement/data basis for the PlasticBoy model and should consider it just as an estimate of the structure of the lymphatic system.
The anatomical model was used to identify some basic characteristics of the lymphatic network topology. We developed algorithms to transform the reference anatomical model developed using a polygonal surface framework to various geometric models, which can be used in computational studies of lymph flow in both 3D and 1D spatial settings.
There is another 3D polygonal model of the lymphatic system by CGTrader (© CGTrader 2011–2017) at
https://www.cgtrader.com/3d-models/character/anatomy/lymphatic-system-in-human-body. Some parts of the lymphatic system in the CGTrader version appear to be somewhat more detailed (e.g., the chest and abdominal parts) and can be used in future updates of the model, whereas some (e.g., the head, cervical and brachial parts, the lower limb) are less elaborate as compared to PlasticBoy. The PlasticBoy and CGTrader versions have a similar number of polygons, being about 700,000 and 600,000, respectively. However, there is a principal difference between the models; i.e., the elements of the lymphatic system are not annotated in the CGTrader model. This implies that additional major processing is required to specify the anatomy-related network structure of the system and the system’s network graph.
Our study is the very first step at understanding the structural organization of the lymphatics system in a way that should be amenable to mathematical modeling (e.g., [
25]), similar to the angiogenesis models [
26,
27,
28]. As the lymphatic system plays a key role in tumor dissemination, tissue fluid balance and systemic infections’ development (e.g., HIV), the mechanistically-oriented modeling based on anatomically-consistent representation of the system structure should provide the research community with novel analytical tools for 3D simulation-assisted resection of lymph nodes, transplantation of lymph nodes [
29], understanding the pathogenesis of sepsis, the cure of HIV infection and drug pharmacokinetics.
Acknowledgments
This research work was supported by the Russian Foundation for Basic Research, Grant Number 17-01-00636 (biological formulation of the problem and interpretation of the results), and the Russian Science Foundation, Grant Number 15-11-00029 (computational algorithm development and the lymphatic network graph construction).
Author Contributions
G.B. and G.L. conceived of and designed the study. R.T., R.S. and G.B. developed the computational algorithms. G.L. analyzed the data. R.T., R.S., G.L. and G.B. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Randolph, G.J.; Ivanov, S.; Zinselmeyer, B.H.; Scallan, J.P. The lymphatic system: Integral roles in immunity. Annu. Rev. Immunol. 2017, 35, 31–52. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.; von der Weid, P.Y. Lymphatic system: An active pathway for immune protection. Semin. Cell Dev. Biol. 2015, 38, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Padera, T.P.; Meijer, E.F.; Munn, L.L. The lymphatic system in disease processes and cancer progression. Annu. Rev. Biomed. Eng. 2016, 18, 125–158. [Google Scholar] [CrossRef] [PubMed]
- Munn, L.L.; Padera, T.P. Imaging the lymphatic system. Microvasc. Res. 2014, 96, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Margaris, K.N.; Black, R.A. Modeling the lymphatic system: Challenges and opportunities. J. R. Soc. Interface 2012, 9, 601–612. [Google Scholar] [CrossRef] [PubMed]
- Abakumov, N.V.; Ashmetkov, I.V.; Esikova, N.B.; Koshelev, V.B.; Mukhin, S.I.; Sosnin, N.V.; Tishkin, V.F.; Favorski, A.P.; Khrulenko, A.B. Strategy of mathematical cardiovascular system modeling. Matem. Mod. 2000, 12, 106–117. (In Russian) [Google Scholar]
- Bunicheva, A.Y.; Mukhin, S.I.; Sosnin, N.V.; Favorskii, A.P. An Averaged Nonlinear Model of Hemodynamics on the Vessel Graph. Differ. Equ. 2001, 37, 949–956. [Google Scholar] [CrossRef]
- Bunicheva, A.Y.; Mukhin, S.I.; Sosnin, N.V.; Khrulenko, A.B. Mathematical modeling of quasi-one-dimensional hemodynamics. Comput. Math. Math. Phys. 2015, 55, 1381–1392. [Google Scholar] [CrossRef]
- Borzov, A.G.; Dreval, A.V.; Mukhin, S.I. Modeling of blood glucose dynamics with account of systemic loop topology. Math. Model. 2015, 27, 3–24. [Google Scholar]
- Grinberg, L.; Anor, T.; Madsen, J.R.; Yakhot, A.; Karniadakis, G.E. Large-scale simulation of the human arterial tree. Clin. Exp. Pharmacol. Physiol. 2009, 36, 194–205. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Sequeira, A.; Simakov, S.; Vassilevskii, Y.; Volpert, V. Methods of blood flow modeling. Math. Model. Nat. Phenom. 2016, 11, 1–25. [Google Scholar] [CrossRef]
- Reddy, N.P.; Krouskop, T.A.; Newell, P.H., Jr. A computer model of the lymphatic system. Comput. Biol. Med. 1977, 7, 181–197. [Google Scholar] [CrossRef]
- Mozokhina, A.S.; Mukhin, S.I.; Koshelev, V.B. Quasi-Onedimensional Approach for Modeling the Lymph Flow in the Lymphatic System; MAKS Press: Moscow, Russia, Preprint; 2017; 20p, ISBN 978-5-317-05592-9. [Google Scholar]
- Nakaoka, S.; Iwami, S.; Sato, K. Dynamics of HIV infection in lymphoid tissue network. J. Math. Biol. 2016, 72, 909–938. [Google Scholar] [CrossRef] [PubMed]
- Qatarneh, S.M.; Kiricuta, I.C.; Brahme, A.; Tiede, U.; Lind, B.K. Three-dimensional atlas of lymph node topography based on the visible human data set. Anat. Rec. Part B New Anat. 2006, 289, 98–111. [Google Scholar] [CrossRef] [PubMed]
- Kesler, C.T.; Liao, S.; Munn, L.L.; Padera, T.P. Lymphatic vessels in health and disease. Wiley Interdiscip. Rev. Syst. Biol. Med. 2013, 5, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Jeltsch, M.; Tammela, T.; Alitalo, K.; Wilting, J. Genesis and pathogenesis of lymphatic vessels. Cell Tissue Res. 2003, 314, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Zdanov, D.A. General Anatomy and Physiology of Lymphatic System; Medgis: Saint Petersburg, Russia, 1952; 336p. (In Russian) [Google Scholar]
- Borodin, Y.I.; Sapin, M.R.; Etingen, L.E.; Grigoriev, V.N.; Trufakin, V.A. Functional Anatomy of Lymph Node; Nauka: Novosobirsk, Russia, 1992; 257p. [Google Scholar]
- Plasticboy. © Plasticboy Pictures 2009 CC. Available online: http://www.plasticboy.co.uk/store/Human_Lymphatic_System_no_textures.html (accessed on 21 December 2017).
- Autodesk 3ds Max: 3D Modeling, Animation, and Rendering Software. © 2017 Autodesk Inc. Available online: https://www.autodesk.eu/products/3ds-max/overview (accessed on 21 December 2017).
- Kislitsyn, A.; Savinkov, R.; Novkovic, M.; Onder, L.; Bocharov, G. Computational approach to 3D modeling of the lymph node geometry. Computation 2015, 3, 222–234. [Google Scholar] [CrossRef]
- Savinkov, R.; Kislitsyn, A.; Watson, D.J.; van Loon, R.; Sazonov, I.; Novkovic, M.; Onder, L.; Bocharov, G. Data-driven modeling of the FRC network for studying the fluid flow in the conduit system. Eng. Appl. Artif. Intell. 2017, 62, 341–349. [Google Scholar] [CrossRef]
- Grebennikov, D.; van Loon, R.; Novkovic, M.; Onder, L.; Savinkov, R.; Sazonov, I.; Tretyakova, R.; Watson, D.J.; Bocharov, G. Critical issues in modeling lymph node physiology. Computation 2017, 5, 3. [Google Scholar] [CrossRef]
- Jamalian, S.; Davis, M.J.; Zawieja, D.C.; Moore, J.E., Jr. Network scale modeling of lymph transport and its effective pumping parameters. PLoS ONE 2016, 11, e0148384. [Google Scholar] [CrossRef] [PubMed]
- Chaplain, M.; Anderson, A. Mathematical modeling of tumour-induced angiogenesis: Network growth and structure. Cancer Treat. Res. 2004, 117, 51–75. [Google Scholar] [PubMed]
- Santos-Oliveira, P.; Correia, A.; Rodrigues, T.; Ribeiro-Rodrigues, T.M.; Matafome, P.; Rodríguez-Manzaneque, J.C.; Seiça, R.; Giräo, H.; Travasso, R.D. The force at the tip—Modeling tension and proliferation in sprouting angiogenesis. PLoS Comput. Biol. 2015, 11, e1004436. [Google Scholar] [CrossRef] [PubMed]
- McDougall, S.R.; Anderson, A.R.; Chaplain, M.A.; Sherratt, J.A. Mathematical modeling of flow through vascular networks: Implications for tumour-induced angiogenesis and chemotherapy strategies. Bull. Math. Biol. 2002, 64, 673–702. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.J.; Gardenier, J.C.; Hespe, G.E.; García Nores, G.D.; Kataru, R.P.; Ly, C.L.; Martínez-Corral, I.; Ortega, S.; Mehrara, B.J. Lymph node transplantation decreases swelling and restores immune responses in a transgenic model of lymphedema. PLoS ONE 2016, 11, e0168259. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).