Analysis, Synchronization and Circuit Design of a 4D Hyperchaotic Hyperjerk System
Abstract
:1. Introduction
2. Description of the 4D Hyperchaotic Hyperjerk System
2.1. Model of the 4D Hyperjerk System
2.2. Equilibrium Point Analysis
2.3. Dissipativity and Invariance
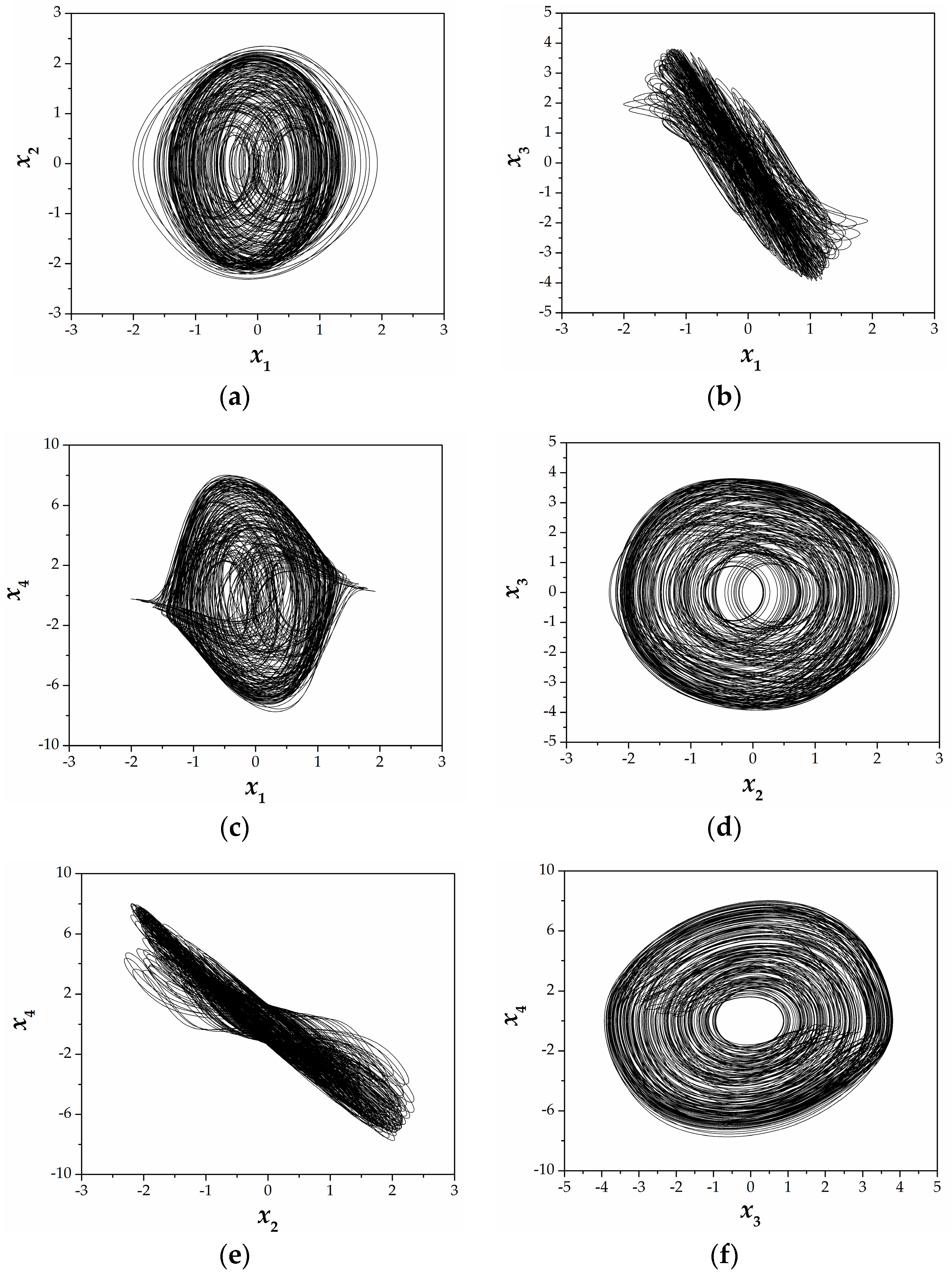
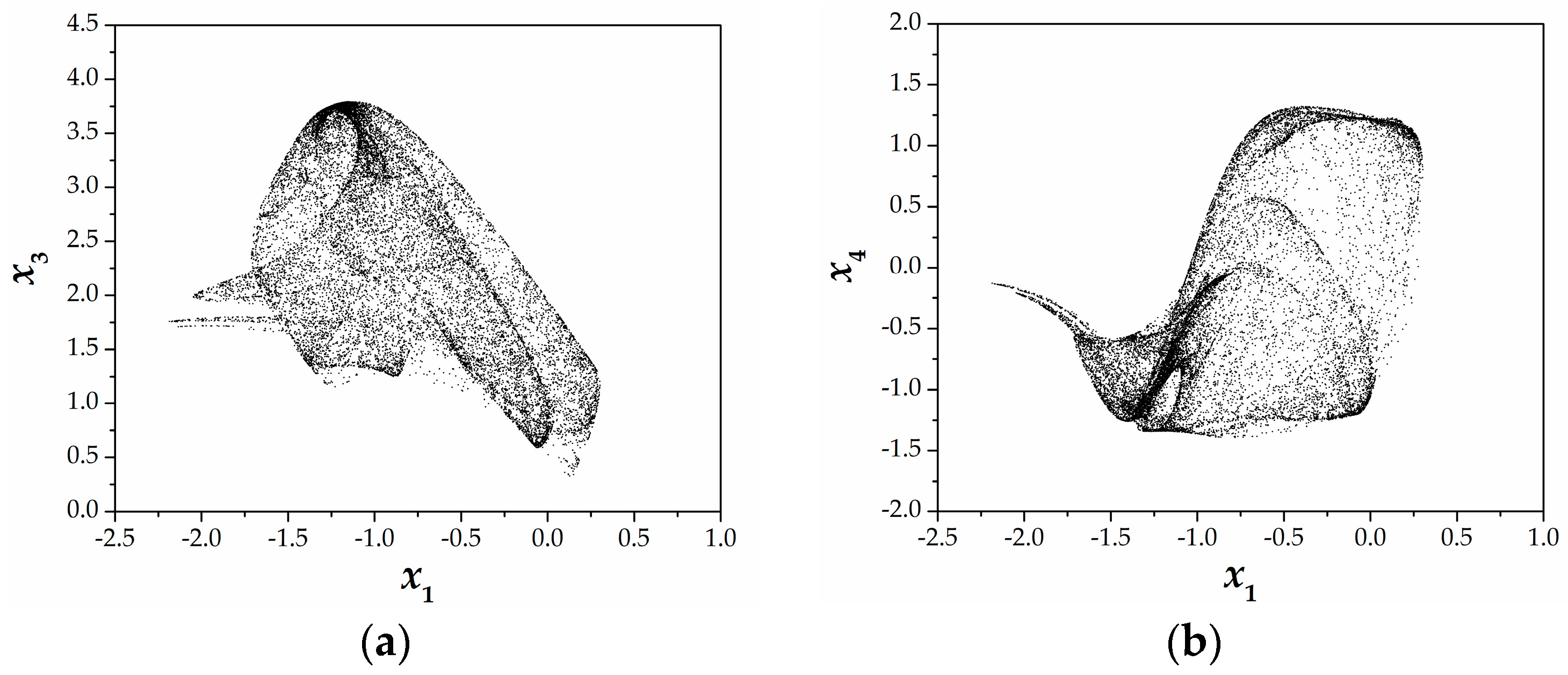
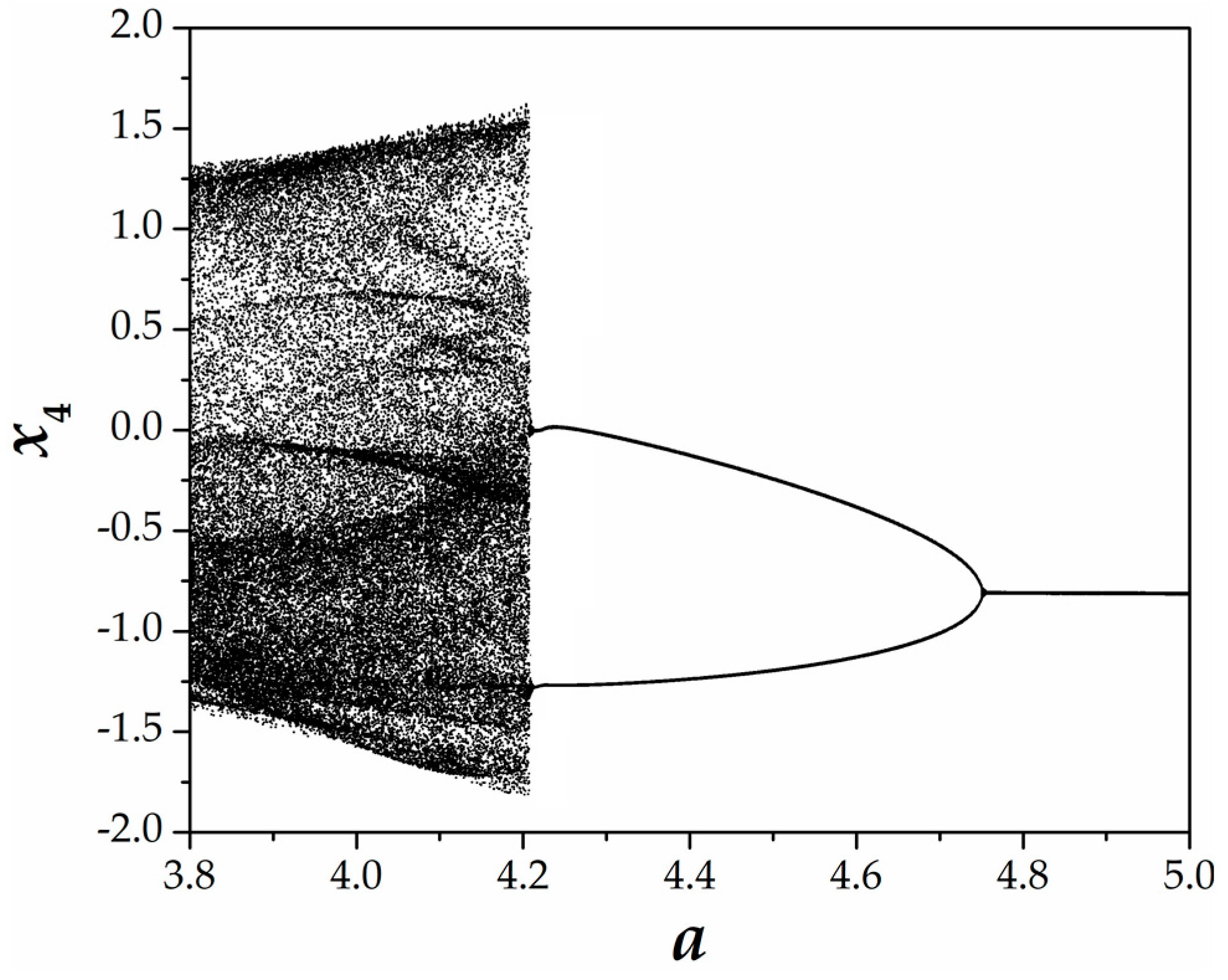
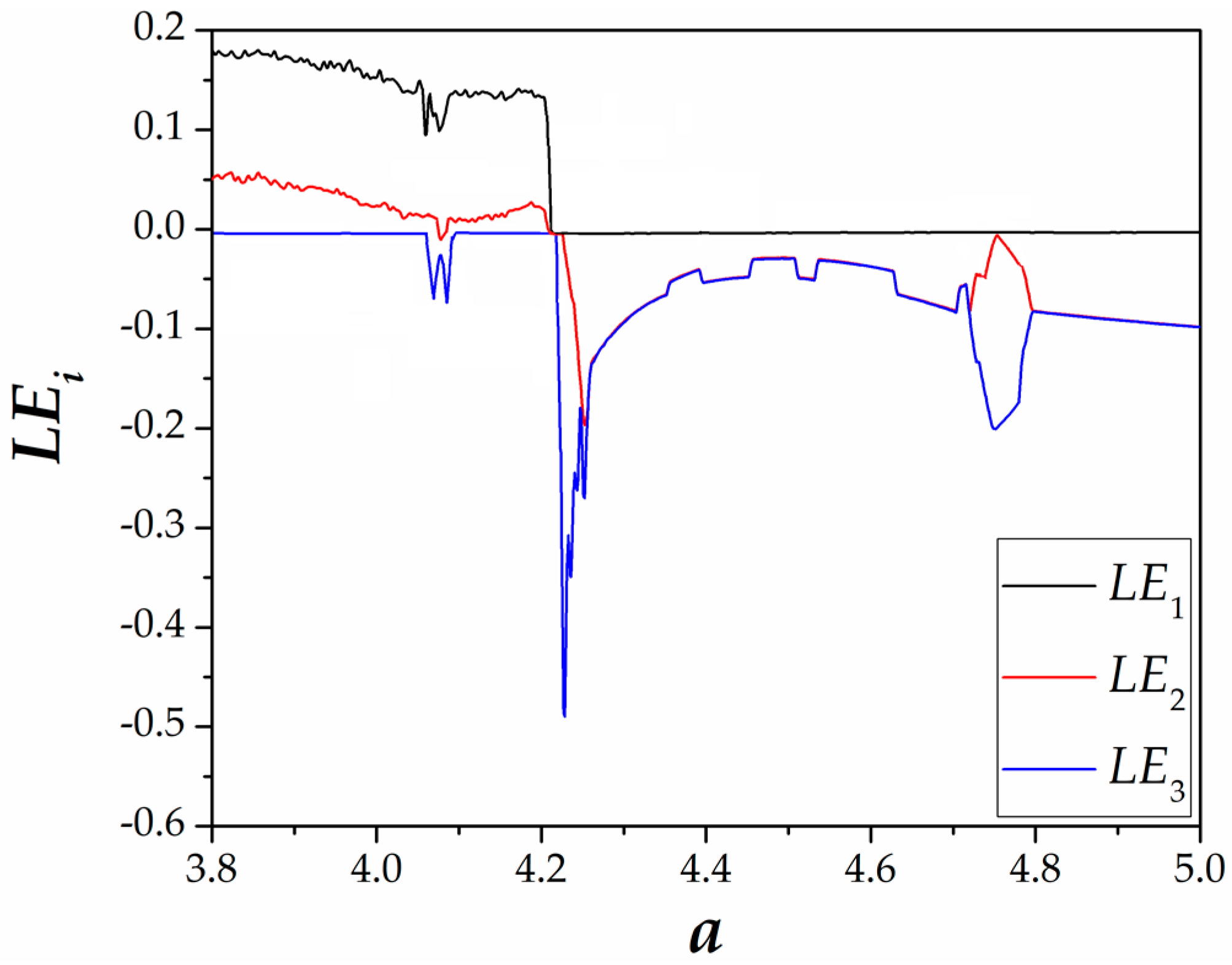
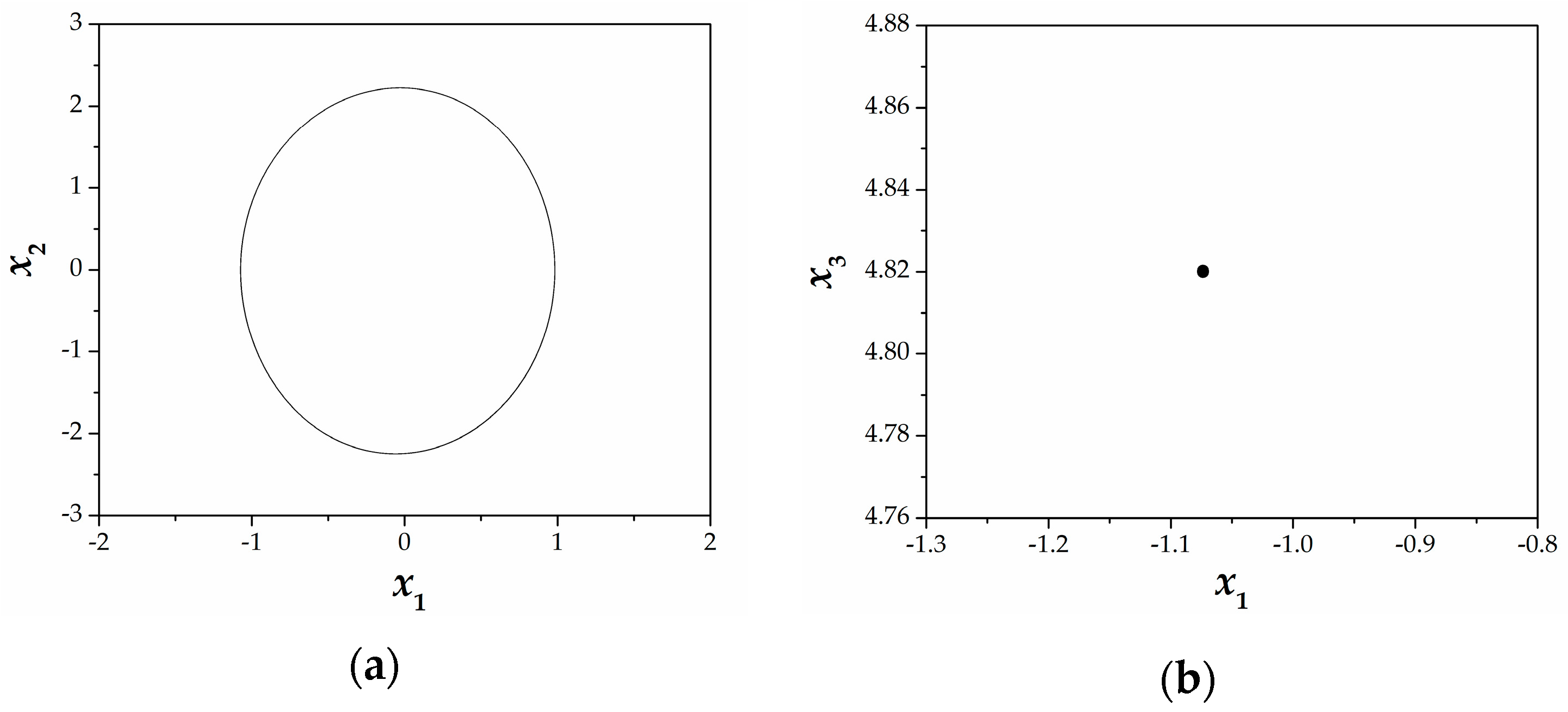
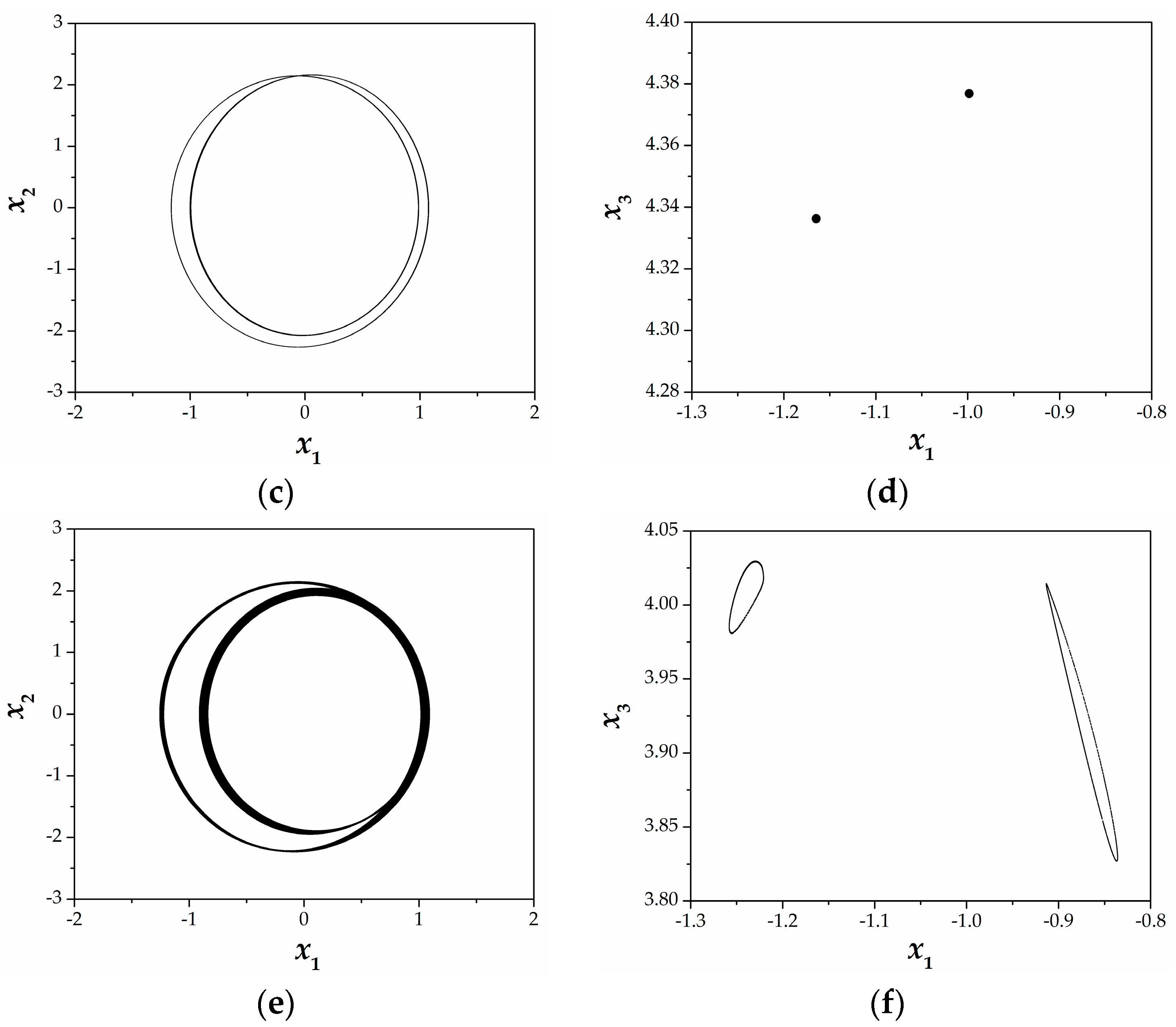
3. Analysis of the 4D Hyperjerk Dynamics
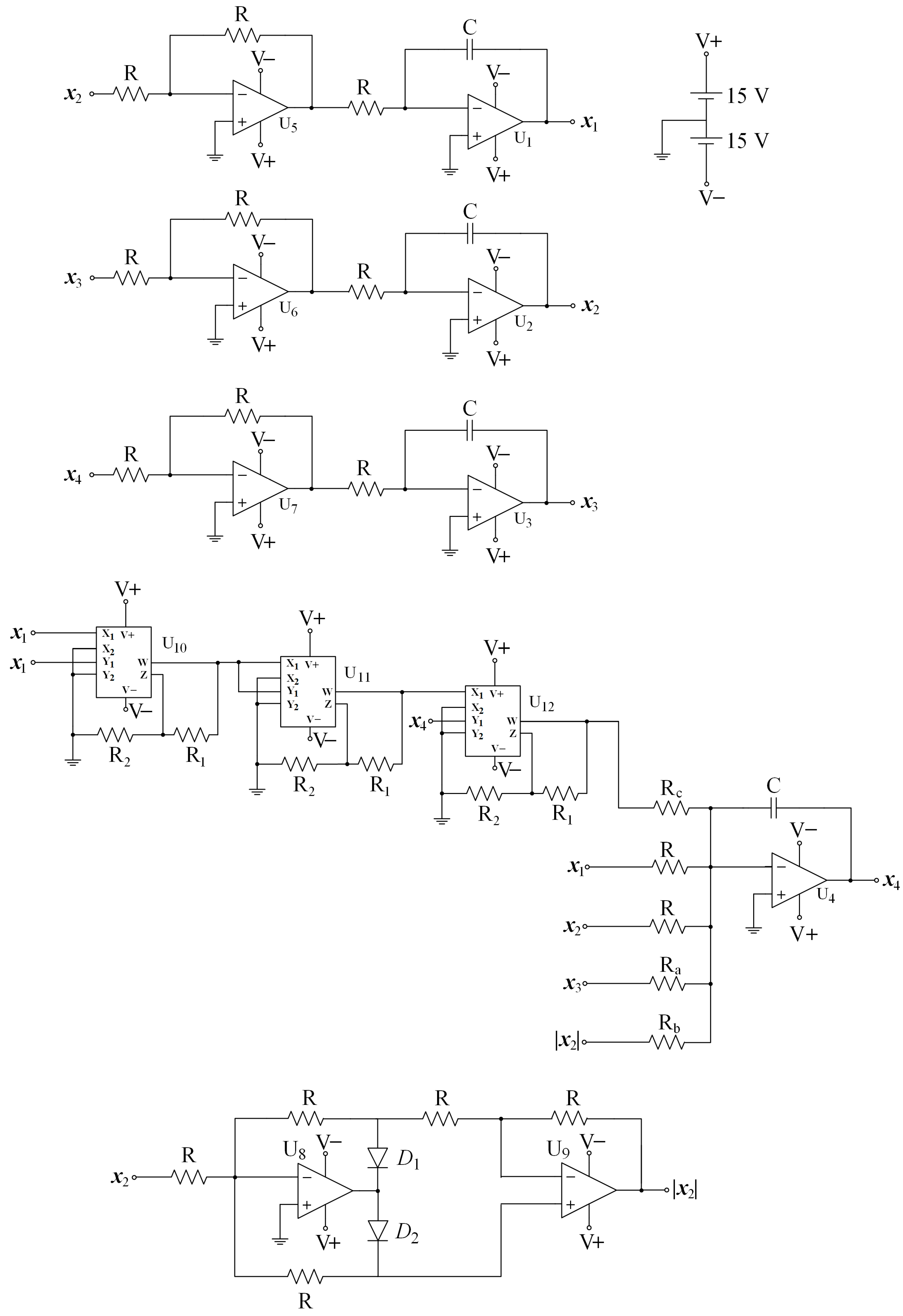
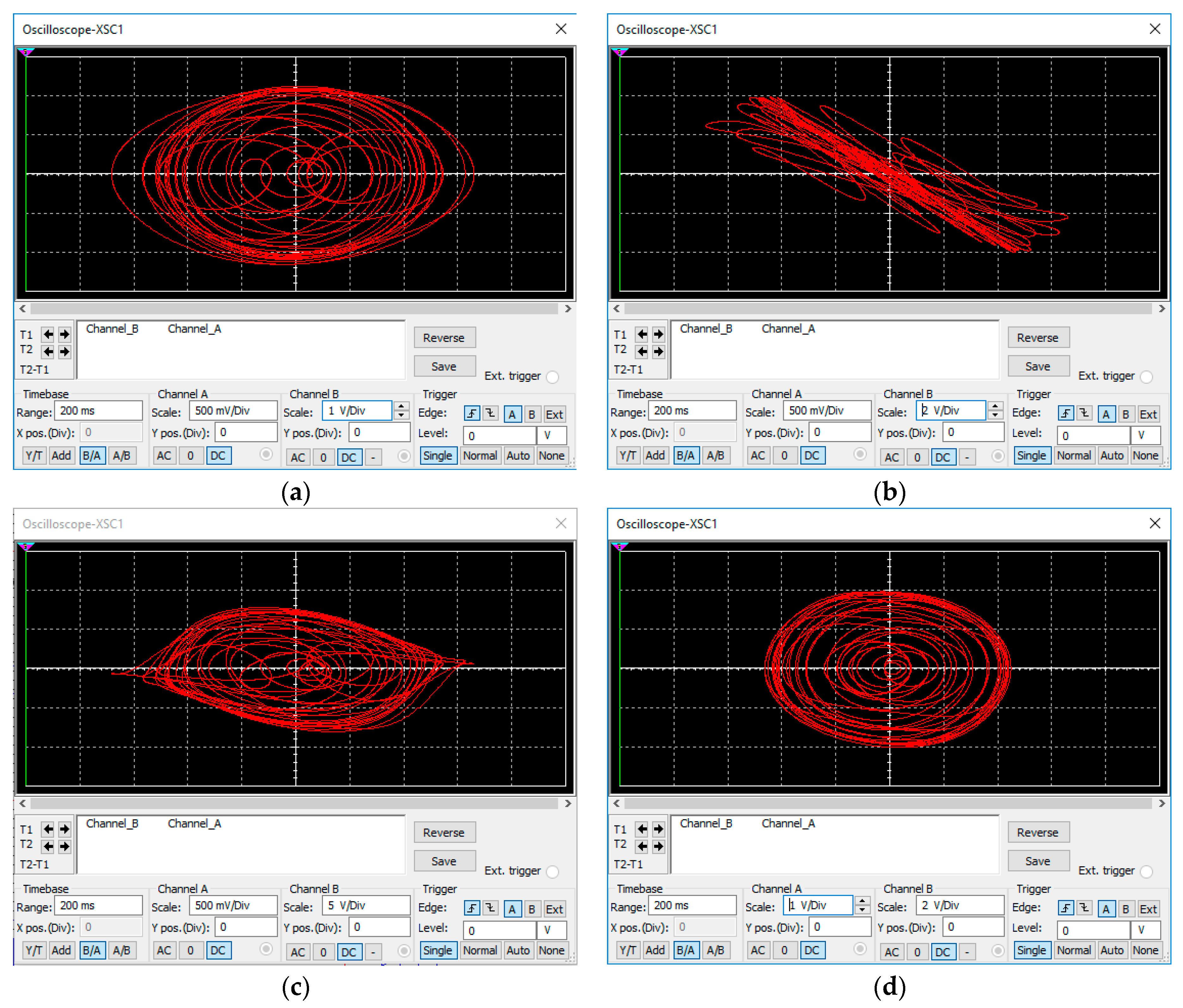
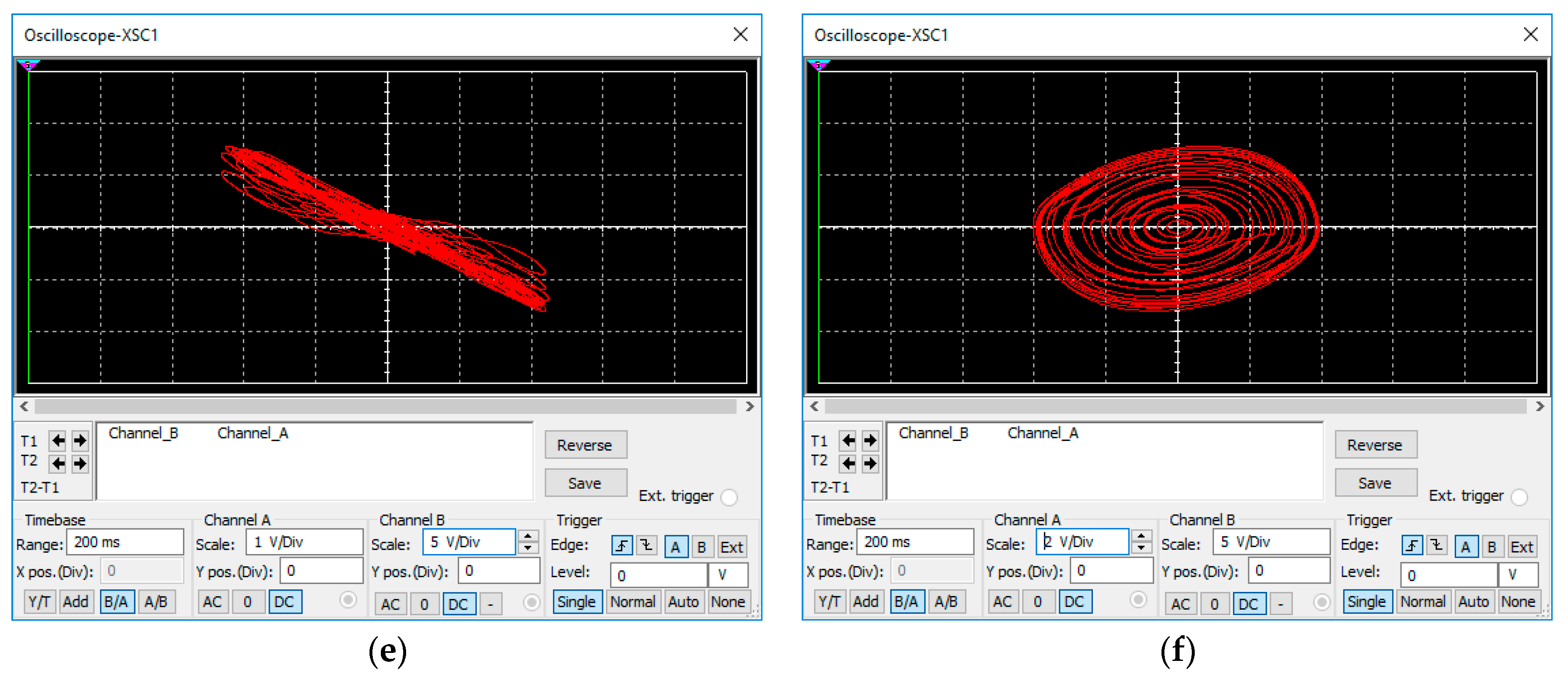
4. Circuit Realization of the Proposed System
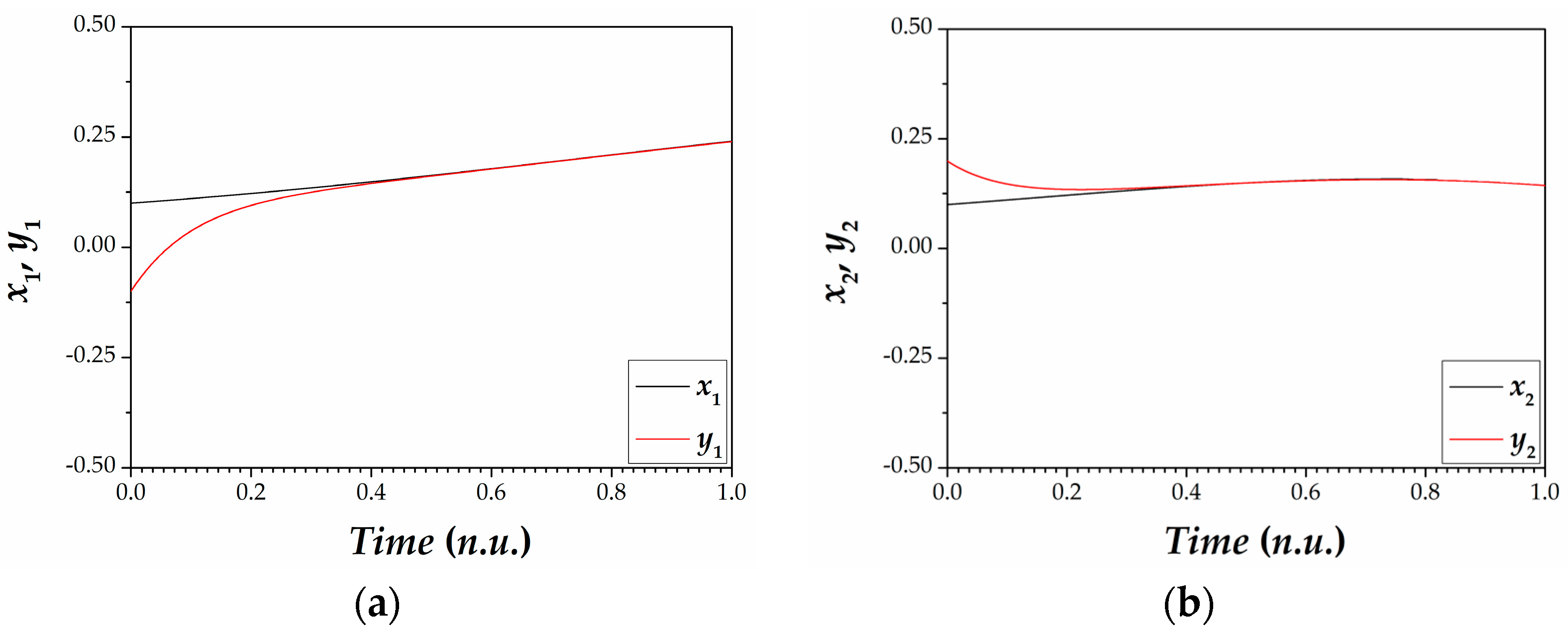
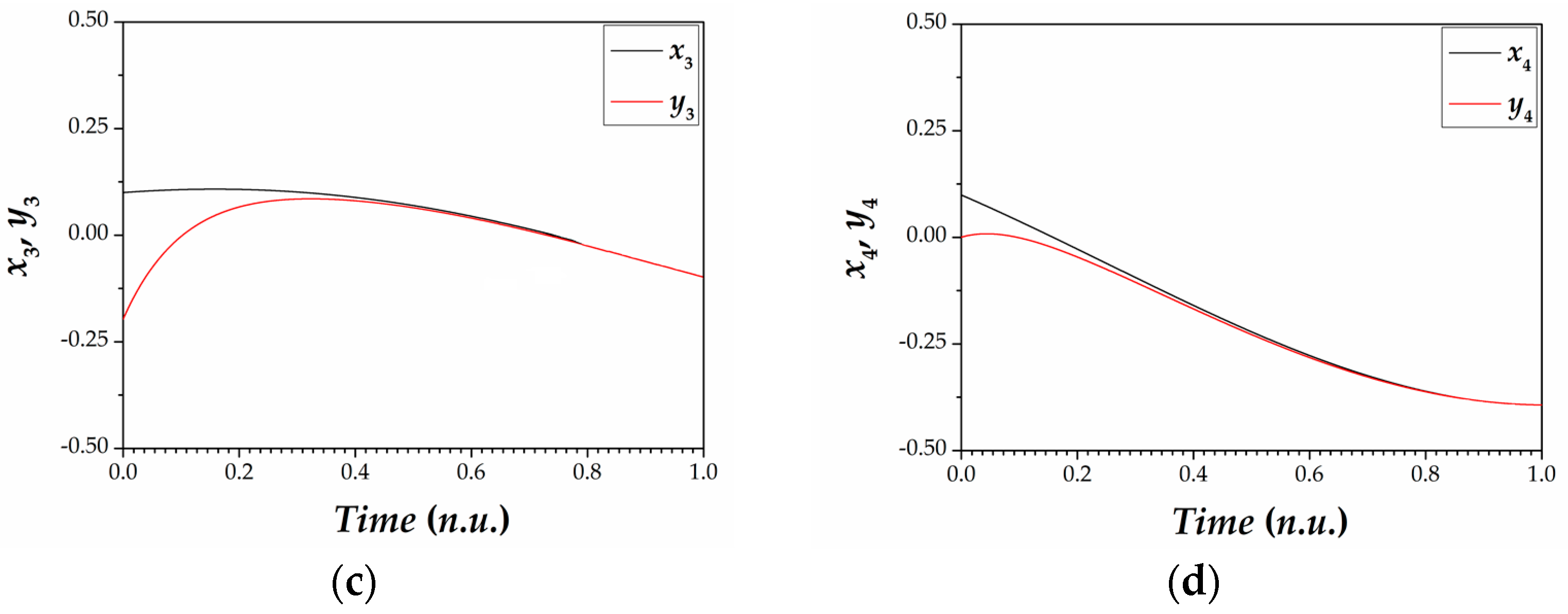
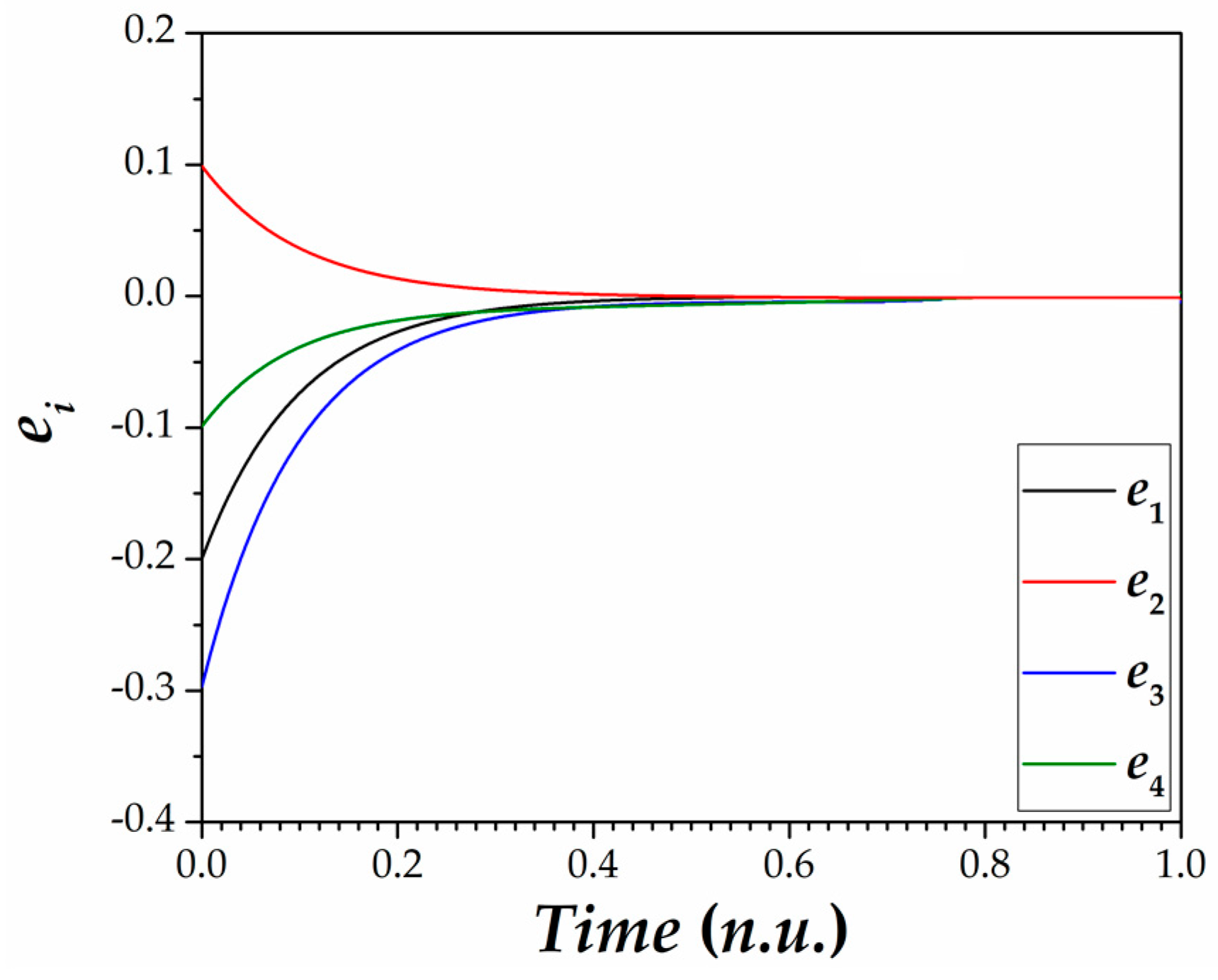
5. Synchronization Scheme
6. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rössler, O.E. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155157. [Google Scholar] [CrossRef]
- Jia, Q. Hyperchaos generated from the Lorenz chaotic system and its control. Phys. Lett. A 2007, 366, 217–222. [Google Scholar] [CrossRef]
- Chen, A.; Lu, J.; Lü, J.; Yu, S. Generating hyperchaotic Lü attractor via state feedback control. Physics A 2006, 364, 103–110. [Google Scholar] [CrossRef]
- Li, X. Modified projective synchronization of a new hyperchaotic system via nonlinear control. Commun. Theor. Phys. 2009, 52, 274–278. [Google Scholar]
- Wang, J.; Chen, Z. A novel hyperchaotic system and its complex dynamics. Int. J. Bifurcat. Chaos 2008, 18, 3309–3324. [Google Scholar] [CrossRef]
- Ghost, D.; Bhattacharya, S. Projective synchronization of new hyperchaotic system with fully unknown parameters. Nonlinear Dyn. 2010, 61, 11–21. [Google Scholar]
- Jia, Q. Projective synchronization of a new hyperchaotic Lorenz system. Phys. Lett. A 2007, 370, 40–45. [Google Scholar] [CrossRef]
- Vaidyanathan, S. A ten-term novel 4-D hyperchaotic system with three quadratic nonlinearities and its control. Int. J. Control Theory Appl. 2013, 6, 97–109. [Google Scholar]
- Schot, S.H. Jerk: The time rate of change of acceleration. Am. J. Phys. 1978, 46, 1090–1094. [Google Scholar] [CrossRef]
- Coullet, P.; Tresser, C.; Arneodo, A. A transition to stochasticity for a class of forced oscillators. Phys. Lett. A 1979, 72, 268–270. [Google Scholar] [CrossRef]
- Elhadj, Z.; Sprott, J.C. Transformation of 4-D dynamical systems to hyperjerk form. Palestine J. Math. 2013, 2, 38–45. [Google Scholar]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Feng, R.; Wang, M. Synchronization of chaotic systems via nonlinear control. Phys. Lett. A 2004, 320, 271–275. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T.; Rajagopal, K.; Alexander, P. Design and SPICE implementation of a 12-term novel hyperchaotic system and its synchronization via active control. Int. J. Model. Identif. Control 2015, 23, 267–277. [Google Scholar] [CrossRef]
- Baz, A.; Poh, S. Performance of an active control system with piezoelectric actuators. J. Sound Vib. 1988, 126, 327–343. [Google Scholar] [CrossRef]
- Åström, K.J.; Wittenmark, B. Adaptive Control; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Craig, J.J.; Hsu, P.; Sastry, S.S. Adaptive control of mechanical manipulators. Int. J. Robot. Res. 1987, 6, 16–28. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.K.; Pham, V.T. Hyperchaos, adaptive control and synchronization of a novel 5-Dhyperchaotic system with three positive Lyapunov exponents and its SPICE implementation. Arch. Control Sci. 2014, 24, 409–446. [Google Scholar]
- Yang, T.; Chua, L.O. Control of chaos using sampled-data feedback control. Int. J. Bifurcat. Chaos 1999, 9, 215–219. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Y.; Hu, J.; Nie, Z. Synchronization for general complex dynamical networks with sampled-data. Neurocomputing 2011, 74, 805–811. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, O.M. A novel criterion for delayed feedback control of time-delay chaotic systems. Chaos Soliton Fract. 2003, 17, 709–716. [Google Scholar] [CrossRef]
- Sun, J. Delay-dependent stability criteria for time-delay chaotic systems via time-delay feedback control. Chaos Soliton Fract. 2004, 21, 143–150. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Idowu, B.A.; Azar, A.T. Backstepping controller design for the global chaos synchronization of Sprott’s jerk systems. In Chaos Modeling and Control Systems Design; Azar, A.T., Vaidyanathan, S., Eds.; Springer: Basel, Switzerland, 2015; Volume 581, pp. 39–58. [Google Scholar]
- Yang, J.H.; Wu, J.; Hu, Y.M. Backstepping method and its applications to nonlinear robust control. Control Decis. 2002, 17, 641–647. [Google Scholar]
- Chen, X.; Park, J.H.; Cao, J.; Qiu, J. Sliding mode synchronization of multiple chaotic systems with uncertainties and disturbances. Appl. Math. Comput. 2017, 308, 161–173. [Google Scholar] [CrossRef]
- Chen, X.; Park, J.H.; Cao, J.; Qiu, J. Adaptive synchronization of multiple uncertain coupled chaotic systems via sliding mode control. Neurocomputing 2018, 273, 9–21. [Google Scholar] [CrossRef]
- Huang, X.; Cao, J.; & Li, Y. Takagi-Sugeno fuzzy-model-based control of hyperchaotic Chen system with norm-bounded uncertainties. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2010, 224, 223–234. [Google Scholar] [CrossRef]
- Lu, J.; Cao, J. Adaptive complete synchronization of two identical or different chaotic (hyperchaotic) systems with fully unknown parameters. Chaos 2005, 15, 043901. [Google Scholar] [CrossRef] [PubMed]
- Liao, T.L. Adaptive synchronization of two Lorenz systems. Chaos Soliton Fract. 1998, 9, 1555–1561. [Google Scholar] [CrossRef]
- Feki, M. An adaptive chaos synchronization scheme applied to secure communication. Chaos Soliton Fract. 2003, 18, 141–148. [Google Scholar] [CrossRef]
- Kocarev, L.; Parlitz, U. General approach for chaos synchronization with applications to communications. Phys. Rev. Lett. 1995, 74, 5028–5030. [Google Scholar] [CrossRef] [PubMed]
- Murali, K.; Lakshmanan, M. Secure communication using a compound signal using sampled-data feedback. J. Appl. Math. Mech. 2003, 11, 1309–1315. [Google Scholar]
- Yang, J.; Zhu, F. Synchronization for chaotic systems and chaos-based secure communications via both reduced-order and step-by-step sliding mode observers. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 926–937. [Google Scholar] [CrossRef]
- Daltzis, P.A.; Volos, C.K.; Nistazakis, H.E.; Tzanakaki, A.Α.; Tombras, G.S. Synchronization of Hyperchaotic Hyperjerk circuits with application in secure communications. In Proceedings of the 7th International Conference on “Experiments/Process/System Modeling/Simulation/Optimization—IC-EPSMSO”, Athens, Greece, 5–8 July 2017. [Google Scholar]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Trans. Circuits Syst. I 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Experimental demonstration of a chaotic cryptographic scheme. WSEAS Trans. Circuits Syst. 2006, 5, 1654–1661. [Google Scholar]
- Wang, Y.; Wang, K.W.; Liao, X.; Chen, G. A new chaos-based fast image encryption. Appl. Soft Comput. 2011, 11, 514–522. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z.; Wang, J. Chaotic image encryption based on circular substitution box and key stream buffer. Signal Process. Image Commun. 2014, 29, 902–913. [Google Scholar] [CrossRef]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 1983, 69, 32–47. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Pecora, L.M.; Carroll, T.L. Synchronizing chaotic circuits. IEEE Trans. Circuits Syst. 1991, 38, 453–456. [Google Scholar]
- Liu, Y.; Takiguchi, Y.; Davis, P.; Aida, T.; Saito, S.; Liu, J.M. Experimental observation of complete chaos synchronization in semiconductor lasers. Appl. Phys. Lett. 2002, 80, 4306–4308. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Complete synchronization of chaotic complex nonlinear systems with uncertain parameters. Nonlinear Dyn. 2010, 62, 875–882. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 1996, 76, 1804. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.M.; Chen, C.C. Phase synchronization of coupled chaotic multiple time scales systems. Chaos Soliton Fract. 2004, 20, 639–647. [Google Scholar] [CrossRef]
- Wang, Y.W.; Guan, Z.H. Generalized synchronization of continuous chaotic system. Chaos Soliton Fract. 2006, 27, 97–101. [Google Scholar] [CrossRef]
- Rulkov, N.F.; Sushchik, M.M.; Tsimring, L.S.; Abarbanel, H.D. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Sampath, S. Anti-synchronization of identical chaotic systems via novel sliding control method with application to Vaidyanathan—Madhavan chaotic system. Int. J. Control Theory Appl. 2016, 9, 85–100. [Google Scholar]
- Kim, C.M.; Rim, S.; Kye, W.H.; Ryu, J.W.; Park, Y.J. Anti-synchronization of chaotic oscillators. Phys. Lett. A 2003, 320, 39–46. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Generalized projective synchronization of novel 3-D chaotic systems with an exponential non-linearity via active and adaptive control. Int. J. Control Theory Appl. 2014, 22, 207–217. [Google Scholar]
- Sivaperumal, S. Hybrid synchronization of identical chaotic systems via novel sliding control with application to hyperchaotic Vaidyanathan—Volos system. Int. J. Control Theory Appl. 2016, 9, 261–278. [Google Scholar]
- Park, J.H. Adaptive synchronization of hyperchaotic Chen system with uncertain parameters. Chaos Soliton Fract. 2005, 26, 959–964. [Google Scholar] [CrossRef]
- Chlouverakis, K.E.; Sprott, J.C. Chaotic hyperjerk systems. Chaos Soliton Fract. 2006, 28, 739–746. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Physica D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: Cambridge, MA, USA, 1994. [Google Scholar]
- Daltzis, P.; Vaidyanathan, S.; Pham, V.T.; Volos, C.; Nistazakis, E.; Tombras, G. Hyperchaotic attractor in a novel hyperjerk system with two nonlinearities. Circ. Syst. Signal Proc. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.K.; Pham, V.T.; Madhavan, K. Analysis, adaptive control and synchronization of a novel 4-D hyperchaotic hyperjerk system and its SPICE implementation. Arch. Control Sci. 2015, 25, 135–158. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Analysis, adaptive control and synchronization of a novel 4-D hyperchaotic hyperjerk system via backstepping control method. Arch. Control Sci. 2016, 26, 311–338. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.K.; Jafari, S.; Wang, X. A chaotic hyperjerk system based on memristive device. In Advances and Applications in Chaotic Systems; Springer: Berlin, Germany, 2016; pp. 39–58. [Google Scholar]
- Wang, X.; Vaidyanathan, S.; Volos, C.K.; Pham, V.T.; Kapitaniak, T. Dynamics, circuit realization, control and synchronization of a hyperchaotic hyperjerk system with coexisting attractors. Nonlinear Dyn. 2017, 89, 1673–1687. [Google Scholar] [CrossRef]
- Vaidyanathan, S. A conservative hyperchaotic hyperjerk system based on memristive device. In Advances in Memristors, Memristive Devices and Systems; Springer: Berlin, Germany, 2017; pp. 393–423. [Google Scholar]
- Yalcin, M.E.; Suykens, J.A.K.; Vandewalle, J. True random bit generation from a double-scroll attractor. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1395–1404. [Google Scholar] [CrossRef]
- Ergun, S.; Ozoguz, S. Truly random number generators based on a nonautonomous chaotic oscillator. AEÜ Int. J. Electron. Commun. 2007, 61, 235–242. [Google Scholar] [CrossRef]
- Cavusoglu, U.; Akgul, A.; Kacar, S.; Pehlivan, I.; Zengin, A. A novel chaos-based encryption algorithm over TCP data packet for secure communication. Secur. Commun. Netw. 2016, 9, 1285–1296. [Google Scholar] [CrossRef]
- Kacar, S. Analog circuit and microcontroller based RNG application of a new easy realizable 4D chaotic system. Optik 2016, 127, 9551–9561. [Google Scholar] [CrossRef]
- Lin, Z.; Yu, S.; Li, C.; Lü, J.; Wang, Q. Design and smartphone-based implementation of a chaotic video communication scheme via wan remote transmission. Int. J. Bifurcat. Chaos 2016, 26, 1650158. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Li, Y. Audio encryption scheme by confusion and diffusion based on multi-scroll chaotic system and one-time keys. Optik 2016, 127, 7431–7438. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. A chaotic path planning generator for autonomous mobile robots. Robot. Auton. Syst. 2012, 60, 651–656. [Google Scholar] [CrossRef]
- Varnosfaderani, I.S.; Sabahi, M.F.; Ataei, M. Joint blind equalization and detection in chaotic communication systems using simulation-based methods. AEÜ Int. J. Electron. Commun. 2015, 69, 1445–1452. [Google Scholar] [CrossRef]
- Abdullah, A.H.; Enayatifar, R.; Lee, M. A hybrid genetic algorithm and chaotic function model for image encryption. AEÜ Int. J. Electron. Commun. 2012, 66, 806–816. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L.; Wei, X. Improved algorithm for image encryption based on DNA encoding and multi-chaotic maps. AEÜ Int. J. Electron. Commun. 2014, 69, 186–1892. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. Self-adaptive permutation and combined global diffusion for chaotic color image encyption. AEÜ Int. J. Electron. Commun. 2014, 68, 361–368. [Google Scholar] [CrossRef]
- Min, L.; Yang, X.; Chen, G.; Wang, D. Some polynomial chaotic maps without equilibria and an application to image encryption with avalanche effects. Int. J. Bifurcat. Chaos 2015, 25, 1550124. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Ozoguz, S. Chaos in a pulse-excited resonator with self feedback. Electron. Lett. 2003, 39, 831–833. [Google Scholar] [CrossRef]
- Piper, J.R.; Sprott, J.C. Simple autonomous chaotic circuits. IEEE Trans. Circuits Syst. II Exp. Briefs 2010, 57, 730–734. [Google Scholar] [CrossRef]
- Trejo-Guerra, R.; Tlelo-Cuautle, E.; Jimenez-Fuentes, J.M.; Sanchez-Lopez, C.; Munoz-Pacheco, J.M.; Espinosa-Flores-Verdad, G.; Rocha-Perez, J.M. Integrated circuit generating 3- and 5-scroll attractors. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4328–4335. [Google Scholar] [CrossRef]
- Trejo-Guerra, R.; Tlelo-Cuautle, E.; Jimenez-Fuentes, J.M.; Munoz-Pacheco, J.M.; Sanchez-Lopez, C. Multi-scroll floating gate-based integrated chaotic oscillator. Int. J. Circuit Theory Appl. 2013, 41, 831–843. [Google Scholar] [CrossRef]
- Pano-Azucena, A.D.; Rangel-Magdaleno, J.J.; Tlelo-Cuautle, E.; Quintas-Valles, A.J. Arduino-based chaotic secure communication system using multi-directional multi-scroll chaotic oscillators. Nonlinear Dyn. 2017, 87, 2203–2217. [Google Scholar] [CrossRef]
- Koyuncu, I.; Ozcerit, A.T.; Pehlivan, I. Implementation of FPGA-based real time novel chaotic oscillator. Nonlinear Dyn. 2014, 77, 49–59. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.J.; Pano-Azucena, A.D.; Obeso-Rodelo, P.J.; Nunez-Perez, J.C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Rangel-Magdaleno, J.J.; Carbajal-Gomez, V.H.; Rodriguez-Gomez, G. Generating a 50-scroll chaotic attractor at 66 MHz by using FPGAs. Nonlinear Dyn. 2016, 85, 2143–2157. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
| Reported Work | Maximal Lypunov Exponent | Kaplan–Yorke Dimension |
|---|---|---|
| [53] | 0.1320 | 3.1300 |
| [57] | 0.1555 | 3.1171 |
| [59] | 0.1448 | 3.1573 |
| [60] | 0.1422 | 3.1348 |
| [61] | 0.0730 | 3.1300 |
| [62] | 0.1250 | 3.1325 |
| [63] | 0.1320 | 3.1300 |
| This work | 0.1809 | 3.1405 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daltzis, P.A.; Volos, C.K.; Nistazakis, H.E.; Tsigopoulos, A.D.; Tombras, G.S. Analysis, Synchronization and Circuit Design of a 4D Hyperchaotic Hyperjerk System. Computation 2018, 6, 14. https://doi.org/10.3390/computation6010014
Daltzis PA, Volos CK, Nistazakis HE, Tsigopoulos AD, Tombras GS. Analysis, Synchronization and Circuit Design of a 4D Hyperchaotic Hyperjerk System. Computation. 2018; 6(1):14. https://doi.org/10.3390/computation6010014
Chicago/Turabian StyleDaltzis, Petros A., Christos K. Volos, Hector E. Nistazakis, Andreas D. Tsigopoulos, and George S. Tombras. 2018. "Analysis, Synchronization and Circuit Design of a 4D Hyperchaotic Hyperjerk System" Computation 6, no. 1: 14. https://doi.org/10.3390/computation6010014
APA StyleDaltzis, P. A., Volos, C. K., Nistazakis, H. E., Tsigopoulos, A. D., & Tombras, G. S. (2018). Analysis, Synchronization and Circuit Design of a 4D Hyperchaotic Hyperjerk System. Computation, 6(1), 14. https://doi.org/10.3390/computation6010014







