Deformable Cell Model of Tissue Growth
Abstract
1. Introduction
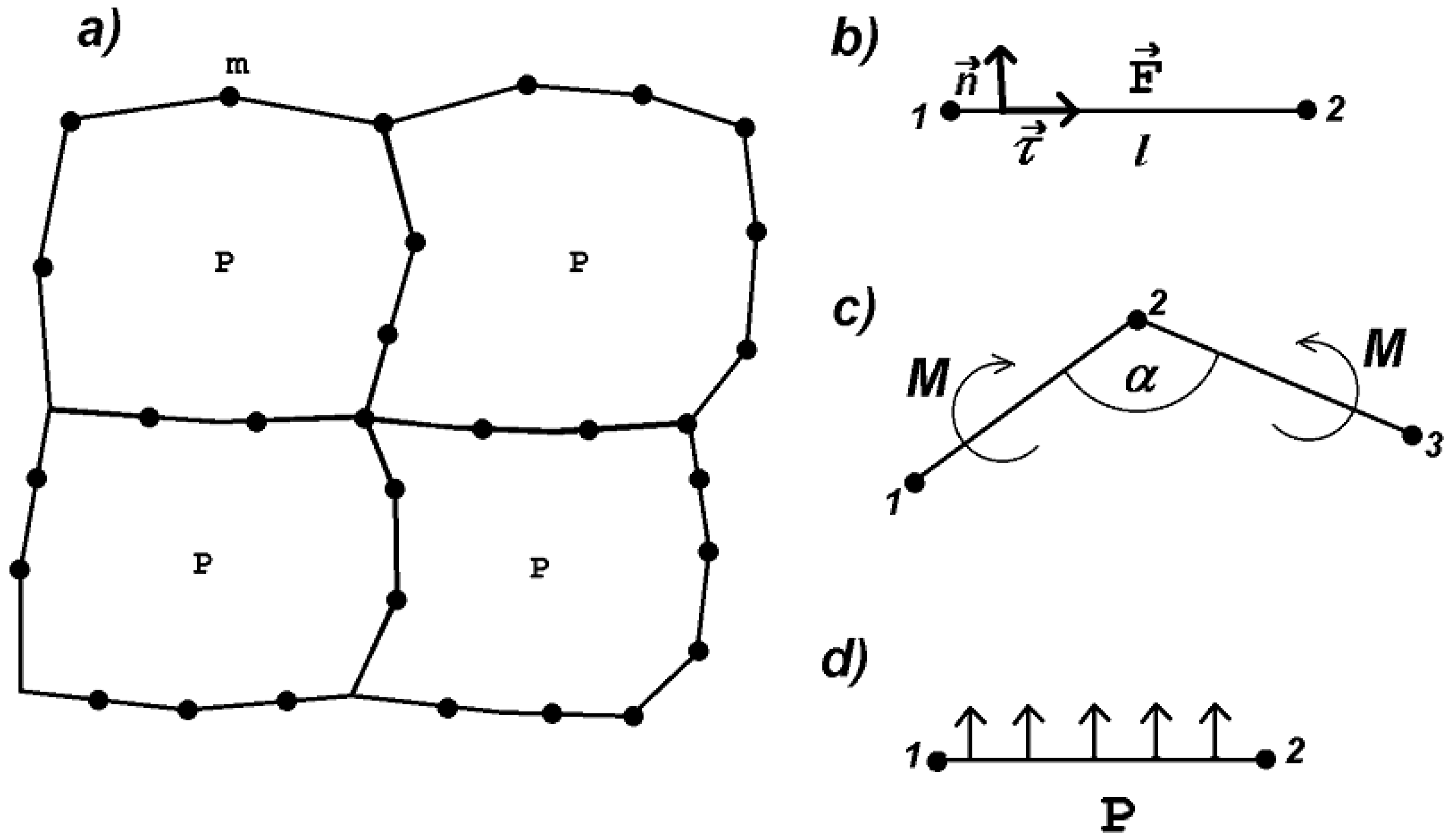
2. Deformable Cell Model
2.1. Forces
- If the length of a side becomes twice as large as its initial length , then an additional vertex is introduced in the middle of the side. At the moment of side division, the stretching force is preserved. Hence the number of vertices depends on cell deformation. This allows us to better describe cell shape in the case of large deformations.
- If the length l of a side becomes sufficiently large, that is , with some , , then the initial length increases irreversibly in such a way that it satisfies the equality . In this case, if the stretching force is removed, then the spring will not return to its initial length but to some greater length. This corresponds to the irreversible deformation of the cell wall when it grows. Here, is a material parameter characterizing plastic deformation observed for biological tissues. In the simulations presented below, we set .
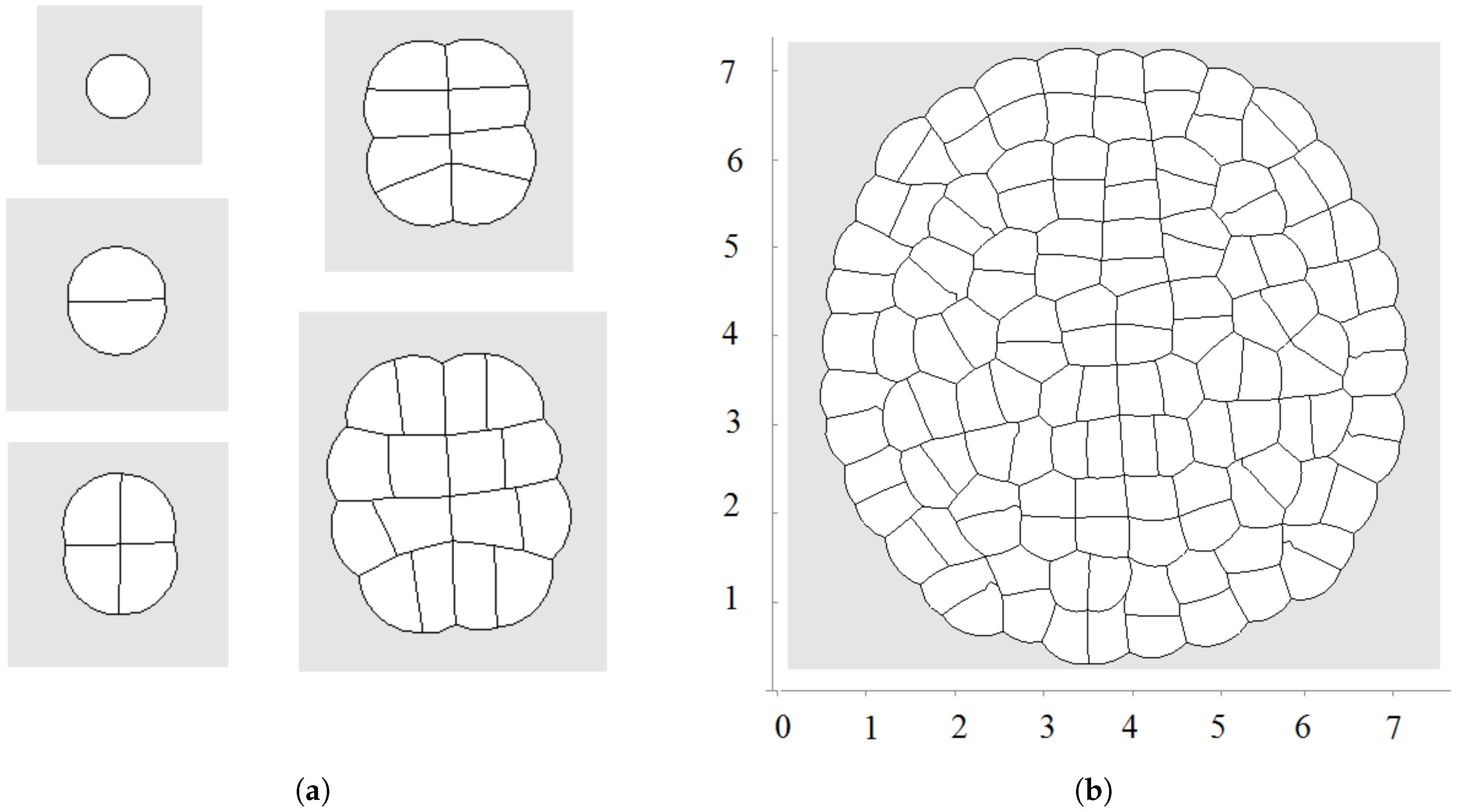
2.2. Cell Growth and Division
2.2.1. Cell Growth
2.2.2. Cell Division
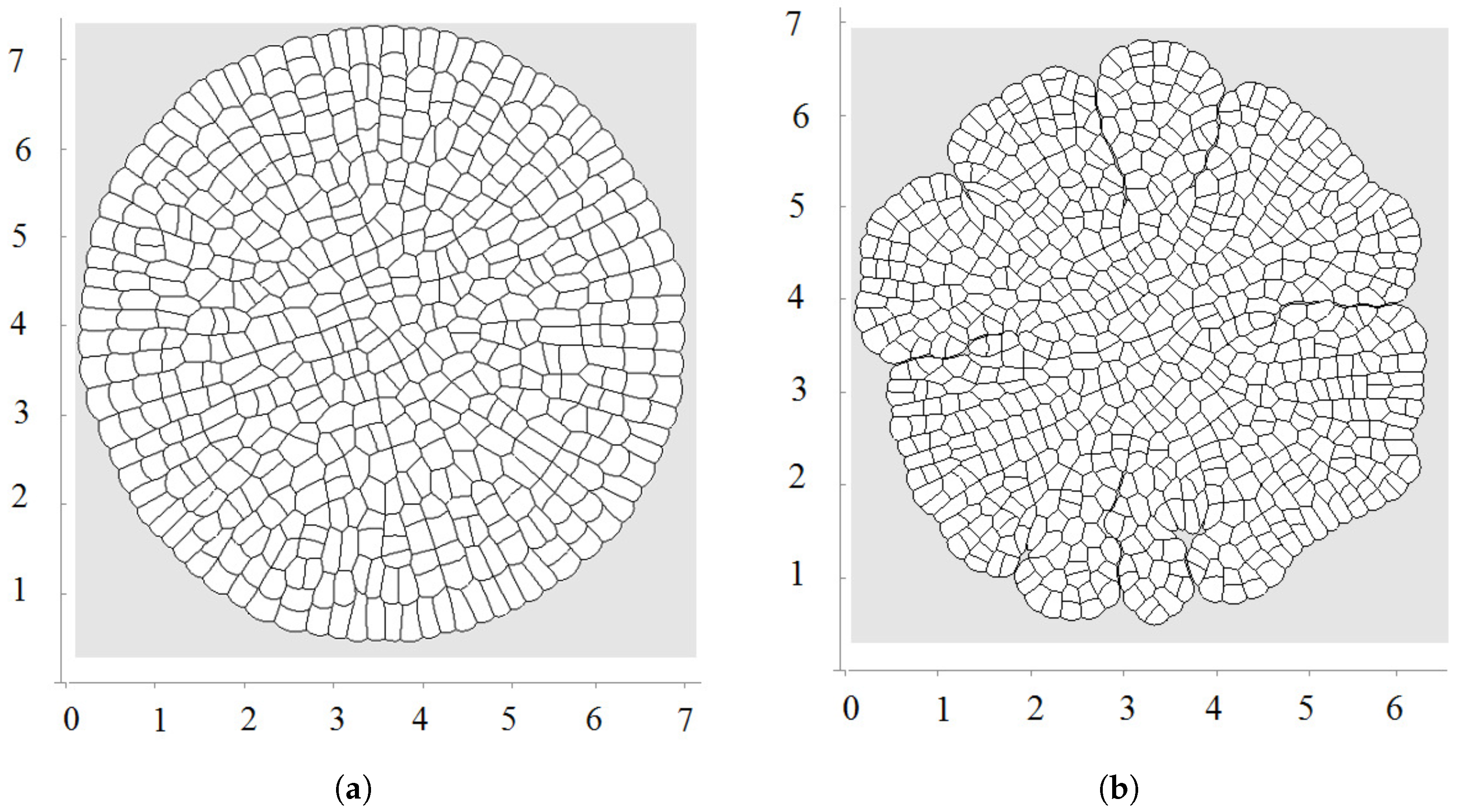
3. Numerical Modelling of Tissue Growth
3.1. All Cells Grow and Divide
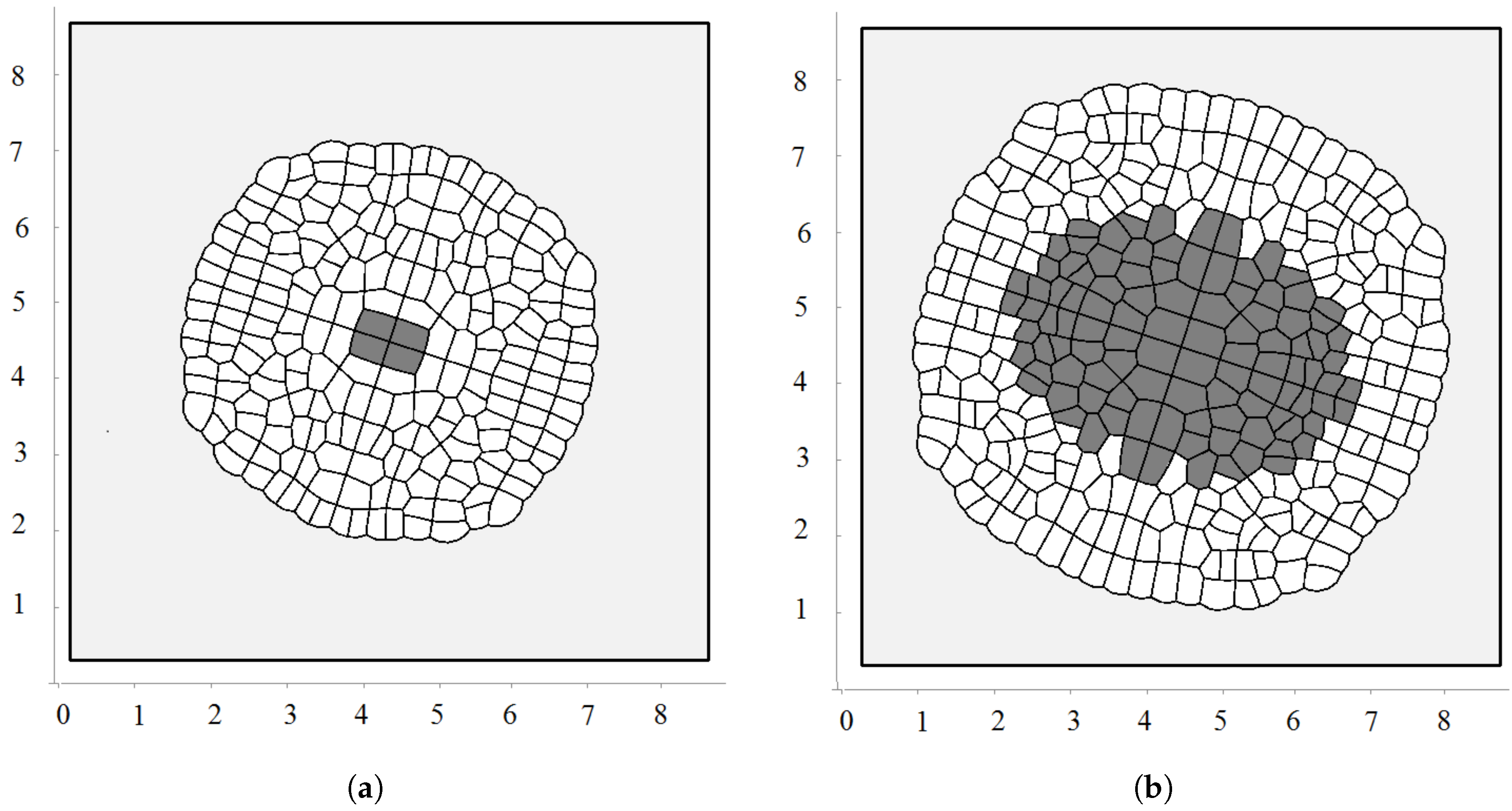
3.2. Pressure-Dependent Proliferation
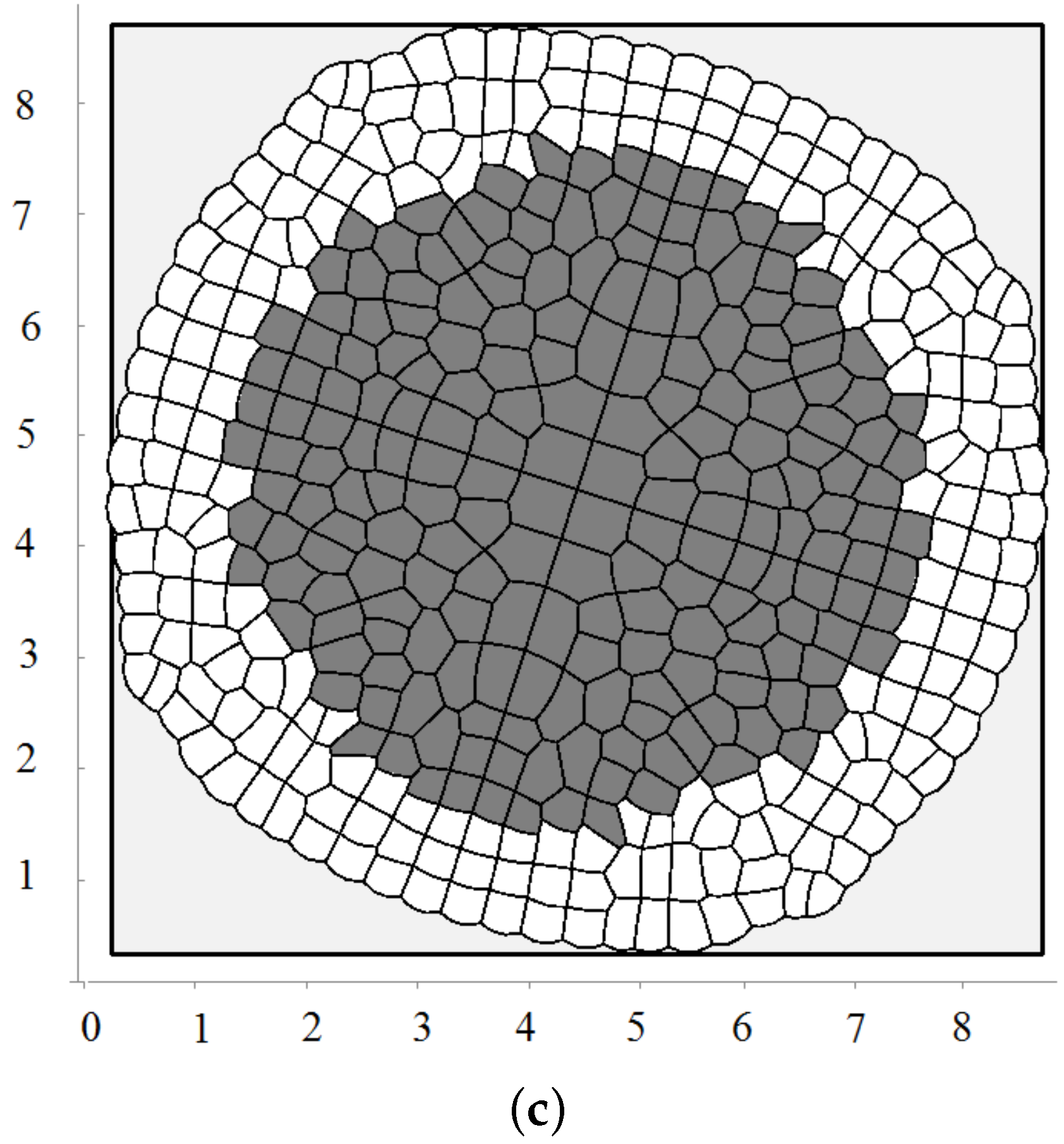
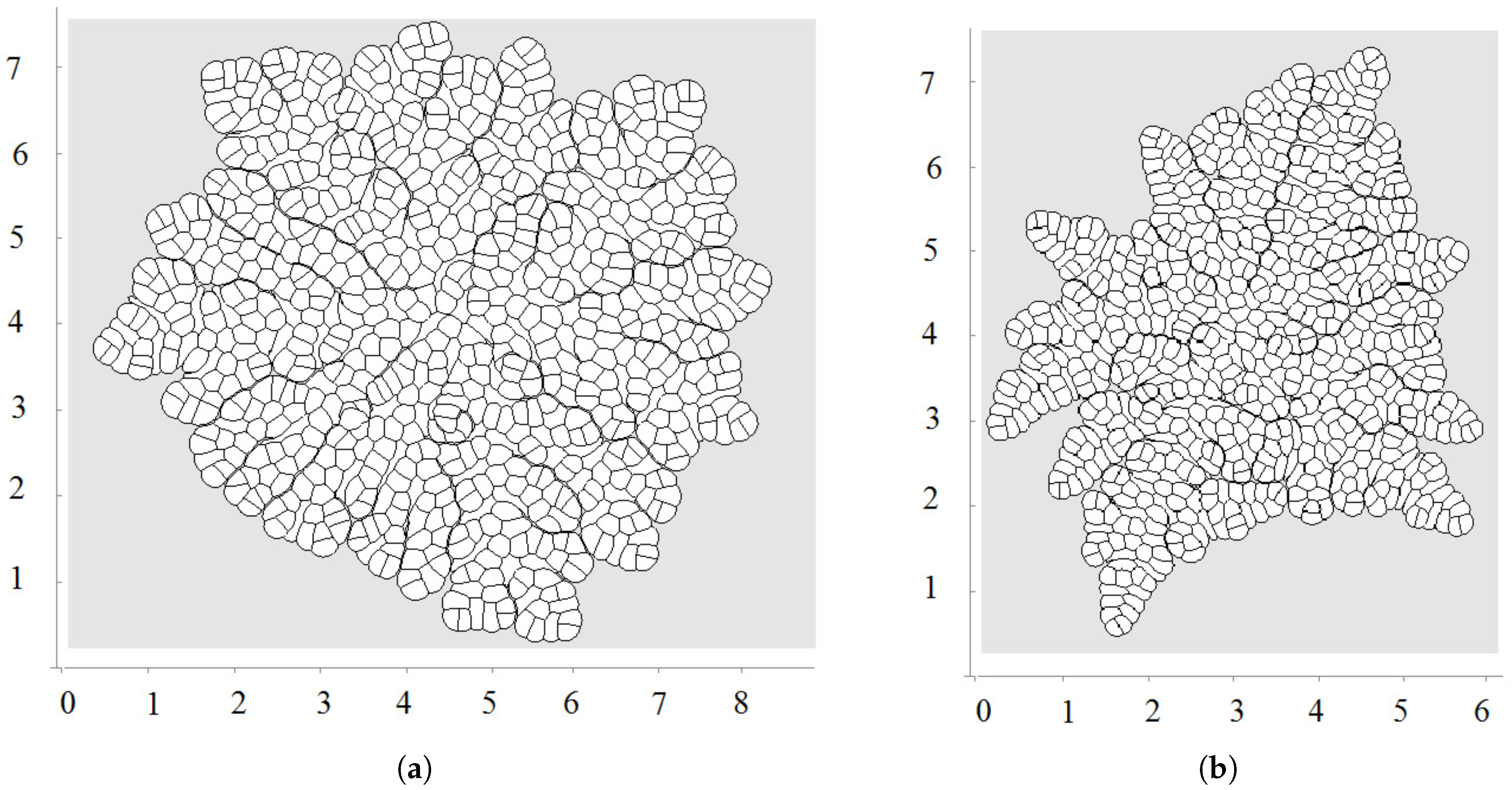
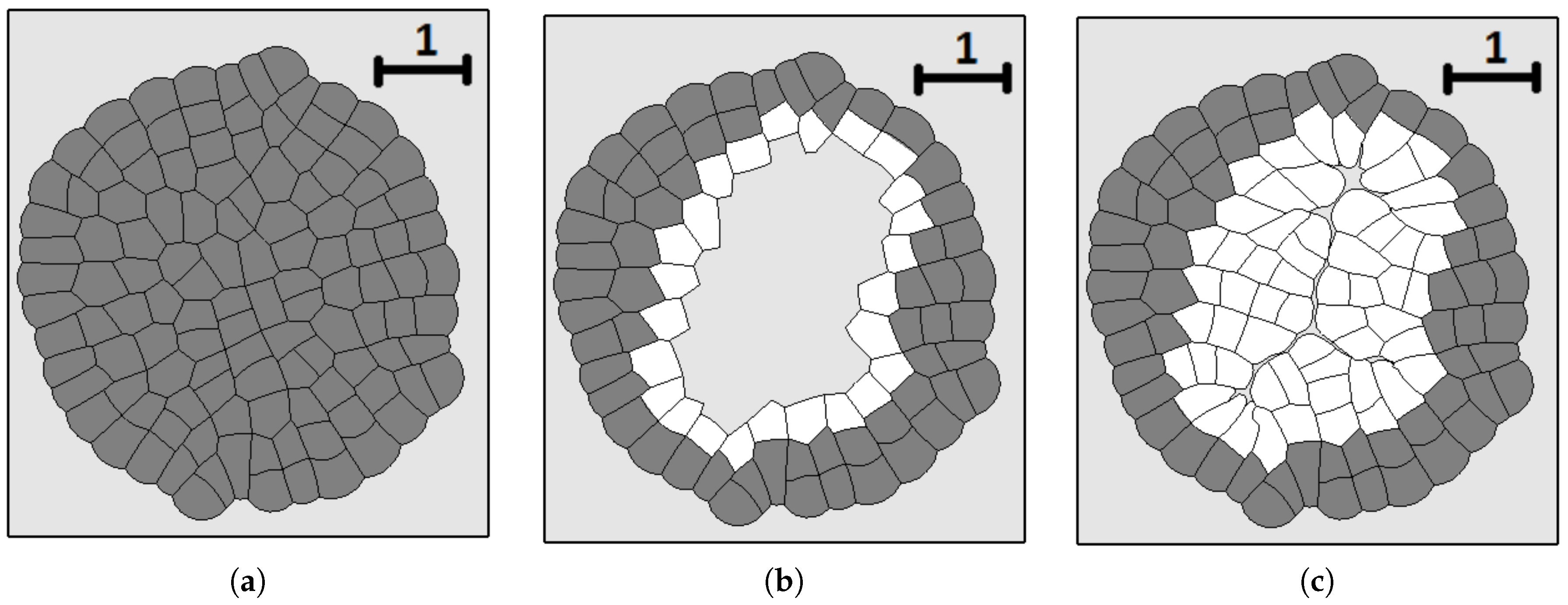
3.3. External Supply of Nutrients
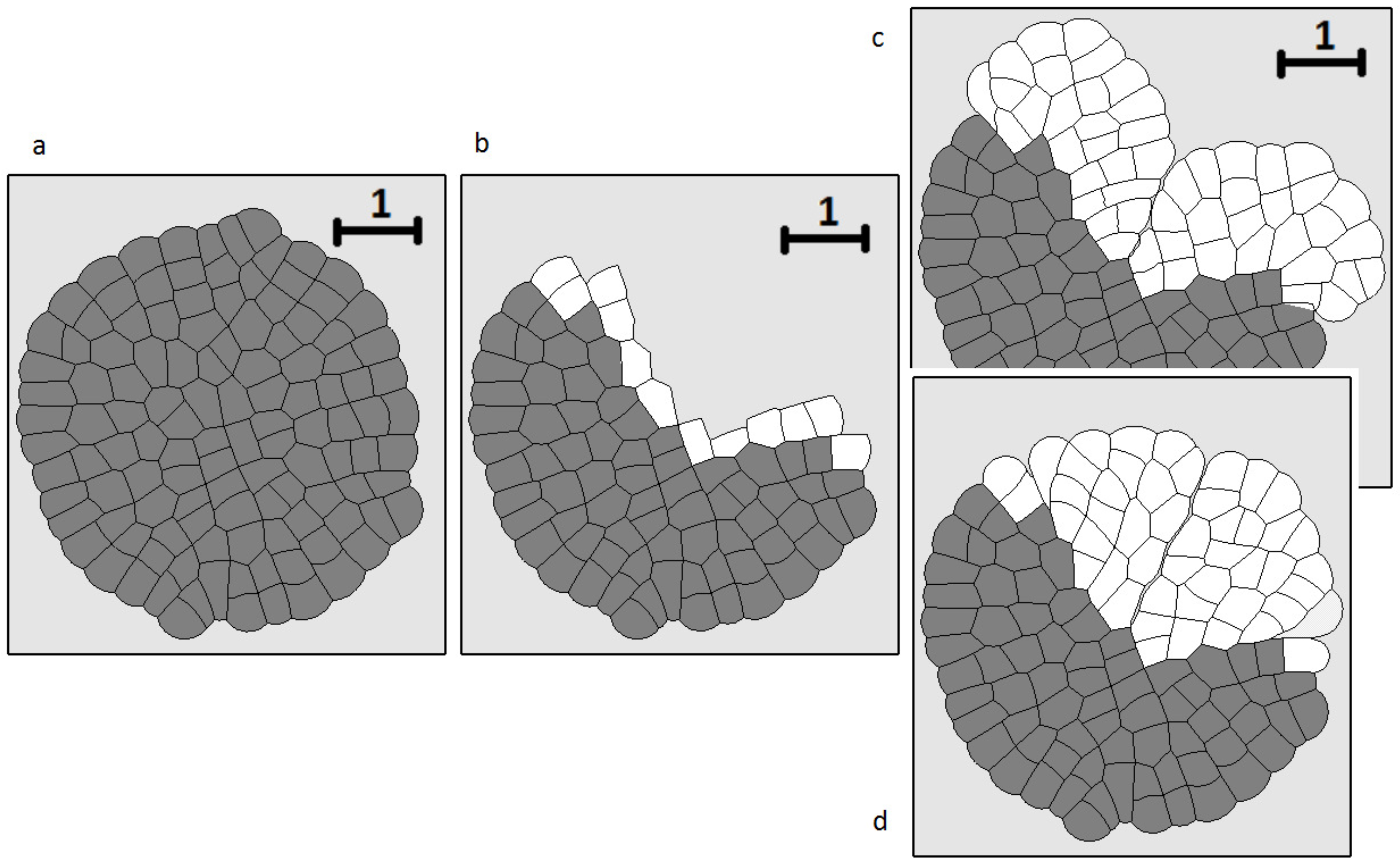
3.4. Wound Healing
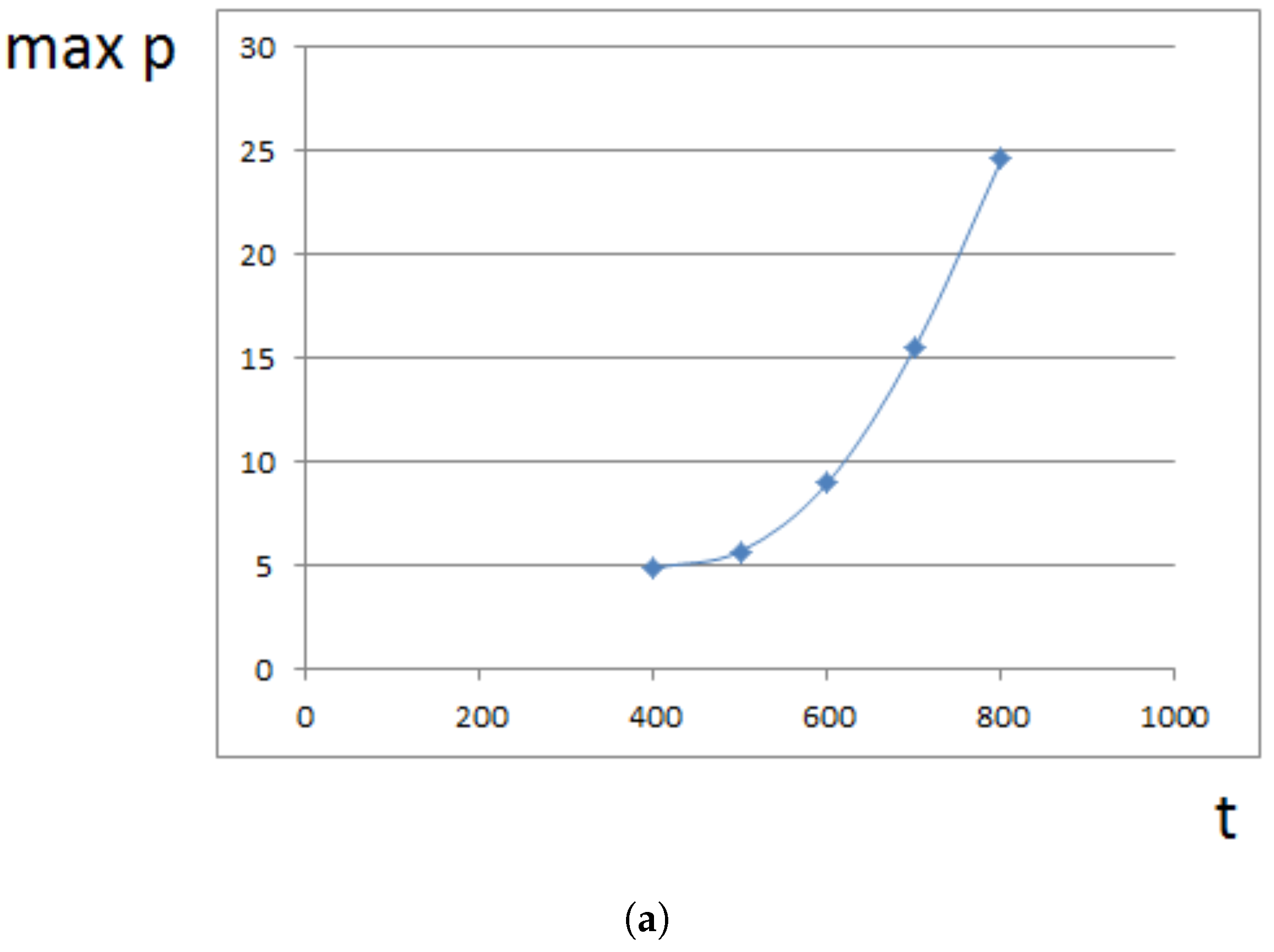
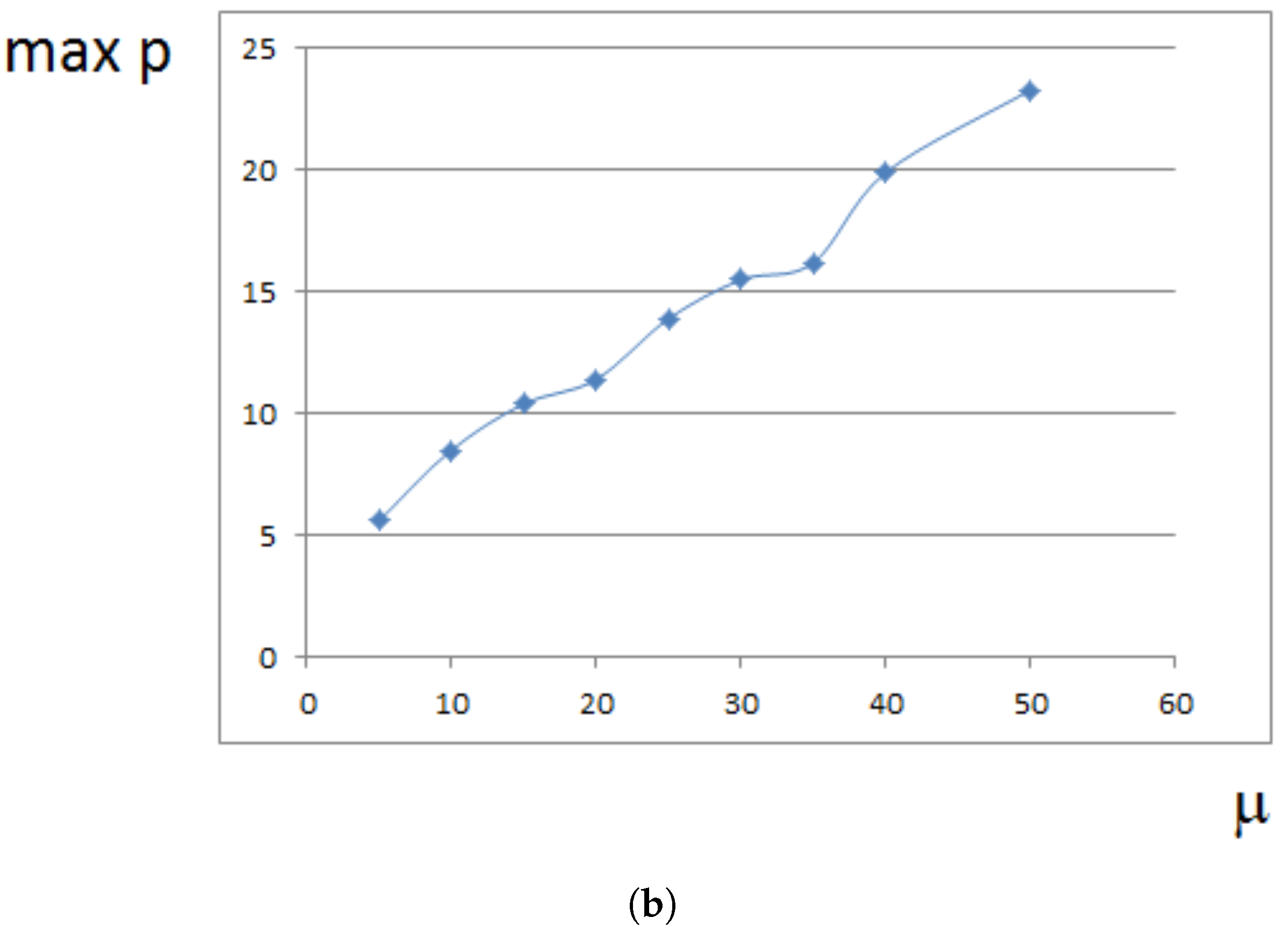
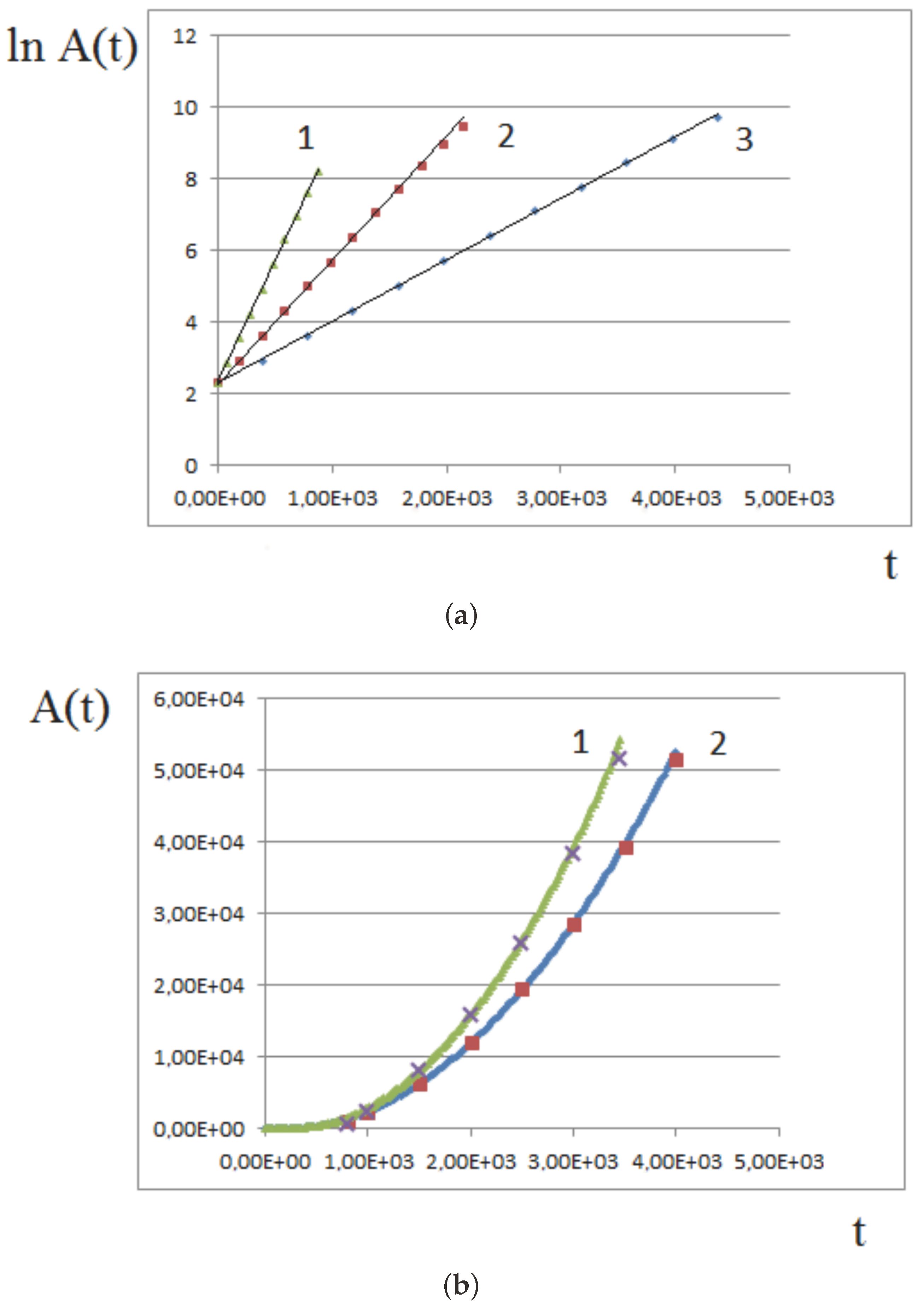
4. Analytical Approximation of the Growth Rate
4.1. Approximate Model
4.2. Constant Proliferation
4.3. Pressure-Dependent Proliferation
5. Discussion
Author Contributions
Conflicts of Interest
References
- Basan, M.; Elgeti, J.; Hannezo, M.; Rappel, W.-J.; Levine, H. Alignment of cellular motility forces with tissue flow as a mechanism for efficient wound healing. Proc. Natl. Acad. Sci. USA 2013, 110, 2452–2459. [Google Scholar] [CrossRef] [PubMed]
- Chauviere, A.; Preziozi, L.; Verdier, C. (Eds.) Cell Mechanics: From Single Cell-Based Models to Multi-Scale Modeling; CRC Press: London, UK, 2010. [Google Scholar]
- Friedman, A. (Ed.) Tutorials in Mathematical Biosciences III; Cell Cycle, Proliferation, and Cancer; Springer: Berlin, Germany, 2006. [Google Scholar]
- Capasso, V.; Gromov, M.; Harel-Bellan, A.; Morozova, N.; Pritchard, L. (Eds.) Pattern Formation in Morphogenesis. In Springer Proceedings in Mathematics; Springer: Berlin, Germany, 2012; Volume 15. [Google Scholar]
- Glade, N.; Stephanou, A. (Eds.) Le Vivant Entre Discret et Continu; Editions Matériologiques: Paris, France, 2013. [Google Scholar]
- Karttunen, M.; Vattulainen, I.; Lukkarinen, A. A Novel Methods in Soft Matter Simulations; Springer: Berlin, Germany, 2004. [Google Scholar]
- Bodenstein, L. A dynamic simulation model of tissue growth and cell patterning. Cell Differ. 1986, 19, 19–33. [Google Scholar] [CrossRef]
- Markov, M.A.; Markov, A.V. Computer simulation of the ontogeny of organisms with different types of symmetry. Paleontol. J. 2014, 48, 1–9. [Google Scholar] [CrossRef]
- Drasdo, D.; Loeffler, M. Individual-based models to growth and folding in one-layered tissues: Intestinal crypts and early development. Nonlinear Anal. 2001, 47, 245–256. [Google Scholar] [CrossRef]
- Bessonov, N.; Pujo-Menjouet, L.; Volpert, V. Cell modelling of hematopoiesis. Math. Model. Nat. Phenom. 2006, 1, 81–103. [Google Scholar] [CrossRef]
- Bessonov, N.; Demin, I.; Pujo-Menjouet, L.; Volpert, V. A multi-agent model describing self-renewal or differentiation effect of blood cell population. Math. Comput. Model. 2009, 49, 2116–2127. [Google Scholar] [CrossRef]
- Bessonov, N.; Crauste, F.; Demin, I.; Volpert, V. Dynamics of erythroid progenitors and erythroleukemia. Math. Model. Nat. Phenom. 2009, 4, 210–232. [Google Scholar] [CrossRef]
- Bessonov, N.; Demin, I.; Kurbatova, P.; Pujo-Menjouet, L.; Volpert, V. Multi-Agent Systems and Blood Cell Formation. In Multi-Agent Systems—Modeling, Interactions, Simulations and Case Studies; Alkhateeb, F., Al Maghayreh, E., Doush, I.A., Eds.; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Ranfta, J.; Basan, M.; Elgeti, J.; Joanny, J.-F.; Prost, J.; Jülicher, F. Fluidization of tissues by cell division and apoptosis. PNAS 2010, 107, 20863–20868. [Google Scholar] [CrossRef] [PubMed]
- Meineke, F.A.; Potten, C.S.; Loeffer, M. Cell migration and organization in the intestinal crypt using a lattice-free model. Cell Prolif. 2001, 34, 253–266. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen, I.M.; Mirams, G.R.; Walter, A.; Fletcher, A.; Murray, P.; Osborne, J.; Varma, S.; Young, S.J.; Cooper, J.; Doyle, B.; et al. An integrative computational model for intestinal tissue renewal. Cell Prolif. 2009, 42, 617–636. [Google Scholar] [CrossRef] [PubMed]
- Kansal, A.R.; Torquato, S.; Harsh, G.R.; Ciccaeb, E.A.; Deisboeck, T.S. Simulated Brain Tumor Growth Dynamics Using a Three-Dimensional Cellular Automaton. J. Theor. Biol. 2000, 203, 367–382. [Google Scholar] [CrossRef] [PubMed]
- Kansal, A.R.; Torquato, S.; Harsh, G.R.; Chiocca, E.A.; Deisboeck, T.S. Cellular automaton of idealized brain tumor growth dynamics. BioSystems 2000, 55, 119–127. [Google Scholar] [CrossRef]
- Ramis-Conde, I.; Drasdo, D.; Anderson, A.R.A.; Chaplain, M.A.J. Modeling the Influence of the E-Cadherin-b-Catenin Pathway in Cancer Cell Invasion: A Multiscale Approach. Biophys. J. 2008, 95, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Ramis-Conde, I.; Chaplain, M.A.J.; Anderson, A.R.A.; Drasdo, D. Multi-scale modelling of cancer cell intravasation: The role of cadherins in metastasis. Phys. Biol. 2009, 6, 016008. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Eymard, N.; Kurbatova, P.; Volpert, V. Mathematical modelling of erythropoiesis in vivo with multiple erythroblastic islands. Appl. Math. Lett. 2012, 25, 1217–1221. [Google Scholar] [CrossRef]
- Eymard, N.; Bessonov, N.; Gandrillon, O.; Koury, M.J.; Volpert, V. The role of spatial organization of cells in erythropoiesis. J. Math. Biol. 2015, 70, 71–97. [Google Scholar] [CrossRef] [PubMed]
- Fischer, S.; Kurbatova, P.; Bessonov, N.; Gandrillon, O.; Volpert, V.; Crauste, F. Modelling erythroblastic islands: Using a hybrid model to assess the function of central macrophage. J. Theor. Biol. 2012, 298, 92–106. [Google Scholar] [CrossRef] [PubMed]
- Kurbatova, P.; Eymard, N.; Volpert, V. Hybrid Model of Erythropoiesis. Acta Biotheor. 2013, 61, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Tosenberger, A.; Ataullakhanov, F.; Bessonov, N.; Panteleev, M.; Tokarev, A.; Volpert, V. Modelling of thrombus growth in flow with a DPD-PDE method. J. Theor. Biol. 2013, 337, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Tosenberger, A.; Bessonov, N.; Volpert, V. Influence of fibrinogen deficiency on clot formation in flow by hybrid model. Math. Model. Nat. Phenom. 2015, 10, 36–47. [Google Scholar] [CrossRef]
- Bessonov, N.; Kurbatova, P.; Volpert, V. Particle dynamics modelling of cell populations. Math. Model. Nat. Phenom. 2010, 5, 42–47. [Google Scholar] [CrossRef]
- Colombi, A.; Scianna, M.; Preziosi, L. A measure-theoretic model for collective cell migration and aggregation. Math. Model. Nat. Phenom. 2015, 10, 4–35. [Google Scholar] [CrossRef]
- Kurbatova, P.; Panasenko, G.; Volpert, V. Asymptotic numerical analysis of the diffusion-discrete absorption equation. Math. Methods Appl. Sci. 2012, 35, 438–444. [Google Scholar] [CrossRef]
- Anderson, A.R.A.; Chaplain, M.; Rejniak, K.A. Single Cell Based Models in Biology and Medicine; Birkhäuser: Basel, Switzerland, 2007. [Google Scholar]
- Deutsch, A.; Dormann, S. Cellular Automaton Modeling of Biological Pattern Formation; Birkhäuser: Boston, MA, USA, 2005. [Google Scholar]
- Gerlee, P.; Anderson, A.R.A. A hybrid cellular automaton model of clonal evolution in cancer: The emergence of the glycolytic phenotype. J. Theor. Biol. 2008, 250, 705–722. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.A.; Gawlinskia, E.T.; Lemieuxe, S.K.; Gatenby, A.A. A Cellular Automaton Model of Early Tumor Growth and Invasion: The Effects of Native Tissue Vascularity and Increased Anaerobic Tumor Metabolism. J. Theor. Biol. 2001, 213, 315–331. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.J.; Merrifield, A.; Landman, K.A.; Hughes, B.D. Simulating invasion with cellular automata: Connecting cell-scale and population-scale properties. Phys. Rev. E 2007, 76, 021918. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.J.; Landman, K.A.; Hughes, B.D. Distinguishing between Directed and Undirected Cell Motility within an Invading Cell Population. Bull. Math. Biol. 2009, 71, 781–799. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.R.A.; Rejniak, K.A.; Gerlee, P.; Quaranta, V. Microenvironment driven invasion: A multiscale multimodel investigation. J. Math. Biol. 2009, 58, 579–624. [Google Scholar] [CrossRef] [PubMed]
- Stephanou, A.; McDougall, S.R.; Anderson, A.R.A.; Chaplain, M.A.J. Mathematical modelling of the influence of blood rheological properties upon adaptative tumour-induced angiogenesis. Math. Comput. Model. 2006, 44, 96–123. [Google Scholar] [CrossRef]
- Chung, C.A.; Lin, T.H.; Chen, S.D.; Huang, H.I. Hybrid cellular automaton modeling of nutrient modulated cell growth in tissue engineering constructs. J. Theor. Biol. 2010, 262, 267–278. [Google Scholar] [CrossRef] [PubMed]
- Binder, B.J.; Landman, K.A.; Simpson, M.J. Modeling proliferative tissue growth: A general approach and an avian case study. Phys. Rev. E 2008, 78, 031912. [Google Scholar] [CrossRef] [PubMed]
- Merks, R.M.H.; Glazier, J.A. A cell-centered approach to developmental biology. Phys. A 2005, 352, 113–130. [Google Scholar] [CrossRef]
- Albert, P.J.; Schwarz, U.S. Dynamics of Cell Ensembles on Adhesive Micropatterns: Bridging the Gap between Single Cell Spreading and Collective Cell Migration. PLoS Comput. Biol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Scianna, M.; Preziosi, L. Cellular Potts Models: Multiscale Extensions and Biological Applications; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Bessonov, N.; Babushkina, E.; Golovashchenko, S.F.; Tosenberger, A.; Ataullakhanov, F.; Panteleev, M.; Tokarev, A.; Volpert, V. Numerical modelling of cell distribution in blood flow. Math. Model. Nat. Phenom. 2014, 9, 69–84. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Newman, T.J. Modeling multicellular systems using subcellular elements. Math. Biosci. Eng. 2005, 2, 613–624. [Google Scholar] [CrossRef] [PubMed]
- Koumoutsakos, P.; Bayati, B.; Milde, F.; Tauriello, G. Particle simulations of morphogenesis. Math. Models Methods Appl. Sci. 2011, 21, 955–1006. [Google Scholar] [CrossRef]
- Rejniak, K.A.; Anderson, A.R.A. A Computational Study of the Development of Epithelial Acini: I. Sufficient Conditions for the Formation of a Hollow Structure. Bull. Math. Biol. 2008, 70, 677–712. [Google Scholar] [CrossRef] [PubMed]
- Rejniak, K.A.; Anderson, A.R.A. A Computational Study of the Development of Epithelial Acini: II. Necessary Conditions for Structure and Lumen Stability. Bull. Math. Biol. 2008, 70, 1450–1479. [Google Scholar] [CrossRef] [PubMed]
- Rejniak, K.A.; Dillon, R.H. A single cell based model of the ductal tumour microarchitecture. Comput. Math. Methods Med. 2007, 8, 51–69. [Google Scholar] [CrossRef]
- Tozluoglu, M.; Tournier, A.L.; Jenkins, R.P.; Hooper, S.; Bates, P.A.; Sahai, E. Matrix geometry determines optimal cancer cell migration strategy and modulates response to interventions. Nat. Cell Biol. 2013, 15, 751–762. [Google Scholar] [CrossRef] [PubMed]
- Lober, J.; Ziebert, F.; Aranson, I.S. Collisions of deformable cells lead to collective migration. Sci. Rep. 2015. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Mironova, V.; Volpert, V. Deformable cell model of root growth. Math. Model. Nat. Phenom. 2013, 8, 62–79. [Google Scholar] [CrossRef]
- Merks, R.M.; Guravage, M.; Inze, D.; Beemster, G.T. VirtualLeaf: An open-source framework for cell-based modeling of plant tissue growth and development. Plant Physiol. 2011, 155, 656–666. [Google Scholar] [CrossRef] [PubMed]
- Brú, A.; Albertos, S.; Subiza, J.L.; Garcıa-Asenjo, J.L.; Brú, I. The Universal Dynamics of Tumor Growth. Biophys. J. 2003, 85, 2948–2961. [Google Scholar] [CrossRef]
- Bessonov, N.; Kurbatova, P.; Volpert, V. Pattern Formation in Hybrid Models of Cell Populations. In Pattern Formation in Morphogenesis: Problems and Mathematical Issues Series; Capasso, V., Gromov, M., Harel-Bellan, A., Morozova, N., Pritchard, L., Eds.; Springer: Berlin, Germany, 2012; pp. 107–119. [Google Scholar]
- Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed.; Springer: Berlin, Germany, 2003. [Google Scholar]
- Bessonov, N.; Levin, M.; Morozova, N.; Reinberg, N.; Tosenberger, A.; Volpert, V. On a model of pattern regeneration based on cell memory. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Caraguel, F.; Bessonov, N.; Demongeot, J.; Dhouailly, D.; Volpert, V. Wound healing and scale modelling in Zebrafish. Acta Biotheor. 2016, 64, 343–358. [Google Scholar] [CrossRef] [PubMed]
- Tosenberger, A.; Bessonov, N.; Levin, M.; Reinberg, N.; Volpert, V.; Morozova, N. A conceptual model of morphogenesis and regeneration. Acta Biotheor. 2015, 63, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A.; Hu, B. Bifurcation from stability to instability for a free boundary problem arising in a tumor model. Arch. Ration. Mech. Anal. 2006, 180, 293–330. [Google Scholar] [CrossRef]
- Friedman, A.; Hu, B. Asymptotic stability for a free boundary problem arising in a tumor model. J. Differ. Equ. 2006, 227, 598–639. [Google Scholar] [CrossRef]
- Friedman, A.; Hu, B. Bifurcation from stability to instability for a free boundary problem modeling tumor growth by Stokes equation. J. Math. Anal. Appl. 2007, 327, 643–664. [Google Scholar] [CrossRef]
- Friedman, A.; Hu, B. Bifurcation for a free boundary problem modeling tumor growth by Stokes equations. SIAM J. Math. Anal. 2007, 39, 174–194. [Google Scholar] [CrossRef]
- Hogea, C.S.; Murray, B.T.; Sethian, J.A. Simulating complex tumor dynamics from avascular to vascular growth using a general level-set method. J. Math. Biol. 2006, 53, 86–134. [Google Scholar] [CrossRef] [PubMed]
- Stephanou, A.; Volpert, V. Hybrid Modelling in Biology: A Classification Review. Math. Model. Nat. Phenom. 2016, 11, 37–48. [Google Scholar] [CrossRef]
- Netti, P.A.; Berk, D.A.; Swartz, M.A.; Grodzinsky, A.J.; Jain, R.K. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000, 60, 2497–2503. [Google Scholar] [PubMed]
- Roca-Cusachs, P.; Conte, V.; Trepat, X. Quantifying forces in cell biology. Nat. Cell Biol. 2017, 19, 742–751. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bessonov, N.; Volpert, V. Deformable Cell Model of Tissue Growth. Computation 2017, 5, 45. https://doi.org/10.3390/computation5040045
Bessonov N, Volpert V. Deformable Cell Model of Tissue Growth. Computation. 2017; 5(4):45. https://doi.org/10.3390/computation5040045
Chicago/Turabian StyleBessonov, Nikolai, and Vitaly Volpert. 2017. "Deformable Cell Model of Tissue Growth" Computation 5, no. 4: 45. https://doi.org/10.3390/computation5040045
APA StyleBessonov, N., & Volpert, V. (2017). Deformable Cell Model of Tissue Growth. Computation, 5(4), 45. https://doi.org/10.3390/computation5040045




