Abstract
Human Immunodeficiency Virus (HIV) infection of humans represents a complex biological system and a great challenge to public health. Novel approaches for the analysis and prediction of the infection dynamics based on a multi-scale integration of virus ontogeny and immune reactions are needed to deal with the systems’ complexity. The aim of our study is: (1) to formulate a multi-scale mathematical model of HIV infection; (2) to implement the model computationally following a hybrid approach; and (3) to calibrate the model by estimating the parameter values enabling one to reproduce the “standard” observed dynamics of HIV infection in blood during the acute phase of primary infection. The modeling approach integrates the processes of infection spread and immune responses in Lymph Nodes (LN) to that observed in blood. The spatio-temporal population dynamics of T lymphocytes in LN in response to HIV infection is governed by equations linking an intracellular regulation of the lymphocyte fate by intercellular cytokine fields. We describe the balance of proliferation, differentiation and death at a single cell level as a consequence of gene activation via multiple signaling pathways activated by IL-2, IFNa and FasL. Distinct activation thresholds are used in the model to relate different modes of cellular responses to the hierarchy of the relative levels of the cytokines. We specify a reference set of model parameter values for the fundamental processes in lymph nodes that ensures a reasonable agreement with viral load and CD4+ T cell dynamics in blood.
1. Introduction
Human Immunodeficiency Virus (HIV) type 1 infection represents a complex biological system [1,2,3,4] and a great challenge for cure strategies [5,6]. Novel approaches for the analysis and prediction of the infection dynamics based on a multi-scale integration of virus ontogeny and immune reactions are needed to deal with the systems’ complexity [7,8,9,10]. Such approaches have not yet been developed in the HIV modeling field [11,12,13].
The term “multi-scale models” is used with different meanings in different sciences. In mathematics, it implies the presence of one or several small parameters, homogenization and averaging techniques. In physics, it is understood in the sense of microscopic-macroscopic scales (e.g., molecular dynamics versus continuum mechanics). These questions are exhaustively discussed in particular in [14]. Multi-scale modeling in biology has been intensively developed during the last decade. It implies that the model includes different biological scales: cells, intracellular regulation, extracellular matrix, the tissue under study and other organs (not necessarily all of them in the same model). It is in this sense that we understand multi-scale modeling in this work.
A multiscale framework turned out to be insightful for understanding the mechanisms and identifying potential therapeutic targets for human infection with Mycobacterium tuberculosis [15,16,17]. Other specific examples of immune system analysis based on multiscale models are the studies of early CD8+ T cell immune responses in Lymph Nodes (LN) [18,19], the NF-κB signaling pathway [20] and immune processes in lymph nodes [21,22]. The gained experience led to the formulation of some more general principles for developing and computationally implementing integrative models of immune responses [16,23,24]. A recent study integrating the spatial structure of the T cell zone of lymph nodes and the dynamics of T cell responses in HIV infection has quantified the effect of the destruction of the Fibroblastic Reticular Cell (FRC) network on T cell reactivity [25]. The aim of our study is: (1) to formulate a multi-scale mathematical model of HIV infection; (2) to implement the model computationally following a hybrid approach; and (3) to calibrate the model by estimating the parameter values enabling one to reproduce the “standard” dynamics of HIV infection in blood during the acute phase of primary infection.
The major targets of HIV infection are macrophages and CD4+ T cells [4]. Both cell types play a key role in the regulation of immune responses by producing cytokines, such as IL-2 and interferons. The activation state of CD4+ T cells has a strong effect on the replication of the virus [26]. Naive resting CD4+ T cells do not support HIV replication, whereas activated cells are the major source of newly-secreted virus particles. HIV selectively infects and destroys memory CD4+ T cells in lymphoid tissues. After mucosal infection, some period of local replication and amplification takes place, finally resulting in the migration of the infected cells to the draining lymph nodes and, from there, to the rest of the body [26]. Dendritic cells (DC), which are highly efficient Antigen-Presenting Cells (APC), play a key role in disseminating HIV from mucosal tissues to the draining lymph nodes [27]. Intravenous infection leads to fast direct dissemination of the virus to all lymphoid organs. In these organs, the productive infection is initially observed in the T cell zone. The development of AIDS occurs when the level of mucosal CD4+ T cells drops to 5%–10% of their normal homeostatic level. Although about half of the gut-associated lymphoid tissue CD4+ T cells is depleted after acute infection [28], the prolonged maintenance of CD4+ T cells is explained by an increased turnover of the cells resulting from a chronic immune activation [26].
HIV viremia is controlled primarily by CD8+ T Lymphocytes (CTL) [28]. The infection is characterized by the production of up to new virus particles per day [27]. The viral load drops from ∼1–5 × viral copies/mL to a steady state of ∼3 × viral copies/mL [28]. It is remarkable that despite massive HIV-specific CTL responses (up to ), a full control of HIV viremia is not achieved. The magnitude and rapidity of the CD8+ T cell response correlate with the viral set point [29]. The set point is a strong predictor of the rate of the progression to AIDS [27]. The failure of HIV-specific CTLs to control HIV infection is attributed to functional defects of these cells associated with apoptosis [29,30]. The development of CTL responses in lymphoid organs is much less characterized than those in the peripheral blood [28]. Therefore, relating the immune processes in LNs to those in peripheral blood is important for a deeper understanding of the control of HIV infection.
Overall, the failure of the immune system to generate a protective antiviral response to HIV infections is linked to exhaustion of virus-specific immunity, the destruction of lymphoid organs, chronic immune activation and viral escape from the cellular and humoral immunity and is, therefore, multifactorial and multistage [4]. To analyze the regulatory mechanisms causing the chronicity of HIV infections, a multidisciplinary approach is required based on mathematical modeling and animal model systems. In this study, we propose a computational approach for a multi-scale integrative modeling of HIV infection. The approach is based on our previous experience in modeling erythropoiesis in blood diseases [31,32,33,34,35,36].
2. Methods
2.1. Multiscale Framework
The traditional approaches to model HIV dynamics focus only on one scale [9,11,12,13]. The multiscale and multi-physics approach [14] provides unprecedented opportunities for understanding HIV via linking microscopic (intracellular) regulations in the immune system to the macroscopic environment of the lymphoid organs, resulting in a system level dynamics as observed and monitored in blood. The potential of such a multiscale approach is illustrated by a recent study on HIV spread in an HIV risk population [37]. For a general guideline on the principles of multiscale modeling, we refer to our recent review [38] and a textbook [14]. The model of acute HIV infection developed in this study belongs to the category of coupled-intricate models. It considers two macroscopic compartments, i.e., the blood and lymph nodes, and the cell population dynamics in the T cell zone of the lymph nodes at the mesoscopic level. The individual cell dynamics is regulated by cytokine fields created by APCs and T cells via intracellular signaling cascades linking cellular receptors with gene transcription factors. The conceptual scheme of our modeling approach is summarized in Figure 1.
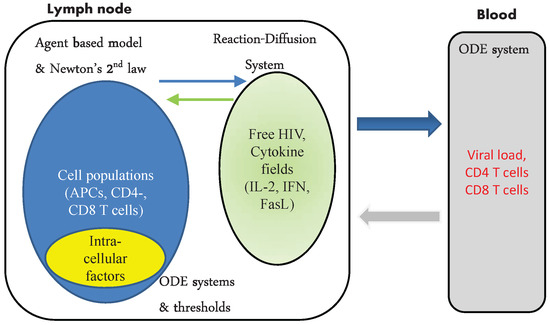
Figure 1.
General structure of the multiscale model of HIV infection.
2.1.1. Cell Displacement
In the developed model, cells are represented by individual elastic spheres. The cells are supposed to move randomly in a 2D domain. When they meet, the mechanical interaction takes place via an elastic force acting on cells and influencing their motion. The motion of the cell (idealized as the motion of their centers) is governed by Newton’s second law:
where m is the mass of the cell and μ is the friction factor due to contact with the surrounding medium. The potential force between two cells is modeled by:
where is the distance between the two cell centers i and j, is the sum of their radii, K is a positive parameter and is the sum of the incompressible part of each cell. The repulsion force between the cells tends to infinity as decreases to . The random force has a constant modulus and random direction.
2.1.2. Cell Division and Differentiation
Cells enter the computational domain Ω of the LN at some rate if there is free space. Naive T cells move in the computational domain randomly. If they contact APC, they divide (Figure 2). When the cell reaches half of its life cycle, it will increase its size. When it divides, two daughter cells appear; the direction of the axis connecting their centers is chosen randomly from 0–. The duration of the cell cycle is 18 h with a random perturbation ranging from to 3 h. We consider two levels of maturity for CD4+ T cells and three levels for CD8+ T cells. If a differentiated cell has enough IL-2, then it divides and gives two mature daughter cells. Finally, differentiated cells leave the lymph node. In the simulations, this means that they are removed from the computational domain. The overall cell fate regulation is determined by a hierarchy of the gene activation thresholds for signaling coming via TCR, IL-2, IFNa and Fas receptors, as shown in Figure 3. Different activation thresholds uncouple the distinct modes of cellular responses depending on the cytokine levels and intracellular signaling, yielding context-specific functional responses [39].
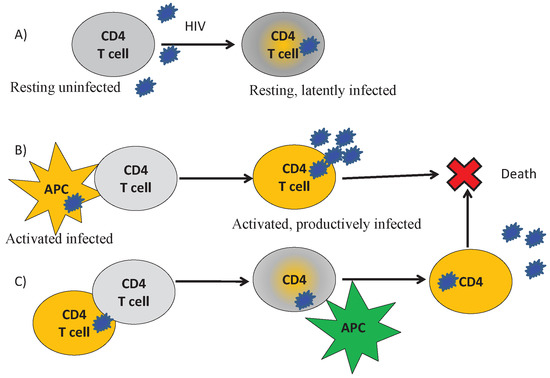
Figure 2.
Scenarios of virus modes of infection of CD4 T cells. (A) Free virus infection of resting CD4 T cells resulting in a latent infection; (B) interaction between infected APC and uninfected CD4 T lymphocytes resulting in a productive infection; (C) cell-to-cell spread of HIV from infected to uninfected CD4 T lymphocytes resulting in a productive infection upon activation by HIV antigen-presenting APC.
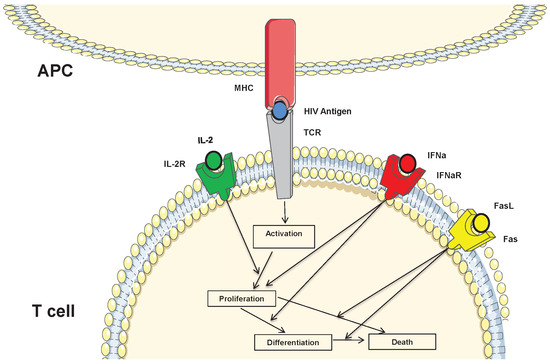
Figure 3.
Scheme of the cell fate regulation via TCR, IL-2, IFNa and Fas receptor-mediated signaling in naive T cells to adaptively program the balance of growth-differentiation and death.
2.2. Biological Assumptions
The model is based on the following assumptions:
- HIV enters the lymph node with infected antigen-presenting cells. These cells secrete HIV and transmit it to uninfected (both HIV-specific and non-specific) CD4+ T cells by cell-cell interaction;
- Each APC or CD4+ T cell is determined by an intracellular viral RNA concentration (). The cell is considered to be infected if reaches some threshold level . HIV upregulates the concentration of caspase, which can result in cell apoptosis;
- The CD8+ T cells produce FasL, as well as other apoptosis-inducing factors. They also activate the caspase cascade through direct cell-cell contact with infected cells resulting in target cell apoptosis. These two mechanisms only affect infected CD4+ T cells and not uninfected cells;
- HIV impairs the immune response by reducing the number of CD4+ T cells in the lymph node. These cells are killed by cytotoxic CD8+ T cells or by the virus itself. As a result, fewer mature helper CD4+ T cells are left, and less IL-2 and type I IFN are produced. This leads to a decrease in the survival and differentiation of CD8+ T cells, which ultimately results in the relapse of the infection.
We will consider three groups of variables characterizing infection development:
Blood:
- 1.
- , the viral load in blood;
- 2.
- , the abundance of infected CD4+ T cells in blood;
- 3.
- , the abundance of uninfected CD4+ T cells in blood;
- 4.
- , the abundance of HIV-specific effector CD8+ T cells in blood.
Lymph node:
- 5.
- , the density of APCs in the T cell zone of LN, uninfected or infected;
- 6.
- , the density of uninfected CD4+ T cells in the T cell zone of LN; and , the density of infected cells;
- 7.
- , the density of CD8+ T cells in the T cell zone of LN;
- 8.
- , the concentration of free HIV in the T cell zone;
- 9.
- , the concentration of IL-2 in the T cell zone;
- 10.
- , the concentration of type I IFN in the T cell zone;
- 11.
- , the concentration FasL in the T cell zone.
Different cells in the lymph node (APC, CD4, CD8, uninfected, infected) are considered as individual objects. The cell densities represent the number of cells in the unit volume. They are encountered in the model at two levels: locally as sources of IL-2, I IFN and FasL; and globally through their total quantity in the lymph node, which determines cell flux from the lymph node to the blood.
Intracellular factors:
- 12.
- , the intracellular concentration of viral genomes in the i-th cell;
- 13.
- , the intracellular concentration of IL-2-induced signaling molecules in the i-th cell;
- 14.
- , the intracellular concentration of type I IFN-induced signaling molecules in the i-th cell;
- 15.
- , the intracellular concentration of FasL-induced signaling molecules in the i-th cell.
3. The Model of Acute HIV Infection
3.1. Blood Compartment
In this section, we formulate equations relating the T cell and virus population dynamics in blood (i.e., in an observable compartment) and lymph nodes for which a detailed description of the HIV infection process is given. The HIV-specific CD8+ T cells are generated in the course of the antiviral immune response occurring in LN. The concentration of the cells in blood results from their migration from LN via efferent lymphatic vessels to blood and further to peripheral tissues. A simple description of the above processes is provided by the equation:
where stands for the concentration of HIV-specific CD8+ T cells in blood and is the density of HIV-specific CD8+ T cells in LNs,
The first term in the right-hand side of this equation describes the production of effector cells in the lymph nodes and the second term their death in the body.
For the equations of the systemic dynamics of APCs, T cells and infected cell populations, the parameters were specified according to available experimental and clinical data as follows:
- 1.
- , rate of T cell production and release into the body: ;
- 2.
- , death rate of T cells in the body: ;
- 3.
- , elimination rate of the infected cells by T cells ;
- 4.
- a, a growth rate parameter of infected cells: ;
- 5.
- h, a parameter in the growth function of infected cells: .
For the migration and decay rate constants, the following estimates can be used:
- 6.
- , migration rate constant of CD8+ T cells from LN to blood. The fraction of HIV-specific CTLs in acute HIV infection can reach 10% of the total number of CD8+ T cells, i.e., about 100 cell/L [11]. Therefore, the value of should be within the range 0.004–0.04 ;
- 7.
- , the disappearance rate of HIV-specific effector CD8+ T cells from blood [11]: = 0.0013 .
As the infection process takes place mainly in organized lymphoid tissues, a similar equation applies to the number of HIV-infected CD4+ T cells in blood (). We describe the dynamics of the infected cells in blood by the equation:
The first term in the right-hand side of this equation describes the growth of the number of infected cells through the accumulation from the lymph nodes; the second term their elimination by the effector cells; the next term describes contamination of uninfected cells by infected cells; and the last terms the death of the HIV-infected cell due to the cytopathic effect of the virus. The function f is considered in the form:
where a and h are some positive constants and is the total number of CD4+ T cells in the lymph node,
For the migration-accumulation, effector cell- and virus-mediated killing rate constants, the following estimates can be used:
- 8.
- a, the accumulation rate constant of HIV-infected CD4+ T cells in blood due to the migration of cells from LNs and other peripheral tissues: the reference value 0.1 suggested in [1] was tuned to 0.35 ;
- 9.
- h, the inverse of the threshold of infected T cells density in LN that leads to 50% reduction of the maximal accumulation rate of the infected cells in blood: 1/100 ·L;
- 10.
- , the elimination rate of HIV-infected CD4+ T cells by CTL-mediated killing. We used the value estimated in [9] 0.0004 L/(cell·h). For a strong T cell response, this value reaching 10% of the total CTL population in blood, this value will ensure the elimination rate of the infected cells from blood of about 1 per day;
- 11.
- , the death rate of HIV-infected CD4+ T cells in blood due to virus cytopathicity: 0.017–0.17 [11,12]; with the geometric mean estimate 0.05 . We consider a death rate of 0.061 .
We describe the dynamics of the uninfected CD4+ T cells in blood by the commonly-used equation:
The first term in the right-hand side of this equation describes the influx of healthy CD4+ T cells from the lymph node,
The second term in the right-hand side of Equation (4) describes the contamination of uninfected cells by infected cells, and the last term describes the death of uninfected T cells. The following estimates can be used for the parameters adjusted from the values reported in [11,12]:
- 12.
- λ, the influx rate of CD4+ from the lymph nodes: 0.45 (L·h)−1;
- 13.
- , the inverse of the threshold of uninfected T cells density in LN that leads to 50% reduction of the maximal accumulation rate of the uninfected cells in blood: 1/200 ·L;
- 14.
- , the infection rate of the CD4+ T cells in blood: 0.00042 (L·h)−1;
- 15.
- , the death rate of uninfected CD4+ T cells in blood: .
Finally, an equation for the HIV concentration in blood has to be specified. We utilize a commonly-used description:
For the HIV transfer and elimination rate constants, the following estimates are used:
- 16.
- k the influx of HIV from LNs to blood was estimated in [40]. Taking into account the volume differences of our computational domain (0.001 L) and the unit of blood volume L, we used the following value 100 virion/(L·h);
- 17.
- , the elimination rate of free HIV from blood [11,12]: 0.5–21 ; with the geometric mean taken as an initial guess 3.2 further tuned to 6 .
3.2. Population Dynamics of Infection in LN
3.2.1. Free HIV
We describe the concentration of HIV in the extracellular matrix as follows:
For the diffusion coefficient of the virus, we used the available estimates [41,42,43], which provide the following broad range for mm2/h, with the geometric mean taken to be the baseline value mm2/h.
HIV is secreted by two types of infected cells: APCs and CD4+ T cells. The production depends on the intracellular concentration of HIV DNA in a threshold manner; once the DNA level is above a certain value in the activated cell, the secretion starts to take place. Virus production is presented by the source term ,
with specifying the per capita secretion rate by activated cells located at some positions . It is a sum of Dirac delta functions, and due to the singularity of the terms, the equation is understood in the weak sense. The maximum secretion rate of HIV by an activated CD4+ T cell is taken to be virion/(cell·h) [11]. The clearance rate of free virus is taken to be about = 0.5 [11].
3.2.2. HIV Infection in Target Cells
The virus is introduced to the lymph node by infected APCs and CD4+ T cells. We suppose that the number of infected APCs CD4+ T cells entering the lymph node and the concentration of proviral HIV DNA inside of them depend on the level of HIV infection. The proportion of the infected APCs and HIV-specific CD4+ entering the lymph node corresponds to the actual level of HIV of infection divided by virion/L. The concentration of intracellular HIV DNA is equal to the infection level divided by virion/L. HIV infects the CD4+ T cells in the lymph node, resulting potentially in the apoptosis of activated cells. Otherwise, the virus stays latent inside of the cell. Furthermore, infected APCs do not induce the differentiation of CD4+ T cells. To describe the number of the integrated proviral HIV DNA D by () in each CD4 T cell or APC, we use the equation:
Here, denotes the concentration of HIV in the extracellular matrix; n is the number of CD4 T cells and APCs in direct contact with infected cell. When in direct contact with uninfected CD4 cells, the virus is transmitted, but remains latent. Hence, the value of the virus inside the previously uninfected cell is set to . Furthermore, is equal to zero when the virus is latent. Otherwise, it is equal to a positive constant. Virus multiplication is activated upon a direct contact with an APC (infected or not). We take equal to 100 virion. The concentration of the integrated DNA in the cell determines if the cell itself is infected or not. To account for this, we consider the cell to be infected if reaches the value . It starts emitting the virus to the extracellular matrix and become susceptible to elimination by CD8 T cells.
For the intracellular HIV replication parameters, we used the following values:
- , the infection rate constant for susceptible cells by free virus. It can be evaluated using the estimates in [44]: L/(virion·h);
- , specifies the maximal production rate of HIV DNA in the activated cell. We used the following estimate virion/(cell·h) [11];
- , specifies the protective effect of type I interferon on HIV DNA growth in the activated cell. The following estimate [45] is used to reproduce a 50% reduction in the viral DNA synthesis rate due to the availability of type I IFN: = 467 L/pg;
- , the probability that a susceptible cell is infected when it contacts infected cells was estimated in [44] to be .
3.3. Cytokine Fields in LN
3.3.1. IL-2
Immature T cells differentiate via direct cell-cell contact with uninfected APCs. Proliferation and differentiation of T cells in the lymph node depend on the concentration of IL-2. It is produced by mature CD4+ T cells. Its spatial distribution is described by the reaction-diffusion equation:
Here, is the extracellular concentration of IL-2; D is the diffusion coefficient; is the rate of its production by CD4+ T cells; and the last term in the right-hand side of this equation describes its consumption and degradation. The production rate is determined by mature CD4+ T cells. We consider each such cell as a source term with a constant production rate at the area of the cell. Let us note that we do not take into account explicitly consumption of IL-2 by immature cells in order not to introduce an additional parameter. Implicitly, this consumption is taken into account in the degradation term. The following estimates of the parameters were used:
- , the secretion rate of IL-2 by a single CD4+ T cell: molec/h;
- , the degradation rate of extracellular IL-2: 0.5 .
3.3.2. Type I IFN
For type I IFN, the equation and the terms in it have a similar interpretation:
For the type I IFN-controlled processes, the following parameter values were used, taken from [45]:
- , the secretion rate of type I IFN by single activated APC (plasmacytoid dendritic cell): molec/h;
- , the degradation rate of extracellular type I IFN: 0.012 .
, , the diffusion coefficients of IL-2 and type I IFN. As the molecular weights of IL-2 and type I IFN are close to that of myoglobin, we used the following estimate of the diffusion coefficient: mm3/h. Initial and boundary conditions for both concentrations IL-2 and IFN are taken to be zero. As before, the production rate equals at the area filled by APC cells and zero otherwise.
3.3.3. FasL
We also describe the concentration of FasL and other cytokines secreted by CD8+ T cells:
The molecular weight of FasL is estimated to be around 40 kD; therefore, we assumed the diffusion coefficient to be proportionally smaller than that of myoglobin, i.e., mm2/h. The production rate of FasL by activated T cells can be estimated from the data in [46] to be around – (molecules/(cell·h) [46] with the geometric mean value of molecules/(cell·h). The degradation rate constant of the soluble FasL is assumed to range from 0.3 (characteristic of the decay rate of Fas receptor [18]) through 0.5 (estimated degradation rate of extracellular IL-2 [47]) to 14 [46], and we used the geometric mean value 2 .
3.4. Intracellular Regulation of Cell Fate
3.4.1. IL-2 Signaling
The survival and differentiation of both CD4 and CD8 T cells depend on the intracellular concentration of IL-2 () and interferon (). We describe these two concentrations by the following equations:
Here, is the intracellular concentration of signaling molecules accumulated as a consequence of IL-2 signals transmitted through transmembrane receptor IL2R downstream of the signaling pathway to control the gene expression in the i-th cell. The concentrations inside two different cells are in general different from each other. The first term in the right-hand side of this equation shows the cumulative effect of IL-2 signaling. The extracellular concentration is taken at the coordinate of the center of the cell. The second term describes the degradation of IL-2-induced signaling molecules inside the cell. Furthermore, is the number of molecules internalized by T cell receptors. For the IL-2 controlled processes, the following parameter values were used taken from [47]:
- , the number of IL-2 molecules internalized by T cells via IL-2 receptors: 2000–5000 per T cell, with used in simulations;
- , the saturation concentration of IL-2 for T cell division in vitro: molec/mL for cells/mL.
3.4.2. Type 1 IFN Signaling
The IFN-dependent regulatory signal dynamics in individual cells can be described by the following equation:
Here, is the intracellular concentration of signaling molecules accumulated as a consequence of IFN signals transmitted through transmembrane receptor IFNR downstream of the signaling pathway to control the gene expression in the i-th cell. The concentrations inside two different cells are in general different from each other. The first term in the right-hand side of this equation shows the cumulative effect of IFN signaling. The extracellular concentration is taken at the coordinate of the center of the cell. The second term describes the degradation of IFN-induced signaling molecules inside the cell.
The quantitative specification of the effect of signaling on gene activation requires a separate study. To illustrate the model performance, it was enough to assume some reference values as follows: ∼∼ 1 molec/h and ∼∼ 0.1 . The proliferation and differentiation thresholds have been arbitrarily set to be units (U) and U.
To model the fate regulation of growth versus differentiation of the activated cells in relation to the timing of the IL-2 and type I IFN signaling, we implement the following decision mechanism.
- C1
- If the concentration of activation signals induced by type I IFN, , is greater than some critical level at the beginning of the cell cycle and that of is smaller than the critical level at the end of the cell cycle, then the cell will differentiate, resulting in a mature cell.
- C2
- If the concentration of activation signals induced by IL-2, , is greater than some critical level at the end of the cell cycle, then the cell will divide, producing two more mature cells.
- C3
- If at the beginning of cell cycle and at the end of cell cycle, then the cell will die by apoptosis and will be removed from the computational domain.
3.4.3. FasL Signaling
HIV also upregulates the level of caspase inside the cell. We describe its concentration as follows:
Here, denotes the effective concentration of extracellular FasL and other cytokines (e.g., TRAIL, PD1L) secreted by CD8 T cells. n denotes the number of CD8 T cells in direct contact with the cell. The cell dies if .
For the apoptosis-related regulation processes, the following estimates were used:
- , the rate of pro-apoptotic signals accumulation because of the viral replication. As the death rate of the infected CD4 T cells is , then we used it to quantify the cytopathic effect of the intracellular HIV DNA on the cell. It can be further scaled depending on the choice of the threshold . The latter was estimated in [12], and we set it M;
- , specifies the FasL-Fas-induced caspase accumulation rate. It was estimated to be in [12];
- , the killing rate of infected cells by effector CTL. It has been indicated in [46] that once in contact with a target cells, the CTL can program them to undergo apoptosis within 5 min. This value results in the following estimate for the impact of CTL on death likelihood ;
- , the caspase degradation rate is taken from [18] .
3.5. Population Dynamics of Immune Response in LN
The influx of APC cells into the lymph nodes is proportional to the number of infected cells . It corresponds to each 25 h where is the floor function of x. This influx is limited by the place available in the lymph node. If there is a free place sufficient to put a cell, the new cells are added. Let us also note that the lymph nodes can increase due to infection in order to produce more effector cells.
For a hybrid multi-scale agent-based model with many parameters, the standards for specifying the model to make it reproducible remain to be developed in immunology. We note that in other fields, such as ecological modeling, the standards for presenting agent-based models in the scientific literature have already been formulated [48,49].
4. Numerical Simulation Results
We consider a 2D computational domain in the T cell zone of lymph node of about 100 m × 100 m. The corresponding number of T cells in the computational domain is ∼ with the proportions of CD4+ and CD8+ T cells being 2:1 and the number of APCs ranging from 30–300 cells. The maximal number of HIV-specific T cells in the computational domain is assumed to be ∼. This corresponds to ∼ of the lymph node space that can be occupied by T cells.
The average CPU time of the acute phase of HIV simulation was around 3 h on a computer with four cores and 6 GB of RAM. The code was written under C++ in the Object Oriented Programming (OOP) style. The characteristic units of the model are the minute for time and the domain length for space. Further details of the numerical methods are described in the Appendix to [50]. The numerical code implementing the model is available upon request to the first author or can be directly assessed at https://github.com/MPS7/MultiScale-HIV.
Reaction-diffusion equations were solved using the Alternating Direction Implicit (API) algorithm. We set the initial values for the four fields described by reaction-diffusion equations to zero. Dirichlet conditions were prescribed to the four boundaries of the computational domain. Naive CD4+ and CD8+ T cells are periodically introduced to the middle of the domain when there is available space.
4.1. Dynamics of APCs, CD4+ and CD8+ T Cells in LN
The initial spread of infection to lymphoid organs is caused by the migration of a few infected APCs from mucosal compartments. The dynamics of infection in LN described by the model is shown in Figure 4. It characterizes the population dynamics of the total number of HIV-infected APCs and CD4+ T cells over the first 30 days after a few infected APCs appear in LN.
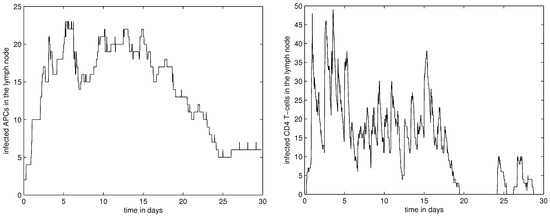
Figure 4.
(left) The dynamics of the population of HIV-infected APCs in the lymph node; (right) The dynamics of the population of HIV-infected CD4+ T cells in the lymph node.
The activation of APCs by HIV induces HIV-specific CD8+ T cell response as reproduced in Figure 5. It is characterized by a sequence of ongoing bursts in the expansion and contraction of CTLs. The strength of the cytotoxic T cell response is enough to limit the spread of infection and to reduced the number of infected APCs and CD4+ T cells from Days 15–20 by four-fold.
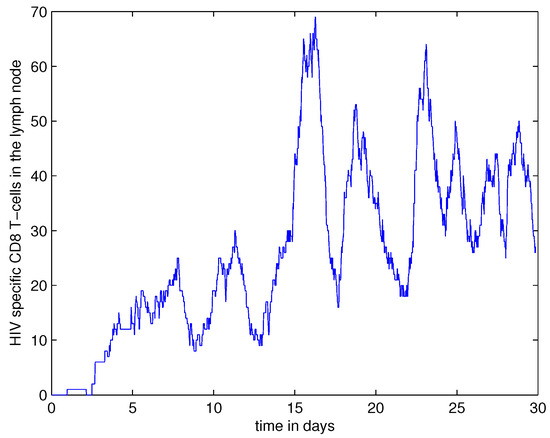
Figure 5.
The dynamics of HIV-specific effector CD8+ T cell response in the lymph node.
The overall comparative dynamics of HIV-specific T cell responses (CD4+ and CD8+) is detailed in Figure 6. The responses are dynamically regulated by the cytokine and HIV distribution in the computational domain.
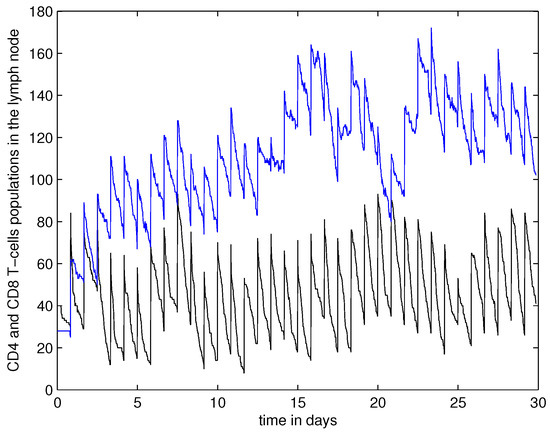
Figure 6.
The dynamics of populations of naive and mature HIV-specific CD4+ (black curve) and CD8+ (blue curve) T cells in the lymph node.
4.2. HIV and Cytokine Fields in LN
The spatial distribution of the virus, IL-2, type I IFN and FasL at Days 3 and 12 post the start of the LN infection is shown in Figure 7, Figure 8, Figure 9 and Figure 10. In addition to cytokine fields, different cells are shown: uninfected APCs (green), infected APCs (red), naive uninfected CD4+ T cells (black), infected CD4+ T cells (orange), naive CD8+ T cells (white), three maturity levels of differentiated CD8+ T cells (blue) and two maturity levels of uninfected CD4+ T cells (yellow).
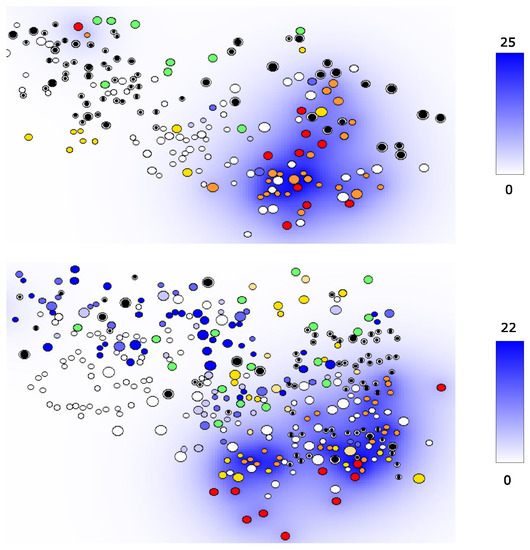
Figure 7.
Snapshots of the simulation in which the concentration of HIV (in virions/L) is shown in blue color gradient. Different cell types are represented as follows: uninfected APCs (green), infected APCs (red), naive uninfected CD4+ T cells (black), infected CD4+ T cells (orange), naive CD8+ T cells (white), three maturity levels of differentiated CD8+ T cells (blue) and two maturity levels of uninfected CD4+ T cells (yellow). (top) Three days after the virus transmission; (bottom) 12 days after virus transmission.
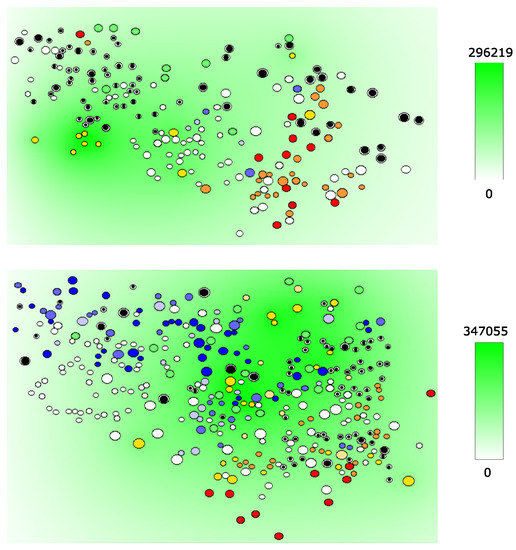
Figure 8.
Snapshots of the simulation in which the concentration of IL-2 (in molecules/L) is shown in green gradient. For cell notations, the same color code as in Figure 7 is used. (top) Three days after the virus transmission; (bottom) 12 days after virus transmission.
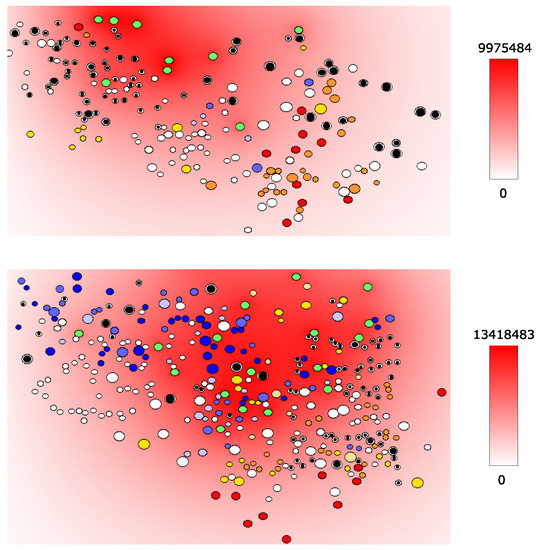
Figure 9.
Snapshots of the simulation in which the concentration of type I interferon (in molecules/L) is shown in red color gradient. For cell notations, the same color code as in Figure 7 is used. (top) Three days after the virus transmission; (bottom) 12 days after virus transmission.
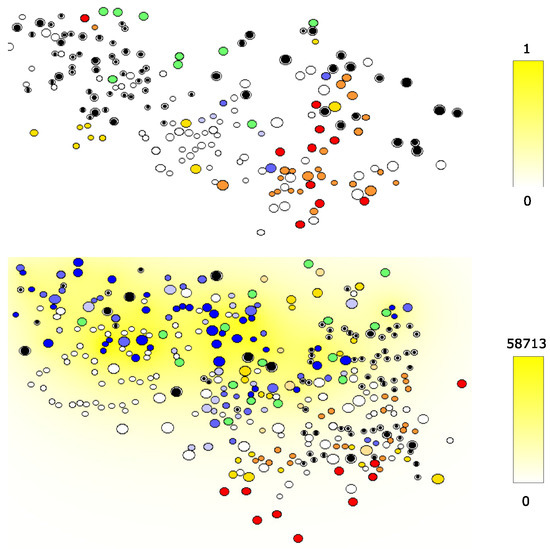
Figure 10.
Snapshots of the simulation in which the concentration of FasL (in molecules/L) is shown in yellow color gradient. For cell notations, the same color code as in Figure 7 is used. (top) Three days after the virus transmission; (bottom) 12 days after virus transmission.
Infected APCs and CD4+ T cells secrete HIV as shown in Figure 7 in blue. Mature CD4+ T cells produce IL-2, whose concentration in the extracellular matrix is shown by the level of green; see Figure 8. Activated APCs produce type I IFN shown in red in Figure 9. Finally, the distribution of the apoptosis-inducing ligands is depicted in Figure 10. The simulations clearly indicate that the cytokines and HIV distributions are non-homogeneous and not identical. The relative shifts and differences underlie the existence of compartments differing in the preferential fate of immune cells (division vs. differentiation vs. death) and the niche for infection continuation (domain with a low interferon level).
To illustrate the dynamics of infection process in LN, the animation of the single run of the model can be viewed via the Supplementary File (Video).
4.3. Systemic Dynamics of HIV Infection in Blood
The model offers a unique tool to link the dynamics of the infection and immune responses in blood and the lymph node. The viral load in LN and blood is shown in Figure 11. One can see that their kinetics are pretty similar. The population dynamics of normal CD4+ T cells and infected and CD4+ T cells is presented in Figure 12.
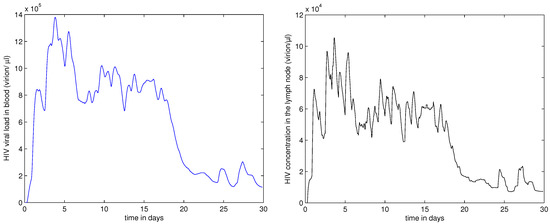
Figure 11.
(left) The viral load in blood (virion/L); (right) The HIV concentration in the lymph node over time.
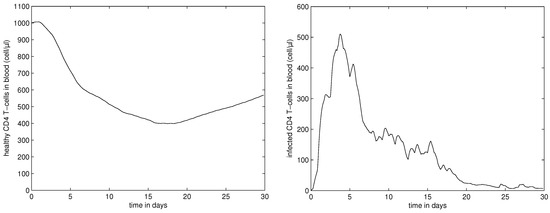
Figure 12.
Dynamics of infection in blood. (left) The population of uninfected CD4+ T cells (cell/L); (right) The population of infected CD4+ T cells (cell/L).
The elimination of infected T cells is due to the CD8+ T cells’ response developing in LN. The HIV-specific CD8+ T cells migrate to blood, as shown in Figure 13. The restoration of naive uninfected CD4+ T cells is only partial and takes longer.
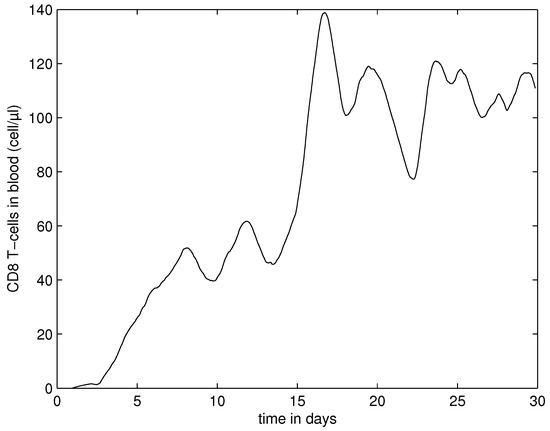
Figure 13.
Dynamics of immune response in blood. The population of HIV-specific CD8+ T cells over time (cell/L).
Overall, the simulations indicate that the model consistently reproduces the dynamics of major HIV infection characteristics in blood (viral load and CD4+ T cells during the initial acute phase of infection. These are determined by the specified and calibrated processes of infection spread and immune response development that occur in LN according to the biological schemes implemented in the model equations.
Sensitivity analysis of the model solutions to parameter variations is an important aspect of the assessment of the model performance. A comprehensive analysis of the local and global sensitivity aspects goes beyond the scope of this study. In Figure 14 and Figure 15, we illustrate how the variation in the value of the migration rate of effector CD8+ T cells from lymph node to blood () affects the dynamics of the observed characteristics of HIV infection. A variation by % of the rate from its reference values has a strong impact on the dynamics of viral load and reduction in the blood number of uninfected CD4+ T cells.
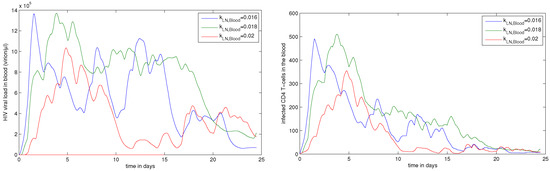
Figure 14.
Sensitivity analysis for blood. The effect of the variation of the rate of CD8+ T cell migration from lymph node to blood () by ± 11%. (left) Viral load (virion/L); (right) Infected CD4+ T cells (cell/L).
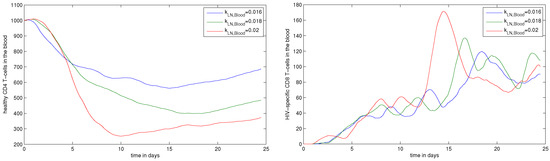
Figure 15.
Sensitivity analysis for blood. The effect of the variation of the rate of CD8+ T cell migration from lymph node to blood () by ± 11%. (left) Uninfected CD4+ T cells (cell/L); (right) HIV-specific CD8+ T cells (cell/L).
The simulations before represent a single run of the model. To illustrate the variations in individual model realizations due to random effects built into the model, Figure 16 shows an ensemble of three single runs of the model from the same starting conditions.
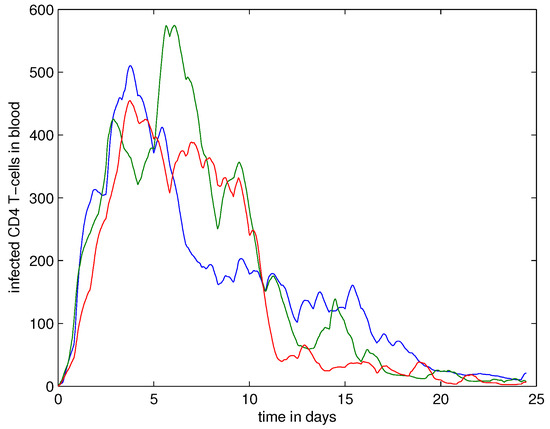
Figure 16.
Three single runs of the model from the same starting conditions showing the effect of randomness on the dynamics of infected CD4+ T cells in blood (cell/L).
5. Discussion
In this study, we formulated a multiscale model of an acute HIV infection, which integrates the processes of infection spread and immune responses in lymph nodes and links to HIV dynamics observed in blood. The spatio-temporal population dynamics of T lymphocytes in LN is governed by equations linking an intracellular regulation of the T lymphocyte fate by intercellular cytokine fields. We describe the balance of proliferation, differentiation and death at a single-cell level as a consequence of gene activation via multiple signaling events activated by IL-2, IFNa and FasL. Distinct activation thresholds uncouple the different modes of cellular responses depending on the relative levels of the cytokines. This scheme is consistent with recent findings of the rules for signal discrimination between qualitatively similar microbial products yielding context-specific functional responses [39].
The calibration of the model in a way that links the observed kinetics in the blood compartment with that in LNs in a quantitatively consistent way is a non-trivial task. We managed to specify a reference set of model parameters that provides a reasonable agreement with viral load and CD4+ T cell dynamics in blood [4,51]. Further refinement of the model and parameter estimates requires data on virological and immunological characteristics of HIV-infected individuals at the earliest stage of infection similar to those that have started to be gathered recently [51,52].
The virus growth in HIV infection is a result of multiple local bursts of the infection-production-elimination occurring randomly in the lymphoid tissue. Indeed, clinical and experimental studies of HIV and SIV infections indicate that the virus growth occurs in multiple local bursts reflecting local non-equilibrium interactions between HIV and immune-activated cells [53]. It was further discussed in [2] that in chronic HIV infection, the efficient transmission of the virus is limited to microscopic clusters of T cells in lymphoid tissues, suggesting that the continuity of virus production is a result of spatially-separated bursts. In view of the above paradigm, the patterns of the model solution seem to be more realistic than the deterministic curves with an exponential pattern.
The multiscale model of HIV infection formulated in our study is based on a number of simplifying assumptions of which the following have to be outlined:
- the spatial dynamics of cells and cytokines in LNs is considered in a 2D regular domain;
- the model is restricted to primary acute HIV infection and concomitant cytotoxic T cell responses;
- intracellular regulation of cell fate by multiple cytokine signaling is described via a hierarchy of activation thresholds;
- HIV infection is considered in LN and blood compartments.
Detailed sensitivity analysis is an important issue of the developed model to be used for examining the HIV pathogenesis mechanisms. However, it goes beyond the scope of this particular work and will be comprehensively examined in a follow up study.
The here formulated model can be extended along many lines, depending on the questions to be explored and the data available for that. For example, the model allows a straightforward incorporation of a more detailed description of the intracellular fate regulation by considering regulatory networks. The ontogeny of HIV in infected cells can be described in much greater detail [54]. Additional cell fate regulation factors, such as PD1, can be incorporated [55,56]. Finally, elaborate mechanisms for dynamic tuning of lymphocytes [57,58], genetic evolution of HIV [59], viral latency [6], chronic immune activation [60] and complementary arms of the immune system [61] need to be considered for extending this model to describe the long-term HIV infection dynamics. The development of respective fine resolution mechanistic “elementary” modules and their integration into the developed multi-scale modeling framework will allow one to study via the sensitivity analysis the efficacy of multi-modal treatment approaches of HIV infection combining ART, anti-fibrotic and immuno-modulatory drugs. The insight should assist clinicians in progressing towards an ambitious aim of a perfect long-term control/cure of the infection with minimal side effects.
Supplementary Materials
The video is available online at http://www.mdpi.com/2079-3197/5/1/6/s1.
Acknowledgments
This study was supported by the grant of the Russian Science Foundation, Project No. 15-11-00029 (to G.B., A.M. and V.V.).
Author Contributions
All authors of this paper have contributed to the study design. A.B., G.B. and V.V. developed the multi-scale model. A.B. and V.V. conducted the numerical simulations. A.B., G.B., A.M. and V.V. conceived of the study design and manuscript preparation. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HIV | Human Immunodeficiency Virus |
| LN | Lymph Mode |
| FRC | Fibroblastic Reticular Cell |
| APC | Antigen-Presenting Cell |
| IL-2 | Interleukin 2 |
| IFN | Type I Interferon |
| FasL | Fas Ligand |
References
- Levy, J.A. HIV and the Pathogenesis of AIDS, 3rd ed.; ASN Press: Washington, DC, USA, 2007. [Google Scholar]
- Grossman, Z.; Meier-Schellersheim, M.; Paul, W.E.; Picker, L.J. Pathogenesis of HIV infection: What the virus spares is as important as what it destroys. Nat. Med. 2006, 12, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Grossman, Z.; Meier-Schellersheim, M.; Sousa, A.E.; Victorino, R.M.; Paul, W.E. CD4+ T cell depletion in HIV infection: Are we closer to understanding the cause? Nat. Med. 2002, 8, 319–323. [Google Scholar] [CrossRef] [PubMed]
- Chereshnev, V.A.; Bocharov, G.; Bazhan, S.; Bachmetyev, B.; Gainova, I.; Likhoshvai, V.; Argilaguet, J.M.; Martinez, J.P.; Rump, J.A.; Mothe, B.; et al. Pathogenesis and treatment of HIV infection: The cellular, the immune system and the neuroendocrine systems perspective. Int. Rev. Immunol. 2013, 32, 282–306. [Google Scholar] [CrossRef] [PubMed]
- Kent, S.J.; Reece, J.C.; Petravic, J.; Martyushev, A.; Kramski, M.; De Rose, R.; Cooper, D.A.; Kelleher, A.D.; Emery, S.; Cameron, P.U.; et al. The search for an HIV cure: Tackling latent infection. Lancet Infect. Dis. 2013, 13, 614–621. [Google Scholar] [CrossRef]
- Melkova, Z.; Shankaran, P.; Madlenakova, M.; Bodor, J. Current views on HIV-1 latency, persistence, and cure. Folia Microbiol. 2016, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Kidd, B.A.; Peters, L.A.; Schadt, E.E.; Dudley, J.T. Unifying immunology with informatics and multiscale biology. Nat. Immunol. 2014, 15, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Carlson, J.M.; Le, A.Q.; Shahid, A.; Brumme, Z.L. HIV-1 adaptation to HLA: A window into virus-host immune interactions. Trends Microbiol. 2015, 23, 212–224. [Google Scholar] [CrossRef] [PubMed]
- Banks, H.T.; Davidian, M.; Hu, S.; Kepler, G.M.; Rosenberg, E.S. Modelling HIV immune response and validation with clinical data. J. Biol. Dyn. 2008, 2, 357–385. [Google Scholar] [CrossRef] [PubMed]
- Ludewig, B.; Stein, J.V.; Sharpe, J.; Cervantes-Barragan, L.; Thiel, V.; Bocharov, G. A global “imaging” view on systems approaches in immunology. Eur. J. Immunol. 2012, 42, 3116–3125. [Google Scholar] [CrossRef] [PubMed]
- Bocharov, G.; Chereshnev, V.; Gainova, I.; Bazhan, S.; Bachmetyev, B.; Argilaguet, J.; Martinez, J.; Meyerhans, A. Human Immunodeficiency Virus Infection: From Biological Observations to Mechanistic Mathematical Modelling. Math. Model. Nat. Phenom. 2012, 7, 78–104. [Google Scholar] [CrossRef]
- Alizon, S.; Magnus, C. Modelling the course of an HIV infection: Insights from ecology and evolution. Viruses 2012, 4, 1984–2013. [Google Scholar] [CrossRef] [PubMed]
- Canini, L.; Perelson, A.S. Viral kinetic modeling: State of the art. J. Pharmacokinet. Pharmacodyn. 2014, 41, 431–443. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E. Principles of Multiscale Modelling; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Fallahi-Sichani, M.; El-Kebir, M.; Marino, S.; Kirschner, D.E.; Linderman, J.J. Multi-scale computational modeling reveals a critical role for TNF receptor 1 dynamics in tuberculosis granuloma formation. J. Immunol. 2011, 186, 3472–3483. [Google Scholar] [CrossRef] [PubMed]
- Cilfone, N.A.; Kirschner, D.E.; Linderman, J.J. Strategies for efficient numerical implementation of hybrid multi-scale agent-based models to describe biological systems. Cell. Mol. Bioeng. 2015, 8, 119–136. [Google Scholar] [CrossRef] [PubMed]
- Simeone Marino, S.; Kirschner, D.E. A multi-compartment hybrid computational model predicts key roles for dendritic cells in tuberculosis infection. Computation 2016, 4, 39. [Google Scholar] [CrossRef]
- Prokopiou, S.A.; Barbarroux, L.; Bernard, S.; Mafille, J.; Leverrier, Y.; Arpin, C.; Marvel, J.; Gandrillon, O.; Crauste, F. Multiscale Modeling of the Early CD8 T-Cell Immune Response in Lymph Nodes: An Integrative Study. Computation 2014, 2, 159–181. [Google Scholar] [CrossRef]
- Gao, X.; Arpin, C.; Marvel, J.; Prokopiou, S.A.; Gandrillon, O.; Crauste, F. IL-2 sensitivity and exogenous IL-2 concentration gradient tune the productive contact duration of CD8(+) T cell-APC: A multiscale modeling study. BMC Syst. Biol. 2016, 10. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.A.; Jon Timmis, J.; Qwarnstrom, E.E. Computational Models of the NF-κB Signaling Pathway. Computation 2014, 2, 131–158. [Google Scholar] [CrossRef]
- Baldazzi, V.; Paci, P.; Bernaschi, M.; Castiglione, F. Modeling lymphocyte homing and encounters in lymph nodes. BMC Bioinform. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.; Mattila, J.T.; Miller, M.; Flynn, J.L.; Linderman, J.J.; Kirschner, D. Predicting lymph node output efficiency using systems biology. J. Theor. Biol. 2013, 335, 169–184. [Google Scholar] [CrossRef] [PubMed]
- Palsson, S.; Hickling, T.P.; Bradshaw-Pierce, E.L.; Zager, M.; Jooss, K.; O’Brien, P.J.; Spilker, M.E.; Palsson, B.O.; Vicini, P. The development of a fully-integrated immune response model (FIRM) simulator of the immune response through integration of multiple subset models. BMC Syst. Biol. 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Germain, R.; Meier-Schellersheim, M.; Nita-Lazar, A.; Fraser, I. Systems biology in immunology—A computational modeling perspective. Annu. Rev. Immunol. 2011, 29, 527–585. [Google Scholar] [CrossRef] [PubMed]
- Donovan, G.M.; Lythe, G. T cell and reticular network co-dependence in HIV infection. J. Theor. Biol. 2016, 395, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Lackner, A.A.; Lederman, M.M.; Rodriguez, B. HIV pathogenesis: The host. Cold Spring Harb. Perspect. Med. 2012, 2, a007005. [Google Scholar] [CrossRef] [PubMed]
- McMichael, A.; Dorrell, L. The immune response to HIV. Medicine 2009, 37, 321–325. [Google Scholar] [CrossRef]
- Walker, B.; McMichael, A. The T cell response to HIV. Cold Spring Harb. Perspect. Med. 2012, 2, a007054. [Google Scholar] [CrossRef] [PubMed]
- Ndhlovu, Z.M.; Kamya, P.; Mewalal, N.; Kløverpris, H.N.; Nkosi, T.; Pretorius, K.; Laher, F.; Ogunshola, F.; Chopera, D.; Shekhar, K.; et al. Magnitude and Kinetics of CD8+ T Cell Activation during Hyperacute HIV Infection Impact Viral Set Point. Immunity 2015, 43, 591–604. [Google Scholar] [CrossRef] [PubMed]
- Petrovas, C.; Mueller, Y.M.; Katsikis, P.D. Apoptosis of HIV-specific CD8+ T cells: An HIV evasion strategy. Cell Death Differ. 2005, 12, 859–870. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Eymard, N.; Kurbatova, P.; Volpert, V. Mathematical modeling of erythropoiesis in vivo with multiple erythroblastic islands. Appl. Math. Lett. 2012, 25, 1217–1221. [Google Scholar] [CrossRef]
- Fischer, S.; Kurbatova, P.; Bessonov, N.; Gandrillon, O.; Volpert, V.; Crauste, F. Modelling erythroblastic islands: Using a hybrid model to assess the function of central macrophage. J. Theor. Biol. 2012, 298, 92–106. [Google Scholar] [CrossRef] [PubMed]
- Kurbatova, P.; Bernard, S.; Bessonov, N.; Crauste, F.; Demin, I.; Dumontet, C.; Fischer, S.; Volpert, V. Hybrid model of erythropoiesis and leukemia treatment with cytosine arabinoside. SIAM J. Appl. Math. 2011, 71, 2246–2268. [Google Scholar] [CrossRef]
- Volpert, V.; Bessonov, N.; Eymard, N.; Tosenberger, A. Modèle multi-échelle de la dynamique cellulaire. In Le Vivant Discret et Continu; Glade, N., Stephanou, A., Eds.; Editions Materiologiques: Paris, France, 2013. [Google Scholar]
- Kurbatova, P.; Eymard, N.; Volpert, V. Hybrid Model of Erythropoiesis. Acta Biotheor. 2013, 61, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Eymard, N.; Bessonov, N.; Gandrillon, O.; Koury, M.J.; Volpert, V. The role of spatial organization of cells in erythropoiesis. J. Math. Biol. 2015, 70, 71–97. [Google Scholar] [CrossRef] [PubMed]
- Yeghiazarian, L.; Cumberland, W.G.; Yang, O.O. A stochastic multi-scale model of HIV-1 transmission for decision-making: Application to a MSM population. PLoS ONE 2013, 8, e70578. [Google Scholar] [CrossRef] [PubMed]
- Stéphanou, A.; Volpert, V. Hybrid modeling in biology: A classification review. Math. Model. Nat. Phenom. 2016, 11, 37–48. [Google Scholar] [CrossRef]
- Gottschalk, R.A.; Martins, A.J.; Angermann, B.R.; Dutta, B.; Ng, C.E.; Uderhardt, S.; Tsang, J.S.; Fraser, I.D.; Meier-Schellersheim, M.; Germain, R.N. Distinct NFkB and MAPK Activation Thresholds Uncouple Steady-State Microbe Sensing from Anti-pathogen Inflammatory Responses. Cell Syst. 2016, 2, 378–390. [Google Scholar] [CrossRef] [PubMed]
- Nakaoka, S.; Iwami, S.; Sato, K. Dynamics of HIV infection in lymphoid tissue network. J. Math. Biol. 2016, 72, 909–938. [Google Scholar] [CrossRef] [PubMed]
- Stancevic, O.; Angstmann, C.N.; Murray, J.M.; Henry, B.I. Turing patterns from dynamics of early HIV infection. Bull. Math. Biol. 2013, 7, 774–795. [Google Scholar] [CrossRef] [PubMed]
- Dunia, R.; Bonnecaze, R. Mathematical modeling of viral infection dynamics in spherical organs. J. Math. Biol. 2013, 67, 1425–1455. [Google Scholar] [CrossRef] [PubMed]
- Strain, M.C.; Richman, D.D.; Wong, J.K.; Levine, H. Spatiotemporal dynamics of HIV propagation. J. Theor. Biol. 2002, 218, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhou, S.; Groppelli, E.; Pellegrino, P.; Williams, I.; Borrow, P.; Chain, B.M.; Jolly, C. Hybrid spreading mechanisms and T cell activation shape the dynamics of HIV-1 infection. PLoS Comput. Biol. 2015, 11, e1004179. [Google Scholar] [CrossRef] [PubMed]
- Bocharov, G.; Züst, R.; Cervantes-Barragan, L.; Luzyanina, T.; Chiglintsev, E.; Chereshnev, V.A.; Thiel, V.; Ludewig, B. A Systems Immunology Approach to Plasmacytoid Dendritic Cell Function in Cytopathic Virus Infections. PLoS Pathog. 2010, 6, e1001017. [Google Scholar] [CrossRef] [PubMed]
- Webb, S.D.; Sherratt, J.A.; Fish, R.G. Cells behaving badly: A theoretical model for the Fas/FasL system in tumour immunology. Math. Biosci. 2002, 179, 113–129. [Google Scholar] [CrossRef]
- Baker, C.T.H.; Bocharov, G.A.; Paul, C.A.H. Mathematical Modelling of the Interleukin-2 T-Cell System: A Comparative Study of Approaches Based on Ordinary and Delay Differential Equation. J. Theor. Med. 1997, 1, 117–128. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; Bastiansen, F.; Eliassen, S.; Ginot, V.; Giske, J.; Goss-Custard, J.; Grand, T.; Heinz, S.K.; Huse, G.; et al. A standard protocol for describing individual-based and agent-based models. Ecol. Model. 2006, 198, 115–126. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; DeAngelis, D.L.; Polhill, J.G.; Giske, J.; Railsback, S.F. The ODD protocol: A review and first update. Ecol. Model. 2010, 221, 2760–2768. [Google Scholar] [CrossRef]
- Bouchnita, A.; Bocharov, G.; Meyerhans, A.; Volpert, V. Hybrid approach to model the spatial regulation of T cell responses. BMC Immunol. 2016. accepted. [Google Scholar]
- Ananworanich, J.; Chomont, N.; Eller, L.A.; Kroon, E.; Tovanabutra, S.; Bose, M.; Nau, M.; Fletcher, J.L.; Tipsuk, S.; Vandergeeten, C.; et al. HIV DNA Set Point is Rapidly Established in Acute HIV Infection and Dramatically Reduced by Early ART. EBioMedicine 2016, 11, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Ananworanich, J.; Sacdalan, C.P.; Pinyakorn, S.; Chomont, N.; de Souza, M.; Luekasemsuk, T.; Schuetz, A.; Krebs, S.J.; Dewar, R.; Jagodzinski, L.; et al. Virological and immunological characteristics of HIV-infected individuals at the earliest stage of infection. J. Virus Erad. 2016, 2, 43–48. [Google Scholar] [PubMed]
- Grossman, Z.; Polis, M.; Feinberg, M.B.; Grossman, Z.; Levi, I.; Jankelevich, S.; Yarchoan, R.; Boon, J.; de Wolf, F.; Lange, J.M.; et al. Ongoing HIV dissemination during HAART. Nat. Med. 1999, 5, 1099–1104. [Google Scholar] [CrossRef] [PubMed]
- Likhoshvai, V.A.; Khlebodarova, T.M.; Bazhan, S.I.; Gainova, I.A.; Chereshnev, V.A.; Bocharov, G.A. Mathematical model of the Tat-Rev regulation of HIV-1 replication in an activated cell predicts the existence of oscillatory dynamics in the synthesis of viral components. BMC Genom. 2014, 15. [Google Scholar] [CrossRef] [PubMed]
- Petrovas, C.; Yamamoto, T.; Price, D.A.; Rao, S.S.; Klatt, N.R.; Brenchley, J.M.; Douek, D.C.; Gostick, E.; Angermann, B.R.; Grossman, Z.; et al. High production rates sustain in vivo levels of PD-1high simian immunodeficiency virus-specific CD8 T cells in the face of rapid clearance. J. Virol. 2013, 87, 9836–9844. [Google Scholar] [CrossRef] [PubMed]
- Peligero, C.; Argilaguet, J.; Güerri-Fernandez, R.; Torres, B.; Ligero, C.; Colomer, P.; Plana, M.; Knobel, H.; García, F.; Meyerhans, A. PD-L1 Blockade Differentially Impacts Regulatory T Cells from HIV-Infected Individuals Depending on Plasma Viremia. PLoS Pathog. 2015, 11, e1005270. [Google Scholar] [CrossRef] [PubMed]
- Grossman, Z.; Paul, W.E. Dynamic tuning of lymphocytes: Physiological basis, mechanisms, and function. Annu. Rev. Immunol. 2015, 33, 677–713. [Google Scholar] [CrossRef] [PubMed]
- Paul, W.E.; Grossman, Z. Pathogen-sensing and regulatory T cells: Integrated regulators of immune responses. Cancer Immunol. Res. 2014, 2, 503–509. [Google Scholar] [CrossRef] [PubMed]
- Bocharov, G.A.; Telatnikov, I.S.; Chereshnev, V.A.; Martinez, J.; Meyerhans, A. Mathematical modeling of the within-host HIV quasispecies dynamics in response to antiviral treatment. Russ. J. Numer. Anal. Math. Model. 2015, 30, 157–170. [Google Scholar] [CrossRef]
- Okoye, A.; Meier-Schellersheim, M.; Brenchley, J.M.; Hagen, S.I.; Walker, J.M.; Rohankhedkar, M.; Lum, R.; Edgar, J.B.; Planer, S.L.; Legasse, A.; et al. Progressive CD4+ central memory T cell decline results in CD4+ effector memory insufficiency and overt disease in chronic SIV infection. J. Exp. Med. 2007, 204, 2171–2185. [Google Scholar] [CrossRef] [PubMed]
- Paul, W.E.; Milner, J.D.; Grossman, Z. Pathogen-sensing, regulatory T cells, and responsiveness-tuning collectively regulate foreign- and self-antigen mediated T cell responses. Cold Spring Harb. Symp. Quant. Biol. 2013, 78, 265–276. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).