Abstract
We present some details of our recently-proposed Time-Dependent Density-Functional Theory (TDDFT) for strongly-correlated materials in which the exchange-correlation (XC) kernel is derived from the charge susceptibility obtained using Dynamical Mean-Field Theory (the TDDFT + DMFT approach). We proceed with deriving the expression for the XC kernel for the one-band Hubbard model by solving DMFT equations via two approaches, the Hirsch–Fye Quantum Monte Carlo (HF-QMC) and an approximate low-cost perturbation theory approach, and demonstrate that the latter gives results that are comparable to the exact HF-QMC solution. Furthermore, through a variety of applications, we propose a simple analytical formula for the XC kernel. Additionally, we use the exact and approximate kernels to examine the nonhomogeneous ultrafast response of two systems: a one-band Hubbard model and a Mott insulator YTiO3. We show that the frequency dependence of the kernel, i.e., memory effects, is important for dynamics at the femtosecond timescale. We also conclude that strong correlations lead to the presence of beats in the time-dependent electric conductivity in YTiO3, a feature that could be tested experimentally and that could help validate the few approximations used in our formulation. We conclude by proposing an algorithm for the generalization of the theory to non-linear response.
1. Introduction
Materials with strong electron-electron correlations form an important class of condensed matter systems with unusual physical properties and numerous technological applications (see, for example, [1]), which are expected to significantly increase with advances in nanotechnologies [2,3,4,5,6]. The non-equilibrium properties of these strongly-correlated materials are particularly interesting for several reasons: (1) they allow better understanding of the excitation spectrum, orbital occupancies, lattice potential profile and other “inherent” properties of the unperturbed system; (2) systems may be driven into new phases that cannot be achieved when in equilibrium [7]; (3) potential applications in “bulk-” and nano-technologies, such as switches [8], microelectromechanical system (MEMS) devices [9], biosensors [10] and ultrafast lithium storage batteries [11].
An accurate theoretical description of experimental results, as well as the prediction of the desired properties of Strongly-Correlated Materials (SCMs) out of equilibrium is a very complex task. The power of many-body approaches is remarkably limited in this case, since one needs to deal with multi-orbital systems with no translational and temporal invariance. As a result, the corresponding simulations, which involve very large (especially for nanoscale systems) Green’s function matrices with multiple arguments (atom coordinate, electron orbital and spin indices and complex time variable), are extremely slow. As an alternative, the ab initio Time-Dependent Density-Functional Theory (TDDFT) approach [12], because of its technical simplicity, seems to be a better candidate for the purposes mentioned above. However, to make TDDFT applicable to SCMs, one needs to construct an appropriate exchange-correlation (XC) potential, since the available ones are not very successful in describing these systems, even in the static (DFT) case.
The most straightforward way to construct such a potential is to use a many-body theory approach in which some of the strongly-correlated problems can be solved either exactly or by using an accurate and physically-transparent approximation. In this case, the XC potential (kernel) is found by taking functional derivative(s) of the obtained XC action with respect to the electron charge density with the corresponding boundary terms arising from the requirements of causality (in the adiabatic case, one differentiates the XC energy with no boundary terms). Indeed, most of the progress in building the XC potential for SCMs has been made for the exactly-solvable systems (using, e.g., the Bethe ansatz approach [13]) or systems that can be solved with a high numerical accuracy: small clusters [14,15,16,17,18,19,20,21], including one- and a few-impurity junctions [22,23,24,25], and one-dimensional systems [15,21,26,27,28] (for an over-review of the relationship between static DFT and the two-site Hubbard model, see [29,30]). Thus, so far, most of the results have been obtained for “small” systems: small clusters and chains. Nevertheless, these results already give an idea about the structure of the XC potential and XC kernel needed for SCMs and the possible physical phenomena that may be described within TDDFT. In order to “converge” to a universal potential (kernel) valid in all dimensions, further analytical and/or numerical studies, especially of two-dimensional systems, surface and bulk materials, are required. The power of the analytical methods for “large” (extended) strongly-correlated systems is mainly constrained to some limiting cases, such as systems with low particle densities for which it is possible to obtain an accurate result for the exchange-correlation energy [31,32].
Probably, the most powerful, modern, numerical, many-body approach to study extended SCMs is Dynamical Mean-Field Theory (DMFT) [33,34]. In particular, combined with DFT (DFT + DMFT) [35,36], it was successfully applied to analyze the equilibrium properties of bulk systems and films [37,38] and recently even nanostructures (see, e.g., [39,40]). The success of DMFT is based on an “impurity approximation”, i.e., neglecting the non-local correction to the electron self-energy, which is an accurate approximation for systems with a large atomic coordination number (or in high dimensions). This approximation enables one to solve strongly-correlated problems with reasonable computational resources. Recently, the approach was also generalized to examine systems in non-equilibrium [41,42,43], though the application has so far been restricted to systems with computational super-cells that contain less than ten non-equivalent atoms. On the other hand, one can use the equilibrium DMFT solution to construct the XC potential, which could be used to examine the non-equilibrium response of SCMs within TDDFT. In this regard, Karlsson et al. applied DMFT to obtain the adiabatic XC potential for the three-dimensional one-band Hubbard model [44]. To test the theory, the authors used the exact numerical solution for a cubic cluster with a finite local Coulomb repulsion on the central atom. In this important work, the authors showed that their adiabatic TDDFT + DMFT can successfully describe the response of the system when correlations are not very strong and/or the electron density is not very close to half-filling. Since memory effects (non-adiabaticity or frequency dependence of the XC potential) were neglected in their approach, one expects that inclusion of these effects into the theory will make it more robust.
The importance of non-adiabatic effects has already been demonstrated for some strongly correlated systems of different sizes and geometries. For example, in the case of the Hubbard dimer, we have recently demonstrated [17] that the non-adiabaticity of the XC kernel is essential for obtaining an electronic spectrum with the characteristic satellite peaks resulting from dynamical (time-resolved) local interactions between electrons. Furthermore, Fuks and Maitra [18,19] showed that the adiabatic approximation leads to the wrong results for the charge-transfer dynamics for the Hubbard dimer. In the case of the Hubbard chain, it was indicated that non-adiabatic effects are important at some values of doping [28]. Recently, we have proposed a non-adiabatic TDDFT + DMFT approach [45], which allows one to take into account non-adiabatic effects in practically all types of systems, from clusters to bulk materials. In this approach, the XC kernel is obtained from the charge susceptibility for an effective (many-body theory) Hubbard model solved using DMFT. We have also applied this TDDFT + DMFT method to the bulk Hubbard model and demonstrated that non-adiabatic effects significantly modify the adiabatic results for the excitation spectrum and the non-equilibrium charge response of the system. To test the accuracy of the results, we compared the TDDFT + DMFT solutions with those from non-equilibrium DMFT calculations to find better agreement when non-adiabatic effects are included in the former.
In this work, we review some details of the non-adiabatic TDDFT + DMFT approach [45], including the algorithm, to obtain the non-adiabatic XC kernel. We derive numerical results for the XC kernel for the 3D one-band Hubbard model by using two routes to solve the DMFT equations, a numerically-exact Hirsch–Fye Quantum Monte Carlo (HF-QMC) and an approximate, computationally-efficient Iterative Perturbation Theory (IPT) approach, and show that the latter is a reasonable approximation for getting preliminary, semi-quantitative or even quantitative results, as well as insight into the properties of the system. We also propose an analytical fitting formula for the frequency dependence of the XC kernel for the 3D one-band Hubbard model. Next, we compare some results obtained with the XC kernel, solved using the HF-QMC and IPT approaches for two prototypical systems, focusing on the role of non-adiabatic effects in the response of the systems (excited charge density and conductivity). Finally, we formulate the main steps for further extension of the proposed methodology for the general non-linear response.
2. The TDDFT + DMFT Formalism
2.1. The Linear Response TDDFT
In TDDFT, the effective electronic wave function is propagated in time by solving the Kohn–Sham (KS) equation [12]:
In this equation, the first term in the brackets is the kinetic energy operator; Vion(r) is the ion potential; is the Hartree potential; and is the external potential that describes, for example, laser pulse fields. The remaining and the most nontrivial term is the XC potential that takes into account the effects of electron-electron interaction, including memory effects (non-adiabaticity). Since and are functionals of the electron charge density, Equation (1) has to be solved self-consistently with the particle number equation:
where the summation is performed over the states that are occupied in the ground state ( is the Fermi momentum).
Strictly speaking, to find the expression for the time-dependent by using the many-body technique, one has to minimize the XC action functional in both charge density and the electron self-energy with the corresponding boundary (causality) terms (for details, see, e.g., [46] for the case of TDDFT and [37] for the static case). Such challenging steps may be avoided by resorting to the linear-response regime, for which we can write:
where:
is the XC kernel. The first term in Equation (3), , is the static part of the potential, which can be calculated with methods such as DFT + DMFT and be included in the electronic spectrum of the system. The focus here is on the dynamical part of the potential (the last term in Equation (3)); to obtain which, we provide some details below.
The XC kernel can be obtained from the many-body approach by using the following relationship (in the frequency domain):
where:
is the charge susceptibility of the interacting system ( is the time-ordering operator applied to the charge density operators) and is that for the non-interacting Kohn–Sham electrons [46]. The frequency-dependent susceptibilities in Equation (5) can be obtained from the Fourier transform of the function in Equation (6): (because of time translation invariance, the susceptibility depends on the difference of its time arguments ).
To find the charge susceptibility Equation (6), which in the general, multi-orbital case is a sum of the corresponding orbital spin susceptibilities,
( and are the orbital and the spin indices), we use the many-body DMFT approach as described in the next subsection.
2.2. Dynamical Mean-Field Theory and the XC Kernel
2.2.1. Single-Electron Green’s Functions
In DMFT, the electronic system is often approximated by the following Hubbard Hamiltonian:
where are the electron annihilation and creation operators, are the (inter- and intra-site) hopping parameters and are the on-site Coulomb interaction energy parameters ( are the site, the orbital and the spin indices). Finally, is the chemical potential, which fixes the charge density in the system. Most of the single-particle properties can be obtained from the single-particle spin-orbital Green’s function:
In general, the solution for this Green’s function in the frequency-momentum representation, which can be written as:
where a and b now represent combined orbital and spin indices and and are the DFT spectrum and the self-energy matrices with respect to these indices (diagonal and non-diagonal matrices, correspondingly). In the DMFT approximation, one neglects the momentum dependence of the self-energy,, i.e., one takes into account the time-resolved fluctuations and neglects the spatial ones. The problem then reduces to that for a single-site with the local-in-space Green’s function:
where both the electron local Green’s function and self-energy are the same for the original (extended) and the single-site systems. In the single-site model, the on-site electrons interact with the bath of other electrons described by the field , called the dynamical mean-field, which is related to the local Green’s function by means of the Dyson equation:
Finally, to close the system of equations for three unknown matrix functions, and one adds the so-called “impurity equation”, the path integral expression for the single-site Green’s function:
where and are Grassmann variables, is the inverse temperature, and we assume summation over the repeating indices c and d. The function in the denominator:
is the partition function. Equations (12)–(14) are written in imaginary time (Matsubara) representation, which is most convenient to perform the path integration. Once the imaginary-time Green’s function is found, one can find its real frequency dependence in the following way. First, the corresponding imaginary (Matsubara) frequency Green’s function is calculated (, and then, the analytical continuation of the Green’s function to the real frequency branch, , is carried out.
In summary, the DMFT part of the methodology involves solving the set of Equations (11)–(13). The only nontrivial equation in this set is the impurity equation, Equation (13). In this work, we solve it in two different ways: by using a non-expensive Iterative Perturbation Theory (IPT) approximation (Appendix A) and by performing exact numerical path integration with the HF-QMC algorithm (Appendix B).
2.2.2. Two-Electron Green’s Functions
To calculate the XC kernel by using Equations (5)–(7), one needs to go beyond the single-electron picture, namely one needs the two-particle correlation functions . In general, these functions can be obtained by using the Bethe–Salpeter equation (BSE) formalism [46], starting from generalized susceptibilities:
where, as usual, are the spin-orbital indices and and are the corresponding electron site and time coordinates (we make one of the time arguments equal to zero due to time translation invariance). More precisely, we need the frequency transform of the susceptibilities Equation (15):
In the single-site (impurity) approximation used in DMFT, one approximates the susceptibilities Equation (16) by local functions connected to the local vertex function by means of the following equation:
where are the corresponding free-electron generalized susceptibilities. To make the notations shorter, we omit the spin-orbital indices. The vertex function that enters the last equation is the key function in the proposed formalism, since one can use it to calculate the required susceptibilities in Equations (6) and (7) as:
where:
and the Green’s functions are defined in Equation (10).
In the framework of DMFT, to calculate usually, the Dynamical Vertex Approximation () [47] is employed. Namely, in the scheme, one first calculates the local generalized susceptibility (left-hand side of Equation (17)) by using the single-site (impurity) approximation:
(here, simple single-particle correlation functions from Equation (15) are omitted for brevity). Then, after Fourier transformation of the resulting function (Equation (16)) and its substitution into Equation (17), one gets the vertex function and, finally, the susceptibility and the XC kernel from Equations (18) and (5). In , the vertex is momentum independent and depends only on frequencies, , which justifies the name for the approximation.
Another approach, which is more transparent and numerically efficient as compared to the one described above, is to calculate the vertex function by using a truncated perturbation theory with respect to U. For this, it is convenient to use the Bethe–Salpeter equation (BSE), which connects the vertex function in Equations (17) and (18) with the so-called irreducible vertex function :
In this case, the problem is shifted to finding the irreducible vertex function. In the lowest order approximation, one uses (see, e.g., [48]), which gives the RPA susceptibility [46]. This function together with Equation (5) gives the following XC kernel:
where is the non-interacting (DFT) susceptibility and is the one-loop susceptibility equal to the susceptibility defined in Equation (18) and calculated at . Higher-order U corrections to the XC kernel can be systematically included through the corresponding corrections to the solution of Equations (21).
Below, we use the kernel Equation (22) to demonstrate the ability of TDDFT to grasp the main characteristic properties of SCMs caused by time-resolved, electron-electron interactions.
3. The DMFT XC Kernel for the One-Band Hubbard Model
We apply the above formalism to the prototypical case of the one-band bulk Hubbard model Equation (8) with a Gaussian free electron Density Of States (DOS): . A system with such a DOS is most relevant to DMFT, since it corresponds to a cubic lattice with infinite coordination number. In this case, the electron self-energy is momentum independent, and the DMFT solution is the exact one [34]. On the other hand, the Gaussian DOS corresponds to a general physical situation of a narrow-band system with the bandwidth of order of several t’s (where is the hopping parameter). Below, we analyze the most important case of half-filling, assuming that the system is in the paramagnetic phase.
3.1. Density of States
We begin with calculations of the single-particle DOS, obtained from the local Green’s function:
at different values of U and temperature by using the IPT and HF-QMC approaches. The numerical results are presented in Figure 1 and Figure 2.
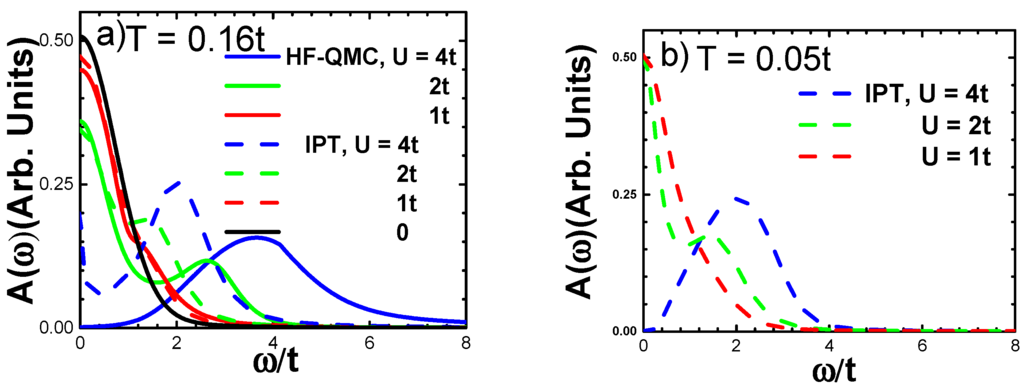
Figure 1.
The single particle Density Of States (DOS) as a function of frequency obtained for U = 1t, 2t and 4t: (a) for T = 0.16t with both the Hirsch–Fye Quantum Monte Carlo (HF-QMC) and the Iterative Perturbation Theory (IPT) approaches; (b) for T = 0.05t using IPT only.
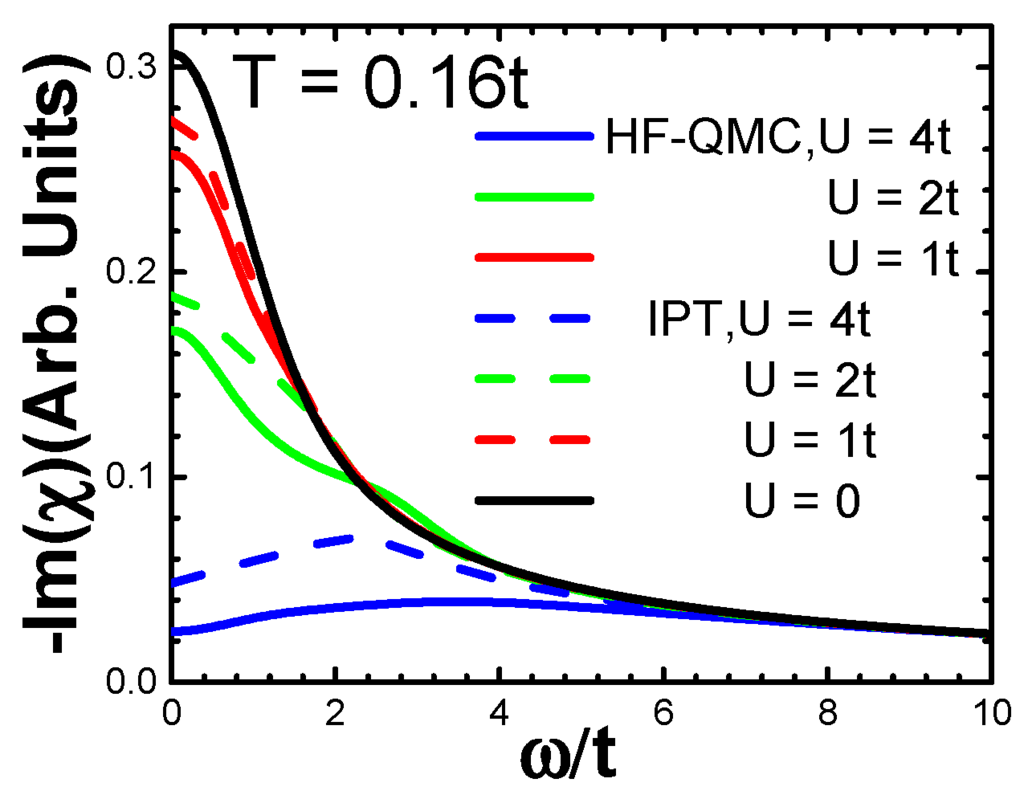
Figure 2.
The imaginary part of the charge susceptibility as a function of frequency obtained with the HF-QMC and the IPT approaches at U = 1t, 2t and 4t and temperature T = 0.16t.
In Figure 1, we present the results for the DOS for U = 1t, 2t and 4t obtained within these two approaches at temperature T = 0.16t (this corresponds to the low temperature regime, since the temperature is much smaller than two other energy scales in the system: ). Only the positive frequency part of the DOS is shown, since at half-filling, is an even function of frequency. Figure 1 shows that the two approaches give qualitatively and semi-quantitatively the same dependence of the DOS on U: at small U’s (red curves), it is close to the non-interacting electron Gaussian DOS; at larger U’ (green curves), three quasi-bands (actually, peaks of the redistributed electron spectral function) emerge: two Hubbard quasi-bands, with the peaks separated by a frequency and the central quasi-particle peak around zero frequency. Finally, at large U’s (blue curves), the system is in a Mott insulator regime with the two Hubbard sub-bands separated by the gap .
The difference between the exact HF-QMC and approximated IPT DOS increases with U, though the shape of the curves remains the same. It is important that the computationally-inexpensive IPT solution gives results similar to the exact ones, except the case U = 4t (see below). A good performance of IPT can be especially beneficial for complex systems with many non-equivalent atoms and orbitals, for which IPT can be used relatively easily as the first approximation to get an intuitive insight on the general features of the XC kernel and even on the properties of the materials. We will focus on the exact HF-QMC results, presenting the IPT solutions, only to gauge its accuracy at different strengths of correlations. We also used the IPT solution to check the temperature dependence of the results (Figure 1b). It follows from Figure 1a,b that the IPT DOS for T = 0.16t and T = 0.05t are very similar, except for a large U (U = 4t). At a lower temperature, the gap opens in the spectrum due to suppression of the central peak, while other parts of the spectrum remain the same. Since in the HF-QMC case, the gap is already open at U = 4t, T = 0.16t, one does not expect to get any difference in the spectrum at lower temperatures, which are computationally much more demanding, within this approach.
3.2. Charge Susceptibility
As the next step, we obtained the excitation spectrum of the system for parameters used in Figure 1 by calculating the imaginary part of the one-loop susceptibility in the local-in-space approximation:
(for the inclusion of the spatial dependence of the kernel in this scheme, see Appendix C). The results are given in Figure 2.
It follows from Figure 2 that the excitation spectrum is in agreement with the DOS of the system. That is, at small U’s (red), the main excitation processes take place around zero frequency (“Fermi level”) states, at which the DOS has the sharp peak. At medium U’s (green), for which the DOS is three-peaked, the excitations mainly take place around the central (“Fermi level”) quasi-particle peak, though now, this peak is much lower compared to the small-U case as a result of reduced zero-frequency DOS. More importantly, such a peak, known to play a very important role in the properties of many SCMs, cannot be obtained with DFT + U and other “non-dynamic” approximations. In addition, there is another pronounced type of the excitations at intermediate U’s, between the left and right Hubbard sub-bands, revealed in the (not very sharp) peak of at . Finally, at large U’s (blue), the excitation spectrum is dominated by the transitions between the Hubbard sub-bands, separated by the energy. Again, qualitatively and semi-quantitatively, the HF-QMC and IPT results are rather similar, which is not surprising since they are the consequence of very similar results for the DOS in Figure 1.
Below, we show that the features of the excitation spectrum in Figure 2, including the zero-energy quasi-particle peak, define the structure of .
3.3. The XC Kernel
We calculate the XC kernel Equation (5) in the local-in-space approximation by using the local susceptibility Equation (22). The static part in Equation (5) is ignored by assuming that it is much smaller than the dynamic term in SCMs (which has much stronger dependence on U).
3.3.1. Numerical Results
In Figure 3, the HF-QMC and the IPT results for for the one-band Hubbard model for the values of U used in Figure 1 and Figure 2 are presented.
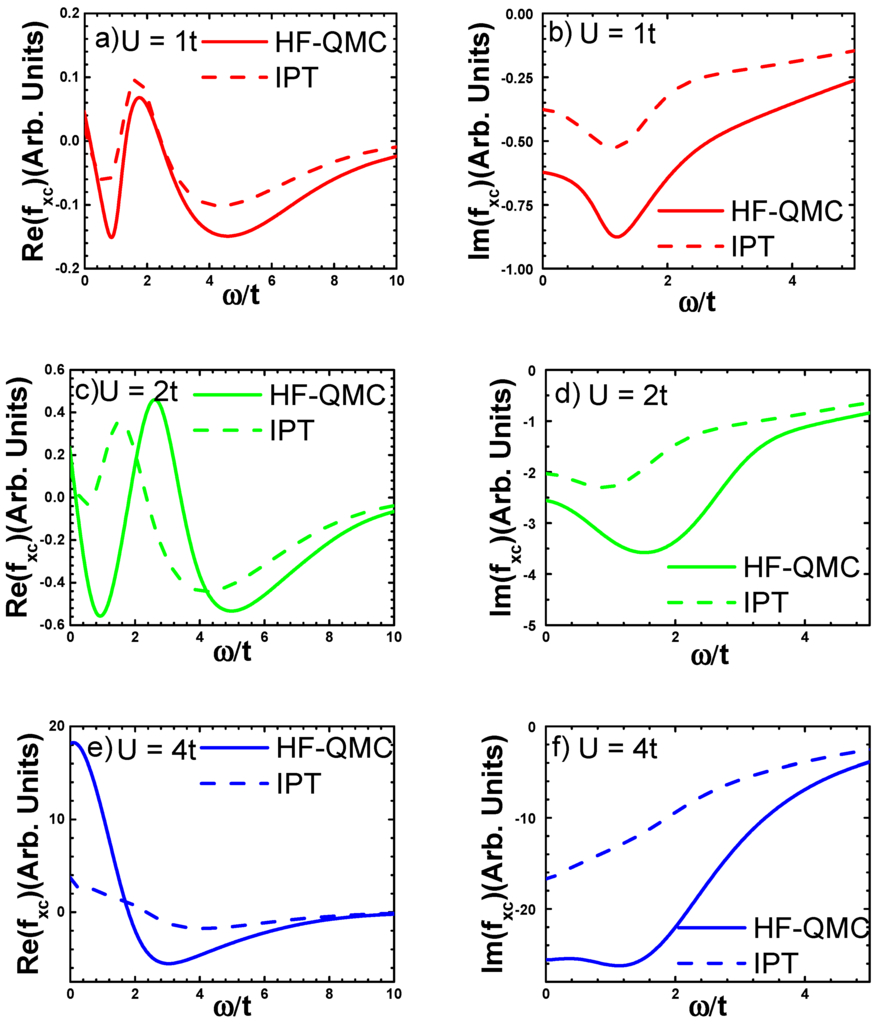
Figure 3.
The real (left column) and imaginary (right column) parts of for the one-band Hubbard model at different values of U and temperature T = 0.16t obtained by using the IPT and the HF-QMC approaches.
One can make several conclusions about the qualitative frequency dependence of the XC kernel: (1) the magnitude of the kernel grows with U; (2) the real part of XC is a decaying oscillating function of frequency with the oscillation period proportional to U; (3) its imaginary part has one peak at a frequency and also decays at large frequencies; (4) in all cases (surprisingly), both the real and imaginary parts decay with approximately the same decay constant . Again, the IPT and the HF-QMC results are in a good qualitative and semi-quantitative agreement with each other.
The physical interpretation of the shape of the XC kernel is as follows: in real-time representation, the kernel is an oscillating function of time with the period of oscillations ~U, which corresponds to scattering between singly- and doubly-occupied “sub-bands” separated in energy by approximately U. The decay constant corresponds to the memory (scattering) time of the system, defined by the XC kernel. Indeed, our kernel includes the effects of time-resolved electron-electron interactions successfully captured by DMFT.
Comparison of our results for the XC kernel with another available rare result for the frequency-dependent XC kernel for strongly-correlated systems, namely for a cubic cluster [14], shows that despite significant differences between the system considered in this work and [14], both kernels share several similarities: a peak in the imaginary part of the kernel and an oscillatory (rather irregular in the case of the cluster) feature of the real part of the kernel, with oscillation and decay periods ~U (though in the case of the cluster, the proportionality coefficients are a couple of times larger than in the extended system). Given these generalities, we were motivated to find an analytical (and at least semi-quantitatively correct) frequency-dependent kernel common for systems of different sizes and geometries. It is also important to mention that in constructing an accurate analytical kernel, one also needs to take into account known constraints that come from many-body theory, such as the generalized translational invariance and the zero-force theorem (see [20] for some discussion in this regard).
3.3.2. Analytical Fitting
To accompany the numerical results for the XC kernel in Figure 3 with a simple analytical fitting expression, we begin with the approximate Gross–Kohn XC kernel for the Homogeneous Electron Gas (HEG) [49,50] with the imaginary part (the real part can be found by using the Kramers–Kronig relation). This kernel has correct analytically derived low- and high-frequency asymptotes analytically obtained for the HEG (see also [46] for an over-review of the subject). It appears that one can reproduce the numerical curves in Figure 3 reasonably accurately by using the following simple kernel:
obtained by multiplying the Gross–Kohn kernel by the term consisting of two exponential parts and shifting the zero-frequency value (Figure 4). The fitting parameters at different U’s are given in Table 1.
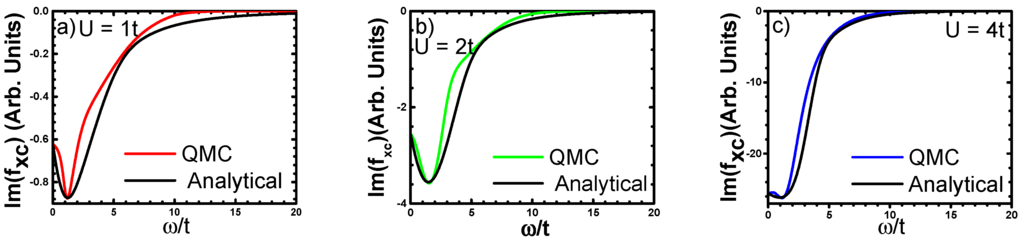
Figure 4.
HF-QMC and analytical fitting (Equation (25)) results for the imaginary parts of the XC kernels from Figure 3.

Table 1.
Fitting parameters for the analytically-approximated expression for the imaginary part of the XC kernel Equation (25) at different values of U.
From the fitting formula, it is clear that the kernel decays faster with the frequency growth when the electron charge density is strongly nonhomogeneous (in SCMs, it is mostly localized around the atoms, i.e., the situation is opposite that for HEG). Such a difference between the kernels of the homogeneous and nonhomogeneous electron gases might be explained by stronger scattering effects at short times (large frequencies) in the nonhomogeneous case (since the scattering time is proportional to 1/U), which leads to a weaker dependence on frequency at large frequencies. Otherwise, the structures of the kernel are rather similar.
Further, thorough examination of the structure of the DMFT XC kernel for SCMs, especially for systems with reduced dimensionality and/or many electron orbitals, is needed in order to arrive at an analytical formula for that is proven to be accurate. However, despite the over-simplified fitting above, one can already get an intuitive feeling of the connection between the frequency dependence of the XC kernel and the strong spatial non-homogeneity of the electronic charge distribution (charges localized around the atoms).
4. Applications: Ultrafast Charge Response
4.1. One-Band Hubbard Model
As the first application of the kernels in Figure 3, we analyze the charge response of the Hubbard system excited by a homogeneous electric laser pulse (the electric field , the field magnitude , the pulse duration ). Here and in the next subsection, we solved the KS Equation (1) within the density-matrix formalism, expanding the KS wave function in the basis of static (DFT) wave functions (for the details of the formalism and the form of the laser pulse, see Appendix C). The results for the excited change density in the case of different U’s and approximations for the XC kernel are shown in Figure 5.
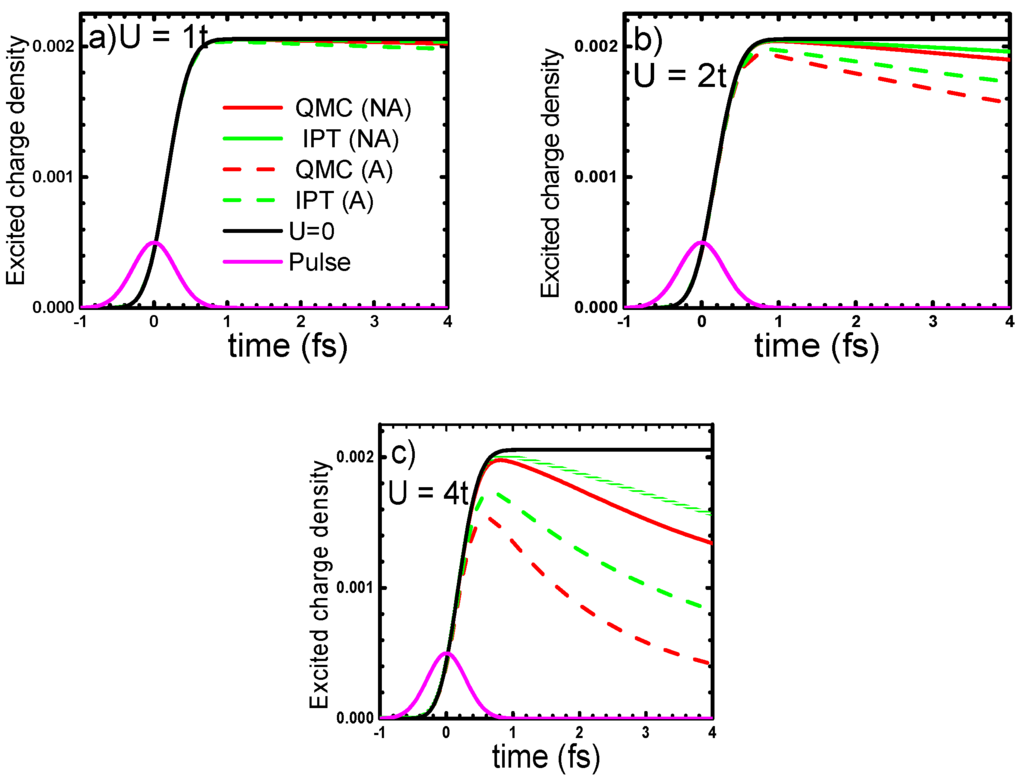
Figure 5.
Time dependence of the excited charge density in the one-band Hubbard model in the case of 0.8-fs laser pulse perturbation at different values of U and adiabatic (A) and non-adiabatic (NA) exchange-correlation (XC) kernels.
Several conclusions can be made from Figure 5. First, the electrons get “quasi-ballistically” excited during the pulse excitation. Then, the excited charge density starts to decrease, but at the time scale an order of magnitude longer, as compared to the charge pumping time. This indicates that the main process at this stage is not repopulation of the lower band, but excitation relaxation of the electronic system to a new quasi-equilibrium state with high electronic temperature. The duration of this process strongly depends on the value of U and may vary from several to hundreds of femtoseconds. These results are in a qualitative and (very probably) semi-quantitative agreement with recent experimental results on the ultrafast breakdown of the Mott insulating state in VO2 [51], where at initial times, the electronic and lattice subsystems are disentangled (i.e., the lattice is frozen at times below ~100 fs), and the metallization happens without the lattice transformation. The last process takes place on a ps to ns time scale, when the lattice undergoes a transformation to the stable (metallic, high-temperature) rutile phase. Theoretical analysis based on the solution of phenomenological (spatially-averaged) Bloch equations is also in agreement with this scenario [52]. The advantage of the TDDFT + DMFT approach is that it can be easily applied to study also a spatially non-homogeneous response by properly taking the exact electronic structure of the material. To study the longer time response, one needs to include the lattice dynamics, which is one of our primary tasks for the near future.
On comparing the results for the system response for different XC kernels, one can find from Figure 5 that the HF-QMC gives a faster relaxation of the system, though the order of the timescales of the excitation and relaxation stages for both HF-QMC and IPT solutions are the same.
Finally, we would like to discuss the difference between the solutions with the full kernel and its instant (adiabatic) approximation, when the non-adiabatic effects are neglected, i.e., when or the kernel is frequency independent. This is the case of the DFT + U approximation. It follows from our calculations above that the memory (dynamical) effects slow down the relaxation of the system, since the scattering is more efficient on “frozen” electrons (for the complex role of “movable” and “frozen” (heavy) charges and between both subsystems, see, e.g., [53]). Thus, it appears that consideration of non-adiabaticity is important even at the femtosecond time scale.
4.2. Mott Insulator YTiO3
Another example we consider here is the charge response of the effective three d-band insulator YTiO3. We refer the reader to [45,54,55,56] for details on the static properties of the system obtained with DFT + DMFT and other approaches. The free-electron spectrum of YTiO3 was obtained by using a tight-binding model with the parameters given in [54]. In this subsection, we focus mainly on the role of the spatial overlap of the interacting orbital charges in the system response. To model this overlap, we multiply the local kernel Equation (5) at U = 4t by a parameter A, which might be regarded as the strength of the kernel (for details, see Appendix C). The results for the charge response of this system at U = 4 eV, relevant to YTiO3, and different values of A are presented in Figure 6a.
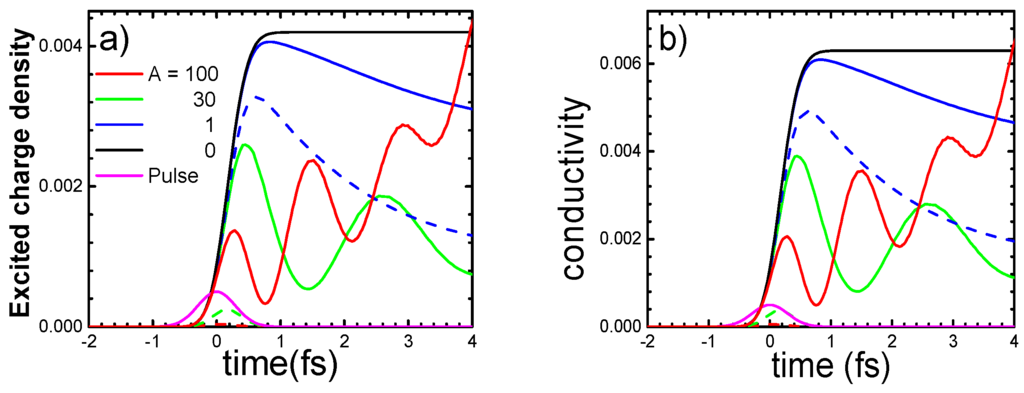
Figure 6.
Time-dependence of the excited charge density (a) and Brugemman’s conductivity (b) for YTiO3 excited by a 0.8-fs homogeneous Gaussian laser pulse (field magnitude ). The results correspond to U = 4 eV and to different XC kernels (see the text for details). The dashed lines correspond to the solution with the adiabatic XC kernel.
One can see from Figure 6a that at small A, the relaxation time decreases with increasing A, which is natural for the linear response regime (the relaxation time is inversely proportional to the strength of the effective electron-electron interaction described by the XC kernel). With the further increase of A, the system response transforms from a monotonous decrease of the excited charge density to a decrease with beatings (green curve) and even to a nonlinear growing of the excited charge density with beatings at very large A (red curve). Of course, only further experimental testing will allow one to estimate the values of the parameter A relevant to YTiO3. Using Brugemman’s theory of conductivity [57], in which the current is proportional to the fraction of the metallic area of the excited insulator or to the excited charge density, one can easily find these beatings also in the time-dependent conductivity (Figure 6b). Similar to the previous subsection, the beatings can be explained by the charge transitions between singly-occupied and empty orbital levels, i.e., by dynamical effects. As one can see from Figure 6, the results for the conductivity obtained with the adiabatic kernel do not show this effect.
5. The Non-Linear Response: A Possible Extension of the Formalism
In the above, we have focused on the linear response of systems to an external perturbation. In this section, we briefly describe a possible way to extend the above approach to the nonlinear response of systems. For this, we propose to use van Leeuwen’s non-equilibrium (TDDFT) generalization [58] of the equilibrium (DFT) Sham-Schlueter equation [59,60] that connects the XC potential with the electron self-energy:
where is the TDDFT Kohn–Sham one-electron Green’s function and and are the many-body theory one-electron Green’s function and self-energy, respectively. The time integrations in Equation (26) are performed over the three-branch complex time contour (see, e.g., [41,42,43]). Since both sides of the last equation have integration over and , the corresponding expressions under the integral must also be equal, which gives:
This equation gives the exact expression for the XC potential in terms of the many-body XC self-energy and Green’s function. This opens the door to controllable analytical approximations for , in particular by using known analytical properties of the self-energy, such as its high-frequency dependence and different sum rules (see, for example, [61,62]).
To make Equation (27) relevant to TDDFT, one needs to express the expression on the right-hand side in terms of the KS wave functions. At this point, some approximations have to be made to solve the above equations. As the most straightforward step, we assume that the has its DMFT form (see Equation (11), in which the electron self-energy has no index XC). Next, we approximate the many-body Green’s function by the “non-interacting” Kohn–Sham Green’s function:
With the above, the proposed DMFT XC potential Equation (27) becomes an orbital TDDFT potential. The approximation Equation (28) can be justified as follows. We would like to include correlation effects in the XC potential at the DMFT level described by . Indeed, the last function describes the contribution of the electron-electron interaction effects to the electronic spectrum, which follows, for example, from Equation (11). In TDDFT, the XC potential has a similar role, describing the effects of the electron-electron interactions, which leads to a correction to the electron spectrum. This can be seen by comparing the many-body equation for the Green’s function that involves , (where is the kinetic energy of non-interacting system) and the TDDFT KS Equation (1). Therefore, it is not surprising that two functions, and , are proportional to each other in Equation (27). To take into account the correlation effects in both theories, many-body DMFT and TDDFT, at the same level means to neglect the contribution of these effects to Equation (27) that come from other functions, i.e., Green’s functions , so one can put . This approximation gives the time-dependent generalization of the Local Density Approximation (LDA) potential proposed by Sham [60]:
The approximation for the XC potential for SCM Equation (29) can be further improved by correcting the result for in Equation (27). For example, it can be done by using the equation:
Indeed, from Equation (30) at fixed (DMFT solution) and (defined in Equation (29)), one can find a more accurate result for Green’s function with respect to the one given in Equation (29), .
6. Summary
We have presented a summary of our recently-developed linear-response non-adiabatic TDDFT + DMFT approach for SCMs. The key element of the theory, the XC kernel, is defined by the DMFT self-energy of the electron. We established the main features of the dependence of the kernel on frequency by solving the DMFT equations exactly with HF-QMC and by using an approximate (IPT) approach and demonstrated that both results are in reasonable agreement, which makes the computationally-efficiently IPT solver attractive for initial considerations of systems of interest. We also proposed a simple analytical expression for the XC kernel.
We used the XC kernels calculated with both approaches to study the ultrafast electronic response in two systems and found that the inclusion of the non-adiabatic, or memory, effects significantly modifies the femtosecond response; in particular, they may lead to beatings in the conductivity of excited insulator YTiO3.
Finally, we formulated a scheme for generalizing the theory for the case of nonlinear response.
We hope these results will be helpful in constructing full self-consistent TDDFT for some of the most challenging condensed matter systems: materials with strong electron-electron correlations.
Acknowledgments
We thank DOE for partial support under grant DOE-DE-FG02-07ER46354.
Author Contributions
T.S.R. guided the project. V.T. led the development of the formalism. S.R.A. performed the calculations. S.R.A., V.T and T.S.R. analyzed and discussed the results and contributed to the writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Density Functional Theory |
| DA | Dynamical Vertex Approximation |
| DMFT | Dynamical Mean-Field Theory |
| DOE | Department of Energy |
| DOS | Density Of States |
| HEG | Homogeneous Electron Gas |
| HF-QMC | Hirsch–Fye Quantum Monte Carlo |
| IPT | Iterative Perturbation Theory |
| KS | Kohn–Sham |
| LDA | Local Density Approximation |
| MEMS | Microelectromechanical Systems |
| RPA | Random Phase Approximation |
| SCMs | Strongly-Correlated Materials |
| TDDFT | Time-Dependent Density-Functional Theory |
| XC | Exchange-Correlation |
Appendix A. Iterative Perturbation Theory Approximation
In the multi-orbital IPT approximation [63], the expression for the orbital- and spin-dependent self-energy is:
where , and . In the last two functions, and are the spin-orbital charge densities in the case of lattice and “non-interacting” impurity electrons, respectively, and is the density-density correlation function.
This approximation evolved from the perturbation theory expansion for the impurity electron self-energy in the case of the one-band model at half-filling, where:
It was shown that this approximation is exact in the limits of small and large U’s and describes qualitatively correctly the main features of the DMFT spectrum at other values of U. The generalization Equation (A1) was obtained by requiring the known exact asymptotic dependence of the self-energy on frequency in the limit of large frequencies (for details, see [37,63]). The approximation was used by different groups and, despite its limitations, led to encouraging results, even in the case of systems with reduced dimensionality (see, e.g., [64,65]).
Appendix B. The Hirsch–Fye Quantum Monte Carlo Scheme
Here, we present some details of the HF-QMC formalism [66] to calculate numerically exactly the impurity Green’s function Equation (13) in the case of the one-band Hubbard model. The main idea of this approach is in splitting of the effective action in the exponent of the impurity Equation (13):
into the free and interacting part with consequent Hubbard–Stratonovich transformation of the “interacting” parts of the exponent:
where and are the “Ising spin” variables for each of the L time point of the discretized time contour in Equation (B1).
Since in this case, the effective action in the exponent in Equation (13) is quadratic, one can easily perform the path integration and get:
In the last two equations, are the time matrices that depend on both time and Ising spin variables . The explicit form of the inverse of these matrices is:
where:
Thus, the problem is reduced to calculating the inverses of matrix Equation (B5) for all possible Ising spin configurations on the “L-atom time chain” and summing up the corresponding terms in Equations (B3) and (B4). Since the computational time increases with as , the exact calculations are usually performed only at . For practical needs, at temperatures of order of room or lower, one typically needs L’s of order one to several hundreds. Therefore, the summations in Equation (B3) and Equation (B4) are usually performed for a randomly-chosen set of configurations , i.e., by using QMC methods (for details, see, e.g., [34]).
Appendix C. The Density-Matrix TDDFT Formalism
To solve the TDDFT Equation (1) in the case of a laser pulse perturbation described by the potential:
we expand the electron wave function in basis wave functions, , where are the static (DFT) wave functions ( can be regarded as a generalized index that includes the s-, p-, d- or f-orbital index and other quantum numbers). In this case, the equation may be reduced to a set of equations for the time-dependent coefficients, , or, more conveniently, to the equations for the density matrix elements . The diagonal elements of this matrix describe the time-resolved state occupancies and the non-diagonal: the polarization processes. The elements of the density matrix satisfy the Liouville matrix equation , where are the matrix elements of the KS Hamiltonian with respect to the basis wave functions. Using , where are the static KS energy levels, one can obtain the following density-matrix TDDFT equations:
where and . The last two equations give:
where:
Using the matrix elements defined in Equation (C2) , Equation (C3) has to be solved with the initial conditions:
where are the initial state occupancies.
No approximation within the density-matrix formalism has been made so far. In the case of DGA, we use , which gives the following simplified expressions for the matrix elements (C3):
where:
are static coefficients. In the calculations, we also assume that are momentum independent . This is equivalent to the standard Bloch wave-function approximation: . From the structure of the integral of Equation (C6), one can also see that the following approximation may be used: ; since the product of two conjugated functions has maximal overlap when they are the same orbital functions. For the same reason, one can make further simplification, , which gives:
where:
These numbers may be regarded as the spatial strength of the XC kernel, which we used in our calculations in the case of YTiO3 (more explicitly, we used one averaged over the orbital parameter A).
We refer the reader to [67] for more details.
References
- Anisimov, V.; Izyumov, Y. Electronic Structure of Strongly Correlated Materials; Springer: Berlin, Germany; London, UK, 2010. [Google Scholar]
- Loth, S.; Baumann, S.; Lutz, C.P.; Eigler, D.; Heinrich, A.J. Bistability in atomic-scale antiferromagnets. Science 2012, 335, 196–199. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Shibuya, K.; Okuyama, D.; Hatano, T.; Ono, S.; Kawasaki, M.; Iwasa, Y.; Tokura, Y. Collective bulk carrier delocalization driven by electrostatic surface charge accumulation. Nature 2012, 487, 459–462. [Google Scholar] [CrossRef] [PubMed]
- Tsunekawa, S.; Ishikawa, K.; Li, Z.-Q.; Kawazoe, Y.; Kasuya, A. Origin of anomalous lattice expansion in oxide nanoparticles. Phys. Rev. Lett. 2000, 85, 3440. [Google Scholar] [CrossRef] [PubMed]
- Hailstone, R.; DiFrancesco, A.; Leong, J.; Allston, T.; Reed, K. A study of lattice expansion in CeO2 nanoparticles by transmission electron microscopy. J. Phys. Chem. C 2009, 113, 15155–15159. [Google Scholar] [CrossRef]
- Sundaresan, A.; Bhargavi, R.; Rangarajan, N.; Siddesh, U.; Rao, C. Ferromagnetism as a universal feature of nanoparticles of the otherwise nonmagnetic oxides. Phys. Rev. B 2006, 74, 161306. [Google Scholar] [CrossRef]
- Ao, T.; Ping, Y.; Widmann, K.; Price, D.F.; Lee, E.; Tam, H.; Springer, P.T.; Ng, A. Optical properties in nonequilibrium phase transitions. Phys. Rev. Lett. 2006, 96, 055001. [Google Scholar] [CrossRef] [PubMed]
- Markov, P.; Marvel, R.E.; Conley, H.J.; Miller, K.J.; Haglund Jr, R.F.; Weiss, S.M. Optically monitored electrical switching in VO2. ACS Photonics 2015, 2, 1175–1182. [Google Scholar] [CrossRef]
- Merced, E.; Torres, D.; Tan, X.; Sepúlveda, N. An Electrothermally Actuated VO2-Based MEMS Using Self-Sensing Feedback Control. J. Microelectromec. Syst. 2015, 24, 100–107. [Google Scholar] [CrossRef]
- Nie, G.; Zhang, L.; Lei, J.; Yang, L.; Zhang, Z.; Lu, X.; Wang, C. Monocrystalline VO2 (B) nanobelts: Large-scale synthesis, intrinsic peroxidase-like activity and application in biosensing. J. Mater. Chem. A 2014, 2, 2910–2914. [Google Scholar] [CrossRef]
- Yang, S.; Gong, Y.; Liu, Z.; Zhan, L.; Hashim, D.P.; Ma, L.; Vajtai, R.; Ajayan, P.M. Bottom-up approach toward single-crystalline VO2-graphene ribbons as cathodes for ultrafast lithium storage. Nano Lett. 2013, 13, 1596–1601. [Google Scholar] [CrossRef] [PubMed]
- Runge, E.; Gross, E.K. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Lieb, E.H.; Wu, F.Y. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension. Phys. Rev. Lett. 1968, 20, 1445. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. Exchange-correlation kernel in time-dependent density functional theory. Phys. Rev. B 2002, 66, 165119. [Google Scholar] [CrossRef]
- López-Sandoval, R.; Pastor, G. Properties of the exact correlation-energy functional in Hubbard models. Phase Transit. 2005, 78, 839–850. [Google Scholar] [CrossRef]
- Carrascal, D.; Ferrer, J. Exact Kohn–Sham eigenstates versus quasiparticles in simple models of strongly correlated electrons. Phys. Rev. B 2012, 85, 045110. [Google Scholar] [CrossRef]
- Turkowski, V.; Rahman, T.S. Nonadiabatic time-dependent spin-density functional theory for strongly correlated systems. J. Phys. Condens. Matter 2014, 26, 022201. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fuks, J.I.; Maitra, N.T. Challenging adiabatic time-dependent density functional theory with a Hubbard dimer: The case of time-resolved long-range charge transfer. Phys. Chem. Chem. Phys. 2014, 16, 14504–14513. [Google Scholar] [CrossRef] [PubMed]
- Fuks, J.; Maitra, N. Charge transfer in time-dependent density-functional theory: Insights from the asymmetric Hubbard dimer. Phys. Rev. A 2014, 89, 062502. [Google Scholar] [CrossRef]
- Lani, G.; Di Marino, S.; Gerolin, A.; van Leeuwen, R.; Gori-Giorgi, P. The adiabatic strictly-correlated-electrons functional: Kernel and exact properties. Phys. Chem. Chem. Phys. 2016. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Chen, A.-H.; Tokatly, I.V.; Kurth, S. Lattice density functional theory at finite temperature with strongly density-dependent exchange-correlation potentials. Phys. Rev. B 2012, 86, 235139. [Google Scholar]
- Stefanucci, G.; Kurth, S. Towards a description of the Kondo effect using time-dependent density-functional theory. Phys. Rev. Lett. 2011, 107, 216401. [Google Scholar] [CrossRef] [PubMed]
- Uimonen, A.-M.; Khosravi, E.; Stan, A.; Stefanucci, G.; Kurth, S.; van Leeuwen, R.; Gross, E. Comparative study of many-body perturbation theory and time-dependent density functional theory in the out-of-equilibrium Anderson model. Phys. Rev. B 2011, 84, 115103. [Google Scholar] [CrossRef]
- Liu, Z.-F.; Bergfield, J.P.; Burke, K.; Stafford, C.A. Accuracy of density functionals for molecular electronics: The Anderson junction. Phys. Rev. B 2012, 85, 155117. [Google Scholar] [CrossRef]
- Liu, Z.-F.; Burke, K. Density functional description of Coulomb blockade: Adiabatic versus dynamic exchange correlation. Phys. Rev. B 2015, 91, 245158. [Google Scholar] [CrossRef]
- Schönhammer, K.; Gunnarsson, O.; Noack, R. Density-functional theory on a lattice: Comparison with exact numerical results for a model with strongly correlated electrons. Phys. Rev. B 1995, 52, 2504. [Google Scholar] [CrossRef]
- Verdozzi, C. Time-dependent density-functional theory and strongly correlated systems: Insight from numerical studies. Phys. Rev. Lett. 2008, 101, 166401. [Google Scholar] [CrossRef] [PubMed]
- Mancini, L.; Ramsden, J.; Hodgson, M.; Godby, R. Adiabatic and local approximations for the Kohn–Sham potential in time-dependent Hubbard chains. Phys. Rev. B 2014, 89, 195114. [Google Scholar] [CrossRef]
- Capelle, K.; Campo, V.L., Jr. Density functionals and model Hamiltonians: Pillars of many-particle physics. Phys. Rep. 2013, 528. [Google Scholar] [CrossRef]
- Carrascal, D.; Ferrer, J.; Smith, J.C.; Burke, K. The Hubbard dimer: A density functional case study of a many-body problem. J. Phys. Condens. Matter 2015, 27, 393001. [Google Scholar] [CrossRef] [PubMed]
- Lieb, E.H.; Seiringer, R.; Solovej, J.P. Ground-state energy of the low-density Fermi gas. Phys. Rev. A 2005, 71, 053605. [Google Scholar] [CrossRef]
- Giuliani, A. Ground state energy of the low density Hubbard model: An upper bound. J. Math. Phys. 2007, 48, 023302. [Google Scholar] [CrossRef]
- Metzner, W.; Vollhardt, D. Correlated lattice fermions in d=∞ dimensions. Phys. Rev. Lett. 1989, 62, 324. [Google Scholar] [CrossRef] [PubMed]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Anisimov, V.; Poteryaev, A.; Korotin, M.; Anokhin, A.; Kotliar, G. First-principles calculations of the electronic structure and spectra of strongly correlated systems: Dynamical mean-field theory. J. Phys. Condens. Matter 1997, 9, 7359. [Google Scholar] [CrossRef]
- Lichtenstein, A.; Katsnelson, M. Ab initio calculations of quasiparticle band structure in correlated systems: LDA++ approach. Phys. Rev. B 1998, 57, 6884. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865. [Google Scholar] [CrossRef]
- Held, K.; Nekrasov, I.; Keller, G.; Eyert, V.; Blümer, N.; McMahan, A.; Scalettar, R.; Pruschke, T.; Anisimov, V.; Vollhardt, D. Realistic investigations of correlated electron systems with LDA+ DMFT. Phys. Status Solidi (b) 2006, 243, 2599–2631. [Google Scholar] [CrossRef]
- Turkowski, V.; Kabir, A.; Nayyar, N.; Rahman, T.S. A DFT+ DMFT approach for nanosystems. J. Phys.: Condens. Matter 2010, 22, 462202. [Google Scholar] [CrossRef] [PubMed]
- Turkowski, V.; Kabir, A.; Nayyar, N.; Rahman, T.S. Dynamical mean-field theory for molecules and nanostructures. J. Chem. Phys. 2012, 136, 114108. [Google Scholar] [CrossRef] [PubMed]
- Freericks, J.; Turkowski, V.; Zlatić, V. Nonequilibrium dynamical mean-field theory. Phys. Rev. Lett. 2006, 97, 266408. [Google Scholar] [CrossRef] [PubMed]
- Turkowski, V.; Freericks, J.K. Strongly Correlated Systems, Coherence and Entanglement; Carmelo, J.M.P., Lopes dos Santos, J.M.B., Vieira, V.R., Sacramento, P.D., Eds.; World Scientific: Singapore, 2007; p. 187. [Google Scholar]
- Aoki, H.; Tsuji, N.; Eckstein, M.; Kollar, M.; Oka, T.; Werner, P. Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 2014, 86, 779. [Google Scholar] [CrossRef]
- Karlsson, D.; Privitera, A.; Verdozzi, C. Time-dependent density-functional theory meets dynamical mean-field theory: Real-time dynamics for the 3d Hubbard model. Phys. Rev. Lett. 2011, 106, 116401. [Google Scholar] [CrossRef] [PubMed]
- Turkowski, V.; Rahman, T.S. Nonadiabatic exchange-correlation kernel for strongly correlated materials. ArXiv Preprint 2014. [Google Scholar]
- Ullrich, C.A. Time-Dependent Density-Functional Theory: Concepts and Applications; Oxford University Press: Oxford, NY, USA, 2012. [Google Scholar]
- Toschi, A.; Katanin, A.; Held, K. Dynamical vertex approximation: A step beyond dynamical mean-field theory. Phys. Rev. B 2007, 75, 045118. [Google Scholar] [CrossRef]
- Rohringer, G.; Valli, A.; Toschi, A. Local electronic correlation at the two-particle level. Phys. Rev. B 2012, 86, 125114. [Google Scholar] [CrossRef]
- Gross, E.; Kohn, W. Local density-functional theory of frequency-dependent linear response. Phys. Rev. Lett. 1985, 55, 2850. [Google Scholar] [CrossRef] [PubMed]
- Iwamoto, N.; Gross, E. Correlation effects on the third-frequency-moment sum rule of electron liquids. Phys. Rev. B 1987, 35, 3003. [Google Scholar] [CrossRef]
- Wegkamp, D.; Stähler, J. Ultrafast dynamics during the photoinduced phase transition in VO2. Prog. Surf. Sci. 2015, 90, 464–502. [Google Scholar] [CrossRef]
- He, Z.; Millis, A.J. Photoinduced phase transitions in narrow-gap Mott insulators: The case of VO2. Phys. Rev. B 2016, 93, 115126. [Google Scholar] [CrossRef]
- Freericks, J.K.; Turkowski, V.M.; Zlatić, V. F-electron spectral function of the Falicov-Kimball model in infinite dimensions: the half-filled case. Phys. Rev. B 2005, 71, 115111. [Google Scholar] [CrossRef]
- Pavarini, E.; Yamasaki, A.; Nuss, J.; Andersen, O. How chemistry controls electron localization in 3d1 perovskites: A Wannier-function study. New J. Phys. 2005, 7, 188. [Google Scholar] [CrossRef]
- Pavarini, E.; Biermann, S.; Poteryaev, A.; Lichtenstein, A.; Georges, A.; Andersen, O. Mott transition and suppression of orbital fluctuations in orthorhombic 3d1 perovskites. Phys. Rev. Lett. 2004, 92, 176403. [Google Scholar] [CrossRef] [PubMed]
- Arita, M.; Sato, H.; Higashi, M.; Yoshikawa, K.; Shimada, K.; Nakatake, M.; Ueda, Y.; Namatame, H.; Taniguchi, M.; Tsubota, M. Unoccupied electronic structure of Y1−xCaxTiO3 investigated by inverse photoemission spectroscopy. Phys. Rev. B 2007, 75, 205124. [Google Scholar] [CrossRef]
- Bruggemann, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. (Leipzig) 1935, 24, 636. [Google Scholar] [CrossRef]
- Van Leeuwen, R. The Sham-Schlüter equation in time-dependent density-functional theory. Phys. Rev. Lett. 1996, 76, 3610. [Google Scholar] [CrossRef] [PubMed]
- Sham, L.; Schlüter, M. Density-functional theory of the energy gap. Phys. Rev. Lett. 1983, 51, 1888. [Google Scholar] [CrossRef]
- Sham, L. Exchange and correlation in density-functional theory. Phys. Rev. B 1985, 32, 3876. [Google Scholar] [CrossRef]
- Turkowski, V.M.; Freericks, J.K. Spectral moment sum rules for strongly correlated electrons in time-dependent electric fields. Phys. Rev. B 2006, 73, 075108, Erratum: Phys. Rev. B 2006, 73, 209902. [Google Scholar] [CrossRef]
- Turkowski, V.M.; Freericks, J.K. Nonequilibrium sum rules for the retarded self-energy of strongly correlated electrons. Phys. Rev. B 2008, 77, 205102, Erratum: Phys. Rev. B 2010, 82, 119904. [Google Scholar] [CrossRef]
- Craco, L.; Laad, M.; Müller-Hartmann, E. Orbital Kondo Effect in CrO2: A Combined Local-Spin-Density-Approximation Dynamical-Mean-Field-Theory Study. Phys. Rev. Lett. 2003, 90, 237203. [Google Scholar] [CrossRef] [PubMed]
- Wernsdorfer, J.; Harder, G.; Schollwoeck, U.; Hofstetter, W. Signatures of delocalization in the fermionic 1d Hubbard model with box disorder: Comparative study with DMRG and R-DMFT. ArXiv Preprint 2011. [Google Scholar]
- Semmler, D.; Byczuk, K.; Hofstetter, W. Anderson-Hubbard model with box disorder: Statistical dynamical mean-field theory investigation. Phys. Rev. B 2011, 84, 115113. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Fye, R.M. Monte Carlo method for magnetic impurities in metals. Phys. Rev. Lett. 1986, 56, 2521. [Google Scholar] [CrossRef] [PubMed]
- Turkowski, V.; Ullrich, C.A. Time-dependent density-functional theory for ultrafast interband excitations. Phys. Rev. B 2008, 77, 075204. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).