The Influence of One-Electron Self-Interaction on d-Electrons
Abstract
:1. Introduction
2. Counteracting Electronic Self-Interaction with Hybrid Functionals
3. Computational Details
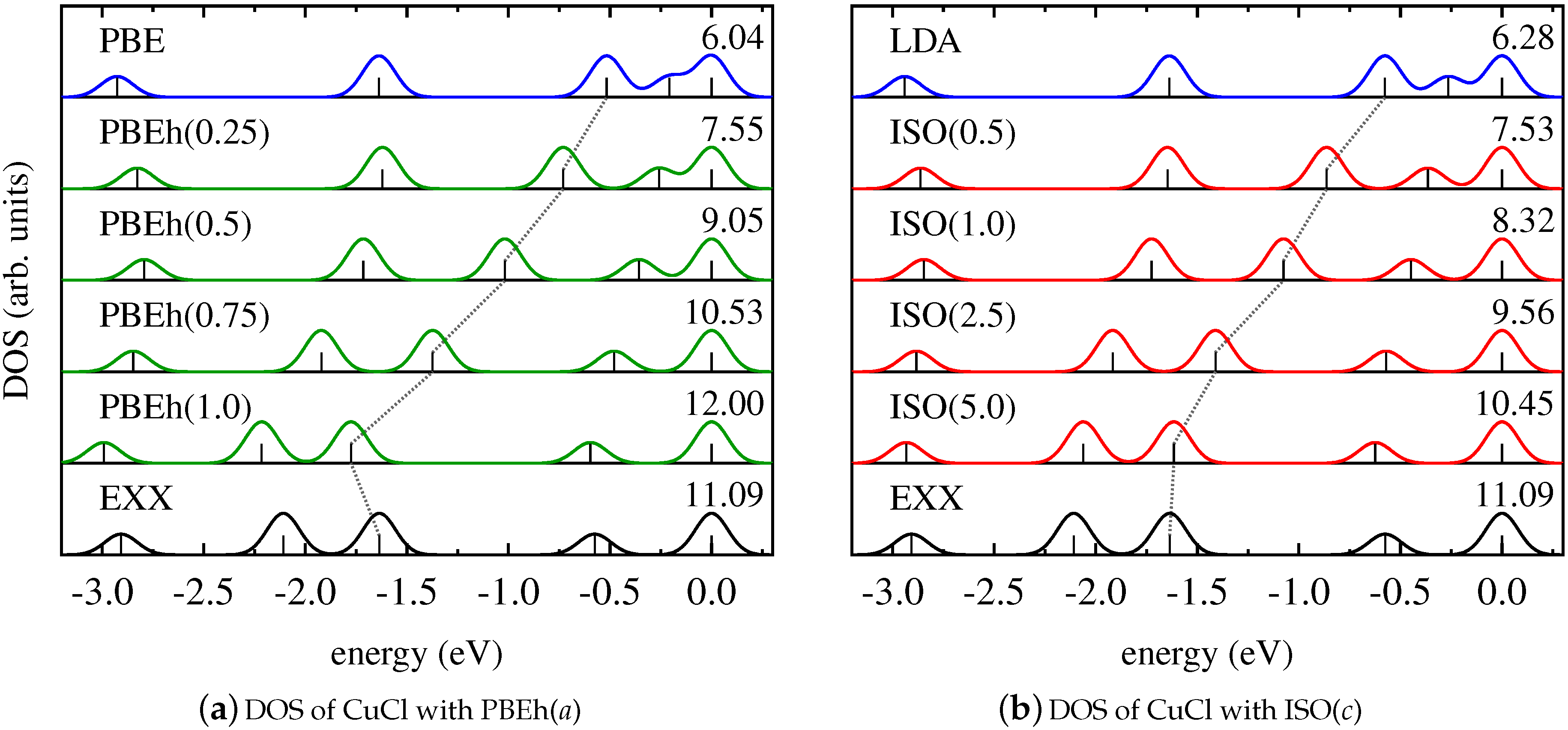
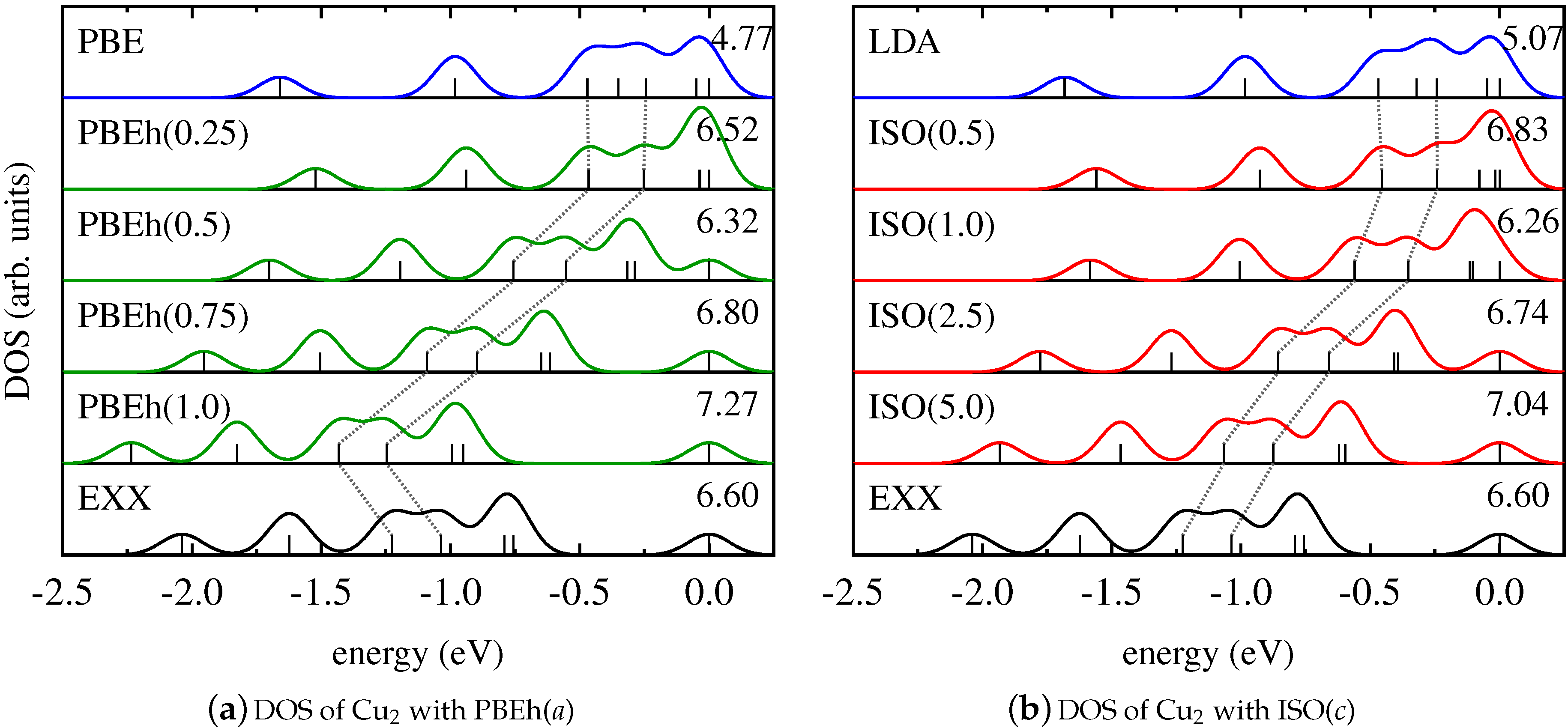
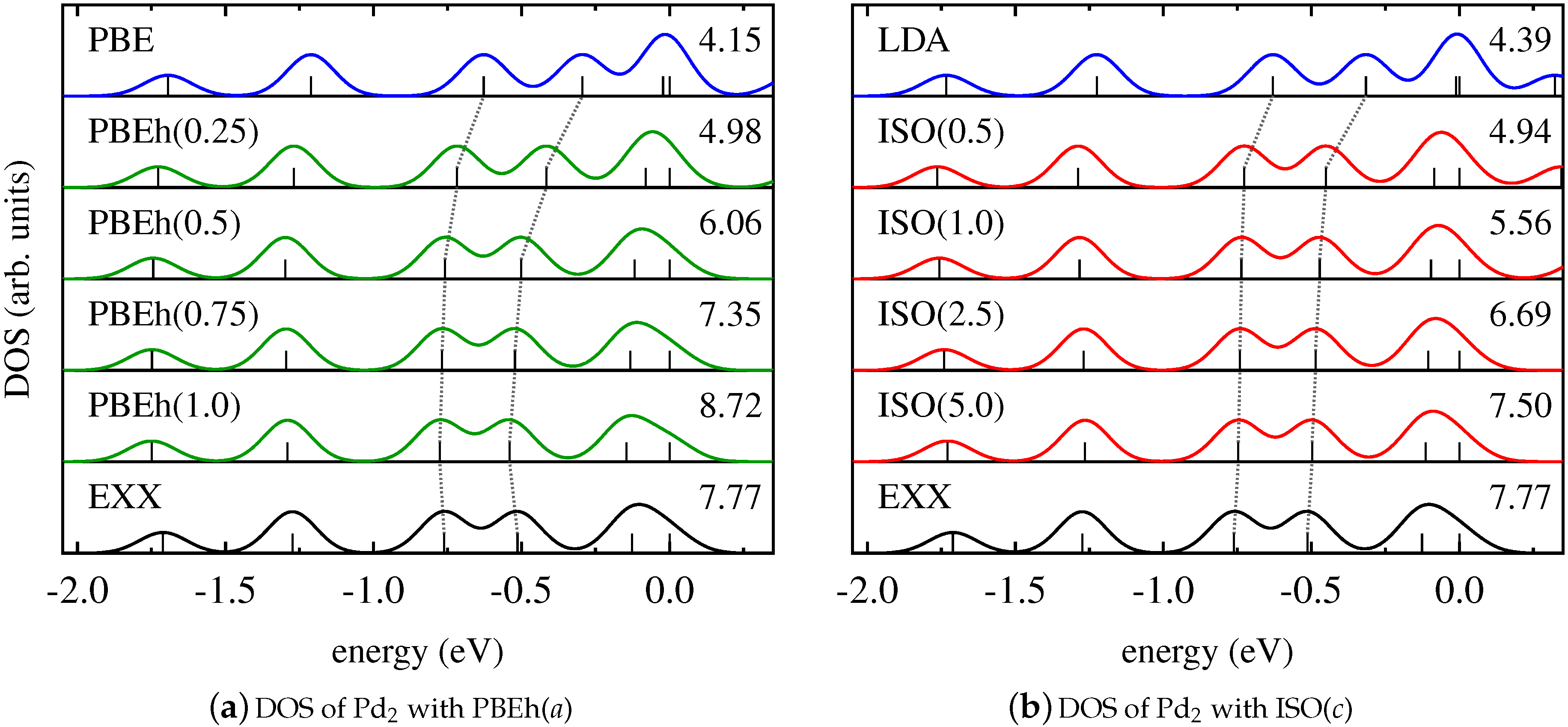
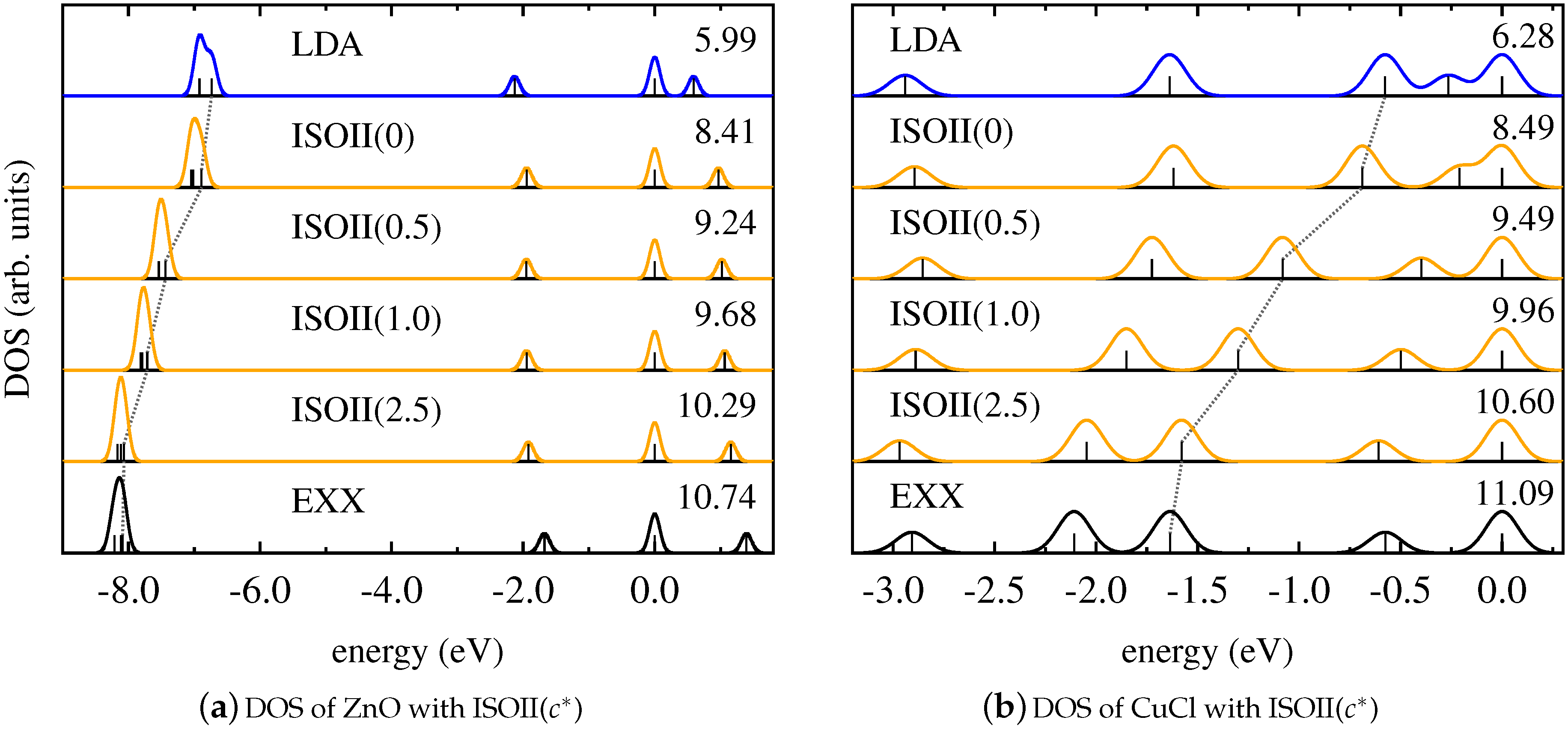
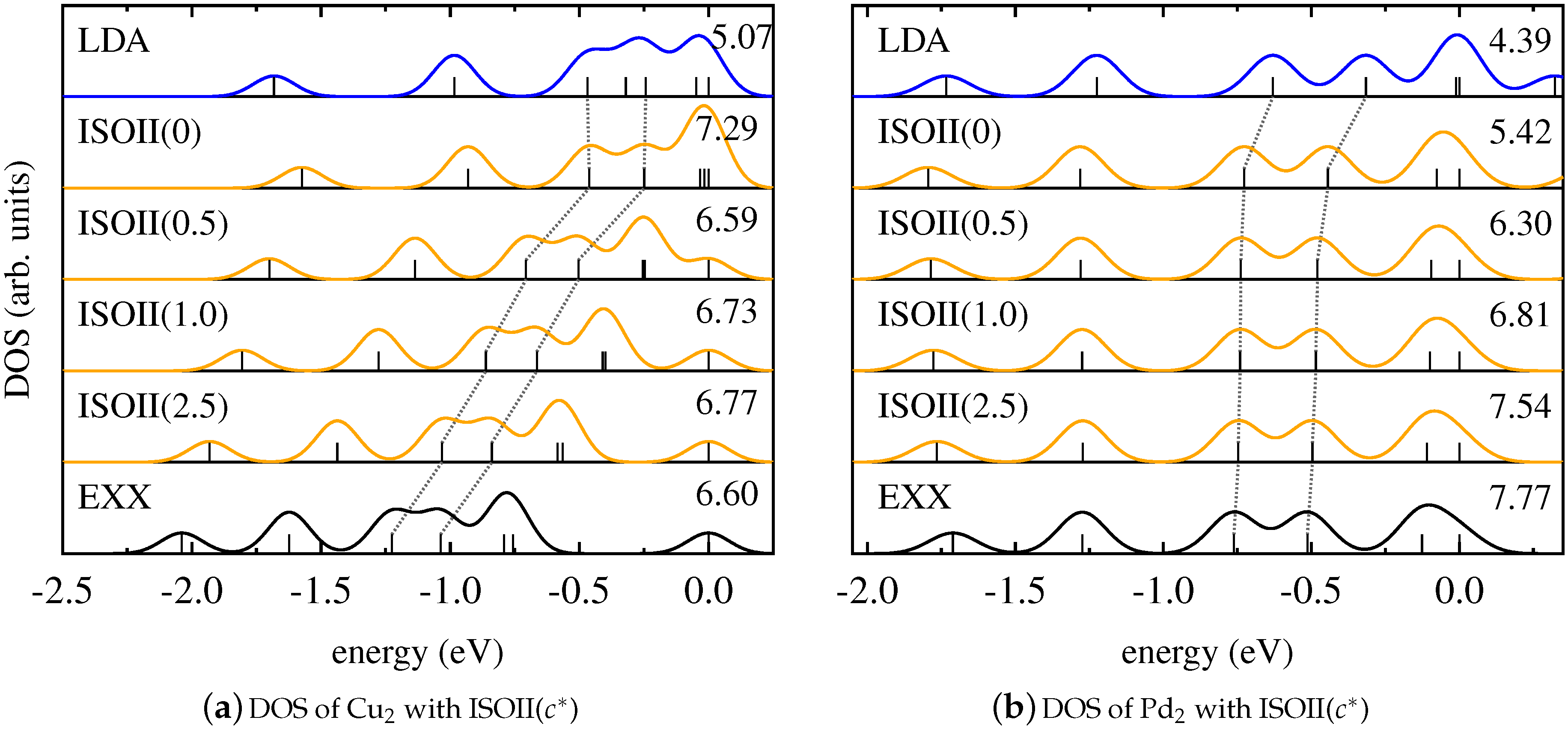
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Becke, A.D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014, 140, 18A301. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef] [PubMed]
- Szotek, Z.; Temmerman, W.M.; Winter, H. Application of the self-interaction correction to transition-metal oxides. Phys. Rev. B 1993, 47, 4029–4032. [Google Scholar] [CrossRef]
- Schulthess, T.C.; Temmerman, W.M.; Szotek, Z.; Butler, W.H.; Stocks, G.M. Electronic structure and exchange coupling of Mn impurities in III–V semiconductors. Nat. Mater. 2005, 4, 838–844. [Google Scholar] [CrossRef]
- Strange, P.; Svane, A.; Temmerman, W.M.; Szotek, Z.; Winter, H. Understanding the valency of rare earths from first-principles theory. Nature 1999, 399, 756–758. [Google Scholar] [CrossRef]
- Perdew, J.P. Orbital functional for exchange and correlation: Self-interaction correction to the local density approximation. Chem. Phys. Lett. 1979, 64, 127–130. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Kümmel, S.; Kronik, L. Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 2008, 80, 3–60. [Google Scholar] [CrossRef]
- Tsuneda, T.; Hirao, K. Self-interaction corrections in density functional theory. J. Chem. Phys. 2014, 140, 18A513. [Google Scholar] [CrossRef] [PubMed]
- Körzdörfer, T.; Kümmel, S.; Marom, N.; Kronik, L. When to trust photoelectron spectra from Kohn–Sham eigenvalues: The case of organic semiconductors. Phys. Rev. B 2009, 79, 201205(R). [Google Scholar] [CrossRef]
- Körzdörfer, T.; Kümmel, S.; Marom, N.; Kronik, L. Erratum: When to trust photoelectron spectra from Kohn–Sham eigenvalues: The case of organic semiconductors [Phys. Rev. B 79, 201205 (2009)]. Phys. Rev. B 2010, 82, 129903. [Google Scholar] [CrossRef]
- Handy, N.C.; Cohen, A.J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Cremer, D. Density functional theory: Coverage of dynamic and non-dynamic electron correlation effects. Mol. Phys. 2001, 99, 1899–1940. [Google Scholar] [CrossRef]
- Polo, V.; Kraka, E.; Cremer, D. Electron correlation and the self-interaction error of density functional theory. Mol. Phys. 2002, 100, 1771–1790. [Google Scholar] [CrossRef]
- Fermi, E.; Amaldi, E. Le Orbite [infinito] s Ddegli Elementi; R. Accademia d’Italia: Roma, Italy, 1934; Volume 6, p. 119. [Google Scholar]
- Cortona, P. New self-interaction-corrected local-density approximation to tzhe density-functional theory. Phys. Rev. A 1986, 34, 769–776. [Google Scholar] [CrossRef]
- Guo, Y.; Whitehead, M.A. An alternative self-interaction correction in the generalized exchange local-density functional theory. J. Comput. Chem. 1991, 12, 803–810. [Google Scholar] [CrossRef]
- Lundin, U.; Eriksson, O. Novel method of self-interaction corrections in density functional calculations. Int. J. Quantum Chem. 2001, 81, 247–252. [Google Scholar] [CrossRef]
- Unger, H.J. Self-interaction correction with an explicitly density-dependent functional. Phys. Lett. A 2001, 284, 124–129. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. A simple method to selectively scale down the self-interaction correction. J. Chem. Phys. 2006, 124, 191101. [Google Scholar] [CrossRef] [PubMed]
- Vieira, D.; Capelle, K. Investigation of self-interaction corrections for an exactly solvable model system: Orbital dependence and electron localization. J. Chem. Theory Comput. 2010, 6, 3319–3329. [Google Scholar] [CrossRef] [PubMed]
- Constantin, L.A.; Fabiano, E.; Della Sala, F. Improving atomization energies of molecules and solids with a spin-dependent gradient correction from one-electron density analysis. Phys. Rev. B 2011, 84, 233103. [Google Scholar] [CrossRef]
- Dinh, P.M.; Reinhard, P.G.; Suraud, E.; Vincendon, M. The two-set and average-density self-interaction corrections applied to small electronic systems. In Advances in Atomic, Molecules, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 64, pp. 87–103. [Google Scholar]
- Borghi, G.; Ferretti, A.; Nguyen, N.L.; Dabo, I.; Marzari, N. Koopmans-compliant functionals and their performance against reference molecular data. Phys. Rev. B 2014, 90, 075135. [Google Scholar] [CrossRef]
- Nguyen, N.L.; Borghi, G.; Ferretti, A.; Dabo, I.; Marzari, N. First-principles photoemission spectroscopy and orbital tomography in molecules from koopmans-compliant functionals. Phys. Rev. Lett. 2015, 114, 166405. [Google Scholar] [CrossRef] [PubMed]
- Pederson, M.R.; Heaton, R.A.; Lin, C.C. Local-density Hartree-Fock theory of electronic states of molecules with self-interaction correction. J. Chem. Phys. 1984, 80, 1972. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Effect of the Perdew-Zunger self-interaction correction on the thermochemical performance of approximate density functionals. J. Chem. Phys. 2004, 121, 8187–8193. [Google Scholar] [CrossRef] [PubMed]
- Messud, J.; Dinh, P.M.; Reinhard, P.G.; Suraud, E. Time-dependent density-functional theory with a self-interaction correction. Phys. Rev. Lett. 2008, 101, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Ruzsinszky, A.; Perdew, J.P.; Csonka, G.I.; Scuseria, G.E.; Vydrov, O.A. Understanding and correcting the self-interaction error in the electrical response of hydrogen chains. Phys. Rev. A 2008, 77, 060502. [Google Scholar] [CrossRef]
- Körzdörfer, T.; Mundt, M.; Kümmel, S. Electrical Response of Molecular Systems: The Power of Self-Interaction Corrected Kohn–Sham Theory. Phys. Rev. Lett. 2008, 100, 133004. [Google Scholar] [CrossRef] [PubMed]
- Kümmel, S. Self-interaction correction as a Kohn–Sham scheme in ground-state and time-dependent density functional theory. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 64, pp. 143–151. [Google Scholar]
- Chen, J.; Krieger, J.B.; Li, Y.; Iafrate, G.J. Kohn–Sham calculations with self-interaction-corrected local-spin-density exchange-correlation energy functional for atomic systems. Phys. Rev. A 1996, 54, 3939–3947. [Google Scholar] [CrossRef] [PubMed]
- Garza, J.; Nichols, J.A.; Dixon, D.A. The optimized effective potential and the self-interaction correction in density functional theory: Application to molecules. J. Chem. Phys. 2000, 112, 7880. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Autschbach, J.; Ziegler, T. Curing difficult cases in magnetic properties prediction with self-interaction corrected density functional theory. J. Chem. Phys. 2001, 115, 26–42. [Google Scholar] [CrossRef]
- Legrand, C.; Suraud, E.; Reinhard, P.G. Comparison of self-interaction-corrections for metal clusters. J. Phys. B Atomic Mol. Opt. Phys. 2002, 35, 1115–1128. [Google Scholar] [CrossRef]
- Vieira, D.; Capelle, K.; Ullrich, C.A. Physical signatures of discontinuities of the time-dependent exchange-correlation potential. Phys. Chem. Chem. Phys. 2009, 11, 4647–4654. [Google Scholar] [CrossRef] [PubMed]
- Pemmaraju, C.D.; Sanvito, S.; Burke, K. Polarizability of molecular chains: A self-interaction correction approach. Phys. Rev. B 2008, 77, 121204(R). [Google Scholar] [CrossRef]
- Körzdörfer, T.; Kümmel, S.; Mundt, M. Self-interaction correction and the optimized effective potential. J. Chem. Phys. 2008, 129, 014110. [Google Scholar] [CrossRef] [PubMed]
- Körzdörfer, T.; Kümmel, S. Self-interaction correction in the Kohn–Sham framework. In Theoretical Computational Developments in Modern Density Functional Theory; Roy, A.K., Ed.; Nova Science Publishers: New York, NY, USA, 2012. [Google Scholar]
- Svane, A.; Gunnarsson, O. Transition-metal oxides in the self-interaction-corrected density-functional formalism. Phys. Rev. Lett. 1990, 65, 1148–1151. [Google Scholar] [CrossRef] [PubMed]
- Temmerman, W.M.; Szotek, Z.; Winter, H. Self-interaction-corrected electronic strucutre of La2CuO4. Phys. Rev. B 1993, 47, 11533–11536. [Google Scholar] [CrossRef]
- Goedecker, S.; Umrigar, C.J. Critical assessment of the self-interaction-corrected-local-density-functional method and its algorithmic implementation. Phys. Rev. A 1997, 55, 1765–1771. [Google Scholar] [CrossRef]
- Pederson, M.R.; Heaton, R.A.; Lin, C.C. Density-functional theory with self-interaction correction: Application to the lithium molecule. J. Chem. Phys. 1985, 82, 2688. [Google Scholar] [CrossRef]
- Pederson, M.R.; Lin, C.C. Localized and canonical atomic orbitals in self-interaction corrected local density functional approximation. J. Chem. Phys. 1988, 88, 1807–1817. [Google Scholar] [CrossRef]
- Klüpfel, S.; Klüpfel, P.; Jónsson, H. Importance of complex orbitals in calculating the self-interaction- corrected ground state of atoms. Phys. Rev. A 2011, 84, 050501. [Google Scholar] [CrossRef]
- Hofmann, D.; Klüpfel, S.; Klüpfel, P.; Kümmel, S. Using complex degrees of freedom in the Kohn–Sham self-interaction correction. Phys. Rev. A 2012, 85, 062514. [Google Scholar] [CrossRef]
- Klüpfel, S.; Klüpfel, P.; Jónsson, H. The effect of the Perdew-Zunger self-interaction correction to density functionals on the energetics of small molecules. J. Chem. Phys. 2012, 137, 124102. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, D.; Körzdörfer, T.; Kümmel, S. Kohn–Sham Self-Interaction Correction in Real Time. Phys. Rev. Lett. 2012, 108, 146401. [Google Scholar] [CrossRef] [PubMed]
- Lehtola, S.; Jónsson, H. Variational, self-consistent implementation of the Perdew-Zunger self-interaction correction with complex optimal orbitals. J. Chem. Theory Comput. 2014, 10, 5324–5337. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsdóttir, H.; Jónsson, E.Ö.; Jónsson, H. Calculations of Al dopant in α-quartz using a variational implementation of the Perdew-Zunger self-interaction correction. New J. Phys. 2015, 17, 83006. [Google Scholar] [CrossRef]
- Lehtola, S.; Jónsson, E.Ö.; Jónsson, H. Effect of complex-valued optimal orbitals on atomization energies with the Perdew–Zunger self-interaction correction to density functional theory. J. Chem. Theory Comput. 2016. [Google Scholar] [CrossRef] [PubMed]
- Lehtola, S.; Head-Gordon, M.; Jónsson, H. Complex orbitals, multiple local minima and symmetry breaking in Perdew-Zunger self-interaction corrected density-functional theory calculations. J. Chem. Theory Comput. 2016, 12, 3195–3207. [Google Scholar] [CrossRef] [PubMed]
- Pederson, M.R.; Ruzsinszky, A.; Perdew, J.P. Communication: Self-interaction correction with unitary invariance in density functional theory. J. Chem. Phys. 2014, 140, 121103. [Google Scholar] [CrossRef] [PubMed]
- Pederson, M.R.; Baruah, T. Self-interaction corrections within the fermi-orbital-based formalism. In Advance in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 64, pp. 153–180. [Google Scholar]
- Hahn, T.; Liebing, S.; Kortus, J.; Pederson, M.R. Fermi orbital self-interaction corrected electronic structure of molecules beyond local density approximation. J. Chem. Phys. 2015, 143, 224104. [Google Scholar] [CrossRef] [PubMed]
- Ruzsinszky, A.; Perdew, J.P.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E. Spurious fractional charge on dissociated atoms: Pervasive and resilient self-interaction error of common density functionals. J. Chem. Phys. 2006, 125, 194112. [Google Scholar] [CrossRef] [PubMed]
- Mori-Sánchez, P.; Cohen, A.J.; Yang, W. Many-electron self-interaction error in approximate density functionals. J. Chem. Phys. 2006, 125, 201102. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Parr, R.G.; Levy, M.; Balduz, J.L. Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy. Phys. Rev. Lett. 1982, 49, 1691–1694. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Sai, N.; Barbara, P.F.; Leung, K. Hole localization in molecular crystals from hybrid density functional theory. Phys. Rev. Lett. 2011, 106, 226403. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.; Autschbach, J.; Govind, N.; Kronik, L.; Baer, R. Curvature and frontier orbital energies in density functional theory. J. Phys. Chem. Lett. 2012, 3, 3740–3744. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zheng, X.; Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Local scaling correction for reducing delocalization error in density functional approximations. Phys. Rev. Lett. 2015, 114, 053001. [Google Scholar] [CrossRef] [PubMed]
- Dauth, M.; Caruso, F.; Kümmel, S.; Rinke, P. Piecewise linearity in the GW approximation for accurate quasiparticle energy predictions. Phys. Rev. B 2016, 93, 121115. [Google Scholar] [CrossRef]
- Schmidt, T.; Kümmel, S. One- and many-electron self-interaction error in local and global hybrid functionals. Phys. Rev. B 2016, 93, 165120. [Google Scholar] [CrossRef]
- Atalla, V.; Zhang, I.Y.; Hofmann, O.T.; Ren, X.; Rinke, P.; Scheffler, M. Enforcing the linear behavior of the total energy with hybrid functionals: Implications for charge transfer, interaction energies, and the random-phase approximation. Phys. Rev. B 2016, 94, 035140. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Peach, M.J.G.; Helgaker, T.; Sałek, P.; Keal, T.W.; Lutnæs, O.B.; Tozer, D.J.; Handy, N.C. Assessment of a Coulomb-attenuated exchange-correlation energy functional. Phys. Chem. Chem. Phys. 2006, 8, 558–562. [Google Scholar] [CrossRef] [PubMed]
- Iikura, H.; Tsuneda, T.; Yanai, T.; Hirao, K. A long-range correction scheme for generalized-gradient- approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- De Queiroz, T.B.; Kümmel, S. Tuned range separated hybrid functionals for solvated low bandgap oligomers. J. Chem. Phys. 2015, 143, 034101. [Google Scholar] [CrossRef] [PubMed]
- Karolewski, A.; Kronik, L.; Kümmel, S. Using optimally tuned range separated hybrid functionals in ground-state calculations: Consequences and caveats. J. Chem. Phys. 2013, 138, 204115. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Cruz, F.G.; Lam, K.C.; Burke, K. Exchange-correlation energy density from virial theorem. J. Phys. Chem. A 1998, 102, 4911–4917. [Google Scholar] [CrossRef]
- Jaramillo, J.; Scuseria, G.E.; Ernzerhof, M. Local hybrid functionals. J. Chem. Phys. 2003, 118, 1068–1073. [Google Scholar] [CrossRef]
- Arbuznikov, A.V.; Kaupp, M.; Bahmann, H. From local hybrid functionals to “localized local hybrid” potentials: Formalism and thermochemical tests. J. Chem. Phys. 2006, 124, 204102. [Google Scholar] [CrossRef] [PubMed]
- Janesko, B.G.; Scuseria, G.E. Local hybrid functionals based on density matrix products. J. Chem. Phys. 2007, 127, 164117. [Google Scholar] [CrossRef] [PubMed]
- Bahmann, H.; Rodenberg, A.; Arbuznikov, A.V.; Kaupp, M. A thermochemically competitive local hybrid functional without gradient corrections. J. Chem. Phys. 2007, 126, 011103. [Google Scholar] [CrossRef] [PubMed]
- Kaupp, M.; Bahmann, H.; Arbuznikov, A.V. Local hybrid functionals: An assessment for thermochemical kinetics. J. Chem. Phys. 2007, 127, 194102. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Staroverov, V.N.; Tao, J.; Scuseria, G.E. Density functional with full exact exchange, balanced nonlocality of correlation, and constraint satisfaction. Phys. Rev. A 2008, 78, 052513. [Google Scholar] [CrossRef]
- Schmidt, T.; Kraisler, E.; Makmal, A.; Kronik, L.; Kümmel, S. A self-interaction-free local hybrid functional: Accurate binding energies vis-à-vis accurate ionization potentials from Kohn–Sham eigenvalues. J. Chem. Phys. 2014, 140, 18A510. [Google Scholar] [CrossRef] [PubMed]
- de Silva, P.; Corminboeuf, C. Local hybrid functionals with orbital-free mixing functions and balanced elimination of self-interaction error. J. Chem. Phys. 2015, 142, 074112. [Google Scholar] [CrossRef] [PubMed]
- Kümmel, S.; Perdew, J.P. Two avenues to self-interaction correction within Kohn–Sham theory: Unitary invariance is the shortcut. Mol. Phys. 2003, 101, 1363–1368. [Google Scholar] [CrossRef]
- Duffy, P.; Chong, D.P.; Casida, M.E.; Salahub, D.R. Kohn–Sham density-functional orbitals as approximate Dyson orbitals scattering for the calculation. Phys. Rev. A 1994, 50, 4707–4728. [Google Scholar] [CrossRef] [PubMed]
- Chong, D.P.; Gritsenko, O.V.; Baerends, E.J. Interpretation of the Kohn–Sham orbital energies as approximate vertical ionization potentials. J. Chem. Phys. 2002, 116, 1760–1772. [Google Scholar] [CrossRef]
- Kronik, L.; Kümmel, S. Gas-phase valence-electron photoemission spectroscopy using density functional theory. In First Principles Approaches to Spectroscopic Properties of Complex Materials; Topics in Current Chemistry; di Valentin, C., Botti, S., Coccoccioni, M., Eds.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Akola, J.; Manninen, M.; Häkkinen, H.; Landman, U.; Li, X.; Wang, L.S. Aluminum cluster anions: Photoelectron spectroscopy and ab initio simulations. Phys. Rev. B 2000, 62, 13216. [Google Scholar] [CrossRef]
- Khanna, S.N.; Beltran, M.; Jena, P. Relationship between photoelectron spectroscopy and the magnetic moment of Ni7 clusters. Phys. Rev. B 2001, 64, 235419. [Google Scholar] [CrossRef]
- Kronik, L.; Fromherz, R.; Ko, E.; Ganteför, G.; Chelikowsky, J.R. Highest electron affinity as a predictor of cluster anion structures. Nat. Mater. 2002, 1, 49–53. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Moseler, M.; Huber, B.; Häkkinen, H.; Landman, U.; Wrigge, G.; Hoffmann, M.A.; Issendorff, B.V. Thermal effects in the photoelectron spectra of Na-N clustres (N = 4–19). Phys. Rev. B 2003, 68, 165413. [Google Scholar] [CrossRef]
- Häkkinen, H.; Moseler, M.; Kostko, O.; Morgner, N.; Hoffmann, M.A.; Issendorff, B.V. Symmetry and electronic structure of noble-metal nanoparticles and the role of relativity. Phys. Rev. Lett. 2004, 93, 093401. [Google Scholar] [CrossRef] [PubMed]
- Mundt, M.; Kümmel, S.; Huber, B.; Moseler, M. Photoelectron spectra of sodium clusters: The problem of interpreting Kohn–Sham eigenvalues. Phys. Rev. B 2006, 73, 205407. [Google Scholar] [CrossRef]
- Leppert, L.; Kümmel, S. The electronic structure of gold-platinum nanoparticles: Collecting clues for why they are special. J. Phys. Chem. C 2011, 115, 6694–6702. [Google Scholar] [CrossRef]
- Leppert, L.; Albuquerque, R.Q.; Foster, A.S.; Kümmel, S. Interplay of electronic structure and atomic mobility in nanoalloys of Au and Pt. J. Phys. Chem. C 2013, 117, 17268–17273. [Google Scholar] [CrossRef]
- Zamudio-Bayer, V.; Leppert, L.; Hirsch, K.; Langenberg, A.; Rittmann, J.; Kossick, M.; Vogel, M.; Richter, R.; Terasaki, A.; Möller, T.; et al. Coordination-driven magnetic-to-nonmagnetic transition in manganese-doped silicon clusters. Phys. Rev. B 2013, 88, 115425. [Google Scholar] [CrossRef]
- Capelo, R.G.; Leppert, L.; Albuquerque, R.Q. The concept of localized atomic mobility: Unraveling properties of nanoparticles. J. Phys. Chem. C 2014, 118, 21647–21654. [Google Scholar] [CrossRef]
- Leppert, L.; Kempe, R.; Kümmel, S. Hydrogen binding energies and electronic structure of Ni–Pd particles: A clue to their special catalytic properties. Phys. Chem. Chem. Phys. 2015, 17, 26140–26148. [Google Scholar] [CrossRef] [PubMed]
- Cherepanov, P.V.; Melnyk, I.; Skorb, E.V.; Fratzl, P.; Zolotoyabko, E.; Dubrovinskaia, N.; Dubrovinsky, L.; Avadhut, Y.S.; Senker, J.; Leppert, L.; et al. The use of ultrasonic cavitation for near-surface structuring of robust and low-cost AlNi catalysts for hydrogen production. Green Chem. 2015, 17, 2745. [Google Scholar] [CrossRef]
- Aslan, M.; Davis, J.B.A.; Johnston, R.L. Global optimization of small bimetallic Pd–Co binary nanoalloy clusters: A genetic algorithm approach at the DFT level. Phys. Chem. Chem. Phys. 2016, 18, 6676. [Google Scholar] [CrossRef] [PubMed]
- Grabo, T.; Kreibich, T.; Gross, E.K.U. Optimized effective potential for atoms and molecules. Mol. Eng. 1997, 7, 27–50. [Google Scholar] [CrossRef]
- Kümmel, S.; Perdew, J.P. Simple Iterative Construction of the Optimized Effective Potential for Orbital Functionals, Including Exact Exchange. Phys. Rev. Lett. 2003, 90, 043004. [Google Scholar] [CrossRef] [PubMed]
- Makmal, A.; Kümmel, S.; Kronik, L. Fully Numerical All-Electron Solutions of the Optimized Effective Potential Equation for Diatomic Molecules. J. Chem. Theory Comput. 2009, 5, 1731–1740. [Google Scholar] [CrossRef] [PubMed]
- Makmal, A.; Kümmel, S.; Kronik, L. Dissociation of diatomic molecules and the exact-exchange Kohn–Sham potential: The case of LiF. Phys. Rev. A 2011, 83, 062512. [Google Scholar] [CrossRef]
- Burke, K.; Cruz, F.G.; Lam, K.C. Unambiguous exchange-correlation energy density. J. Chem. Phys. 1998, 109, 8161–8167. [Google Scholar] [CrossRef]
- Arbuznikov, A.V.; Kaupp, M. Towards improved local hybrid functionals by calibration of exchange-energy densities. J. Chem. Phys. 2014, 141, 204101. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Erratum: Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Körzdörfer, T.; Kümmel, S. Single-particle and quasiparticle interpretation of Kohn–Sham and generalized Kohn–Sham eigenvalues for hybrid functionals. Phys. Rev. B 2010, 82, 155206. [Google Scholar] [CrossRef]
- Imamura, Y.; Kobayashi, R.; Nakai, H. Linearity condition for orbital energies in density functional theory (II): Application to global hybrid functionals. Chem. Phys. Lett. 2011, 513, 130–135. [Google Scholar] [CrossRef]
- Atalla, V.; Yoon, M.; Caruso, F.; Rinke, P.; Scheffler, M. Hybrid density functional theory meets quasiparticle calculations: A consistent electronic structure approach. Phys. Rev. B 2013, 88, 165122. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Wang, Y.; Perdew, J.P. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar]
- Schmidt, T.; Kraisler, E.; Kronik, L.; Kümmel, S. One-electron self-interaction and the asymptotics of the Kohn–Sham potential: An impaired relation. Phys. Chem. Chem. Phys. 2014, 16, 14357–14367. [Google Scholar] [CrossRef] [PubMed]
- Kurth, S.; Perdew, J.P.; Blaha, P. Molecular and solid-state tests of density functional approximations: LSD, GGAs, and meta-GGAs. Int. J. Quantum Chem. 1999, 75, 889–909. [Google Scholar] [CrossRef]
- Krieger, J.B.; Li, Y.; Iafrate, G.J. Construction and application of an accurate local spin-polarized Kohn–Sham potential with integer discontinuity: Exchange-only theory. Phys. Rev. A 1992, 45, 101–126. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 92nd ed.; CRC: London, UK, 2011.
- Gritsenko, O.V.; Mentel, L.M.; Baerends, E.J. On the errors of local density (LDA) and generalized gradient (GGA) approximations to the Kohn–Sham potential and orbital energies. J. Chem. Phys. 2016, 144, 204114. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, T.; Kümmel, S. The Influence of One-Electron Self-Interaction on d-Electrons. Computation 2016, 4, 33. https://doi.org/10.3390/computation4030033
Schmidt T, Kümmel S. The Influence of One-Electron Self-Interaction on d-Electrons. Computation. 2016; 4(3):33. https://doi.org/10.3390/computation4030033
Chicago/Turabian StyleSchmidt, Tobias, and Stephan Kümmel. 2016. "The Influence of One-Electron Self-Interaction on d-Electrons" Computation 4, no. 3: 33. https://doi.org/10.3390/computation4030033
APA StyleSchmidt, T., & Kümmel, S. (2016). The Influence of One-Electron Self-Interaction on d-Electrons. Computation, 4(3), 33. https://doi.org/10.3390/computation4030033




