Abstract
Local effective potential theory, both stationary-state and time-dependent, constitutes the mapping from a system of electrons in an external field to one of the noninteracting fermions possessing the same basic variable such as the density, thereby enabling the determination of the energy and other properties of the electronic system. This paper is a description via Quantal Density Functional Theory (QDFT) of the electron correlations that must be accounted for in such a mapping. It is proved through QDFT that independent of the form of external field, (a) it is possible to map to a model system possessing all the basic variables; and that (b) with the requirement that the model fermions are subject to the same external fields, the only correlations that must be considered are those due to the Pauli exclusion principle, Coulomb repulsion, and Correlation–Kinetic effects. The cases of both a static and time-dependent electromagnetic field, for which the basic variables are the density and physical current density, are considered. The examples of solely an external electrostatic or time-dependent electric field constitute special cases. An efficacious unification in terms of electron correlations, independent of the type of external field, is thereby achieved. The mapping is explicated for the example of a quantum dot in a magnetostatic field, and for a quantum dot in a magnetostatic and time-dependent electric field.
1. Introduction
This paper is concerned with the electron correlations within local effective potential theory (LEPT) such as Kohn–Sham [1] (KS) and Quantal (Q) [2,3] density functional theory (DFT). We begin with a brief description of the electron correlations that must be accounted for within LEPT. The understanding and definitions of these electron correlations is achieved via the equations of Quantal density functional theory (QDFT) [2,3]. QDFT is a description in terms of “classical” fields and quantal sources based on the “Quantal Newtonian” second [4,5,6] and first [7,8,9] laws for each electron. In this work, a comprehensive unification in terms of electron correlations is arrived at through QDFT for electrons in the presence of both an external static and a time-dependent electromagnetic field.
As readers may be more familiar with KS–DFT and its various extensions, a brief description of the ideas underlying QDFT is provided in the Appendix.
Stationary-ground-state LEPT such as Kohn–Sham (KS) [1] and QDFT constitute the mapping from an interacting system of N electrons in an external electrostatic field to one of noninteracting fermions, also in their ground state, with the same nondegenerate ground state density . The choice of density as the property of equivalence is governed by the fact that it constitutes a basic variable of quantum mechanics. According to the first Hohenberg–Kohn (HK) [10] theorem, a basic variable is a gauge invariant property knowledge of which determines the wave functions of the system. Thus, knowledge of the density uniquely determines the external scalar potential to with a constant. With the kinetic and electron-interaction potential energy operators assumed to be known, so is the Hamiltonian. Solution of the Schrödinger equation then leads to the wave functions of the system for both ground and excited states. In the mapping, it is further assumed that the model noninteracting fermions also experience the same external electrostatic field . Hence, the local effective potential of the model (S system) fermions is written as , where , the effective electron-interaction potential, is the component in which all the many-body effects are incorporated. The electron correlations that the model system must account for via are those due to the Pauli exclusion principle and Coulomb repulsion. However, the potential must also account for correlations which arise because of the difference in kinetic energies of the interacting and model systems having the same density , viz. the Correlation–Kinetic contribution. In KS–DFT, the many-body correlations are all subsumed in the electron-interaction energy functional of the density, and thereby via its functional derivative, in the potential . Within QDFT, the contributions of these correlations to both the potential and the corresponding Pauli, Coulomb, and Correlation–Kinetic components of the total energy E are separately delineated and explicitly defined [2,3,7,8] (As a point of interest, we note that within QDFT [2,3], it is also possible to map the interacting system in its ground state to a model system in an arbitrary excited state but with the same ground state density . The contribution to the corresponding potential of correlations due to the Pauli principle and Coulomb repulsion remain unchanged in each case. The difference in the potentials is solely due to Correlation–Kinetic effects).
In time-dependent LEPT, such as Runge–Gross (RG) [11] DFT or QDFT [4], the electrons are subject to a time-dependent external field . In this case, as proved by the RG theorem [11], a basic variable is the density . Knowledge of the density determines the external potential to within a time-dependent function, hence the Hamiltonian, and thereby the wave function (as an important point of note, the RG theorem also proves the current density to be a basic variable). Once again, it is assumed that the model fermions are also subject to the same external potential , and in traditional time-dependent LEPT, the mapping is such as to reproduce solely the density . As shown by QDFT, the correlations that must be accounted for in this LEPT are, of course, those due to the Pauli exclusion principle, Coulomb repulsion and Correlation–Kinetic effects. However, there is, in general, an additional correlation [2,4,5,6] due to the difference in the current densities of the interacting and noninteracting fermions, viz. the Correlation–Current–Density effects, which must also be considered. In RG–DFT, these correlations are all subsumed in the corresponding electron-interaction action functional of the density and its functional derivative . Within QDFT, the separate contribution of all these correlations to the electron-interaction potential is explicitly defined. Correlation–Current–Density effects do not contribute explicitly to the (non-conserved) energy , but do so implicitly via their contribution to .
Finally, consider the case of N electrons in both an external electrostatic and magnetostatic field (This case, and the corresponding basic variables [12], is discussed in greater detail in the following section. Here, we focus on the correlations within the corresponding LEPT). A QDFT [13] can be formulated in the traditional manner, i.e., via the construction of both an effective scalar and vector potential for the model S system. The correlations that must be accounted for in this LEPT are those due to the Pauli exclusion principle, Coulomb repulsion, and Correlation–Kinetic effects. However, in addition, Correlation–Magnetic effects, i.e., correlations due to the difference in an internal magnetic field component of the interacting and model systems must also be considered.
To summarize, we observe that the correlations in LEPT as presently construed, are a function of the external potential. We provide here, via QDFT, a generalization of all LEPT such that the only correlations that need to be accounted for are solely those due to the Pauli exclusion principle, Coulomb repulsion, and Correlation–Kinetic effects. This requires that the noninteracting fermions (a) possess all the basic variables; and (b) be subject to the same external fields as those of the interacting system. In Section 2, we prove this for the case of an external electrostatic and magnetostatic field, a special case of which is stationary state KS–DFT and QDFT. In Section 3, the proof for an external time-dependent electromagnetic field is provided, a special case of which is time-dependent RG–DFT and QDFT. For the proof, we derive the “Quantal Newtonian” second law for electrons in an external time-dependent electromagnetic field, as well as the law for the corresponding model S system fermions (The derivation of these “Quantal Newtonian” laws is provided in Supplementary Material). The stationary state case is explicated by the example of a harmonically confined quantum dot in a magnetostatic field, and the time-dependent case via the quantum dot in a magnetostatic field perturbed by a time-dependent electric field. Concluding remarks are made in Section 4.
2. Case of External Static Electromagnetic Field
Consider a system of N electrons in a static external electric and magnetic field, where and are the corresponding scalar and vector potentials, respectively. The Schrödinger equation in atomic units (charge of electron , ) together with the assumption of is
where the terms of the Hamiltonian are the physical kinetic , electron-interaction potential , and external potential energy operators; the eigenfunctions and eigenvalues; ; ; the spatial and spin coordinates of each electron.
In recent work [12], we have proved that the basic variables for the physical system described above, in which the interaction of the magnetic field is solely with the orbital angular momentum, are the nondegenerate ground state density and the physical current density . The proof is for uniform magnetic fields and for fixed electron number N and canonical angular momentum . The proof is rigorous in the original HK sense in that knowledge of uniquely determines the potentials to within a constant and the gradient of a scalar function, respectively. Thereby, the Hamiltonian is now known, and the wave functions of the system determined via solution of the Schrödinger equation of Equation (1) (The proof has also been extended to the Schrödinger–Pauli Hamiltonian, which additionally involves the interaction of the magnetic field with the spin angular momentum. We do not consider that case here). The theorem extends the applicability of LEPT to yrast states, which are states of lowest energy for fixed angular momentum—in particular, to harmonically trapped electrons in the presence of a uniform perpendicular magnetic field [14].
The “Quantal Newtonian” first law for each electron for the above interacting system states that the sum of the external and internal fields experienced by each electron vanish [13,15]:
The law is valid for arbitrary gauge, and satisfies the continuity condition . The external field is the sum of the electrostatic and Lorentz fields:
where is defined in terms of the Lorentz “force” as , with the density; the density operator; ; the physical current density; with the physical current density operator.
The internal field is the sum of the electron-interaction , kinetic , differential density , and internal magnetic fields:
These fields are defined in terms of the corresponding ‘forces’ , , , and (each ‘force’ divided by the density constitutes the corresponding field). The “force” , representative of electron correlations due to the Pauli exclusion principle and Coulomb repulsion, is obtained via Coulomb’s law via its quantal source, the pair-correlation function , with the expectation of the pair operator ; the kinetic “force” , representative of kinetic effects, is obtained from its quantal source, the single-particle density matrix , where the kinetic energy tensor with the expectation of the operator , , , with a translation operator such that ; the differential density ‘force’, representative of the density is , the quantal source being the density ; and internal magnetic force whose quantal source is the current density , . The components of the total energy E—the kinetic, electron-interaction, internal magnetic, and external—can each be expressed in integral virial form in terms of the respective fields [13].
We next map the interacting system to one of noninteracting fermions possessing the same basic variables , the same electron number N, and orbital angular momentum . We assume the model fermions experience the same external fields and . The corresponding model S system LEPT differential equation is then
with
and where all the many-body effects are incorporated in the effective electron-interaction potential . The wave function of the S system is the Slater determinant of the orbitals ; the density and physical current density are the expectations and .
The mapping to the model system possessing the same basic variables ensure the constancy [12] of both the electron number N and orbital angular momentum .
With the above assumption, the “Quantal Newtonian” first law for the S system is then
where is the same as Equation (3), and the internal field is
Here, the kinetic field is defined in a manner similar to that of the interacting system but in terms of the Dirac density matrix . The differential density and internal magnetic field components remain the same as in Equation (4).
On comparing the “Quantal Newtonian” laws of Equations (2) and (7), we see that the effective electron-interaction potential is the work done to move a model fermion from a reference point at infinity to its position at in the force of a conservative effective field :
where
with the Correlation–Kinetic field defined as
Note that since , the work done is path-independent. The total energy E as obtained from the S system is
where the electron-interaction energy is
and the Correlation–Kinetic energy is
For completeness, we note [2,3] that the electron-interaction field can be decomposed in terms of its Hartree , Pauli , and Coulomb components. This is accomplished by writing the pair–correlation density , where is the Fermi-Coulomb hole: , with the Fermi hole defined as , and the Coulomb hole defined thereby. The density, Fermi, and Coulomb hole charge distributions then constitutes the quantal sources of the fields , , and as determined via Coulomb’s law.
The QDFT equations for the local potential and total energy E show that for electrons in an external static electric and magnetic field it is (a) possible to map to a model system of noninteracting fermions possessing the same basic variables ; and (b) that the only correlations that need to be considered in the mapping are those of the Pauli exclusion principle, Coulomb repulsion, and Correlation–Kinetic effects.
To elucidate the above, we consider the mapping from the ground state of the two-dimensional two-electron quantum dot in a magnetic field [16,17] to one of noninteracting fermions possessing the same also in its ground state. The external scalar potential in the Hamiltonian of Equation (1) is then with the harmonic frequency. The ground [13] state wave function of the quantum dot in the symmetric gauge , is , where , , , , the effective force constant with the Larmor frequency. In Figure 1a, we plot the components and of the effective field of Equation (10). In this example, the fields and are separately conservative. Thus, in Figure 1b, we plot the potentials and , which are, respectively, the work done in the fields and . The sum of and is the local effective electron-interaction potential , which is also plotted in Figure 1b. The local potential then generates single-particle orbitals, which lead to the same as that of the interacting system quantum dot. As a consequence of the reduction in dimensionality, Correlation–Kinetic effects are significant: , , , , . A similar mapping [18] from an excited state of the quantum dot can be accomplished. Once again, it is observed that Correlation–Kinetic effects play a significant role.
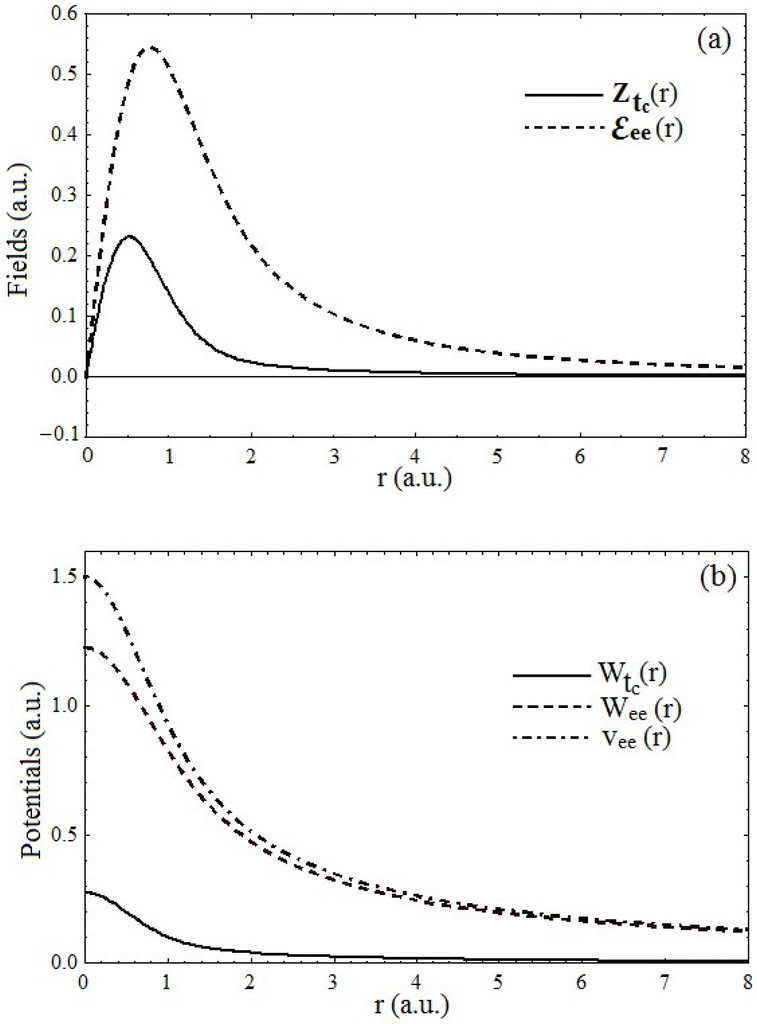
Figure 1.
Fields and potentials of the model noninteracting fermions in their ground state for the mapping from a quantum dot in a magnetic field also in a ground state: (a) the electron-interaction (Pauli–Coulomb) and Correlation–Kinetic fields; (b) the local effective electron-interaction potential and its Pauli–Coulomb and Correlation–Kinetic components.
Finally, we note that the sole presence of an external electrostatic field with the density as the basic variable, constitutes the special case of Kohn–Sham theory. The expressions for remain the same. Hence, the electron correlations that must be accounted for in the mapping to the corresponding model system of density are also the same [2,3].
3. Case of External Time-Dependent Electromagnetic Field
Consider next a system of N electrons, in an external time-dependent electric field ; , in the presence of an electromagnetic field , , with scalar and vector potentials (a special case is when the electric field is static, i.e., ). The corresponding time-dependent Schrödinger equation is then
where the terms of the Hamiltonian are the physical kinetic , electron-interaction potential , and external scalar potential energy operators; , and the wave function.
It has been proved [19,20] that for the physical system described by the above Hamiltonian, the basic variables are the density and the physical current density . Thus, knowledge of uniquely determines the external scalar potentials to within a time-dependent function, and the vector potential to within the gradient of a scalar function of time, and thereby the Hamiltonian and the wave function. The properties are also the basic variables for the special case when the only external field is . This then corresponds to the Runge–Gross [11] theorem (we note that the proofs given in [19,20] are different).
The “Quantal Newtonian” second law for each electron for the system of Equation (15) is (see Supplementary Material for the Derivation)
where the response of the electron to the external and internal fields is the current density field . Here, the density and physical current density are the expectations of the density and current density operators defined previously taken with respect to the wave function . The law is gauge invariant and derived using the continuity equation . The external field is
where the Lorentz field , with the Lorentz “force” .
The internal field is
where the component fields , , , are defined as in the previous section but from time-dependent quantal sources obtained via the wave function (a special case [4] of the ‘Quantal Newtonian’ second law of Equation (16) corresponds to an external field . The term is then absent from Equation (19)).
In mapping to the model S system such that it possesses the same basic variables , we again assume the noninteracting fermions are subject to the same external fields as those of the electrons. The LEPT differential equation for the single-particle orbitals is then
with
where all the many-body effects are incorporated into the local effective electron-interaction potential . The S system wave function is the Slater determinant of these orbitals.
For the above described model system, the “Quantal Newtonian” second law is (see Supplementary Material for the Derivation)
Here, the S system current density field , with the current density defined as the expectation of the operator taken with respect to the determinant . The last equality of Equation (22) follows from the equivalence of of the interacting system to of the model system.
The internal field is
The kinetic field is defined as in the previous section but in terms of the time-dependent Dirac density matrix . The remaining fields and are the same as in Equation (19).
Hence, on comparing the “Quantal Newtonian” second law of Equations (16) and (22), the potential is then the work done at each instant of time, to move the model fermion from some reference point at infinity to its position at in the force of a conservative effective field :
where
with the electron-interaction, and the Correlation–Kinetic field defined as . As , the work done , at each instant of time, is path-independent.
The QDFT equations for the above LEPT once again show that the only correlations that need to be accounted for are those due to the Pauli exclusion principle, Coulomb repulsion, and Correlation–Kinetic effects.
The expression for of Equation (24) remains the same for the special case when the external potential is solely . This then means that the correlations that must be accounted for in the corresponding mapping to the model system are also the same.
For harmonically confined electrons in a magnetostatic field , perturbed by a time-dependent electric field , the corresponding wave function referred to as the Generalized Kohn Theorem, has been recently derived [21]. It is comprised of a phase factor times the unperturbed wave function in which the coordinates of each electron are translated by a value that satisfies the classical equation of motion (In the absence of the harmonic external potential, the wave function reduces to the Kohn Theorem [22] wave function. In the absence of the external magnetic field, the wave function reduces to the Harmonic Potential Theorem [23] wave function). Hence, if the unperturbed wave function is known, the time evolution of all properties is known. Observables represented by non-differential Hermitian operators, such as the density then correspond to the unperturbed value translated by a time-dependent function. Thus, the example of the QDFT mapping of the quantum dot in a magnetostatic field given in the previous section is equally representative of the case when the time-dependent field is additionally present. In this example, both the density and physical current density satisfy the above translational property. The results of Figure 1 correspond to (the case of the quantum dot in a time-dependent electromagnetic field is not provided because the corresponding wave function has not yet been derived).
4. Conclusions
The conclusions of this work, arrived at via QDFT, are the following: (a) in traditional LEPT, one maps a system of electrons in external time-independent or time-dependent electromagnetic fields, to one of noninteracting fermions possessing the same density or , a basic variable. However, what is proved here is that, within QDFT, it is possible and efficacious to map to a model system such that it possesses all the same basic variables. In the presence of both an electric and magnetic field, the basic variables are the density and physical current density (the reason for treating the time-independent and time-dependent cases separately is because, for the former, in addition to the constraint of fixed electron number, there is the constraint of fixed canonical angular momentum). External fields that are solely either electrostatic or time-dependent electric fields for which the basic variables are or constitute a special case; (b) in order to map to such a model system, the external fields experienced by the interacting electrons and noninteracting fermions must be the same. Hence, within QDFT, it is only the effective S system scalar potential , or equivalently the effective electron-interaction potential in which all the many-body effects are incorporated that must be determined (In traditional LEPT (see e.g., [19]), although one also assumes the model fermions are subject to the same external fields, both an effective scalar and vector (containing an additional electron-interaction component) potential must be obtained); (c) finally, given the requirement that the noninteracting fermions possess the same basic variables and are subject to the same external fields, then, irrespective of the form of external field, the only many-body correlations that must be accounted for in the mapping to the model system are those due to the Pauli exclusion principle, Coulomb repulsion, and Correlation–Kinetic effects. This provides a unification of all LEPT in terms of the electron correlations that must be considered. It also provides a considerable simplification in that Correlation–Current–Density and Correlation–Magnetic effects need no longer be addressed. Additionally, in three-dimensional, high density, low-electron-correlation systems, Correlation–Kinetic effects are usually small. For such systems, these effects can therefore be ignored in a first approximation. On the other hand, in lower dimensional systems and in the low density, high-electron-correlation Wigner regime, these effects play a significant role [24,25] and must be considered.
Supplementary Materials
Supplementary files are available online at http://www.mdpi.com/2079-3197/ 4/3/30/s1.
Acknowledgments
V.S. thanks Agnes Nagy and Karlheinz Schwarz for their invitation to contribute to the volume commemorating the 50th Anniversary of Kohn–Sham theory. The work of V.S. was supported in part by the Research Foundation of the City University of New York, and that of X.P. by the National Natural Science Foundation of China (Grant No: 11275100).
Author Contributions
This paper arose as a result of collaborative discussions between the authors over the past four years. V.S. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix Brief Summary of Quantal Density Functional Theory
The Quantal density functional theory (QDFT) described in this work is based on recent developments in Schrödinger theory and the fundamental theorems of density functional theory. Consider a system of N electrons in an external static or time-dependent electromagnetic field (the coordinate could be either , or , as the case may be). QDFT maps this system of electrons as described by the Schrödinger equation to one of noninteracting fermions possessing the same basic variables. A basic variable is a gauge invariant property, knowledge of which uniquely determines the wave function of the system. For the quantum-mechanical systems described, the basic variables are the density and the physical current density .
The next step is the description of Schrödinger theory from the perspective of the individual electron. This perspective is described via the “Quantal Newtonian” second and first laws, which are the equations of motion of the single electron in the sea of electrons in the external field . These laws are in terms of “classical” fields that pervade all space, and whose sources are quantum-mechanical expectations of Hermitian operators taken with respect to the wave function (with or . In addition to the external field , there is an internal field experienced by each electron. The internal field is comprised of components representative of properties of the system such as the correlations due to the Pauli exclusion principle and Coulomb repulsion, the density, kinetic effects, and an internal magnetic field component. There is then the response of the electron to all the fields described by a current density field (in summing over all the electrons, the contribution of the internal field vanishes, thereby leading to Ehrenfest’s theorem). The energy E and the nonconserved energy , and their components can be written in integral virial form in terms of the individual fields.
With the assumption of the existence of a noninteracting fermion model system possessing the same basic variables , and the assumption of the model fermions experiencing the same external field , one then derives the corresponding “Quantal Newtonian” second law. The resulting internal field now contains a field involving the local electron-interaction potential in which all the many-body effects are incorporated. It also contains the fields corresponding to the density, kinetic effects, and an internal magnetic field component. The density and internal magnetic field components are the same as those of the interacting system by the assumptions above. The kinetic field differs as can be understood from the Heisenberg uncertainty principle. There is finally the response of the model fermion represented by the field , which is also equivalent to of the interacting system, as the currents densities are also assumed to be the same.
As experienced by the electron and the model fermion is the same, equating the corresponding “Quantal Newtonian” laws then leads to the potential being the work done by the model fermion in a conservative effective field. This field is the sum of the electron-interaction field representative of Pauli and Coulomb correlations, and the Correlation–Kinetic field, which arises from the difference in the kinetic fields. Note that the expression for the potential is explicitly defined and solely in terms of these electron correlations of the system. Additionally, irrespective of the form of external field, whether it be static or time-dependent, the correlations are the same. Finally, the electron interaction and Correlation–Kinetic components of the energy can be expressed in terms of the respective fields.
The most general derivation of the “Quantal Newtonian” second law is given in Supplementary Material. For further derivations of the individual quantal sources and fields, approximation methods and applications, we refer the reader to [2,3].
References
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A 1133. [Google Scholar] [CrossRef]
- Sahni, V. Quantal Density Functional Theory, 2nd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Sahni, V. Quantal Density Functional Theory II: Approximation Methods and Applications; Springer-Verlag: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Qian, Z.; Sahni, V. Quantum mechanical interpretation of the time-dependent density functional theory. Phys. Lett. A 1998, 247, 303–308. [Google Scholar] [CrossRef]
- Qian, Z.; Sahni, V. Time-dependent differential virial theorems. Int. J. Quantum Chem. 2000, 78, 341–347. [Google Scholar] [CrossRef]
- Qian, Z.; Sahni, V. Sum rules and properties in time-dependent density-functional theory. Phys. Rev. A 2001, 63, 042508. [Google Scholar] [CrossRef]
- Sahni, V. Quantum-mechanical interpretation of density functional theory. Top. Curr. Chem. 1996, 182, 1–39. [Google Scholar]
- Sahni, V. Physical Interpretation of Density Functional Theory and of Its Representation of the Hartree-Fock and Hartree Theories. Phys. Rev. A 1997, 55, 1846. [Google Scholar] [CrossRef]
- Holas, A.; March, N.H. Exact exchange-correlation potential and approximate exchange potential in terms of density matrices. Phys. Rev. A 1995, 51, 2040. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1994, 136, B864. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Pan, X.-P.; Sahni, V. Hohenberg-Kohn Theorems in Electrostatic and Uniform Magnetostatic Fields. J. Chem. Phys. 2015, 143, 174105. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Pan, X.-P.; Sahni, V. Quantal Density Functional Theory in the Presence of a Magnetic Field. Phys. Rev. A 2011, 83, 042518. [Google Scholar] [CrossRef]
- Saarikovski, H.; Saarikoski, H.; Reimann, S.M.; Harju, A.; Manninen, M. Vortices in quantum droplets: Analogies between boson and fermion systems. Rev. Mod. Phys. 2010, 82, 2785. [Google Scholar] [CrossRef]
- Holas, A.; March, N.H. Density matrices and density functionals in strong magnetic fields. Phys. Rev. A 1997, 56, 4595. [Google Scholar] [CrossRef]
- Taut, M. Two electrons in a homogeneous magnetic field: Particular analytical solutions. [CrossRef]
- Taut, M.; Eschrig, H. Exact solutions for a two-electron Quantum Dot model in a magnetic field and application to more complex systems. Z. Phys. Chem. 2010, 224, 631–649. [Google Scholar] [CrossRef]
- Slamet, M.; Sahni, V. Study of a Quantum Dot in an Excited State. Bull. Am. Phys. Soc. 2016, 61, 357. [Google Scholar]
- Ghosh, S.K.; Dhara, A.K. Density-functional theory of many-electron systems subjected to time-dependent electric and magnetic fields. Phys. Rev. A 1988, 38, 1149. [Google Scholar] [CrossRef]
- Vignale, G. Mapping from current densities to vector potentials in time-dependent current density functional theory. Phys. Rev. B 2004, 70, 201102. [Google Scholar] [CrossRef]
- Zhu, H.-M.; Chen, J.-W.; Pan, X.-Y.; Sahni, V. Wave Function for Harmonically Confined Electrons in Time-Dependent Electric and Magnetostatic Fields. J. Chem. Phys. 2014, 140, 024318. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W. Cyclotron Resonance and de Haas-Van Alphen Oscillations of an Interacting Electron Gas. Phys. Rev. 1961, 123, 1242. [Google Scholar] [CrossRef]
- Dobson, J. Harmonic-Potential Theorem: Implications for Approximate Many-Body Theories. Phys. Rev. Lett. 1994, 73, 2244. [Google Scholar] [CrossRef] [PubMed]
- Achan, D.; Massa, L.; Sahni, V. Wigner High Electron Correlation Regime in Nonuniform Electron Density Systems: Kinetic and Correlation-Kinetic Aspects. Comput. Theor. Chem. 2014, 1035, 14–18. [Google Scholar] [CrossRef]
- Achan, D.; Massa, L.; Sahni, V. Wigner High Electron Correlation Regime of Nonuniform Density Systems: A Quantal Density Functional Theory Study. Phys. Rev. A 2014, 90, 022502. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).