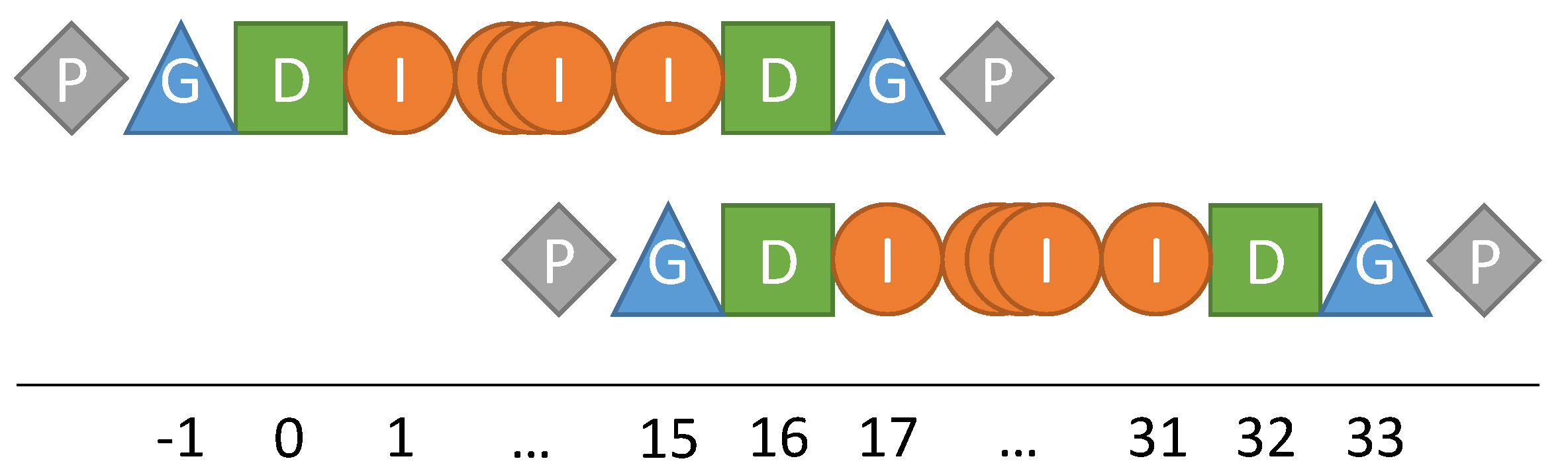Automatic Generation of Massively Parallel Codes from ExaSlang

Abstract

Domain-specific languages (DSLs) have the potential to provide an intuitive interface for specifying problems and solutions for domain experts. Based on this, code generation frameworks can produce compilable source code. However, apart from optimizing execution performance, parallelization is key for pushing the limits in problem size and an essential ingredient for exascale performance. We discuss necessary concepts for the introduction of such capabilities in code generators. In particular, those for partitioning the problem to be solved and accessing the partitioned data are elaborated. Furthermore, possible approaches to expose parallelism to users through a given DSL are discussed. Moreover, we present the implementation of these concepts in the ExaStencils framework. In its scope, a code generation framework for highly optimized and massively parallel geometric multigrid solvers is developed. It uses specifications from its multi-layered external DSL ExaSlang as input. Based on a general version for generating parallel code, we develop and implement widely applicable extensions and optimizations. Finally, a performance study of generated applications is conducted on the JuQueen supercomputer.

1. Introduction and Related Work

Heterogeneity and variance in available hardware components are increasing, especially in the field of high-performance computing (HPC). This makes the development of applications that attain optimal performance and retain their level of performance when changing the execution hardware more challenging than ever. One traditional approach is developing highly specialized codes that are tuned towards the target hardware and the problem to be solved. On the other end of the spectrum stands the creation and maintenance of large-scale libraries and software frameworks. However, both approaches become increasingly unsuited for the task at hand. One technology that has been emerging since the last decade and that represents a possible remedy is given by domain-specific languages (DSLs) in conjunction with code generation techniques.

Within the larger research scope, one particularly attractive class of applications is given by stencil computations. Here, the potential to gain greatly improved performance through well-known optimization techniques is given. Moreover, stencil codes and their derivatives can be encountered in many components of numerical codes, especially in the context of partial differential equations (PDEs) and ordinary differential equations (ODEs). Quite a few research projects with different aims and features have been started in the past years. Among them is STELLA [1], a DSL embedded in C++ recently used in accelerating COSMO, a weather prediction and regional climate model. Its main focus is on stencil computations on structured grids and it supports using accelerators through CUDA, as well as distributed memory parallelization using MPI. However, the latter is restricted to two dimensions for 3D problems. Other projects are Pochoir [2], PATUS [3] and Liszt [4]. Their respective main focuses are cache-oblivious stencil computations, auto-tuning methods and unstructured grids. One tool especially focused on low-level optimizations is SDSL (Stencil Domain Specific Language) [5] and its compiler. More specialized to the domain of stencil computations in image processing algorithms is HIPAcc [6]. Its applicability is, however, restricted to 2D problems. Another project in the image processing domain is PolyMage [7], which aims at optimizing kernel pipelines.

Generally speaking, many stencil compilers and frameworks limit themselves to a very restricted feature set by dropping support for distributed memory parallelization approaches and/or accelerators, as well as 3D problems. In contrast, ExaStencils aims at supporting all of these features and goes one step further: it additionally specializes in a distinct class of problems and numerical solvers, namely PDEs and geometric multigrid solvers [8]. 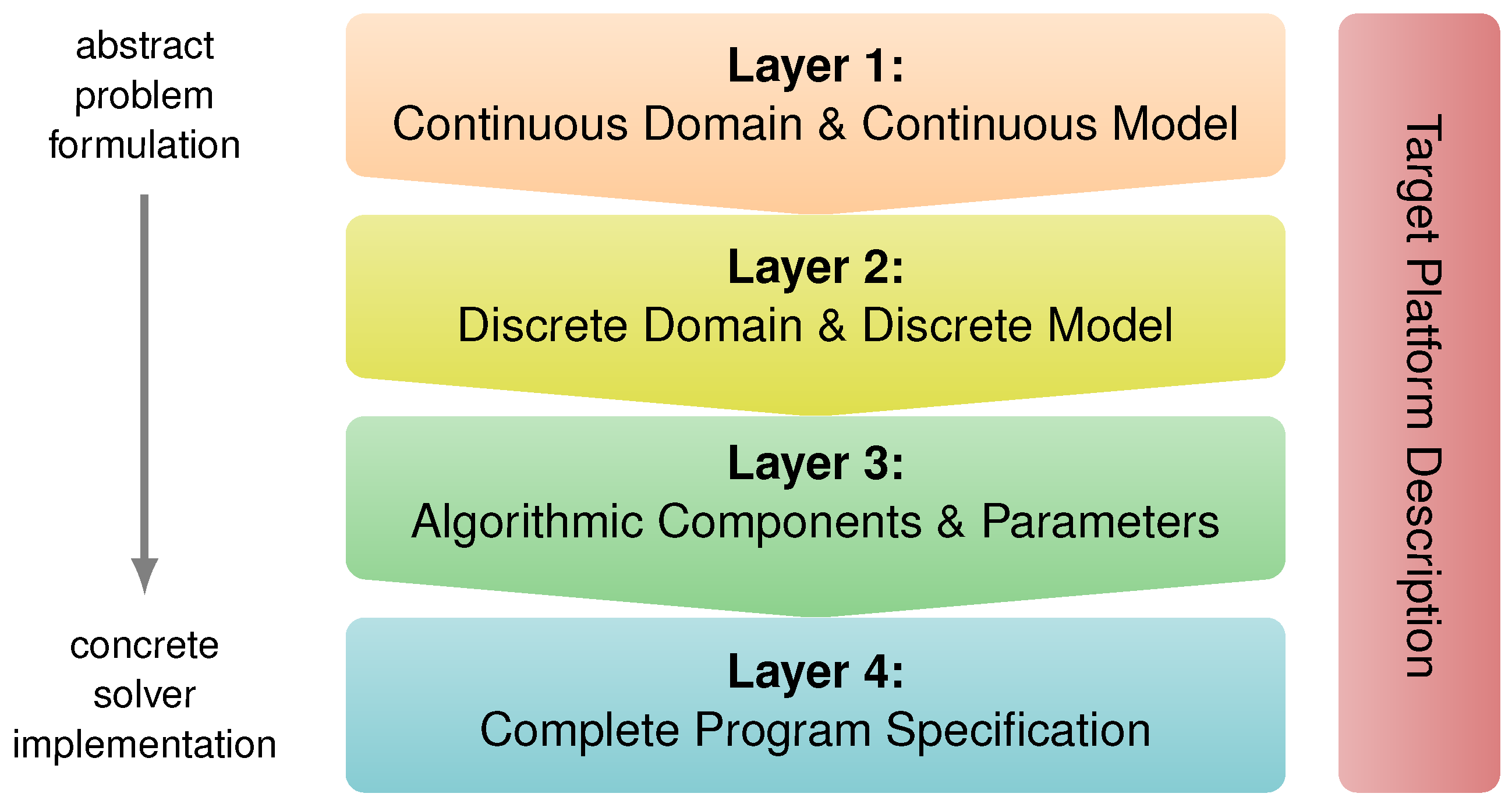In its scope, a multi-layered, external DSL named ExaSlang (ExaStencils language) is developed [9]. As illustrated in Figure 1, it consists of four distinct layers, which target different aspects of the problem and solver specification. Essentially, Layer 1 allows providing continuous formulations of PDEs and computational domains. On Layer 2, their discretized counterparts can be expressed. In most cases, finite differences and finite volumes are used for the discretization. Furthermore, certain restrictions towards the utilized computational grid are imposed, such as being structured or at least composed of structured patches (block-structured). After describing the problem and its discretization, a suitable solver can be composed on Layer 3. At this stage, the code is still serial and does not include information about potential domain partitions. This changes on Layer 4, where the complete program is assembled and automatically annotated with communication statements. Apart from adapting communication schemes and data layouts, this layer also allows adding utility functionality, such as timings and data in- and out-put, as well as some general program flow, thus finalizing a fully specified application. Additionally, an orthogonal layer solely dedicated to the specification of target hardware platforms is available, as well. Roughly speaking, information from this description and the first three layers is used to create a stand-alone application on Layer 4. It is then used as input for our code generation framework, which applies a series of fine-grained transformations to ultimately produce a detailed syntax tree. At this point, output to source code in a chosen target language, such as C++ or CUDA, is possible.

Besides stencil codes, particle dynamics are a highly relevant domain occurring in a wide array of industrial and academical applications. One example for a DSL from this domain is PPML [10], a DSL embedded in Fortran 2003 that can be used to implement particle simulations.

Apart from specialized DSLs for a distinct class of applications, there are also frameworks targeting rapid development of DSLs. One of the most promising projects following this approach is AnyDSL [11]. It is designed similar to established solutions like language workbenches, which are discussed in detail in [12]. However, AnyDSL has the potential to facilitate the automatic application of hardware-specific optimizations and the introduction of parallelization concepts.

Independent of the domain, any DSL has to be combined with a code generator or compiler. Apart from mapping DSL code to a compilable or executable representation, fully exploiting target machines by utilizing a wide range of possible hardware components is one of the most challenging problems. It requires carefully optimizing the code, which luckily can be done almost in a fully-automated manner, as recent work demonstrates [13].

Another issue is exposing and exploiting parallelism in a given application. In most domains of today’s research, such as stencil computations and particle simulations, exposition is not the dominant challenge. Instead, techniques for mapping general, usually not explicitly parallel DSL code to, e.g., distributed compute resources and accelerators are required. These techniques are also the main focus of this paper. In detail, we discuss possible approaches, as well as necessary steps and illustrate them with the example of our own framework ExaStencils and its multi-layered DSL ExaSlang.

ExaSlang’s Layer 4, or ExaSlang 4 for short, is most relevant for influencing a possible (automatic) parallelization. The language is described in detail in [9] and used in the code examples of this paper. Previous publications within the scope of ExaStencils focused on general concepts [8], choosing an appropriate technology for implementing the DSL and generator [12], an initial specification of ExaSlang 4 [9], low-level optimizations employed by the code generator [13] and evaluating special target hardware, such as FPGAs [14]. In contrast, this work discusses the concepts for the generation of highly scalable parallel code, as well as their implementation in the ExaStencils framework. Furthermore, the implemented optimizations concerning the parallelization are discussed and, in part, evaluated. All presented concepts generalize towards other domains as, e.g., particle simulations. Their concrete application and implementation, however, is beyond the scope of this work. This is also the case for extensions towards target architectures beyond CPUs, such as, e.g., ARMs and FPGAs.

The remainder of this paper is structured as follows: In Section 2, concepts that must be supported by any compiler or code generator are presented. There are two main challenges: the partition of data and the associated accesses to local and remote data. They are examined in Section 3 and Section 4, respectively. After showing how these concepts can be incorporated in code generators, we go into detail about possible ways to expose such functionality to potential users in Section 5. This is followed by suitable extensions and optimizations for our exemplary domain of stencil computations on (block-)structured grids in Section 6. Lastly, we verify our approach by presenting performance results for fully-generated and highly parallel geometric multigrid solvers in Section 7 before a conclusion is drawn in Section 8.

2. Required Concepts

This section addresses mainly one question: which concepts are required for generating parallel code from abstract DSL specifications?

Generally speaking, performing parallel computations requires two steps: First, the work to be done has to be distributed on the available hardware resources. This can be done statically or dynamically, either by hand or by relying on a suitable runtime system. Second, data required for the actual computations must be distributed, as well, usually taking care that limited resources, such as memory, are not exhausted. In this step, data may be duplicated to increase performance or to reduce implementation effort. When choosing a strategy for the second step, it makes sense to investigate the data access patterns of the application at hand. To this end, data are correlated with (a) parts of the work to be performed and (b) dependencies between data. While the first point usually refers to the part of the problem updated by the target computations, the second one is harder to describe. Usually, either global data access, as, e.g., in the case of matrix-matrix-multiplications, or data access within a restricted neighborhood is performed. Prominent examples for the latter are given by stencil computations where the neighborhood is defined by the extent of the stencil and the topology of the grid and by particle computations based on fast decaying potentials where the neighborhood can be derived from particle properties, such as positions and extents.

This work focuses on restricted data access patterns since, in our opinion, they are widespread, and the importance of implementing (or generating) specialized solutions is more relevant with respect to attainable performance. In this case, the partitioning of work and data often follows a common strategy. Possible approaches are discussed in the next section. Due to the nature of the domain, data access mapping between different partitions is required, which is elaborated in Section 4. While the discussed topics are widely applicable, we want to illustrate them using their implementations in the ExaStencils framework. Its focus is on stencil computations, and especially those arising in the context of specifying geometric multigrid solvers, on regular or at least block-structured grids. Of course, any concept implemented in such a code generator has to be flexible enough to support conventional and novel solutions alike. In our context, this means that established approaches like dividing the computational domain into sub-domains, embedding ghost (or halo) layers and exchanging them via MPI are essential. On the other hand, they have to be easily extendable to other types of hardware, such as GPUs, ARMs and FPGAs, other parallelization interfaces, such as CUDA and OpenMP, as well as specialized models and run-times, such as DASH [15], which implements the partitioned global address space (PGAS) approach, and task-based approaches, like OmpSs [16] and CHARM++ [17].

3. Data Partition

In order to support a field of application as large as possible, multiple layers of data partitioning are necessary. First, data need to be distributed physically, thus mapping to available hardware resources. This step includes, e.g., assignment to MPI ranks or CUDA devices. Since available hardware is usually organized hierarchically, any flexible concept must take this into account. Nevertheless, in our experience, a very flat hierarchy of only three levels is sufficient for most applications. Concurrently, data on each of the physical partitions need to be partitioned logically. That is, data are not stored separately in this step, but assigned to logical groups. This allows the distinction between data points owned by the respective partition and those existing only as a copy (or ghost/halo data). Furthermore, this mechanism can be used to mark data available for synchronization. Schemes for both kinds of partitioning are presented in the following.

3.1. Physical Data Partition

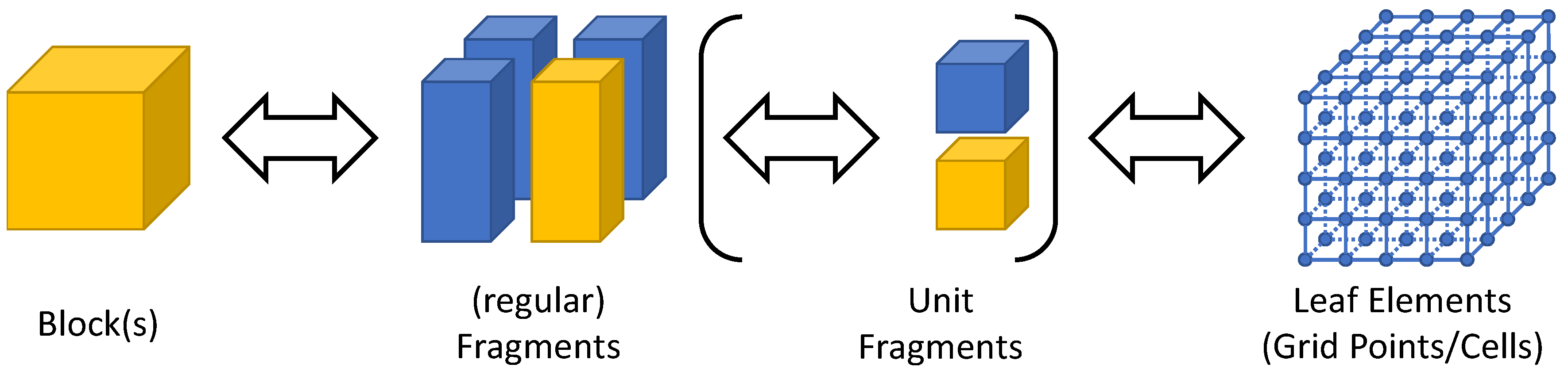
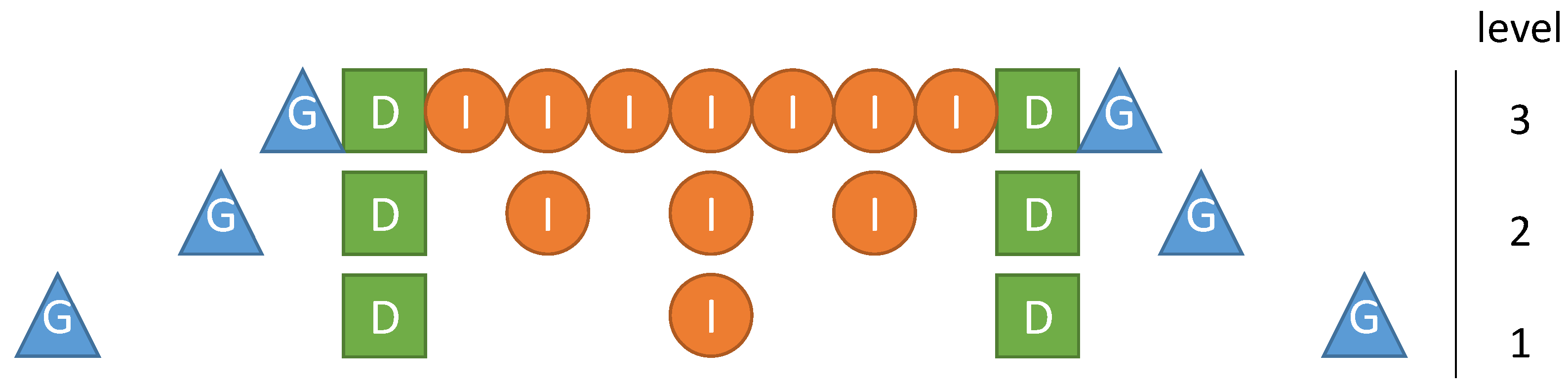
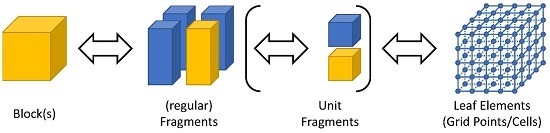
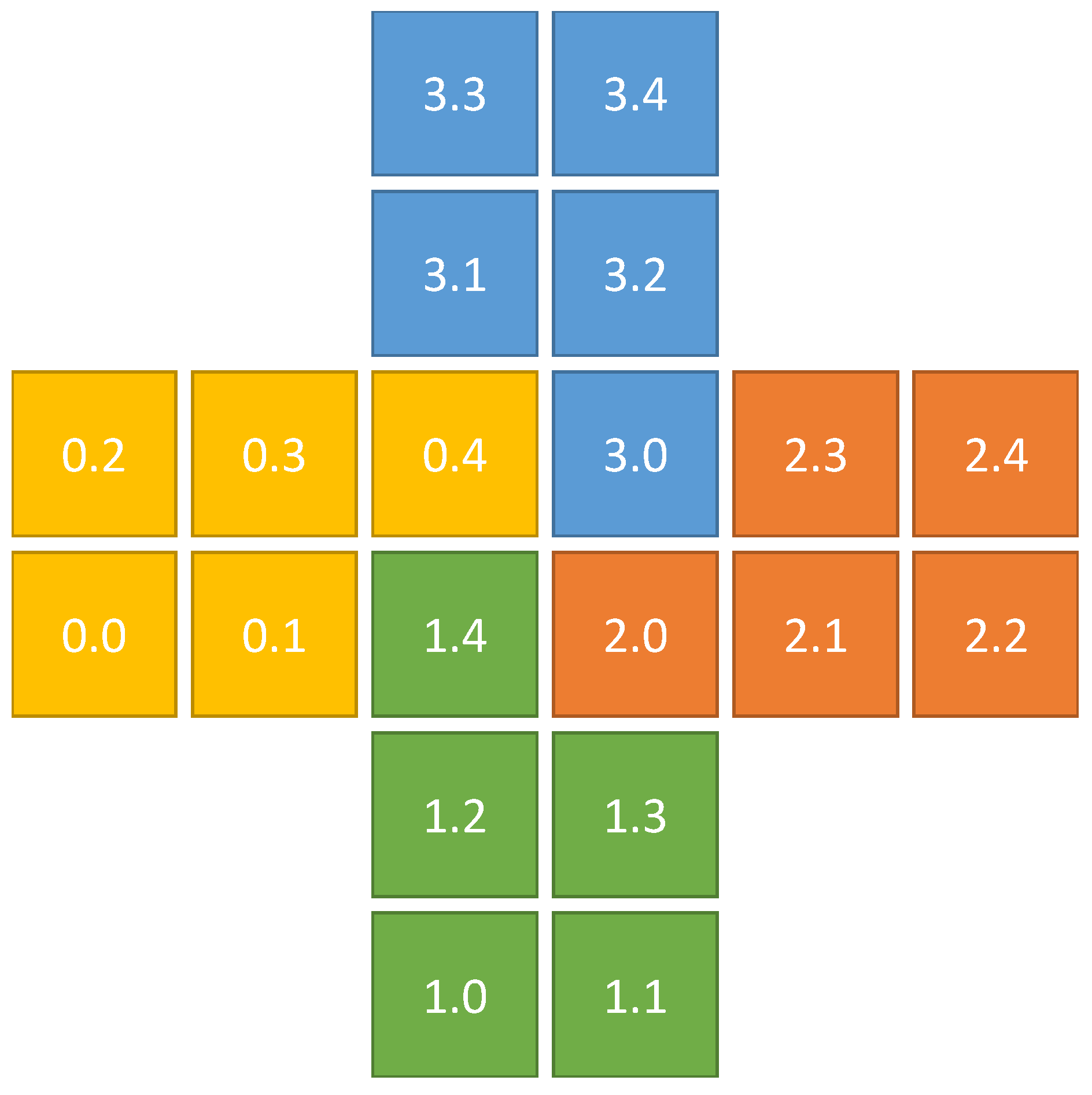
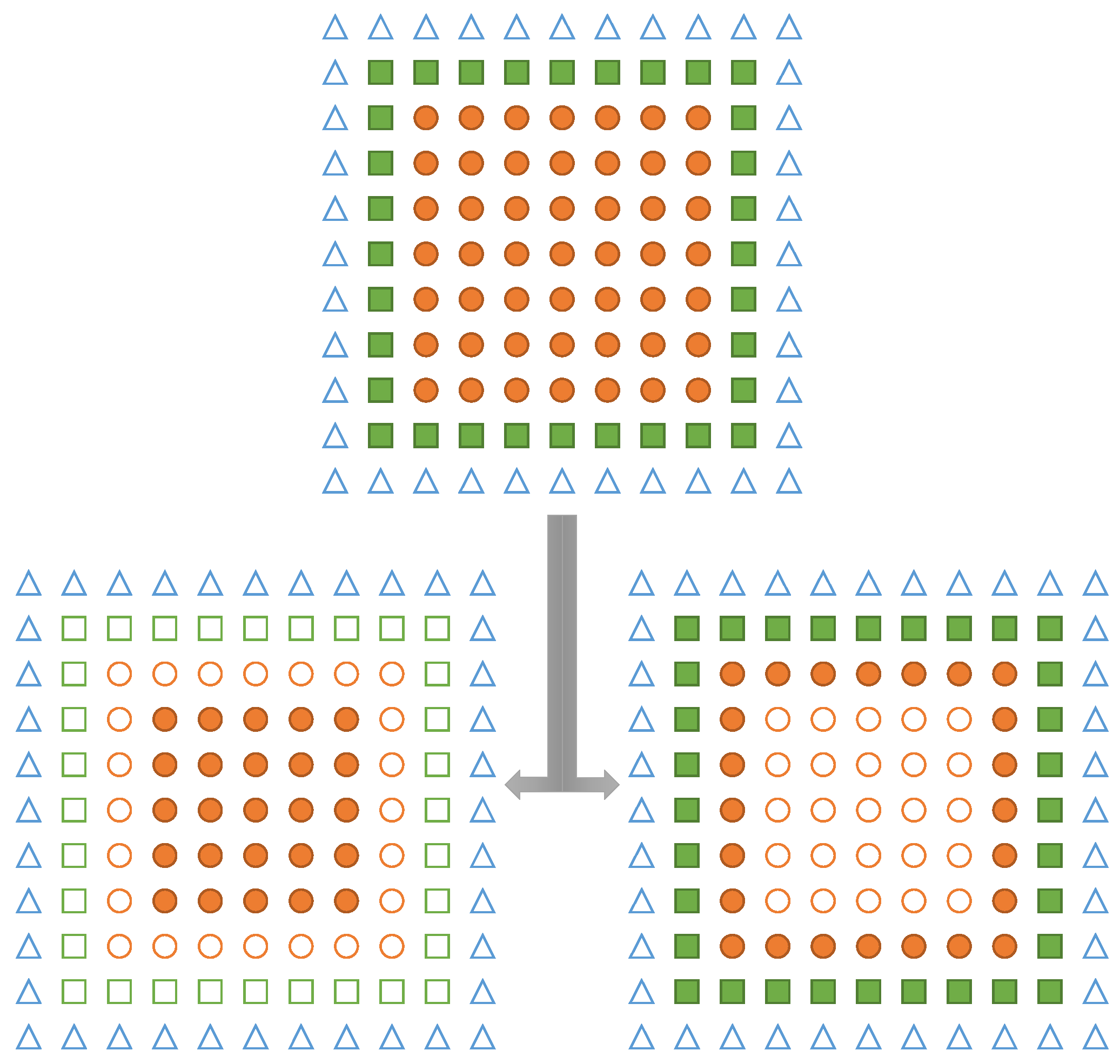
We propose the (physical) data distribution according to a three-level hierarchy as is also implemented in ExaStencils. First, the smallest unit of partition, which we call leaf elements, is determined. In the case of block-structured grids, this is given by the single nodes or cells of the grid. As illustrated in Figure 2, sets of leaf elements, in our case parts of the computational grid, are accumulated in so-called fragments. These can, amongst others, be used to represent different sockets or accelerators. One or more fragments are then used to compose a so-called block. Each block can, amongst others, be used to represent compute units in a distributed memory context. Within the domain of stencil computation on (semi-)regular grids, blocks are usually rectangular and composed of equivalently-sized fragments. However, other configurations, as illustrated in Figure 3, are also possible. Note that in ExaStencils fragments are technically composed of unit fragments, i.e., cubic fragments with a fixed number of grid points. This specialization, however, is only relevant in the context of multigrid solvers, as explained in Section 3.2. While demonstrated for patch-based grids, this concept is not restricted to such cases, but can easily be applied to unstructured grids and graphs, as well as mesh-less problems, such as particle-based methods.

With the presented approach, mapping data to a wide range of hardware configurations and parallelization models is possible. One of the most frequently encountered ones is a hybrid MPI/OpenMP parallelization. Here, each MPI rank is assigned a single block, while fragments are mapped to single OpenMP threads. In case of very irregular domains, i.e., in cases where a high number of fragments needs to be processed, over-subscription in the form of multiple fragments assigned to a single OpenMP thread may be suitable. For the basic case of fully regular blocks, however, aggregating all fragments within one block and concurrently applying OpenMP parallelization to suited kernels may yield improved performance. In general, it is always possible to have only one fragment per block if a block-fragment distinction is not required. This essentially collapses the primitive hierarchy.

Another feature is being able to control different levels of parallelism very intuitively. Considering, e.g., the common configuration of large-scale GPU clusters, a suitable mapping is given by the following: Each compute node is managed by a single MPI rank, which corresponds to a single block. Within each block, one fragment per accelerator device is instantiated. Computations within one fragment are parallelized using CUDA, where the degree of parallelism is limited by the number of leaf elements.

Besides these more conventional configurations, the presented concept is flexible enough to support code generation for other parallel programming models. One very tempting option is given by targeting PGAS models, as the required implementation effort for the code generation routines is significantly lower than for, e.g., MPI. On the other hand, certain optimizations may be inhibited by this approach, and the overall performance of the application may be limited by the employed PGAS implementation.

Another potentially suitable target is given by task-based models, such as implemented by OmpSs [16] and StarPU [18]. Here, operations acting on a single fragment can simply be modeled as a distinct task, while a suitable shared memory parallelization is applied within each fragment/task. The biggest advantage of this approach is the built-in adaptive load balancing and the possibility of easily extending towards fault tolerance and resilience. However, similar to the PGAS approach, in the end, performance is dependent on the implementation of the parallelization framework on which it is built.

Independent of the chosen combination of hardware and parallelization backends, blocks and fragments need to be instantiated according to some prescribed strategy in the final (generated) program. Usually, this requires some additional information, e.g., which block owns which fragments and how primitives are connected to one another. Other, more use-case-specific information, such as MPI ranks assigned to connected primitives, negotiated communication tags or CUDA device ids, may be added if necessary. In the most basic case, all of these parameters are read from one or more files. In practice, however, it often is more efficient to embed a suitable routine in the generated application, which determines relevant parameters at execution time. This optimization is mainly used if the original computational domain can be described in a very abstract and concise fashion, as is the case with, e.g., simple shapes, such as cuboids and spheres.

Lastly, memory for the actual problem data, i.e., the leaf elements, needs to be allocated. This is normally done with respect to fragments, that is each fragment holds a container for storing data associated with the leaf elements. In the case of ExaStencils, this container corresponds to one or more linearized n-dimensional grids stored consecutively in memory.

3.2. Logical Data Partition

As discussed in Section 3.1, a three-level hierarchy allows efficient mapping of data associated with leaf elements to a multitude of hardware platforms and parallelization paradigms. The next step is supporting updates of data within a given fragment. To this end, many applications require access to leaf elements of different, usually neighboring fragments. Possible mechanisms that allow such accesses are discussed in Section 4. We want to prepare for the most common case given by maintaining read-only copies of certain leaf elements on neighboring primitives. These copies, which are usually named ghosts, shadows or halos, allow batched synchronization of data and aligned access patterns. For easy reference, we refer to them as ghost elements. By convention, no calculations are performed on ghost elements, apart from updating them according to their original counterparts as described in the next section. Although no write access is performed, for most applications, it makes sense to integrate those ghost elements in the regular storage in order to optimize, e.g., read accesses. Apart from “regular” and ghost elements, we propose a third kind, so-called duplicate elements. These are elements occurring within multiple fragments, like ghost elements, but are handled as regular elements with respect to updating. The reason for keeping these elements in a separate group is that even though the same calculations are performed for each fragment, certain key details, such as the order of operands, may differ. As a consequence, slight variations in the values of duplicated elements can occur, and additional synchronization with a specialized protocol is required. Moreover, reductions may need to be adapted, such that the contributions of duplicate elements are only considered once. Details on both aspects are given in Section 4.

In the scope of ExaStencils, that is in the scope of geometric multigrid solvers on regular grids, the different groups of leaf elements refer to specific regions of the computational grid. This is illustrated in Figure 4: the inner region, which contains all regular leaf elements, is surrounded by the duplicate region, which is in turn wrapped by the ghost layers. For performance optimizations, padding regions may be added on both sides of the field. In our framework, all layers/regions are defined separately per dimension and can be of zero size if not required. Ghost and padding layer widths may additionally vary depending on the side of the fragment on which they are located. Due to this layout, it is not required to store group affiliations explicitly in the generated program since they are implicitly available through the grid indices of given leaf elements.

While the distinction between duplicate and ghost elements is not intuitive, it is particularly useful in the context of multilevel methods. Under certain conditions, operations mapping data between grids can be specified independently of the fragment to which they are applied. As illustrated in Figure 5, duplicate points remain at a constant (geometric) position independent of the level, if $c_{dim}{2}^{level}+1$ grid points per dimension (without ghost and padding layers) are used. For cell-based data localizations, $c_{dim}{2}^{level}$ cells per dimension are used, and duplicate layers are eliminated. In both cases, $c_{dim}$ is an arbitrary, usually small, dimension-wise defined constant, which corresponds to the number of unit fragments per fragment in the corresponding dimension.

Depending on the application, it may be useful to introduce another group of elements. This group marks all leaf elements that have corresponding ghost elements in other fragments, i.e., elements that may need to be read in a synchronization step. However, in the domain of ExaStencils, this is generally not necessary, since the presented region concept already allows intuitive specifications of communication patterns, as described in the next section.

4. Access to Data

Using the partitioning concepts presented in Section 3, it is evident that almost all applications will require access to data of other fragments when updating their own. As described in Section 2, the focus of this work is given by applications that require data access only within a certain, limited neighborhood. Consequently, the number of fragments, from which data are required, is generally small. Depending on the actual primitive hierarchy and the used parallel programming models, different routines for such data accesses are required. Consider, e.g., using an OpenMP parallelization on the fragment level, while blocks are handled by designated MPI threads. In this case, access to other fragments’ data within one block can be implemented by simple indirect memory accesses. However, this approach leads to potential race conditions and performance penalties due to unaligned accesses. For better control of performance characteristics, we propose a more structured approach: we rely on the logical groups of leaf elements, e.g., regular, ghost and duplicate, within fragments that have been introduced in the previous section. This allows keeping all fragment accesses local, i.e., within one fragment. However, synchronization of ghost, and possibly duplicate, data is required at some point. To minimize latency, it is beneficial to always communicate all elements within one set in a single operation. Sets are usually defined by the data to be communicated (in the case of multiple data elements per leaf node) and communication characteristics, such as the fragment with which to be communicated. Considering the domain of stencil operations, this corresponds to handling parts of regions associated with a given neighboring fragment as a whole.

In the case of synchronizing ghost elements, the ownership, and thus origin, of the data is clear. Similarly, the target is known, and the communication is bidirectional, i.e., every sender is also a receiver for the same neighboring fragment, as illustrated in Figure 6a. For handling duplicate data, however, additional work is necessary. Computations on duplicate elements are usually performed in the same fashion for each fragment, but due to a locally changed order of operands or other minor details, results may diverge. Since it is not known which version of the data is the more ‘correct’ one, different approaches are possible. Taking the mean value of different element instances and using them as the new value of every participating element is frequently used, for instance. Another, potentially more efficient method is declaring a dominant instance, e.g., defined by the lowest id of the parent fragment, and using its value to overwrite all other instances. The latter is the default choice in our framework and visualized in Figure 6b.

Orthogonal to the different communication patterns, code generators need to support a range of parallelization backends and combinations thereof. This renders the generation of robust and fast code for each variant challenging. Since the actual choice of backends is usually left open when formulating DSL code, input influencing the communication behavior of the program is mostly quite abstract (details on embedding them in DSLs are given in Section 5). In ExaStencils, we implement different modules capable of generating specific code for different parallelization backends. The most straightforward of these modules handles the exchange of data between fragments located in shared memory, as is the case of an OpenMP parallelization over multiple fragments within one block. Here, data can be exchanged directly without the use of temporary buffers. More precisely, data can be copied in shared memory, either through single assignments or through memcpy’s if permitted by the access pattern. Nevertheless, avoiding buffered communication needs additional synchronization when, e.g., computation and communication are to be overlapped. Depending on the direction of the implemented communication, that is if data are pulled from or pushed to other primitives, problems might occur when data were not updated in time. To avoid this, we allow the generation of additional volatile synchronization variables. They can be used to keep track of whether data may be read or written at any given time. Relying on these mechanism may deteriorate performance initially. However, the increased asynchronicity of the control flow may counterbalance these effects, depending on the application at hand.

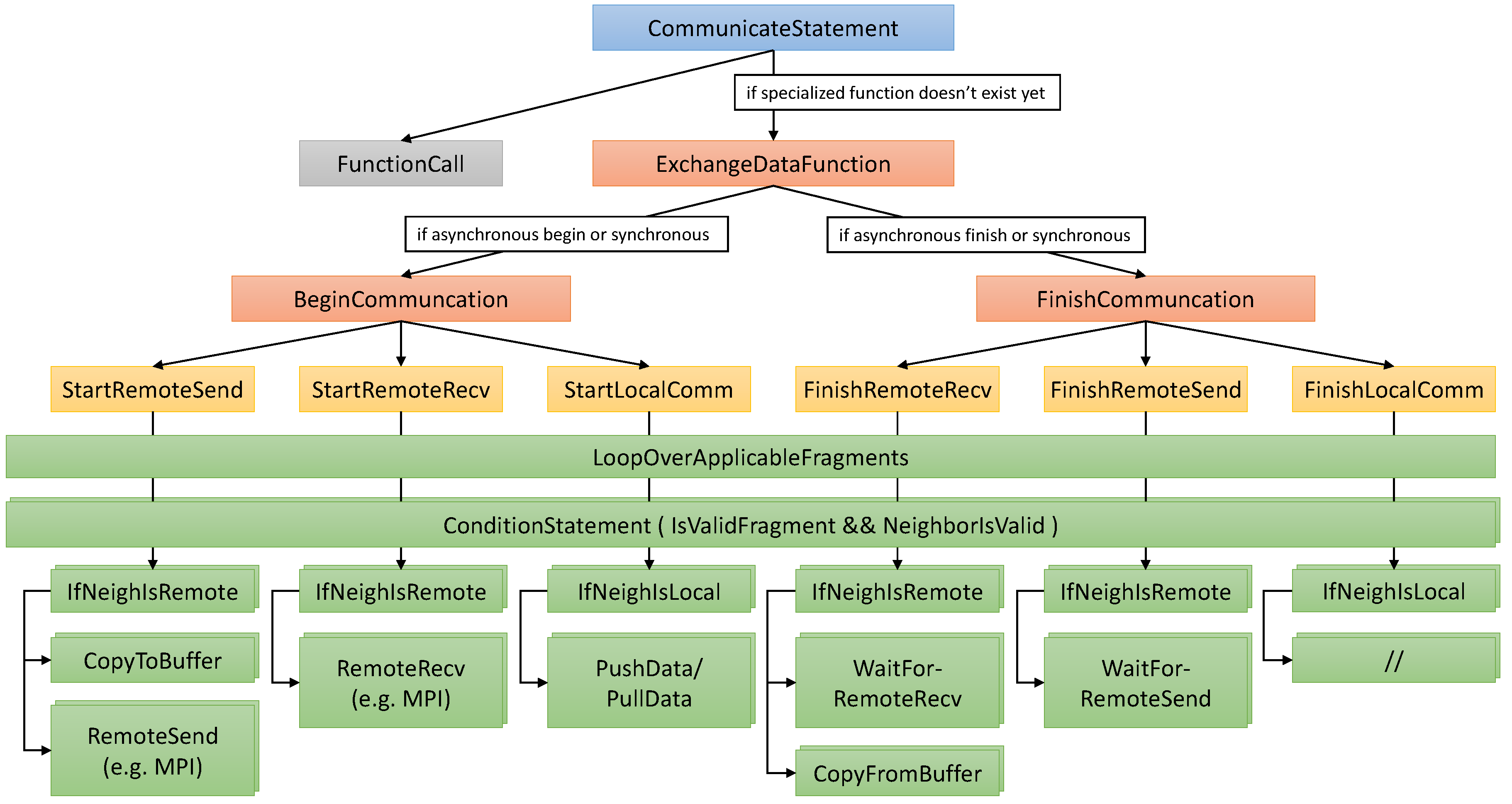
Data exchange between fragments located in different memory spaces, where the most prominent example is MPI communication, is more complicated. In our code generator, we break up such communication statements into multiple smaller building blocks, as illustrated in Figure 7. First, the statement is transformed into a function call to a specialized communication function providing the required functionality. This allows encapsulating and reusing the complete routine, which can become quite complex. If the requested function does not exist yet, i.e., was not already generated for an identical communication statement, it is added. To this end, the body is initialized with placeholders representing a start and/or a finish phase, depending on the original statement. Through this, an otherwise synchronous statement can also be split at the DSL level, effectively allowing users to overlap the communication with other statements. Next, the placeholders are transformed into more fine-grained operations, such as starting and finishing stages of local and remote communications, that is communications taking place between fragments held by the same or different blocks. These are then further refined into distinct copy to/from buffer and send/receive operations, as well as synchronization statements, if required. Since each fragment exchanges data with multiple neighbors, these nodes are instantiated for each of these cases, and the type of communication (local/remote) is chosen at runtime depending on the type of neighborhood connection. In the case of multiple fragments per block, it is beneficial to wrap the generated statements with loops over all fragments to allow for easy parallelization using, e.g., OpenMP. Here, multiple different approaches are possible. One is wrapping at different stages of the processing pipeline, such as at the green nodes in Figure 7, for instance. Another option is combining some nodes in the hierarchy, e.g., buffer packing and send/receive nodes. Ultimately, all generated operations are mapped to loops, conditions and specialized statements chosen according to the desired parallelization backend.

Overall, many performance-influencing choices have to be made, including to what extent asynchronous operations are replaced with their synchronous counterparts, how the different building blocks are arranged and if and how loops are split or merged. Currently, our code generator supports all of these cases and allows setting external flags to specify the desired behavior. This interface also allows automatic tuning of these choices, but a robust implementation is currently a work in progress. Our flexible approach also allows applying more advanced optimization techniques, such as those presented in Section 6. One of these techniques is interweaving local and remote communication stages, as also already used in Figure 7.

In addition to generating communication functions, a code generator has to take care of making sure that temporary buffers are available in the generated code. This includes instantiation and memory management. A simple approach is generating these buffers in place as part of the routine described above. This, however, may deteriorate performance. Allocating buffers at the start of the program and then re-using them throughout is a better option. Since some buffers may not be shared, as they are used concurrently, the first step is identifying these groups. For the code generation, distinguishing features between these buffers need to be extracted. In our applications, they may include the fragment index, the direction of the data exchange as a vector in the dimensionality of the computational domain, the operation itself, i.e., send or receive and the multigrid level on which the operation is taking place. After establishing a minimal set of concurrently-used buffers, the maximum required size of each buffer is determined. With this information, the generation of appropriate instantiations, allocations and deallocations is straightforward. As a last step, accesses to buffers have to be adapted if necessary. In ExaStencils, this pipeline is implemented as a set of automatically applied transformations. Distinguishing features can be adapted by the user via external parameters if required.

At this point, most communication patterns can be handled within the DSL and code generator. However, there is one more operation that needs to be modeled specifically: reductions. Here, we propose to follow the primitive hierarchy. This means performing reductions on leaf elements of every fragment, followed by reductions across fragments in one block and, finally, a reduction across blocks. In the case of OpenMP and MPI, the generation of the additionally required clauses or statements is easy. For other parallelization backends, such as CUDA, this is more complex. Here, we propose to generate specialized reduction kernels in conjunction with injecting specialized, sharable buffers similar to the regular communication buffers described before. The latter is required due to the fact that CUDA reductions are usually performed in-place, and the original data must not be compromised. Another special case is given by duplicate elements, as their contributions must be considered only once. To this end, we discard contributions from all fragments but the one with the lowest index. In ExaSlang 4, reductions must currently be annotated explicitly. All further processing is then done automatically by the code generator using the concepts above.

Concluding, we consider the presented concepts to be flexible enough to support novel architectures and parallelization backends alike.

5. Exposing Parallelism to Potential Users

A more high-level question is how parallelism can be exposed to potential users on a DSL level. In practice, specifications from DSLs have to be mappable to a multitude of backends. At the same time, DSLs need to be concise and not unnecessarily bloated. As a consequence, only very abstract parallelization interfaces are practical at the DSL level. In the extreme case, parallelism can even be completely hidden from the user. How an interface is modeled in the end depends strongly on the target domain and user group. A common requirement for all approaches, however, is to support the presented strategies for data partitioning and synchronization. In the following, we illustrate one potential implementation with the example of ExaStencils.

Users describe the computational domain, i.e., the computational grids, within the DSL. Additionally, information about grid partitioning, usually corresponding to the number and size of fragments and blocks, is required. Alternatively, the domain partition can be read from a separate input file, allowing for more complicated use-cases.

In terms of data layout, ExaSlang allows the definition of so-called field layouts describing the extents of the regions presented in Section 3.2. Examples are shown in Listing 1. All encoded information can be determined automatically and serves only the purpose of being visible and, if required, adaptable, to users.

        $1 /* \mathit{\text{layout for scalar, node-located grid data; simple stencils can be applied}} */$
      
	  
        $2 \mathbf{\text{Layout}} \text{DefaultNodeLayout} < \mathbf{\text{Real}} , \text{Node} >@\text{all} \{$
      
	  
        $3 \text{duplicateLayers} = [ 1, 1, 1 ] \text{with} \text{communication}$
      
	  
        $4 \text{ghostLayers} = [ 1, 1, 1 ] \text{with} \text{communication}$
      
	  
        $5 \}$
      
	  
        $6$
      
	  
        $7 /* \mathit{\text{layout omits duplicate layers as values are now cell-centered}};$
      
	  
        $8 \mathit{\text{features extended ghost layers for larger stencils or temporal blocking}} */$
      
	  
        $9 \mathbf{\text{Layout}} \text{ExtendedCellLayout} < \mathbf{\text{Real}} , \text{Cell} >@\text{all} \{$
      
	  
        $10 \text{duplicateLayers} = [ 0, 0, 0 ]$
      
	  
        $11 \text{ghostLayers} = [ 3, 3, 3 ] \text{with} \text{communication}$
      
	  
        $12 \}$
      

Listing 1: Defining field layouts in ExaSlang 4. Both layouts are defined for all levels of the multigrid hierarchy. Layers to be communicated can be annotated. The number of inner points is chosen automatically dependent on the multigrid level.

Synchronization of data is either determined automatically, as discussed in Section 6, or set up manually. We support a set of coarse-grain synchronization operations, which can directly be mapped to generated communication functions, as explained in Section 4. As evident from Listing , simple statements are used to trigger data exchange. They can be specialized for a specific set of regions and sub-sets of those regions or split into begin and end operations to account for the overlap of computation and communication.

        $1 /* \mathit{\text{communicates all layers marked for communication}} */$
      
	  
        $2 \mathbf{\text{communicate}} \text{Solution}@\text{current}$
      
	  
        $3$
      
	  
        $4 /* \mathit{\text{communicates only ghost layers}} */$
      
	  
        $5 \mathbf{\text{communicate ghost}} \text{of} \text{Solution}@\text{current}$
      
	  
        $6$
      
	  
        $7 /* \mathit{\text{communicates duplicate and first two ghost layers}} */$
      
	  
        $8 \mathbf{\text{communicate dup}}\mathbf{,} \mathbf{\text{ghost}}[0, 1] \text{of} \text{Solution}@\text{current}$
      
	  
        $9$
      
	  
        $10 /* \mathit{\text{asynchronous communication of all marked layers}} */$
      
	  
        $11 \mathbf{\text{begin communicate}} \text{Residual}@\text{current}$
      
	  
        $12 //\dots$
      
	  
        $13 \mathbf{\text{finish communicating}} \text{Residual}@\text{current}$
      

Listing 2: Communicate statements in ExaSlang 4. Fields are accessed using (multigrid) level specifiers as in [9]. Each field is tied to a specific field layout with layers marked for communication.

6. Extensions and Optimizations

Based on the presented concepts, it is possible to extend code generation frameworks with more sophisticated optimizations. Although some of these extensions are dependent on the actual problem domain of the DSL and code generator, we highlight some possibilities within ExaStencils.

6.1. Automatic Generation of Communication Statements

Considering the domain of stencil codes on (semi-)regular grids, specific data synchronization patterns emerge. This allows for the automatic injection of communication statements, which makes writing DSL code even easier. For this, we first implement a transformation that gathers and transforms all suitable loops. For each loop, the body is checked for read and write accesses to specific data, as well as for stencil convolutions. With this information and also taking the current loop bounds into account, read and write accesses to duplicate and ghost data are determined. At this point, one of two strategies may be applied:

• Data are fetched when required, i.e., communication statements are added in front of the loop according to relevant read accesses.
• Data are propagated after they have been updated, i.e., communication statements are added behind the loop according to relevant write accesses.

This method already works reasonably well in practice and, additionally, allows the presentation of an updated version of the given DSL code to the user, such that a review of injected communication statements is possible. Nevertheless, further optimizations are possible when handling loops that are only applied to a specific subset of grid points, as, e.g., in multi-color kernels. Here, the set of applicable points can be specified using conditions, such as 0 == (i0 + i1 + i2) % 2, which targets all even points for a red-black Gauss–Seidel smoother. In these cases, it is not necessary to do a full data exchange if a reduced set of read and write accesses can be determined.

Another optimization is given by eliminating unnecessary data exchange steps. These occur, e.g., when two loops synchronize the same set of data points without any of them being changed between the loops. An analysis finding those cases is possible by creating a detailed call-graph or data flow graph. However, in most cases, this is only possible when the code generator knows and understands the whole program. This is generally only true for external DSLs without coupled third-party code, such as legacy applications or other libraries. Otherwise, the user may still use his or her knowledge about the algorithm to manually edit the automatically-generated communication statements.

6.2. MPI Data Types

In many application domains targeted by DSLs and code generation techniques, data access patterns emerging from synchronizing data points have some inherent structure and regularity. In this case, it can be beneficial to avoid explicitly buffering data to be sent and received via MPI. Instead, a program may rely on MPI data types that allow a given MPI implementation to optimize internal processes. In theory, this leads to an improved performance and/or decreased memory consumption. We implement this approach by extending the expansion strategies mentioned in Section 4 with a specialized transformation targeting all applicable communication statements. These are usually the ones occurring between fragments of different blocks, i.e., the ones to be mapped to MPI. There are different implementations for send and receive operations, but conceptually, both are transformed into one of the following:

• a direct (unbuffered) send/receive operation if only one element is to be exchanged, or
• an MPI send/receive with an MPI data type if enabled and possible, or
• a fallback to a copy to/from a communication buffer and an MPI send/receive using that buffer as the default case.

Evidently, this requires the initialization and de-initialization of all employed MPI data types at some point. To allow for the generation of clean, robust and performant code, we re-use identical MPI data types. In that context, data types with the same access patterns are identified as identical. Their setup and destruction is merged and added to the general initialization and de-initialization phases of the generated program. In code, this relates to creating a transformation that collects all utilized data types and sets up the required routines.

6.3. Communication Pattern Optimization

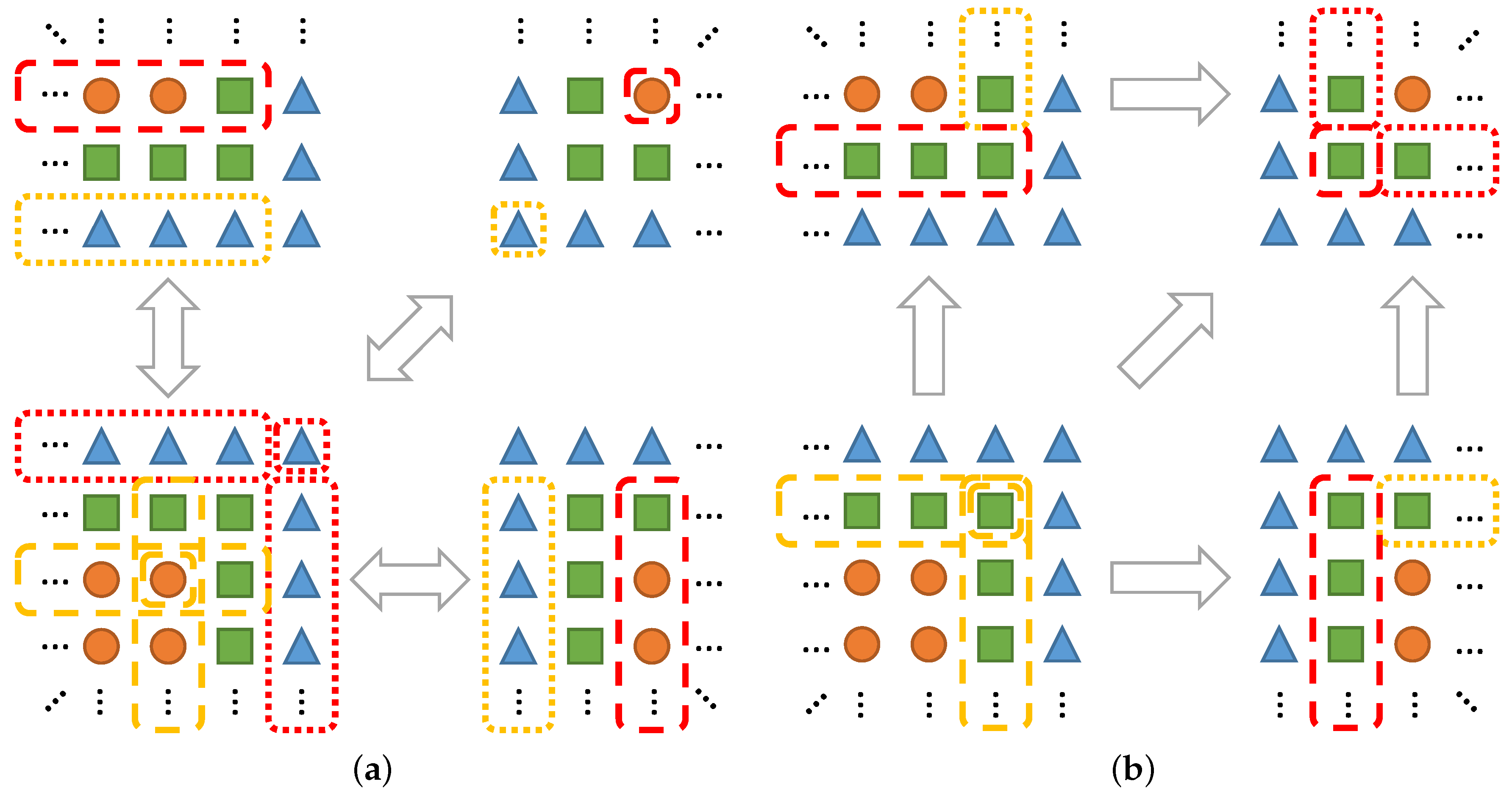
Another possible point of optimization is optimizing the number and/or size of messages exchanged. Consider, e.g., a regular grid divided into fragments as described in Section 3. For most stencil codes, it is sufficient to communicate with direct neighbors. In 2D and 3D, this relates to eight and 26 exchanges per fragment, respectively. In order to reduce the number of messages and neighbors to communicate with, we propose an automatic adaptation of such communication schemes to rely only on four and six neighbors in 2D and 3D, respectively. To this end, data exchanges with diagonal neighbors, i.e., neighbors sharing only a vertex in 2D or a vertex or edge in 3D, are performed in multiple stages. This approach is also visualized in Figure 8: extended regions of communication allow relaying data via multiple fragments. For correct results, it is necessary to sequentialize the communication in some fashion, e.g., per spatial dimension. In ExaStencils, this is implemented through a transformation splitting and grouping the communication into d steps, where d is the dimensionality of the computational domain.

Evidently, this approach requires that blocks and fragments can be aligned on regular grids, i.e., that each primitive can be assigned a d-dimensional index that correctly maps neighborhood information. For cases where this is not possible, similar approaches build on the partition and data exchange properties at hand may be devised.

Note that this approach may require the adaptation of other optimizations or even prevent them to a certain degree, such as the interweaving of OpenMP and MPI communications, as described in the next paragraph. Nevertheless, the reduced number of messages and the lowered risk of congestion may make this optimization worthwhile.

6.4. Interweaving Intra- and Inter-Block Communication

Another opportunity for optimization arises in the context of hybrid parallelization, i.e., when fragments and blocks are mapped to different parallelization interfaces. More precisely, it is often possible to overlap both types of data exchange, such as in the prominent example of MPI and OpenMP. To this end, we allow communication statements to be expanded in the following fashion, which is also illustrated in Figure 7: Initially, the first half of the inter-block, in this example MPI, communication is started. This includes the packing of data and starting the asynchronous send process and is performed for all applicable neighbors. It is also possible to already start the asynchronous receive operations at this point. Next, the intra-block communication is performed. In this case, a simple OpenMP synchronization is mapped to memory copy operations in shared memory, as described in Section 4. Finally, the inter-block communication is finished. This means starting the asynchronous receive operations (if not done in the first step) and waiting for the receives to finish. After each finished receive, the corresponding buffer is unpacked. As a last step, waiting for all send operations is necessary.

If MPI data types are used as described before, manual buffering is eliminated (as usual, MPI implementations may buffer internally). Moreover, if communication patterns are optimized as described above, the described mapping must be done after splitting into d sequential steps.

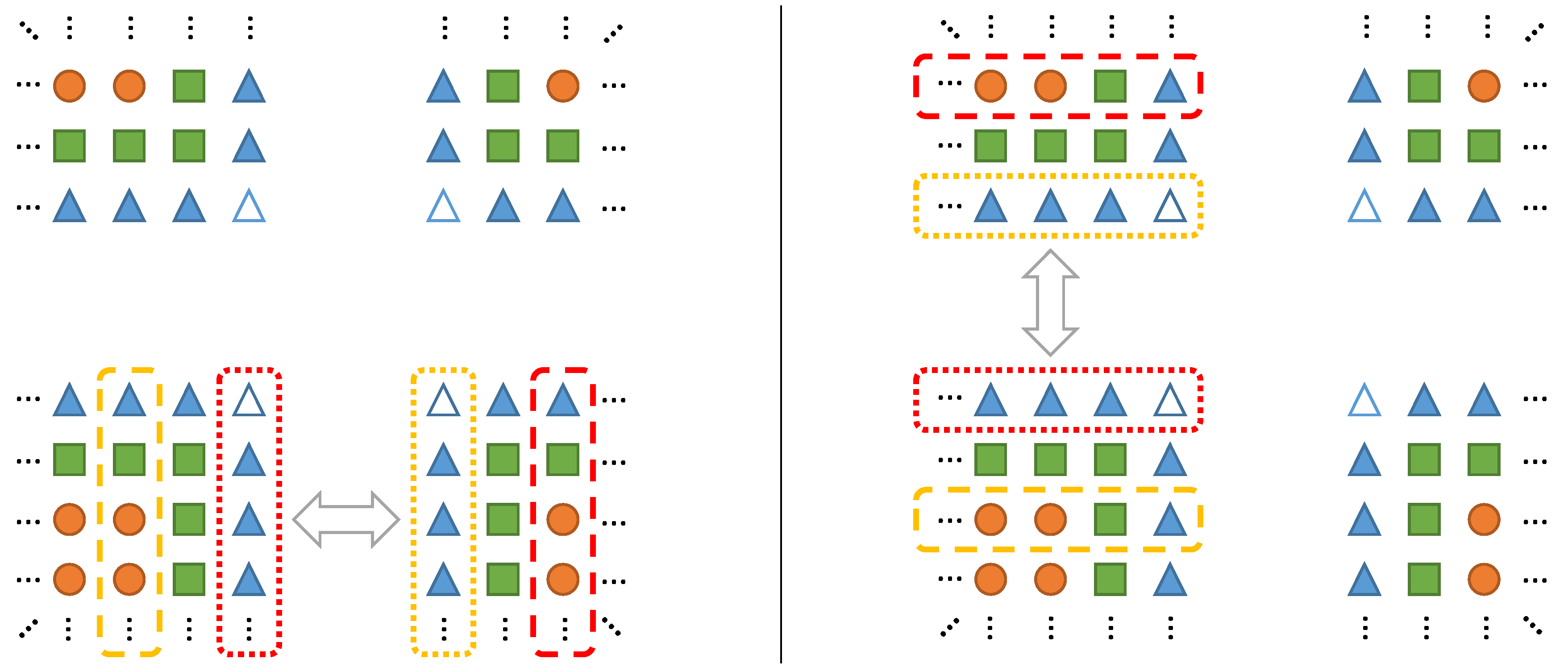
6.5. Automatic Overlapping of Computation and Communication

A common optimization for codes relying on asynchronous communication is overlapping computation and communication to hide communication overhead. To allow for an automated application of this technique, we follow a two-step approach. First, we apply a preparatory transformation targeting loops with communication statements before or after them. These communication statements are then added as loop annotations. If communication statements are added automatically, as described above, it is also possible to directly add them to the processed loops. Secondly, since each loop knows which data must be synchronized, another transformation may now split the loop into multiple smaller loops and partly overlap them with communication. This split, as illustrated in Figure 9, is dependent on the data access patterns, as well as the specified communication statements. In detail, there are two cases to be handled: If communication would have been done before the loop was entered, the split is performed such that all iterations are separated that do not access any data that is part of the communication. This loop is then overlapped with the communication. Afterwards, the remaining loop iterations can be performed. If communication was scheduled after the loop, the order of operations is reversed. More precisely, we first perform all loop iterations connected to data to be synchronized. Next, communication is initiated and the bulk of the computation is performed in parallel. Afterwards, the communication is finished.

In any case, this optimization is only possible if there are no dependencies between loop iterations. The fact that this restriction is not violated can either be specified at the DSL level or determined automatically inside the code generator. In ExaStencils, the latter is available as part of the polyhedron loop optimization strategies, which perform a suitable dependency analysis.

Further extensions of this approach are possible, such as enlarging the outer region (in specific dimensions) to optimize cache-line utilization and vectorizability.

7. Results

To demonstrate the applicability of the presented concepts, we perform a weak scaling for the well-known model problem given by Poisson’s equation:

$$\begin{array}{ccc}\hfill -△u& =& f\text{in}\Omega ,\hfill \\ \hfill u& =& g\text{on}\partial \Omega \hfill \end{array}$$

(1)

For our experiments, we choose the JuQueen supercomputer located at Jülich, Germany. It features 458,752 cores across 28,672 nodes. Considering the problem size, we solve for roughly 16 million unknowns per physical core, which corresponds to about 4 million unknowns per thread. In total, the largest solved problem contains close to 4.4 trillion unknowns using more than half of the JuQueen supercomputer at 16,384 nodes.

We consider fully-generated 2D and 3D multigrid solvers based on finite difference discretizations of Equation (1) on $\Omega ={(0,1)}^d$. They perform v-cycles with three pre- and three post-smoothing steps using damped Jacobi iterations as the smoother, until the L2 norm of the initial residual is reduced by a factor of 10⁻⁵. Our code generation framework features an array of automatic optimizations that can be activated [13], from which we choose the following for our experiment: Architecture-specific vectorization and the concomitant memory layout adaptions to favor aligned loads and stores, address pre-calculation, polyhedral loop optimizations and spatial blocking according to the L2 cache size. Furthermore, we examine the employment of MPI data types and communication pattern optimization as explained in Section 6. In all configurations, the varying number of blocks is mapped to MPI, and the number of fragments per block is fixed to one. Computations on each fragment are either serial (pure MPI) or parallelized using OpenMP and four threads. In total, there are always 64 threads (MPI and OpenMP combined) per compute node.

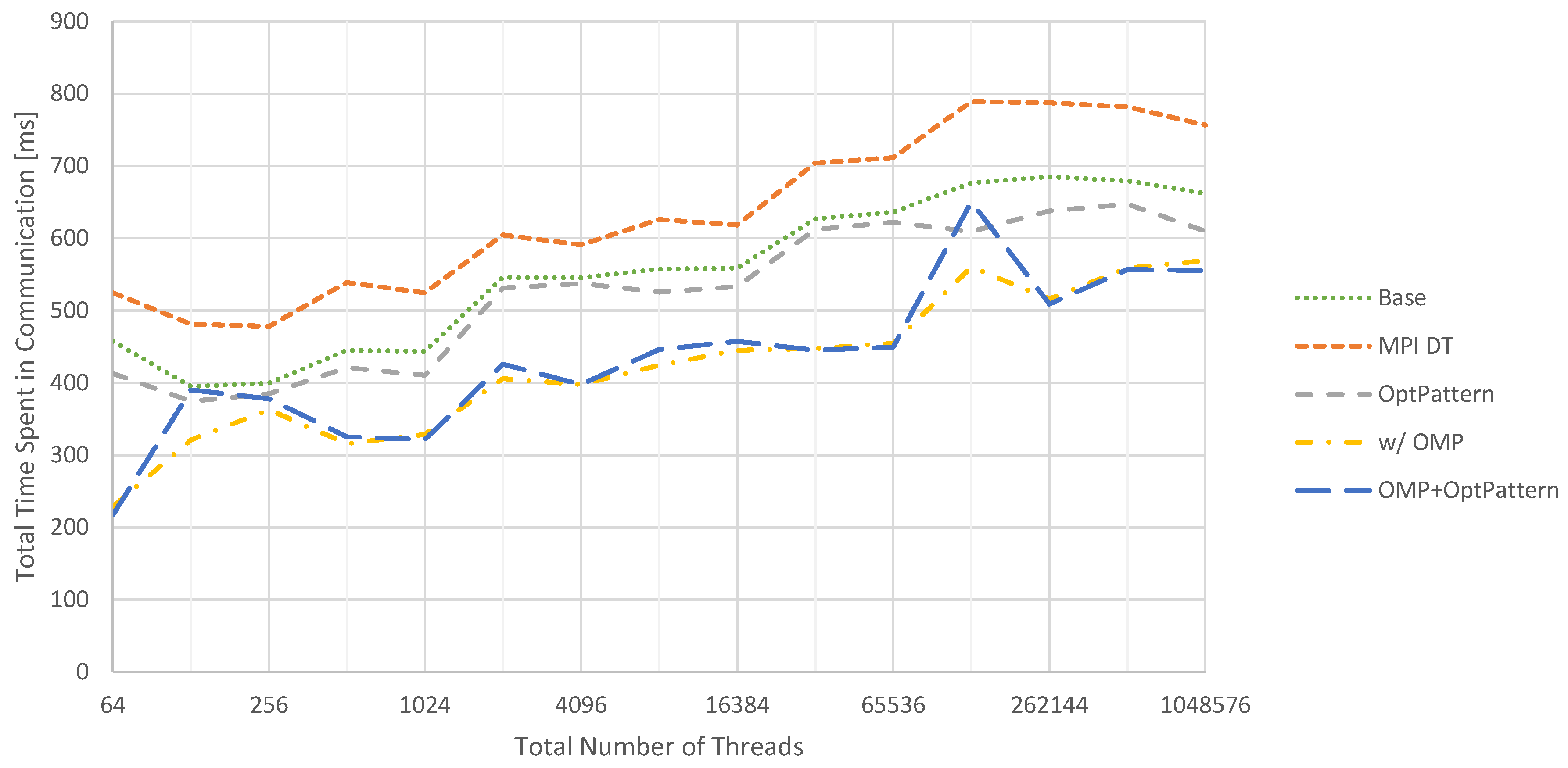
In Figure 10, the accumulated time spent in communication routines is summarized for the 2D test problem. These measurements do not include any performance impacts on the computational parts of the solver, such as potentially introduced by using OpenMP. The baseline corresponds to generating these communication routines without any of the presented optimizations applied. Compared to this version, adding MPI data types decreases performance on the chosen hardware. On the other hand, optimizing the communication patterns to reduce the number of messages helps to improve performance. Yet, the biggest improvement can be observed when switching from pure MPI to a hybrid MPI/OpenMP parallelization. Unfortunately, activating the communication pattern optimization in addition does not yield a benefit in this case.

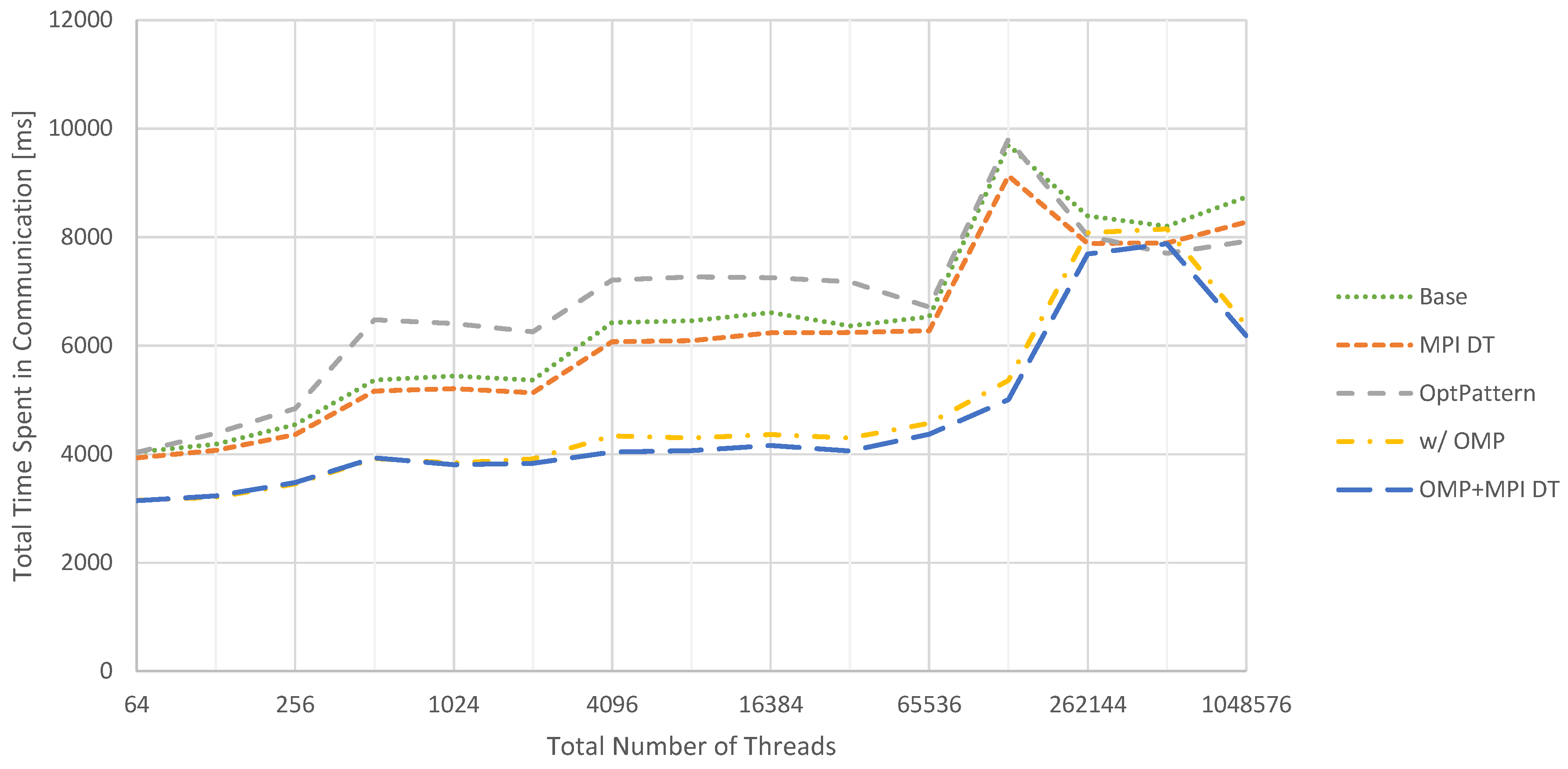
In comparison with the 2D case, the 3D case visualized in Figure 11 behaves differently. Here, injecting MPI data types improves performance. Furthermore, communication pattern optimization decreases performance for most configurations and is only beneficial for very big problems. This behavior can be explained by two circumstances. First, when using larger portions of the supercomputer, MPI messages have to travel larger distances. This increases latencies. Second, the increased number of messages in a weak scaling scenario promotes congestion for larger configurations. Both issues are mitigated by the employment of the communication pattern optimization, thus increasing performance.

Switching to a hybrid parallelization yields an improved performance for most cases, which can be further improved by combining this approach with MPI data types. In total, the communication times are increased greatly compared to the 2D cases. One, however only minor, reason for this is the higher number of multigrid cycles required to achieve a satisfactory residual reduction (seven for 3D vs. five for 2D). The main reason is the increased volume of communication. Considering, e.g., two fragments with 4097 × 4097 and 257 × 257 × 257 data points, respectively, both contain a comparable number of unknowns in the range of 17 million. However, the total communication volume for one layer is given by roughly 16 thousand data points for 2D and 400 thousand data points for 3D. Furthermore, instead of eight messages, 26 messages need to be sent or, using the communication pattern optimization, four and six, respectively.

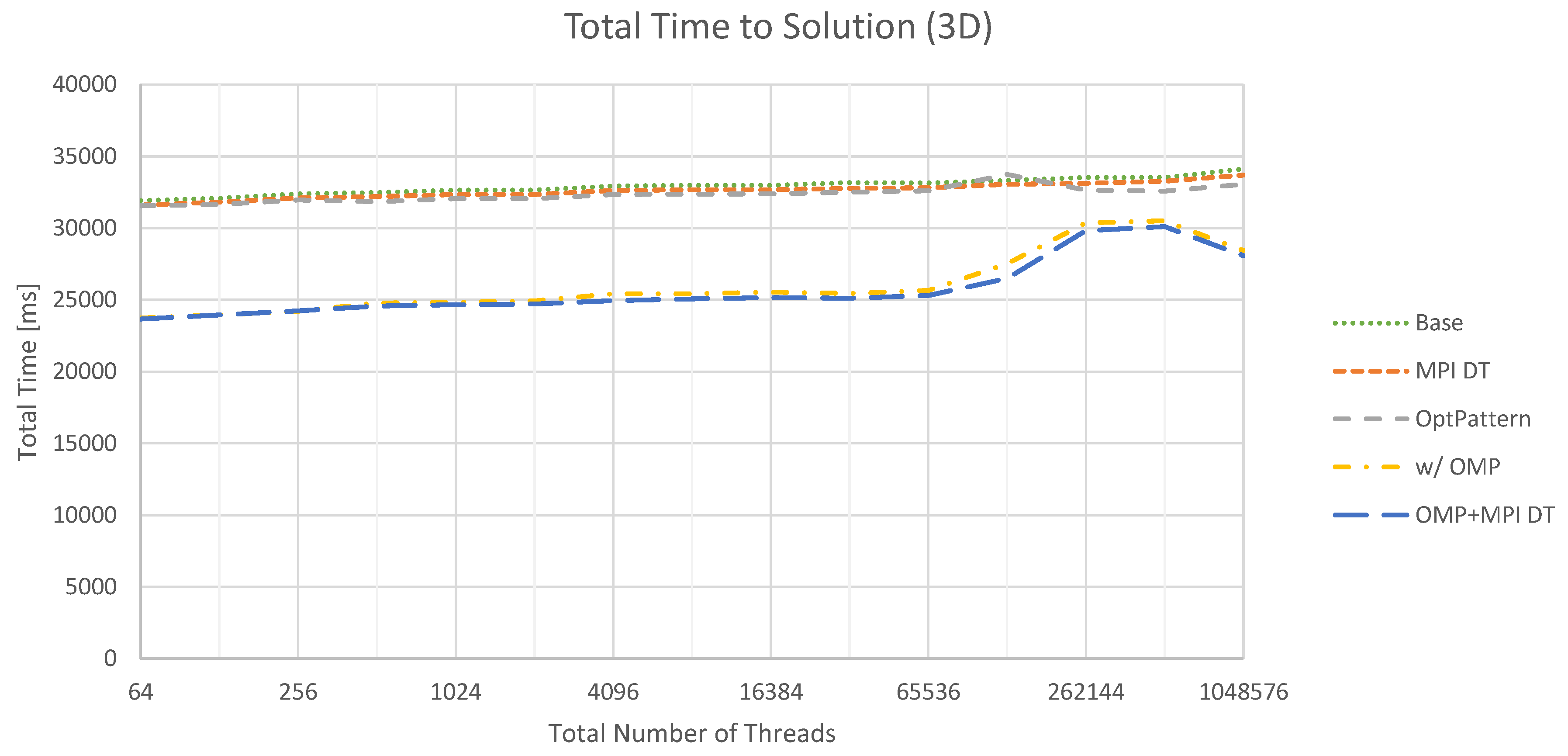
This behavior is also reflected in the comparison between the time spent in communication routines and the full time to solution. For 2D, we observe an average share of around 3.5%, while it increases to roughly 20% for 3D. For the latter case, the total time to solution is depicted in Figure 12. It is evident that the trend set by the communication times determines the total performance to a certain extent. Moreover, switching to a hybrid parallelization increases performance beyond the savings in communication time. However, it is important to relate these numbers to the problem solved. For Poisson’s equation, the communication effort is extremely high compared to the time required by the actual kernels. We expect that switching to more complex problems, which also require more complex solver components, will increase the relative and absolute cost of executing kernels. As a consequence, the influence of communication will be mitigated. Moreover, overlapping communication and computation appears to be very promising in this context. This is currently analyzed in detail, and thus, concrete results are deferred to future work.

8. Conclusions and Future Work

Concepts for equipping code generators with capabilities to emit parallelized code have been discussed. Initially, data are distributed physically according to a chosen hierarchy, allowing assignment to hardware resources. Here, we propose a flat hierarchy consisting of leaf elements, fragments and blocks. Next, data within one level of the hierarchy, usually at the leaf element level, are partitioned logically according to their roles in communication steps. To this end, inner, ghost and duplicate elements are identified. Using these groups, statements for exchanging data can be specified at the DSL level or generated automatically if applicable. For each statement, a dedicated routine implementing the data exchange is generated. These routines are first described in an abstract form, independent of the employed parallelization backend. This also allows applying optimizations, such as the overlap of computation and communication and the overlap of inter- and intra-block communication. Finally, a specialization to the target hardware and parallelization backends is performed, and compilable code can be emitted.

These concepts and extensions are already fully implemented in the ExaStencils framework. In the future, we aim for supporting PGAS and task-based parallelization backends, as well as multi-GPUs. Moreover, a thorough investigation of performance characteristics of the presented optimization techniques for different hardware platforms has to be conducted.

Orthogonally, our code generation approach allows for automatic deduction of simple performance models for kernels. It is highly desirable to extend these models with a priori assessments for communication routines based on benchmarks and hardware properties. Based on these predictions or on measurements, an auto-tuning approach is feasible to automatically decide how communication routines are to be composed.