Kinetic and Exchange Energy Densities near the Nucleus
Abstract
:1. Introduction
2. Kinetic and Exchange Energy Densities at the Nuclear Cusp in Spherical Systems
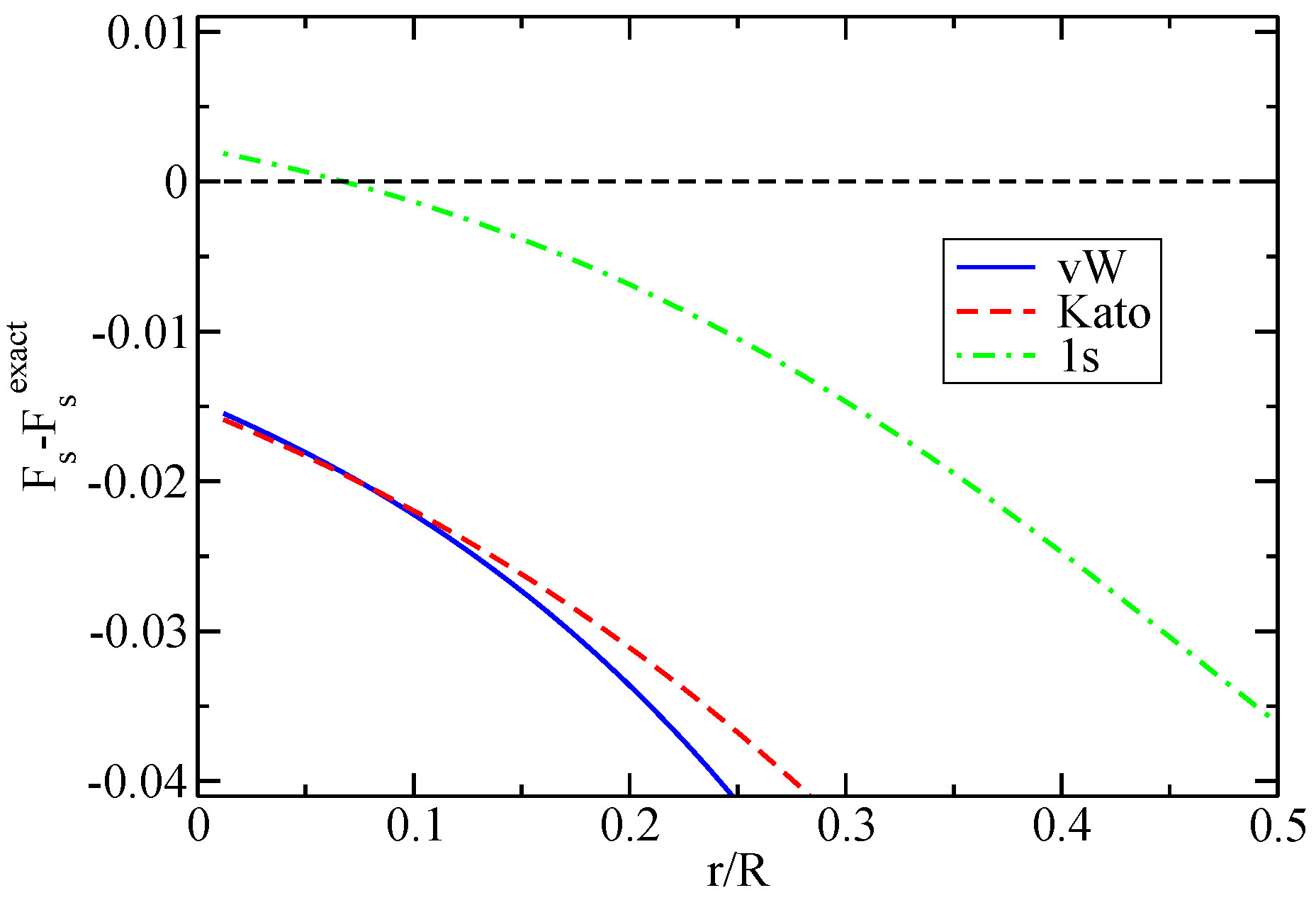
2.1. Hydrogenic Shells
2.2. Ten-Electron Hydrogenic Model
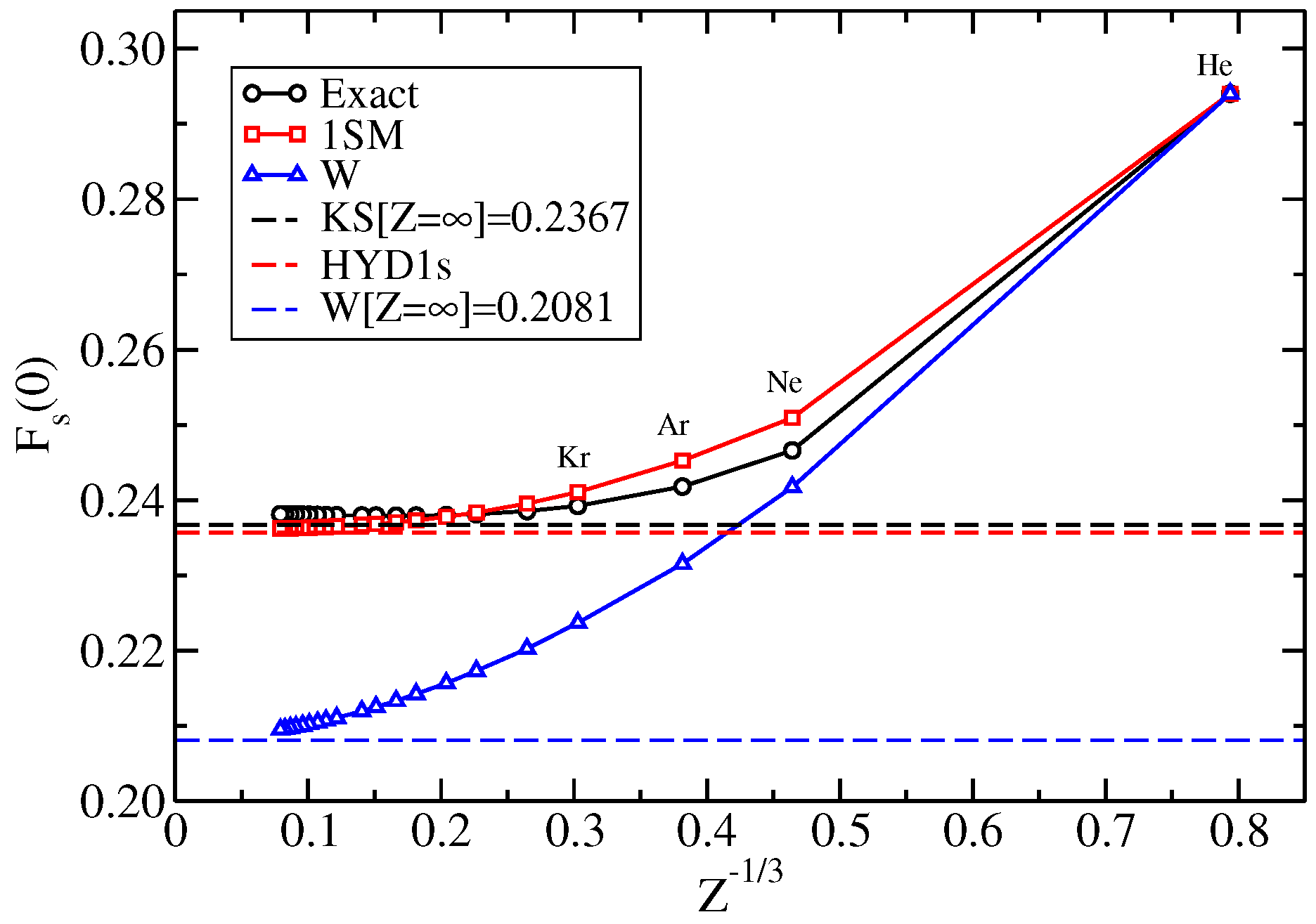
2.3. The Asymptotic Neutral Atom with an Infinite Number of Electrons
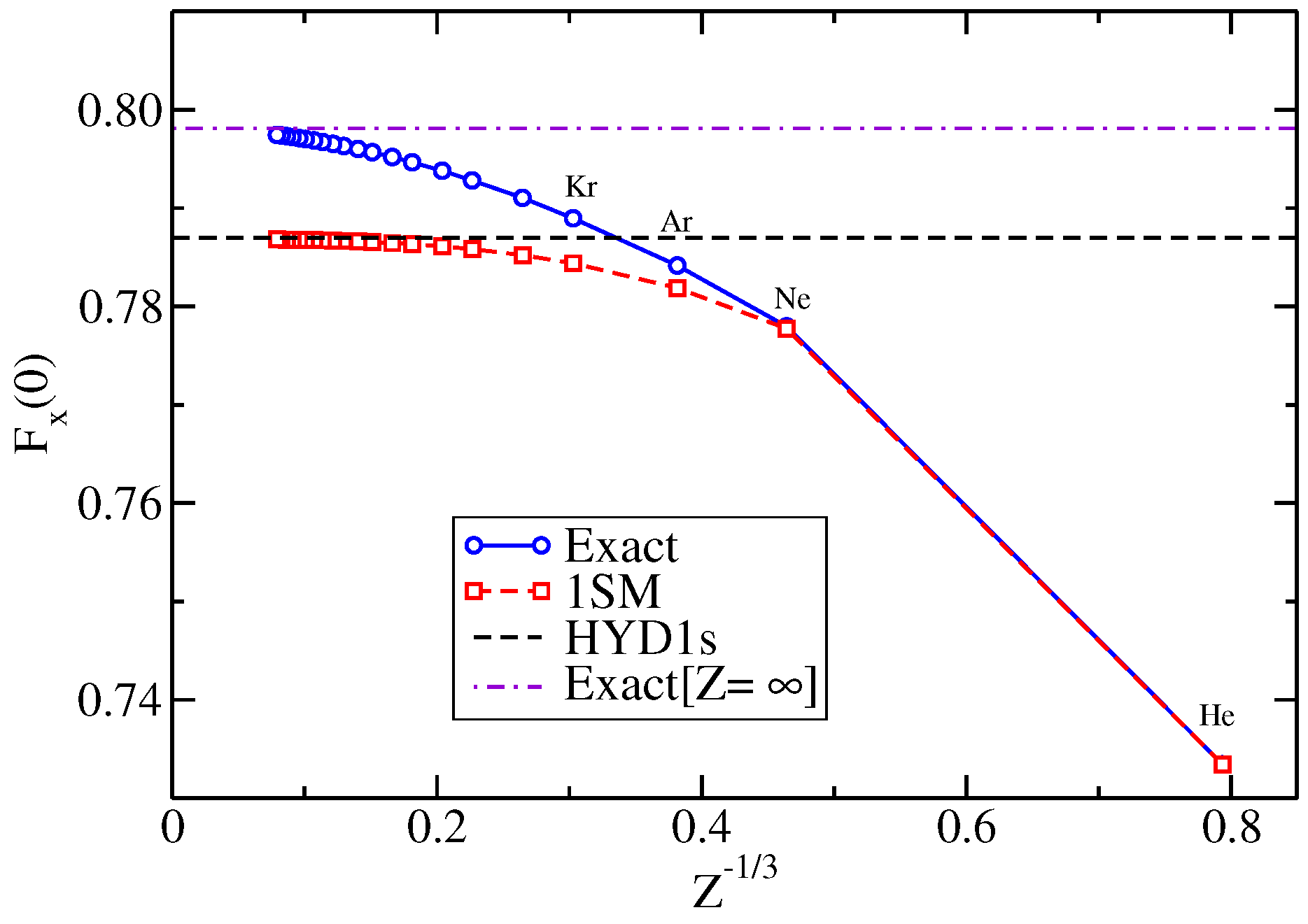
2.4. 1s-Shell Model
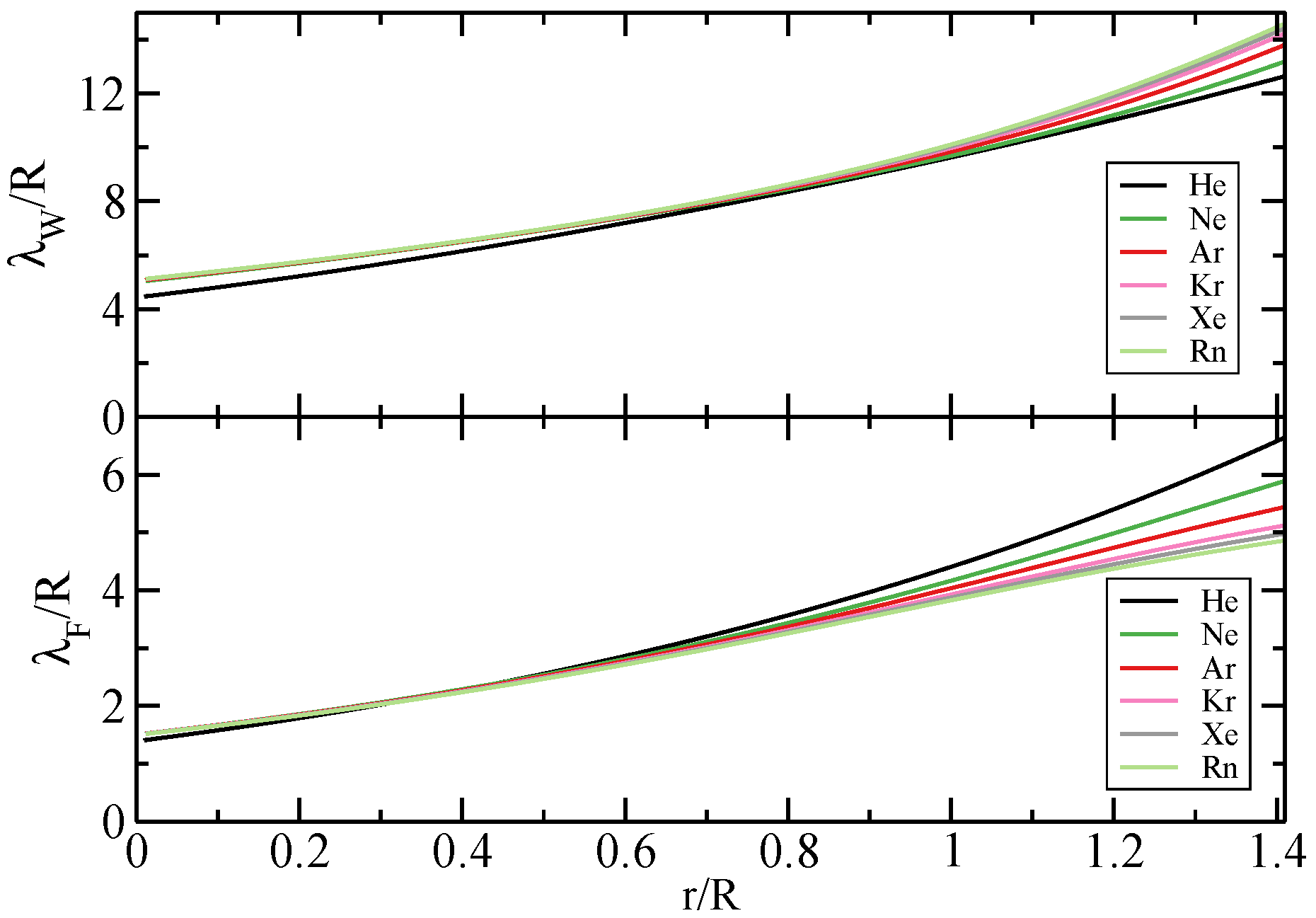
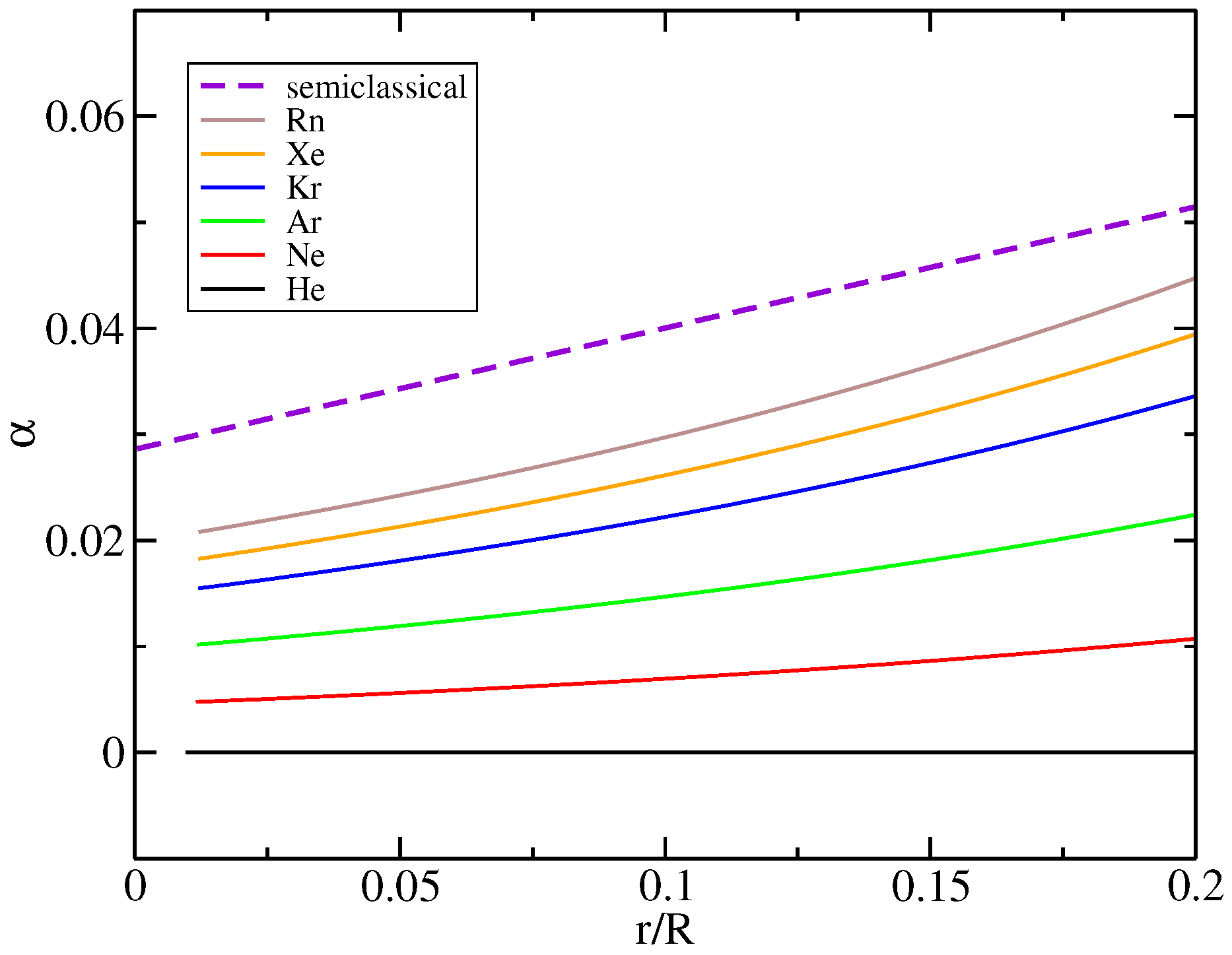
2.5. Real Atoms
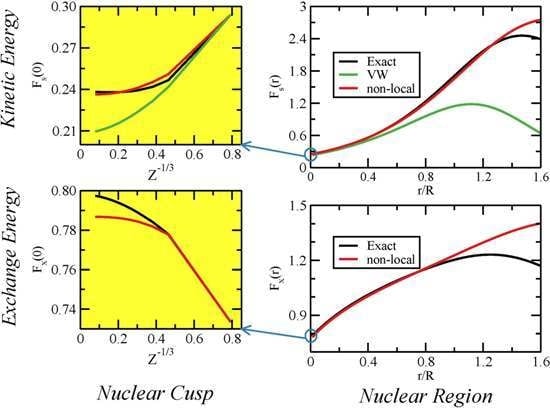
3. Non-Local Approximations for Exchange and Kinetic Energies, at and near the Nucleus
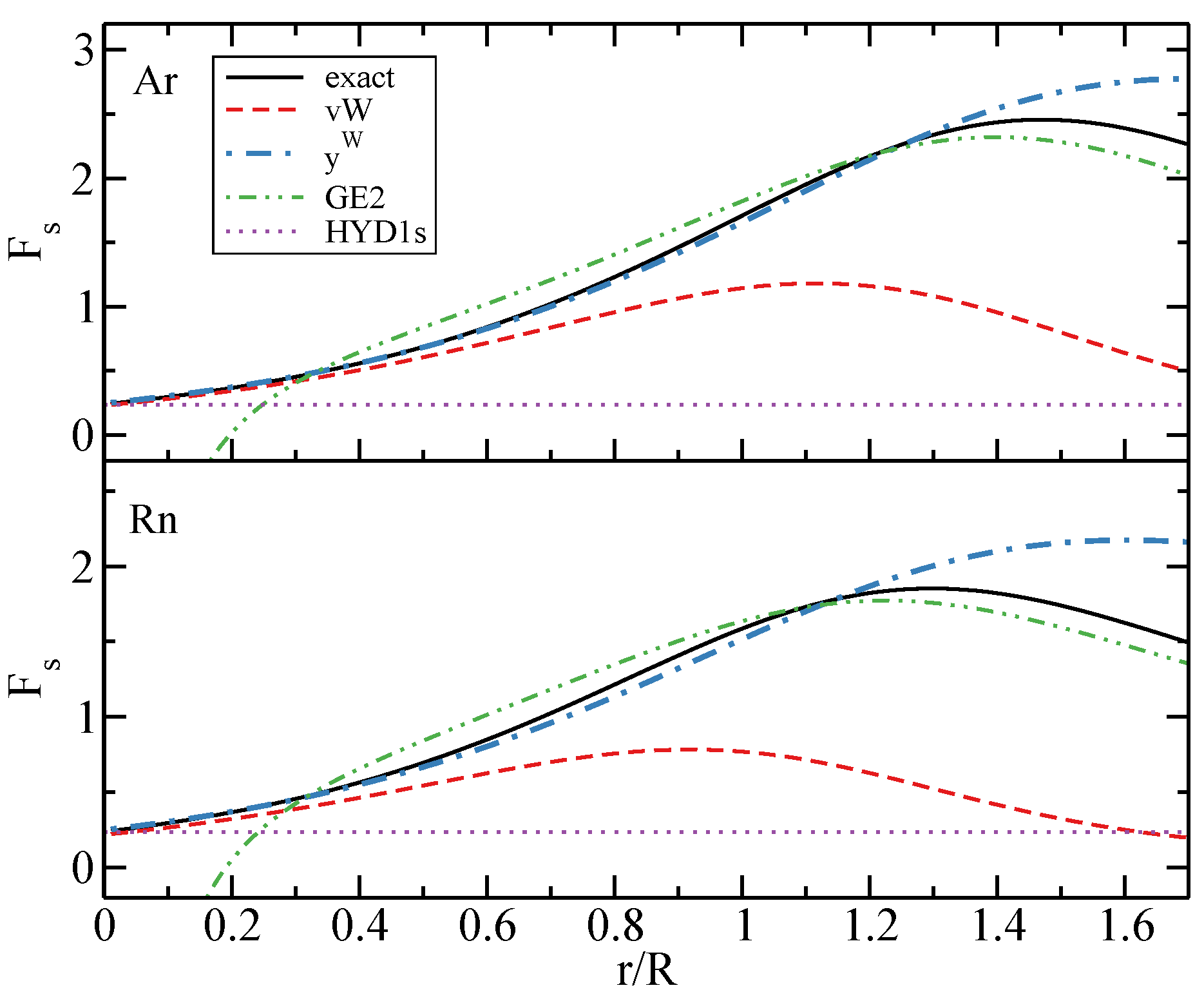
3.1. Kinetic Energy
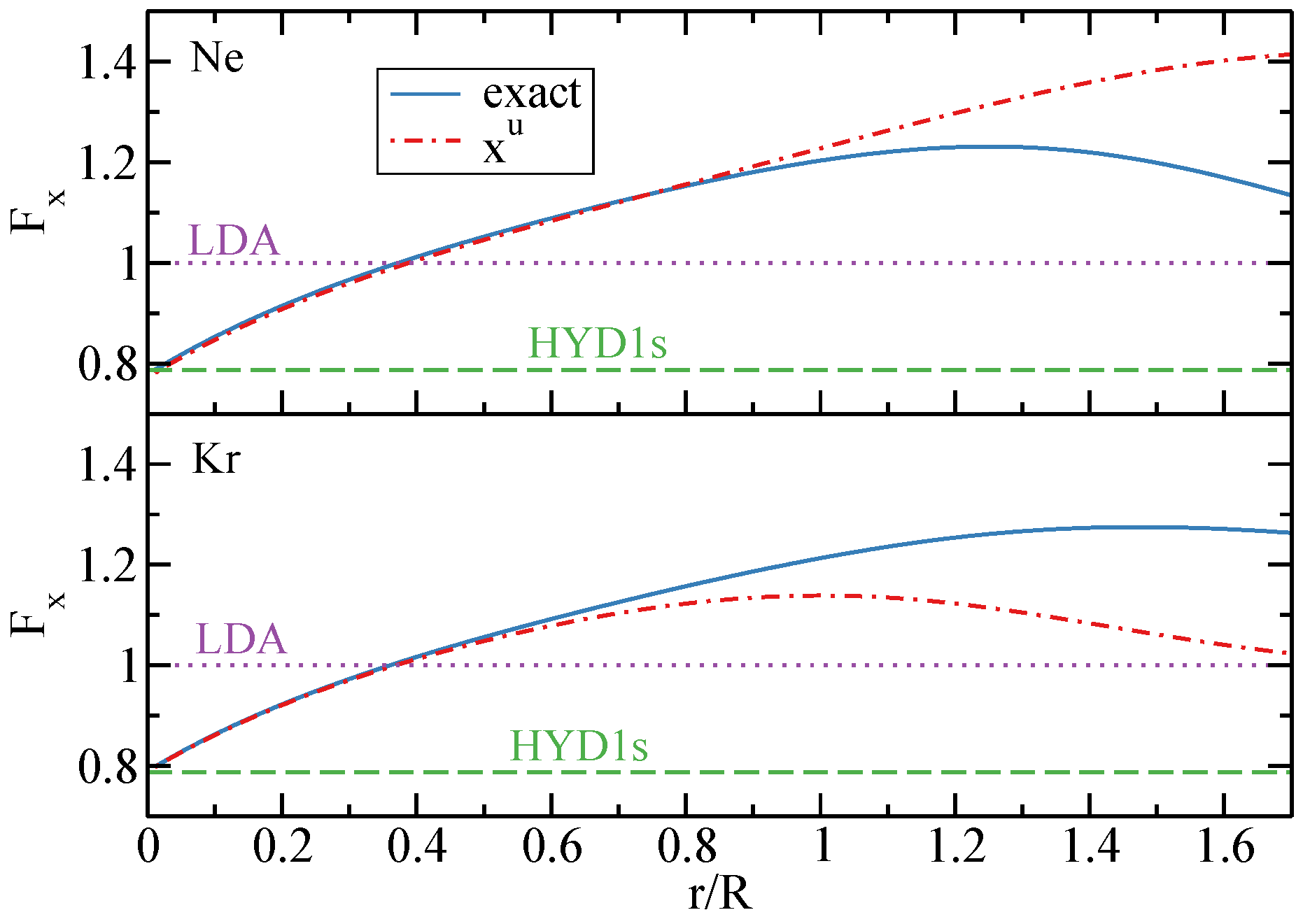
3.2. Exchange Energy
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Dreizler, R.M.; Gross, E.K.U. Density Functional Theory; Springer: New York, NY, USA, 1990. [Google Scholar]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Scuseria, G.E.; Staroverov, V.N. Progress in the development of exchange-correlation functionals. In Theory and Applications of Computational Chemistry: The First 40 Years (A Volume of Technical and Historical Perspectives); Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 669–724. [Google Scholar]
- Becke, A.D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. Quest for a universal density functional: The accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Phil. Trans. A 2014, 372. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, T.A.; Shedge, S.; Zhou, X. Frozen-density embedding strategy for multilevel simulations of electronic structure. Chem. Rev. 2015, 115, 5891–5928. [Google Scholar] [CrossRef] [PubMed]
- Jacob, C.R.; Neugebauer, J. Subsystem density-functional theory. WIRE 2014, 4, 325–362. [Google Scholar] [CrossRef]
- Krishtal, A.; Sinha, D.; Genova, A.; Pavanello, M. Subsystem density-functional theory as an effective tool for modeling ground and excited states, their dynamics and many-body interactions. J. Phys. Condens. Matter 2015, 27, 183202. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Carter, E.A. Orbital-free kinetic-energy density functional theory. In Progress in Theoretical Chemistry and Physics; Schwartz, S., Ed.; Kluwer: Dordrecht, The Netherlands, 2000; p. 117. [Google Scholar]
- Wesolowsky, T.A.; Wang, Y.A. Recent Progress in Orbital-Free Density Functional Theory; World Scientific: Singapore, 2013. [Google Scholar]
- Xia, J.; Huang, C.; Shin, I.; Carter, E.A. Can orbital-free density functional theory simulate molecules? J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Karasiev, V.; Trickey, S. Issues and challenges in orbital-free density functional calculations. Comput. Phys. Commun. 2012, 183, 2519–2527. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized gradient approximation made simple”. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Haas, P.; Tran, F.; Blaha, P.; Schwarz, K. Construction of an optimal GGA functional for molecules and solids. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Constantin, L.A.; Fabiano, E.; Laricchia, S.; Della Sala, F. Semiclassical Neutral Atom as a Reference System in Density Functional Theory. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Del Campo, J.M.; Gazquez, J.L.; Trickey, S.B.; Vela, A. Non-empirical improvement of PBE and its hybrid PBE0 for general description of molecular properties. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. Exchange-Correlation Functional with Good Accuracy for Both Structural and Energetic Properties while Depending Only on the Density and Its Gradient. J. Chem. Theory Comput. 2012, 8, 2310–2319. [Google Scholar] [CrossRef] [PubMed]
- Armiento, R.; Mattsson, A.E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Vela, A.; Pacheco-Kato, J.C.; Gázquez, J.L.; del Campo, J.M.; Trickey, S.B. Improved constraint satisfaction in a simple generalized gradient approximation exchange functional. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Fabiano, E.; Constantin, L.A.; Della Sala, F. Generalized gradient approximation bridging the rapidly and slowly varying density regimes: A PBE-like functional for hybrid interfaces. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
- Constantin, L.A.; Fabiano, E.; Della Sala, F. Spin-dependent gradient correction for more accurate atomization energies of molecules. J. Chem. Phys. 2012, 137. [Google Scholar] [CrossRef] [PubMed]
- Chiodo, L.; Constantin, L.A.; Fabiano, E.; Della Sala, F. Nonuniform scaling applied to surface energies of transition metals. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Zhao, Y.; Truhlar, D.G. Generalized gradient approximation that recovers the second-order density-gradient expansion with optimized across-the-board performance. J. Phys. Chem. Lett. 2011, 2, 1991–1997. [Google Scholar] [CrossRef]
- Constantin, L.A.; Terentjevs, A.; Della Sala, F.; Cortona, P.; Fabiano, E. Semiclassical atom theory applied to solid-state physics. Phys. Rev. B 2016, 93. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical Meta–Generalized gradient approximation designed for Mo lecules and solids. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Constantin, L.A.; Sun, J. Workhorse semilocal density functional for condensed matter physics and quantum chemistry. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Xiao, B.; Ruzsinszky, A. Communication: Effect of the orbital-overlap dependence in the meta generalized gradient approximation. J. Chem. Phys. 2012, 137. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Perdew, J.P.; Ruzsinszky, A. Semilocal density functional obeying a strongly tightened bound for exchange. Proc. Nat. Acad. Sci. USA 2015, 112, 685–689. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. M11-L: A local density functional that provides improved accuracy for electronic structure calculations in chemistry and physics. J. Phys. Chem. Lett. 2012, 3, 117–124. [Google Scholar] [CrossRef]
- Constantin, L.A.; Fabiano, E.; Della Sala, F. Meta-GGA exchange-correlation functional with a balanced treatment of nonlocality. J. Chem. Theory Comput. 2013, 9, 2256–2263. [Google Scholar] [CrossRef] [PubMed]
- Mardirossian, N.; Head-Gordon, M. Mapping the genome of meta-generalized gradient approximation density functionals: The search for B97M-V. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Del Campo, J.M.; Gazquez, J.L.; Trickey, S.; Vela, A. A new meta-GGA exchange functional based on an improved constraint-based GGA. Chem. Phys. Lett. 2012, 543, 179–183. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. An improved and broadly accurate local approximation to the exchange-correlation density functional: The MN12-L functional for electronic structure calculations in chemistry and physics. Phys. Chem. Chem. Phys. 2012, 14, 13171–13174. [Google Scholar] [CrossRef] [PubMed]
- Wellendorff, J.; Lundgaard, K.T.; Jacobsen, K.W.; Bligaard, T. mBEEF: An accurate semi-local Bayesian error estimation density functional. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Hartree-Fock exchange energy of an inhomogeneous electron gas. Int. J. Quantum Chem. 1983, 23, 1915–1922. [Google Scholar] [CrossRef]
- Armiento, R.; Kümmel, S. Orbital localization, charge transfer, and band gaps in semilocal density- functional theory. Phys. Rev. Lett. 2013, 111. [Google Scholar] [CrossRef] [PubMed]
- Constantin, L.A.; Fabiano, E.; Della Sala, F. Construction of a general semilocal exchange-correlation hole model: Application to nonempirical meta-GGA functionals. Phys. Rev. B 2013, 88. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Perdew, J.P. Generalized gradient approximation to the angle-and system-averaged exchange hole. J. Chem. Phys. 1998, 109, 3313–3320. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Heyd, J.; Krukau, A.V.; Scuseria, G.E. Importance of short-range versus long-range Hartree-Fock exchange for the performance of hybrid density functionals. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef] [PubMed]
- Tao, J. Exchange energy density of an atom as a functional of the electron density. J. Chem. Phys. 2001, 115, 3519–3530. [Google Scholar] [CrossRef]
- Cancio, A.C.; Wagner, C.E.; Wood, S.A. Laplacian-based models for the exchange energy. Int. J. Quantum Chem. 2012, 112, 3796–3806. [Google Scholar]
- Lembarki, A.; Chermette, H. Obtaining a gradient-corrected kinetic-energy functional from the Perdew-Wang exchange functional. Phys. Rev. A 1994, 50, 5328–5331. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Wesoloski, T.A. Link between the kinetic- and exchange-energy functionals in the generalized gradient approximation. Int. J. Quantum Chem. 2002, 89. [Google Scholar] [CrossRef]
- Lee, H.; Lee, C.; Parr, R.G. Conjoint gradient correction to the Hartree-Fock kinetic- and exchange-energy density functionals. Phys. Rev. A 1991, 44, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Thakkar, A.J. Comparison of kinetic-energy density functionals. Phys. Rev. A 1992, 46, 6920–6924. [Google Scholar] [CrossRef] [PubMed]
- Laricchia, S.; Fabiano, E.; Constantin, L.A.; Della Sala, F. Generalized gradient approximations of the noninteracting kinetic energy from the semiclassical atom theory: Rationalization of the accuracy of the frozen density embedding theory for nonbonded interactions. J. Chem. Theory Comput. 2011, 7, 2439–2451. [Google Scholar] [CrossRef] [PubMed]
- Laricchia, S.; Constantin, L.A.; Fabiano, E.; Della Sala, F. Laplacian-Level kinetic energy approximations based on the fourth-order gradient expansion: Global assessment and application to the subsystem formulation of density functional theory. J. Chem. Theory Comput. 2014, 10, 164–179. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Wesolowski, T.A. Semilocal Approximation for the Kinetic Energy. In Recent Advances in Computational Chemistry 6; Wesolowski, T.A., Wang, Y.A., Eds.; World Scientific: Singapore, 2013; pp. 429–442. [Google Scholar]
- García-Aldea, D.; Alvarellos, J.E. Approach to kinetic energy density functionals: Nonlocal terms with the structure of the von Weizsäcker functional. Phys. Rev. A 2008, 77. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Jones, R.S.; Trickey, S.B.; Harris, F.E. Properties of constraint-based single-point approximate kinetic energy functionals. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Garcia Lastra, J.M.; Kaminski, J.W.; Wesolowski, T.A. Orbital-free effective embedding potential at nuclear cusps. J. Chem. Phys. 2008, 129, 074107. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Constantin, L.A. Laplacian-level density functionals for the kinetic energy density and exchange-correlation energy. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Chakraborty, D.; Shukruto, O.A.; Trickey, S.B. Nonempirical generalized gradient approximation free-energy functional for orbital-free simulations. Phys. Rev. B 2013, 88. [Google Scholar] [CrossRef]
- Della Sala, F.; Fabiano, E.; Constantin, L.A. Kohn–Sham kinetic energy density in the nuclear and asymptotic regions: Deviations from the von Weizsäcker behavior and applications to density functionals. Phys. Rev. B 2015, 91. [Google Scholar] [CrossRef]
- Qian, Z. Exchange and correlation near the nucleus in density functional theory. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Nagy, A.; March, N.H. Exact potential-phase relation for the ground state of the C atom. Phys. Rev. A 1989, 40, 554–557. [Google Scholar] [CrossRef]
- Santamaria, R.; March, N. Kinetic energy density as a function of subshell electron densities. J. Mol. Struct. 1990, 205, 35–41. [Google Scholar] [CrossRef]
- Zhou, Z.; Chu, S.I. Spin-dependent localized Hartree-Fock density-functional calculation of singly, doubly, and triply excited and Rydberg states of He- and Li-like ions. Phys. Rev. A 2005, 71. [Google Scholar] [CrossRef]
- Howard, I.A.; March, N.H.; Van Doren, V.E. r- and p-space electron densities and related kinetic and exchange energies in terms of s states alone for the leading term in the 1/Z expansion for nonrelativistic closed-shell atomic ions. Phys. Rev. A 2001, 63. [Google Scholar] [CrossRef]
- Heilmann, O.J.; Lieb, E.H. Electron density near the nucleus of a large atom. Phys. Rev. A 1995, 52, 3628–3643. [Google Scholar] [CrossRef] [PubMed]
- Constantin, L.A.; Snyder, J.C.; Perdew, J.P.; Burke, K. Communication: Ionization potentials in the limit of large atomic number. J. Chem. Phys. 2010, 133. [Google Scholar] [CrossRef] [PubMed]
- March, N.H.; Nagy, A. Pauli potential in terms of kinetic energy density and electron density in the leading Coulombic term of the nonrelativistic 1/Z expansion of spherical atomic ions. Phys. Rev. A 2010, 81. [Google Scholar] [CrossRef]
- Bogár, F.; Bartha, F.; Bartha, F.A.; March, N.H. Pauli potential from Heilmann-Lieb electron density obtained by summing hydrogenic closed-shell densities over the entire bound-state spectrum. Phys. Rev. A 2011, 83. [Google Scholar] [CrossRef]
- Lee, D.; Constantin, L.A.; Perdew, J.P.; Burke, K. Condition on the Kohn–Sham kinetic energy and modern parametrization of the Thomas–Fermi density. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed]
- Elliott, P.; Lee, D.; Cangi, A.; Burke, K. Semiclassical Origins of Density Functionals. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Kato, T. On the eigenfunctions of many-particle systems in quantum mechanics. Commun. Pure Appl. Math. 1957, 10, 151–177. [Google Scholar] [CrossRef]
- Liu, S.; Parr, R.G.; Nagy, A. Cusp relations for local strongly decaying properties in electronic systems. Phys. Rev. A 1995, 52, 2645–2651. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, C.M.; Constantin, L.A.; Proetto, C.R.; Pitarke, J.M. Position-dependent exact-exchange energy for slabs and semi-infinite jellium. Phys. Rev. B 2009, 80, 235101. [Google Scholar] [CrossRef]
- Engel, E.; Vosko, S.H. Accurate optimized-potential-model solutions for spherical spin-polarized atoms: Evidence for limitations of the exchange-only local spin-density and generalized-gradient approximations. Phys. Rev. A 1993, 47. [Google Scholar] [CrossRef]
- Engel, E. Orbital-dependent functionals for the exchange-correlation energy: A third generation of density functionals. In A Primer in Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 2003; pp. 56–122. [Google Scholar]
- March, N.H. Spatially dependent generalization of Kato’s theorem for atomic closed shells in a bare Coulomb field. Phys. Rev. A 1986, 33, 88–89. [Google Scholar] [CrossRef]
- Seidl, A.; Görling, A.; Vogl, P.; Majewski, J.A.; Levy, M. Generalized Kohn–Sham schemes and the band-gap problem. Phys. Rev. B 1996, 53, 3764–3774. [Google Scholar] [CrossRef]
- Talman, J.D.; Shadwick, W.F. Optimized effective atomic central potential. Phys. Rev. A 1976, 14. [Google Scholar] [CrossRef]
- Kümmel, S.; Kronik, L. Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 2008, 80, 3–60. [Google Scholar] [CrossRef]
- Della Sala, F.; Görling, A. Efficient localized Hartree-Fock methods as effective exact-exchange Kohn–Sham methods for molecules. J. Chem. Phys. 2001, 115. [Google Scholar] [CrossRef]
- Perdew, J.P.; Staroverov, V.N.; Tao, J.; Scuseria, G.E. Density functional with full exact exchange, balanced nonlocality of correlation, and constraint satisfaction. Phys. Rev. A 2008, 78. [Google Scholar] [CrossRef]
- Odashima, M.M.; Capelle, K. Nonempirical hyper-generalized-gradient functionals constructed from the Lieb-Oxford bound. Phys. Rev. A 2009, 79. [Google Scholar] [CrossRef]
- Haunschild, R.; Odashima, M.M.; Scuseria, G.E.; Perdew, J.P.; Capelle, K. Hyper-generalized-gradient functionals constructed from the Lieb-Oxford bound: Implementation via local hybrids and thermochemical assessment. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Constantin, L.A.; Fabiano, E.; Della Sala, F. Kinetic and Exchange Energy Densities near the Nucleus. Computation 2016, 4, 19. https://doi.org/10.3390/computation4020019
Constantin LA, Fabiano E, Della Sala F. Kinetic and Exchange Energy Densities near the Nucleus. Computation. 2016; 4(2):19. https://doi.org/10.3390/computation4020019
Chicago/Turabian StyleConstantin, Lucian A., Eduardo Fabiano, and Fabio Della Sala. 2016. "Kinetic and Exchange Energy Densities near the Nucleus" Computation 4, no. 2: 19. https://doi.org/10.3390/computation4020019
APA StyleConstantin, L. A., Fabiano, E., & Della Sala, F. (2016). Kinetic and Exchange Energy Densities near the Nucleus. Computation, 4(2), 19. https://doi.org/10.3390/computation4020019