Abstract
Finite-temperature density functional theory (DFT) has become of topical interest, partly due to the increasing ability to create novel states of warm-correlated matter (WCM). Warm-dense matter (WDM), ultra-fast matter (UFM), and high-energy density matter (HEDM) may all be regarded as subclasses of WCM. Strong electron-electron, ion-ion and electron-ion correlation effects and partial degeneracies are found in these systems where the electron temperature is comparable to the electron Fermi energy . Thus, many electrons are in continuum states which are partially occupied. The ion subsystem may be solid, liquid or plasma, with many states of ionization with ionic charge . Quasi-equilibria with the ion temperature are common. The ion subsystem in WCM can no longer be treated as a passive “external potential”, as is customary in DFT dominated by solid-state theory or quantum chemistry. Many basic questions arise in trying to implement DFT for WCM. Hohenberg-Kohn-Mermin theory can be adapted for treating these systems if suitable finite-T exchange-correlation (XC) functionals can be constructed. They are functionals of both the one-body electron density and the one-body ion densities . Here, j counts many species of nuclei or charge states. A method of approximately but accurately mapping the quantum electrons to a classical Coulomb gas enables one to treat electron-ion systems entirely classically at any temperature and arbitrary spin polarization, using exchange-correlation effects calculated in situ, directly from the pair-distribution functions. This eliminates the need for any XC-functionals. This classical map has been used to calculate the equation of state of WDM systems, and construct a finite-T XC functional that is found to be in close agreement with recent quantum path-integral simulation data. In this review, current developments and concerns in finite-T DFT, especially in the context of non-relativistic warm-dense matter and ultra-fast matter will be presented.
Keywords:
exchange and correlation; warm dense matter; density functional theory; ultra-fast matter; high-energy density matter; finite-temperature effects PACS:
52.25.Os; 52.35.Fp; 52.50.Jm; 78.70.Ck
1. Introduction
Although there are no systems at zero temperature available to us, it is the quantum mechanics of the simpler T = 0 systems that has engaged the attention of theorists. Thermal ensembles usually require the study of extended systems attached to a “heat bath”, and within some statistical ensemble. Even perturbation-theory approaches to model systems like the electron gas at finite-T were full of surprises [1,2].
Condensed matter physics and chemistry could get by with quantum mechanics as the input to some sort of thermal theory which is not integrated into the many-body problem. Much of plasma physics and astrophysics could manage with simple extensions of hydrogenic models, Thomas-Fermi theory, extended-Debye theory, and classical “one-component-plasma” models as long as the accuracy of observations, experiments and theoretical models did not demand anything more from quantum mechanics. On the other hand, at the level of foundations of quantum mechanics, the whole issue of quantized thermo-field dynamics has been an open problem [3]. Similarly, the theory of “mixed” systems with classical and quantum components is also a topic of discussion [4]. It is in this context that we need to look at the advent of density-functional theory (DFT) as a great step forward in the quantum many-body problem. The Hohenberg-Kohn theorem published in 1964 was soon followed by its finite-T generalization by Mermin, providing a “thermal” density-functional theory (th-DFT) in 1965 [5,6,7], which also saw the advent of Kohn-Sham theory. Hence, in 2015, we are celebrating the fiftieth anniversary of both Kohn-Sham theory, and Mermin’s extension of Hohenberg-Kohn theory to finite-T [8].
While DFT provided chemistry and condensed-matter physics, an escape from the intractable “n-electron” problem, in addition to its computational implications, DFT has deep epistemological implications in regard to the foundational ideas of physics. DFT claims that the many-body wavefunction can be dispensed with, and that the physics of a given system can be discussed as a functional of the one-body density. Thus, even entanglement can be discussed in terms of density functionals [9,10]. However, it is the computational power of DFT that has been universally exploited in many fields of physics.
The interest in thermonuclear fusion via laser compression and related techniques, and the advent of ultra-fast lasers, have created novel states of matter where the electron temperature is usually of the order of the Fermi energy , under conditions where they are identified as warm dense matter (WDM) [11]. When WDM is created using a fast laser within femto-second time-scales, the photons couple strongly to the electrons which are heated very rapidly to many thousands of degrees, while the ions remain essentially at the initial “ambient” temperature [12,13]. In addition to highly non-equilibrium systems, this often leads to two-temperature systems with the ion temperature , with . Alternatively, if shock waves are used to generate a WDM, we may have . Such ultra-fast matter (UFM) systems can be studied using a fs-probe laser within timescales t such that , where is the electron-ion temperature relaxation time [14,15] of the UFM system. These WCM systems are of interest in astrophysics and planetary science [16], inertial fusion [11], materials ablation [17,18], machining, and in the hot-carrier physics of field-effect transistors, nano-devices etc. [19,20].
Early attempts to apply thermal-DFT (also called finite-T DFT, th-DFT) to WDM-like systems were undertaken by the present author and François Perrot in the early 1980s as reviewed in Reference [21]. This involved a reformulation of the neutral-pseudoatom (NPA) model that had been formulated by Dagens [22] for zero-T problems, as it has the versatility to treat solids, liquids and plasmas.
Originally it was Ziman [23] (and possibly others, see [24]) who had proposed the NPA model as an intuitive physical idea in the context of solid-state physics. The electronic structure of matter is regarded as a superposition of charge densities located on each nuclear centre at . In other words, if the total charge density in momentum space was , then this is considered as being made up of the individual charge distributions put together using the ionic structure factor . This was more explicitly implemented in muffin-tin models of solids, or “atoms-in molecules” models of chemical bonds that were actively pursued in the 1960s, with the increasing availability of fast computers. The NPA model was formulated rigorously within DFT by Dagens who showed that it was capable of the same level of accuracy, at least for “simple metals”, as the Linear Muffin-Tin Orbital (LMTO) method, Augmented Plane-Wave (APW) method or the Korringa-Kohn-Rostoker codes that were becoming available in the 1970s [22]. Wigner’s exchange-correlation (XC) “functional” in the local-density approximation (LDA) was used by Dagens.
In the finite-T NPA that we have used as our “work-horse”, we solve the Kohn-Sham Mermin equation for a single nucleus placed at the centre of a large “correlation sphere” of radius which is of the order of 10, where is the Wigner-Seitz radius per ion. Here, , where is the ion density given as the number of ions per unit atomic volume. For WDM aluminium at normal compression, a.u. All types of particle correlations induced by the nucleus at the centre of the “correlation sphere” would have died down to bulk-values when . The ion distribution is approximated as a spherical cavity of radius surrounding the nucleus, and then becoming a uniform positive background [25,26]. This is simpler to implement than the full method implemented in Reference [27]. The latter involved a self-consistent iteration of the ion density and the electron density obtained from the Kohn-Sham procedure coupled to a classical integral equation or even molecular dynamics; the simpler NPA procedure is sufficient in most cases.
There have also been several practical formulations of NPA-like models in more recent times. Some of these [28] are extensions of the INFERNO cell-model of Lieberman [29], while others [30] use a mixture of NPA ideas as well as elements of Chihara’s “quantal-hyper-netted-chain (QHNC)” models [31]. We have discussed Chihara’s model to some extent in Reference [32]. In true DFT models, the electrons are mapped to a non-interacting Kohn-Sham electron gas having the same interacting density but at the non-interacting chemical potential. This feature is absent in INFERNO-like cell-models where the chemical potential is determined via an integration within the ion-sphere or by some such consideration. Thus, different physical results may arise (e.g., for the conductivity) depending on how the chemical potential is fixed. Chihara’s models use an ion subsystem and an electron subsystem coupled via a “quantal Ornstein-Zernike” equation. However, if a one-component electron-gas calculation was attempted via the “quantal HNC”, the known are not recovered. In the two component case, as far as we can ascertain, the ion- limit is not correctly related to the electron compressibility.
Thus, the Kohn-Sham NPA calculation provides the free-electron charge density pile-up around the nucleus. This is sufficient to calculate an electron-ion pseudopotential , and hence an on-ion pair potential as discussed in, say, Reference [26]. Once the pair-potential is available, the Hyper-Netted Chain equation (and its modified form incorporating a bridge function) can be used to calculate an accurate if desired, rather than via the direct iterative procedure used in Reference [27]. This finite-T NPA approach is capable of accurate prediction of phonons (i.e., milli-volt energies) in WDM systems, as shown explicitly by Harbour et al. [33] using comparisons with results reported by Recoules et al. [34] who used the Vienna Ab Initio Simulation Package (VASP).
Since the XC-functional of DFT is directly connected with the pair-distribution function (PDF), or equivalently with the two-particle density matrix [35], we sought to formulate the many-body problem of ion-electron systems directly in terms of the pair distribution functions of the system, where α and β count over types of particles (ions and electrons, with two types of electrons with spin up, or down) [25,26,27]. The ionic species may be regarded as classical particles without spin as their thermal de Broglie length is in the femto-meter regime at WDM temperatures. This approach led to the formulation of the Classical-map Hyper-Netted-Chain (CHNC) method that will be briefly described in Section 3.1.
The attempt to use thermal DFT for actual calculations naturally required an effort towards the development of finite-T XC-functionals [36,37,38,39,40,41,42]. Meanwhile, large-scale codes implementing DFT (e.g., CASTEP [43], VASP [44], ABINIT [45], Amasterdam density-functional (ADF) code [46], Gaussian [47] etc.) became available, where well-tested XC-functionals (e.g., the PBE functional [48]) as well as DFT-based pseudopotentials are implemented. Currently, these codes also included versions where the single-particle states could be chosen as a Fermi distribution [49] at a given temperature, while they do not include the finite-T XC functionals that are needed for a proper implementation of thermal DFT. These codes are meant to be used at or small T since finite-T calculations require a very rapid increase in the basis sets needed for such calculations. It should also be mentioned that Karasiev et al. [50] have recently implemented finite-T XC within the “Quantum Espresso” code, as well as given an “orbital-free” implementation, although, as far as we can see, the non-locality problem in the kinetic-energy functional has not been resolved.
However, the availability of DFT-electronic structure codes have opened up the possibility of using them even in the WDM regime. We give several references to such work that contain additional citations to other calculations [34,51,52,53,54,55]. This renewed interest has re-kindled an interest in the theory of thermal DFT in the context of current concerns [56]. In the following, we discuss some of the typical issues that arise in applying thermal-DFT to current problems, as these may range from basic issues to the simple question of “if one can get away with” just using the XC functional.
The use of a functional, augmented with gradient approximations etc. is satisfactory as long as the “external potential” can be considered fixed, as is the usual case in quantum chemistry and solid-state physics. In situations where the external potential arises from a dynamic ion distribution , since as well as the electron distribution depend self-consistently on each other, it is clear that the XC-contribution is a functional of both ρ and n, i.e., the XC-functional is of the form . Under such circumstances, a direct in situ calculation of the electron in the presence of the ion distribution has to be carried out, and an “on-the-fly” coupling constant integration is needed for each self-consistent loop determining and . We presented examples of such calculations for a system of electrons and protons at finite temperatures, in [57,58], using the classical-map Hyper-Netted Chain technique (CHNC) that enables an easy in situ calculation of the and . This approach is at once non-local and hence avoids the need for gradient approximations. Furthermore, the ion-ion correlations are highly non-local and the LDA or its extensions are totally inadequate since they are described by the HNC approximation.
2. Exchange-Correlation at Finite-T
It may be useful to present this section as an “FAQ” (Frequently Asked Questions) rather than a formal discussion on thermal-XC functionals.
2.1. Do We Have Reliable Thermal-XC Functionals?
The finite-T XC-functional in the random-phase approximation (RPA) [37,38,39] has been available since 1982, while formulations and parametrizations that go beyond RPA have been available since the late 1980s [40,41,42]. Finite-T XC-data from quantum simulations for the uniform finite-T electron fluid were provided in 2013 by Brown et al. [59], while an analytical fit to their data is found in Karasiev et al. [60]. The XC-parametrization of Perrot and Dharma-wardana given in 2000, Reference [42], was based on a coupling-constant evaluation of the finite-T electron-fluid PDF calculated via the Classical-map Hyper-Netted-Chain (CHNC) [61] method. It closely agrees with the recent quantum-simulation results (Figure 1). Finite-T CHNC-based results are available for the 2D- [62] and 3D-[61] electron gas, as well as other electron-layer systems [63,64,65]. They are in good agreement with path-integral and other Monte Carlo (PIMC) calculations where available.
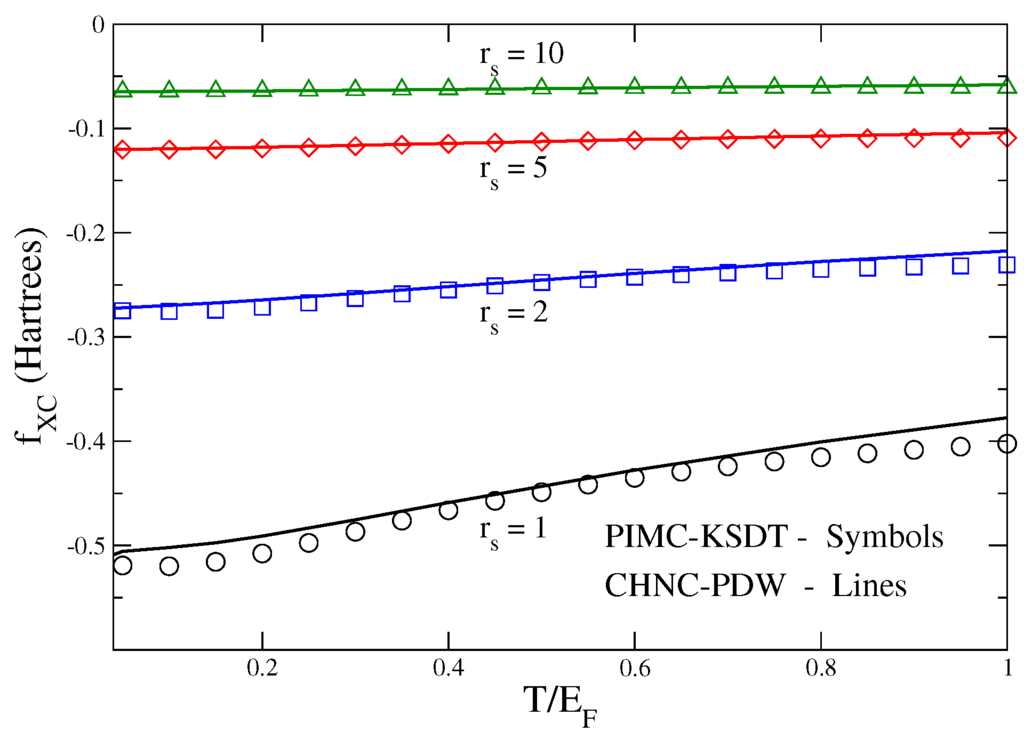
Figure 1.
(Color online) Finite-T exchange and correlation free energy per electron (Hartrees) versus the reduced temperature in units of the Fermi energy. The symbols, labeled PIMC-KSDT are the fit given by Karasiev et al. (Reference [60] to the path-integral Monte Carlo (PIMC) data of Brown et al. [59]). The continuous lines, labeled CHNC-PDW are from the classical-map HNC procedure of Perrot and Dharma-wardana [42]. The temperature range is the region of interest for WDM studies.
We consider the data for the 3D system that have been conveniently parametrized by Karasiev et al. (labeled KSDT in Figure 1). The CHNC at high temperatures (beyond what is displayed in the figure) show somewhat less correlation than given by PIMC, but correctly approaches the Debye-Hückel limit at high temperatures. In the high-density regime (), the RPA-functionals become increasingly accurate as . The small- regime has also been recently treated by Schoof et al. [66]. It should be stated that when the CHNC mapping was constructed, Fran  is Perrot and the present author did not attempt to map the regime in detail as it is fairly well treated by RPA methods. Recent simulations by Malone et al. [67] find some differences between their work, and that of Brown et al. [59] for in the neighbourhood of unity. Similarly, the CHNC data show differences for the curve, as shown in Figure 1. However, it is too early to re-examine the small regime and review the data of Reference [67] which are given as the internal energy and not converted to a free energy.
is Perrot and the present author did not attempt to map the regime in detail as it is fairly well treated by RPA methods. Recent simulations by Malone et al. [67] find some differences between their work, and that of Brown et al. [59] for in the neighbourhood of unity. Similarly, the CHNC data show differences for the curve, as shown in Figure 1. However, it is too early to re-examine the small regime and review the data of Reference [67] which are given as the internal energy and not converted to a free energy.
 is Perrot and the present author did not attempt to map the regime in detail as it is fairly well treated by RPA methods. Recent simulations by Malone et al. [67] find some differences between their work, and that of Brown et al. [59] for in the neighbourhood of unity. Similarly, the CHNC data show differences for the curve, as shown in Figure 1. However, it is too early to re-examine the small regime and review the data of Reference [67] which are given as the internal energy and not converted to a free energy.
is Perrot and the present author did not attempt to map the regime in detail as it is fairly well treated by RPA methods. Recent simulations by Malone et al. [67] find some differences between their work, and that of Brown et al. [59] for in the neighbourhood of unity. Similarly, the CHNC data show differences for the curve, as shown in Figure 1. However, it is too early to re-examine the small regime and review the data of Reference [67] which are given as the internal energy and not converted to a free energy.However, it is clear that there is no shortage of reliable finite-T XC-functionals for those who wish to use them.
2.2. Can We Ignore Thermal Corrections and Use the Implementations?
While finite-T XC functionals can be easily incorporated into the NPA model or average-atom cell models etc. [29], this is much more difficult in the context of large DFT codes like VASP or ABINIT. Hence, the already installed XC-functionals have been used as a part of the “package” for a significant number of calculations for WDM materials, ranging from equation of state (EOS), X-ray Thomson scattering, conductivity etc. Hence, the question has been raised as to whether the thermal corrections to the XC-functional may be conveniently disregarded.
The push for accurate XC-functionals in quantum chemistry came from the need for “chemical accuracy” in predicting molecular interactions in the milli-Rydberg range. The current level of accuracy in WDM experiments is nowhere near that. Furthermore, many properties (e.g., the EOS and the total energy) are insensitive to details since total energies are usually very large compared to XC-energies, even at , unless one is dealing with unusually contrived few-particle systems. However, one can give a number of counter examples which are designed to show that there are many situations where the thermal modification of the XC-energy and XC-potential are important.
As a model system, we may consider the uniform electron fluid with a density of n electrons per atomic volume, and thus having an electron-sphere radius . Since the Fermi momentum , where , the kinetic energy at scales as , while the Coulomb energy scales as . Hence, the ratio of the Coulomb-interaction energy to the kinetic energy scales as . Thus, the electron-sphere radius is also the “coupling constant” that indicates the deviation of the system from the non-interacting independent particle model. The RPA is valid when for systems, for Coulomb fluids. On the other hand, at very high temperatures, the kinetic energy becomes T (or where in our units), while the Coulomb energy is , where for the electron fluid. Hence the ratio of the Coulomb energy to the kinetic energy, viz., for Classical Coulomb systems. Here, the role of is reversed to that at , and the system behaves as an “ideal gas” for large in systems where . The equivalent of the RPA-theory in the high-T limit is the Debye-Hückel theory which is valid for . A generalized coupling constant that “switches over” correctly from its behavior to the classical-fluid behavior at high T can be given as in Equations (1) and (2):
The equivalent kinetic temperature referred to in the above equation can be constructed from the mean kinetic energy as in Equation (A2) given in the appendix to [42]. However, the main point here is that there are two non-interacting limits for studying Coulomb fluids. We can start from the non-interacting limit and carry out perturbation theory, or coupling-constant integrations to include the effect of the Coulomb interaction , with λ moving from 0 to unity (e.g., see Equation (71) of Reference [56] for a discussion and references). Alternatively, we can start from the non-interacting limit. This high temperature limit is the “classical limit” where the system is a non-interacting Boltzmann gas. One can do perturbation theory as well as coupling constant integrations over going from 0 to its required value Γ. The latter approach is well known in the theory of classical fluids. Such results provide standard “benchmarks” in the context of the classical one-component plasma [68,69], just as the electron gas does for the quantum many-electron problem. However, there is no clear way of evolving from a classical Boltzmann gas at into a quantum fluid by increasing the Coulomb coupling to its full value, as the anti-symmetry of the underlying wavefunction needs to be included. This problem does not arise if we start from a non-interacting Fermi gas at . How this problem is solved within a classical scheme is discussed below, in the context of the CHNC method. The “temperature connection formula” referred to recently by Burke et al. [70] in a thermal-DFT context may be closely related to this discussion.
Although XC effects are important, it is a small fraction of the total energy. They become negligible as T becomes very large, when the total energy itself becomes very large. Thus, it is easy to understand that finite-T XC effects are most important, for any given , in the WDM range, where , with . Furthermore, in any electron-ion system containing even one bound state, the electron density becomes large as one approaches the atomic core, and hence there are spatial regions r where , when finite-T XC comes into play. Since the “free-electron” states are orthogonal to the core states, the free-electron density pile-up near a nucleus immersed in a hot-electron fluid is also equally affected, directly and via the core. Furthermore, is a property that directly enters into the calculation of the X-Ray Thomson scattering signal as well as the electron-ion pseudopotential . Hence, the effect of finite-T XC, and the need to include thermal-XC functionals in such calculations can be experimentally ascertained.
In Figure 2, we present the near an Aluminium nucleus in an electron fluid of density electrons/cm, i.e., at and at eV, calculated using the neutral-pseudo-atom method. This temperature corresponds to . Calculations using VASP code for an actual experiment covering this regime has also been given by Plageman et al. [52]. Although the difference in charge densities that arises from the difference between the XC and the finite-T XC shown in Figure 2 may seem small, such charge-density differences translate into significant energy differences as well as into significant X-ray scattering features.
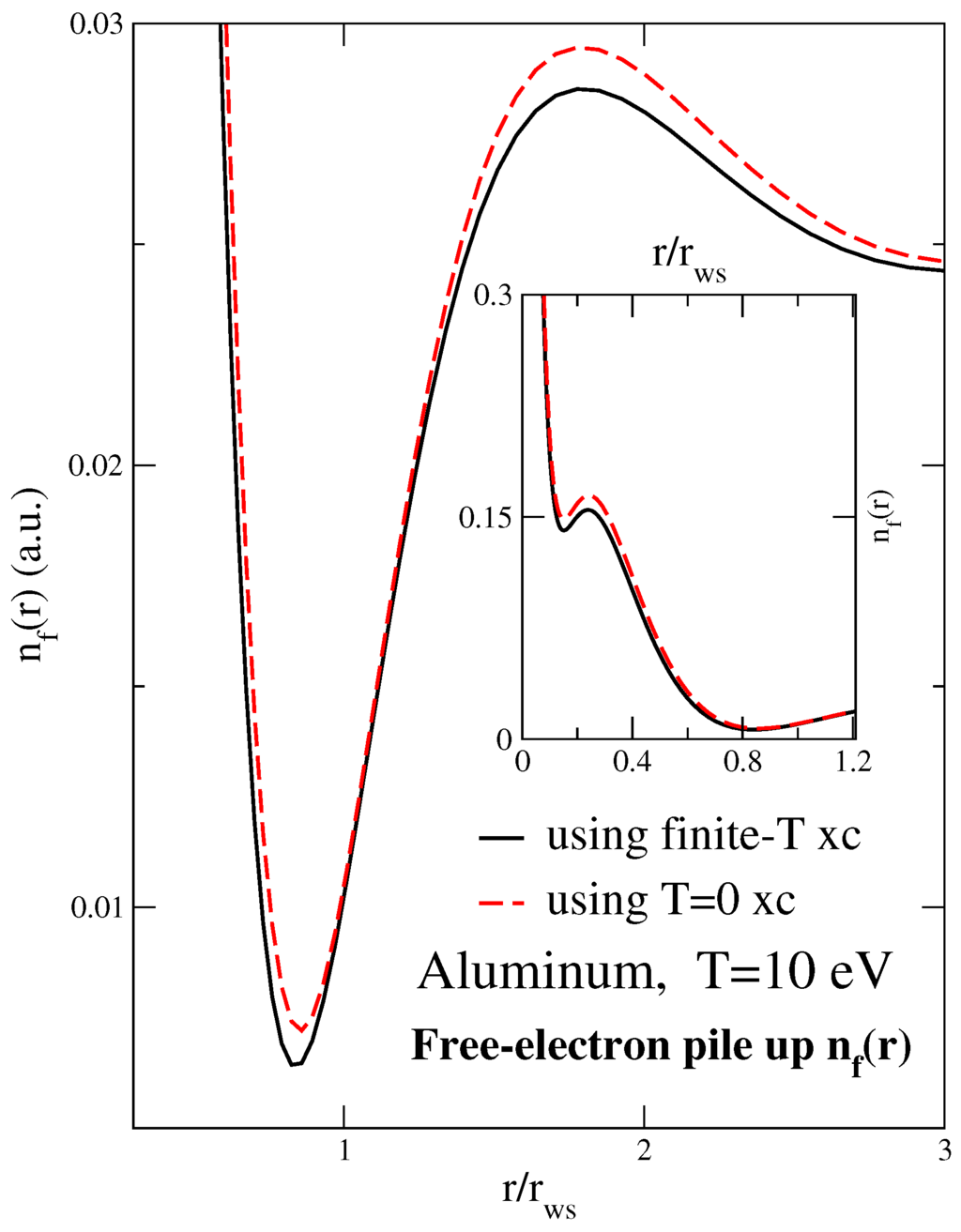
Figure 2.
(Color online) The NPA free-electron density using PDW finite-T XC and with the XC. Inset: inside the Wigner-Seitz sphere, with 3.0 Bohr.
Although Kohn-Sham energies are not to be interpreted as the one-particle excitation energies of the system, they can be regarded as the one-particle energies of the non-interacting electron fluid (at the interacting density) that appears in Kohn-Sham theory. These eigen-energies are also sensitive to whether we use the XC-functional, or even to different finite-T functionals. For instance, in Section 6 of Reference [42] we give the Kohn-Sham energy spectrum of warm-dense Aluminium at 15 eV calculated using the PDW-finite-T XC-functional [42], as well as the finite-T Iyatomi-Ichimaru (YI) functional. In summary, the Kohn-Sham (KS)-bound states obtained by the two methods (with YI given second) are: at energies (in Rydbergs) of 2115.044 and 2110.199 for the 1s level, 27.86214 and 27.53968 for the 2s level. The outermost level, the 2p-state, has an energy of 25.05646 and 24.81116 from Perrot and Dharma-wardana (PWD) and YI, respectively. Similar proportionate changes are seen in the phase shifts of the continuum states. Thus, it is clear that the XC-potentials should have a significant impact, especially in determining the regimes of plasma phase transitions [26,71], finite-T magnetic transitions, as well as in the theory of ionization processes [54] and transport properties.
Another example of the need for finite-T XC functionals is given by Sjostrom and Daligault [72] in their discussion of gradient-corrected thermal functionals. They conclude that “finite-temperature functionals show improvement over zero-temperature functionals, as compared to path-integral Monte Carlo calculations for deuterium equations of state, and perform without computational cost increase compared to zero-temperature functionals and so should be used for finite-temperature calculations”.
Karasiev et al. [50] have recently implemented the PDW-finite-T XC functional as well as their new fit to the PIMC data in the “Quantum Espresso” code. They have made calculations of the bandstructure and electrical conductivity of WDM Aluminium. They find that the use of finite-T XC is necessary if significant errors (up to 15% at 0.11 in the case of Al) are to be avoided [73].
2.3. Can We Define Free and Bound Electrons in an “Unambiguous” Manner?
In a “fully-ionized” plasma, all the electrons are in delocalized states. Thus, in stark contrast to quantum chemistry, most plasma physics deals with continuum processes. WDM systems usually contain some partially occupied bound states as well as continuum states. Thus, if the Hamiltonian is bounded, and if there is no frequency dependent external field acting on the system, there is no difficulty in identifying the bound states and continuum states of the non-interacting electron system used in Kohn-Sham theory. If a strong frequency-dependent external field is acting on the system, the concept of “bound” electrons as distinct from “free” electrons becomes much more hazy and will not be discussed here.
Depending on the nature of the “external potential”, a system at may be such that all electrons are in “bound states”. The latter are usually eigenstates whose square becomes rapidly negligible as r goes beyond a region of localization. The spectrum contains occupied and unoccupied “bound states” as well as positive-energy states which are not localized within a given region. All states become partially occupied in finite-T systems, and treatments that restrict themselves to a small basis set of functions localized over a finite region of space become too restrictive. Most DFT codes use a simulation cell of linear dimension L with periodic boundary conditions. In such a model, the smallest value of k in momentum space is , and this prevents the direct evaluation of various properties (e.g., ) as . In the NPA model, a large sphere of radius R such that all particle correlations have died out is used, and phase shifts of continuum states, taken as plane waves, are calculated. This procedure allows an essentially direct access to properties as well as the bound and continuum spectrum of the ion in the plasma. However, the difficulty arises when the electronic bound-states spread beyond the Wigner-Seitz radius of the ion.
The question of determining the number of free electrons per ion, viz., is usually posed in the context of the mean-ionic charge used in metal physics and plasma theory. If the nuclear charge is , and if the total number of bound electrons attributed to that nucleus is , then clearly if the charge distribution is fully contained within the Wigner-Seitz sphere of the ion. While is well-defined in that sense for many elements under standard conditions, giving, for example for Al at normal compression and up to about T = 20 eV, this simple picture breaks down for many elements even under normal conditions. If the electronic charge density cannot be accurately represented as a superposition of individual atomic charge densities, the definition of becomes more complicated since a bound electron may be shared between two or more neighbouring atoms that form bonds. Transition-metal solids and WDMs have d-electron states, which extend outside the atomic Wigner-Seitz sphere. Hence, assigning them to a particular nuclear centre becomes a delicate exercise. However, even in such situations, there are meaningful ways to define and that lead to consistence with experiments. In such situations, the proper value of may differ from one physical property to another as the averaging involved in constructing the mean value may change. A similar situation applies to the effective electron mass which deviates from the ideal value of unity (in atomic units), and takes on different values according to whether we are discussing a thermal mass, an optical effective mass, or a band mass that we may use in a Luttinger-Kohn calculation.
Experimentally, is a measure of the number of free electrons released per atom. This can be measured from the limit of the optical conductivity . Thus, although transition metals like gold have delocalized d-electrons, the static conductivity up to about 2 eV is found to indicate that , with the optical mass . Another property which measures is the electronic specific heat. Here again, the specific heat evaluated from DFT calculations that use a pseudopotential for Au agrees with experimental data up to 2 eV, while those that use the density of states from all 11 electrons as free-electron states will obtain significantly different answers [74,75] that need to be used with circumspection. That is, such a calculation will be valid only if the d-electrons are fully delocalized and partake in the heating process by being coupled with the pump laser creating the WDM.
The argument that is not a valid concept or a quantum property because there is no “operator” corresponding to it has no merit. The temperature also does not correspond to the mean value of a quantum operator. In fact, T is a Lagrange multiplier ensuring the constancy of the Hamiltonian within the relevant times scales, while is the Lagrange multiplier that sets the charge neutrality condition relating the average electron density to the average ion density [27].
Additional discussions regarding may be found in References [21,58] and in Reference [26] where the case of a WDM mixture of ions with different ionization, viz., Al is treated within a first-principles DFT scheme.
3. Future Challenges in Formulating Finite-T XC Functionals
In considering a system of ions with a distribution , and an electron distribution interacting with it, the free energy F has to be regarded as a functional of both and . Hence, the ground state has to be determined by a coupled variational problem involving a constrained-search minimization with respect to all physically possible electron charge distributions , and ion distributions , subject to the usual formal constraints of n-representability etc. The Euler-Lagrange variational equation from the derivative of F with respect to , for a fixed would yield the usual Kohn-Sham procedure with the rigid electrostatic potential of providing the external potential. However, if no static approximation or Born-Oppenheimer approximation is made, we can obtain another Euler-Lagrange variational equation from the derivative of F with respect to ρ. This coupled pair of equations treated via density-functional theory involves not only the , but also and , the latter involving correlations (but no exchange) as it arises from ion-ion interactions beyond the self-consistent-field approximation. In effect, just as the electron many-body problem can be reduced to an effective one-body problem in the Kohn-Sham sense, we can thus reduce the many-ion problem into a “single-ion problem”. Such an analysis was given by us long ago [27].
The ion-ion correlations cannot be approximated by any type of local-density approximation, or even with a sophisticated gradient approximation. However, Perrot and the present author were able to show that a fully non-local approximation where an ion-ion pair-distribution can be constructed in situ using the HNC equation provides a very satisfactory solution. This is equivalent to positing that the ion-ion correlation functional is made up of the hyper-netted-chain diagrams. However, significant insights are needed in regard to the electron-ion correlation functionals which involve the coupling between a quantum subsystem and a classical subsystem [4]. This is largely an open problem that we have attempted to deal with via the classical-map HNC approach, to be discussed below.
The advent of WDM and ultra-fast matter has thrown out a number of new challenges to the implementation of thermal DFT. A simple but at the moment unsolved problem in UFM may be briefly described as follows. A metallic solid like Al at room temperature () is subject to a short-pulse laser which heats the conduction electrons to a temperature that may be 6 eV. The core electrons (which occupy energy bands deep down in energy and hence not excitable by the laser) remain essentially unperturbed in the core region and at the core temperature, i.e., at 0.026 eV. The temperature relaxation by electron-ion processes is “slow”, i.e., it occurs in pico-second times scales. On the other hand, electron-electron processes are “fast”, and hence one would expect that the conduction-band electrons at to undergo exchange as well as Coulomb scattering within femto-second time scales, consistent with electron-electron interactions timescales. Thus, while we have a quasi-equilibrium of a two-temperature system holding for up to pico-second timescales, the question arises if one can meaningfully calculate an exchange and correlation potential between the bound electrons in the core at the temperature , and the conduction-band electrons at , with . While we believe on physical grounds that a thermal DFT is applicable at least in an approximate sense, an unambiguous method for calculating the two-temperature XC-energies and potentials is as yet unavailable.
3.1. Classical-Map Hyper-Netted Chain Method
Once the pair-distribution function of a classical or quantum Coulomb system is known, all the thermodynamic functions of the system can be calculated from . The XC-information is also in the . Only the ground-state correlations are needed in calculating the linear transport properties of the system. Hence, most properties of the system become available. It is well known that correlations among classical charges (i.e., ions) can be treated with good accuracy via the the hyper-netted-chain equation, but dealing with the quantum equivalent of hyper-netted-chain diagrams for quantum systems is difficult, even at [76].
When we have an electron subsystem interacting with the ion subsystem, obtaining the PDFs becomes a difficult quantum problem even via more standard methods. We need to solve for a many-particle wavefunction which rapidly becomes intractable as the number of electrons is increased beyond a small number. The message of DFT is that the many-body wavefunction is not needed, and that the one-particle charge distribution is sufficient. While the charge distribution at involves a sum over the squares of the occupied Kohn-Sham wavefunctions, at very high T, the classical charge distribution is given by a Boltzmann distribution containing an effective potential felt by a single “field” particle and characterized by the temperature which is directly proportional to the classical kinetic energy.
In CHNC, we attempt to replace the quantum-electron problem by a classical Coulomb problem where we can use a simple method like the ordinary HNC equation to directly obtain the needed PDFs, at some effective “classical fluid” temperature having the same density distribution as the quantum fluid. The electron PDF of the non-interacting quantum electron fluid is known at any temperature and embodies the effect of quantum statistics (Pauli principle). Hence, we can ask for the effective potential which, when used in the HNC, gives us the , an idea dating back to a publication by Lado [77]. This ensures that the non-interacting density has the required “n-representable” form of a Slater determinant. Of course, only the product can be determined by this method, and it exists even at . Then the total pair potential to be used in the equivalent classical fluid is taken as . How does one choose since the Pauli term is independent of it?
To a very good approximation, if is chosen such that the classical fluid has the same Coulomb correlation energy as the quantum electron fluid, then it is found that the PDF of the classical Coulomb fluid is a very close approximation to the PDF of the quantum electron fluid at . There is of course no mathematical proof of this. However, from DFT, we know that only the “correct” ground state distribution will give us the correct energy, and perhaps it is not surprising that this choice is found to work. The that works for the quantum electron gas is called the “quantum temperature” . More details of the method are given in Reference [42]. There it is argued that, to a good approximation, for a finite-T electron gas at the physical temperature T, the effective classical fluid temperature . This has been confirmed independently by Datta and Dufty [78] in their study of classical approximations to the quantum electron fluid. Thus, CHNC provides all the tools necessary for implementing a classical HNC calculation of the PDFs of the quantum electron gas at finite-T.
We display in Figure 3 pair-distribution functions calculated using CHNC, and those available in the literature from quantum simulations at , as finite-T PDFs from quantum simulations are hard to find. In any case, the classical map is expected to be better as T increases and the comparison is important. In the figure, diffusion Monte Carlo (DMC) and variational Monte Carlo (VMC) data [79] are compared with CHNC results. In Figure 3, the parallel-spin PDF is marked , while the anti-parallel spin PDF is marked . The latter has a finite value as as there is no Pauli exclusion principle operating on them. Furthermore, the the mean value of the operator of the Coulomb potential, i.e., , is of the form , where is the thermal de Broglie wavelength of the electron pair, as discussed in [61]. This “quantum-diffraction” correction ensures that has a finite value, as seen in the figure. It is in good agreement with Quantum Monte Carlo results. Thus, the CHNC is capable of providing a good interpretation of the physics underlying the results of quantum simulations. Needless to say, unlike Quantum Monte Carlo or Path-Integral simulation methods, the CHNC integral equations can be implemented on a laptop and the computational times are imperceptible.
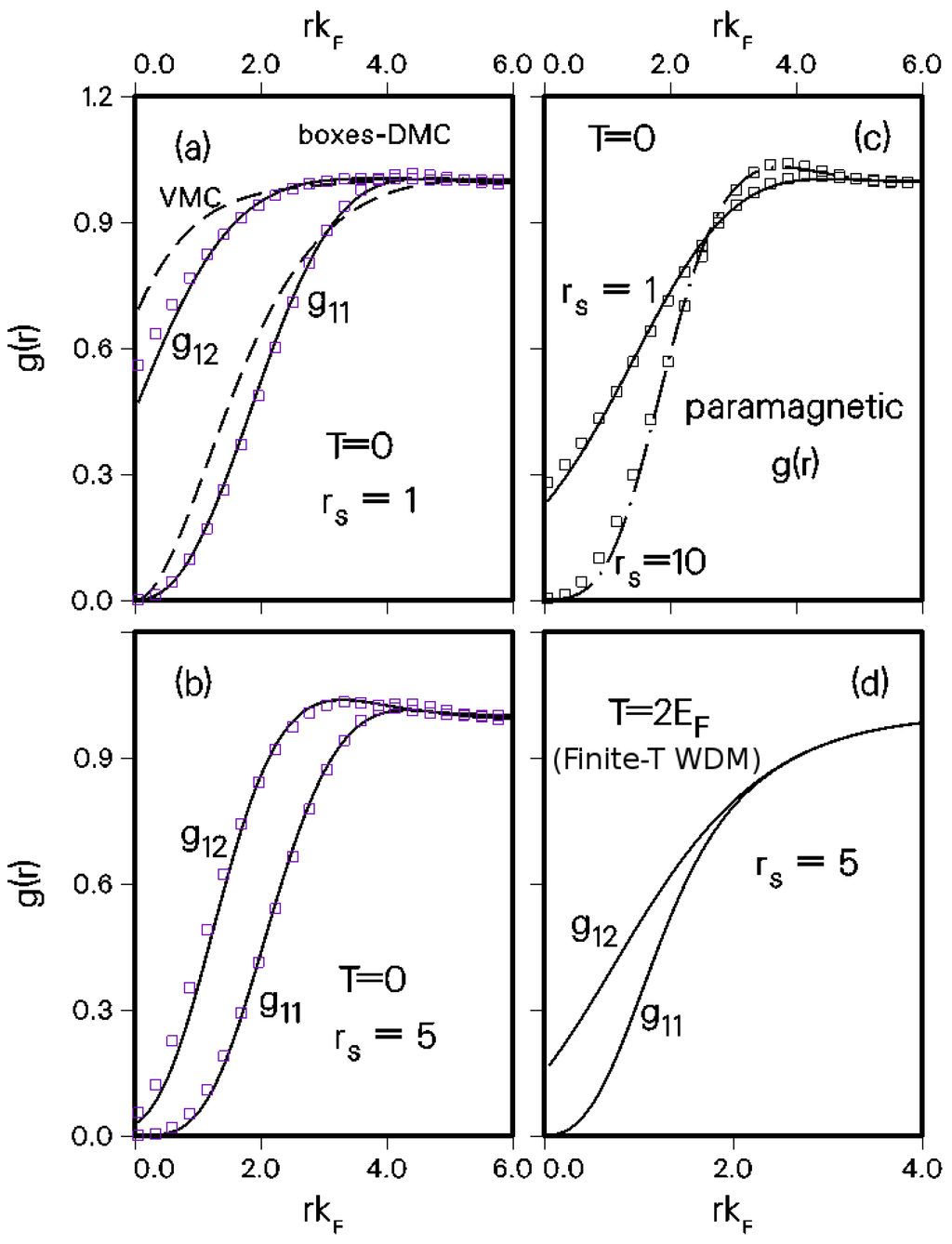
Figure 3.
(a) Here, the CHNC g(r) are compared with VMC and DMC simulation results: the interacting PDFs and at = 1 are shown. Solid lines: CHNC, boxes: DMC, dashed line: VMC [79]; Panel (b) , DMC [79] and HNC; In (c), the paramagnetic at = 1 and = 10, T = 0 are compared with DMC; (d) Finite temperature PDFs (CHNC) for = 2, = 5 would correspond to a WDM at ≃ 3.6 eV (∼ 42,000 K).
Using the PDFs calculated with a scaled Coulomb potential , a coupling constant integration over λ can be carried out to obtain the XC-free energy as described in detail in Reference [42]. As seen from Figure 1, this procedure leads to good agreement with the thermal-XC results from the PIMC method, while only the spin-polarized data were used in constructing . Furthermore, since tends to the physical temperature at high T, and since the HNC provides an excellent approximation to the PDFs of the high-T electron system, the method naturally recovers the high-T limit of the classical one-component plasma. Note that we could NOT have started from the high-T limit of an ideal classical gas and used the well-known classical coupling constant (i.e., Γ integration method, e.g., see Baus and Hansen or Ichimaru [68,69]) to determine from an integration that ranges from to the needed temperature (i.e., the needed Γ). This is because there is no clear method of capturing the physics contained in , and ensuring that Fermi statistics are obeyed (e.g., via the introduction of a ), as there is only Boltzmann statistics at .
The ability of the CHNC to correctly capture the thermal-DFT properties of the finite-T quantum fluid suggests its use for electron-ion systems like compressed hydrogen (electron-proton gas), or complex plasmas with many different classical ions interacting with electrons [57], without having to solve the Kohn-Sham equations, as demonstrated in Bredow et al. [80]. The extensive calculations of Bredow et al. establish the ease and rapidity provided by CHNC, without sacrificing accuracy. CHNC has potential applications for electron-positron systems or electron-hole systems where both quantum components can be treated via the classical map. It also provides a partial solution to the still unresolved problem of formulating a fully-nonlocal “orbital-free” approach that directly exploits the Hohenberg-Kohn-Mermin theory, without the need to go via the Kohn-Sham orbital formulation.
4. Conclusions
We have argued that our current knowledge of the thermal XC-functionals is satisfactory and the stage is set for their implementation in practical DFT codes. Noting the complexity of warm-dense matter, we have emphasized simplifications as well as extensions which do not sacrifice accuracy. In this respect, the neutral-pseudo atom model can, in most cases, do the work of the ab initio codes like VASP, and handle high-temperature problems that are beyond their scope. Orbital-free approaches [50] will also become increasingly useful, especially at intermediate and high . Nevertheless, the ab initio codes are needed at low-temperature low-density situations involving molecular formation, where the NPA breaks down as it is a “single-centre” approach. However, in many WDM cases, we need to go beyond the picture where the ion subsystem is held static, and the electrons only feel them as an “external potential”. Hence, we have emphasized the need for calculating not just the XC-functionals for electrons, but also the classical correlation functionals for ions, as well as the ion-electron correlations directly, in situ, via direct coupling-constant integrations of all the pair-distribution functions of the system, ensuring a fully non-local formulation where gradient expansions are not needed. In fact, there is no need for any XC-functionals in such a scheme. To do this efficiently and accurately, we have proposed a classical map of the quantum electrons and implemented it in the CHNC scheme that depends on DFT ideas. This capacity is not found in any of the currently available methods. CHNC has been used to construct a finite-T XC functional for electrons more than a decade before PIMC results became available, and it turns out that the CHNC results are accurate. The CHNC scheme has been successfully used for calculating the equation of state and other properties of warm dense matter as well as multi-component electron-layer systems, thick layers etc., that are expensive to treat by quantum simulation methods, but relevant for nanostructure physics.
Conflicts of Interest
The author declares no conflict of interest.
References
- Luttinger, J.M.; Ward, J.C. Ground-State Energy of a Many-Fermion System—II. Phys. Rev. 1960, 118, 1417. [Google Scholar] [CrossRef]
- Kohn, W.; Luttinger, J.M. Ground-State Energy of a Many-Fermion System. Phys. Rev. 1960, 118, 41. [Google Scholar] [CrossRef]
- Takahashi, Y.; Umezawa, H. Thermofield Dynamics. In Collective Phenomena; Gordon and Beach: New York, NY, USA, 1975; Volume 2, pp. 55–80, Reprinted in Int. J. Mod. Phys. B 1996, 10, 1755. [Google Scholar] [CrossRef]
- Heslot, A. Quantum mechanics as a classical theory. Phys. Rev. D 1985, 31, 1341. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Mermin, N.D. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 1965, 137, A1441. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. Current Issues in Finite-T Density-Functional Theory and Warm-Correlated Matter. In Proceedings of the 16th International Conference on Density Functional Theory and Its Applications, Celebrating the 50th Anniversary of the Kohn-Sham Theory, Debrecen, Hungary, 31 August–4 September 2015.
- Dharma-wardana, M.W.C. A Physicists’s View of Matter and Mind; World Scientific: Singapore, 2014. [Google Scholar]
- Dharma-wardana, M.W.C. Density-Functional Theory, finite-temperature classical maps, and their implications for foundational studies of quantum systems. ArXiv E-Prints 2013. [Google Scholar]
- Graziani, F.; Desjarlais, M.P.; Redmer, R.; Trickey, S.B. (Eds.) Frontiers and Challenges in Warm Dense Matter; Lecture Notes in Computational Science and Engineering; Springer International Publishing: Heidelberg, Germany, 2014; Volume 96.
- Milchberg, H.M.; Freeman, R.R.; Davy, S.C.; More, R.M. Resistivity of a Simple Metal from Room Temperature to 106 K. Phys. Rev. Lett. 1988, 61, 2364. [Google Scholar] [CrossRef] [PubMed]
- Ng, A. Outstanding questions in electron-ion energy relaxation, lattice stability, and dielectric function of warm dense matter. Int. J. Quant. Chem. 2012, 112, 150–160. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. Results on the energy-relaxation rates of dense two-temperature aluminum, carbon, and silicon plasmas close to liquid-metal conditions. Phys. Rev. E 2001, 64, 035401(R). [Google Scholar] [CrossRef] [PubMed]
- Benedict, L.X.; Surh, M.P.; Castor, J.; Khairallah, S.A.; Whitley, H.D.; Richards, D.F.; Glosli, D.N.; Murillo, M.S.; Scullard, C.R.; Grabowski, P.E.; et al. Molecular dynamics simulations and generalized Lenard-Balescu calculations of electron-ion temperature equilibration in plasmas. Phys. Rev. E 2012, 86, 046406. [Google Scholar] [CrossRef] [PubMed]
- Driver, K.P.; Militzer, B. All-Electron Path Integral Monte Carlo Simulations of Warm Dense Matter: Application to Water and Carbon Plasmas. Phys. Rev. Lett. 2012, 108, 115502. [Google Scholar] [CrossRef] [PubMed]
- Lorazo, P.; Lewis, L.J.; Meunier, M. Short-Pulse Laser Ablation of Solids: From Phase Explosion to Fragmentation. Phys. Rev. Lett. 2003, 91, 225502. [Google Scholar] [CrossRef] [PubMed]
- Lorazo, P.; Lewis, L.J.; Meunier, M. Thermodynamic pathways to melting, ablation, and solidification in absorbing solids under pulsed laser irradiation. Phys. Rev. B 2006, 73, 134108. [Google Scholar] [CrossRef]
- Shah, J. Ultrafast Spectroscopy of Semiconductor Nanostructures; Springer: Heidleberg, Germany, 1999. [Google Scholar]
- Dharma-wardana, M.W.C. Coupled-mode hot electron relaxation and the hot-phonon effect in polar semiconductors. Solid State Commun. 1993, 86, 83–86. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. A Review of Studies on Strongly-Coupled Coulomb Systems Since the Rise of DFT and SCCS-1977. Contr. Plasma Phys. 2015, 55, 85–101. [Google Scholar] [CrossRef]
- Dagens, L. A selfconsistent calculation of the rigid neutral atom density according to the auxiliary neutral atom model. J. Phys. C Solid State Phys. 1972, 5, 2333. [Google Scholar] [CrossRef]
- Ziman, J.H. The method of neutral pseudo-atoms in the theory of metals. Adv. Phys. 1964, 13, 89–138. [Google Scholar] [CrossRef]
- Dagens, L. Densité de valence et énergie de liaison d’un métal simple par la méthode de l’atome neutre : Le potentiel ionique Hartree-Fock. J. Phys. France 1975, 36, 521–529. (In French) [Google Scholar] [CrossRef]
- Perrot, F. Ion-ion interaction and equation of state of a dense plasma: Application to beryllium. Phys. Rev. E 1993, 47. [Google Scholar] [CrossRef]
- Perrot, F.; Dharma-wardana, M.W.C. Equation of state and transport properties of an interacting multispecies plasma: Application to a multiply ionized Al plasma. Phys. Rev. E. 1995, 52, 5352. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C.; Perrot, F. Density-functional theory of hydrogen plasmas. Phys. Rev. A 1982, 26, 2096. [Google Scholar] [CrossRef]
- Wilson, B.; Sonnad, V.; Sterne, P.; Isaacs, W. Purgatorio—A new implementation of the Inferno algorithm. J. Quant. Spectrosc. Radiat. Transfer. 2006, 99, 658–679. [Google Scholar] [CrossRef]
- Liberman, D.A. Inferno: A better model of atoms in dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 335–339. [Google Scholar] [CrossRef]
- Starrett, C.E.; Saumon, D. Models of the elastic x-ray scattering feature for warm dense aluminum. Phys. Rev. E 2015, 92, 033101. [Google Scholar] [CrossRef] [PubMed]
- Chihara, J.; Kambayashi, S. Ionic and electronic structures of liquid aluminium from the quantal hypernetted-chain equations combined with the molecular dynamics method. J. Phys. Condens. Matter. 1994, 6, 10221. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. The classical-map hyper-netted-chain (CHNC) method and associated novel density-functional techniques for warm dense matter. Int. J. Quant. Chem. 2012, 112, 53–64. [Google Scholar] [CrossRef]
- Harbour, L.; Dharma-wardana, M.W.C.; Klug, D.D.; Lewis, L.J. Two-Temperature Pair Potentials and Phonon Spectra for Simple Metals in the Warm Dense Matter Regime. Contrib. Plasma Phys. 2015, 55, 144–151. [Google Scholar] [CrossRef]
- Recoules, V.; Clérouin, J.; Zérah, G.; Anglade, P.M.; Mazevet, S. Effect of Intense Laser Irradiation on the Lattice Stability of Semiconductors and Metals. Phys. Rev. Lett. 2006, 96, 055503. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, T.L. Hohenberg-Kohn theorem for nonlocal external potentials. Phys. Rev. B 1975, 12, 2111. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C.; Taylor, T. Exchange and correlation potentials for finite temperature quantum calculations at intermediate degeneracies. J. Phys. C Solid State Phys. 1981, 14, 629–646. [Google Scholar] [CrossRef]
- Gupta, U.; Rajagopal, A.K. Density functional formalism at finite temperatures with some applications. Phys. Rep. 1982, 87, 259–311. [Google Scholar] [CrossRef]
- Perrot, F.; Dharma-wardana, M.W.C. Exchange and correlation potentials for electron-ion systems at finite temperatures. Phys. Rev. A 1984, 30, 2619. [Google Scholar] [CrossRef]
- Kanhere, D.C.; Panat, P.V.; Rajagopal, A.K.; Callaway, J. Exchange-correlation potentials for spin-polarized systems at finite temperatures. Phys. Rev. A 1986, 33, 490. [Google Scholar] [CrossRef] [PubMed]
- Dandrea, R.G.; Ashcroft, N.W.; Carlsson, A.E. Electron liquid at any degeneracy. Phys. Rev. B 1986, 34, 2097. [Google Scholar] [CrossRef]
- Ichimaru, S.; Iyetomi, H.; Tanaka, S. Statistical physics of dense plasmas: Thermodynamics, transport coefficients and dynamic correlations. Phys. Rep. 1987, 149, 91–205. [Google Scholar] [CrossRef]
- Perrot, F.; Dharma-wardana, M.W.C. Spin-polarized electron liquid at arbitrary temperatures: Exchange-correlation energies, electron-distribution functions, and the static response functions. Phys. Rev. B 2000, 62, 16536. [Google Scholar] [CrossRef]
- About CASTEP. Available online: http://www.castep.org/CASTEP/CASTEP (accessed on 21 March 2016).
- VASP. Available online: https://www.vasp.at/ (accessed on 21 March 2016).
- ABINIT. Available online: http://www.abinit.org/ (accessed on 21 March 2016).
- ADF: Powerful DFT Software. Available online: https://www.scm.com/ (accessed on 21 March 2016).
- The Official Gaussian Website. Available online: http://www.gaussian.com/ (accessed on 21 March 2016).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Gonze, X. First-principles responses of solids to atomic displacements and homogeneous electric fields: Implementation of a conjugate-gradient algorithm. Phys. Rev. B 1997, 55, 10337. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Sjostrom, T.; Trickey, S.B. Finite-temperature orbital-free DFT molecular dynamics: Coupling Profess and Quantum Espresso. Comput. Phys. Commun. 2014, 185, 3240–3249. [Google Scholar] [CrossRef]
- Silvestrelli, P.L.; Alavi, A.; Parrinello, M. Electrical-conductivity calculation in ab initio simulations of metals:Application to liquid sodium. Phys. Rev. B 1997, 55, 15515. [Google Scholar] [CrossRef]
- Plagemann, K.U.; Rüter, H.R.; Bornath, T.; Shihab, M.; Desjarlais, M.P.; Fortmann, C.; Glenzer, S.H.; Redmer, R. Ab initio calculation of the ion feature in x-ray Thomson scattering. Phys. Rev. E 2015, 92, 013103. [Google Scholar] [CrossRef] [PubMed]
- Sperling, P.; Gamboa, E.J.; Lee, H.J.; Chung, H.K.; Galtier, E.; Omarbakiyeva, Y.; Reinholz, H.; Röpke, G.; Zastrau, U.; Hastings, J.; et al. Free-Electron X-Ray Laser Measurements of Collisional-Damped Plasmons in Isochorically Heated Warm Dense Matter. Phys. Rev. Lett. 2015, 115, 115001. [Google Scholar] [CrossRef] [PubMed]
- Vinko, S.M.; Ciricosta, O.; Preston, T.R.; Rackstraw, D.S.; Brown, C.R.; Burian, T.; Chalupský, J.; Cho, B.I.; Chung, H.K.; Engelhorn, K.; et al. Investigation of femtosecond collisional ionization rates in a solid-density aluminium plasma. Nat. Commun. 2015, 6, 6397. [Google Scholar] [CrossRef] [PubMed]
- Dharma-wardana, M.W.C. The dynamic conductivity and the plasmon profile of Aluminium in the ultra-fast-matter regime; an analysis of recent X-ray scattering data from the LCLS. ArXiv E-Prints 2015. [Google Scholar]
- Pribram-Jones, A.; Pittalis, S.; Gross, E.K.U.; Burke, K. Thermal Density Functional Theory in Context. In Frontiers and Challenges in Warm Dense Matter; Lecture Notes in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2014; Volume 96. [Google Scholar]
- Dharma-wardana, M.W.C.; Perrot, F. Equation of state and the Hugoniot of laser shock-compressed deuterium: Demonstration of a basis-function-free method for quantum calculations. Phys. Rev. B 2002, 66, 014110. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. Electron-ion and ion-ion potentials for modeling warm dense matter: Applications to laser-heated or shock-compressed Al and Si. Phys. Rev. E 2012, 86, 036407. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.W.; DuBois, J.L.; Holzman, M.; Ceperley, D.M. Exchange-correlation energy for the three-dimensional homogeneous electron gas at arbitrary temperature. Phys. Rev. B 2013, 88, 081102(R). [Google Scholar] [CrossRef]
- Karasiev, V.V.; Sjostrom, T.; Dufty, J.; Trickey, S.B. Accurate Homogeneous Electron Gas Exchange-Correlation Free Energy for Local Spin-Density Calculations. Phys. Rev. Lett. 2014, 112, 076403. [Google Scholar] [CrossRef] [PubMed]
- Dharma-wardana, M.W.C.; Perrot, F. A simple classical mapping of the spin-polarized quantum electron gas distribution functions and local field corrections. Phys. Rev. Lett. 2000, 84, 959. [Google Scholar] [CrossRef] [PubMed]
- Perrot, F.; Dharma-wardana, M.W.C. 2D-Electron Gas at Arbitrary Spin Polarizations and Coupling Strengths: Exchange-Correlation Energies, Distribution Functions, and the Spin-Polarized Phase. Phys. Rev. Lett. 2001, 87, 206404. [Google Scholar] [CrossRef] [PubMed]
- Dharma-wardana, M.W.C.; Perrot, F. Spin-polarized stable phases of the 2DES at finite temperatures. Phys. Rev. Lett. 2003, 90, 136601. [Google Scholar] [CrossRef] [PubMed]
- Dharma-wardana, M.W.C.; Perrot, F. Spin- and valley-dependent analysis of the two-dimensional low-density electron system in Si MOSFETs. Phys. Rev. B 2004, 70, 035308. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. Spin and temperature dependent study of exchange and correlation in thick two-dimensional electron layers. Phys. Rev. B 2005, 72, 125339. [Google Scholar] [CrossRef]
- Schoof, T.; Groth, S.; Vorberger, J.; Bonitz, M. Ab Initio Thermodynamic Results for the Degenerate Electron Gas at Finite Temperature. Phys. Rev. Lett. 2015, 115, 130402. [Google Scholar] [CrossRef] [PubMed]
- Malone, F.D.; Blunt, N.S.; Brown, E.W.; Lee, D.K.K.; Spencer, J.S.; Foulkes, W.M.C.; Shepherd, J.J. Accurate exchange-correlation energies for the warm dense electron gas. Available online: http://arxiv.org/pdf/1602.05104v2.pdf (accessed on 21 March 2016).
- Baus, M.; Hansen, J.-P. Statistical Mechanics of Simple Coulomb Systems. Phys. Rep. 1980, 59, 2. [Google Scholar] [CrossRef]
- Ichimaru, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017. [Google Scholar] [CrossRef]
- Smith, J.C.; Pribram-Jones, A.; Burke, K. Thermal Corrections to Density Functional Simulations of Warm Dense Matter. ArXiv E-Prints 2015. [Google Scholar]
- Norman, G.E.; Starostin, A.N. Failure of the classical description of nondegenerate dense plasma. High Temp. 1968, 6, 394. [Google Scholar]
- Sjostrom, T.; Daligault, J. Gradient corrections to the exchange-correlation free energy. Phys. Rev. B 2014, 90, 155109. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Calderin, L.; Trickey, S.B. The importance of finite-temperature exchange-correlation for warm dense matter calculations. ArXiv E-Prints 2016. [Google Scholar]
- Lin, Z.; Zhigilei, L.V.; Celli, V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys. Rev. B 2008, 77, 075133. [Google Scholar] [CrossRef]
- Chen, Z.; Holst, B.; Kirkwood, S.E.; Sametoglu, V.; Reid, M.; Tsui, Y.Y.; Recoules, V.; Ng, A. Evolution of ac Conductivity in Nonequilibrium Warm Dense Gold. Phys. Rev. Lett. 2013, 110, 135001. [Google Scholar] [CrossRef] [PubMed]
- Zabolitsky, J.G. Advances in Nuclear Physics; Negale, W., Vogt, E., Eds.; Springer US: New York, NY, USA, 1981; pp. 1–58. [Google Scholar]
- Lado, F. Effective Potential Description of the Quantum Ideal Gases. J. Chem. Phys. 1967, 47, 5369. [Google Scholar] [CrossRef]
- Dufty, J.; Dutta, S. Classical representation of a quantum system at equilibrium: Theory. Phys. Rev. E 2013, 87, 032101. [Google Scholar] [CrossRef]
- Ortiz, G.; Ballone, P. Correlation energy, structure factor, radial distribution function, and momentum distribution of the spin-polarized uniform electron gas. Phys. Rev. B 1994, 50, 1391. [Google Scholar] [CrossRef]
- Bredow, R.; Bornath, T.; Kraeft, W.-D.; Dharma-wardana, C.; Redmer, R. Classical-Map Hypernetted Chain Calculations for Dense Plasmas. Contrib. Plasma Phys. 2015, 55, 222–229. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).