Abstract
We model the behavior of an ideal liquid junction, across a porous and possibly charged medium between two ion-containing solutions, by means of the Nernst–Planck equation for the stationary state, in conditions of local electroneutrality. An analytical solution of the equation was found long ago by Planck for the uncharged junction with only ions of valences +1 and −1. Other analytical results, which have later been obtained also for more general situations, seem impractical for performing calculations. In this paper, we obtain analytical solutions for systems with up to three valence classes, which can be applied to perform numerical calculations in a straightforward way. Our method provides a much larger amount of information on the behavior of the system than the well-known Henderson’s approximation. At the same time, it is more simple and reliable, and much less demanding in terms of computational effort, than the nowadays commonly employed numerical methods, typically based on discrete integration and trial-and-error numerical inversions. We present some examples of practical applications of our results. We study in particular the uphill transport (i.e., the transport from the lower-concentration to the higher-concentration region) of a divalent cation in a liquid junction containing also other univalent anions and cations.
PACS:
66.10.Ed, 82.45.Gj
1. Introduction
When two solutions of different electrolytes, or of the same electrolyte but with different concentrations, are put into contact, a potential, called “liquid junction potential”, spontaneously arises between them [1]. Such a potential develops for instance across the porous diaphragm of concentration cells, thus affecting the output potential, and across the diaphragm of the reference electrodes which are commonly used in electrochemistry, thus affecting the measurements of the electrode potentials. On the other hand, since every electrochemical measurement also involves potential differences which arise between the electrodes and the solutions, a reliable experimental measurement of the liquid junction potential alone is often practically unavailable. For this reason, several methods to theoretically calculate the liquid junction potential have been conceived and employed for a long time.
An approximated formula for the junction potential, which gives results sufficiently accurate for most practical purposes, and which is for this reason largely employed still today, has been obtained by Henderson in 1907 [2,3]. A more rigorous approach to the problem had however been adopted by Planck already in 1890 [4,5]. The general behavior of an ion in an ideal liquid junction, which moves under the influence of diffusion and of an electric field, is described by the Nernst–Planck differential equation [4,5,6,7]. Planck obtained an analytical solution of this equation describing the stationary state of an uncharged liquid junction in which only univalent ions are present, under the assumption of local electroneutrality. This assumption means that the Nernst–Planck equations, for all the ionic species present in the junction, are solved with the constraint that the total electric charge vanishes at all points of the junction. In most practically relevant cases the behavior of the electric potential, which is obtained with this method, turns out to be consistent, according to the Poisson equation, with the presence of a charge density which is indeed very low compared with the charge density carried by each individual ionic species. This can be considered as a sound justification for the electroneutrality assumption.
A more rigorous procedure would be to couple the Nernst–Planck equations right from the beginning with the Poisson equation for the electric potential, without invoking electroneutrality. One obtains in this way a closed set of equations which is known as the Poisson–Nernst–Planck system. MacGillvray [8] proved that, for membranes such that the fixed charges are described by a continuum distribution, the solution of the stationary Nernst–Planck equations with electroneutrality represents the zeroth-order term of the expansion of the solution of the full Poisson–Nernst–Planck system, with respect to a parameter which is the square of the ratio of a suitable Debye length in the junction and the junction thickness. Since in practical situations such a parameter is typically very small, this argument represents a mathematically rigorous justification for the use of the electroneutrality condition.
From Planck’s solution, an analytical expression for the potential and the ionic fluxes can be derived. Planck considered a junction with well-defined spatial boundaries, corresponding for instance to the walls of a porous diaphragm between the solutions. The same situation will be considered in the present paper, and is often referred to in modern literature as the “constrained junction”, to distinguish it from the “free junction” which establishes between two solutions when they are simply in contact with one another without any physical separation between them [9]. For ideal junctions the diffusion and mobility coefficients D and μ of each ion are assumed to be constant parameters related to one another by Einstein’s relation D = μkT. For real solutions these conditions are usually approximately satisfied only for low concentrations: in the general case, the dependence of D and μ on the ion concentrations ought to be taken into account.
The Nernst–Planck equation can also be applied to describe the diffusion of ions inside a charged membrane, which can be considered as a porous medium with fixed electric charges. The simplest way to do so is to include in the model a fixed uniform charge density. Membranes have become increasingly important over the years in several technological domains, thanks to their capability to favor the exchange between two solutions of ions with a definite sign, namely the opposite one with respect to the fixed charges [10]. Membranes are also largely studied in connection with the research on nanopores and biological ion channels.
After Planck, several other authors have applied the Nernst–Planck equation to the theoretical study of liquid junctions and charged membranes [11,12,13,14]. In 1954 Schlögl [15] obtained a general analytical solution for a (possibly) charged membrane with arbitrary numbers of ionic species and ionic valences. His formulas are however rather cumbersome and contain parameters which are determined by implicit relations which are impractical to use for numerical computations. For these reasons Schlögl’s work, although occasionally mentioned in advanced textbooks [10], is today essentially neglected in the praxis of scientific research.
Several years later Morf [16] has considered again the problem with ions of only two different valences, providing a new interesting derivation of Planck’s old result, which applies also to the case in which the two valences—a single one for all the cations and another one for all the anions—are arbitrary and not necessarily +1 and −1.
In more recent times, solutions of the Nernst–Planck equations for liquid junctions and membranes have been mainly obtained by means of finite difference numerical integrations, and the development of computers has made possible to treat with these methods a much wider class of situations, including the time-dependent case [17,18,19,20,21]. Several works have also been devoted to the determination of numerical solutions of the full Poisson–Nernst–Planck system. This approach has been used to study the behavior of liquid junctions and membranes in various scientific contexts [9,22,23,24,25,26,27,28,29,30], and in particular in the study of the ions flow across biological cells [31,32,33,34,35,36,37,38,39]. More specifically, the problem of liquid junction potentials has received careful consideration owing to its importance for the correct interpretation of electrophysiological measurements [40].
In the present paper we shall study the Nernst–Planck equations in conditions of local electroneutrality, and we shall present a new analytical method of solution which extends Planck’s results by considering the presence of a fixed charged background and of mobile ions of arbitrary valences. Our main result is that a complete analytical solution can be obtained for an ideal junction across a possibly charged porous diaphragm containing ions with up to three different valences, in the presence of an arbitrary electric current. We obtain in this way, as functions of the total current, the ionic fluxes and the potential difference between the two sides of the junction or membrane, as well as the profiles of the ion concentrations and of the electric potential across the diffusion layer. These results can in particular be applied to the calculation of the potential and ionic fluxes through a diffusion layer between the solutions of two generic binary salts having an ion in common. An interesting phenomenon which can also be described is the uphill transport of a divalent cation (i.e., the transport of the ion against its concentration gradient) driven by the liquid junction or membrane potential at open circuit.
For more than three valence classes the differential equations that we obtain can be integrated with a numerical computer program. A new open source applet to perform these calculations in the case of a liquid junction at zero current has been recently made publicly available on the web [41,42]. This applet also allows considering nonideal junctions for which an analytical dependence of the ion mobilities on the concentrations can be provided.
The paper is organized as follows. In Section 2 we explain the physical assumptions at the basis of the model of liquid junction and charged membrane here considered, and recall the Nernst–Planck equations for the ion concentrations in the stationary state. In Section 3, by a change of variables in the Nernst–Planck equations, we obtain a closed system of differential equations, containing a suitable set of independent parameters which can be determined from the available information on the system, namely the ion concentrations at the two edges of the diffusion layer and the total current density. In Section 4 and Section 5 we show that this system of differential equations can be analytically solved for systems with two and three different ionic species, and obtain explicit formulas ready for use in practical applications. In Section 6 we show how our procedure can be generalized to the case in which more than three ionic species are present, as far as they do not belong to more than three different valence classes. In Section 7 we present and discuss the results which are obtained with our method in particular cases, and show that they allow the study of phenomena which are not described by Henderson’s simplified model. Finally, the conclusions of the paper are summarized in Section 8.
2. Definition of the Problem
We assume that n ion species are present inside the diffusion layer, with concentrations ci, i = 1, …, n, expressed as number of ions per unit volume, and therefore proportional to the molar concentration. We assume that the system has a planar symmetry, so that the concentrations depend only on one spatial coordinate x varying from x = 0 to x = L, where L is the thickness of the diffusion layer. The ion fluxes Φi (number of ions per unit time per unit area) satisfy the Nernst–Planck equations
where Di is the diffusion coefficient of the ion, zi is its relative charge, μi the mobility of the ion in the solution (defined as the ratio between the drift velocity and the total acting force), e the (positive) elementary charge, and V the electric potential. Since charged membranes and—in most cases—also liquid junctions physically consist of porous materials, in the definition of ion fluxes one has to consider an effective area which represents only the porous fraction of the geometrical cross section of the diffusion layer. The numerical value of such a fraction of course depends on the particular material considered, and will not be included in the calculations and in the results which will be presented in the present paper. It can however easily be introduced in the final formulas, whenever this is required for practical applications.
The diffusion coefficient Di and the mobility μi generally depend on the concentrations. However they can be considered approximately constant for very low concentrations, or when the concentrations at the two edges of the diffusion layer are similar. Furthermore, for low concentrations one can apply Einstein’s relation Di = μikT, where k is the Boltzmann constant and T the absolute temperature. Here however we shall make no use of Einstein’s relation and we shall treat Di and μi as two constants such that μi = ηiDi/kT, where ηi a dimensionless coefficient not necessarily equal to 1.
The concentration ci and the flux Φi are connected to each other also by the continuity equation ∂Φi/∂x + ∂ci/∂t = 0. If we assume that the junction has reached a stationary state, all time derivatives vanish. Hence the continuity equation implies that the ionic fluxes are independent both of time and of the position inside the junction. If we introduce the ionic charge densities (divided by e) ρi = zici, the constants χi = ziΦi/Di, and the dimensionless potential φ = eV/kT, Equation (1) can be written as
with ζi = ηjzj (hence ζi = zi when Einstein’s relation is used).
In most practical situations a condition of local electroneutrality is satisfied inside the junction with very good approximation, so that we can assume that the equation
is almost exactly satisfied at all points x. In this formula ρ0 is a constant such that eρ0 represents a charge density due to the presence of fixed charges uniformly distributed throughout a membrane. For the case of liquid junctions one has simply to put ρ0 = 0 here and in all the equations that follow. As a consequence of Equation (3) we can treat only as independent charge densities, while .
Let us denote with a prime all physical quantities evaluated at the edge x = 0 of the diffusion layer, and with a double prime the same quantities evaluated at the edge x = L. So, for instance, , , , , etc. Assuming that the ion concentrations at the two edges of the diffusion layer—i.e., , —are known, our goal is to determine the dependence of the potential difference between the two edges, on the total current density
flowing through the liquid junction. In addition, for any arbitrary point of the J–ΔV curve we aim to fully characterize the stationary state of the junction by determining the fluxes of the individual ionic species and their densities as functions of the position x, together with the behavior of the potential across the diffusion layer.
In the case of the uncharged liquid junction, i.e., for , the concentrations of the ions at the two edges of the junction are the same as those inside the solutions A and B at the two corresponding sides: and . Moreover, each of the two solutions is at the same potential as the neighbouring boundary of the junction, i.e., and . Hence the potential difference between the two solutions is the same as the potential difference between the two boundaries: .
In the case of the charged membrane instead, the concentrations at the edges of the membrane do not coincide with the concentrations in the two solutions, since for the neutrality conditions respectively in the membrane and in the solutions we have
where , . Correspondingly, in order to obtain the full potential difference between the solutions at the two sides of the membrane, one has to respectively add and subtract to the voltage the Donnan potentials and which arise at the two boundaries of the membrane:
The Donnan potentials are related to the ion concentrations at the two boundaries by the Donnan equilibrium relations [43]
where are the partition coefficients. From Equation (5) one then obtains
When the ion concentrations in the two solutions are known, by solving these equations one can determine and . Then the ion concentrations at the two boundaries can be computed using Equations (7) and (8). A rigorous justification of the use of the Donnan equilibrium relations was given by MacGillvray [8], who proved that they lead to a good approximation of the solution of the full Poisson–Nernst–Planck system of equations for the membrane, under the same conditions which justify the use of the electroneutrality condition.
3. Mathematical Procedure
We assume the fixed charges to be uniformly distributes throughout the junction, so that . By summing the Equation (2) over i we thus obtain
where . Multiplying Equation (2) by dx and using Equation (11), we then obtain
where .
It is useful here to introduce the new variables
which satisfy
Note that for . Then Equation (12) can be rewritten
which for n > 2 implies
Putting
and using the relation
We obtain
It is possible to write down two linear relations among the parameters . First of all Equation (4) implies
Furthermore, by dividing each of the Equation (2) by and then summing over i, we obtain using Equation (3)
with
Since the right side of Equation (19) is a constant, we deduce that w is a linear function of x. Hence we can write
and
with , and being the values of w at the boundaries respectively x = 0 and x = L of the diffusion layer. From Equations (18) and (22) it follows that
where
Let us define
As a consequence of Equation (23) and of Equation (25) we have
Therefore, calling , and recalling that , we have
where
It follows that Equation (17) can be rewritten as
These represent a system of n − 2 differential equations in the unknown functions . Note that, according to Equation (16), one has to put in Equation (29), .
The system Equation (29) contains the n − 1 independent parameters and Y, whose physical meaning is expressed by Equations (24) and (25), but which are a priori unknown in practical situations. Let us suppose that , and therefore also ξ, varies monotonically from one side of the junction to the other. If the ion concentrations at the two edges are known, and a value of Y has been assigned, then can be determined by imposing that the solution of Equation (29), with initial data
at , satisfies the n − 2 boundary conditions
at , where , , and
On the right-hand of this formula we put and . Making use of Equation (26) one obtains
with . Note that one has if , and if .
After the system Equation (29) has been solved and the parameters have been determined, by inverting Equations (13) and (16) one can express the ionic charge densities inside the junction as
where is an arbitrary value between and . The corresponding electric potential φ can instead be calculated according to the equation
which follows from Equation (15) for . For the above formula provides the potential difference between the edges of the diffusion layer. For , if can be expressed as functions of one of them, say , which varies monotonically from one side to the other, then the potential φ corresponding to an arbitrary value between and can be calculated according to the equation
which follows from Equation (29) for i = 1.
After having obtained , φ, and therefore also w, it is possible to express the position x by making use of Equation (21):
Equations (34), (35) and (37) provide , φ and x as functions of ξ. Then, by eliminating ξ, it is also possible to express and φ as functions of x. Finally, the ion fluxes can be obtained as
where again on the right-hand side one can make use of Equation (33).
Assuming that the ion concentrations at the edges of a membrane (or liquid junction) are known, the procedure outlined above allows the complete description of the stationary state for an arbitrary value of the parameter Y. According to Equations (20) and (24), in the case of the uncharged liquid junction, i.e., for ρ0 = 0, Y depends only on JL, i.e., on the current density multiplied by the thickness of the junction. Therefore the described procedure allows the calculation of the junction potential ΔV as a function of J. In the case of a charged membrane, instead, once Δφ has been calculated for a given Y, the corresponding current density can be obtained as
Hence the J–ΔV curve of the membrane can be reconstructed using Y as a parameter. Note that for Y = 0 one has J = 0, so with the described procedure one directly obtains the open circuit potential . The membrane potential corresponding to a given value J ≠ 0 can instead be approximated with increasing precision by repeating the above procedure with different values of Y. We shall see later that in some situations, in order to simplify the calculations, it may be convenient to choose in place of Y another independent parameter, such as .
The effective electrical resistivity R of the liquid junction can be defined as
Such a resistivity, for fixed ion concentrations at the two edges, in general depends on the product JL. For , from the definitions Equation (20) of w and Equation (24) of Y one can easily deduce the following expression for the resistivity:
Then for the conductivity σ = 1/R we have
From our results it follows that ΔV can be considered as a function of 2n variables:
and being fixed by the condition of electrical neutrality. In particular, the potential at open circuit is independent of the thickness L. The right-hand side of Equation (42) is a homogeneous function of degree 0, which means that the potential is unaffected by a common rescaling , …, , , , where λ is an arbitrary positive constant.
4. The Solution for Two Ionic Species of Arbitrary Valence
For n = 2 the integrand function in Equation (35) reduces to a constant and, for a given value of the parameter Y, we get the potential
at an arbitrary point of the junction corresponding to a value of between and . Equation (28) here becomes
while from Equations (32) and (33) we have
For Equation (43) provides the potential difference Δφ between the edges of the junction. We obtain
in correspondence with a current density given by Equation (39) and ionic fluxes
For , one can see from Equation (44) that Y can take all real values except those between and . When Y approaches either of these two values both J and Δφ diverge. For instance, if and , then, using also Equation (41), we have
One can also easily prove that, at any inner point of the junction, hence for 0 < x < L, one has
Thus ion concentrations tend to constant values when the current tends to infinity. In particular, the coions (the ions with charge of the same sign as the fixed charges of the membrane, i.e., the negative ones in the present example) tend to assume inside the membrane the same concentration they have at the boundary from which they enter the junction in their drift motion associated with the electric current. This effect, which had already been noticed by Schlögl [15], of course determines also the concentration of the ions of opposite sign (the counterions), due to the condition of charge neutrality. On account of Equations (48) and (49), the limit values of the conductivity given by Equations (46) and (47) assume an obvious physical meaning. The same is true for the limit values of the ionic fluxes which follow from Equation (45):
where −ΔV/L represents the electric field.
For the model describes a liquid junction between two solutions of the same salt, which dissociates into cations of valence , and anions of valence , with . If and are the concentrations of the salt in the two solutions, we have , , , . Formulas simplify considerably and it becomes possible to explicitly express ΔV as a function of J. Since in the present case , we get
from which we derive the junction potential at open circuit
and the effective junction resistivity
Note that in this case R is independent of JL. Moreover, since w is a linear function of either or , the concentrations of the two ions vary linearly with the position x along the junction.
5. The Solution for Three Ionic Species of Arbitrary Valence
5.1. The General Case
When in the diffusion layer there are three ionic species, from Equations (32) and (33) with n = 3 we get
where
If and φ refer to a point inside the junction such that , where , from Equations (29) and (36) we obtain
with
In the above formulas we put
with
The value of the fluxes and , and so also of the parameter , is a priori unknown. Let us put in Equations (57) and (58):
If we assume that the ion concentrations at the two edges of the diffusion layer are given, then all the quantities appearing in Equations (66) and (67) can be expressed as functions of the two only unknown parameters and . For a chosen value of , the former equation can thus be used to determine , and the latter then allows the calculation of the junction potential . Finally, the current density can be obtained as , where the ion fluxes can be expressed using Equation (38) as
In order to solve Equation (66) numerically with respect to , one has first of all to observe that the first member of this equation is real only for , which means that must not lie betweeen and . In the following subsection we shall study how to determine the values of for which the current density J goes to infinity. We shall find that, when there are two counterions, these are finite values which do not coincide with and , so the set of physically acceptable values of must be further restricted.
The existence of the integral at the second member of Equation (66) requires that the integrand function must have no poles between and . This implies that the solution can only be sought within a certain set of intervals of the real axis. Endpoints of these intervals are values of for which any of the two following events occurs:
- Either or coincides with one of the two roots and of the trinomial , with , while the other root does not lie between and .
- and lies between and .
These conditions correspond to simple second-degree algebraic equations, so the endpoints of the intervals can be analytically determined. Using this initial input, it is then easy to set up a numerical algorithm for the solution of Equation (66).
5.2. The Limit of Large Current Densities for the Charged Membrane
For the parameter , and the corresponding solution of Equation (66), approach finite values as the junction potential and the current density J go to infinity. Calling such values and respectively, we can write
According to Equation (41), and represent the two limit values for the effective conductivity of the membrane, with
In general, all points of the J– curve of the membrane are obtained by varying in the set of all real values except those between and .
As for the case with two ions, also in the case with three ion species, for , the ion concentrations inside the junction tend to constant values when the current tends to infinity:
with and
Taking into account Equation (32), these relations are equivalent to for , and this can be directly proved by studying analytically the asymptotic behavior of Equations (57) and (58). The result however acquires an immediate physical meaning if one observes that, as a consequence of Equations (68) and (70), one can then express the limit values of the ionic fluxes as
with . Similarly, for the electrical conductivity of the junction one has
These results are of course the direct analogue of those expressed by Equations (50) and (51) and by Equations (48) and (49) for the case with two ionic species.
In order to study in more detail the behavior of the membrane for high current densities, let us suppose that , , , so that two cations and one anion are present in the membrane (the conclusions we are going to draw can be extended with obvious modifications also to the opposite case). This implies that, for , we have in the junction two coions and only one counterion. In such a case, using Equations (66) and (67) it is possible to show that for , , , where and , with , are the two roots of the trinomial . Hence, by solving with respect to and the system formed by the two equations , , one finds
Similarly, for , , , and the solution of the system , is given by
Using Equations (75)–(77) one then obtains that , for . This means again that the ion concentrations inside the membrane tend, for high current densities, to the concentrations assigned at the boundary from which the coions enter the membrane. Note that in this case, according to Equations (80) and (81), can take all values for which . Moreover, the corresponding limit values of the parameter Y, namely
are similar to those for and respectively, which were introduced in the preceding section for the case with two ions.
Results are different when there are in the membrane one coion and two counterions, as in the case , , , . In such a case one cannot give for and expressions as simple as Equations (80) and (81), and the limit concentrations do not coincide with the ionic concentrations at any of the two boundaries. One can prove that when . Hence it is possible to determine the pair as the solution of the system formed by the two equations , . Similarly, when , and is the solution of the system , .
5.3. The Limit of Large Current Densities for the Uncharged Junction
For , the parameter Y is independent of V and directly proportional to J. Let us suppose again that , , , so that there are two cations and one anion (the conclusions we draw are then valid of course also in the opposite case). By analyzing the behavior of Equations (66) and (67), one finds that for , i.e., when either , , or , . Furthermore, by using Equation (57) one obtains that in this limit everywhere in the junction except a narrow region near the edge . Then Equation (21) implies that
so that the limiting ion distributions are linear in the position x. We have and , where A and B indicate the solutions at the two sides of the junction. It is then easy to realise that the distributions Equation (82) are the same as if on the side there were, in place of B, a solution C with the same ratios between the different ionic species as the solution A, but with concentrations rescaled so that , i.e., . This is reflected also by the limiting value of the resistivity, which is just the value one would obtain for a liquid junction between solutions A and C:
The same is true for the ionic fluxes:
The last member of this equation expresses the fact that the ions of the species k carry in this limit a fraction of the total current density J equal to their transference number in the solution A, i.e., , with
Results are similar if , i.e., when either , , or , . In such a case , and everywhere in the junction except a narrow region near the edge . Hence the ratios between the ionic concentrations become almost everywhere the same as in the solution B, and the junction behaves as if at the side there were in place of A a solution D with . Equations (82)–(84) have to be modified accordingly:
We can thus conclude that in the limit of large current densities, the ionic concentrations inside an uncharged liquid junction depend linearly on the spatial coordinate, and are proportional to the concentrations of the solution at the side where the two ions with the same sign exit the junction according to their drift motion. The ion distributions depart from this behavior only in a narrow region near the opposite side of the junction.
5.4. The Uncharged Junction between Solutions of Binary Salts
Let us finally consider more closely the case of an uncharged liquid junction between two binary salts with one ion species in common. Let us suppose for instance that on the side there is a solution A of concentration of a salt which dissociates into cations of species 1 and valence , and anions of species 3 and valence , while on the side there is a solution B of concentration of another salt which dissociates into cations of species 2 and valence , and anions of species 3 (the same as in solution A) and valence , with , , . We have in this situation , , , , , , whence , . Then, by putting in Equations (66) and (67) and taking the limit , , with , we obtain
For , depends on the current density J but not on the potential . When J is known, the two above formulas express both and the ratio as functions of the single parameter . One can easily determine the interval of the real axis made by all values of for which the integrand functions in Equations (66) and (67) have no poles in . Each point of this interval corresponds to a particular value of between 0 and . Thus the problem can be solved if the concentrations of the two solutions at the two sides of the liquid junction are known.
6. Systems with More Ionic Species Having the Same Valence
Let us suppose that in the diffusion layer there are ions with n different valences , and that there are one or more ionic species for each of these valences. More precisely, we have ionic species with valence , with for , and so altogether different ionic species. In this section, we shall label with a double index quantities which refer to an individual ionic species: for instance , with and , will denote the concentration of the species k with valence . Quantities with a single index will instead refer to a entire valence class, i.e., to all ions having a certain valence.
Let us suppose that the coefficient is the same for all ions having the same valence, so that we shall write for all . This also implies . We want to show that it is possible to reduce the solution of the system of m Nernst–Planck equations
with , to the solution of a system of equations of the form Equation (29) for the same value of n, i.e., for n equal to the number of valences and not to the actual number of ionic species.
Let us introduce, for , the quantities
We can then also define , which represents a suitably averaged diffusion coefficient of the ions with valence . From Equations (2)–(4) we then obtain
It is then clear that the above equations are formally identical to those already studied in Section 2 and Section 3. It follows that one can write a system of differential equations of the form Equation (29) which, as we have seen, admits an analytical solution for either or . In this case however, for all those i such that , the value of the coefficient is unknown, since by definition it depends on all the with . We recall that coefficients appear in the term β of Equation (29) through Equations (27) and (28). However, it is not necessary to use all the fluxes as free parameters in the equations, as the following analysis will show.
By direct integration of the differential Equation (91) we get
and similarly from Equation (95)
By eliminating the integral from these two equations, it follows that we can express the charge densities of the individual ionic species along the diffusion layer in terms of φ and of the as
For the above equation provides
Hence, since , we get
This formula shows that, if the all the concentrations and at the two boundaries are known, it is possible to express all the as functions of the one unknown parameter . Therefore, with respect to the situation considered in Section 3, in the present case we have in Equation (29) just one more free parameter, namely , in addition to and Y. Once has been arbitrarily fixed, the remaining parameters are determined by equations, represented by the boundary conditions Equations (30) and (31) and by the equation for given by Equation (35) with .
After the Equation (29) have been solved and all the parameters have been determined, as in Section 3 one can obtain the current density J and the fluxes with the analogue of Equations (38) and (39). One can also calculate the densities and the electric potential as functions of the spatial coordinate x along the diffusion layer. Then the fluxes and the densities of the individual ionic species can be calculated using Equations (98) and (99).
7. Applications and Results
7.1. Henderson’s Approximation
An approximated formula for the liquid junction potential at open circuit was obtained by Henderson [2,3]. His calculation is based on the assumption that the solution at any point inside the diffusion layer is simply given by a mixture of the solutions at the two sides, according to a “mixing factor” κ which varies from 0 to 1 as one moves across the layer from one side to the other. In this way, in the ideal case (i.e., when the diffusion coefficients and the mobilities are treated as constants) one obtains a potential at open circuit
where
, , etc. These equations do not contain , and they apply to both charged and uncharged liquid junctions.
In the ideal case with two ions, Equation (101) coincides with Equation (44) for Y = 0, so the value of the potential at open circuit given by Henderson’s model is the same as that given by Nernst–Planck’s model. As we are going to see, the predictions of the two models are however no more identical already in the case with three ions. In the following subsections we shall study some examples of concrete problems to which our method of solution can be applied. We shall see that it leads to many analytical results which cannot be obtained using Henderson’s approximation, and which could only be reproduced by making use of numerical routines for the integration of Nernst–Planck differential equations.
7.2. A Neutral Junction between KCl and MgCl2 Solutions
Let us consider an uncharged liquid junction between a solution 0.1 M of KCl on the first side, and a solution 0.1 M of MgCl2 on the second one, at temperature T = 298.15 K. We can apply our equations with n = 3, identifying ions 1, 2 and 3 with K+, Mg2+ and Cl− respectively. Assuming that the solutions behave ideally, with diffusion coefficients D1 = 1.957 × 10−9 m2·s−1, D2 = 0.706 × 10−9 m2·s−1, D3 = 2.032 × 10−9 m2·s−1 [44], and with , we obtain using the formulas of Section 5.4 a liquid junction potential at open circuit mV, to be compared with the value mV provided by Equation (101).
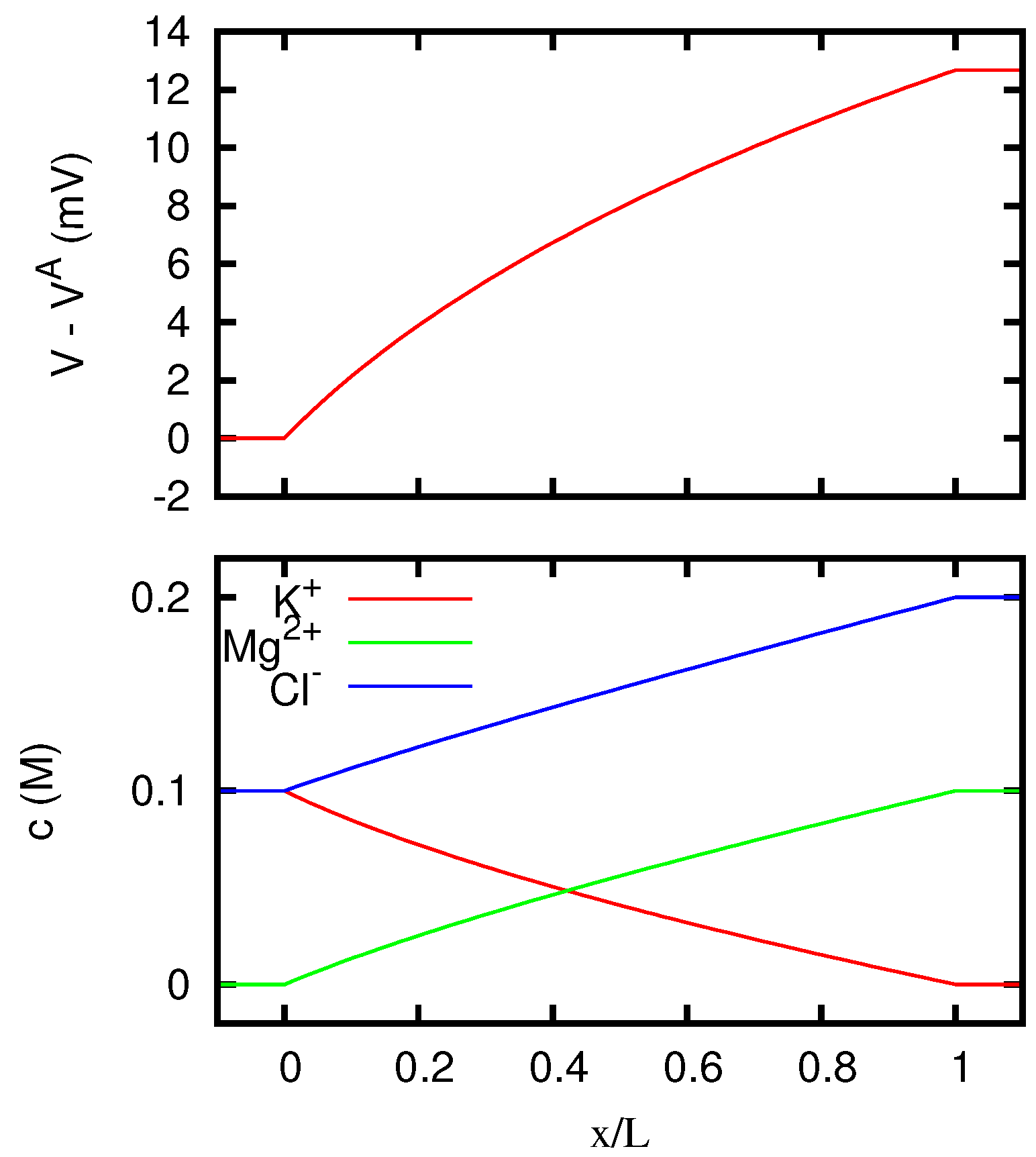
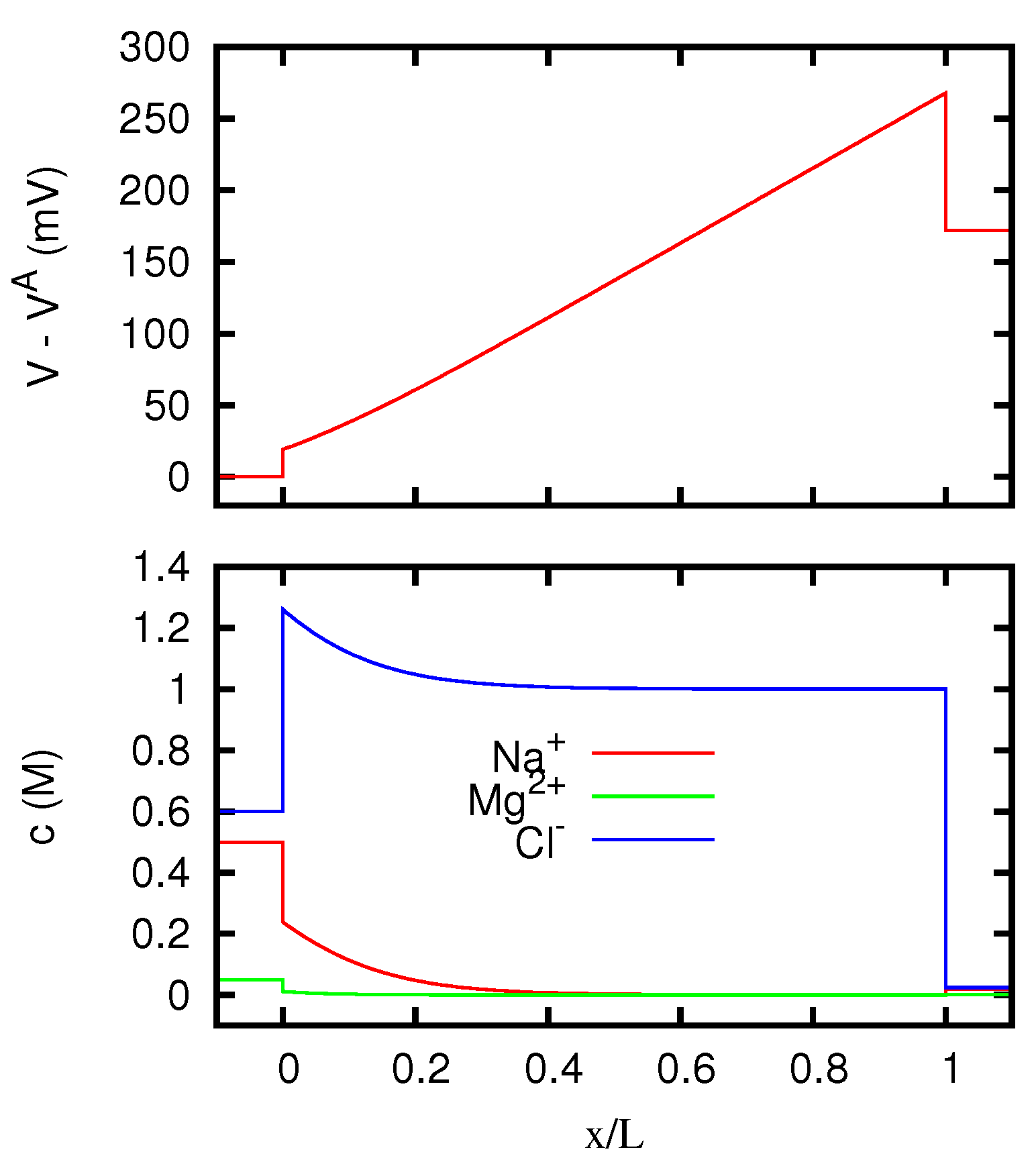
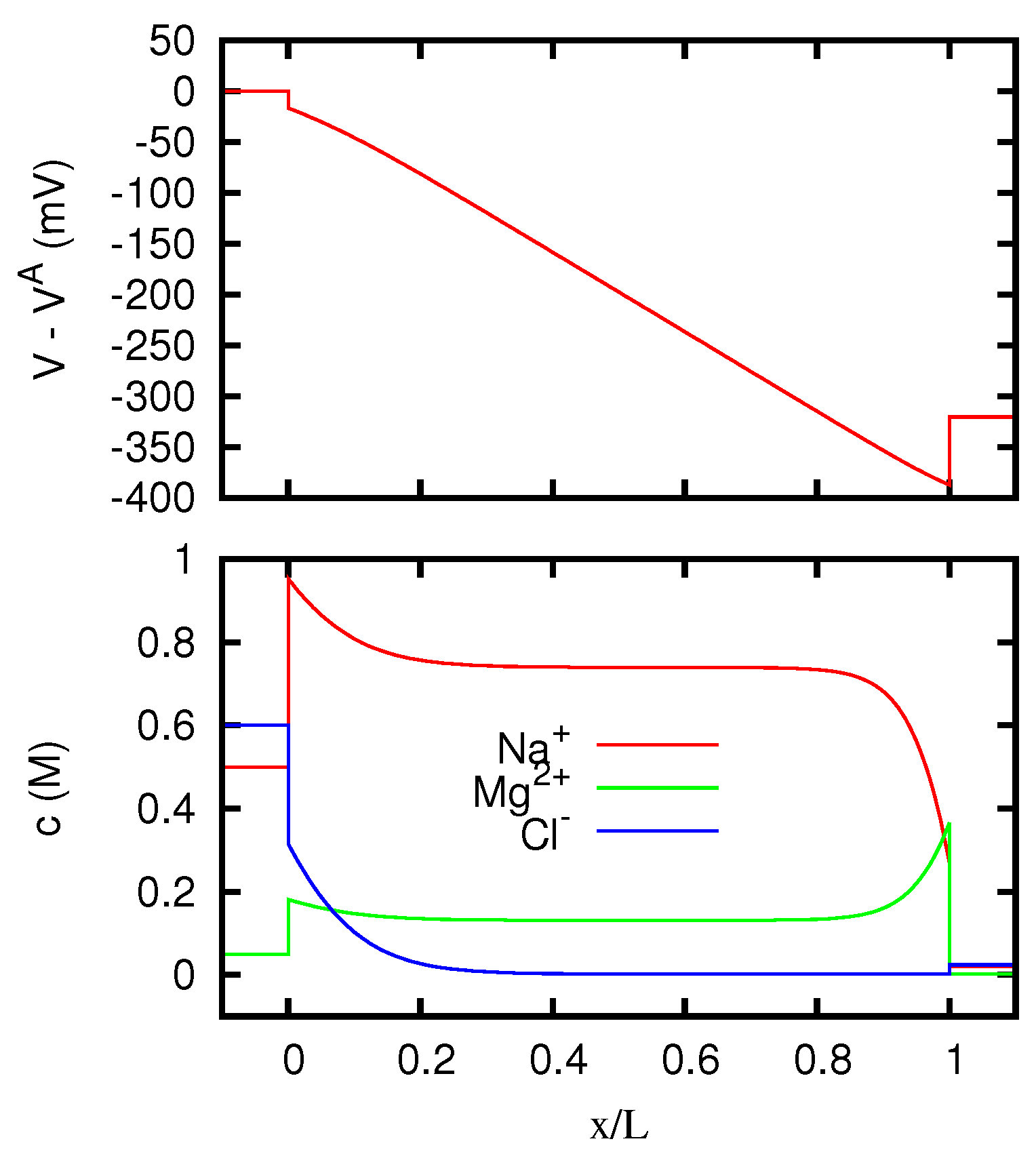
In Figure 1 we display the behavior of the electric potential and of the ionic concentrations inside the junction according to the Nernst–Planck equation. We see that for vanishing current the concentrations inside the junction are with good approximation linearly dependent on the position, and this explains why the discrepancy between Nernst–Planck’s and Henderson’s predictions for the junction potential is quite small.
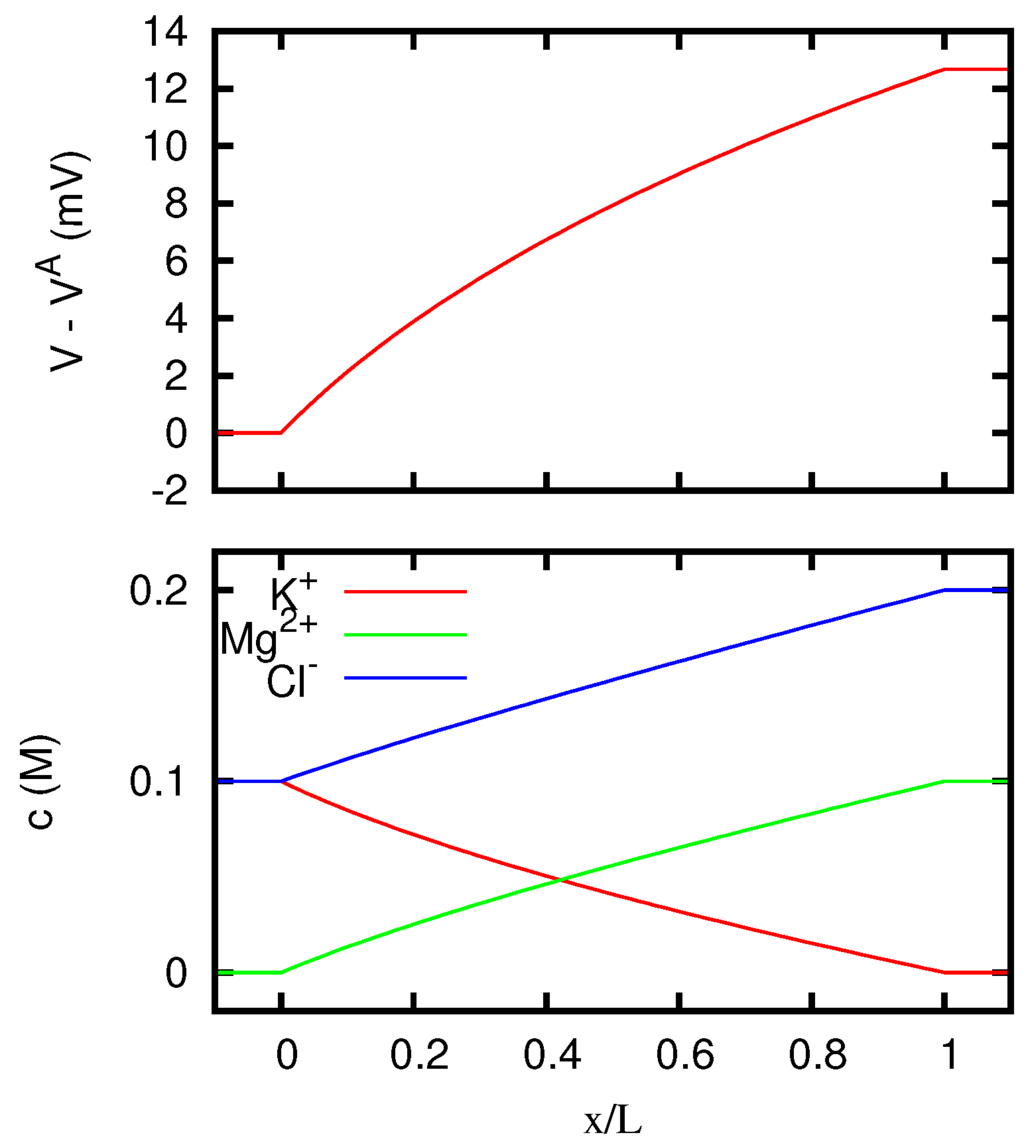
Figure 1.
Electric potential and ionic concentrations c as functions of the position x inside a neutral liquid junction, for vanishing electric current. The regions and correspond to the solutions at the two sides of the junction, which are KCl 0.1 M at the first one, and MgCl2 0.1 M at the second one.
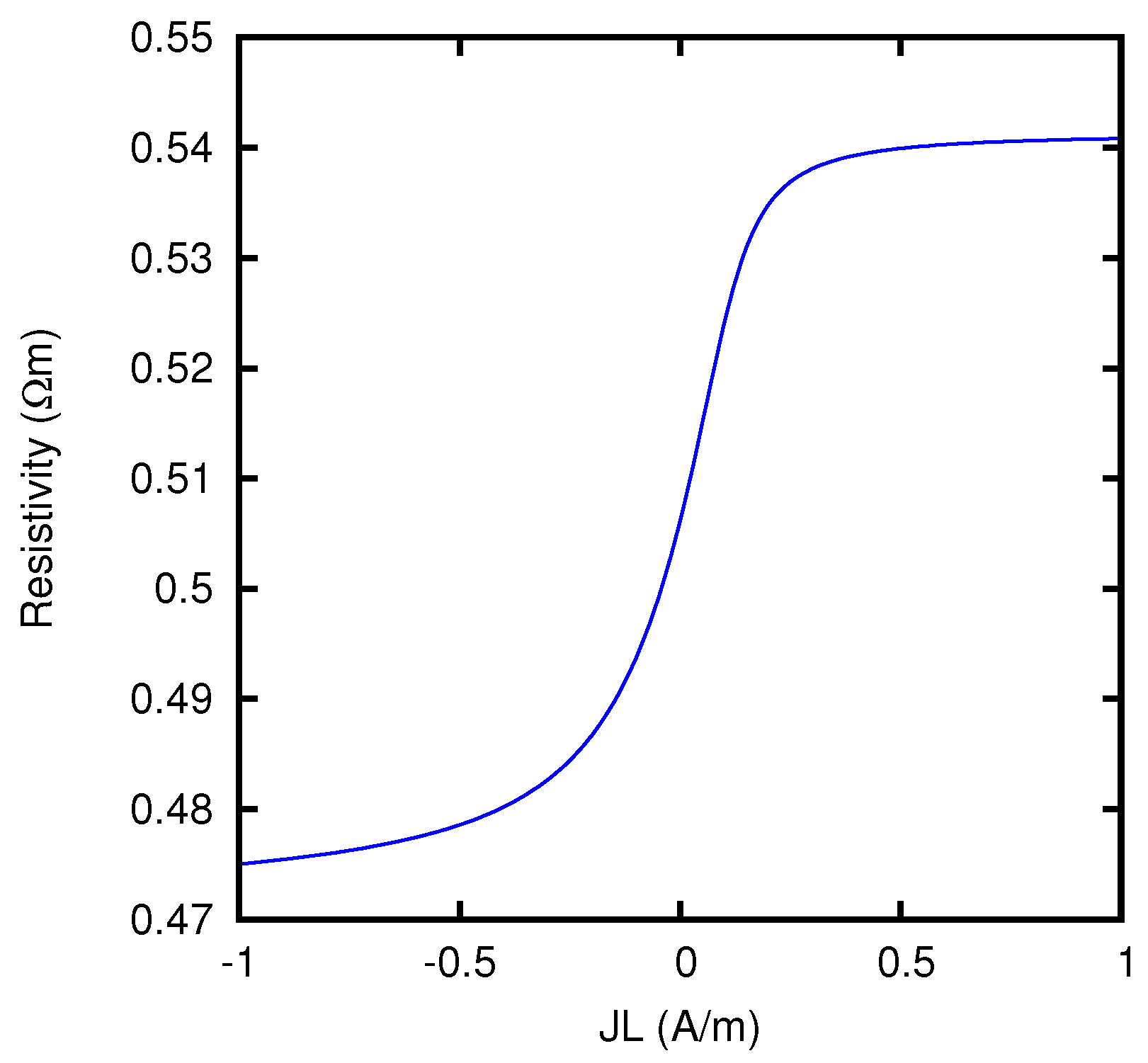
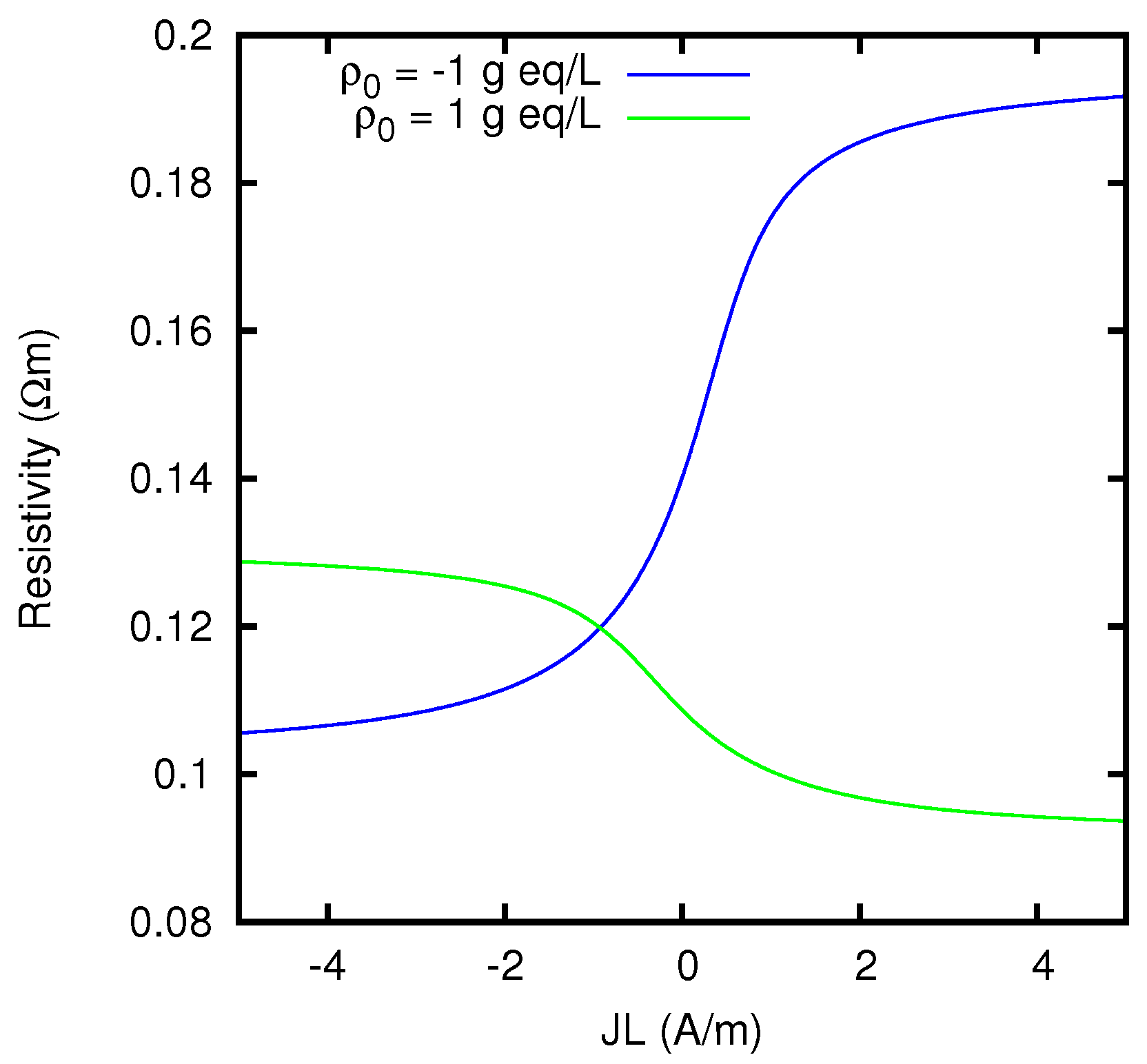
By using the formulas of Section 5.4, we can also calculate the junction potential as a function of the current flowing through the junction. If we then evaluate the effective resistivity of the junction according to Equation (40), we obtain the results which are displayed in Figure 2. We see that, when a large current flows from the KCl solution to the MgCl2 solution, the Nernst–Planck resistivity is more than 10% larger than when a large current flows in the opposite direction.
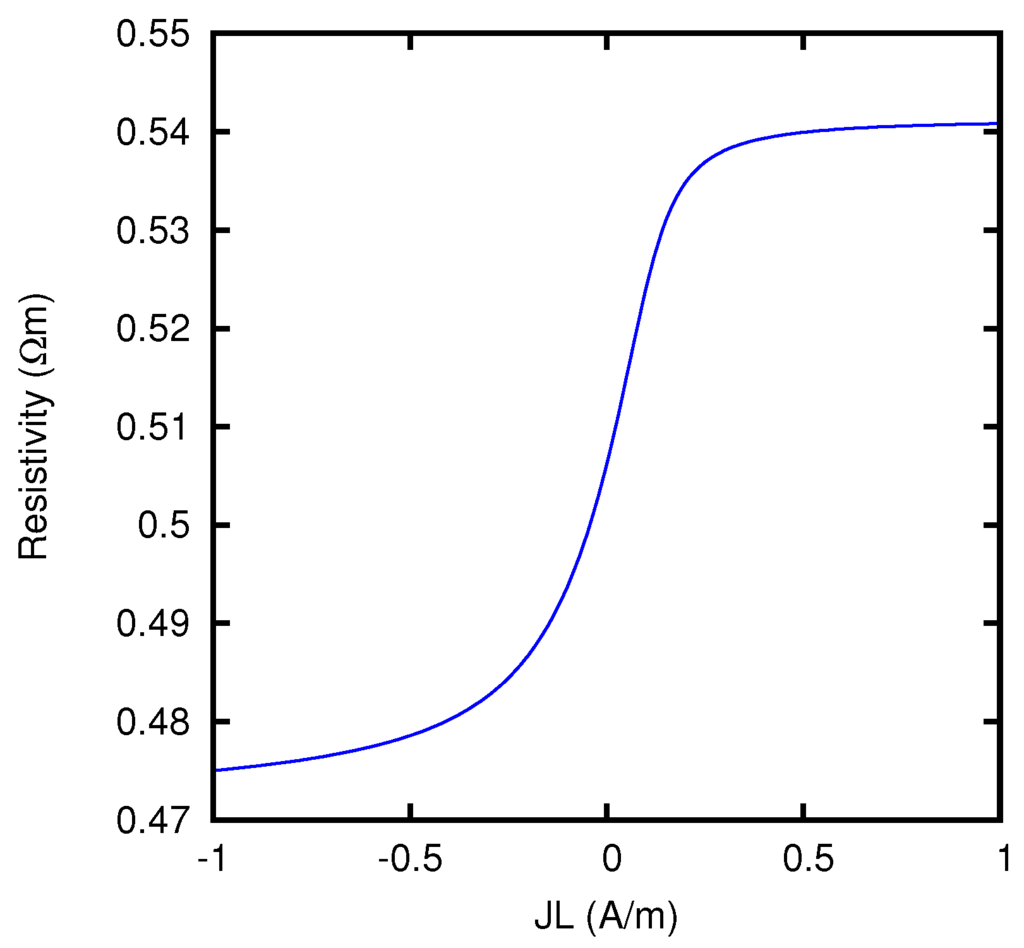
Figure 2.
Effective resistivity of a liquid junction between KCl 0.1 M and MgCl2 0.1 M, as a function of the current density multiplied by the thickness of the junction, according to the Nernst–Planck model.
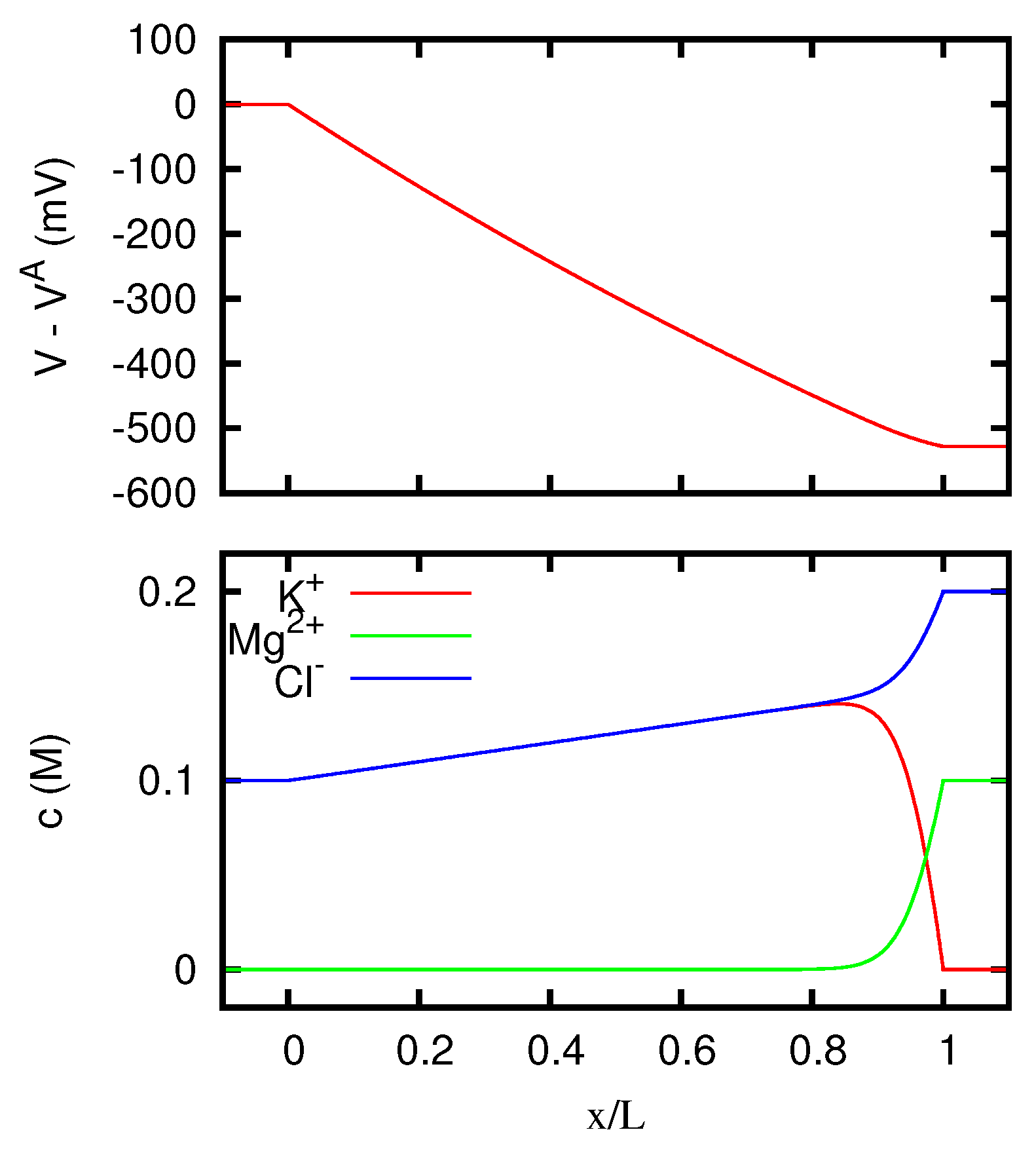
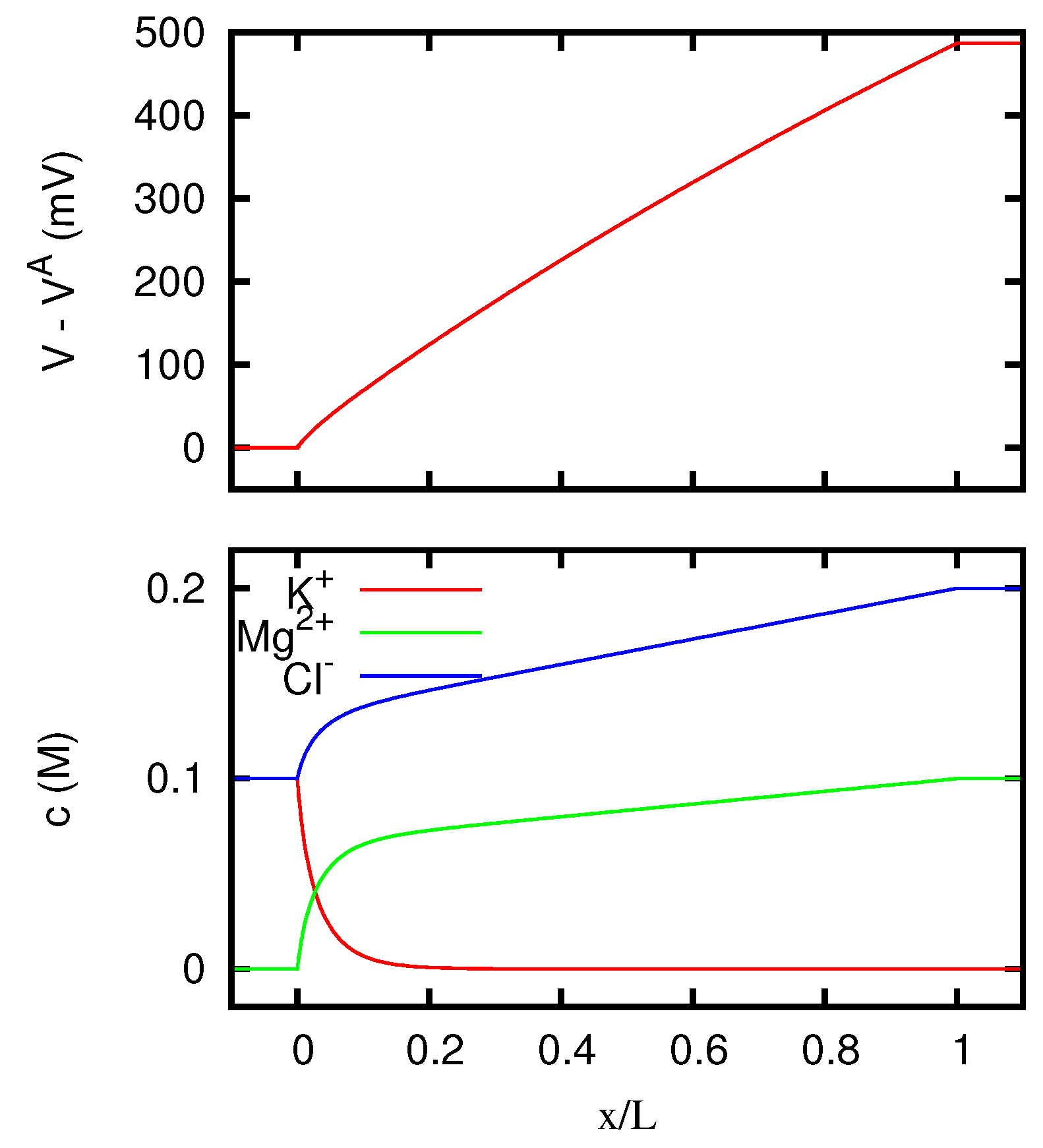
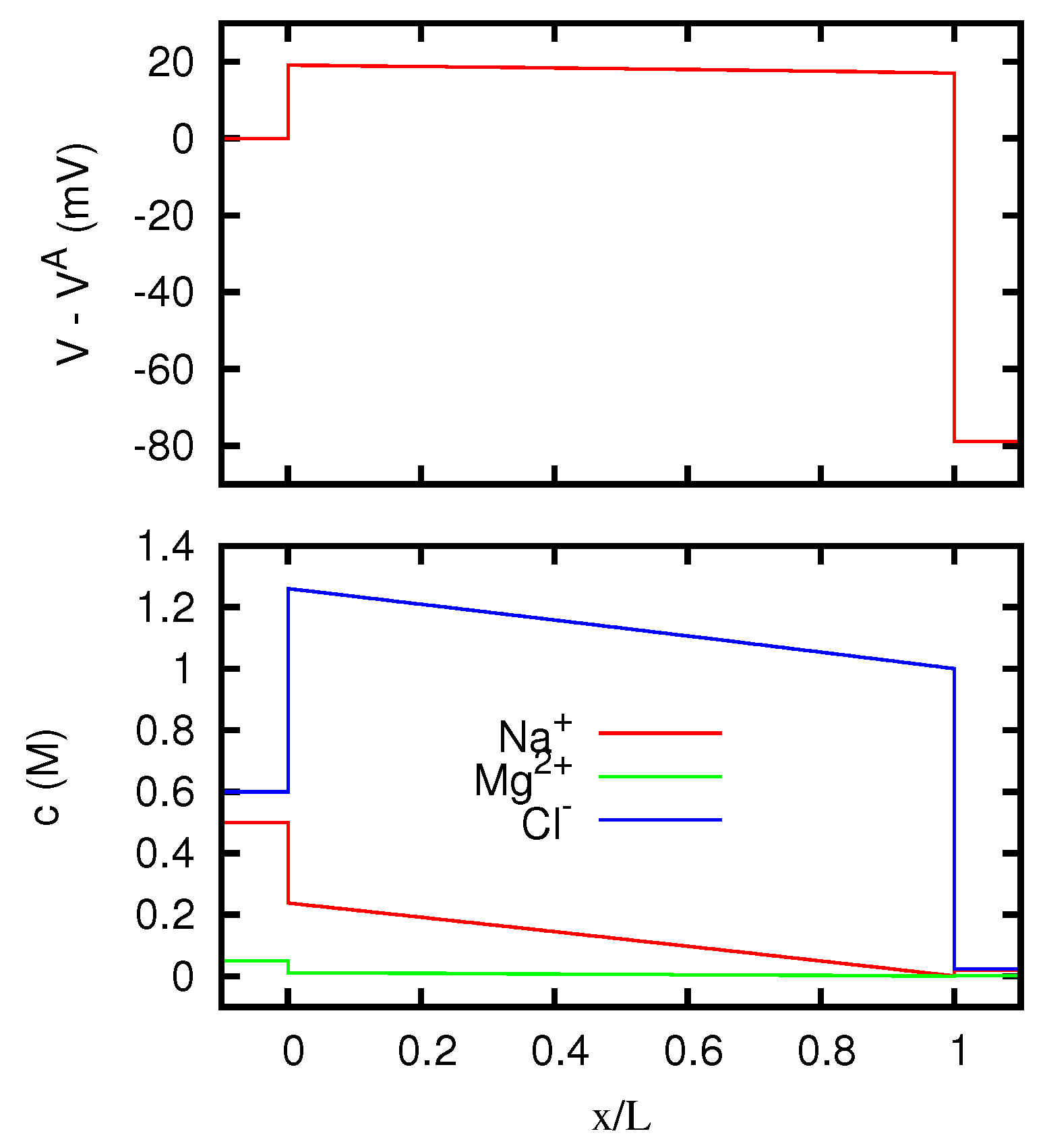
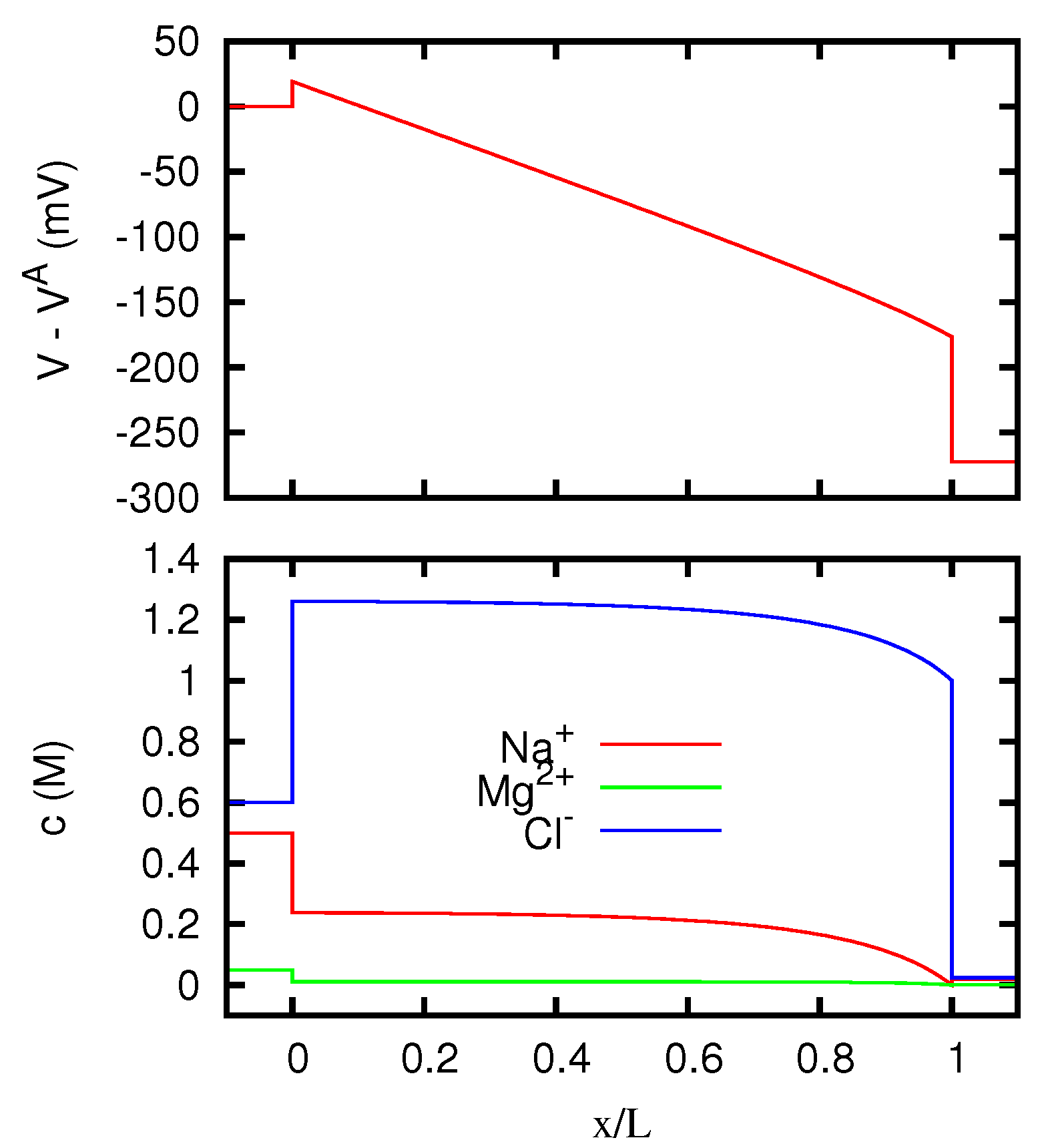
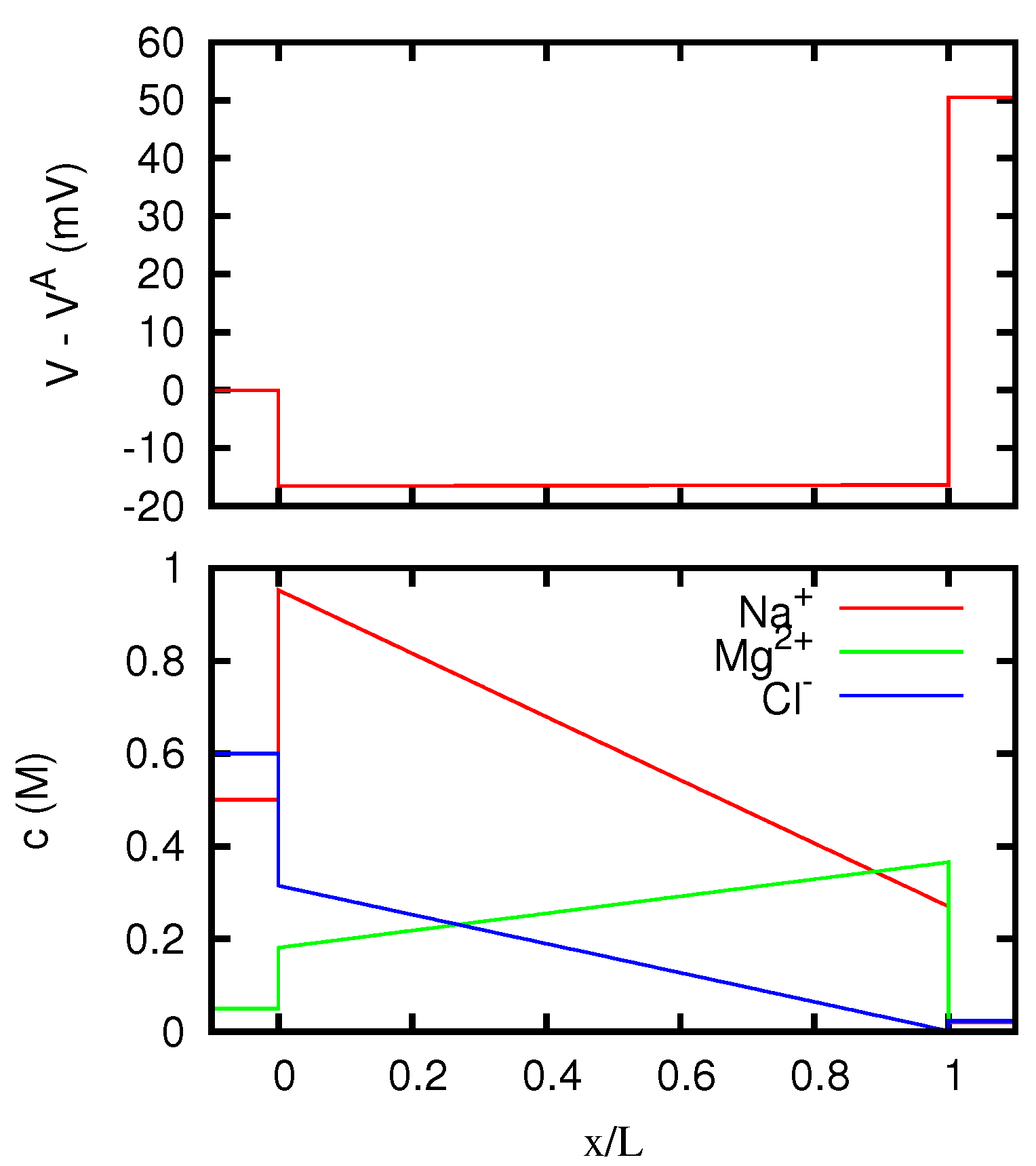
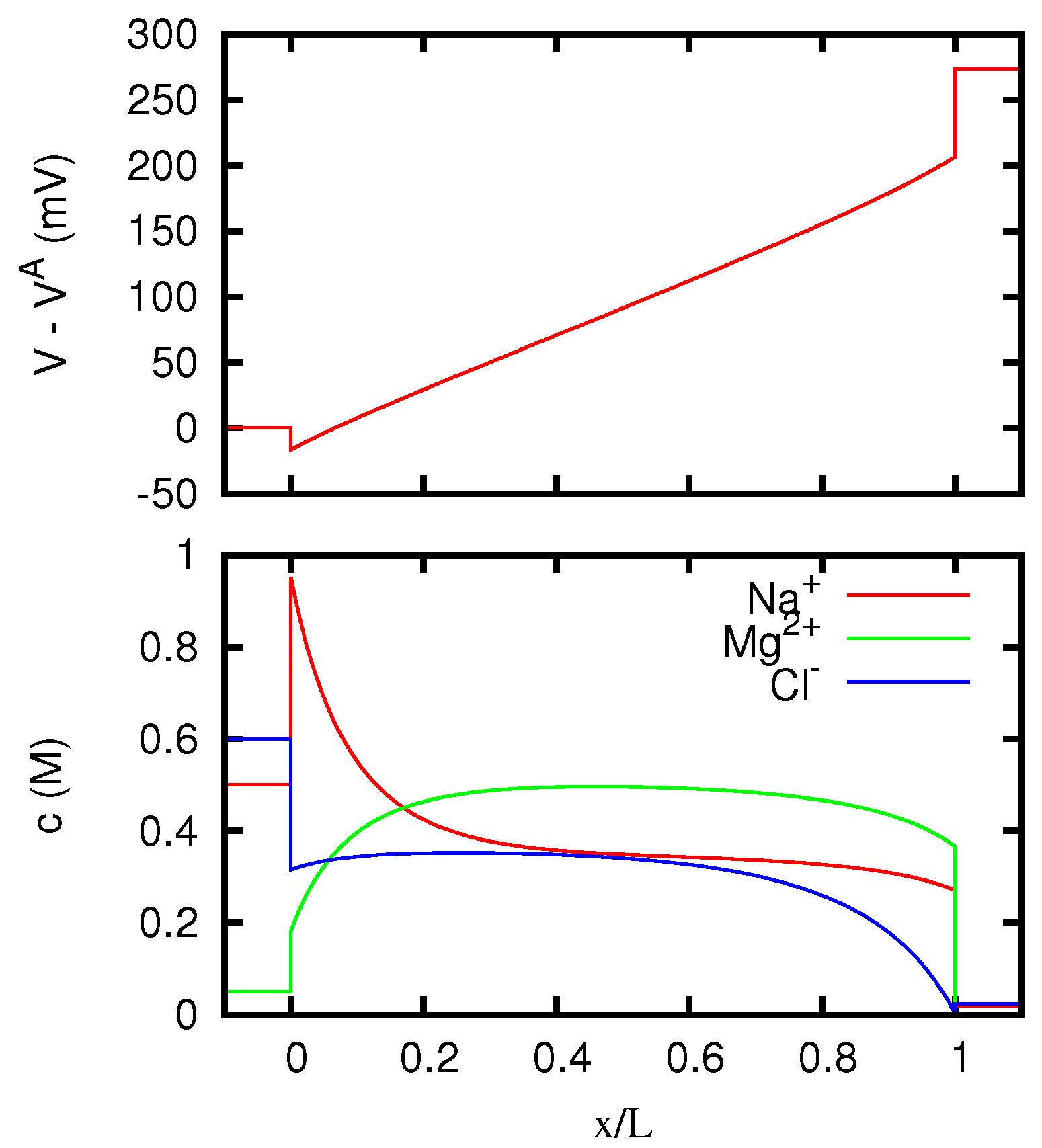
The behavior of the ionic concentrations inside the junction is displayed in Figure 3 for JL = 1 A/m, and in Figure 4 for JL = −1 A/m. We see that the results are in agreement with the conclusions of Section 5.3. Note in fact that a solution 0.1 M of MgCl2 has the same w as a solution 0.15 M of KCl. For large positive current densities, the concentration profiles inside the junction are thus similar to the linear profiles of a junction between two KCl solutions 0.1 M and 0.15 M respectively. The effective resistivity of such a junction, according to Equation (53), is 0.5413 Ωm, and this is in fact the value that the curve of Figure 2 approaches for JL → +∞. In this limit, Mg2+ ions are present inside the junction only in a narrow region near to the right side. Similarly, since a solution 0.1 M of KCl has the same w as a solution 0.06667 M of MgCl2, for large negative current densities the concentration profiles inside the junction tend to the linear profiles of a junction between two MgCl2 solutions 0.06667 M and 0.1 M respectively. Such a junction has an effective resistivity of 0.4703 Ωm, which indeed corresponds to the limit of the curve of Figure 2 for JL → −∞. In this limit, K+ ions are present inside the junction only in a narrow region near to the left side.

Figure 3.
Electric potential and ionic concentrations c as functions of the position inside a neutral junction for A/m, where J is the current density. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 1.
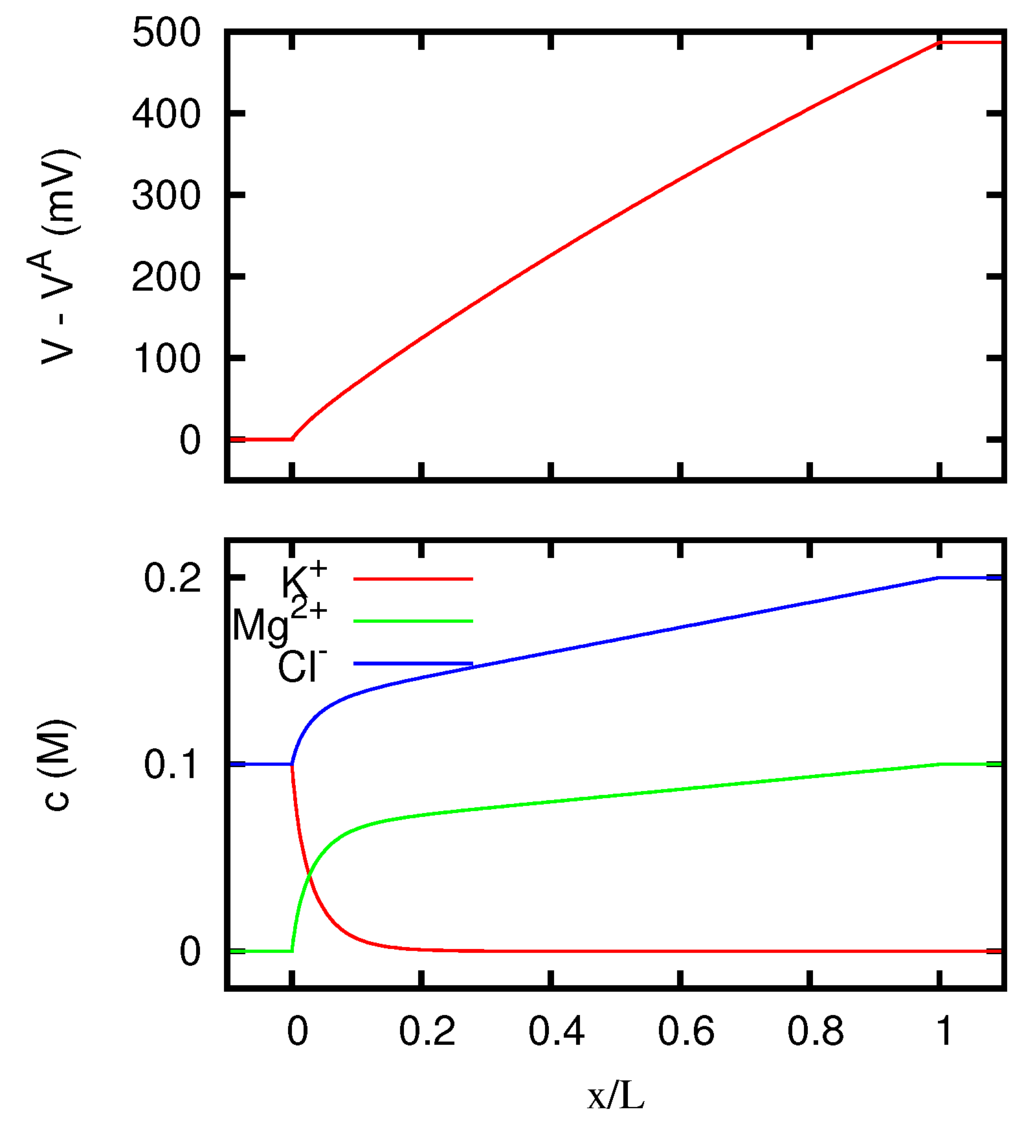
Figure 4.
Electric potential and ionic concentrations c as functions of the position inside a neutral junction for A/m, where J is the current density. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 1.
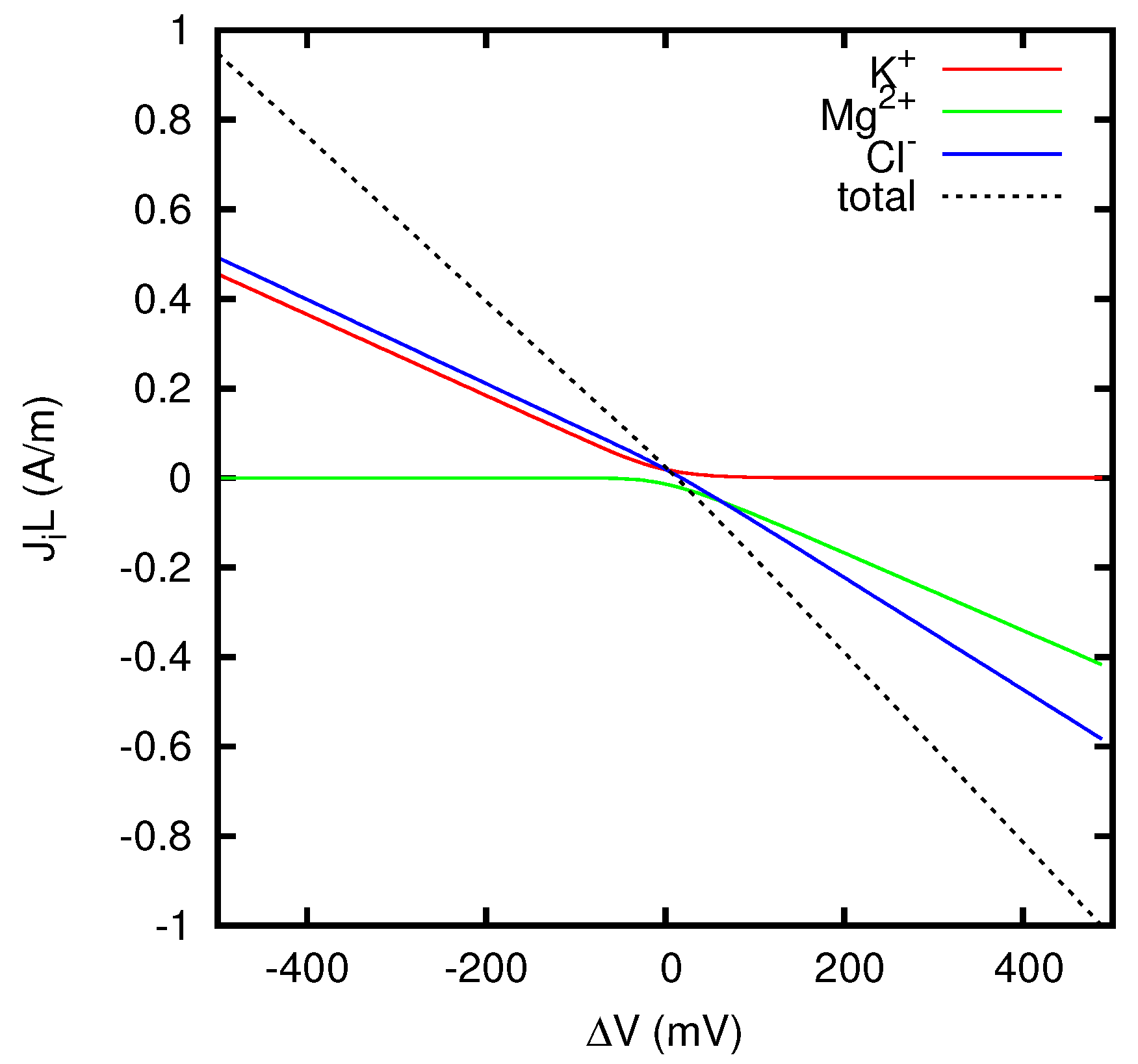
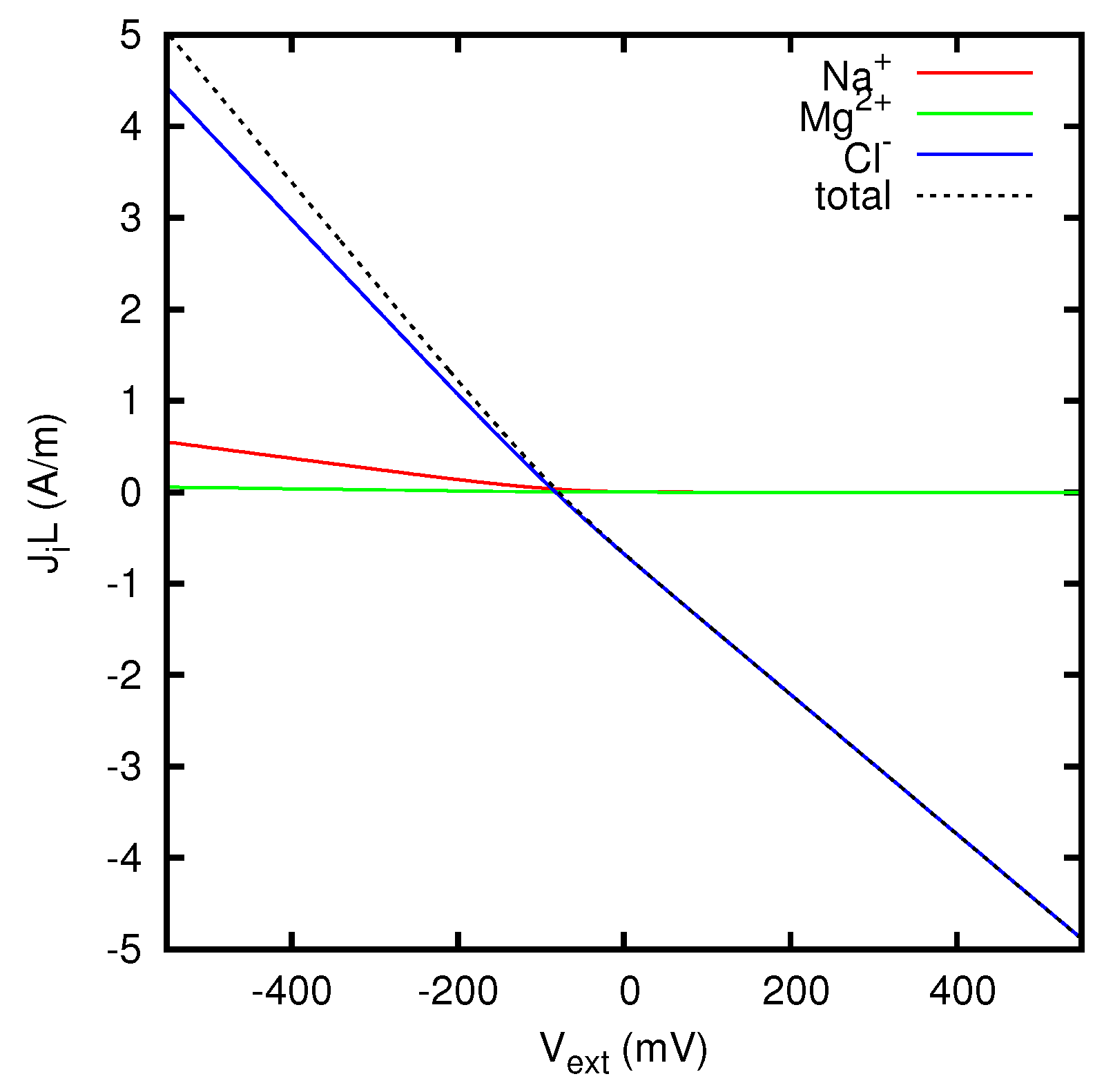
In Figure 5 we report the contributions to the quantity JL which come from the individual ion species. The contribution of the ion i is defined as , where can be calculated using Equations (68)–(70). For JL = 1 A/m, the ratios between the partial currents of the ions and the total current are reported in the first column of Table 1. These values are very close to the corresponding transference numbers in a KCl solution, as shown in the second column of Table 1. Similarly, for JL = −1 A/m, the ratios are very close to the corresponding transference numbers in a MgCl2 solution (see third and fourth columns of Table 1). These results are clearly in agreement with Equations (84) and (88).
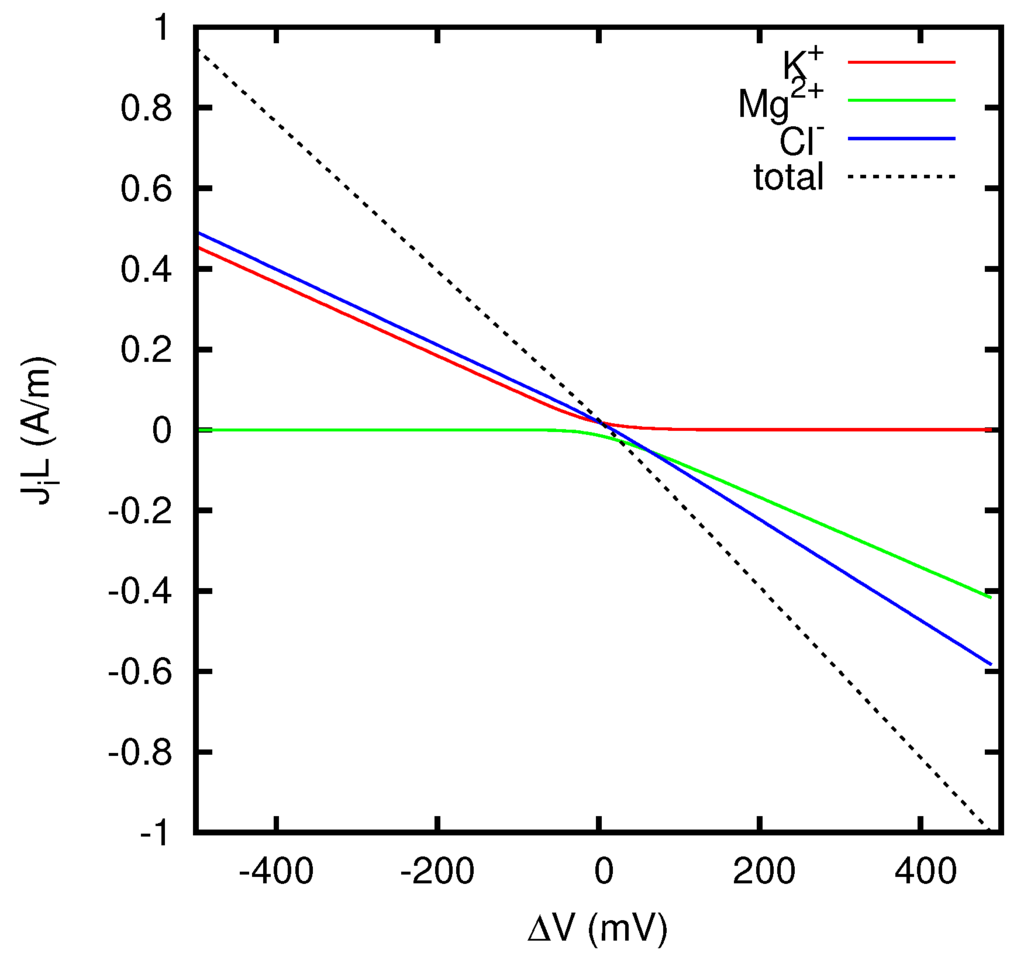
Figure 5.
Ionic current densities and total current density J, multiplied by the junction thickness L, as functions of the junction potential , for a liquid junction between KCl 0.1 M and MgCl2 0.1 M.

Table 1.
Partial currents in a liquid junction between KCl 0.1 M and MgCl2 0.1 M, for JL = 1 A/m (column 2) and JL = −1 A/m (column 4), compared respectively with transference numbers in a KCl solution (column 3) and in a MgCl2 solution (column 5).
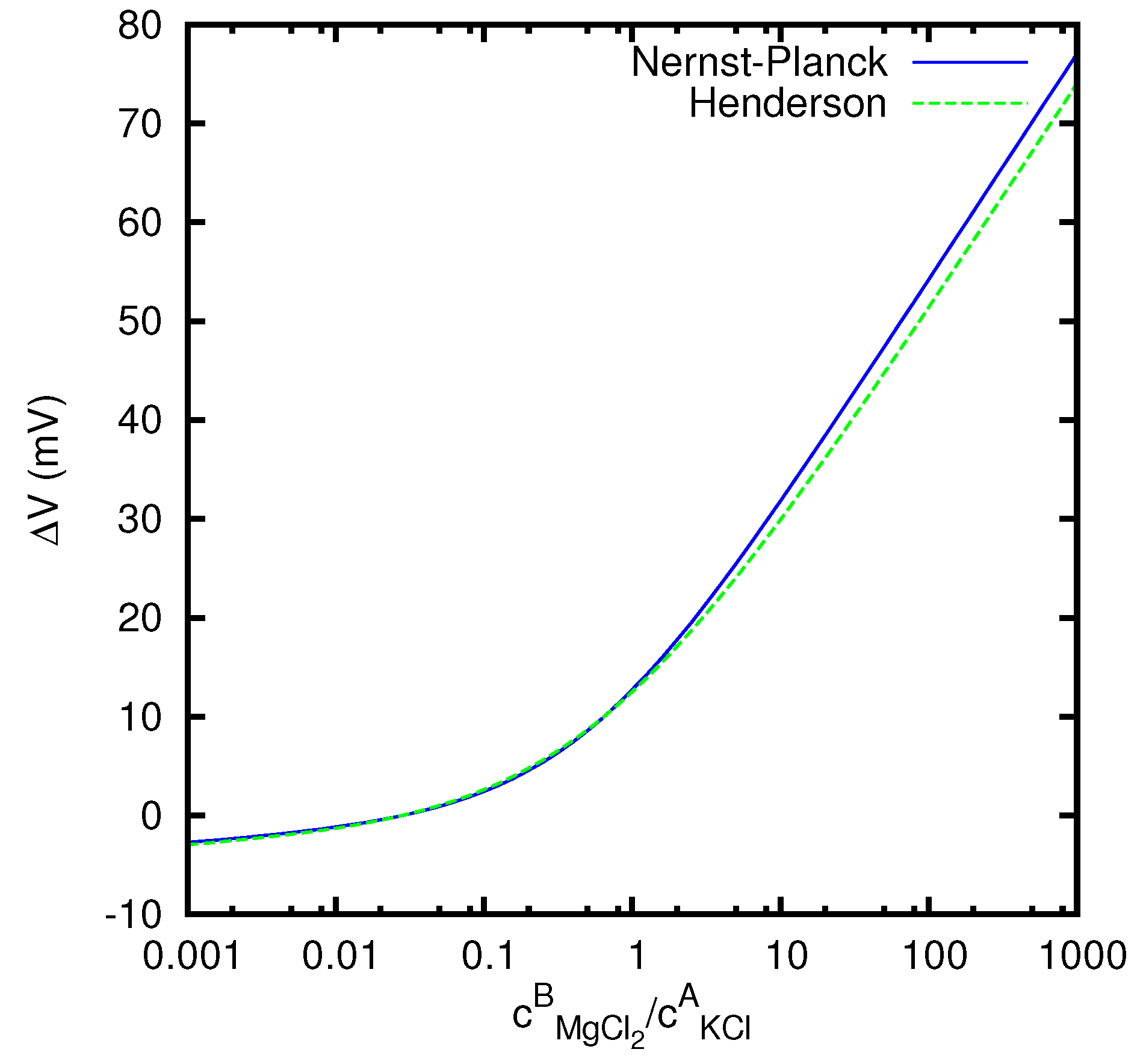
Finally, in Figure 6 we study the dependence of the junction potential, for vanishing current, on the ratio between the concentrations of the MgCl2 solution on the first side and of the KCl solution on the second side. We see that the absolute value of the junction potential is considerably higher when the concentration of the MgCl2 solution prevails with respect to the concentration of the KCl solution. This is related to the fact that the mobility of the Mg2+ ion is about 65% lower than the mobility of the Cl− ion, whereas the difference between the mobilities of K+ and Cl− is less than 4%. This implies that MgCl2 gives to the junction potential a stronger contribution than KCl.
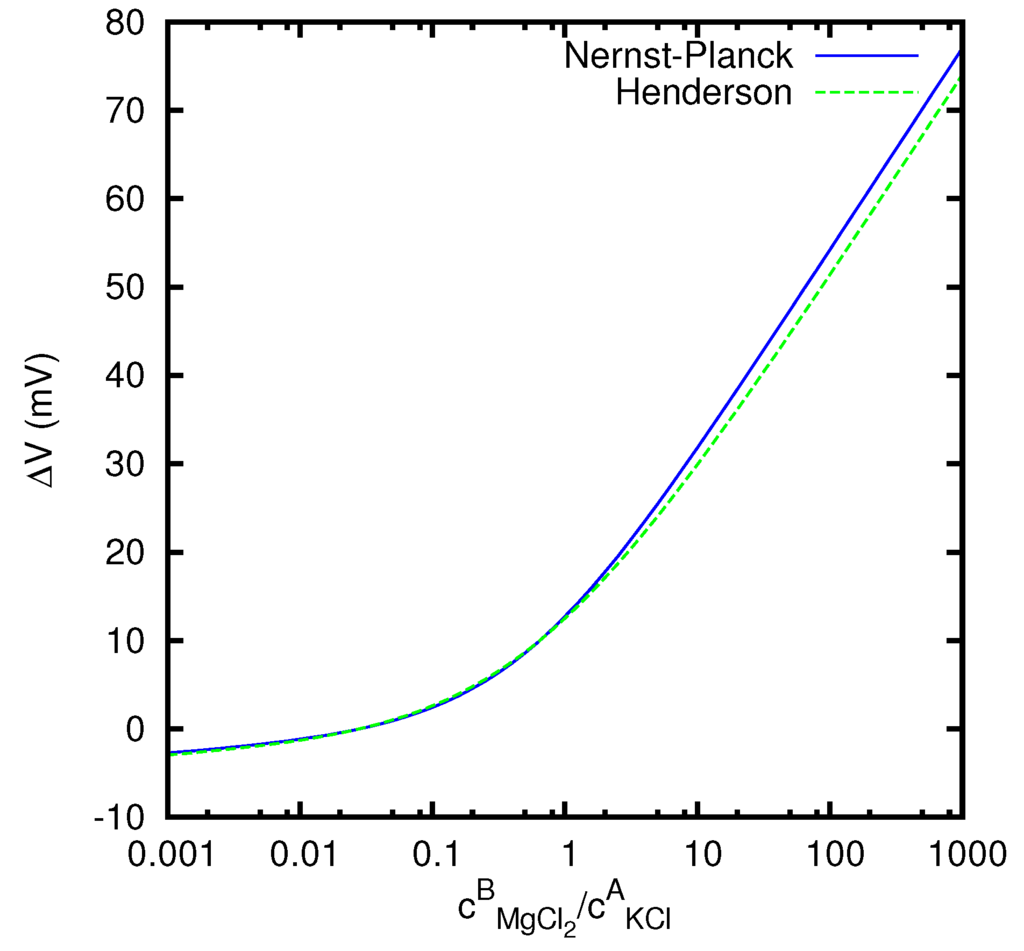
Figure 6.
Liquid junction potential at open circuit between solutions of KCl and MgCl2, as a function of the ratio between the two concentrations, according to the Nernst–Planck’s and Henderson’s models.
7.3. Uphill Transport of Minority Ionic Species
In a system with at least three different ionic species, it is possible to observe in some cases the interesting phenomenon called “uphill transport”, in which one species is transported by the electric field, generated by the liquid junction at open circuit, against its concentration gradient. This effect has been well studied in perm-selective membranes [45,46] and is relevant for the reverse electrodialysis technique for the production of energy from salinity differences [47,48], since it generates an unwanted accumulation of magnesium ions from sea water that affects the performances of the device.
An application of our method to the theoretical prediction of this phenomenon for charged membranes will be presented in Section 7.4. The uphill transport can however be observed also in neutral liquid junctions, and Figure 7 shows the results of the calculations for two systems in which this phenomenon indeed takes place. We consider a liquid junction between two solutions of HCl, with concentration 10 mM at the side x = 0 (solution A) and 100 mM at the side x = L (solution B), at T = 298.15 K. Solutions with Hydrogen ions are considered in this example, since their high mobility (we have D = 9.311 × 10−9 m2 s−1 for the diffusion coefficient of H+ at 25 °C [44]) enhances the phenomenon which we want to study (see [18] for the investigation of a similar situation in charged membranes). We suppose that the two solutions also contain a second electrolyte, namely the chloride of a different cation, with much smaller concentrations which we shall call and , since they correspond to the concentrations of the minority cation in the two solutions A and B. We fix mM at x = 0, and we study the flux of the minority cation as a function of the concentration at x = L (roughly speaking, as a function of the concentration gradient), at zero total current. We shall consider two situations: in the first one the minority electrolyte in the two solutions is KCl, and so we have in the junction a univalent minority cation K+; in the second one the electrolyte is instead MgCl2, and so we have a divalent minority cation Mg2+.
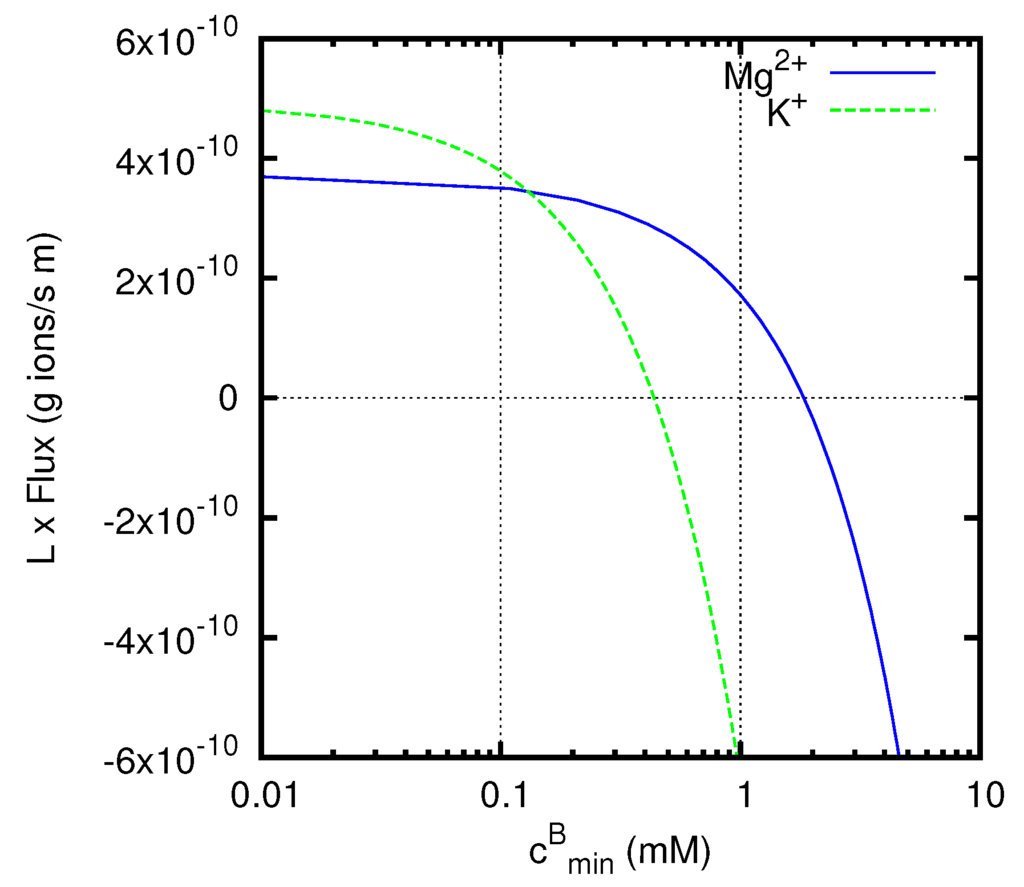
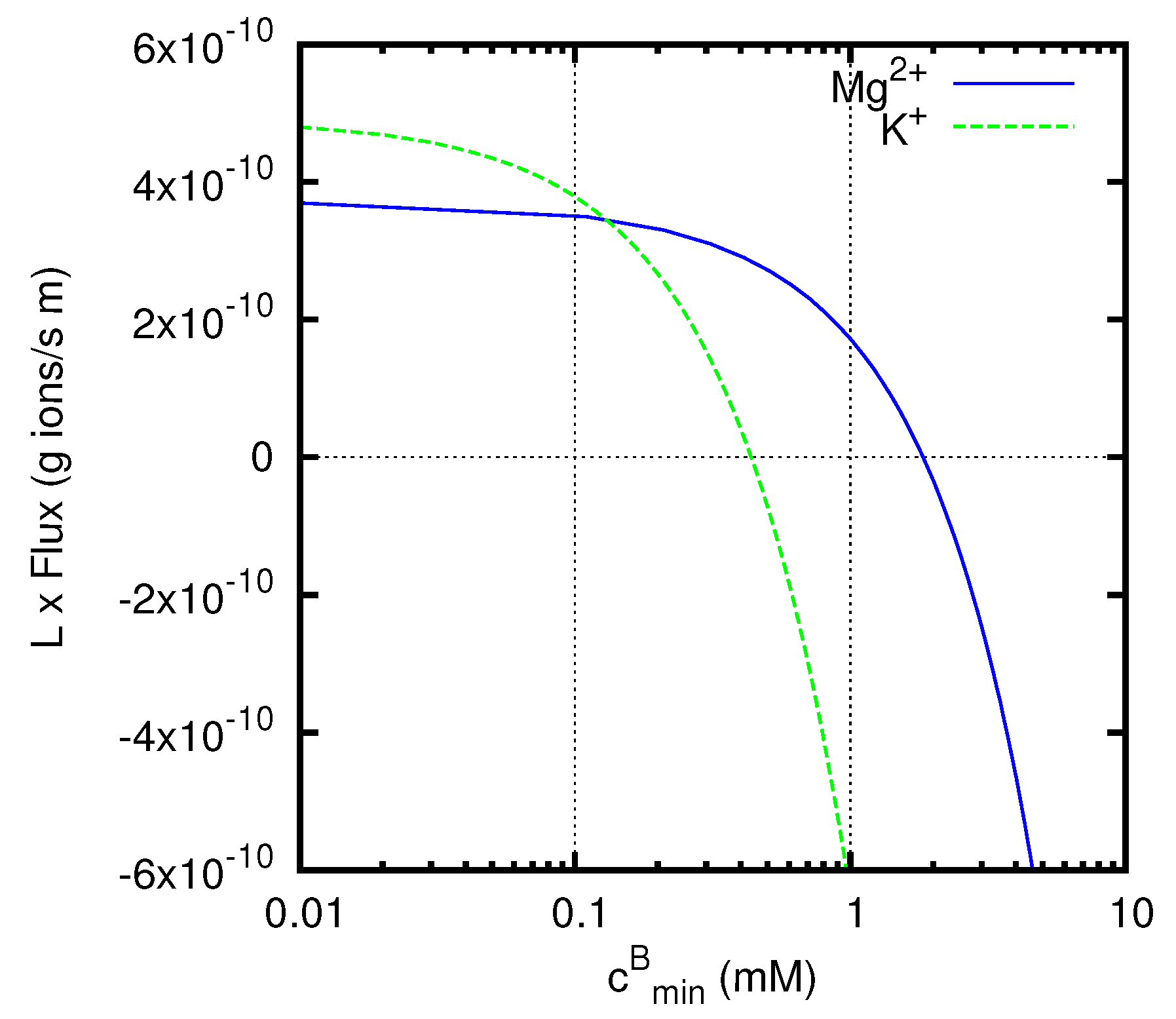
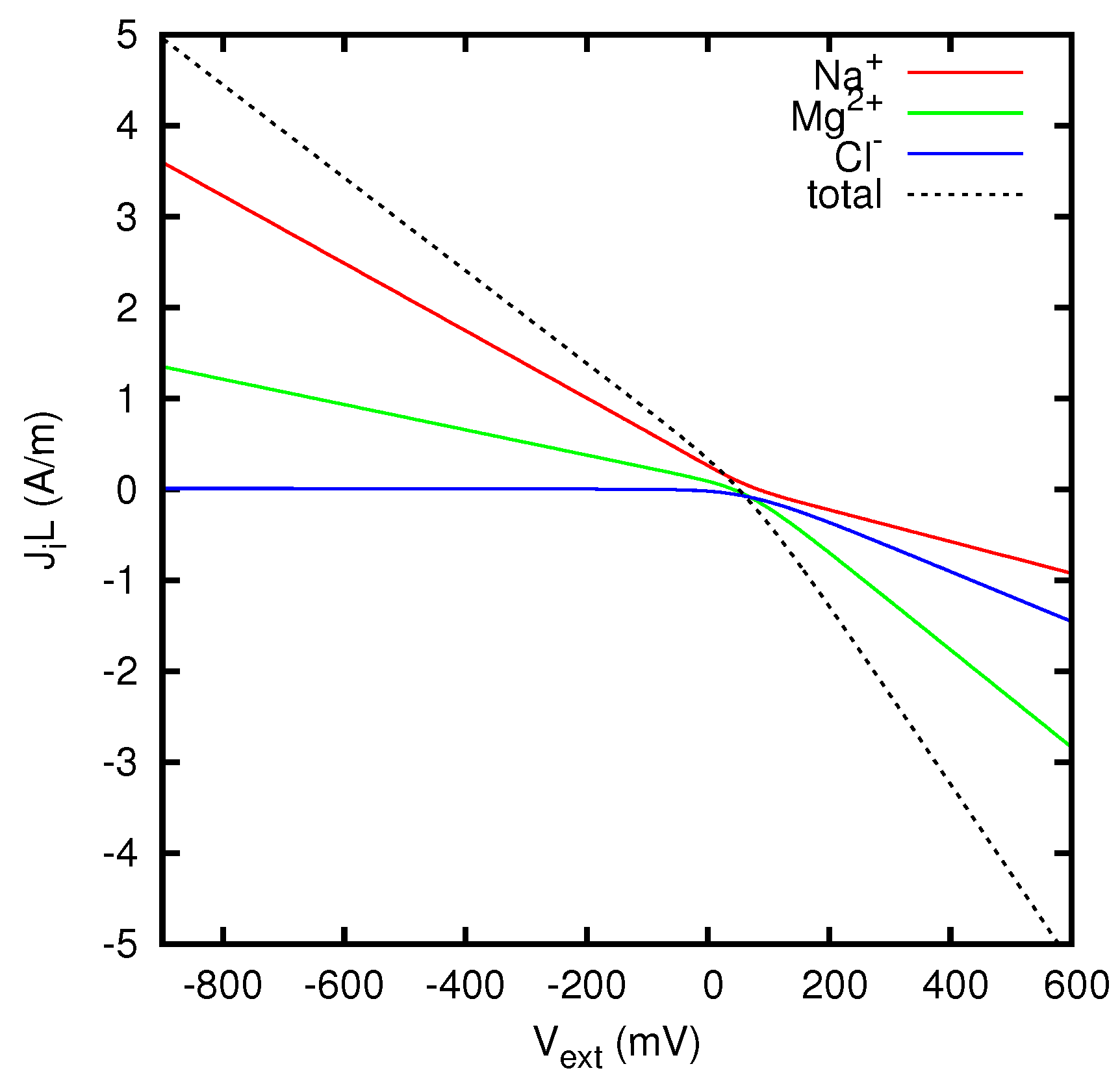
Figure 7.
Fluxes (multiplied by the thickness L of the junction) of K+ or Mg2+ ions in a liquid junction mainly containing H+ and Cl− ions, at zero total current. The concentrations of HCl are 10 and 100 mM respectively at and . The x-axis represents the concentration of the second electrolyte, KCl or MgCl2, at , while the concentration at is fixed at 0.1 mM. For mM, a positive value of the flux represents an uphill transport of the ions, i.e. a transport against the diffusion Fick’s flow of that ion.
The graph in Figure 7 reports the fluxes of the minority cations (multiplied by the thickness L of the junction) calculated by means of Equation (69). The positive direction of the fluxes corresponds to that of the x-axis, and so goes from solution A to solution B. In the region of the graph for mM the diffusive Fick’s flux for the minority cation would be negative. Nevertheless, we observe positive values of the actual flux in a considerable range of concentrations above that value, especially for Mg2+ ions, representing an uphill transport of the ion, i.e., a transport against the diffusive Fick’s flow.
The fluxes of the majority ions H+ and Cl− are weakly affected by the presence of the minority electrolyte, and are not shown in the figure. We have from Equations (68) and (70) g ions/s m. A liquid junction potential of approximately −38 mV, essentially independent of the minority electrolyte, develops across the liquid junction, due to the fact that the mobility of H+ ions is significantly larger than that of Cl− ions. This potential generates an electric field directed along the positive x axis.
At values of less than the concentration mM of the minority cation at x = 0, both the diffusive Fick’s flux and the flux induced by the electric field are positive. At values of approaching the concentration at x = 0, i.e., , the concentration gradient, and thus the diffusive Fick’s flux, vanish. In this situation, the minority cations (Mg2+ or K+) will be dragged by the electric field generated by the liquid junction and will generate a flux with positive sign, i.e., directed as the positive x-axis. The same will be true in the presence of an opposing concentration gradient, provided that the diffusive Fick’s flux it generates is small compared to the flux induced by the electric field. This phenomenon is responsible for the uphill transport observed for both K+ and Mg2+ ions at concentrations .
At higher values of , the behaviors of K+ and Mg2+ ions become remarkably different from one another. A particularly significant value of concentration is mM, at which the ratio between the concentration of the minority electrolyte and that of HCl takes the same value (namely 1/100) at the two sides of the junction. At this concentration, the system can be formally treated as containing a single electrolyte with three different ion species, and the concentrations of all the ions have fixed ratios along the liquid junction. This implies that all the cations with the same charge will have the same flux direction. In particular, both H+ and K+ ions will be transported towards the less concentrated region, giving the negative flux observed for the K+ ion at mM, which corresponds to the usual downhill transport. Instead, due to its higher charge, the Mg2+ ions still show an uphill transport, that also persists at even higher values of opposing concentration gradients.
For both K+ and Mg2+ ions, when the concentration gradient becomes strong enough, the diffusive Fick’s flux finally overcomes the uphill transport generated by the liquid junction potential, and thus negative values of the flux are observed for sufficiently high values of .
It is worth noting that, when the ratio between the concentrations of the two electrolytes is the same at the two sides of the junction (i.e., for mM in the example considered above), the assumptions at the basis of Henderson’s method become verified, and the values of the fluxes resulting from the Nernst–Planck equations can be computed by rather elementary means. However, for arbitrary concentrations Henderson’s method does not provide results comparable with those reported in Figure 7, since in general it does not allow definite predictions for the fluxes of the individual ion species. Note also that the most interesting situation for the uphill transport, i.e., that with both univalent (H+) and divalent (Mg2+) ions present together, cannot be treated with Planck’s method of solution, and so can be solved analytically only with more advanced procedures as those presented in this paper.
7.4. Charged Membranes between Solutions of NaCl and MgCl2
As an example of application of our methods to the study of charged membranes, let us consider a membrane between solutions of a mixture of two salts, with identical ratios with respect to one another at the two sides of the membrane, but with concentrations which are considerably higher at one side than at the other. In particular, we shall consider a solution NaCl 0.5 M, MgCl2 50 mM at the first side, and a solution NaCl 20 mM, MgCl2 2 mM at the second side. Thus in this section indexes 1, 2, and 3 will refer to ions Na+, Mg2+, and Cl− respectively, and we will use the diffusion coefficients D1 = 1.334 × 10−9 m2 s−1, D2 = 0.706 × 10−9 m2 s−1, D3 = 2.032 × 10−9 m2 s−1 [44], at T = 298.15 K. We also assume and, in Equations (7) and (8), .
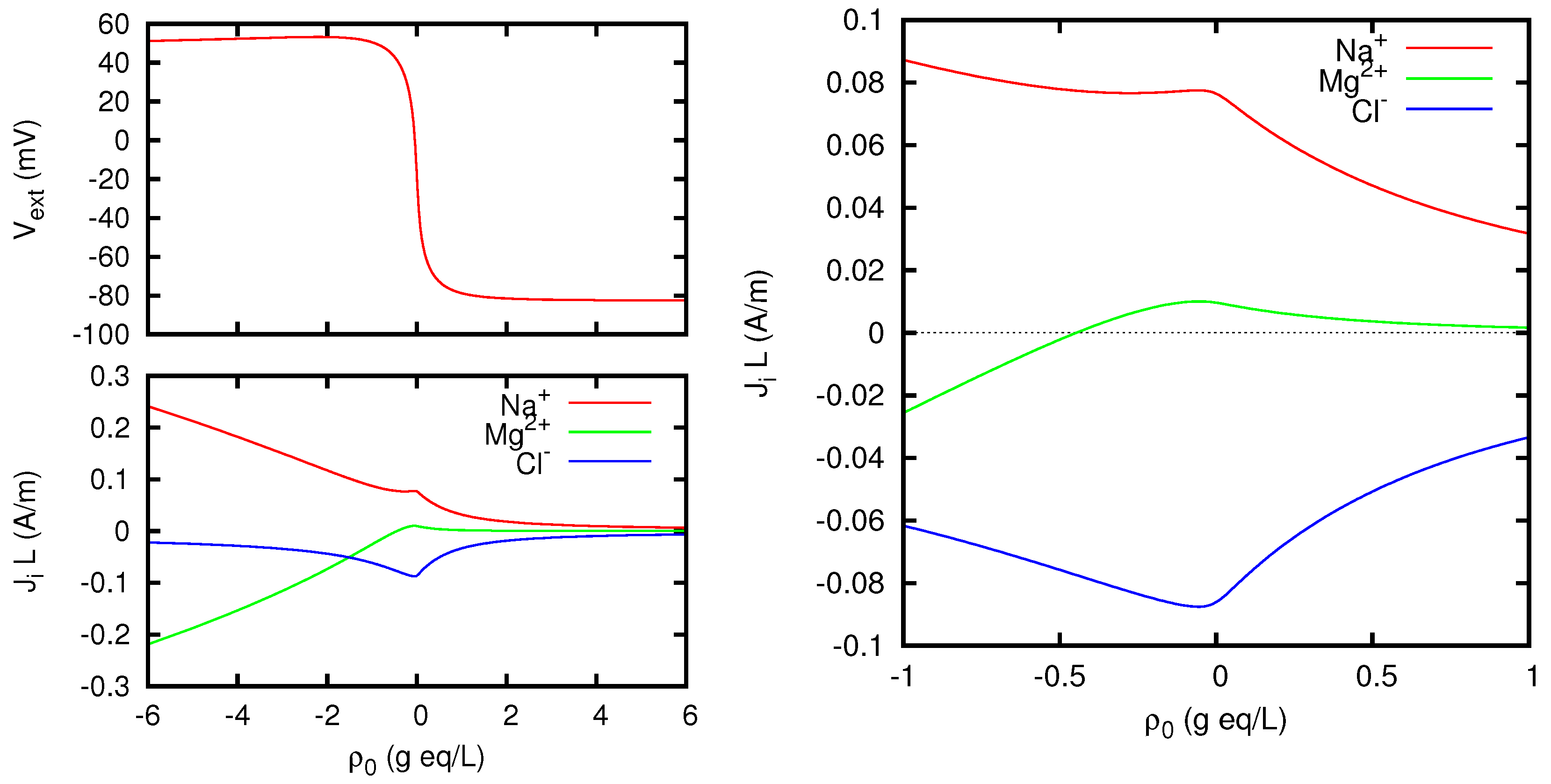
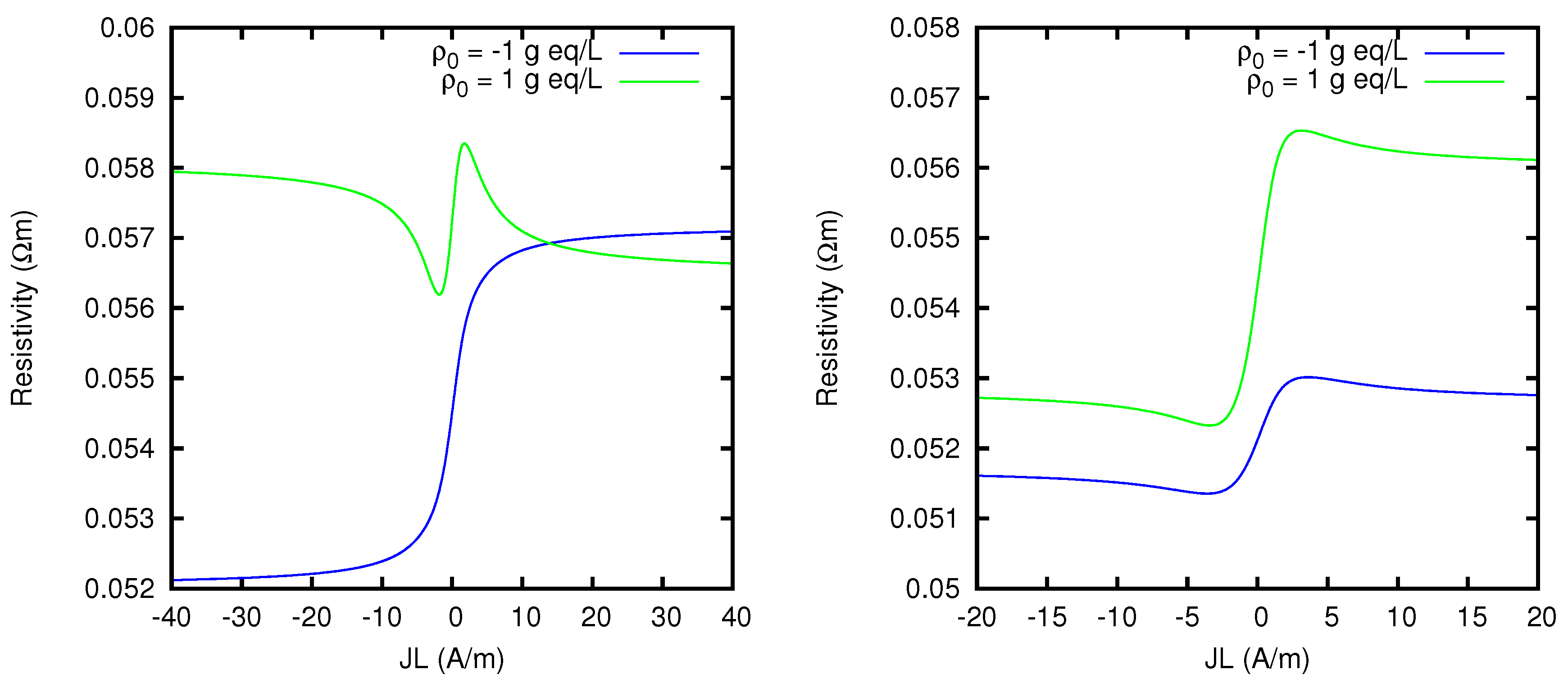
In Figure 8 we show the potential difference between the two solutions, and the current carried by each ionic species, for vanishing total current, as functions of the density of fixed charges in the membrane, represented as in Equation (3) by the quantity ( g eq/L corresponds to a charge density of 96,485 C/L). It can be noticed that for the membrane potential tends to the Donnan limit mV. For the Donnan potential is mainly determined by the divalent cation, and the limiting value of the membrane potential is mV. However, the presence also of univalent ions affects the behavior of the membrane in such a way that a maximum potential of 53.24 mV is reached for a finite value of the background charge density, namely g eq/L. A remarkable fact is that local maxima of all the ion fluxes are reached for g eq/L. One can also notice that for g eq/L the flux of Mg2+ ions becomes negative, which corresponds to the well-known phenomenon of the uphill transport of minority ions, already discussed in the preceding section.
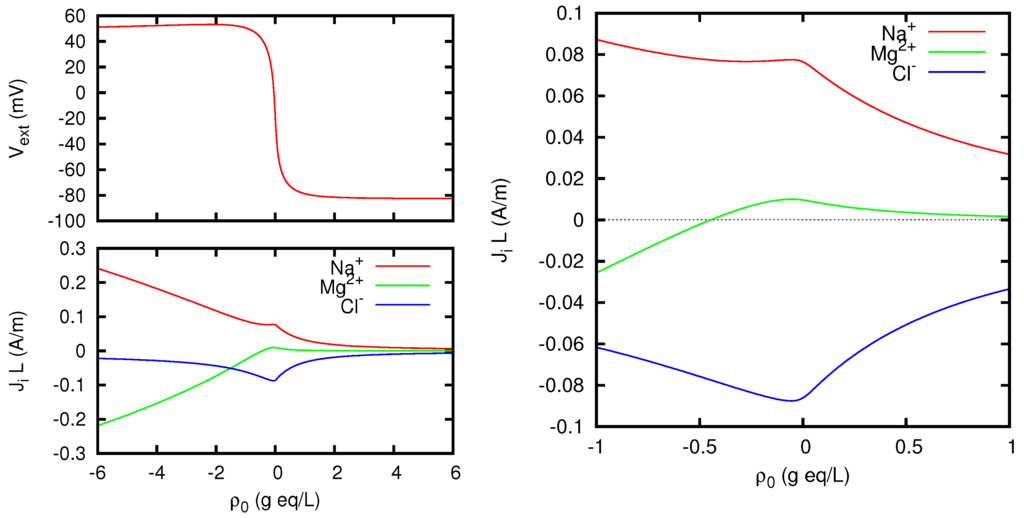
Figure 8.
Membrane potential (including Donnan potentials at the two boundaries) and ionic electric currents multiplied by the membrane thickness L, for vanishing total current density J, as functions of the fixed charge density . The solutions at the two sides of the membrane are: NaCl 0.5 M, MgCl2 50 mM at ; NaCl 20 mM, MgCl2 2 mM at . The graph on the right is a zoom of the region near the origin of the left bottom graph, showing in more detail the occurrence of the uphill transport (here corresponding to negative current) of the Mg2+ ions for sufficiently negative values of the charge density of the membrane.
In Figure 9 we display the ionic currents as functions of the potential difference between the two solutions, for an AEM (anion exchange membrane) with a density of positive fixed charges such that g eq/L. A similar study is presented in Figure 10 for a CEM (cation exchange membrane) with g eq/L. The resulting behavior of the effective resistivity of the junction as a function of the current is shown in Figure 11. The difference between the limiting values of the resistivity at the two sides of the graph is due to the dependence of the ionic concentrations on the current, as mathematically discussed in Section 5. Such a dependence is illustrated for the AEM in Figure 12, Figure 13 and Figure 14, and for the CEM in Figure 15, Figure 16 and Figure 17, by considering the potential and concentration profiles inside the junction for particular values of the current. One can observe that the results are in agreement with the general analysis of Section 5.2. In particular, in the case of the AEM (for which only one counterion is present) the ion concentrations inside the membrane approach for high currents the values at the boundary from which the coions Na+ and Mg2+ enter the membrane. According to Equations (78) and (79), the curve for g eq/L of Figure 11 tends to the limits 0.1309 Ωm for and 0.0915 Ωm for . The limits of the curve for g eq/L are instead 0.1014 Ωm for and 0.1959 Ωm for . So the limiting resistivity of the CEM between the two solutions considered is in one of the two directions almost twice as big as in the other.
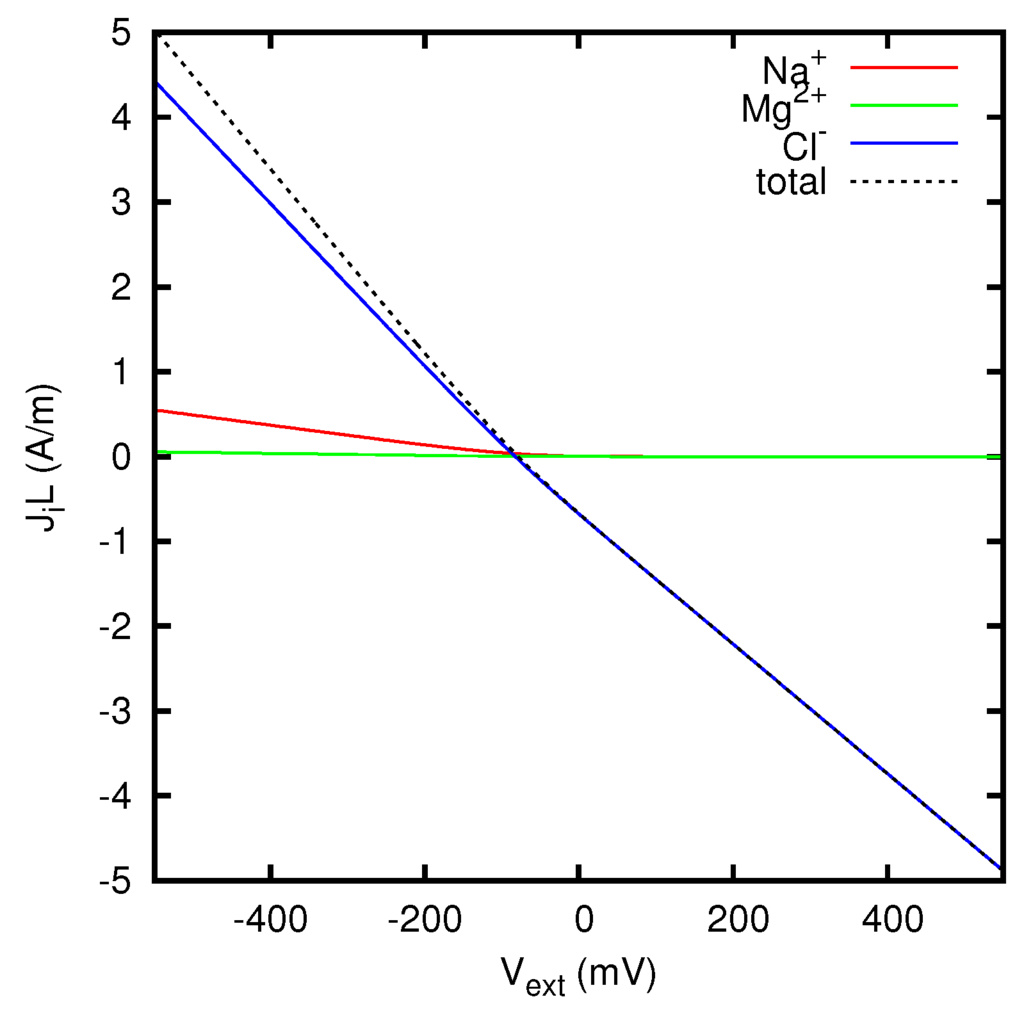
Figure 9.
Ionic current densities and total current density J, multiplied by the thickness L of the porous membrane, for g eq/L, as functions of the membrane potential (including the Donnan potentials at the two boundaries). The solutions at the two sides of the membrane are: NaCl 0.5 M, MgCl2 50 mM at ; NaCl 20 mM, MgCl2 2 mM at .
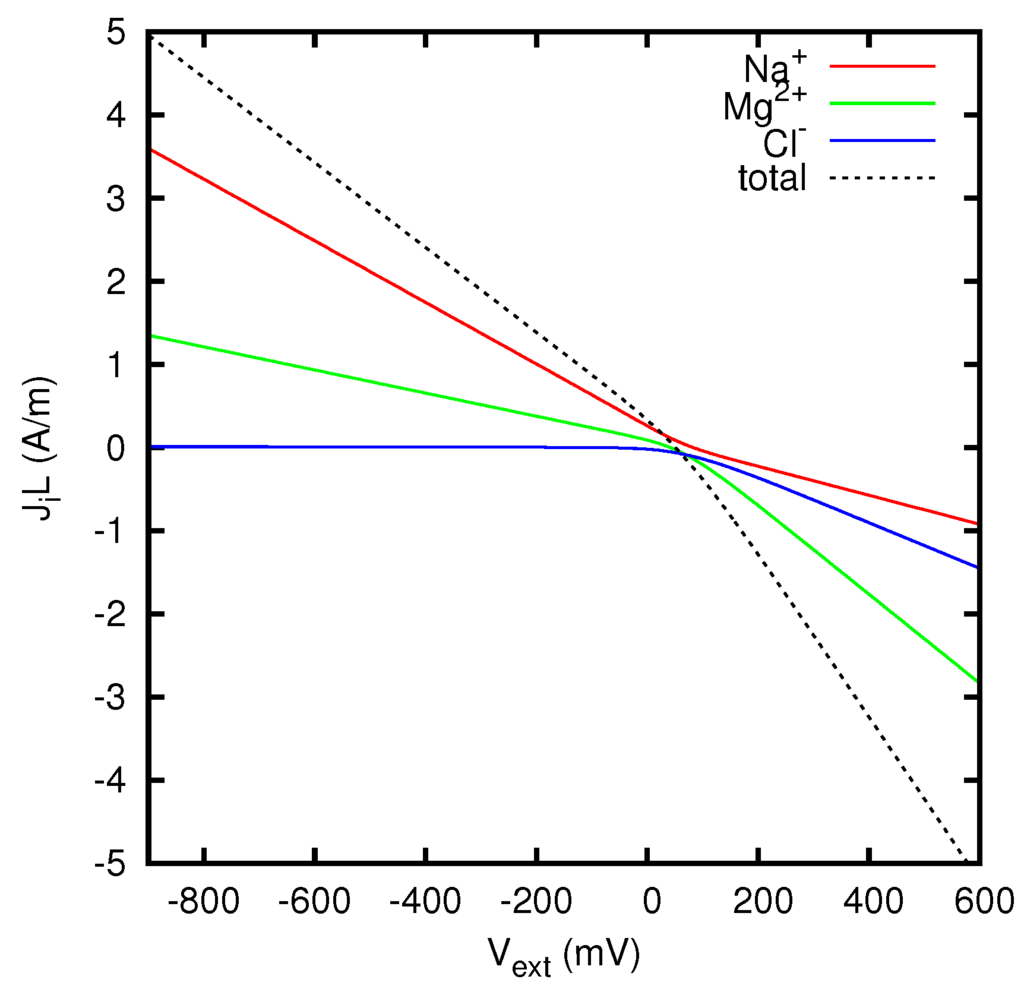
Figure 10.
Ionic current densities and total current density J, multiplied by the thickness L of the porous membrane, for g eq/L, as functions of the membrane potential (including the Donnan potentials at the two boundaries). The solutions at the two sides of the membrane are: NaCl 0.5 M, MgCl2 50 mM at ; NaCl 20 mM, MgCl2 2 mM at .
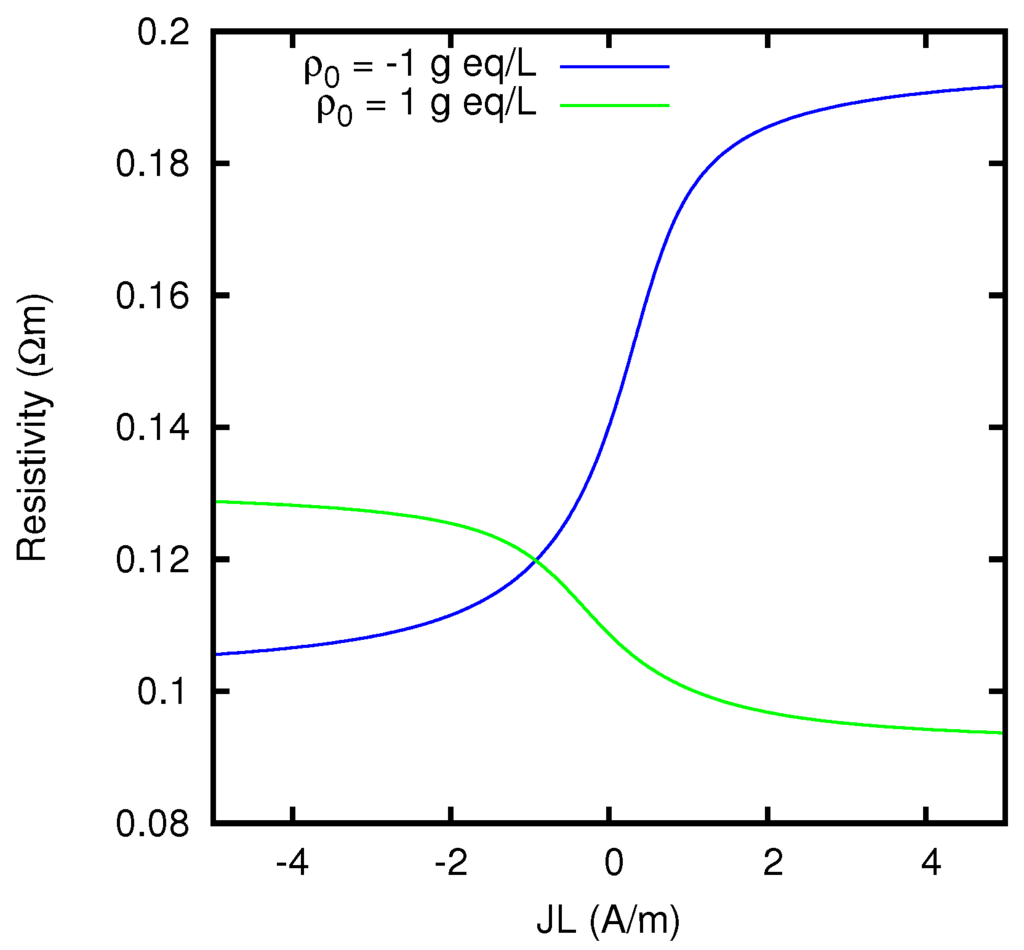
Figure 11.
Effective resistivity of a negatively charged membrane (blue line) and a positively charged membrane (green line) between the solutions considered in Figure 8, as functions of the current density multiplied by the thickness of the membrane.
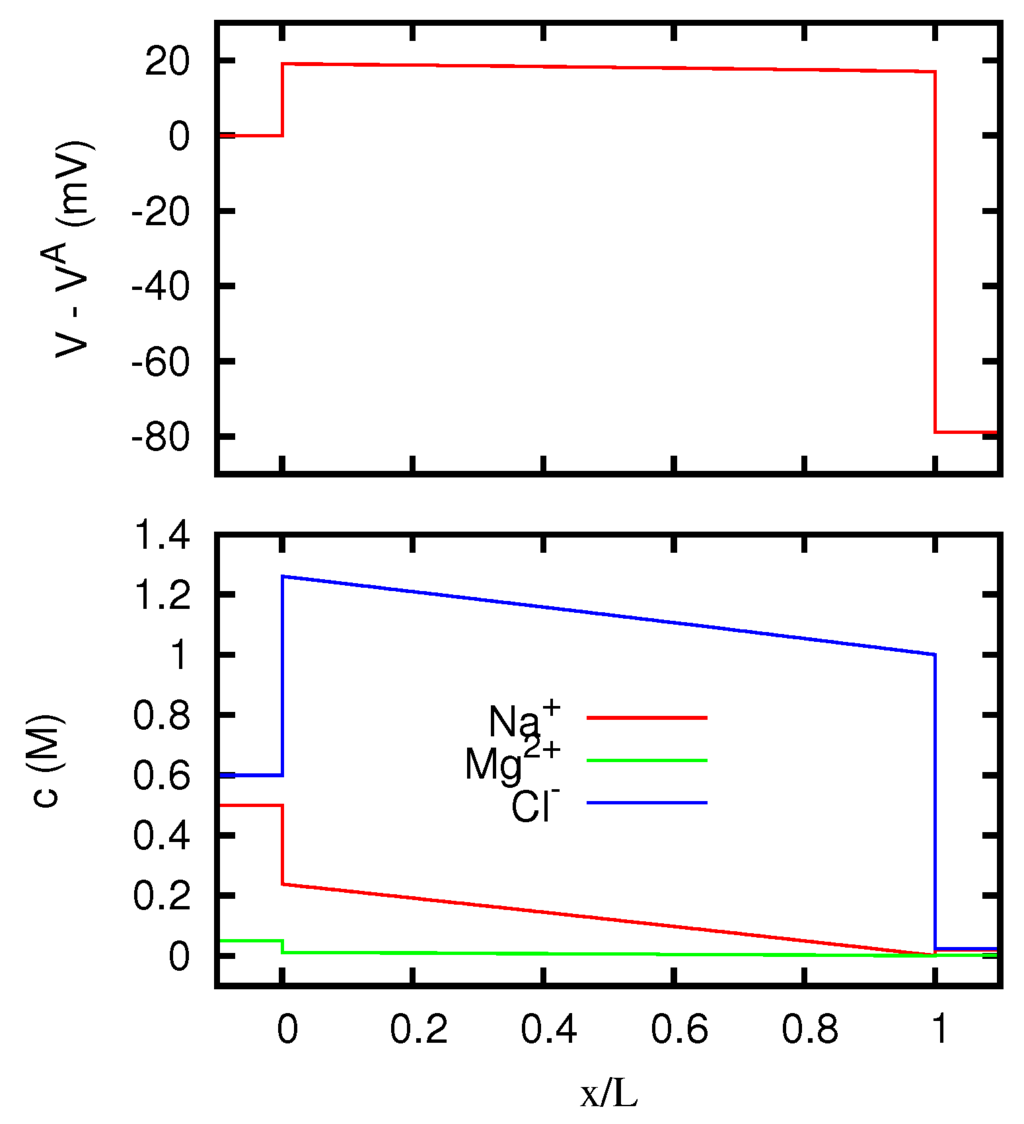
Figure 12.
Electric potential and ionic concentrations c as functions of the position x inside a membrane with g eq/L, for vanishing electric current. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 8.
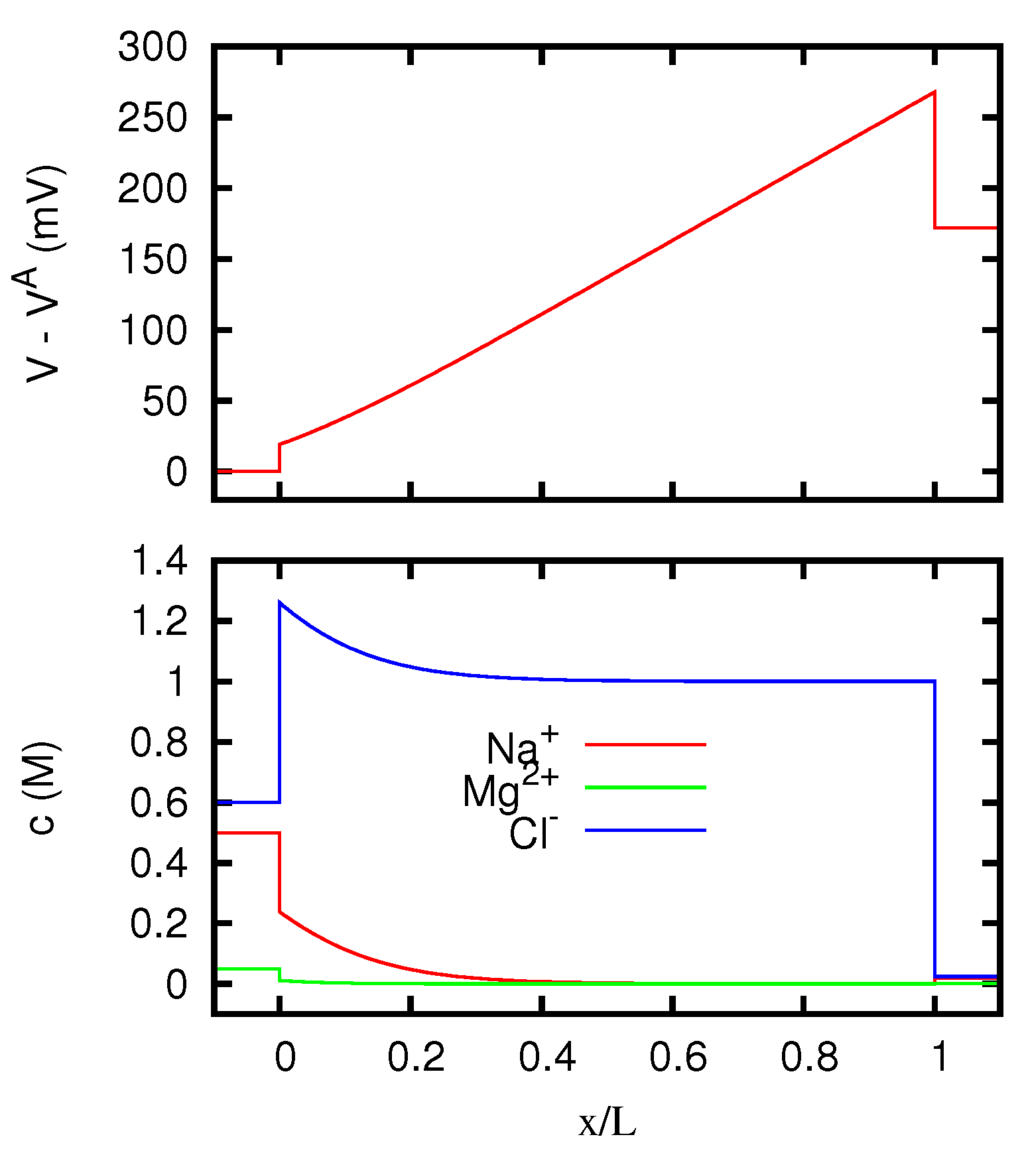
Figure 13.
Electric potential and ionic concentrations c as functions of the position x inside a membrane with g eq/L, for A/m, where J is the current density. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 8.
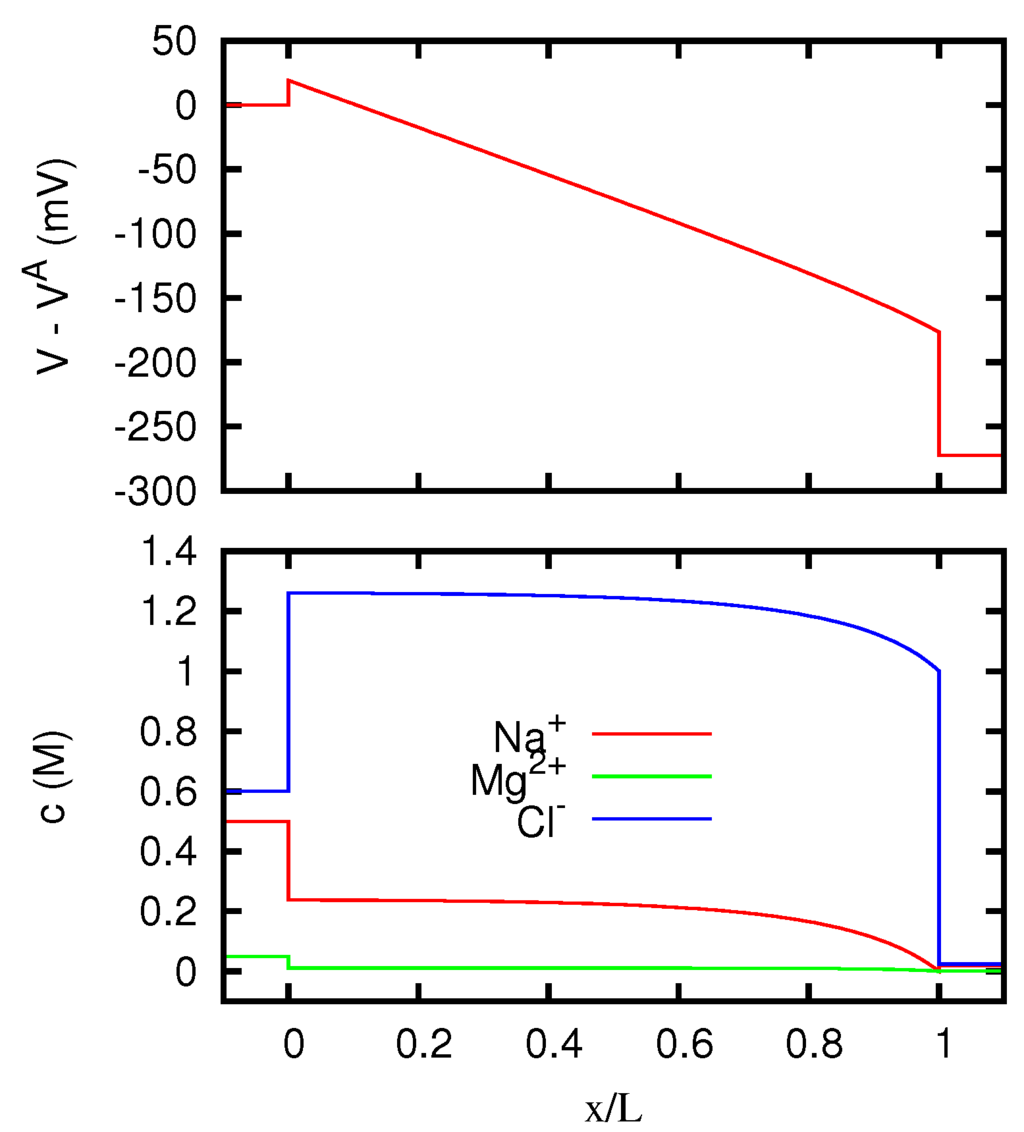
Figure 14.
Electric potential and ionic concentrations c as functions of the position inside a membrane with g eq/L, for A/m, where J is the current density. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 8.
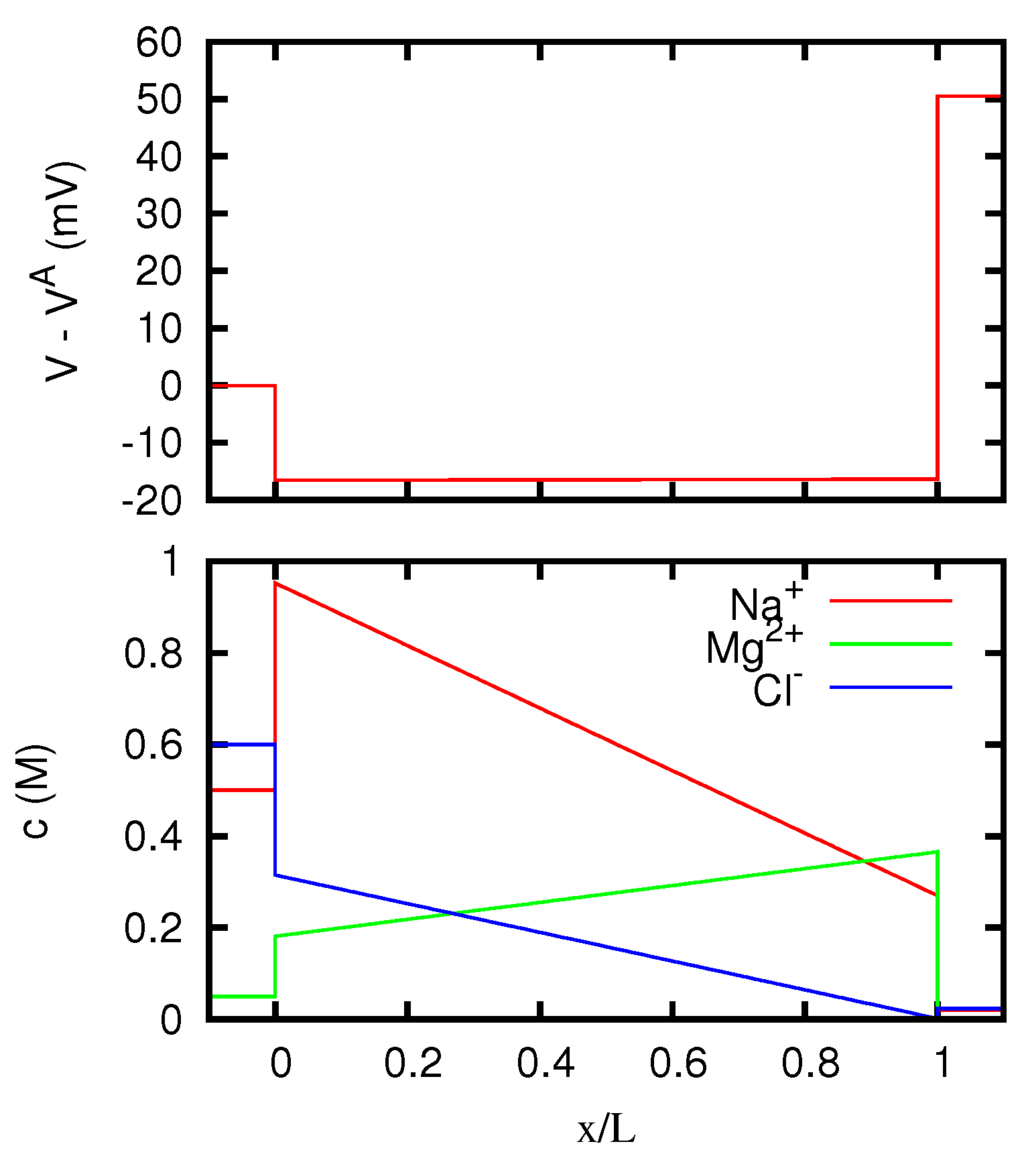
Figure 15.
Electric potential and ionic concentrations c as functions of the position x inside a membrane with g eq/L, for vanishing electric current. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 8.
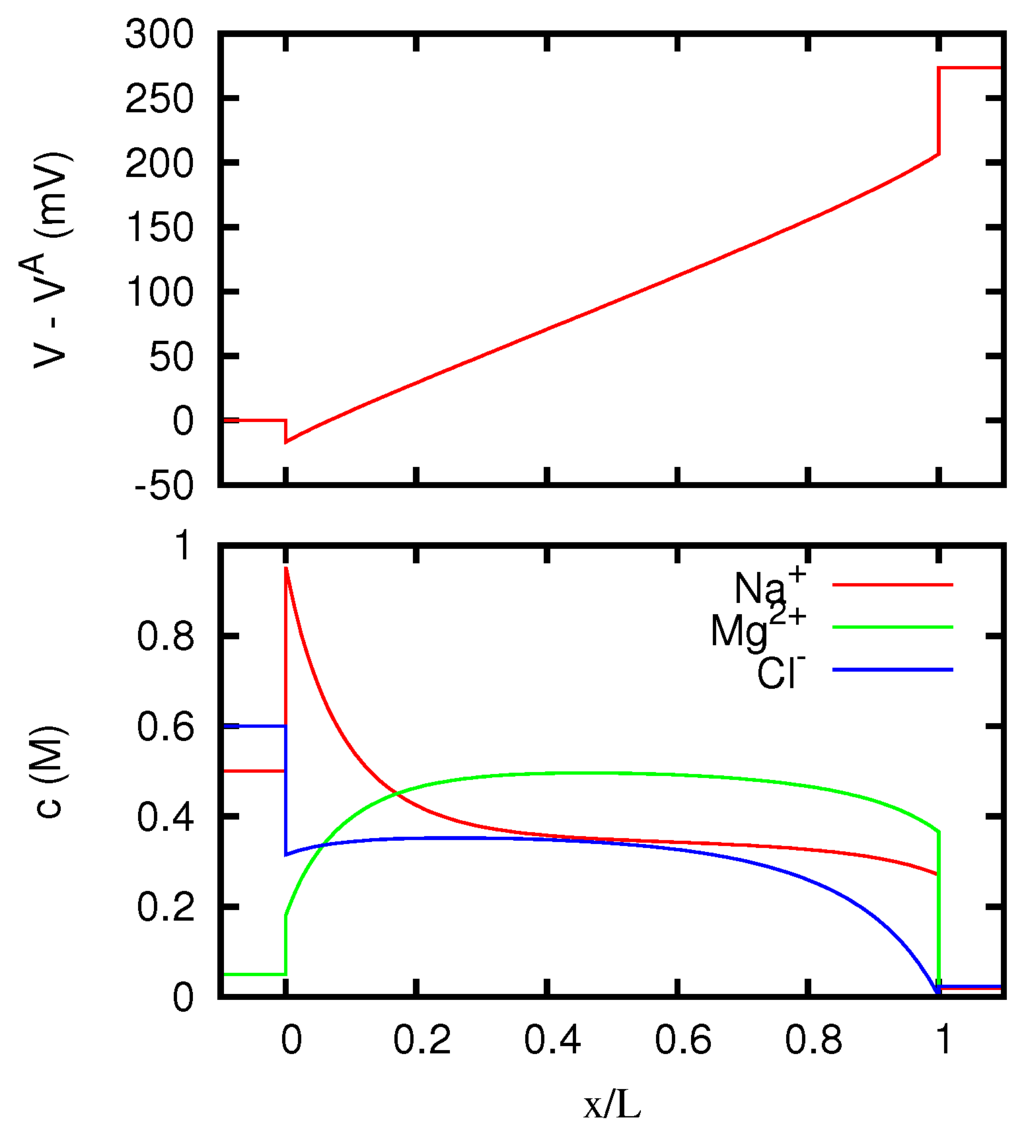
Figure 16.
Electric potential and ionic concentrations c as functions of the position x inside a membrane with g eq/L, for A/m, where J is the current density. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 8.
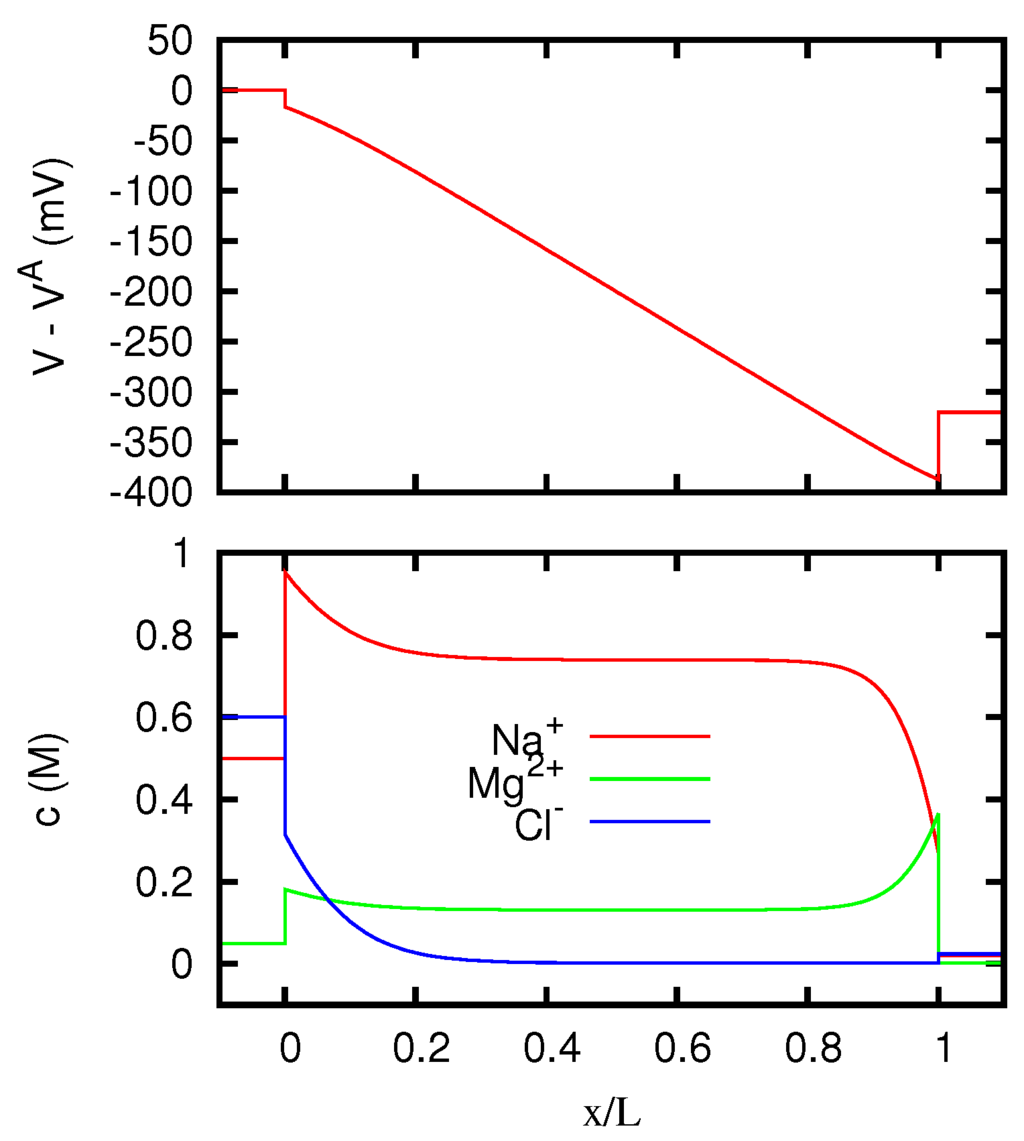
Figure 17.
Electric potential and ionic concentrations c as functions of the position inside a membrane with g eq/L, for A/m, where J is the current density. The regions and correspond to the solutions at the two sides of the junction, which are the same as in Figure 8.
The Nernst–Planck model is able to reveal detailed features of the behavior of a charged membrane which, although not necessarily relevant from a quantitative point of view, are nevertheless qualitatively quite remarkable. As an example, we show in Figure 18 the effective resistivity of charged membranes between solutions of mixtures of NaCl and MgCl2, with different concentrations from those previously considered. We see that small variations in the composition of the two solutions affect in a significant way the behavior of the resistivity, which can present minima and maxima as a function of the current density flowing through the membrane.
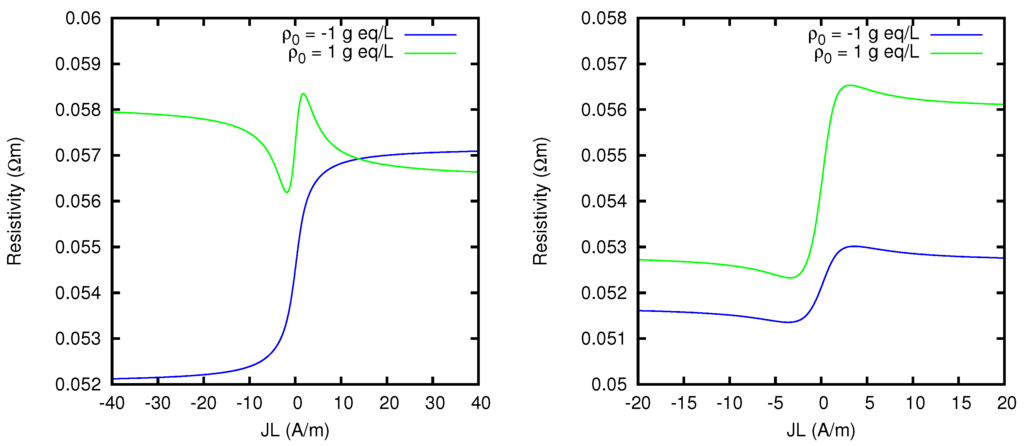
Figure 18.
Effective resistivity of a negatively charged membrane (blue line) and a positively charged membrane (green line) between two solutions A and B specified below, as functions of the current density multiplied by the thickness of the membrane. (left) Solution A NaCl 500 mM + MgCl2 400 mM, solution B NaCl 100 mM + MgCl2 600 mM. (right) Solution A NaCl 550 mM + MgCl2 380 mM, solution B NaCl 130 mM + MgCl2 655 mM.
8. Conclusions
In the present paper we have solved the Nernst–Planck equations for an ideal constrained liquid junction or charged membrane, and we have provided analytical expressions for the junction potential, the resistivity and the ionic fluxes, as well as for the potential and concentration profiles inside the diffusion layer. These analytical expressions have been given for an arbitrary value of the total current density flowing through the junction or membrane, and are valid for systems containing up to three different ionic species with arbitrary valence. We have also shown that the results can be generalized with not too much difficulty to the case of an arbitrary number of ionic species, provided that the total number of valences is not greater than three.
Although the problem considered in this paper has already been the subject of several investigations, the form of our analytical results is new, and they can be rather easily applied to obtain quantitative predictions in a wide range of practical situations. The only step which needs to be performed with a computer is as simple as locating the zero of a function of one real variable. Using these methods it is thus possible to obtain in a simple and reliable way a set of results which are usually derived by means of heavy ad hoc numerical routines. Therefore our results may represent a useful tool for researchers having to study problems involving the behavior or either charged or uncharged liquid junctions in not too complex chemical systems.
We have applied our procedure to the study of a few concrete situations. Our results confirm that the simple Henderson model generally agrees with the predictions of the Nernst–Planck model, as far as the value of the junction potential at zero current is concerned. Nevertheless, the Nernst–Planck model provides a much more general and complete description of the system, including the ionic fluxes and distributions for arbitrary values of the total electric current flowing through the junction. As a result, it is able to highlight interesting features of the behavior of a system, that disappear in the rougher description given by Henderson’s model. A remarkable example is given by the uphill transport of a divalent ion, i.e. its global flow from the side with lower concentration to the side with higher concentration of a liquid junction or of a charged membrane, which may occur at open circuit in the presence of a majority of univalent ions with the same sign.
Acknowledgments
We are grateful to Andrea Carati and Luigi Galgani for interesting discussions.
Author Contributions
Doriano Brogioli has proposed the object and aim of the work. Both authors have worked out together the general plan of the research. Massimo Marino has elaborated the mathematical methods and carried out the numerical calculations. Both authors have contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
List of Symbols
| A | Solution in contact with the liquid junction at x = 0 |
| b | Defined by Equation (62) |
| B | Solution in contact with the liquid junction at x = L |
| c | Defined by Equation (63) |
| ci | Concentration of the i-th ion expressed as number of ions per unit volume |
| cmin | Concentration of the minority ion |
| cS | Concentration of the salt S |
| Di | Diffusion coefficient of the i-th ion |
| Defined as | |
| e | Absolute value of the elementary charge |
| F | Defined by Equation (102) |
| f(r) | Defined by Equation (59) |
| G | Defined by Equation (102) |
| g(r) | Defined by Equation (60) |
| hi | Defined as hi = χi/X |
| J | Total current density, defined by Equation (4) |
| Ji | Current density carried by the i-th ion, Ji = eziΦi |
| k | Boltzmann constant |
| ki | Partition coefficient of the i-th ion |
| L | Thickness of the diffusion layer |
| mi | Number of ionic species with the i-th valence in Section 6 |
| m | Total number of ionic species (sum of the mi) in Section 6 |
| n | Number of ionic species, or of valences in Section 6 |
| R | Effective electrical resistivity of the liquid junction, defined by Equation (40) |
| ri | Defined by Equation (16) |
| r | Stands for r1 for n = 3 |
| An arbitrary value of ri | |
| r−, r+ | Roots of the trinomial r2 + br + c, with r− < r+ |
| si | Defined by Equation (28) |
| Transference number of the i-th ion in solution A, defined by Equation (85) | |
| T | Absolute temperature |
| u | Defined by Equation (64) |
| V | Electric potential |
| Donnan potential at x = 0, defined as | |
| Donnan potential at x = L, defined as | |
| Vext | Potential difference between the solutions A and B, Vext = VB − VA |
| w | Defined by Equation (20) |
| x | Spatial coordinate across the junction, from x = 0 to x = L |
| X | Defined as |
| Y | Defined by Equation (24) |
| Z | Defined by Equation (65) |
| zi | Relative charge of the i-th ion |
| αi | Defined by Equation (25) |
| α | Stands for α1 when n = 3 |
| Defined as | |
| Stands for when n = 3 | |
| β | Defined as 1/hn−1 |
| Defined as | |
| δ | Defined by Equation (61) |
| ζi | Defined as ζi = ηjzj |
| ηi | Ratio between μi and Di/kT; ηi = 1 if Einstein relation holds |
| κ | Mixing factor used in Henderson theory |
| μi | Mobility of the i-th ion in the solution (ratio between drift velocity and total force) |
| ξ | Defined by Equation (16) |
| An arbitrary value of ξ | |
| ρ0 | Charge density of the fixed charges in the porous membrane divided by e |
| ρi | Charge density carried by the i-th ion divided by e, ρi = zici |
| σ | Effective electrical conductivity of the liquid junction, σ = 1/R |
| τi | Defined by Equation (13) |
| φ | Dimensionless potential, φ = eV/kT |
| Φi | Flux of the i-th ion, expressed as number of ions per unit time per unit area |
| χi | Defined as χi = ziΦi/Di |
| ☐jk | A symbol with two subscripts refers to the ion k of the valence class j |
| ☐′ | Represents the value of ☐ at the boundary x = 0 |
| ☐″ | Represents the value of ☐ at the boundary x = L |
| Δ☐ | Difference of ☐ across the liquid junction, defined as Δ☐ = ☐″ − ☐′ |
| ☐A | Represents the value of ☐ in the solution A, in contact with the boundary x = 0 |
| ☐B | Represents the value of ☐ in the solution B, in contact with the boundary x = L |
| ☐+ | Represents the limiting value of ☐ for J → +∞, or for ρ0 → +∞ |
| ☐− | Represents the limiting value of ☐ for J → −∞, or for ρ0 → −∞ |
References
- MacInnes, D. The Principles of Electrochemstry; Reinhold Publishing Corp.: New York, NY, USA, 1939. [Google Scholar]
- Henderson, P. Zur Thermodynamik der Flüssigkeitketten. Z. Phys. Chem. 1907, 59, 118. (In German) [Google Scholar]
- Henderson, P. Zur Thermodynamik der Flüssigkeitketten. Z. Phys. Chem. 1908, 63, 325. (In German) [Google Scholar]
- Planck, M. Über die Erregung von Elektrizität und Wärme in Elektrolyten. Ann. Phys. u. Chem. 1890, 39, 161. (In German) [Google Scholar] [CrossRef]
- Planck, M. Über die Potentialdifferenz zwischen zwei verdünnten Lösungen binärer Electrolyte. Ann. Phys. u. Chem. 1890, 40, 561. (In German) [Google Scholar] [CrossRef]
- Nernst, W. Zur Kinetik der in Lösung befindlichen Körper. Z. Phys. Chem. 1888, 2, 613. (In German) [Google Scholar]
- Nernst, W. Die Elektromotorische Wirksamskeit der Ionen. Z. Phys. Chem. 1889, 4, 129. (In German) [Google Scholar]
- MacGillvray, A.D. Nernst–Planck Equations and the Electroneutrality and Donnan Equilibrium Assumptions. J. Chem. Phys. 1967, 48, 2903. [Google Scholar] [CrossRef]
- Dickinson, E.J.F.; Freitag, L.; Compton, R.G. Dynamic Theory of Liquid Junction Potentials. J. Phys. Chem. B 2010, 114, 187–197. [Google Scholar] [CrossRef] [PubMed]
- Helfferich, F. Ion Exchange; McGraw-Hill Book Co.: New York, NY, USA, 1962. [Google Scholar]
- Behn, U. Über wechselseitige Diffusion von Elektrolyten in verdünnten Lösungen, insbesonders über Diffusion gegen das Conzentrationsgefälle. Ann. Phys. u. Chem. 1897, 62, 54. (In German) [Google Scholar] [CrossRef]
- Pleijel, H. Die Potentialdifferenz zwischen zwei elektrolytischen Lösungen. Z. Phys. Chem. 1910, 72, 1. (In German) [Google Scholar]
- Goldman, D.E. Potential, impedance, and rectification in membranes. J. Gen. Physiol. 1943, 27, 37–60. [Google Scholar] [CrossRef] [PubMed]
- Teorell, T. Zur quantitativen Behandlung der Membranpermeabilität (Eine erweiterte Theorie). Z. Elektrochem. 1951, 55, 460. (In German) [Google Scholar]
- Schlögl, R. Elektrodiffusion in freier Lösung und geladenen Membranen. Z. Phys. Chem. 1954, 1, 305. (In German) [Google Scholar] [CrossRef]
- Morf, W.E. Calculation of Liquid-Junction Potentials and Membrane Potentials on the Basis of the Planck Theory. Anal. Chem. 1977, 49, 810–813. [Google Scholar] [CrossRef]
- Cohen, H.; Cooley, J.W. The numerical solution of the time-dependent Nernst-Planck equation. Biophys. J. 1965, 5, 145–162. [Google Scholar] [CrossRef]
- Ramírez, P.; Alcaraz, A.; Mafé, S. Model calculations of ion transport against its concentration gradient when the driving force is a pH difference across a charged membrane. J. Membr. Sci. 1997, 135, 135–144. [Google Scholar] [CrossRef]
- Ku, J.R.; Lai, S.M.; Ileri, N.; Ramírez, P.; Mafe, S.; Stroeve, P. pH and Ionic Strength Effects on Amino Acid Transport through Au-Nanotubule Membranes Charged with Self-Assembled Monolayers. J. Phys. Chem. C 2007, 111, 2965–2973. [Google Scholar] [CrossRef]
- Wang, W.; Wang, A.; Zhang, X.; Xu, T. The concentration, resistance, and potential distribution across a cation exchange membrane in 1:2 (Na2SO4) type aqueous solution. Desalination 2012, 284, 106–115. [Google Scholar] [CrossRef]
- MacGillvray, A.D. Asymptotic Solutions of the Time-Dependent Nernst-Planck Equations. J. Chem. Phys. 1969, 52, 3126–3132. [Google Scholar] [CrossRef]
- Brumleve, T.R.; Buck, R.P. Numerical solution of the Nernst-Planck and Poisson equation system with applications to membrane electrochemistry and solid state physics. J. Electroanal. Chem. Interfacial Electrochem. 1978, 90, 1–31. [Google Scholar] [CrossRef]
- Sokalski, T.; Lewenstam, A. Application of Nernst-Planck and Poisson equations for interpretation of liquid-junction and membrane potentials in real-time and space domains. Electrochem. Commun. 2001, 3, 107–112. [Google Scholar] [CrossRef]
- Sokalski, T.; Lingenfelter, P.; Lewenstam, A. Numerical Solution of the Coupled Nernst-Planck and Poisson Equations for Liquid Junction and Ion Selective Membrane Potentials. J. Phys. Chem. B 2003, 107, 2443–2452. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Chu, K.T.; Bayly, B.J. Current-voltage relations for electrochemical thin films. SIAM J. Appl. Math. 2005, 65, 1463–1484. [Google Scholar] [CrossRef]
- Xue, J.M.; Zou, X.Q.; Xie, Y.B.; Wang, Y.G. Molecular dynamics simulations on the ionic current through charged nanopores. J. Phys. D Appl. Phys. 2009, 42, 105308. [Google Scholar] [CrossRef]
- Zheng, Q.; Wei, G.W. Poisson–Boltzmann–Nernst–Planck model. J. Chem. Phys. 2011, 134, 194101. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.S.; He, D.; Wylie, J.J.; Huang, H. Singular perturbation solutions of steady-state Poisson–Nernst–Planck systems. Phys. Rev. E 2014, 89, 022722. [Google Scholar] [CrossRef] [PubMed]
- Ward, K.R.; Dickinson, E.J.F.; Compton, R.G. Dynamic Theory of Membrane Potentials. J. Phys. Chem. B 2010, 114, 10763. [Google Scholar] [CrossRef] [PubMed]
- Levitt, D.G. General continuum theory for multi-ion channel. I. Theory. Biophys. J. 1991, 59, 271–277. [Google Scholar] [CrossRef]
- Levitt, D.G. General continuum theory for multi-ion channel. II. Application to acetylcholine channel. Biophys. J. 1991, 59, 278–288. [Google Scholar] [CrossRef]
- Barcilon, V. Ion Flow through Narrow Membrane Channels: Part I. SIAM J. Appl. Math. 1992, 52, 1391–1404. [Google Scholar] [CrossRef]
- Barcilon, V.; Chen, D.P.; Eisenberg, R.S. Ion Flow through Narrow Membrane Channels: Part II. SIAM J. Appl. Math. 1992, 52, 1405–1425. [Google Scholar] [CrossRef]
- Chen, D.P.; Eisenberg, R.S. Charges, currents, and potentials in ionic channels of one conformation. Biophys. J. 1993, 64, 1405–1421. [Google Scholar] [CrossRef]
- Nonner, W.; Chen, D.P.; Eisenberg, B. Anomalous Mole Fraction Effect, Electrostatics, and Binding in Ionic Channels. Biophys. J. 1998, 74, 2327–2334. [Google Scholar] [CrossRef]
- Gillespie, D.; Eisenberg, R.S. Modified Donnan potentials for ion transport through biological ion channels. Phys. Rev. E 2001, 63, 061902. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.; Eisenberg, R.S. Physical descriptions of experimental selectivity measurements in ion channels. Eur. Biophys. J. 2002, 31, 454–466. [Google Scholar] [CrossRef] [PubMed]
- Bolintineanu, D.S.; Sayyed-Ahmad, A.; Davis, H.T.; Kaznessis, Y.N. Poisson–Nernst–Planck Models of Nonequilibrium Ion Electrodiffusion through a Protegrin Transmembrane Pore. PLoS Comput. Biol. 2009, 5, e1000277. [Google Scholar] [CrossRef] [PubMed]
- Barry, P.H. JPCalc, a software package for calculating liquid junction potential corrections in patch-clamp, intracellular, epithelial and bilayer measurements and for correcting junction potential measurements. J. Neurosci. Methods 1994, 51, 107–116. [Google Scholar] [CrossRef]
- Liquid junction potential. Available online: http://jljp.sourceforge.net (accessed on 28 March 2016).
- Marino, M.; Misuri, L.; Brogioli, D. A new open source software for the calculation of the liquid junction potential between two solutions according to the stationary Nernst–Planck equation. ArXiv E-Prints 2014. arXiv:1403.3640. 2014. [Google Scholar]
- Teorell, T. Transport processes and electrical phenomena in ionic membranes. Prog. Biophys. Mol. Biol. 1953, 3, 305–369. [Google Scholar]
- CRC Handbook of Chemistry and Physics, 94th ed.; CRC Press: Boca Raton, FL, USA, 2014.
- Castilla, J.; Garcia-Hernandez, M.T.; Moya, A.A.; Hayas, A.; Horno, J. A study of the transport of ions against their concentration gradient across ion-exchange membranes using the network method. J. Membr. Sci. 1997, 130, 183–192. [Google Scholar] [CrossRef]
- Higa, M.; Tanioka, A.; Miyasaka, K. Simulation of the transport of ions against their concentration gradient across charged membranes. J. Membr. Sci. 1988, 37, 251–266. [Google Scholar] [CrossRef]
- Post, J.W.; Hamelers, H.V.M.; Buisman, C.J.N. Influence of multivalent ions on power production from mixing salt and fresh water with a reverse electrodialysis system. J. Membr. Sci. 2009, 330, 65–72. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Veerman, J.; Saakes, M.; Nijmeijer, K. Influence of multivalent ions on renewable energy generation in reverse electrodialysis. Energy Environ. Sci. 2014, 7, 1434–1445. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).