Abstract
In tissue engineering, porous biodegradable scaffolds are used as templates for regenerating required tissues. With the advances in computational tools, many modeling approaches have been considered. For example, fluid flow through porous medium can be modeled using the Brinkman equation where permeability of the porous medium has to be defined. In this review, we summarize various models recently reported for defining permeability and non-invasive pressure drop monitoring as a tool to validate dynamic changes in permeability. We also summarize some models used for scaffold degradation and integrating mass transport in the simulation.
1. Introduction
Tissue engineering refers to the in vitro regeneration or growth of a tissue or an organ for the purpose of biomedical studies in areas such as toxicology, tissue/organ repair, and medical device development. The technology is based on using biodegradable porous scaffolds to guide and support the in-growth of cells during tissue regeneration either at the site of grafting or in vitro [1]. The scaffold transiently degrades leaving only the necessary healthy tissue. Currently, the primary goal of tissue engineering is to address the massive discrepancy between organ/tissue transplant needs and availability. Another goal is to use engineered tissue to develop safe and effective medication, treatments, and medical devices without threat to life [2]. In vitro cell culture can help achieve these goals, although the growth of cells outside of the body can be difficult due to cell sensitivity. For this reason, cell culture environments closely mimic body conditions such as temperature, pH, and shear stress, as well as mechanical stimuli in some cases. Advancements in tissue engineering have led to the development of numerous techniques and housing environments in cell culture including bioreactors that aim to meet such requirements [3]. However, due to the complex nature of cell systems, gaps exist in the knowledge of the interactions occurring within.
Tissue regeneration is a dynamic process where cell numbers are expected to increase. These cells also need to secrete matrix elements native to that tissue and matrix components need to assemble in the scaffold while the scaffold material degrades. These processes reduce the pore size available for fluid flow to reach a permeability matching that of the healthy tissues. Purely experimentally driven studies to determine parameter change and stimuli effects are costly in time and money, and do not provide a complete understanding of dynamic process [4]. Computational modelling and simulation for optimization of in vitro tissue growth environments decreases experimental costs and allows easy variable manipulation to determine effect. Modeling is currently limited to activities that are capable of predicting or characterizing all of the processes that occur within a given cell culture system, but the success lies in the combination of well validated models into one simulation to tell the entire story of molecular metabolism, mass transport, scaffold decomposition, and many other phenomena on multiple levels. The combination of multiple models in simulation is necessary to build a complete understanding of what occurs throughout the tissue engineering process and what is needed to produce healthy, fully functional tissue [5].
The field of tissue engineering will find great success due to understanding gained from modeling and simulation compilations. This review will focus on the mathematical models currently available for describing mass transport in static and dynamic cell culture environments, as well as discuss methods for describing fluid flow effects on scaffolds.
2. Cell Culture
Numerous in vitro cell culturing techniques, such as growth on tissue culture plastic, cell suspension, cell aggregates, and bioreactors, have been investigated in an attempt to mimic body tissue. Each technique has advantages and faces varying challenges. Two-dimensional (2D) cell culture involves the growth of cells on pre-treated, flat, polystyrene plastic surfaces (Figure 1a). Cells attach to the stiff, plastic surface and spread until surface area runs out. Cells in 2D environments are submerged in nutrient-rich media, typically changed every 48 h, to promote cell vitality and proliferation.
Two-dimensional cell culturing techniques have had success in maintaining cell proliferation, and are easy to set up and maintain; however, 2D cultures are poor approximations of tissue in vivo. Two-dimensional cell cultures lack necessary architectural structure and face significant exposure limitations [6]. Three-dimensional (3D) cell culture can provide necessary architectural structure, generally via a biocompatible, biodegradable scaffold. The scaffold is a porous medium that supports cell organization and motility and allows nutrient transport inside the 3D structure, creating an environment that more closely mimics tissue formations in vivo [7,8,9]. In addition, 3D culture allows for higher cell density seeding over a given surface area, allowing for increased sensitivity and stronger signal strength during system analysis. Three-dimensional cultures are generally preferred to 2D cultures in tissue engineering, and for that purpose, the remainder of this review will focus on simulation of 3D cultures only.
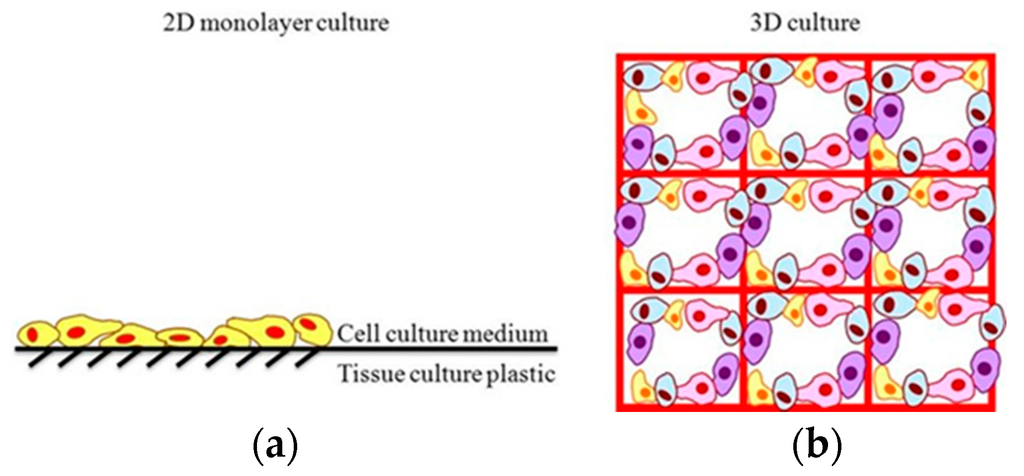
Figure 1.
Structural comparison of (a) Two-dimensional cell culture and (b) Three-dimensional cell culture.
2.1. Cell Culture under Static Conditions
Static cell culture systems are easy to maintain, but require regular media replenishment to maintain adequate nutrient supply. Mass transport of molecules, such as nutrients, can be modelled mathematically. The distribution of components in static condition is driven by diffusion as described by Fick’s first law. Hence, theoretical models used in simulation apply some form of Fick’s law to characterize mass transport in a system [10],
where represents the diffusive mass flux through the system, represents the effective diffusivity of the component, ∇ represents the gradient operator used when evaluating a function in more than one dimension and ∇Ci represents the gradient of concentration. The conservation of mass is given as,
where t represents time. Substitution of Equation (1) into Equation (2) yields:
Assumptions for simplification of a system are commonly made in simulation, especially in the beginning stages. For example, the assumption of a constant diffusion coefficient gives Equation (3) as:
And for a steady state assumption, Equation (3) becomes:
As most of the systems considered in tissue engineering evaluate consumption of nutrients or formation of signature products, a reactive term, , is added to Equation (3) giving [11]:
The sign convention of the reaction term depends upon whether the molecule is being consumed (negative) or produced (positive). Unlike convection where nutrient transport can be estimated by the flow rate and concentration gradient, diffusion transport mainly requires evaluating the diffusivity of the nutrient molecule. The major factors affecting diffusion include porosity and morphology, scaffold biodegradation, swelling due to biodegradation, and shrinkage due to deposition of new biopolymers and cells. Standard approach to defining Di [12] in the literature of flow through porous medium is
where τ is the tortuosity of the porous medium, εp is the porosity of the scaffold, and D∞ is the free diffusivity of the component in water. Since determining τ of the porous medium is difficult, some use that of cells. Alternatively, Mackie-Meares relationship can be used to determine the effective diffusivity. An example of Mackie-Meares relationship [13] is
Since there are many techniques to determine the porosity of the porous medium particularly in tissue engineering scaffolds, those porosity values can be directly utilized to determine effective diffusivity.
2.2. Cell Culture Involving Fluid Flow
Many 3D cell culture environments encounter challenges due to nonhomogeneous molecular distribution, particularly those on the interior of 3D cultures [14]. Further, many body parts are exposed to stresses either due to the weight they carry (such as bone), function they perform (such as bladder and cartilage) or due to the flow of fluid (lung and blood vessels). These parts regenerate if mechanical stimulus is applied. In an effort to address distribution issues and applications of mechanical stimulus, some have investigated convection driven cell culture environments. In the case of bioreactors, convection can be introduced by a flow of fresh, nutrient-rich media into the environment as seen in parallel-flow and flow-through bioreactors. Convection can be introduced into a system via agitation or stirring, as seen in spinner flasks and rotating wall vessel bioreactors. Bioreactors of different flow configurations and sizes have been with an even wider array of nutrient distributing and mechanical simulating techniques [15].
Appropriate characterization of transport phenomena in cell culture simulation is vital to obtaining results that could be utilized for optimizing tissue regeneration. Mathematical modelling of fluid behavior, due to the addition of convection, increases the complexity and number of equations required to describe fluid behavior. Characterization of fluid behavior in a system where convection is present requires the addition of a momentum equation. Fluid momentum in non-porous regions is characterized by the Navier-Stokes equation written as:
where represents fluid pressure, µ represents the fluid kinematic viscosity, ∇u represents the gradient of fluid velocity, ρ represents fluid mass density, I represents the identity matrix, and F represents the sum of the external forces (like gravity) applied to the fluid. The Navier-Stokes equation is used for Newtonian fluids, such as growth medium used in cell culture. Assumptions, such as steady state operation and negligible external forces, are often applied to simulation, eliminating the and F terms respectively from Equation (10). In addition to these two assumptions, consideration of the fluid as incompressible with a constant density and viscosity would yield Equation (8) as:
Use of the conservation of momentum equation must also include the use of the conservation of mass equation, or continuity equation, when solving. The continuity equation is given as:
And if considered at steady state and constant density:
Velocity selection does not affect equation selection for characterization of non-porous regions, but has a direct impact on the equation for characterizing the effect of fluid flow through porous scaffolds. In order to determine the applicable fluid flow equations, the Reynolds number within the pores (and/or Forchheimer number) is calculated. Based on the local Reynolds number, one can determine whether Darcy, Brinkman or Forchheimer equations are most appropriate. The Darcy equation is based on experimental observations of the one-dimensional flow of water at low velocities through a porous medium made of sand particles, and is written as:
where is the direction of fluid flow, v represents the superficial velocity, and κ represents the porous structure permeability. Many derivations for Darcy’s law are used but one must be cautious, as this assumption is only valid when the local Reynolds number is below one [16]. When the local Reynolds number is in the order of 100 or greater, the Forchheimer equation is used to incorporate the turbulent flow conditions. Forchheimer added a quadratic velocity term to the Darcy equation to account for microscopic inertial effects. The Forchheimer equation for one-dimensional flow is written as:
where β is the non-Darcy coefficient. Taking into account local shearing effects between the fluid and porous walls, and the gradient pressure forces involved in transport of fluids from non-porous regions into porous regions, second order derivatives of the velocity are added to the Darcy equation, yielding the Brinkman equation:
where , , and represent directions that are mutually perpendicular. The Brinkman equation is useful when the local Reynolds numbers are in the range of one and 100. Brinkman equation can be viewed as an equation consisting of two terms (i) Darcy’s equation and (ii) a viscous term, similar to Navier-Stokes equation, which provides molecular transport due to convection.
where represents the convective mass flux, represents the average velocity of the fluid, and again, represents the species concentration. Combining Equations (1) and (16) gives an expression for the transport of solutes within the fluid to give the advective-diffusive equation:
Cell metabolism equations are not affected by the inclusion of convection for molecular transport. However, local concentrations of molecules are dictated by the advective-diffusive equation. Hence the rate of reactions are altered, which further leads to altered concentration profiles.
3. Modeling Porous Medium Properties
3.1. Incorporating Permeability
Properties of the porous scaffolds used in tissue engineering, such as biocompatible material, porosity, and tensile strength, play an important role in characterizing mass transport. The Darcy, Forchheimer, and Brinkman equations, which characterize fluid flow through porous scaffolds, require an important porous structure parameter, the permeability, κ. Sensitivity of model predictions are directly dependent on the accurate κ values, which depend on the geometric parameters of the pores in the scaffold [17]. In order to predict flow properties with high fidelity, determining the permeability using physical characteristics of the porous scaffold such as porosity and the pore shape is an approach. Kozeny proposed a relationship in 1927 given as:
where S represents the specific surface area, the ratio of total interstitial surface area to the bulk volume of the porous scaffold and KC represents the Kozeny constant, a dimensionless parameter that depends on the pore geometry. In human physiology, permeability of various tissues is defined using this Kozeny definition [18]. The above expression of κ does not depend on fluid viscosity and density, which helps in extrapolating the simulation results to different fluids and flow conditions. There are a number of approaches available for calculating permeability, based on fiber orientation and size or pore area and number, depending on method and materials used for porous scaffold development. When scaffolds are formed through the process of electrospinning, fibers are randomly oriented (Figure 2a). In order to calculate the permeability in randomly packed fibers, there have been many correlations. One popular equation that seem to agree with the electrospun scaffolds is:
where r is the radius of the fibers. Since these scaffolds are very thin relative to their surface area, one could assume negligible porosity across the thickness. Then, porosity can be estimated using digital micrographs collected from scanning electron microscopy. Image analysis is performed to calculate the ratio of the open pore area to the total area of the image analyzed, which is considered as the porosity of the scaffold [19]. If the fiber sizes are large, another correlation is developed using Lattice-Boltzmann method. In that case, the permeability is calculated using:
Other methods do not use fibers to create scaffolds, but rather create pores within a solid medium. For example, freeze drying of water-based polymer solutions such as collagen, chitosan, and alginate produce pores mimicking water crystals. Permeability for such scaffolds are calculated [20], assuming pores to be cylindrical (Figure 2b), and calculated using the equation,
where d is the pore diameter and nA represents the number of pores per unit area. However, some porous medium preparation techniques using leaching salt from organic solvent-based polymeric blocks such as polycaprolactone and poly lactic-co-glycolic acid (Figure 2c). One could assume the pores to be rectangular and then calculate the permeability using the expression:
where L is the pore length, and W is the pore width. Utilizing permeability equations based on pore geometric characteristics such as pore size, shape, and nA is advantageous because experimental data can be used from scaffold analyses, typically reported in tissue engineering literature.
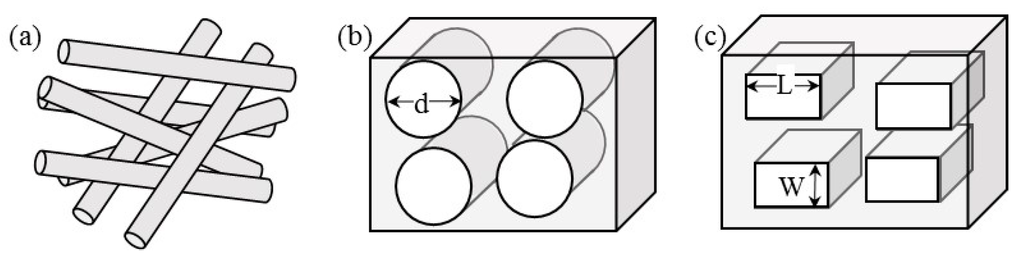
Figure 2.
Schematic of different pore configurations in porous scaffolds used in tissue engineering. These are in the flow direction. (a) Fibrous scaffolds formed by electrospinning; (b) Scaffolds with nearly circular pores when formed using freeze-drying; (c) Scaffolds with rectangular pores when formed using salt-leaching technique.
Scaffold permeability depends on a combination of factors including pore size, porosity, pore geometry, and pore distribution [21]. Alterations in any of these parameters affects permeability, and changes in scaffold permeability directly affects the structural integrity of the scaffold [22]. Increased pore size decreases solid material volume and, as a result, the strength of the material. Scaffold strength is of particular importance during the initial cell seeding, as the extracellular matrix (ECM) that provides stability in vivo is not yet formed. In order to mimic the ECM and promote appropriate cellular behavior, scaffold strength should match in vivo tissue strength [23]. Permeability also influences diffusion of nutrients into and waste out of the porous medium. The transport of nutrients necessary for cell survival into the scaffold, and waste metabolites which can be toxic to cells, is controlled by permeability [21]. Thus, selection of appropriate scaffold permeability for achieving desired effects is critical.
The majority of scaffolds are designed with homogeneous porosity and pore distribution due to manufacturing and design limitations [24]. Homogenous scaffolds or scaffolds of constant porosity are a common assumption employed in tissue engineering simulations. Many reports confirm that this to be a good assumption and useful in calculating scaffold permeability [25,26]. However, many issues arise when considering uniform scaffold permeability. For example, natural tissue is not structurally homogeneous. Additionally, homogeneously porous scaffolds cannot address all of the mechanical and biological tissue requirements. Hence, heterogeneous scaffold development is currently of particular interest to researchers. Scaffolds with separate regions of porosity and scaffolds with porosity gradients have been investigated [27]. In some cases, a multi-scale simulation approach is advantageous in accounting for environmental heterogeneity. Multi-scale approaches allow simultaneous investigation of the interaction and dependence of various factors on the micro (cellular) and macro (entire scaffold) scale [28].
3.2. Incorporating Scaffold Degradation
Characterization of scaffold degradation over time is important to producing and maintaining high-integrity, engineered tissue for in vivo use. If scaffolds degrade too quickly, the necessary structural architecture for promoting appropriate cell proliferation and functionality is lost, resulting in cell death. Computational modelling and simulation can provide a better understanding of the mechanism driving structural degradation. Some mathematical models consider scaffold degradation by chemical reactions and erosion due to fluid flow. Many studies have investigated the effects of environment (i.e., fluid velocity), porosity, and scaffold material on degradation rates by surface and bulk erosion, as well as by chemical reactions [29,30]. For example [31], polymer degradation by hydrolysis is modeled using the following coupled equations,
and
where is the mole concentration of ester bonds of polymer chains, is the mole concentration of monomers, k1 is the rate constant of the reaction which is independent of any catalyst, is the rate constant of a reaction catalyzed by the previously formed products, and γ is the disassociation power of the acid end group. These reactions are then related to the MW of the polymer present in the scaffold, which can be measured and then the model can be validated. The rate of scaffold degradation by hydrolysis is not restricted to the combination of Equations (23) and (24), but can also be characterized by an exponential decay or first order equation. Other research has considered enzymatic degradation according to Michaelis Menten kinetics in addition to degradation by hydrolysis [32]. Scaffold degradation can take on many forms and is highly dependent upon scaffold composition and component concentrations.
3.3. Incorporating Scaffold Deformation
Most porous scaffolds used in soft tissue regeneration i.e., except in bone regeneration, have low mechanical strength and are very elastic. In addition, porosity of the scaffolds affects their mechanical characteristics. Further, cells respond to stresses in the substrates [33]. Hence, velocity selection in flow-through systems can directly impact cell vitality and scaffold structural stability. In order to understand how fluid flow deforms the porous scaffold, novel computational tools offer a moving mesh that can be used to predict deformation. The simulation needs generalized mechanical property of the scaffolds such as elastic modulus and Poisson ratio in drained conditions [20]. Initial simulation with Navier-Stokes equation without moving mesh is used to create boundary condition such as the initial total load (FT) applied by the fluid on the scaffold. This is calculated using,
where n represents the normal vector. In addition to the stress due to the elastic nature of the scaffold, there is a hydrodynamic stress from fluid pore pressure, which is incorporated by coupling the strain using the relationship,
where σ represents the Cauchy stress tensor, ε-represents the strain tensor, C represents the elasticity matrix, αB represents the Biot-Willis coefficient, and Pf is the fluid pore pressure. Equation (26) reduces to Hooks Law of linear elasticity when αB is zero. Poroelasticity models in earth sciences for understanding soil consolidation use similar models in conjunction with Darcy’s equation. However, these models have to use Brinkman or Forchheimer equations based on the flow regimes, as described above. Assuming the material to behave isotropically, and porosity to remain constant, elasticity matrix is obtained using the values of elastic modulus, E, and the shear modulus, G. In the linear region, shear modulus and elastic modulus can be coupled using the equation.
where ν represents the Poisson’s ratio of the porous scaffold. Some have used quasistatic approximations and solved the equations analytically [34]. Similar models have been attempted in cartilage and other tissues [35]. In order to use these simulations, mechanical characteristics in particular elastic modulus and Poisson’s ratio have to be analyzed in wet conditions similar to the condition where scaffolds are used. Currently, some of these properties are not available for many scaffolds and hence, they need to be determined. Nevertheless, adding these simulations help understand the local stresses experienced by cells. These can be then analyzed with the biological response of cells, and further optimization of the flow can be performed to improve the quality of the regenerated tissues.
4. Validation Techniques
One of the primary requirements for successful mathematical modelling and computational simulation is validation of the experimental results. Well-validated, mathematical characterizations of phenomena occurring within a tissue culture environment would help close knowledge gaps in tissue engineering. The computational approach summarized above utilizes scaffold properties routinely measured and reported in literature and pressure drop can be predicted by using an appropriate flow through porous medium equation. Further, pressure drop profiles for various flow regions can be simulated using a range of permeability encompassing scaffold permeability to healthy tissue.
In order to utilize these profiles, experimental validation can be performed at various flow rates using scaffolds alone. A simple flow-scheme for such purposes is shown in Figure 3. Placing a pressure transducer at the inlet of the bioreactor and another at the outlet will provide pressure drop across the scaffold. The pressure transducers would be connected to a computer to record pressure values for both the transducers. In addition, performing experiments without the scaffold could be used to account for pressure drop occurring without the scaffold. These experiments can help validate the simulations.
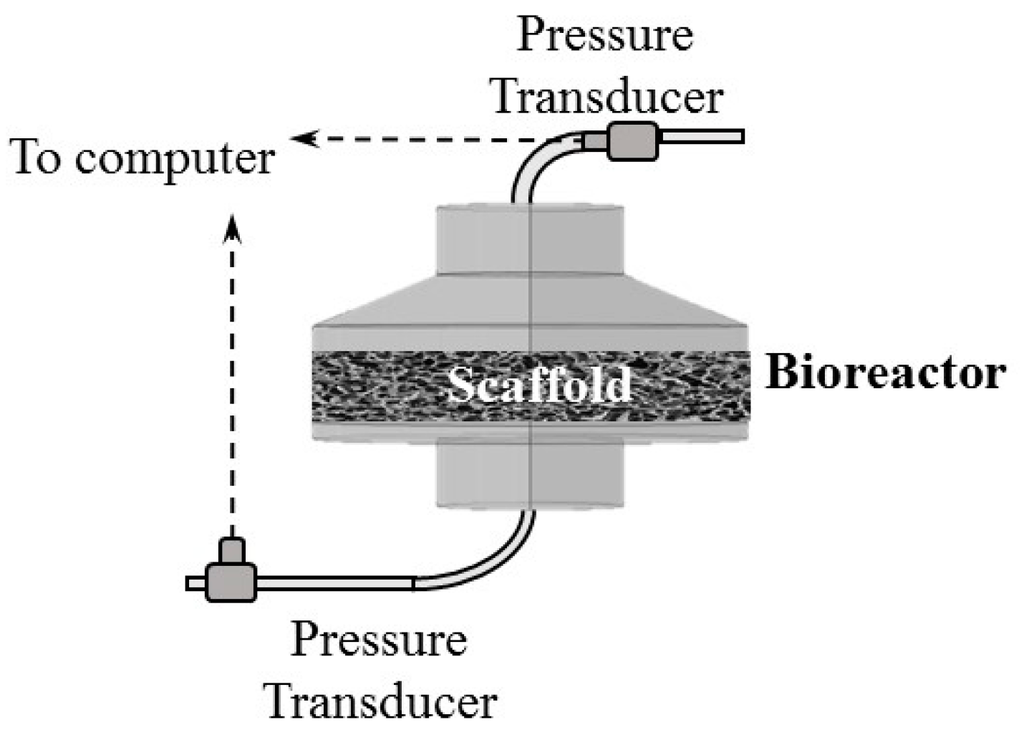
Figure 3.
Flow-scheme to determine the pressure drop across the porous scaffold.
The advantage of this approach is that pressure drop can be continuously monitored non-invasively, even when biological experiments are performed in sterile environment. The method allows for simulation validation without harming or contaminating the cell cultures. This is unlike many of the destructive assays performed for understanding the quality of the regenerated tissues. Permeability is expected to change during the course of tissue regeneration as cells will proliferate, synthesize extracellular matrix elements that are deposited in the porous scaffolds. Hence, the pressure drop increases as the permeability decreases.
In order to understand the implications of dynamic changes in permeability, simulations with decreasing pore sizes can be utilized. Matching with the simulated pressure drop to flow rate correlation can be utilized to understand the changes in permeability, quality of the regenerated tissue, and adjusting the flow rate in order to ensure nutrient distribution. There are a few commercialized products available to measure the permeability of the porous scaffolds by Darcy’s Law that is used to monitor bone growth. The primary caveat is that pressure drop is a significant function of the flow pattern. Hence, for each bioreactor configuration, few profiles have to be generated. Nevertheless, these advances of monitoring pressure drop in real time would be invaluable to the tissue regeneration process.
5. Conclusion
Computational simulation of flow through porous medium is gaining significant attention in tissue engineering. As we validate developed correlations between pressure drop and scaffold pore architecture for wide variety of porous media used in tissue engineering, they can be utilized as a standard quality assessment method for regenerated tissues. Furthermore, simulation and modeling can guide preparation of better scaffolds and bioreactors for regenerating high quality tissues. These can be used in transplantation, drug screening, or understanding of disease progression. Modelling and simulation will allow ideas to be tested without waste of materials. The growth of an entire organ requires the inclusion of multiple cell types, as well as a vascular system. Addressing the physical and mechanical requirements of multiple cell types in a single environment is extremely difficult and too complex for current application. Perhaps, modeling will help develop individualize medicine. This is the future of tissue engineering.
Acknowledgments
Financial support provided by the Oklahoma Center for Advancement of Science and Technology (HR15-142) and the Edward Joullian Endowment. Financial support also provided by Jerry and Nona Wilhm. There are no conflict of interests to disclose.
Author Contributions
Carrie L. German worked on the paper. Sundararajan V. Madihally helped with the concept and editing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Place, E.S.; Evans, N.D.; Stevens, M.M. Complexity in biomaterials for tissue engineering. Nat. Mater. 2009, 8, 457–470. [Google Scholar] [CrossRef] [PubMed]
- Astashkina, A.; Mann, B.; Grainger, D.W. A critical evaluation of in vitro cell culture models for high-throughput drug screening and toxicity. Pharmacol. Ther. 2012, 134, 82–106. [Google Scholar] [CrossRef] [PubMed]
- Ravi, M.; Paramesh, V.; Kaviya, S.R.; Anuradha, E.; Solomon, F.D. 3D cell culture systems: Advantages and applications. J. Cell. Physiol. 2015, 230, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Haycock, J. 3D cell culture: A review of current approaches and techniques. In 3D Cell Culture; Haycock, J.W., Ed.; Humana Press: New York, NY, USA, 2011; pp. 1–15. [Google Scholar]
- Sander, E.A.; Stylianopoulos, T.; Tranquillo, R.T.; Barocas, V.H. Image-based multiscale modeling predicts tissue-level and network-level fiber reorganization in stretched cell-compacted collagen gels. Proc. Natl. Acad. Sci. USA 2009, 106, 17675–17680. [Google Scholar] [CrossRef] [PubMed]
- ElectrospinningCompany. Why 3d Cell Culture? Availabe online: http://www.electrospinning.co.uk/why-3d-cell-culture/ (accessed on 1 February 2016).
- Pal, A.; Kleer, C.G. Three dimensional cultures: A tool to study normal acinar architecture vs. Malignant transformation of breast cells. J. Vis. Exp. 2014, 86. [Google Scholar] [CrossRef] [PubMed]
- Edmondson, R.; Broglie, J.J.; Adcock, A.F.; Yang, L. Three-dimensional cell culture systems and their applications in drug discovery and cell-based biosensors. Assay Drug Dev. Technol. 2014, 12, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Shamir, E.R.; Ewald, A.J. Three-dimensional organotypic culture: Experimental models of mammalian biology and disease. Nat. Rev. Mol. Cell Biol. 2014, 15, 647–664. [Google Scholar] [CrossRef] [PubMed]
- Granot, Y.; Rubinsky, B. Mass transfer model for drug delivery in tissue cells with reversible electroporation. Int. J. Heat Mass Transf. 2008, 51, 5610–5616. [Google Scholar] [CrossRef] [PubMed]
- Patrachari, A.R.; Podichetty, J.T.; Madihally, S.V. Application of computational fluid dynamics in tissue engineering. J. Biosci. Bioeng. 2012, 114, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Curcio, E.; Macchiarini, P.; De Bartolo, L. Oxygen mass transfer in a human tissue-engineered trachea. Biomaterials 2010, 31, 5131–5136. [Google Scholar] [CrossRef] [PubMed]
- Podichetty, J.T.; Dhane, D.V.; Madihally, S.V. Dynamics of diffusivity and pressure drop in flow-through and parallel-flow bioreactors during tissue regeneration. Biotechnol. Prog. 2012, 28, 1045–1054. [Google Scholar] [CrossRef] [PubMed]
- Vunjak-Novakovic, G.; Martin, I.; Obradovic, B.; Treppo, S.; Grodzinsky, A.J.; Langer, R.; Freed, L.E. Bioreactor cultivation conditions modulate the composition and mechanical properties of tissue-engineered cartilage. J. Orthop. Res. 1999, 17, 130–138. [Google Scholar] [CrossRef] [PubMed]
- Martin, I.; Wendt, D.; Heberer, M. The role of bioreactors in tissue engineering. Trends Biotechnol. 2004, 22, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.W.; Grigg, R. A criterion for non-darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Pennella, F.; Cerino, G.; Massai, D.; Gallo, D.; Falvo D’Urso Labate, G.; Schiavi, A.; Deriu, M.A.; Audenino, A.; Morbiducci, U. A survey of methods for the evaluation of tissue engineering scaffold permeability. Ann. Biomed. Eng. 2013, 41, 2027–2041. [Google Scholar] [CrossRef] [PubMed]
- Swartz, M.A.; Fleury, M.E. Interstitial flow and its effects in soft tissues. Annu. Rev. Biomed. Eng. 2007, 9, 229–256. [Google Scholar] [CrossRef] [PubMed]
- Podichetty, J.T.; Bhaskar, P.R.; Khalf, A.; Madihally, S.V. Modeling pressure drop using generalized scaffold characteristics in an axial-flow bioreactor for soft tissue regeneration. Ann. Biomed. Eng. 2014, 42, 1319–1330. [Google Scholar] [CrossRef] [PubMed]
- Podichetty, J.T.; Madihally, S.V. Modeling of porous scaffold deformation induced by medium perfusion. J. Biomed. Mater. Res. Part B Appl. Biomater. 2014, 102, 737–748. [Google Scholar] [CrossRef] [PubMed]
- O'Brien, F.J.; Harley, B.A.; Waller, M.A.; Yannas, I.V.; Gibson, L.J.; Prendergast, P.J. The effect of pore size on permeability and cell attachment in collagen scaffolds for tissue engineering. Technol. Health Care 2007, 15, 3–17. [Google Scholar] [PubMed]
- Loh, Q.L.; Choong, C. Three-dimensional scaffolds for tissue engineering applications: Role of porosity and pore size. Tissue Eng. Part B Rev. 2013, 19, 485–502. [Google Scholar] [CrossRef] [PubMed]
- Leong, K.F.; Chua, C.K.; Sudarmadji, N.; Yeong, W.Y. Engineering functionally graded tissue engineering scaffolds. J. Mech. Behav. Biomed. Mater. 2008, 1, 140–152. [Google Scholar] [CrossRef] [PubMed]
- Sogutlu, S.; Koc, B. Stochastic modeling of tissue engineering scaffolds with varying porosity levels. Computer-Aided Des. Appl. 2007, 4, 661–670. [Google Scholar] [CrossRef]
- Hollister, S.J.; Lin, C.Y. Computational design of tissue engineering scaffolds. Comput. Methods Appl. Mech. Eng. 2007, 196, 2991–2998. [Google Scholar] [CrossRef]
- Sanz-Herrera, J.A.; Garcia-Aznar, J.M.; Doblare, M. A mathematical approach to bone tissue engineering. Philos. Trans. R. Soc. A Math Phys. Eng. Sci. 2009, 367, 2055–2078. [Google Scholar] [CrossRef] [PubMed]
- Khoda, A.K.; Ozbolat, I.T.; Koc, B. Engineered tissue scaffolds with variational porous architecture. J. Biomech. Eng. 2011, 133, 011001. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Vaughan, T.; McNamara, L. Multiscale fluid-structure interaction modelling to determine the mechanical stimulation of bone cells in a tissue engineered scaffold. Biomech. Modeling Mechanobiol. 2015, 14, 231–243. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhou, S.; Li, Q. Mathematical modeling of degradation for bulk-erosive polymers: Applications in tissue engineering scaffolds and drug delivery systems. Acta Biomater. 2011, 7, 1140–1149. [Google Scholar] [CrossRef] [PubMed]
- Shirazi, R.N.; Ronan, W.; Rochev, Y.; McHugh, P. Modelling the degradation and elastic properties of poly(lactic-co-glycolic acid) films and regular open-cell tissue engineering scaffolds. J. Mech. Behav. Biomed. Mate. 2016, 54, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Pan, J.; Han, X.; Sinka, C.; Ding, L. A phenomenological model for the degradation of biodegradable polymers. Biomaterials 2008, 29, 3393–3401. [Google Scholar] [CrossRef] [PubMed]
- Dhote, V.; Vernerey, F.J. Mathematical model of the role of degradation on matrix development in hydrogel scaffold. Biomech. Modeling Mechanobiol. 2014, 13, 167–183. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, B.J.; Madihally, S.V. Cell colonization in degradable 3d porous matrices. Cell Adh. Migr. 2008, 2, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Naili, S.; Oddou, C.; Geiger, D. A method for the determination of mechanical parameters in a porous elastically deformable medium : Applications to biological soft tissues. Int. J. Solids Struct. 1998, 35, 4963–4979. [Google Scholar] [CrossRef]
- Chung, C.-Y.; Mansour, J.M. Using regression models to determine the poroelastic properties of cartilage. J. Biomech. 2013, 46, 1921–1927. [Google Scholar] [CrossRef] [PubMed][Green Version]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).